Introduction

In the last decades, many efforts have been made by archaeometallurgists to disclose technological data recorded in ancient ferrous artifacts.[1,2,3] The main types of key information researchers are interested in the identification of iron-making processes, the pyrometallurgical technology, and the forging strategies reconstruction. The interpretation of these technological data along with a deep understanding of archaeological context of the object allows to address important issues such as the reconstruction of knowledge transmission paths and the evolution of ancient technology both in space and in time under environmental and cultural constraints.[4] For this purpose, many authors effectively employed a reverse engineering method based on the synergic combination of metallography and analysis of slag inclusions (SI), i.e., residues of the slag formed from non-metallic compounds during the metallurgical processes.[5,6,7,8,9,10,11,12] Using this approach, Buchwald[13,14] and other researchers[15,16] observed that, despite the heterogeneity of ancient ferrous objects, in many cases, there is a close correlation between the metal matrix microstructure and the mineralogy of smelting-related SI. In particular, iron oxide-rich wüstite-fayalite SI are typically surrounded by a low-carbon ferritic metal matrix, whereas iron oxide-poor glassy SI are mainly placed in high-carbon pearlitic zones. Moreover, this correlation was occurred for ferrous artifacts obtained through both direct and indirect iron-making processes. It was suggested that it can be explained by assuming in both cases local near-equilibrium conditions, which were reached respectively during the smelting and fining (i.e., cast iron decarburization) processes between SI and metal phases despite the overall temperature and redox fluctuations.[2] It is worth mentioning that the direct method is a solid-state process (namely, carried out below the metal melting point), which takes place inside the so-called “bloomer” furnace, where the iron ore is reduced to metal by chemical interactions with the reducing agent, i.e., carbon monoxide gas generated during charcoal combustion.[17] Conversely, the indirect iron-making route is a two-step process. At first, cast iron is produced in a blast furnace. Subsequently, cast iron is converted to iron or steel by decarburization in a fining hearth, i.e., an open furnace with a large central cavity where cast iron mixed with charcoal is fired and subjected to oxidizing conditions.[17] It was also speculated that post-smelting thermochemical treatments such as carburization and decarburization can greatly bias the inverse correlation between iron oxide in SI and carbon in the metal matrix due to physicochemical alterations of SI-metal systems local equilibria.[18,19]

This research aims to show that a thermodynamic-based approach together with an accurate metallographic analysis and a careful characterization of the object SI-metal systems can be employed to explore the correlation between iron oxide and carbon inside these systems to reconstruct the smelting and post-smelting manufacturing processes. From this perspective, the present work aims to further a widely used approach in archaeometallurgy based on slag inclusions analysis emphasizing the key role of SI-metal systems.

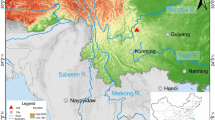
This strategy, inspired by modern metallurgical physical chemistry methods, was applied focusing on the study of a Lombard steel bar which was retrieved in the area “F” of the medieval archaeometallurgical site of Ponte di Val Gabbia I (Brescia, northern Italy), hereafter referred to as PVGI (Figure 1 and Figure S-1 in the electronic supplementary material). The steel bar is currently kept at the Ethnographic Museum of Iron in Bienno (Brescia, northern Italy). PVGI site was dated to the Lombard Period (VI–VII centuries AD), and it is positioned near two other ancient metallurgical sites, i.e., Ponte di Val Gabbia II (PVGII) and Ponte di Val Gabbia III (PVGIII), which were active during the Lombard Period (VI–VII centuries AD) and the Late Antiquity Period (V–VI century AD), respectively.[20,21,22] The archaeological findings at these sites mainly consist of iron-making and iron-working waste (i.e., smelting, and smithing slags), some ferrous artifacts, and smelting furnace fragments (the actual furnaces were not excavated because they were buried by rock falls). It is worth observing that previous research works have underlined a technological diversity between PVGI–II and PVGIII sites.[20,21,22] In particular, it was suggested on the basis of archaeological data that the PVGIII site can be a very early example of an iron-making site where bloomery and indirect methods were both practiced.[21]

Fig. 1
figure 1

Geographical context with positions of the key locations mentioned in this study

Full size image

This hypothesis was judged as being potentially relevant as it backdates the introduction of the indirect method in Europe which is usually dated to about the thirteenth century. The use of the indirect method at the PVGIII site was inferred from the finding of a pig iron block (about 3.5 kg in weight) and the archaeometallurgical analysis of a miner’s chisel.[7,23] On the other hand, Cucini and Tizzoni[20] hypothesized that only the bloomery process was used in both PVGI and PVGII sites. It should be noted that the reasons for this technological evolution have not yet been fully understood even if it is likely related to the local socio-economical changes that occurred in this region between Late Antiquity and the Early Medieval Period.[20] The iron ore (i.e., hematite and goethite) processed in all these ancient iron-making sites was exploited in the nearby mine of Piazzalunga and it is characterized by a high manganese content.[24] In addition, a remarkable metalworking activity has been documented in geographical areas close to the ancient village of Bienno since medieval times.[20] Against this background, the present study aims to provide novel data and methodological tools for furthering the study of ancient iron-making technologies in the complex PVG context.

Materials and Methods

The Bar: Preliminary Description and Macro-observations

The bar was retrieved in a heavily corroded condition (Figure 2(a)). It has a rectangular cross section and its main dimensions are as follows: length = 75 mm, maximum thickness = 11 mm, and maximum width = 20 mm. A single section (S1) was polished from one end side of the bar, as shown in Figure 2. A significant portion of section S1 is constituted by oxidation products since corrosion was deeply penetrated to a depth of approximately half the thickness of the section (Figure 2(b)).

Fig. 2
figure 2

(a) Photographic image of the bar and (b) detail of the sampled section S1

Full size image

Analytical Methods

The sample was submitted to a standard metallographic preparation consisting of grinding with SiC paper (grades from 600 to 1200) and final polishing with polycrystalline diamond pastes (3 and 1 µm). Metallographic observations were performed by LEICA DMI 5000 M optical microscope on the as-polished sample and after chemical etching by immersion in 1 pct Nital solution (1 pct vol HNO3 in ethanol). Vickers microhardness tests were carried out with a Shimadzu Microhardness Tester Type-M under a 300 g load applied for 15 seconds on the etched section to confirm the metallographic observations. After metallographic investigations, the chemical composition of many non-metallic inclusions was measured on the re-polished sample section to prevent any influences of the metallographic etching on the SI chemistry. For each metallurgical zone, a reliable number of SI were selected and analyzed via Scanning Electron Microscope (SEM) in backscattering mode (BSD) to carefully assess their mineralogy and microstructure. Moreover, a semi-quantitative chemical analysis of SI was performed by X-ray Energy Dispersive Spectroscopy (EDS) coupled with SEM. The chemical data of multi-phase SI were obtained by analyzing all SI surfaces through area acquisition. The oxygen amount was obtained by stoichiometry. The SI chemical composition is expressed by the following stoichiometric oxides: Na2O, MgO, Al2O3, SiO2, K2O, CaO, TiO2, MnO, FeO, BaO, P2O5, and CuO. The area of each SI was measured with the ImageJ software environment for Image Analysis. The carbon content of the metal matrix surrounding each analyzed SI was approximately estimated with the inverse lever rule from the volume fraction of ferrite and pearlite which were measured by ImageJ.[25]

Classification of SI

SI entrapped in the metal matrix can originate from both smelting and post-smelting processes. It is worth noting that only SI derived from the smelting and forging stages can potentially encapsulate thermochemical information about the reduction and smithing processes, respectively. Therefore, it is crucial to carefully examine their formation origin.[26,27] To achieve this purpose, the SI classification methods proposed by Dillmann and L’Héritier[1] and Charlton et al.[28] were applied in this study. Both these selection strategies assume that SI can be modeled as multicomponent oxide systems constituted by two main oxide classes: reduced compounds (RCs) and non-reduced compounds (NRCs). It is important to stress that only NRCs (e.g., Al2O3, K2O, MgO) allow discriminating SI with different origins because RCs (e.g., FeO, P2O5, CuO) can be greatly scattered even inside SI with the same origin. Following the approach of Dillmann and L’Héritier,[1] only SI with constant NRCs ratios (e.g., Al2O3–SiO2 ratio) can be classified as smelting-related SI. Moreover, the approach proposed by Charlton et al.[24] is based on multivariate statistical analysis, i.e., Principal Component Analysis (PCA) and Hierarchical Cluster Analysis (HCA). To employ these models, the raw elemental chemical data of each analyzed SI were converted to oxides weight percentages (wt pct) by stoichiometry. To equalize the NRCs weight magnitude and variance, PCA was applied to compositional data pre-processed by the centered log-ratio transformation (CLR) as suggested by Aitchison.[29] This data transformation is expressed by Formula [1]:

$$ Xi_{{{\text{NRC}}}} = \, \log \left( {Ei_{{{\text{NRC}}}} } \right){-}g\left( {\log E_{{{\text{NRC}}}} } \right) $$
(1)

where XiNRC is the ith transformed value for each NRC (i.e., MgO, Al2O3, SiO2, K2O, CaO, and MnO), EiNRC is the amount of the ith NRC and g(log ENRC) is the geometrical mean of the logged NRCs.

To distinguish the main SI clusters, HCA based on the Ward method with Euclidean distance was adopted. The data treatment was performed using R 3.6.1, Excel, and OriginLab software environment for statistical computing and graphics.[30]

Thermodynamic-Based Model

To extract smelting and post-smelting thermochemical parameters (i.e., temperature and oxygen chemical potential) from the chemistry of SI-metal systems, a thermodynamic approach was adopted in this study. To this aim, SI-metal systems were modeled as shown in Figure 3(a). This simplified model is suitable for describing SI-metal local equilibria reached in both bloomery and fining furnaces where cast iron is decarburized to obtain iron and steel. In both cases, it is assumed that the concentrations of iron oxide (FeO) and carbon (C) in these systems were mainly governed by local thermochemical conditions, i.e., oxygen chemical potential (\(\mu_{{{\text{O}}_{{2}} }}\)) and temperature (T) of the gas phase (g) in equilibrium with both austenitic metal (γ) and SI phases. The gas phase is a CO/CO2/N2 mixture with small traces of oxygen which is generated inside the bloomery furnace or the fining hearth from the reaction of air oxygen with charcoal. Since the smelting and fining furnaces can be modeled as open systems that approximately work at atmospheric pressure, the chemical composition of the gas phase was constrained as follows: \(p_{{{\text{CO}}}} + \, p_{{{\text{CO}}_{2} }} + \, p_{{{\text{N}}_{2} }} = 1\,{\text{bar}}\) (0.1 MPa); where pCO, \(p_{{{\text{CO}}_{2} }}\), and \(p_{{{\text{N}}_{2} }}\) are the partial pressure of the carbon monoxide, carbon dioxide, and nitrogen, respectively.[31,32] Metal and SI phases can be austenite and liquid (or glass), respectively. To model local micro-equilibria, it is assumed that the radius of the metal phase (γ) is of the same order of magnitude as the SI phase. Under the hypothesis of thermodynamic equilibrium, the oxygen chemical potential (\(\mu_{{{\text{O}}_{{2}} }}\)) of the gas phase (g) is the same as metal and SI. At fixed pressure, this equilibrium condition can be formalized by Formula [2]:

$$ \mu_{{{\text{O}}_{2} }} \left( {\left[ {\text{C}} \right], \, T, \, \left[ {w_{{\text{M}}} } \right]} \right) \, = \mu_{{{\text{O}}_{2} }} \left( {\left( {{\text{FeO}}} \right), \, T, \, \left( {w_{{\text{S}}} } \right)} \right) $$
(2)

where [C] and (FeO) are the weight percentages (wt pct) of carbon and iron oxide in the metal (γ) and SI phases, respectively. In addition, [xM] and (xS) refer to the weight percentages (wt pct) of other elements and constituents in the metal and SI phases, respectively.

Fig. 3
figure 3

(a) Model of SI-metal systems equilibrated with gas phase: (γ) austenitic phase, SI phase in the liquid or glassy state, and (g) gas; (b) example of equilibrium conditions (star-shaped symbol) graphically visualized as the intersection of isopleths of carbon and iron oxide weight percentages in the oxygen chemical potential space at 1 bar (0.1 MPa)

Full size image

Graphically, equilibrium conditions correspond to the coordinates of the intersection point between iso-C and iso-FeO concentration curves in the oxygen chemical potential space at a fixed pressure (Figure 3(b)).

Both oxygen chemical potential and temperature can be calculated by Formula [2] if carbon and iron oxide activities are known. In particular, carbon activity in the austenitic phase was computed as a function of temperature and carbon weight percentage in the metal matrix by Formula [3] which is valid for the Fe–C binary system[33]:

$$ \log \, a_{{[{\text{C}}]}} = 2300/T \, {-} \, 2.21 \, + \, 0.15\left[ {\text{C}} \right] + \log \left[ {\text{C}} \right] $$
(3)

where a[C], [C], and T are the activity of carbon (reference state Henrian at 100 pct C), the carbon weight percentage in the austenitic metal phase (γ), and the temperature in kelvin, respectively. It should be noted that Formula [3] can be applied if the amount of alloying elements other than carbon (e.g., phosphorous) is negligible. Otherwise, the effect of each alloying element on the carbon activity must be specifically evaluated.

Moreover, under appropriate conditions, it is possible to consider the hypothesis that the activity–composition relation for iron oxide in the liquid or glassy SI can be predicted following the quadratic regular solution model proposed by Ban-Ya[34] (Formulas [4] and [5]):

$$ a_{{({\text{FeO}})}} = \, x_{{({\text{FeO}})}} f_{{({\text{FeO}})}} \exp \left[ {\left( {{-}8540 \, + \, 7.14T} \right)/{\text{RT}}} \right] $$
(4)
$$ f_{{({\text{FeO}})}} = \, \exp \left\{ {\left[ {\left( {33470 \, \left( {x_{{{\text{MgO}}}} } \right)^{2} {-} \, 41000 \, \left( {x_{{{\text{AlO}}_{3/2} }} } \right)^{2} {-} \, 41840 \, \left( {x_{{{\text{SiO}}_{2} }} } \right)^{2} {-} \, 31380 \, \left( {x_{{{\text{CaO}}}} } \right)^{2} + \, 7110*\left( {x_{{{\text{MnO}}}} } \right)^{2} + \, 63600 \, x_{{{\text{MgO}}}} x_{{{\text{AlO}}_{3/2} }} + \, 58570 \, x_{{{\text{MgO}}}} x_{{{\text{SiO}}_{2} }} + \, 102510 \, x_{{{\text{MgO}}}} x_{{{\text{CaO}}}} {-} \, 21340 \, x_{{{\text{MgO}}}} x_{{{\text{MnO}}}} + \, 44770 \, x_{{{\text{AlO}}_{3/2} }} x_{{{\text{SiO}}_{2} }} + \, 82430 \, x_{{{\text{AlO}}_{3/2} }} x{\text{CaO }} + \, 49790 \, x_{{{\text{AlO}}_{3/2} }} x_{{{\text{MnO}}}} + \, 60670 \, x_{{{\text{SiO}}_{2} }} x_{{{\text{CaO}}}} + \, 40580 \, x_{{{\text{SiO}}_{2} }} x_{{{\text{MnO}}}} + \, 67780 \, x_{{{\text{CaO}}}} x_{{{\text{MnO}}}} } \right)} \right]/\left( {{\text{RT}}} \right)} \right\} $$
(5)

where a(FeO) and f(FeO) are the Raoultian activity and activity coefficient of iron oxide in the SI phase, respectively. Oxides concentrations are expressed as molar fractions (x) and T is the temperature expressed in kelvin.

Computation of carbon concentration and activity isopleths

Carburization, i.e., dissolution of carbon atoms in the metal matrix, is governed by the Boudouard reaction (Formula [6]), which is catalyzed on the metal surface[35,36,37]:

$$ {\text{2CO}} \leftrightarrow \left[ {\text{C}} \right] \, + {\text{ CO}}_{{2}} $$
(6)

where [C] indicates the carbon dissolved in the austenitic metal phase (γ).

The standard Gibbs free energy change (ΔG6°) and the equilibrium constant (K6) of the Boudouard reaction were computed by Formulas [7] and [8] starting from the thermochemical data provided by Barin[38]:

$$ \Delta G_{{6}}^{^\circ } = \, 0.{17}T \, {-}{ 165}.{73 }\left( {{\text{KJ}}/{\text{mol}}} \right) $$
(7)
$$ K_{6} = \, \exp ({-}\Delta G_{6}^{^\circ } /{\text{ RT}}) $$
(8)

According to Lupis,[31] the Boudouard equilibrium curve (η) can be computed by Formulas [9] through [11]:

$$ \eta \left( {a_{{[{\text{C}}]}} , \, T} \right) \, = \, p_{{{\text{CO}}}} /p_{{{\text{CO}}_{2} }} = (2\lambda )/(0.21 \, {-}\lambda ) $$
(9)
$$ \lambda = \, \left[ {{-}0.79A \, + \, \left( {\left( {0.79A} \right)^{2} + \, 4 \, \left( {4 + A} \right) \, 0.21 \, A} \right)^{1/2} } \right] \, / \, \left[ {2 \, \left( {4 + A} \right)} \right] $$
(10)
$$ A = \left( {p_{{{\text{CO}}}} } \right)^{2} /p_{{{\text{CO}}_{2} }} = a_{{[{\text{C}}]}} K_{6} $$
(11)

To determine the oxygen partial pressure \(\left( {p_{{{\text{O}}_{2} }} } \right)\) from the Boudouard equilibrium, the dissociation reaction of carbon dioxide (Formula [12]) was considered. The standard Gibbs free energy change (ΔG12°) and the equilibrium constant (K12) of this reaction were obtained by Formulas [13] and [14] from Barin’s thermochemical data[38]:

$$ 2{\text{CO}}_{2} \leftrightarrow 2{\text{CO}} + {\text{O}}_{2} $$
(12)
$$ \Delta G_{{{12}}}^{^\circ } = {-} \, 0.{17}T + {561}.{26 }\left( {{\text{kJ}}/{\text{mol}}} \right) $$
(13)
$$ K_{12} = \exp ({-}\Delta G_{12}^{^\circ } /{\text{RT}}) = p_{{{\text{O}}_{2} }} \left( {p_{{{\text{CO}}}} /p_{{{\text{CO}}_{2} }} } \right)^{2} = p_{{{\text{O}}_{2} }} \eta^{2} $$
(14)

The oxygen partial pressure was calculated by Formula [15]:

$$ p_{{{\text{O}}_{2} }} = K_{12} /\eta^{2} $$
(15)

By definition of oxygen chemical potential, the isopleths of both carbon concentration and activity in the oxygen chemical potential space (Figures 4(a) and (b)) can be computed by Formula [16]:

$$ \mu_{{{\text{O}}_{2} }} \left( {a_{{[{\text{C}}]}} , \, T} \right) = {\text{RT }}\ln p_{{{\text{O}}_{2} }} = {\text{RT}}\,\ln (K_{12} /\eta^{2} ) \, \left( {{\text{kJ}}/{\text{mol}}} \right) $$
(16)

where the activity of carbon (reference state Henrian at 100 pct C) in the austenitic phase (a[C]) can be expressed as a function of carbon concentration and temperature by Formula [3].

Fig. 4
figure 4

Isopleths of (a) carbon concentration (wt pct) and (b) activity in the oxygen chemical potential space at 1 bar (0.1 MPa)

Full size image

Computation of iron oxide concentration and activity isopleths

To calculate iso-concentration and iso-activity curves of iron oxide in liquid or glassy SI, Formulas [17] and [18] are considered:

$$ \left[ {{\text{Fe}}} \right] + \left[ {\text{O}} \right] \leftrightarrow \left( {{\text{FeO}}} \right) $$
(17)
$$ \left[ {\text{O}} \right] \leftrightarrow 1/2{\text{ O}}_{2} $$
(18)

The equilibrium constants for these reactions (K17 and K18) were computed from Barin’s thermochemical data[38] (Formulas [19] and [20]):

$$ K_{17} = \exp ({-}\Delta G_{17}^{^\circ } /{\text{RT}}) \, = \, a_{{({\text{FeO}})}} /\left( {a_{{[{\text{O}}]}} a_{{[{\text{Fe}}]}} } \right) = \exp \left[ {\left( {523.40 \, {-} \, 0.13T} \right)/{\text{RT}}} \right] $$
(19)
$$ K_{18} = \exp ({-}\Delta G_{18}^{^\circ } /{\text{RT}}) = p_{{{\text{O}}_{2} }}^{1/2} /a_{{[{\text{O}}]}} = \exp \left[ {\left( {254.01 \, {-} \, 0.07T} \right)/{\text{RT}}} \right] $$
(20)

The isopleths of iron oxide concentration and activity are calculated by Formula [21]:

$$ \mu_{{{\text{O}}_{2} }} \left( {a_{{({\text{FeO}})}} , \, T} \right) = {\text{RT }}\ln \, p_{{{\text{O}}_{2} }} = 2{\text{RT }}\ln \left( {a_{{({\text{FeO}})}} K_{17} /K_{18} } \right) \, \left( {{\text{kJ}}/{\text{mol}}} \right) $$
(21)

where the Raoultian activity of iron oxide in the SI phase (a(FeO)) can be defined by Ban–Ya’s model[34] (Formulas [4] and [5]). Examples of iron oxide iso-activity curves are shown in Figure 5.

Fig. 5
figure 5

Isopleths of iron oxide activity in the oxygen chemical potential space at 1 bar (0.1 MPa)

Full size image

Results and Discussion

Metallographic Examination and Microhardness Measurements

The as-polished S1 section was optically investigated (Figure 6(a)). Most of the SI are poorly oriented and featured a fragmented appearance. Some SI bands aligned throughout the main hot plastic deformation directions were also observed (Figure 6(b)). In addition, the majority of SI were preferentially positioned at the section right side as shown in Figure 6(a).

Fig. 6
figure 6

(a) The as-polished S1 section (collage of micrographs with ×50 magnification) and (b) optical micrograph of SI (×50 magnification)

Full size image

The optical examination of the chemically etched S1 section reveals a heterogeneous distribution of different microstructural constituents (Figure 7(a)). The upper portion of the section is mainly characterized by two microstructural constituents arranged in a vein-like pattern. Pearlite-rich areas with some traces of allotriomorphic and Widmanstätten ferrite (P + F*) (Figure 7(b)) are mixed with zones constituted of Widmanstätten ferrite and pearlite (F* + P) (Figure 7(c)). Moreover, bright ghost lines (GL), i.e., light-etching zones caused by the local enrichment of alloying elements in the metal matrix, were detected (Figure 7(d)). On the other hand, the lower region of the section, which corresponds to the bar inner core, is mainly featured by equiaxed ferrite grains with a small fraction of pearlite (F + P) (Figure 7(e)).

Fig. 7
figure 7

(a) Distribution map of the main microstructural constituents and (b) through (e) some representative ×200 magnification optical micrographs (F ferrite, F* Widmanstätten ferrite, P pearlite, GL ghost lines, SI slag inclusions)

Full size image

The microhardness measurement data, summarized in Table I and Figure 8, confirm the metallographic results.

Table I Vickers Microhardness Results (N Sample Amplitude, Min Minimum Value, Max Maximum Value, \(\overline{x }\) Mean Value, s Sample Standard Deviation)
Full size table
Fig. 8
figure 8

(a) Distribution map of Vickers microhardness indentations and (b) measurement results along vertical lines (L1, L2, L3)

Full size image

The microstructural analysis and Vickers microhardness results seem to indicate that the steel bar was shaped by a hot plastic deformation process. In fact, despite SI being oriented and elongated in the plastic deformation directions, no strained ferrite grains were detected. This observation can be explained as follows. Before forging, the material was austenitized by heating above Ac3 temperature. Subsequently, the steel compression by hammering induced the elongation and flattening of both austenitic grains and SI. The plastic deformation of austenitic grains increases the dislocation density and promotes dynamic recovery as well as recrystallization, which preserves good material workability. On the other hand, the steel workability significantly drops owing to a strain-hardening mechanism when it is plastically deformed below the recrystallization temperature. This phenomenon is likely to occur during a forging cycle because the material temperature tends to decrease. Therefore, the bar was probably forged and drawn out with multiple hammering and annealing cycles. This thermo-mechanical process is often involved in iron smithing because it allows proper material workability retention, promoting material recrystallization at each step.[39]

It should be observed that no signs of cold working after hot shaping have been detected, such as twin lines (Neumann bands) in the equiaxed ferrite grains.

In addition, the presence of near-equilibrium and low-undercooling microstructural constituents, i.e., ferrite and pearlite, and the absence of rapid cooling microstructure (e.g., bainite and martensite) indicate that the artifact was probably cooled in the air after the shaping stage. The observed microstructural heterogeneity can be explained by supposing either smelting-related carburization of the ferrous material or a post-smelting carbon enrichment during the smithing stage. Moreover, the ghost lines clearly point out an uneven distribution of alloying elements in the metal matrix. In fact, ghost lines can be observed on the etched sample owing to a local increase in the steel etching resistance due to the presence of alloying elements.[16]

SEM/EDS Analysis

The chemical composition of 79 SI was analyzed by SEM/EDS (Supplementary Tables S-I and S-II). The results of PCA coupled with HCA for each SI are shown in Figure 9. The inclusions were clustered in four main groups on PC space (Figure 9(a)) when the dendrogram plot was truncated at a height of 15 (Supplementary Figure S-2).

Fig. 9
figure 9

(a) through (e) Projection of SI chemical composition on PC1 to PC2 plane with loading vectors plot (the percentage of variation described by each PC is given into brackets) and (f) SI position on the section microstructural constituents map; square, circle, and triangle symbols correspond to SI surrounded by F + P, F* + P and P + F steel microstructures, respectively (F ferrite, F* Widmanstätten ferrite, P pearlite, GL ghost lines, SI slag inclusions)

Full size image

The mean oxides percentages weighted on the SI surfaces were computed for each SI group by Formula [22]:

$$ {\text{Pct}}\,{\text{Oxide}}_{j}^{*} = \sum\limits_{i = 1}^{{n_{j} }} {{\text{Pct}}\,{\text{Oxide}}_{ij} \times \frac{{S_{ij} }}{{S_{{{\text{T}}j}} }}} $$
(22)

where pct Oxide*j refers to the mean weighted percentage of a given oxide for the jth group, pct Oxideij is the oxide weight percentage for the ith SI in the jth cluster, Sij correspond to the ith SI surface in thejth group and STj is the total surface for the jth group. The average oxides weighted percentages are listed in Table II.

Table II Average Weighted Oxides Percentages (Wt Pct) for Each SI Group
Full size table

Group 1 (blue) includes the majority of the analyzed SI and is mainly positioned near the origin of the PC1 to PC2 plane (Figures 9(a) and (b)). In addition, its chemistry is characterized by a significant amount of MnO and traces of BaO, P2O5, and CuO (Table II). Since these oxides are contained in the iron ore gangue, this group is probably derived from the smelting process. Moreover, it is interesting to note that these compounds are specifically detected in the iron ore of the Piazzalunga mine, which was possibly used to produce the bar steel.[20,22,40] Group 2 (yellow) is marked by a low amount of MnO and a high percentage of CaO and K2O (Figures 9(a), (c), and Table II). For these reasons, it can be related to ash contamination. Group 3 (green) includes SI that are mainly characterized by the absence of MgO (Figures 9(a), (d), and Table II). Moreover, the SI of group 3 contains some traces of P2O5 which is related to iron ore gangue. Accordingly to these observations, group 3 could be constituted by smelting-related SI. Group 4 (red) is marked by a great amount of MnO (Figures 9(a), (e), and Table II). Since MnO derives from iron ore gangue, group 4 is probably constituted by smelting-related SI. The high MnO content can be explained by a local concentration effect due to a significant SI fragmentation and consequent local partitioning of Mn-rich spots. SI mineralogy was investigated by SEM/EDS analysis. Examples of chemical measurements for the main detected mineralogical phases are shown in Figure 10 and Table III. Two main SI petrological classes were observed, i.e., two-phase fayalite-wüstite SI (Figures 10(a) and (b)) and single-phase glassy SI (Figure 10(c)). In addition, the two-phase SI are marked by a high iron oxide content and preferentially belong to groups 1 and 3 (Table III). Conversely, the single-phase glassy SI (Figure 10(c)) are generally characterized by a lower iron oxide content (Table III). It was observed that the single-phase type is greatly predominant in all SI groups except for group 3.

Fig. 10
figure 10

SEM micrographs of the two main SI types: (a) and (b) two-phase fayalite (dark gray)—wüstite (gray) SI and (c) single-phase glassy SI (C). The letters A, B, and C indicate the three zones chemically analyzed by SEM/EDS

Full size image
Table III SEM/EDS Microchemical Analyses of the Areas Highlighted in Fig. 10
Full size table

In addition, the correlation between the chemistry and mineralogy of SI and the metal matrix microstructure was assessed. It was noted that fayalite-wüstite SI are primarily placed in the ferrite-rich zone (F + P) whereas the glassy SI type is mainly positioned in the ferritic-pearlitic (F* + P) and in the pearlitic-ferritic (P + F*) zones. Conversely, it was observed that the inverse correlation between iron oxide in SI and carbon in the metal matrix is not satisfied for all SI-metal systems (Figure 11). In fact, some SI in the ferritic-pearlitic (F* + P) and pearlitic-ferritic (P + F*) zones are featured by a relatively high iron oxide content. According to Buchwald,[41] these systems are significantly far from local equilibrium probably as a consequence of post-smelting carburization.

Fig. 11
figure 11

FeO–SiO2 bivariate scatterplot (solid and open versions of the same symbol refer to SI that follow or not the inverse correlation between iron oxide and carbon in the SI-metal systems, respectively)

Full size image

FeO-SiO2 and NRCs bivariate scatterplots were also evaluated to confirm and deepen the SI selection and classification (Figure 12). For the sake of example, the SiO2–Al2O3 biplot is given in Figure 12(b). The point clouds corresponding to SI groups 1 and 3 follow a linear trend because of constant NRC ratios. This feature confirms that these groups include smelting-derived SI. By contrast, groups 2 and 4 appear significantly more scattered than groups 1 and 3, probably as a consequence of ash contamination and local concentration effects.

Fig. 12
figure 12

Bivariate scatterplots: (a) FeO–SiO2 and (b) SiO2–Al2O3 (solid and open versions of the same symbol refer to glassy and fayalite-wüstite SI, respectively)

Full size image

In addition, 16 semi-quantitative chemical measurements were performed by SEM/EDS to investigate the metal matrix chemistry. The steel is alloyed with copper and arsenic in average weight percentages of 1 and 0.47 wt pct, respectively. These elements probably passed from the ore to the metal phase during the reduction stage. Furthermore, the uneven distribution of these alloying elements in the metal matrix can explain the presence of ghost lines on the etched bar cross-section.

The multivariate statistical approach proposed by Disser et al.[42] was applied in this study to evaluate the steel technological origin. This model is based on logistic regression and allows to effectively discriminate between direct and indirect processes starting from the chemical composition of smelting-related SI. The statistical model permits to compute a binary output variable (Y). The value of this variable can be equal to 0 or 1 if the smelting process is direct or indirect, respectively.

Following the protocol suggested by Disser et al.,[42] the mean weight oxides percentages for smelting-related SI (wt pct Oxide*) were converted to subcompositional ratios (Oxide**) by the Formula [23]:

$$ {{\text{Oxide}}^{**}} = ({\text{Wt Pct}}\,{\text{Oxide}}^{*} \, \times 100)/\left( {100{-}{\text{Wt}}\,{\text{Pct}}\,{\text{FeO}}^{*}} \right) $$
(23)

where “Oxide” indicates each oxide involved in the statistical analysis (i.e., MgO, Al2O3, SiO2, P2O5, K2O, CaO, MnO). The logistic model can be written by Formula [24]:

$$ {\text{Logit}}\left( p \right) = \log \, \left[ {p/\left( {1 - p} \right)} \right] = \beta^{0} + \beta^{{{\text{Mg}}}} \left[ {{\text{pct}}\,{\text{MgO}}^{**}} \right] + \beta^{{{\text{Al}}}} \left[ {{\text{pct}}\,{\text{Al}}_{2} {\text{O}}_{3}^{**}} \right]_{{}} + \, \beta^{{{\text{Si}}}} \left[ {{\text{pct}}\,{\text{SiO}}_{2}^{**}} \right] + \beta^{{\text{P}}} \left[ {{\text{pct}}\,{\text{P}}_{2} {\text{O}}_{5}^{**}} \right] + \beta^{{\text{K}}} \left[ {{\text{pct}}\,{\text{K}}_{2} {\text{O}}^{**}} \right] + \beta^{{{\text{Ca}}}} \left[ {{\text{pct}}\,{\text{CaO}}^{**}} \right] + \beta^{{{\text{Mn}}}} \left[ {{\text{pct}}\,{\text{MnO}}^{**}} \right] $$
(24)

where p corresponds to the probability that the binary variable Y is equal to unity. To apply the logistic regression model, the parameters (β0, βMg, βAl, βSi, βP, βK, βCa, βMn) provided by Disser et al.[42] were used (Table IV).

Table IV Logistic Regression Model Parameters
Full size table

In general, three scenarios can occur. In the case that the output value of p is less than 0.3 or greater than 0.7, the iron-making technology can be classified as direct or indirect, respectively.[42] Otherwise, the pyrometallurgical method cannot be determined.

In the present study, only the smelting-related SI of group 1 was considered to assess the technological origin of the bar steel. The computed oxides subcompositional ratios for group 1 are listed in Table V.

Table V Oxides Subcompositional Ratios for Smelting-Derived SI of Group 1
Full size table

The logistic regression model provided a p value equal to 0.01. Since this result is less than 0.3, it can be concluded that the bar steel was produced by a direct iron-making process. It should be noted that this outcome matches the previous archaeological data of the PVGI site where the use of the bloomery process was hypothesized.[20]

Thermodynamic Analysis

The thermochemical equilibrium conditions for the SI-metal systems were computed following the thermodynamic-based model described in the Material and Methods section. The activity of carbon in the austenitic metal matrix was estimated by Formula [3], which is valid for the binary system Fe–C, even if small amounts of Cu and As were semi-quantitatively detected by SEM/EDS analysis. It should be noted that this approximation results in a negligible error of 2 to 3 pct in the computation of the carbon activity if the copper effect was considered as suggested by Williams and Bodsworth.[43] On the other hand, the influence of As on carbon activity cannot be calculated because of the lack of specific thermodynamic data currently available in the literature. The thermodynamic analysis was applied to the glassy SI of group 1 which includes the majority of smelting-related SI.

In addition, the SI-metal systems that do not follow the inverse correlation between iron oxide and carbon were not considered because they are probably very far from the local equilibrium conditions assumed. The thermodynamic analysis results for the SI positioned in the three main zones (F + P, F* + P, and P + F) of the section are shown in Figure 13(a) and Table VI. In particular, the equilibrium temperatures are in the range of 1003 °C to 1171 °C, whereas the computed values of oxygen chemical potential (\(\mu_{{{\text{O}}_{{2}} }}\)) vary between − 447.47 and − 385.79 kJ/mol. It is important to highlight that the SI-metal systems in the carburized zone (F* + P, P + F) show an equilibrium at a lower temperature and oxygen chemical potential compared to the systems in the low-C zones (F + P). Moreover, these results explain the inverse correlation between iron oxide and carbon observed in the FeO–SiO2 bivariate scatterplot (Figure 13(b)) in terms of both temperature and oxygen chemical potential variations of the gas phase in local equilibrium with the SI-metal systems. The estimated thermochemical parameters can give a reasonable indication of the working conditions of the bloomery smelting process.

Fig. 13
figure 13

(a) Equilibrium conditions for the SI-metal systems in the oxygen chemical potential space at 1 bar (0.1 MPa). Quartz-Fayalite-Iron (QFI) and C–CO–CO2 (CCO) buffers are inserted to delimit the austenite stability field (gray-colored area). Data used for drawing the Quartz-Fayalite-Iron (QFI) curve were taken from O’Neill,[44] whereas the C–CO–CO2 (CCO) curve is calculated by Formula [16] imposing carbon activity as unity. (b) FeO-SiO2 bivariate scatterplot

Full size image
Table VI Values of Equilibrium Temperature (T), Oxygen Chemical Potential (\(\mu_{{{\text{O}}_{{2}} }}\)) and SI Liquidus Temperature
Full size table

The liquidus temperatures for the SI considered in the thermodynamic analysis were estimated with MELTS-rhyolite v.1.0.2. software package (details of MELTS-rhyolite calculations are provided in the electronic supplementary material).[45,46] The results for the SI positioned in the three main zones (F + P, F* + P, and P + F) are 1187 °C, 1195 °C, and 1190 °C, respectively. These values can be considered as the lower limits of the maximum temperatures reached during the direct smelting process. In addition, it was noted that in all cases, the liquidus temperatures exceed the equilibrium temperatures; therefore, the computed local equilibria refer to sub-liquidus conditions. Since the thermodynamic-based approach implemented in this research has been applied only to one object, future works will have to confirm its general validity by analyzing a large set of ferrous artifacts related to both bloomery and indirect iron-making processes.

Conclusions

In this study, an archaeometallurgical characterization of a Lombard steel bar retrieved in the medieval site of Ponte di Val Gabbia I (Brescia, northern Italy) was performed to disclose technological data and processing thermochemical parameters by a thermodynamic-based analysis of the slag inclusion-metal systems. Metallographic analysis and Vickers microhardness measurements indicate that the steel bar was forged and drawn out by the hot plastic deformation of a heterogenous steel lump or bloom. Moreover, the presence of low-undercooling microstructural constituents, i.e., ferrite and pearlite, points out that the artifact was cooled in the air at the end of the shaping stage. The SI chemistry was semi-quantitatively measured by SEM/EDS analysis. Starting from these chemical composition data, the SI origin was investigated by multivariate statistical methods, i.e., PCA and HCA, and NRCs ratios analysis. In addition, this strategy allowed the selection of a SI group that can be safely related to the smelting process. The relatively high iron oxide content of some SI in the ferritic-pearlitic (F* + P) and pearlitic-ferritic (P + F*) zones can support the hypothesis that the material has undergone post-smelting carburization. From the chemistry of this SI group, a multivariate statistical approach based on logistic regression was employed to discriminate the steel technological origin. The results allowed us to conclude that the bar steel was obtained following the direct iron-making route. The analysis of the correlation between the iron oxide in the SI and carbon in the metal matrix allowed us to identify those SI-metal systems for which local equilibrium conditions can be assumed. Focusing on these systems, a thermodynamic-based model was applied to compute the temperature and the oxygen chemical potential of the gas phase in equilibrium with the SI-metal systems. In particular, the calculated equilibrium temperatures are in the range of 1003 °C to 1171 °C, whereas the oxygen chemical potential varies between − 447.47 and − 385.79 kJ/mol. The liquidus temperatures of the smelting-related SI were estimated by the MELTS-rhyolite software package. For the SI positioned in the mainly ferritic (F + P), ferritic-pearlitic (F* + P) and pearlitic-ferritic (P + F) zones, it was obtained that the lower limits of the maximum temperature reached during the smelting process are 1187 °C, 1195 °C, and 1190 °C, respectively. These thermochemical parameters possibly give an indication of the working conditions of the bloomery smelting process.