Introduction

The Top Submerged Lance (TSL) furnace is a pyrometallurgical technology invented in the 1970s at CSIRO to enhance the performance of tin smelting processes, and today widely applied in the production chains of several non-ferrous base metals.[1] Given the advantages of high mass and heat transfer, reaction rates, and hence process throughput, in recent decades the TSL furnace has been successfully implemented in processes for copper, lead, zinc, and nickel production.[2,3,4] According to the 2019 Copper Smelting Survey by Watt and Kapusta,[5] the TSL smelting technologies Ausmelt and Isasmelt rank second in the total number of worldwide operating furnaces after flash smelters, accounting for 17 pct of the world’s copper production. Although the Peirce-Smith technology is still predominant, TSL furnaces are also emerging as conversion process,[6] and eventually as recycling technology for metal scrap, e-waste, lead batteries, and slag.[7,8,9]

A key feature of this high flexibility of the TSL smelter is the direct and downward injection of process gas into the slag bath by means of a top lance. The ensuing strong interactions between the gases and the molten bath lead to high mixing in the vessel, and enhance transport phenomena in the reactor.[10] Despite the firm role of this technology in the metals industry, many questions on the basic physics remain unanswered and fundamental research is needed for a thorough comprehension of the process. In-situ experimental investigations are still challenging, because the high temperatures and the aggressive atmosphere complicate the measurement of physical quantities in the furnace. The role of physical and mathematical modeling is therefore crucial to understand the complexity of the metallurgical system,[11] and the development of computer-aided engineering (CAE) tools is key for evaluating the furnace resource efficiency, and for optimizing it so that it can be integrated into a circular economy of metals.[12] In this perspective, many scientific works can be found in the literature on TSL systems at laboratory scale. Experimental investigations into top gas injections in water/oil baths can be found in References 13,14, through 15, and examples of Computational Fluid Dynamics (CFD) being used to simulate small-scale vessels are found in References 16,17,18,19,20, through 21. Morsi et al. presented one of the first comprehensive experimental measurements of a top-submerged gas injection in a water bath, providing 2D distributions of velocity and turbulent kinetic energy in the bath, which are useful for the validation of numerical models.[22] In terms of modeling, the work of Sattar et al. is relevant: they developed a Population Balance Method (PBM) sub-model in the framework of the Two-Fluid-Model (TFM) multiphase method, in order to simulate the bath dynamics with a focus on slag foaming in TSL injection.[23,24,25] The authors were able to predict the foam height for a small-scale lab vessel and the foam behavior as a function of the \({\text{Al}_{2}\text{O}_{3}}\) content.

There are fewer research works related to pilots and industrial-scale furnaces, and most of them involve the development of mathematical and CFD models. Solnordal et al. investigated the fluid dynamics of swirling lances and developed a 1D model to calculate the heat transfer at the lance wall and cooling air for the pilot Sirosmelt furnace.[26,27] The model was able to predict temperatures at the inner walls of the lance and the thickness of the solidified slag layer, also measured in the furnace. Huda et al. carried out a CFD study on the Outotec TSL pilot-scale furnace, investigating the zinc slag fuming process.[28] They applied a TFM method for the multiphase system, including sub-models for interfacial mass and energy transfer, and combustion reactions. The authors were able to reproduce the physical phenomena of the process and calculate the rate of zinc fuming from the slag. Although the model overpredicted the zinc content in the bath, the fuming rate was found to be close to experimental values. With the same modeling approach, the authors also studied the fuming process in a tuyere-blown furnace.[29] Gwynn-Jones et al. performed a single-phase CFD analysis on the offtake system of a large-scale TSL smelter.[30] Their analysis focused only on the region of the exhaust flow, neglecting the multiphase interactions in the bath. Different roof geometries were compared by monitoring for the possible presence of feedstock carryover, thermal asymmetries and recirculation zones. The TFM approach was also applied by Stephens et al. to model the multiphase flow in the HiSmelt furnace, a pyrometallurgical reactor for iron reduction, where submerged lance injection also takes place.[31] A Lagrangian phase was also included to track the ore and coal particles. Although the results revealed the dynamics of the bath with submerged gas injection and species distributions in the reactor, the method was not validated or even compared to experimental data.

The most commonly used approach found in the literature on the CFD modeling of the TSL bath is the TFM method. In all these works, coarse grids have been used for the simulations, making it possible to implement complex phenomena of mass and heat transfer while reducing computational costs, which are otherwise high for this type of method. Indeed, it may be recalled that in the TFM, a set of Navier–Stokes (NS) equations is solved for each of the phases involved in the system. However, in a process such as the TSL bath, the interfacial exchanges between phases depend directly on the exchange surface, the interface between the slag and the gas phase. Since the geometrical reconstruction of the interface is not performed in the TFM method, and low-resolution grids are often used, the quality of the results concerning the interphase exchange phenomena can be questionable. Moreover, the correct modeling of the closure terms for the interphase interactions in TFM is not trivial. A good example of this is drag models, which require the estimation of a representative bubble diameter in the liquid phase.

On the other hand, front-tracking methods such as the Volume Of Fluid (VOF) allow the interface to be directly reconstructed. Furthermore, being one of the so-called “one fluid” models, only one set of NS equations is solved and no closure terms are needed. Despite the disadvantage of high computational costs, the authors believe that a preferable approach for the CFD simulation of TSL furnaces is VOF-based and involves high-resolution grids.

In a recent work, Wang et al. used a VOF-LES approach to simulate the top gas injection in an industrial vessel for the slag stabilization process.[32] The modeling approach was first validated with a lab-scale bath of paraffin oil and then applied to the slag vessel, with the authors focusing their analysis on the free surface sloshing and splashing. Nevertheless, the mesh resolution was not high enough to ensure a sharp reconstruction of the interface. In addition, it is hard to extend their outcomes to TSL furnaces, since the lance-to-vessel diameter ratio considered in their analysis was considerably smaller than those typical of TSL smelters.[3] The VOF method was also employed by the authors in previous works. In a first work, the effect of liquid physical properties on the hydrodynamics of TSL systems was studied using parameter analysis.[19] The CFD study underlined the importance of liquid viscosity and surface tension for the hydrodynamic characterization of a top-submerged gas injection, revealing a weakness in the application of the Froude number to downscale the furnace to lab vessels operating with water or oils. That also revealed the need to investigate new model fluids whose properties were closer to those of real slags. In cooperation with Akashi et al.,[33] the authors investigated TSL gas injection in a quasi-2D metal bath, with an eutectic alloy that is liquid at room temperature. Thanks to X-ray radioscopic imaging, the measurements provided CFD-grade data, allowing the VOF method to be extensively validated for complex fluid systems such as the GaInSn alloy.[20] In a recent publication, the work was extended to metallic baths in cylindrical vessels. With a parametric study on the lance immersion rate and the gas volume flow, three-dimensional phenomena of the TSL hydrodynamics were investigated.[21] The analysis focused particularly on the detection of rotational sloshing waves at the free surface and how these translate into an increase in the rotation speed, and therefore the mixing, in the liquid phase.

The present work is a continuation of these past activities, examining the bath dynamics for a pilot TSL furnace, in which gas is injected into molten slag. The CFD simulations are based on the VOF method and computed on a high-resolution grid. As a result, an insight into the multiphase interactions is presented, with highly resolved tracking of the slag-gas interface and in-depth analysis of key features for a TSL process, such as bubble formation, slag splashing, bath mixing or sloshing waves. The results reveal the predictive capabilities of the VOF-based numerical model also for these scales, making the approach highly reliable and laying solid foundations for future developments.

The Pilot-Scale TSL Furnace

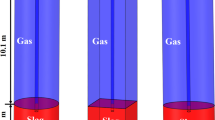
Figure 1 shows a representation of the pilot TSL furnace operating at TU Bergakademie Freiberg. The cylindrical structural vessel is embedded in a platform of reinforced concrete at the base, and it is surmounted by a top flange, where the lance entry system, the feedstock port and the exhaust duct are located. Two launders, displaced in angular and axial positions, allow slag and matte phases to be regularly tapped from the bottom. This external structure has a height of approximately 2.5 m and a diameter of roughly 0.9 m. The furnace is internally lined with refractory material, reducing the diameter to 0.4 m. The stainless steel lance is inserted from a top central port and delivers air or \({\text{O}_{2}}\)-enriched air and fuel, with two concentric tubes. The air is blown in the annular section of the lance and encounters a swirler (if installed) right before the discharge. As with Outotec’s patented lance,[34] the helical vane enhances the lance cooling in this section of the lance, favoring the formation of an outer, protective layer of solidified slag and, at the same time, increasing the efficiency of air and fuel mixing, and therefore of combustion. The specific lance diameters are \(d_{air,in} = 28\) mm, \(d_{air,out} = 32\) mm, \(d_{fuel,in} = 12\) mm and \(d_{fuel,out} = 14\) mm.

The furnace can handle different smelting processes in oxidizing and reducing atmospheres up to temperatures around 1400 °C, and it is operated for various research campaigns. As part of the program of the Center for Innovation Competence for Virtual High Temperature Conversion (CIC Virtuhcon), the virtualization of the TSL process is developed by means of CFD modeling supported by practice knowledge and fundamental research. The present work is therefore a further step towards the achievement of this goal, in line with the authors’ past research, as already discussed above.

Fig. 1
figure 1

Scheme of the pilot-scale TSL furnace operating at TU Bergakademie Freiberg

Full size image

Numerical Setup

Scope and Main Assumptions

The main goal of this numerical investigation is to provide a detailed insight into the bath dynamics of a pilot-scale TSL furnace. The use of real furnace geometry and conditions, with measured physical properties of the slag, fill the gap in the understanding of the fundamental physics of TSL furnace processes, a subject that has still not been fully explored and discussed in the literature. The difficulty in measuring these flows experimentally must be overcome with the help of numerical models, the complexity of which is rising, thanks to advances in computational technology.

With this in mind, the current model was developed under certain assumptions, in order to focus on the dynamics of the slag bath with submerged gas injection. Heat transfer, chemical reactions and the solid feedstock stream are not taken into account. The system is therefore in iso-thermal conditions at \(T_{op} = 1500\) K, in the range of the typical operating temperatures of a TSL furnace.[2,3,35] As a consequence, the physical properties of the slag are kept constant and evaluated at \(T_{op}\) using data that are experimentally measured in-house.[36]

The VOF Model

The CFD approach of the present work is based on the use of the VOF method. In this multiphase model, a marker function is defined as follows, in order to identify the phases of the system:

$$\begin{aligned} \alpha = {\left\{ \begin{array}{ll} \,0 &{} \quad \text {if only gas}\\ \,0< \alpha < 1 &{} \quad \text {at the interface}\\ \,1 &{} \quad \text {if only liquid}. \end{array}\right. } \end{aligned}$$
(1)

Here, \(\alpha \) is the volume fraction, a discrete function which varies from 0 to 1. Based on its value, the interface is reconstructed using an approximation scheme.[37] The Geometric Reconstruction Scheme applied here uses a Piecewise-Linear Interface Construction (PLIC) approach, which calculates the normal vector of the interface. After the reconstruction, \(\alpha \) is advected in the given velocity field following the advection equation

$$\begin{aligned} \frac{\partial \alpha }{\partial t} + \nabla \cdot \vec {u} \alpha = 0 \, . \end{aligned}$$
(2)

These two steps are therefore performed at each time step and allow the interface to be tracked over time. Only one set of the NS equations is solved in the VOF method:

$$\begin{aligned}&\nabla \cdot \vec {u} = 0 \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial \rho (\alpha ) \vec {u}}{\partial t} + \nabla \cdot \rho (\alpha ) \vec {u} \vec {u} = - \vec {\nabla p} + \nabla \cdot \mu (\alpha )\nonumber \\&\quad [\nabla \vec {u}+(\nabla \vec {u})^T] + \vec {f_g} + \vec {f_\sigma } \quad \end{aligned}$$
(4)

where \(\vec {u}\) is the velocity vector, p is the pressure, \( \vec {f_g}\) is the gravitational force and \( \vec {f_\sigma }\) is the interfacial force due to the surface tension. Turbulence is modeled here with a RANS approach, namely the k-\(\omega \)-SST model. The choice of the k-\(\omega \)-SST model is based on the advantage of combining the benefits of the k-\(\epsilon \) model for free shear flows, as for the bubbles in the bath, and those of the k-\(\omega \) model for wall-bounded and adverse pressure gradient flows, for the gas injection against the slag back-pressure.[38] Two additional transport equations are hence solved: one for the turbulent kinetic energy k and one for its specific dissipation rate \(\omega \)

$$\begin{aligned}&\frac{\partial \rho (\alpha ) k}{\partial t} + \nabla \cdot \rho (\alpha ) k \vec {u} \nonumber \\&\quad = \nabla \cdot \left[(\mu (\alpha )+\frac{\mu _t(\alpha )}{\sigma _k})\vec {\nabla k}\right] + G_k - Y_k \quad \end{aligned}$$
(5)
$$\begin{aligned}&\frac{\partial \rho (\alpha ) \omega }{\partial t} + \nabla \cdot \rho (\alpha ) \omega \vec {u} \nonumber \\&\quad = \nabla \cdot \left[\left(\mu (\alpha )+\frac{\mu _t(\alpha )}{\sigma _\omega }\right)\vec {\nabla \omega }\right] + G_\omega - Y_\omega \quad \end{aligned}$$
(6)

where

$$\begin{aligned} \mu _t= & {} \frac{\rho (\alpha ) k}{\omega } \frac{1}{max\left[ \frac{1}{a*},\frac{SF_2}{a_1\omega }\right] },\quad F_2 = tanh({\Phi _2}^2),\nonumber \\ \Phi _2= & {} max \left[ 2 \frac{\sqrt{k}}{0.09\omega y},\frac{500\mu }{\rho (\alpha ) \omega y^2}\right] . \end{aligned}$$
(7)

\(G_k\) and \(G_\omega \) are the generation of turbulent kinetic energy due to the mean velocity gradients and the generation of \(\omega \). \(Y_k\) and \(Y_\omega \) represent the dissipation terms of k and \(\omega \) due to turbulence. In Eq. [7], y is the distance from the nearest surface, S the strain rate and \(\sigma _k\), \(\sigma _\omega \), \(a*\) and \(a_1\) are constants of the model.

The “one-fluid” formulation enables the local fluid properties of density and viscosity to be defined as a function of the local volume fraction:

$$\begin{aligned} \rho (\alpha ) = \rho _l \alpha + \rho _g (1-\alpha ) \end{aligned}$$
(8)
$$\begin{aligned} \mu (\alpha ) = \mu _l \alpha + \mu _g (1-\alpha ) \end{aligned}$$
(9)

where \(\alpha \) is the volume fraction, \(\rho _l\) is the density of the liquid phase, \(\rho _g\) is the density of the gas phase, \(\mu _l\) is the dynamic viscosity of the liquid phase and \(\mu _g\) is the dynamic viscosity of the gas phase.

This approach was chosen with the intention of following the evolution of the free surface of the slag at high resolution. At the expense of high computational costs, this makes it possible to obtain detailed and precise information on the multiphase flow.

Case Setup

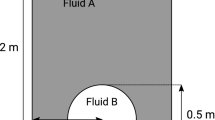
The computational domain is shown in Figure 2 and represents the fluid domain extracted from Figure 1. The inlet is positioned inside the lance and has an annular cross-section, as it lies between the air and the fuel lance. The gas phase is therefore injected downwards into the slag bath, which has an initial height \(H_b = 0.6\) m. The outlet is located at the beginning of the exhaust’s piping system, which is not considered in this work. The tap-holes at the bottom are closed and, along with all the other surfaces of the furnace and the lance, are treated like a no-slip wall.

Fig. 2
figure 2

The computational domain considered in the analysis. The inlet boundary condition is located inside the lance and has an annular cross-section. The outlet is positioned at the exhaust pipe and all other walls are considered as no-slip boundary conditions. \(H_b\) is the initial height of the slag bath and is equal to 0.06 m

Full size image

As mentioned, the slag in the bath has already been described by the authors in Reference 36. It originates from a secondary slag converter, and its composition can be simplified to \( {\text{SiO}}_{2} \cdot {\text{FeO}} \cdot {\text{Al}}_{2} {\text{O}}_{3} \cdot {\text{CaO}} \cdot {\text{Fe}}_{2} {\text{O}}_{3} \cdot {\text{MgO}} \cdot {\text{K}}_{2} {\text{O}} \cdot {\text{P}}_{2} {\text{O}}_{5} \cdot {\text{TiO}}_{2} \). The physical properties are evaluated at \(T_{op} = 1500\) K from data measured in-house and consist of a density \(\rho = 3435\) kg/m3, a dynamic viscosity \(\mu = 0.6072\) kg/ms and a surface tension \(\sigma = 0.1998\) N/m. The furnace is filled with almost 260 kg of slag. The process gas is considered to be air, which enters the system with a gas flow \(Q = 137\) Nm3/h, typical of the furnace operations at TU Bergakademie Freiberg.

Two setup configurations were studied, one ignoring and one taking into account the presence of a swirler in the gas flow. A few works in the literature have already examined the effect of a swirling gas injection on a TSL bath.[16,22] However, they have all focused on lab-scale vessels with simplified air-water fluid systems and, to the best knowledge of the authors, no studies on pilot-scale slag baths have been conducted to date. In the pilot-scale furnace, the swirler consists of a helicoidal support inserted into the annular section between the air and fuel lances, and has a swirl angle at the axis of 65 deg. In the CFD setup, this is included by setting the swirling component of the air flow directly at the inlet, located at the vertical position where the swirler would end.

The simulations were performed with the commercial software ANSYS Fluent© (v.19.2) and a summary of the numerical setup is reported in Table I.

Table I Numerical Setup
Full size table

Computational Grid

The numerical grid was generated with the commercial software ANSA Beta CAE© (v.20); an overview can be seen in Figure 3. A hybrid meshing approach was chosen to mesh the computational domain, to ensure that there was a structured and well resolved region in the core area of the slag bath, as well as controlling the overall number of cells. The lower and central part of the furnace are the regions where the slag-gas interface develops, because of the gas injection and slag splashing. This region is meshed with a structured hexa-block grid. In fact, the GEO-reconstruct scheme used in this work to reconstruct the interface performs with highest accuracy over a grid with hexagonal cells.[39,40] The upper part of the furnace is mainly occupied by the gas-phase flowing to the outlet and is meshed with an unstructured hexa-dominant approach, to reduce the total number of cells and facilitate the generation of a perfectly symmetric grid in the bottom part. Figures 4(a) and (b) show the inner cells distribution of the two zones. The structured zone is made of hexahedral cells with an almost constant spatial step of \(\Delta x = 3\) mm. This permits a resolution above 60-70 pt. per bubble diameter, which has already been adopted and verified by the authors in Reference 20. The unstructured mesh is topologically connected with a transition of polyhedral and tetrahedral cells, and presents a larger spatial discretization for the reason discussed above. This leads to a mesh size of around 2.8 M cells. An additional refinement of the grid would have been prohibitive with the available computing resources. It must be said that a resolution of 3 mm for a pilot-scale multiphase system is high, and is not found elsewhere in the literature on TSL furnace modeling. On one hand, this allows the smaller multiphase structures, such as entrained gas bubbles or splashed droplets, to be resolved to this scale; on the other hand, it restricts the computing capability. Indeed, in order to comply with the Courant–Friedrichs–Lewy condition of \(Courant < 1\), the time step is set equal to \(1\times 10^{-5}\) s. The CFD simulations were carried out to complete an elapsed time of 24 seconds, the first 4 seconds of which were necessary to complete the development of the flow and were excluded from the statistical analysis of the transient result data. The calculation of the elapsed time is completed with a number of computing days of O(10), using 240 CPUs allocated at the HPC Cluster Center for Information Services and High Performance Computing (ZIH) at TU Dresden.

Fig. 3
figure 3

The computational grid used in the CFD calculation. The structured and unstructured zones are highlighted

Full size image
Fig. 4
figure 4

Details of the computational grid: (a) Z-normal cross-section in the bath area, showing the structure of the hexa-block grid; (b) X-normal cross-section in the exhaust area, showing the unstructured hexa-dominant grid and the conjunction with the lower part

Full size image

Results and Discussion

Main Features of the Multiphase Flow

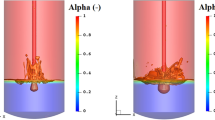
Figures 5(a) and (b) show a qualitative comparison of the multiphase flow, contrasting the no-swirl and the swirl configurations. The slag–gas interface is visualized by computing an iso-surface of the volume fraction \(\alpha _{slag} = 0.5\), offering a view of the multiphase flow as if the slag phase was transparent. Two instants of the simulations are shown, in which the gas bubble formed at the lance tip is at its maximum extension before rising due to gravity. Corresponding movie sequences are available as Electronic Supplementary Material, where the evolution of the interface is recorded for 4 seconds of the elapsed time and reproduced in slow motion, so that the dynamics are perceptible.

The snapshots in Figure 5 clearly present qualitative differences between the two configurations. Focusing first on the bubbles’ shape, whereas in the no-swirl configuration the gas penetrates deeper into the bath, leading to an ellipsoidal-cap bubble with a prolate profile, the bubble assumes an almost spherical shape in the presence of the swirler. This of course has a direct effect on many other features of the multiphase system, such as the bath mixing or the slag-gas interface area, which are discussed in detail in the following paragraphs. The splashing of the slag, also connected to the bubbles’ shape and their consequent disruptions, is another qualitative discrepancy that catches the eye when looking at the snapshots and the movies. In both cases, slag is violently splashed in the furnace. However, in the no-swirl configuration the slag forms an almost vertical spout with long sheet structures that easily reach the top of the furnace. On the other hand, the swirl configuration has a lower splashing region on average, as the slag is mainly spouted radially on the furnace walls.

Fig. 5
figure 5

Two instantaneous snapshots of slag-gas interface for (a) the no-swirl and (b) the swirl configurations

Full size image

Bubble Fequency

For TSL furnaces to operate properly, bubble frequency is an important parameter to monitor and should therefore be assessed during the design phase. In fact, it provides the operators with information about the dynamics of the bath and the actual process conditions.

In this study, the bubble frequency is calculated with a procedure already used by the authors in Reference 20. The surface-weighted average of the gas volume fraction is tracked over a monitoring surface on the XY plane placed at \(Z = 0.45\) m, 50 mm above the injection point. The time signal is recorded with a frequency of 100 Hz, sufficient for the measurement of such phenomena, and oscillates between the values of 0 and 1, respectively, for the detection of slag or gas. Thus, each peak above 0 represents the passage of gas, either with a bubble structure or as a stream. In order to calculate the bubble frequency, this time signal is processed with a Fast Fourier Transform (FFT) and the obtained spectrum fitted with a Gaussian function, applying the nonlinear least-squares (NLLS) Marquardt–Levenberg algorithm. Figures 6 and 7 show the results of the analysis for the no-swirl and swirl configurations, respectively. It is evident that in both cases two clear main frequencies appear. For the no-swirl case, \(f_1 = 5.89\) Hz and \(f_2 = 3.05\) Hz. For the swirl case, \(f_1 = 5.71\) Hz and \(f_2 = 2.46\) Hz. Initial observation of the data would identify the main frequency of the bubbles at values close to 6 Hz. However, the great advantage of numerical analysis lies in the ability to directly access the flow fields and shed light on physical phenomena by visualizing them. Figure 8 shows a correlation between the time signal of the void fraction, as discussed above, and corresponding visualizations of the gas-slag interface, for the no-swirl case. As expected from the analysis of the frequency spectrum, the time signal has a typical waveform: a signal composed of two waves, one with double the frequency of the other, and different amplitudes. Focusing attention on the short time range from \(t_A = 12.17\) seconds to \(t_E = 12.52\) seconds, one period of the wave can be analyzed. The five instants from A to E are visualized with the corresponding snapshots of the interface. In A, the monitoring surface reports a high average void fraction close to 1, indicating the passage of a large gas bubble. This is indeed observed in snapshot A, which shows the rise of the bubble right after its formation. The signal then drops to 0 in B and, as the reader can see from the snapshot, the bubble has already passed and splashed above, and slag is mainly momentarily present in the monitoring position. At the consecutive instant C, a second bubble appears. However, a lower value of void fraction is tracked and a clear bubble structure is not observed as in A. This phenomenon is common in this type of injections and has already been observed and discussed by the authors in References 20, 36. When a large bubble detaches from the lance tip and rises up towards the bath surface, an area of relative depression is formed in the rear wake and the upcoming injected gas is sucked in and therefore accelerated. Flowing into the wake, this gas is unable to form a real bubble, as one can see from the condition at C. After the detachment of this secondary stream in D, a main large bubble is formed again at instant E, confirmed by the high value of the tracked void fraction and the corresponding snapshot. The described mechanism of bubble detachment completes a period of injection which is repeated cyclically over time. With this explanation in mind, \(f_2\) appears to be the main bubble frequency, whereas \(f_1\) identifies the secondary phenomenon of gas embedding in the bubble wake. Frequencies in the range of 2 to 3 Hz are indeed known from practice. Player[41] reported measured bubble frequencies of 2.89 to 3.5 Hz for a pilot-scale Lead Isasmelt and of 2.3 Hz for a commercial-scale Copper Isasmelt. The frequencies were measured by monitoring the gas pressure in the lance, which fluctuates with the formation and collapsing of the bubbles, in line with the behavior calculated and observed in the present work.

Fig. 6
figure 6

Frequency spectrum of the bubble detachment for the no-swirl configuration. The spectrum is fitted with a Gaussian function in order to detect the main frequencies

Full size image
Fig. 7
figure 7

Frequency spectrum of the bubble detachment for the swirl configuration. The spectrum is fitted with a Gaussian function in order to detect the main frequencies

Full size image

.

Fig. 8
figure 8

Overview of the mechanism of bubble formation. The five statuses from A to E describe the mechanism and define one period of the recorded time signal of the void fraction. The dotted black line indicates the location of the monitoring surface

Full size image

The mechanism of bubble formation is identical for the swirl case. The presence of the swirling component in the gas flow has a small effect on the bubble frequency, which is reduced by about 0.5 Hz compared with the no-swirl case. Since the injected axial volume flow is kept constant in the two configurations, larger differences were not expected. However, this slight reduction can be related to the transport of axial velocity in the tangential direction. In fact, the bubbles formed in the swirl configuration are larger and less deep than those in the no-swirl configuration, as shown in Figures 5(a) and (b).

Slag Splashing

The splashing of the slag above the free surface is analyzed by evaluating the Splashing Domain (SD), a parameter already defined and used by the authors in References 19, 21. The definition of SD is based on the time-averaged distribution of the slag volume fraction. This represents the probability of finding slag or gas in a specific location during the time of observation. A value of 1 in a volume cell indicates that the slag phase has occupied that volume for 100 pct. of the elapsed time, and 0 pct. for a value of 0. That said, SD is defined as the volume in m3 above the initial bath level which has a probability of between 0.5 and 100 pct. of being occupied by slag during the 20 seconds of observation. It is calculated by blanking the domain for \(Z < 0.6\) m and \(\alpha _{slag} < 0.005\) and computing the integral volume. For the no-swirl case, a \(SD = 0.088\) m3 was calculated, compared to a \(SD = 0.078\) m3 for the swirl case, with a reduction of more than 11 pct. Figures 9(a) and (b) show a visual representation of SD for the two configurations. The splashing is clearly less intense in the presence of the swirler. The central region close to the lance is less occupied by the slag and, moreover, the height of the splashing region is also lower than in the no-swirl case.

Fig. 9
figure 9

Visual representation of SD for (a) the no-swirl and (b) the swirl configurations

Full size image

As can be seen from the distributions, slag droplets can reach to the top of the furnace, and in the no-swirl configuration they also reach the exhaust duct. The cause of these different splashing phenomena is undoubtedly to be found in the different nature of the gas bubbles created in the slag bath. As previously observed, while in the no-swirl configuration the bubbles elongate, penetrating deep into the bath, in the swirl configuration they tend to lose energy in the axial direction, and consequently develop more in the radial direction, making them larger but less powerful. Since splashing is generated by the rupture of these large gaseous bubbles,[42] the difference in splashing intensity is a direct consequence.

This violent slag splashing, capable of reaching the roof and the exhaust ducts, is well known from practice in TSL furnaces. In its description of the operational performance of the Isasmelt Phelps Dodge Miami Mining Smelter, Voltura includes splashing among the major issues to be addressed, as a cause of accretions in the off-gas hood.[43] The installation of a splash-block panel helped to prevent the deterioration of the off-gas boiler and therefore increase the campaign life from 20 to 36 months, bringing the campaign throughput up to 2,000,000 t. Fundamental knowledge of this phenomenon is therefore crucial for efficient furnace operations and simulation tools can be beneficial to develop expertise.

Gas–Slag Interface Area

The interface area between the gas and the liquid slag is a crucial aspect of the multiphase flow in the TSL process. Due to the intense downward gas injection, the bath is strongly agitated and the interface is developed in four main modes: the free surface of the bath, the main bubble at the lance, the gas entrainment in the bath and the splashed droplets. The interfacial heat and mass transfer are therefore strongly enhanced, giving the TSL process high reaction rates and throughput compared to other furnace technologies.[1,2,4,44] Despite its relevance, it is difficult to measure this contact area in real furnaces and it is only possible to make estimations, based on the bubble frequency and the conversion rates.

CFD modeling allows the overall interface area to be directly tracked during the simulation time. As already mentioned, the interface is identified with an iso-surface at \(\alpha _{slag} = 0.5\) and its surface integral is monitored over time with a frequency of 100 Hz. The plot in Figure 10 displays the temporal evolution of the interface area for the two configurations studied. At \(t = 0\) seconds the bath is in contact with the gas over a surface of 0.125 m2. As soon as the lance injection starts, the contact area increases by more than ten times in less than 1 seconds, for the reasons cited above, and then oscillates around more or less stable values. Averaging over a time range of 20 seconds, it is found that for the no-swirl configuration \(A_i = 1.4405\) m2 and for the swirl configuration \(A_i = 1.3675\) m2. That means a reduction of around 5 pct. when including the swirler for the air jet. This result might be counterintuitive, but it is justified by the reduction in the splashing, as discussed before, and therefore in the contribution made by the slag droplets above the bath.

Fig. 10
figure 10

Time development of the integral slag-gas interface area

Full size image

Rotational Sloshing

When the bubble detachment at the lance enters into resonance with the oscillation of the bath’s free surface, a condition of synchronism between the two motions is established. In cylindrical vessels, as for the TSL furnace, this leads to self-maintained rotational sloshing waves. The phenomenon is well known from the literature on gas injection[45,46,47] and from practice.[4,41] It is a major issue to be addressed during the design of the furnace, since these waves translate into continuous displacements of tons of liquid slag, that subject the support structure of the furnace to enormous stresses.

The rotational sloshing in TSL baths has already been investigated by the authors in Reference 21, and the same analysis method is used here in order to track the dynamics of the slag bath waves. In brief, the idea is to track the Center of Mass (CoM) of the slag phase over time, by monitoring its position with a User-Defined Function (UDF). As explained in the Reference 21, the CoM follows the location of the wave, considering that the slag is displaced towards the slope incline. Figures 11(a) and (b) show the position of the slag CoM in the XY plane over time. Although the paths may seem chaotic, circular motions can be identified for both configurations, suggesting the presence of sloshing in the bath. It is interesting to note, that the intensity of the CoM displacement clearly increases for the swirl configuration, meaning that there is a higher wave amplitude. This is expected, since the presence of the swirler in the lance is a source of axial momentum in the bath, in addition to that arising from the condition of synchronism.

Fig. 11
figure 11

Position of the slag CoM in the XY plane over time for (a) the no-swirl and (b) the swirl configurations

Full size image

In his experimental investigations on the Copper Isasmelt process, Player observed the presence of a resonance condition between the bath and the bubble plume and estimated the frequency of the slope wave at 1.14 Hz, which he found to be half the bubbling frequency.[41] In the present work, the sloshing frequency of the bath can also be calculated using the tracked data for the CoM motion. Figures 12(a) and (b) show the temporal evolution of \(\Theta \), the angular position of the CoM, which locates the angular position of the bath waves in both configurations studied. By applying a FFT to this signal and fitting the spectrum to a Gaussian function with the NLLS method, it is possible to identify the frequency of the rotational wave. Figure 13 shows the result for the no-swirl configuration, with a \(f_{wave} = 1.217\) Hz. Figure 14 shows the result for the swirl configuration, with a \(f_{wave} = 1.199\) Hz. These frequencies, based on CFD calculations, are in the range of that estimated by Player for a real process,[41] and, also in agreement with his investigation, around half the corresponding bubble frequencies. Beyond giving weight to the validity of the VOF simulations in the present work, the result confirms the synchronism between the bubbles and free surface.

Fig. 12
figure 12

Angular position of the slag CoM over time for (a) the no-swirl and (b) the swirl configurations

Full size image
Fig. 13
figure 13

Frequency spectrum of the bath wave for the no-swirl configuration. The spectrum is fitted with a Gaussian function in order to detect the main frequency

Full size image
Fig. 14
figure 14

Frequency spectrum of the bath wave for the swirl configuration. The spectrum is fitted with a Gaussian function in order to detect the main frequency

Full size image

As indicated above, the presence of rotational waves induces an indirect swirl motion in the bath. Figure 15(a) and (b) show contour distributions of the time-averaged swirl velocity in the liquid phase for the two configurations studied. The averaged interface is also shown in green, to help visualize the bath boundaries. The rotational motion clearly develops in the upper part of the bath and around the bubble area in both cases. There, the effect of the waves is indeed stronger. However, in the swirl configuration it extends to the bottom of the furnace. By calculating the volume average of these distributions, the time-averaged swirl velocity of the slag phase can be quantified in 0.0185 m/s for the no-swirl configuration, and 0.0345 m/s for the swirl configuration. The presence of a swirler in the air lance induces a rotary motion in the bath of twice the intensity of the configuration without it, which translates into an improvement of the mixing rate. This result again highlights that the swirler has an important effect on the hydrodynamics of the multiphase system, in addition to its major role in cooling the lance.

Fig. 15
figure 15

Contour distribution of the time-averaged swirl velocity in the slag phase for (a) the no-swirl and (b) the swirl configurations

Full size image

Bath Mixing and Recirculation Patterns

The bath mixing is analyzed by injecting a liquid tracer with same physical properties as the slag into the melt and tracking its distribution over time.[19] Although the elapsed time of the simulations is not sufficient to reach a final homogeneous concentration in the bath, it is still possible to evaluate the trends for both configurations. In the plot of Figure 16, the local maximum mass fraction of the tracer is reported over time.

Fig. 16
figure 16

Time development of the maximum of tracer mass fraction in the slag bath

Full size image

When mixing is completed, this quantity should be the same in both cases and equal to the homogeneous concentration \(mass_{tracer}/mass_{bath}\). The higher mixing efficiency of the swirl configuration is indicated by the faster drop of the curve. The same information is visually reported in Figures 17(a) and (b), where a snapshot of the tracer distribution at \(t = 24\) seconds is shown for the two cases.

Fig. 17
figure 17

Contour distributions of the tracer mass fraction \(w_{tracer}\) for (a) the no-swirl and (b) the swirl configurations

Full size image

The tracer in the bath is more strongly non-uniform in the case of the no-swirl configuration, whereas a more homogeneous distribution is developed in the swirl case. One reason for this difference is undoubtedly the previously discussed rotating bath motion, which is induced by the sloshing and more vigorous with the air swirler. Secondly, the continuous detachment and rising of the bubbles produces recirculation cells in the toroidal direction of the bath. When the bubble rises up, the surrounding liquid is dragged upwards and, at the same time, other liquid is sucked from the bottom into the bubble wake and hence replaced with liquid from adjacent areas.[19,20] These vortex structures are shown in Figures 18(a) and (b) with the visualization of time-averaged streamlines in the slag phase. In both configurations, the eye of the recirculation cells lies quite high in the bath, sustained by the bubble plume activity. Whereas in the swirl configuration, the vortexes develop entirely in the vessel, secondary recirculation regions are spotted in the bottom of the furnace for the no-swirl configuration. These stagnant areas are hidden from the main liquid recirculation. As a consequence, if the tracer enters these secondary vortexes, the achievement of a uniform mixing is limited.

Fig. 18
figure 18

Time-averaged recirculation cells, visualized with the streamlines for (a) the no-swirl and (b) the swirl configurations

Full size image

Exhaust Gas Flow

Besides the dynamics of the slag bath, the off-gas flow is another important aspect of the fluid dynamics of TSL furnaces. It directly interacts with many features of the process, such as the slag splashing, accretions at the roof, the lance entry system, and the feedstock stream. Figures 19(a) and (b) show a series of Z-normal slices above the bath for the two configurations, where the time-averaged axial component of velocity is reported. In both cases, the flow has a nearly perfect axial symmetry inside the furnace. Closer to the bath, the gas flows close to the lance and then homogenizes in the furnace, also due to the restriction of the diameter. No differences are observed between the two configurations, since the swirl velocity component which is present in the swirl configuration is entirely eliminated in the multiphase interaction with the liquid slag and the gas rises straight up.

Flow asymmetries appear at the top of the furnace, where the exhaust gases flow to the laterally displaced offtake. Although this detail might seem obvious, it is in fact an important issue in the industrial practice. Because of such flow asymmetries, the lance can be subjected to high local thermal gradients, since the upcoming flow is hotter than the furnace atmosphere. Added to the mechanical stresses of the bath, this leads to lance bending and “banana-shaped” lances. To avoid this, industrial solutions have been developed to continuously rotate the lance around its axis, leveling out its thermal exposure to the offgases.[48] The CFD study by Gwynn-Jones et al. also reviews several technological solutions for the offtake system of industrial furnaces, with the aim of enhancing the lance performance.[30]

Fig. 19
figure 19

Time-averaged axial velocity plotted on Z-normal slices for (a) the no-swirl and (b) the swirl configurations

Full size image

Summary and Conclusions

The bath dynamics of the pilot-scale TSL furnace operating at TU Bergakademie Freiberg were investigated here by means of CFD simulation. The study focused on top gas injection in a real slag bath, whose physical properties were experimentally measured.[36] The modeling approach is based on the VOF model, which allows the slag–gas interface to be directly tracked during the simulation. This is a great advantage of this method, since many physical phenomena of the process can be reproduced and investigated in depth. Two setup configurations were compared, with or without the air swirler, and the results provided interesting information on the behavior of the slag bath.

The key outcomes of the study can be summarized as follows:

  • This work is a continuation of previous studies by the authors on the TSL furnace technology.[19,20,21,33,36,49] The advancement of mathematical modeling is of great importance to fully understand pyrometallurgical reactors and for them to be integrated into the new technological processes of the circular economy of metals. This investigation demonstrates the capabilities of a highly resolved VOF simulation for the numerical characterization of a pilot-scale furnace.

  • The numerical analysis showed promising results that are in line with knowledge on TSL furnaces gained in practice. The CFD-calculated bubble frequencies are in the range of 2.5 to 3 Hz, close to those measured by Player in a pilot and a commercial-size Isasmelt.[41] Similar agreement is achieved regarding the sloshing waves at the bath’s free surface. The CFD model is able to detect such phenomena with a frequency of around 1.2 Hz, half the frequencies of the bubble detachment. As estimated by Player,[41] and directly observed here from the interface evolution, this relation is the result of the synchronism between the bubbles and the sloshing free surface. By directly observing the flow fields, the mechanisms that govern these phenomena can be visualized and fully understood here, adding value to the empirical knowledge of the furnace.

  • The comparison of two setups, no-swirl and swirl configurations, showed the effect of the lance swirler on the hydrodynamics of the slag bath. The swirler is often included in the lance to enhance heat transfer. The main goal of these helical vanes is indeed to increase the \({O_{2}}\)/fuel mixing before combustion and cool down the lance more efficiently, favoring the formation of a protective solid slag layer from the furnace side.[34] However, relevant consequences on the hydrodynamics of the slag bath are observed and discussed here:

    1. 1.

      The process of bubble formation differs qualitatively between the two cases. In the no-swirl configuration, the bubbles assume an elongated shape, penetrating deeply into the bath, whereas in the swirl configuration, they inflate in the radial direction, taking on an almost spherical shape. The evolution of these two bubble types consequently leads to differences in the bath dynamics, observed by looking at other flow features.

    2. 2.

      The presence of the swirler slightly reduces the bubbling frequency from 3.05 to 2.46 Hz. This can be precisely explained by the different processes of bubble formation. When the gas flow has a swirling component, the axial velocity is also transported in the tangential direction, hence part of it is dissipated. As a consequence, the bubbles are larger and detach at a lower frequency.

    3. 3.

      Another phenomenon linked to the differences in bubble shape is the reduction of slag splashing above the bath. In fact, splashing originates from the bubble collapse. Once the bubble reaches the bath surface and the cavity opens up, the slag at the rim of this structure is spouted upwards in the furnace. As explained above, bubbles formed in the swirling lance lose part of their axial energy, hence they are followed by less intense splashing, with a SD reduction of about 11 pct. However, in both cases this phenomenon is quite violent and the slag droplets reach the top of the furnace and the exhaust pipes. This is a well-known issue in TSL furnaces, and if it is not managed, can significantly reduce the productivity of the process.[43]

    4. 4.

      From the analysis of the slag-gas interface area it is found that reducing the splashing also diminishes the contact area by about 5 pct. This is a crucial parameter of the process, since it determines the kinetics of the multiphase transport phenomena.

    5. 5.

      The free surface sloshing waves are tracked by monitoring the CoM of the slag phase. The induced rotational velocity in the liquid phase is found to be almost double in the presence of the air swirler, with a direct positive effect on the bath mixing efficiency. Whereas intense sloshing is not desired, to avoid the refractory lining being washed out, moderate sloshing is required for the stirring action.[34,50]

    6. 6.

      A final analysis of the exhaust gas flow shows no differences between the two configurations, indicating that the tangential velocity component generated in the swirler is entirely dissipated in the multiphase interaction with the slag bath.

    7. 7.

      The insertion of helical vanes in the air lance gives the process an overall hydrodynamic advantage, besides the improvement of the heat transfer. A part from a slight reduction in the interface area, bath mixing is highly favored and splashing intensity decreased. The achievement of these goals can significantly extend the campaign life and throughput.[43]

  • It should be noted that the present CFD study on the pilot TSL furnace has been performed under the assumptions of an iso-thermal and non-reactive system. In spite of this, the results have shown the validity of the method and lay the foundations for future developments, specifically concerning heat exchange and interphase transport phenomena. Furthermore, a potential for new research is the consideration of fluid-solid interactions, such as those in the feedstock stream or in the generation of magnetite in the bath.