1 Introduction

Precipitation-strengthened Co–Al–W-based alloys exhibit superior high-temperature strength compared to conventional carbide and solid-solution-strengthened Co-based alloys. Their strength even exceeds that of some precipitation-strengthened Ni-base superalloys.[1,2,3] Thus, they are regarded as potential structural materials for future turbine engine applications.[4,5,6] Although this new alloy system was rediscovered just over 1 decade ago,[4] the knowledge regarding the effect of alloying elements,[7,8,9,10,11] oxidation,[12,13,14] and thermodynamic,[15,16,17,18] microstructural,[3,19,20] and mechanical properties[2,21,22,23] has significantly increased since then. Despite the growing understanding, there are still open questions regarding this new class of alloys.

Tantalum is an indispensable alloying element for the development of high-strength Co-based superalloys. It increases the γ′ solvus temperature, the γ′ volume fraction, and according to ab-initio simulations the superlattice intrinsic stacking fault energy of γ′ and, therefore, the strengthening effect of the γ′ precipitates.[7,8,21,24,25,26,27] However, it is not clear how much Ta can be alloyed. High contents of Ta lead to enhanced microsegregation during solidification. It lowers the microstructural stability, which results in the formation of deleterious secondary phases during heat treatment or creep.[8,9,22,28] Most of the experimental investigations on the thermodynamic and microstructural properties so far are confined to temperatures below 1100 °C and to alloys of the composition range Co–(7–10)Al–(7–10)W–(1–2)Ta (all the alloy compositions throughout the text are given in atomic percent) with relatively high γ′ volume fractions.[7,8,29,30] Recently, Epishin et al. investigated alloys with higher Ta contents of up to 4 at. pct.[31] Detailed investigations on the Co–Al–W,[32,33,34] Co–Al–W–Ni,[15,35,36] Co–Al–W–Ti,[10,37,38] and Co–Al–W–Ge[39] system exist, however, more data beyond the investigated temperature and composition range of the Co–Al–W–Ta system are needed for the calculation of phase diagrams and the development of multicomponent Ta-containing Co-based alloys.

Regarding engineering applications, the thermal expansion behavior of the Co-based superalloys is also important. For example, matching of the thermal expansion coefficients of the involved materials over a large temperature range is an important criterion in the development of oxidation protection coatings. From previous investigations, it can be concluded that the thermal expansion coefficients of Co-based superalloys are strongly influenced by the γ′ dissolution processes at higher temperatures.[11,30,40]

Additionally, little is known about the influence of an increasing fraction of the γ′ precipitate phase. In this study, a series of single-crystalline (SX) Co–Al–W–Ta alloys was designed on a tie-line between the pure γ matrix and the γ′ precipitate compositions to obtain microstructures with different γ′ volume fractions from 0 to 100 pct. This enables the investigation of the microstructure as well as the thermodynamic and thermophysical properties of the Co–Al–W–Ta alloys as a function of the γ′ volume fraction with the same chemical and physical properties of the constituent phases. In a previous publication,[41] we already presented the creep properties of these alloy series. We found that the strengthening contribution of the γ′ phase correlates with its volume fraction, that is, an increasing γ′ volume fraction provides a higher strengthening contribution and, subsequently, a higher creep resistance.

2 Experimental Methods and Materials

2.1 Alloy Design

A series of Ta-containing Co-based alloys with different γ′ volume fractions was designed. The alloy ERBOCo-2Ta (Co–9Al–7.5W–2Ta), an already investigated alloy,[42,43] served as a starting point for this development. Atom probe tomography (APT) was performed to obtain the quantitative compositions of the γ matrix and the γ′ precipitate phase of this alloy after a heat treatment at 1300 °C for 12 hours and 900 °C for 200 hours. The compositions of the γ and γ′ phases at 900 °C derived from APT are listed in Table I as γERBOCo-2Ta and γ′ERBOCo-2Ta and were used to draw the schematic Co-(Al,W,Ta) pseudo-binary phase diagram in Figure 1. The nominal compositions of VF0 and VF100 equal the measured γ and γ′ compositions of ERBOCo-2Ta, respectively. As indicated by the red tie-line in Figure 1, the alloys were designed with the aim to vary the γ′ volume fraction systematically in the steps 0, 20, 40, 60, 80, and 100 pct. According to the lever rule, the compositions of the alloys containing different γ′ volume fractions fγ′ at 900 °C are designed by the following equation:

Table I Nominal and Measured (SEM-EDS) Compositions in Atomic Percent of ERBOCo-2Ta and the ERBOCo-VF Alloy Series
Full size table
Fig. 1
figure 1

Schematic pseudo-binary phase diagram of the Co-(Al,W,Ta) system. The red tie-line at 900 °C indicates how the alloy series was designed (Color figure online)

Full size image
$$ C_{\text{Alloy}} = \left( {1 - f_{{\gamma^{\prime}}} } \right)C_{\gamma }^{i} + f_{{\gamma^{\prime}}} C_{{\gamma^{\prime}}}^{i} $$

where Cγ and Cγ′ are the concentrations of the element i (i = Co, Al, W, and Ta) in the γ and γ′ phases, respectively. According to Murakumo et al.,[44] the γ and γ′ phases in the ERBOCo-VF alloys should have the same compositions as the γ and γ′ phases in ERBOCo-2Ta, respectively. However, this only holds true as long as the alloys exhibit a two-phase microstructure and no additional phases form. Otherwise, the compositions of γ and γ′ might vary slightly. The compositions of the six experimental alloys were determined by calibrated energy-dispersive X-ray spectroscopy (EDS) in a Zeiss Cross Beam 1540 EsB and are listed in Table I in comparison to the nominal composition. The alloys are referred to as their intended γ′ volume fractions, for example, ERBOCo-VF20 represents the alloy with an intended γ′ volume fraction of 20 pct. For simplicity, the alloy designations are used without the prefix ERBOCo hereafter in the text.

The experimental alloys were produced by a two-step casting process. First, both the γ and γ′ master alloys were manufactured by MaTeck GmbH (Jülich, Germany) using raw elements of 99.9 wt pct purity. Afterward, by mixing different contents of the master alloys, single crystals of the previously introduced ERBOCo-VF alloys with a length of 120 mm and a diameter of 12 mm were cast in a laboratory scale Bridgman unit (Reference 45 provides further details).

2.2 Modeling and Experimental Procedure

The phase transformation temperatures were characterized by differential scanning calorimetry (DSC) using specimens that were heat treated at 1300 °C for 12 hours and subsequently aged at 900 °C for 200 hours. The measurements were carried out on a Netzsch DSC 404 F1 with a heating and cooling rate of 20 °C/min in the range of 25 °C to 850 °C and 5 °C/min in the range of 850 °C to 1500 °C. Heat treatments at temperatures between 1350 °C and 1390 °C for 24 hours were conducted to homogenize the cast bars. Since higher temperatures did not improve the homogeneity (refer to Figure S1 of the electronic supplementary material), 1350 °C was chosen as the temperature for solution annealing of the alloys. Subsequently, all alloys were additionally aged at 900 °C for 100 hours. This two-step heat treatment was conducted under vacuum and furnace cooling. Additional long-term heat treatments in vacuum, followed by water quenching, at 900 °C, 950 °C, 1000 °C, and 1050 °C for 1000 hours were performed to investigate the microstructural stability. After a standard sample preparation, the as-cast and heat-treated microstructures were characterized by a Zeiss Cross Beam 1540 EsB. The chemical composition and crystallographic structure of secondary phases were measured by calibrated EDS and electron backscattering diffraction (EBSD) in the same Zeiss Cross Beam 1540 EsB. The EBSD experiments were carried out by a Nordlys II EBSD detector and analyzed by the HKL Channel Six software package. The area fraction of the phases was determined using image analysis on at least five representative images with ImageJ.[46] The measured γ′ area fraction was stereographically corrected to calculate the γ′ volume fraction according to Reference 47, assuming that all precipitates are rectangular, have the same size, and are evenly distributed.

For the investigation of thermal expansion, cuboidal samples with edge lengths of about 7 mm were cut by spark erosion from heat-treated cast bars. Temperature-induced strains were recorded between − 170 °C and 1340 °C using a commercial inductive dilatometer type DIL 402 C from Netzsch. The entire temperature range was covered by two different experimental setups. At low temperatures (− 170 °C to 400 °C), a furnace with resistance heater, liquid nitrogen cooling system, thermocouples of type E, and a sample holder made of fused silica was employed. The high-temperature setup (30 °C to 1340 °C) included a furnace with SiC heating element, thermocouples of type S, and a sample holder made of corundum ceramic. Both systems were first calibrated using rod-shaped standard samples from Netzsch made of fused silica or corundum ceramic, respectively. All experiments were carried out with heating/cooling rates of 2 °C/min in a He purge gas atmosphere at a flow rate of about 2 L/h. All measurements were repeated at least twice to check for reproducibility. Thermodynamic calculations were carried out by the CALPHAD method[48,49] using the ThermoCalc (TC) software package with the updated TCNI9 (v9.1) database.

3 Results

3.1 As-Cast Microstructure

The as-cast alloy compositions are given in Table I. The actual compositions are generally consistent with the nominal contents, but the Al and Ta contents in all alloys are slightly lower than the designed ones with an increasing deviation from VF0 (~ 0.4 at. pct) to VF100 (~ 1 at. pct). The difference in the Al and Ta contents between the nominal and measured compositions may be caused by an evaporation loss during fabrication, macrosegregation, or the difficulties in separating the EDS signals of W and Ta.

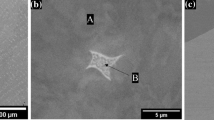
The primary dendrite arm spacing is similar among all alloys and varies from 200 to 250 µm. A γ single-phase microstructure is found in as-cast VF0 and VF20 (Figures 2(a) and (b)), while a small number of intermetallic precipitates with light gray contrast are occasionally observed in the interdendritic regions of VF40 (insert in Figure 2(c)).

Fig. 2
figure 2

As-cast microstructure of the ERBOCo-VF alloy series. (a) through (f) VF0-VF100 with (c) through (f) insets of higher magnifications

Full size image

VF60, VF80, and VF100 show a pronounced fraction of interdendritic phases with light gray contrast (Figures 2(d) through (f)). In addition to the eutectic-like structure, another interdendritic phase with white contrast was formed, which is enveloped by the light gray phase in VF100 (Figure 2(f)). This indicates that a peritectic reaction occurs during the final stages of solidification. According to EDS and EBSD measurements, these interdendritic phases with light gray and white contrast are most likely C14-Laves (Co2Ta) phase and D85-μ (Co7W6) phase, respectively, which fits with the calculated crystallographic structures that exist in the Co–Al–W–Ta system (Table II) and with the reported Co–Al–W–Ta, Co–Ta, and Co–W systems.[29,50,51] The reasons for the intermetallic phase formation are the high levels of W and Ta and the strong segregation of Ta to the interdendritic regions during solidification.[28] The presence of W- and Ta-rich interdendritic phases is also observed in the as-cast state of other alloys containing high W and Ta contents, for example, Co–9Al–10W–2Ta and Co–9Al–10W–4Ta.[8,28] The area fractions of the Laves and µ phases in the interdendritic regions of the ERBOCo-VF alloys are listed in Table III.

Table II Calculated and Experimentally Observed (After Short-Term Aging for 100 Hours and Long-Term Aging for 1000 Hours) Phase Constituents at 900 °C
Full size table
Table III Experimentally Observed Area Fractions of Secondary Phases After Solidification in the ERBOCo-VF Alloy Series
Full size table

3.2 Phase Transformation Temperatures

The phase transformation temperatures of the ERBOCo-VF alloy series were experimentally determined by DSC. The DSC curves are shown in Figure 3. The γ′ solvus temperature Tγ′ increases considerably from 864 °C in VF0 to about 1121 °C in VF100 (see Table IV).

Fig. 3
figure 3

DSC curves of the ERBOCo-VF alloy series. (a) Heating and (b) cooling curves (heating/cooling rate 20 °C/min). The arrow indicates the small endothermic (exothermic) peak in the heating (cooling) curve close to the solidus temperature

Full size image
Table IV Phase Transformation Temperatures of the ERBOCo-VF Alloy Series Calculated by TC and Experimentally Measured by DSC and Thermal Expansion
Full size table

The experimentally determined γ′ solvus temperature Tγ′ is in good agreement with the reported data on Co-based quaternary alloys Co–10.1Al–4.9W–1.7Ta,[10] Co–9Al–7W–2Ta,[30] and Co–9Al–10W–2Ta[4,8,21,22] that have similar compositions compared to the present ones. The solvus temperatures of secondary phases, such as Laves and µ, could not be quantified due to their low volume fractions and absent or overlapping peaks in the DSC curves. The liquidus temperature TL decreases continuously from 1463 °C to 1419 °C in VF0-VF100 (Figure 3 and Table IV). The solidus temperature TS is not well defined in VF80 and VF100, which exhibit a small endothermic peak in the heating curves at approximately 1370 °C, as marked in Figure 3(a). The corresponding exothermic peaks exist in the cooling curves at a lower temperature of ~ 1340 °C in VF60 but at similar temperatures in VF80 and VF100 (Figure 3(b)). These small peaks may indicate a solid reaction or liquid transformation, which is likely related to the secondary phase formation in the final stages of solidification of the alloys VF60, VF80, and VF100 (Figures 2(d) through (f)).

3.3 Microstructure After Short-Term Aging

A heat treatment procedure of homogenization at 1350 °C for 24 hours followed by aging at 900 °C for 100 hours was chosen since solution annealing above 1350 °C did not result in a significantly more homogeneous microstructure. The resulting microstructures are shown in Figure 4 and at lower magnifications in Figure 5.

Fig. 4
figure 4

Microstructures of the ERBOCo-VF alloy series after the heat treatment at 1350 °C for 24 h and subsequent aging at 900 °C for 100 h. (a) Pure γ and (b) through (f) γ/γ′ two-phase microstructures

Full size image
Fig. 5
figure 5

Microstructures of the alloys (a) VF60, (b) VF80, and (c) VF100 after heat treatment at 1350 °C for 24 h and subsequent aging at 900 °C for 100 h at a low magnification show that additional phases in VF60 could be solved while μ, χ, and most likely Laves phases remain in VF80 and VF100

Full size image

A single-phase γ microstructure is present in VF0 (Figure 4(a)), while γ/γ′ two-phase microstructures exist in VF20–VF100 (Figures 4(b) through (f)). However, for VF80 and VF100, additional phases form and the γ/γ′ two-phase microstructure exists only locally. Therefore, Figure 5 shows lower magnifications of the same microstructures of VF60, VF80, and VF100. These images indicate that all additional phases of the as-cast state can be dissolved in VF60; however, the Laves and D85-µ phases still remain in VF80 and VF100 (Figure 5(b) and (c)). Additionally, these phases are surrounded by the newly formed D019-χ phase (Figures 5(b) and (c) and inset). The γ′ volume fraction as well as precipitate size increases continuously from VF20 to VF80, while there is no difference in the local γ–γ′ two-phase microstructure between VF80 and VF100 due to the increasing fraction of χ, Laves, and μ phases (Table V), which consume the γ′-forming elements.

Table V Microstructural Details of the ERBOCo-VF Alloy Series After Heat Treatment at 1350 °C/24 h and 900 °C/100 h
Full size table

3.4 Microstructure After Long-Term Aging

In order to investigate the stability of the microstructures, subsequent long-term aging experiments for 1000 hours were performed at 900 °C, 950 °C, 1000 °C, and 1050 °C. The corresponding microstructures of the alloys VF0 to VF100 are shown in Figures 6(a) through (f). At 900 °C, VF0 shows a small number of bulky precipitates that align preferentially along substructures such as dendrites. Assumingly, these bulky precipitates are µ phases, which form due to inhomogeneities in the local composition or defect densities. The alloy VF20 still exhibits a significant fraction of γ′, since the γ′ solvus temperature is not yet reached. Needle-shaped phases of D019-χ type are also present as well as the small bulky phases similar to that in VF0 (presumably µ phases). The alloys VF40 and VF60 exhibit similar microstructures to each other after 1000 hours at 900 °C. The high γ′ volume fraction is preserved, although these precipitates are coarsened. Additionally, a significant amount of χ needles was formed during aging and also some remaining µ phases aligned along inhomogeneities are visible. VF80 and VF100 do not show the formation of any additional phases to those that are already present after the standard heat treatment at 900 °C. However, in VF80, the area fraction of the χ phase is significantly larger at the expense of γ′, µ, and Laves phases, indicating that the equilibrium is not reached after the 100-hour standard heat treatment.

Fig. 6
figure 6

Long-term heat-treated microstructures of the ERBOCo-VF alloy series (a) through (f) after standard heat treatment and subsequent long-term aging at 900 °C, 950 °C, 1000 °C, and 1050 °C for 1000 h

Full size image

At 950 °C, the alloys VF0 and VF20 show a small number of bulky precipitates that align preferentially along substructures such as dendrites. VF20 also precipitates fine needle-shaped phases that are of D019-χ type. Although the γ′ solvus temperature for VF20 is not reached at 950 °C, no visible γ′ precipitates were found via scanning electron microscopy (SEM). VF40 and VF60 exhibit a significant number of needle-shaped phases. Additionally, the γ′ precipitates are coarsened and their volume fraction is reduced. VF80 and VF100 still show µ, Laves, and χ phases besides γ and γ′; however, the Laves phase and the μ precipitates are dissolving, while χ is growing in size and volume fraction. The γ′ phase is also still present but exhibits significant coarsening, and the volume fraction is decreasing. For VF80, the χ phase is mainly present in bulky shapes, while the plate-like or needle shapes are only rarely visible.

After 1000 hours at 1000 °C, no phases besides the γ matrix are present in VF0 and VF20. VF40 shows an increasing amount of χ needles at this temperature. As a result, the formation of χ consumes also γ′-forming elements, and since the heat treatment temperature is approaching the γ′ solvus temperature, the γ′ volume fraction decreases significantly. Similar effects could be found for VF60. The fraction of the χ phase is increasing, while the γ′ fraction is lowered. However, the γ′ fraction is still quite high compared to VF40. Of course, the γ′ precipitates are coarsening in both alloys VF40 and VF60. VF80 still shows a high fraction of γ′ and additionally µ, Laves, and χ. While γ′ and χ are coarsening, the amount of µ and Laves is decreasing further. This is even more pronounced for VF100, where almost all former γ′ regions are covered with χ. Even if the experimentally determined γ′ solvus temperature is not reached, the formation of χ is absorbing the γ′-forming elements, which results in an almost complete disappearance of γ′.

At 1050 °C, VF0 shows no additional phases besides γ. VF20 exhibits a very small number of bulky precipitates as at 900 °C and 950 °C, which might be the µ phase. However, the precipitation of µ can be found locally, so there are also areas that show only γ, as expected. This strengthens the assumption that the formation of these small undesirable phases is the result of local chemical heterogeneities. Significant local differences are also present in VF40 and VF60 after the heat treatment at 1050 °C, as indicated by the split micrograph in Figures 6(c) and (d), bottom. Some sample areas are covered by fine χ needles. In these areas also γ′ is found in VF60. However, there are also regions where a smaller area fraction of coarsened needles can be found. EBSD and EDS measurements revealed that these phases are Laves and χ. VF80 and VF100 exhibit again γ, µ, Laves, and χ after 1000 hours at 1050 °C. However, in VF80, the fraction of the χ phase is significantly higher in the former γ/γ′ regions compared to 1000 °C, resulting in a dissolution of γ′ since γ′-forming elements are consumed.

3.5 Thermal Expansion

In Figure 7(a), the experimental strain ε(T) of VF100 as a function of the temperature is exemplarily shown. All alloys behave similarly. Their strain curves almost coincide below 530 °C, whereas at higher temperatures, a well-reproducible, marked change in the slope occurs (compare Figure 7(c)). The anomaly becomes particularly evident in the first derivative of the strain curve (Figure 7(b)). More precisely, the thermal expansion coefficient α(T) exhibits a relatively sharp maximum close to the γ′ solvus temperature Tγ′, as indicated by CALPHAD calculations and calorimetric experiments (cf. Sections B and F). From VF100 to VF0, that is, with decreasing content of the γ′ stabilizing elements, the peak temperature decreases and the thermal expansion anomaly becomes less pronounced (Figure 7(c) and Table VI). Similar thermal expansion anomalies have been reported in the literature[11,52] for a series of CMSX-4 type Ni- and Co-base superalloys. The authors demonstrated that the temperature of the thermal expansion peak coincides with the γ′ solvus temperature and suggested dilatometry as a highly sensitive probe for the determination of Tγ′.

Fig. 7
figure 7

(a) Temperature-induced strain and (b) corresponding thermal expansion coefficient as first derivative of the strain curve, exemplarily shown for VF100. Additionally, an Einstein model fitted to the strain data at temperatures below 527 °C is shown in red and the dashed line represents the linear fit of the data above the γ′ solvus temperature. (c) Thermal expansion coefficients of the investigated alloys VF0 through VF100

Full size image
Table VI Parameters of the Einstein Model Fitted to the Experimental Strain Data at Low Temperatures (T < 527 °C), Peak Temperature of the Anomaly in Thermal Expansion (Interpreted as γ′ Solvus Temperature Tγ′), and Thermal Expansion Coefficient at High Temperatures (T > Tγ′) as Obtained by a Linear Fit to the Strain Data
Full size table

At lower temperatures, the thermal expansion of the VF alloys is dominated by vibrational contributions; that is, α(T) is proportional to the heat capacity (Grüneisen relation) and, thus, the temperature-induced strain εEM(T) can be described by an integrated form of the Einstein model:

$$ \varepsilon_{EM} \left( T \right) = \varepsilon_{0} + \alpha_{h} \cdot \frac{{\varTheta_{E} }}{{\left( { - 1 + \exp \left( {\varTheta_{E} /T} \right)} \right)}} $$

where T denotes the absolute temperature, ε0 represents the initial strain at − 273 °C, αh is the high-temperature limit of the thermal expansion coefficient and θE denotes the equivalent of the Einstein temperature. The corresponding thermal expansion is then given by

$$ \alpha_{\text{EM}} \left( T \right) = \frac{{\partial \varepsilon_{\text{EM}} \left( T \right)}}{\partial T} = \alpha_{h} \cdot \left( {\frac{{\varTheta_{E} }}{T}} \right)^{2} \cdot \frac{{{ \exp }\left( {\varTheta_{E} /T} \right)}}{{\left( { - 1 + { \exp }\left( {\varTheta_{E} /T} \right)} \right)^{2} }} $$

Corresponding fits of the Einstein model to strain data below 527 °C reveal only minor differences in the thermal expansion behavior at low temperatures, regardless of the γ′ volume fraction (Table VI). The parameters \( \varepsilon_{0} \), \( \varTheta_{E} \), and \( \alpha_{h} \), which are acquired by fitting of the Einstein model to the strain data below 527 °C, are given in Table VI. At temperatures above Tγ′, on the other hand, the thermal expansion is almost constant but exceeds the high-temperature limit αh of the corresponding Einstein model by roughly 40 pct, as indicated by the arrow in Figure 7(b). The high-temperature part of the strain data above Tγ′ was assumed as linear and the thermal expansion coefficient α was, therefore, determined by a linear fit of this region, as indicated by the dashed line in Figure 7(b). The corresponding values are given in Table VI as well.

3.6 Thermodynamic Calculations

The influence of the addition of 2 at. pct Ta on the phase equilibria in the Co–Al–W ternary system is evaluated by TC calculations to provide a general trend for the thermodynamic calculation of the ERBOCo-VF alloy series. The calculated 900 °C isothermal section of the pseudo-ternary (Co + 2Ta)–Al–W phase diagram is shown in Figure 8, superimposed on the Co–Al–W ternary system, adapted from Reference 4. The addition of Ta causes a shift of the γ′ single-phase and the γ–γ′ two-phase regions from the W-rich to the Al-rich side compared to the ternary system. Figure 8 also depicts the composition of ERBOCo-2Ta, which is calculated to be in a three-phase region with γ, γ′, and an additional D019-χ (Co3W) phase in the quaternary system.

Fig. 8
figure 8

Calculated 900 °C isothermal section of the pseudo-ternary (Co + 2Ta)–Al–W–phase diagram by TC software, superimposed with the Co–Al–W ternary phase diagram, adapted from Ref. 4 in gray and the composition of ERBOCo-2Ta marked in red (Color figure online)

Full size image

Figure 9 shows the calculated phase fractions as a function of temperature above 800 °C based on the nominal compositions of the ERBOCo-VF alloy series listed in Table I. The γ and γ′ phases are calculated to be the only equilibrium phases in VF0 and VF20 (Figures 9(a) and (b)), whereas the D019-χ Co3W phase is also present in the other alloys (Figures 9(c) through (f)). However, VF0 and VF20 also show the formation of additional phases, which are most likely µ, during the heat treatment for 1000 hours at 950 °C (Figure 6). Additionally, the χ phase was found in VF20 after 1000 hours at 900 °C, although it could not be calculated (Figure 9(b)). The intermetallic phases B2-β (CoAl), D85-μ (Co7W6), and C14-Laves (Co2Ta) are further calculated to be in equilibrium in VF80 and VF100 (Figures 9(e) and (f)). Their phase fractions and solvus temperatures increase with increasing content of γ′-forming elements. Comparing the experimentally observed phase constituents (mole fractions and volume fractions should be very similar) after long-term aging at 900 °C, 950 °C, 1000 °C, and 1050 °C and the calculated phase fractions, significant differences could be found. For example, the β phase was never experimentally observed in any of the alloys. Additionally, the strong underestimation of the γ′ stability seems to be a major problem during the calculations, leading to different phase constituents at the tested temperatures. This can be seen, for example, for VF40 and VF60 at 1000 °C and 1050 °C, where γ′ can still be found experimentally, while the calculations only show χ and γ to be stable (Figures 9(c) and (d)). Furthermore, it is possible that the increasing content of refractory elements in the alloys with nominally high γ′ fraction causes significantly reduced kinetics. Thus, the equilibrium might also not be reached after a 1000-hour heat treatment. Conversely, it might also be the case that the kinetics are too slow to solve the phases that are present after casting in a reasonable time, although they are not equilibrium phases.

Fig. 9
figure 9

Calculated property diagrams of the ERBOCo-VF alloy series based on their nominal alloy compositions. (a) through (f) VF0-VF100. The γ single-phase region is marked in blue (Color figure online)

Full size image

The calculated equilibrium phase constituents at 900 °C are given in Table II in comparison to the experimental observations after aging for 100 and 1000 hours. It is interesting that the γ phase is calculated to be unstable at 900 °C in VF80 and VF100, resulting in a γ′–χ two-phase equilibrium in VF80 and a γ′–χ–β three-phase equilibrium in VF100 (Figures 9(e) and (f)).

According to these calculations, only VF0 and VF20 are close to the intended alloy design in terms of phase constituents after a heat treatment for 100 hours (compare Figure 1). However, after 1000 hours at 900 °C, every alloy develops additional phases to the ones found after 100 hours and to the calculated ones. The calculated phase transformation temperatures, γ′-solvus (Tγ′), solidus (TS), and liquidus (TL), are listed in Table IV in comparison with the experimentally determined transformation temperatures.

As the levels of γ′-forming elements increase, the γ′ solvus temperature Tγ′ is calculated to increase from 860 °C in VF0 to 994 °C in VF80 and VF100. The solidus temperature TS decreases continuously from 1440 °C to 1254 °C in alloys VF0 to VF100, which narrows the single-phase γ region (highlighted in blue in Figures 9(a) through (e)). Note that the single-phase γ region is reduced to ~ 25 °C in VF80 (Figure 9(e)) and no single-phase γ region exists over the entire temperature range in VF100 (Figure 9(f)). This indicates that the desired single-phase γ solid solution may not be experimentally obtained during the homogenization heat treatment in VF100 and that no γ/γ′ two-phase microstructure can be obtained at an aging temperature of 900 °C, for example. Another important indication from the calculations is that the melting range widens from ~ 30 °C in VF0 to ~ 165 °C in VF100. This indicates an increasing possibility of elemental segregation during solidification and the likelihood of the formation of secondary phases.

4 Discussion

4.1 Development of the γ′ Volume Fraction in the Alloy Series

Compared to the intended alloy design, an increasing γ′ volume fraction is obtained in VF0–VF60 after short-term heat treatment, whereas VF80 and VF100 additionally contain undesired secondary phases as the phase equilibrium in these alloy series is not in a γ/γ′ two-phase region.

VF0 was intended to exhibit a single-phase γ microstructure. As shown in Figure 4(a), this alloy indeed does not form precipitates during the heat treatment at 900 °C and remains a fcc solid solution. The alloy VF20 was designated to have a γ′ volume fraction of 20 pct. The analysis of the micrographs after the aging heat treatment of 100 hours at 900 °C revealed a γ′ area fraction of about 34 pct, which is, assuming a rectangular shape and an even distribution, equivalent to a γ′ volume fraction of 20 pct (Figure 4 and Table V). Due to local heterogeneities of the microstructure, these values might vary locally (Figure 4). Interestingly, with γ′ volume fractions of 50 and 70 pct, respectively, the alloys VF40 and VF60 exhibit a significantly higher volume fraction as they were designed (Figure 4 and Table V), although the measured concentration of the γ′ formers Al and Ta is lower than the nominal content. However, an accurate measurement of the Ta and W contents in the same alloy by EDS is difficult because their peaks overlap. Since the content of W, which is also known to be enriched in the γ′ phase in Co-base superalloys, is slightly higher compared to the nominal composition, the actual ratio of W to Ta might differ from the measured one. Despite these small issues, the alloy design approach was successful as the γ′ volume fraction systematically increases in the VF series. Especially, the alloys VF0 through VF60 do not show additional phases besides γ and γ′ after the heat treatment at 900 °C for 100 hours. Nevertheless, the χ phase appears in these alloys after long-term aging for 1000 hours, which is in agreement with the thermodynamic calculations. It is known from previous investigations that the γ′ phase in Co–Al–W–based alloys can remain stable up to several thousands of hours before secondary phases reach the phase equilibrium due to the very small Gibbs free energy difference between the γ′ phase and other phases[53] and the resulting sluggish phase transformation.[16,17,29,54]

4.2 Comparison of Transformation Temperatures Between Experiments and Thermodynamic Calculation

The experimentally determined γ′ solvus temperature (DSC) significantly rises from 864 °C to 1117 °C in VF0-VF80 with increasing content of the γ′ stabilizing elements W and Ta (Figure 10 and Table IV). The γ′ solvus temperatures acquired by thermal expansion are in very good agreement with the ones identified by DSC (Figure 10 and Table VI). Though slightly higher, the values are actually within the error bars of the DSC results, indicating that thermal expansion measurements are suitable for determining γ′ solvus temperatures.

Fig. 10
figure 10

Schematic pseudo-phase diagram of the Co-(Al,W,Ta) system based on DSC, TC, thermal expansion, and heat-treated microstructure

Full size image

In comparison between the experimental and calculated γ′ solvus temperatures, an obvious deviation is found, as shown in Figure 10. Although a continuous increase of the γ′ solvus temperature from VF0 to VF80 is well estimated, in most cases, the calculated γ′ solvus temperatures are lower than the measured ones, in particular, in VF40 through VF100, with relatively high levels of alloying additions. This discrepancy between calculated and measured γ′ solvus temperatures of alloys with Ta addition was also reported by Lass.[18] The limited experimental data available on Co-based alloys with high W and Ta content may partly be the reason for the larger deviation of calculations and experiments in VF80 and VF100 compared to that in VF0, although TCNI9 is an updated thermodynamic database with more experimental input from Co-rich compositions. The lack of applicability is possibly due to the less accurate description of the Co–W–Ta and Co–Ta systems. For example, the recently measured thermodynamic data in the Co-Ta system show that the calculated metastable γ′-Co3Ta phase is stable up to 2000 °C.[51] Similarly, the trend of a decreasing solidus temperature TS with increasing γ′-forming element content is calculated well by thermodynamic calculations, but the calculations overestimate the reduction of TS by up to 100 °C (Figure 10). Nevertheless, the experiments and calculations reveal that although the addition of Ta significantly increases the solvus temperature Tγ′ and stability of γ′, it also substantially decreases the solidus temperature TS. Furthermore, Ta enlarges the freezing range and enhances the microsegregation to the interdendritic region during solidification, which agrees well with the literature.[8,21,28] This negative effect has been shown to promote the formation of deleterious secondary phases, which remained after homogenization and aging heat treatment in the alloys VF80 and VF100 similar to the alloy Co–9Al–10W–4Ta.[8] The calculations also show the presence of further intermetallic phases; however, the types of intermetallic phases differ from the ones that are experimentally observed after 100 hours. For example, the increasing probability for the formation of additional intermetallic phases with increasing γ′-forming element content, as described previously, is consistent with the expected phase equilibrium in the calculated (Co + 2Ta)–Al–W isothermal section at 900 °C (Figure 8). As marked in red, the base alloy ERBOCo-2Ta is predicted not to be in the γ/γ′ two-phase region and also small changes in the chemical composition would not shift it to the γ/γ′ phase field.

Additionally, for instance, the D019-χ phase was calculated to be present in all the alloys VF40 through VF100 at 900 °C, but this phase was not found in VF40 and VF60 after the heat treatment for 100 hours. However, after the additional long-term heat treatments for 1000 hours at 900 °C, χ phases could be identified, which suggests that the equilibrium is not reached after just 100 hours. This is also the case for the heat treatment at 950 °C, 1000 °C, and 1050 °C for 1000 hours.

4.3 Anomalies of the Thermal Expansion Behavior

In the alloys investigated here, the dissolution or precipitation of the γ′ phase is always associated with a significant positive contribution to the thermal expansion (Figure 7), which was also observed in other Co- and Ni-based superalloys.[11,40,52] Surprisingly, such an effect, even though a weaker one, also occurs in VF0, which indicates that at low temperatures, VF0 does not have a single-phase microstructure in equilibrium. During slow heating in the dilatometer, precipitation of γ′ starts at about 700 °C in VF0 samples, before the precipitates have dissolved again at the γ′ solvus temperature of 881 °C. A similar but weaker effect is also observed in VF20. It is further remarkable that on the timescale of the dilatometer experiment, the transition from the quasi-static nonequilibrium to the dynamic equilibrium state takes place at relatively low temperatures between 700 °C and 900 °C. Such transitions could be responsible for the discrepancies between the experimentally observed thermal expansion coefficients above the γ′ solvus temperature and the high-temperature limit αh of the fitted Einstein model (Section III–E).

Based on their studies on CMSX-4 type alloys, Horst et al.[52] suggested two major contributions to the thermal expansion anomaly as a consequence of temperature-induced variations of the γ/γ′ volume ratio: changes in the unit cell dimensions of both γ and γ′ phases and an effect of the lattice misfit. However, the latter contribution can now be excluded, as the thermal expansion anomaly is quite similar for Ni-base superalloys with negative constrained lattice misfit and Co-base ones investigated in this work with positive lattice misfit.[42] It should be noted that an additional contribution of the secondary phases to the thermal expansion cannot be excluded, especially in the alloys VF80 and VF100 that exhibit the strongest anomaly (Figure 7(c)) and the highest amount of such phases. On the one hand, the peak maximum close to the γ′ solvus temperature suggests that the anomaly in the coefficient of thermal expansion (CTE) directly correlates with the γ′ phase. On the other hand, the stronger anomaly in VF80 and VF100 might also be related to the dissolution of the χ phase. This occurs in the temperature range between 1050 °C and 1350 °C, as indicated by the long-term heat treatments at 1050 °C (Figure 6), and the additional solution heat-treatment experiments, as shown in Figure S1 of the supplementary materials. This is further supported by the TC calculations, as shown in Figure 9, which give a solvus temperature of the χ phase of about 1150 °C for VF80 and VF100, which is close to the peak temperatures observed in DSC and thermal expansion experiments (Table IV). Therefore, we assume that the pronounced anomaly in these two alloys is related to both the γ′ and χ phases; however, a quantification or separation of both was not possible. Moreover, also changes of the magnetic properties of the alloys might affect their thermal expansion behavior. While the VF alloys are likely to be ferromagnetic at room temperature, there is a transition to paramagnetic behavior in the investigated temperature range. Sato et al.[55] showed that the Curie temperature of binary Co–W alloys with a W content similar to the VF alloys is in the temperature range where we observe the peak in the thermal expansion coefficient. However, the ferro- to paramagnetic transition usually does not lead to a peak but to a steplike increase of the CTE. It might be possible that the differences between αh (as obtained from the fit of an Einstein model below the peak) and the experimental α above the peak are related to this transition. Clarification of this hypothesis will be part of future investigations.

Contrary to the findings in Reference 40, no decreasing thermal expansion coefficient with an increasing γ′ solvus temperature could be found. However, the mean thermal expansion coefficients up to 1000 °C are within the range of the values found for the Ni-base superalloy Rene N5 in Reference 40, indicating that the Co-base superalloys investigated during this work are also suitable for combination with TBC coatings in terms of spallation and delamination.

5 Conclusions

A set of six Co–Al–W–Ta alloys with intended compositions along the γ–γ′ tie-line at 900 °C were designed to contain different γ′ volume fractions based on the phase composition of the alloy ERBOCo-2Ta, that is, Co–9Al–7.5W–2Ta.[42] The microstructural, thermodynamic, and thermophysical properties were investigated. The following conclusions can be drawn.

  1. 1.

    After solution annealing and short-term aging for 100 hours at 900 °C, γ single-phase or γ–γ′ two-phase microstructures are present with increasing γ′ volume fractions as designed in alloys VF0 through VF60.

  2. 2.

    All the experimental alloys exhibit a dendritic structure after solidification. As the content of γ′-forming elements (mainly Ta and W) increases, secondary phases, such as Laves and μ, are formed with increasing area fractions in the interdendritic regions in certain alloys.

  3. 3.

    Calculations and experiments reveal the increasing γ′ solvus temperatures and the continuously decreasing solvus and liquidus temperature as a function of the γ′-forming element content (mainly Ta and W). In most cases, the experimental γ′ solvus and solidus temperatures are substantially higher than the calculated values. The differences in liquidus temperatures are much less significant.

  4. 4.

    Long-term heat treatments for 1000 hours revealed that the χ phase with a D019 structure appears also in VF20, VF40, and VF60, which are free of additional phases after 100 hours at 900 °C. This indicates that the phase equilibrium is not reached after 100 hours. Especially, the strong underestimation of the γ′ stability can be related to the thermodynamic database used for the calculations.

  5. 5.

    The thermal expansion behavior at low temperatures and at temperatures above the γ′ solvus temperature varies only slightly with the composition of Co- and Ni-base superalloys. However, changes of the γ/γ′ phase ratio and the precipitation of additional phases lead to significant positive contributions to the thermal expansion, which, in turn, can be used to monitor the corresponding dissolution/precipitation processes and to determine the γ′ solvus temperature using high-resolution dilatometry.