Analysis of Experimental Grain Boundary Distributions Based on Boundary-Space Metrics

Abstract

Grain boundary distributions in the space of macroscopic boundary parameters are basic statistical characteristics of boundary networks. To avoid artifacts caused by the currently used computation method, it is proposed to utilize the kernel density estimation technique and to determine boundary distributions based on metric functions defined in the boundary space. A distribution is calculated at points of interest by summing areas of boundaries that fall within specified distances from these points. The new method is illustrated on experimental data of a nickel-based superalloy.

A variety of properties of polycrystalline materials are affected by grain boundaries. To explore relationships between boundary structures and material properties, the boundaries need to be investigated at both atomic and “macroscopic” levels. Studies at the atomic scale are limited by experimental capabilities, but the macroscopic boundary parameters (i.e., misorientations between neighboring grains and directions of boundary plane normals[1]) can be relatively easily determined. Experimental methods of three-dimensional microstructure characterization have been improved greatly over the last decade, and large sets of boundary parameters are being collected, e.g., References 2, 3. The sizes of resulting data sets allow for statistical analyses of boundaries.

One of the most basic statistical characteristics of a boundary network is the distribution of grain boundaries with respect to the macroscopic boundary parameters. In relevant reports published so far (e.g., References 4 through 8), the distributions have been computed using a method[4] based on partition of a certain domain in the boundary parameter space into equivolume bins. Although this method has been successfully applied to various materials, it has deficiencies leading to artifacts in computed distributions, and complicating estimation of the reliability of the distributions.

This note presents an alternative approach to computation of the boundary distributions. Suggestions given in Reference 9 are followed to adapt the kernel density estimation technique and to replace the partition of the boundary space by probing the distributions at selected points and counting boundaries that are not farther from those points than an assumed limiting distance defined in the boundary space. It is shown that this change of the computation method leads to significant improvements in the quality of resulting distributions. The new method also allows for a direct estimation of the reliability of the distributions. In the following, deficiencies of the hitherto used approach are discussed. Then, the new approach is described and confronted with the old one. Both methods are applied to grain boundary data of a nickel-based superalloy. For simplicity, only cubic ${(m\bar{3}m)}$ crystal symmetry is considered; similar analysis can be performed for other holohedral symmetries.

The grain misorientations and boundary plane normals are usually parameterized by Euler angles $\varphi _1,\,\Phi ,\,\varphi _2$ and spherical (polar and azimuth) angles $\vartheta$ and $\psi$, respectively. With cubic crystal symmetry, the parameter domain used in the partition-based approach is restricted by $0\,{{\rm{deg}}} \le \varphi _1, \Phi , \varphi _2, \vartheta \le 90\,{\rm{deg}}$ and $0\,{\rm{deg}} \le \psi \le 360\,{\rm{deg}}$. The “rectangular” box $\varphi _1 \times \cos {\Phi } \times \varphi _2 \times \cos {\vartheta } \times \psi$ is partitioned into equivolume rectangular bins of dimensions $\Delta {\varphi _1}=\Delta {\varphi _2}=90\,{\rm{deg}}/k$, $\Delta \psi =90\,{\rm{deg}}/k'$, $\Delta (\cos {\Phi })=1/k$ and $\Delta (\cos {\vartheta })=1/k'$, where $k$, $k'$ are positive integers.[4] Typically, “$10\,{\rm{deg}}$-bins” ($k=9=k'$) are used. It is easy to see that the partition results in elongated bins. For instance, the $\Phi$-dimensions of $10\,{\rm{deg}}$-bins with $\cos {\Phi }$ in the ranges $[0,\frac{1}{9}]$ and $[\frac{8}{9},1]$ are, respectively, 6.4 and $27.3\,{\rm{deg}}$. The disparities in the bin dimensions are schematically illustrated in Figure 1(a). Large bin elongation should be avoided because boundaries at the opposing extremities of a long bin have significantly different geometries. Moreover, the bin sizes do not really correspond to experimental resolutions, which—in the case of EBSD-based data—are believed to be about $1\,{\rm{deg}}$ for misorientations and about $7.5\,{\rm{deg}}$ for boundary planes.[4] With a sufficiently large data set, the volumes of the bins could be reduced by increasing $k$ and $k'$. Such an increase, however, does not eliminate the bin elongation, and it results in even larger relative differences between angular dimensions of the shortest and the longest bins.

Fig. 1

(a) Schematic illustration of the angular dimensions of the “$10\,{\rm{deg}}$-bins” in the partition-based method. (b) $\Sigma 5$ section through the test distribution obtained by the partition-based approach with “$10\,{\rm{deg}}$-bins”. (c) $\Sigma 5$ section calculated using the metric-based method with $\rho _{\rm{m}} = 5\,{\rm{deg}} = \rho _{\rm{p}}$. ($d,e,f$) Essential parts of the sections through the test distribution computed using the partition into “$10\,{\rm{deg}}$-bins” for the misorientations $\Sigma 3$, $[110]/57\,{\rm{deg}}$ and $[111]/50\,{\rm{deg}}$, respectively

In the process of boundary distribution determination, boundary networks are reconstructed in the form of meshes. To calculate the distribution, areas of mesh segments are accumulated in the bins. With the domain used in the partition-based approach, a boundary (of multiplicity 1) is represented by $36$ (different) symmetrically equivalent points. Therefore, at the accumulation step, each segment contributes to multiple bins, and in the end, a value of the grain boundary distribution at a given point is obtained by averaging over the bins containing equivalent points. In the presence of elongated bins, the averaging smooths but also excessively flattens the resulting distributions. As a consequence, weak maxima may become indistinguishable from the background.

To illustrate artifacts in boundary distributions obtained by the partition-based method, let us examine an artificial test function containing two individual boundary types: the symmetric $\Sigma 5$ ($[100]/36.9\,{\rm{deg}}$ misorientation) boundaries with $(012)$ planes and the (fcc twin) boundaries with $\Sigma 3$ ($[111]/60\,{\rm{deg}}$) misorientations and $(111)$ planes. Two nearly point-like maxima are expected at the $(012)$ and $(0\bar{2}1)$ poles in the $\Sigma 5$ section of the distribution, and a single peak at the $(111)$ pole in the $\Sigma 3$ section. Values for all other boundary types should be zero. However, in the distribution obtained by the conventional method, besides the expected peaks, also artifacts are observed. In the $\Sigma 5$ section calculated using $10\,{\rm{deg}}$-bins, the peaks are spread along the $[010]$ direction (Figure 1(b)). In the $\Sigma 3$ section, the peak at the $(111)$ pole has full width at half-maximum of about $7\,{\rm{deg}}$ (Figure 1(d)). Its “tail” is still visible at the neighborhood of the $(\bar{1}11)$ pole for the $[110]/57\,{\rm{deg}}$ misorientation, which is $13.5\,{\rm{deg}}$ away from the $[110]/70.5\,{\rm{deg}}$ misorientation—one of equivalent representatives of $\Sigma 3$ (Figure 1(e)). The tail is also present in the closer $[111] / 50\,{\rm{deg}}$ section (Figure 1(f)); this section has been considered without accounting for the impact of the peak at the twin boundary.[5,6] Clearly, large spread of peaks causes difficulties in interpretation of the distributions.

Boundary distributions can be computed by an alternative method which does not lead to artifacts and uses parameters which can be directly linked to both the experimental resolution and the size of a data set. The idea is to use the kernel density estimation technique and to get a value of the distribution at a given point by summing areas of boundaries that are not farther from that point than an assumed limiting distance. A metric in the boundary space can be defined in a number of ways,[10] but it is essential that two boundaries are close (distant) if they have similar (different) geometric features, and that symmetrically equivalent representations of boundaries are taken into consideration. The boundary space is a Cartesian product of misorientation and boundary plane subspaces. For calculation of distributions of boundary planes for fixed misorientations, it is convenient to consider distances in these subspaces separately. In the misorientation subspace, the difference between two boundary geometries is quantified by the angle $\delta _{\rm{m}}$ ¹ of the rotation relating the misorientations, and in the boundary-plane subspace by $\delta _{\rm{p}}=\sqrt{(\chi _1^2+\chi _2^2)/2}$, with $\chi _i$ denoting the angles between boundary plane normals; there are two angles $\chi _i$ because the boundary planes of two crystallites need to be taken into account. Moreover, $\delta _{\rm{m}}$ and $\delta _{\rm{p}}$ are calculated for all symmetrically equivalent boundary representations and minimum values $\min (\delta _{\rm{m}})$ and $\min (\delta _{\rm{p}})$ are used as the distances. Having separate limiting distances for misorientations $(\rho _{\rm{m}})$ and for boundary planes $(\rho _{\rm{p}})$ allows for adjusting the bin shapes to actual experimental resolutions of measured boundary parameters. This option would not be available if a single distance defined in the complete boundary space was used.

To obtain a section through a distribution for a fixed misorientation, all boundary segments whose distances $\min (\delta _{\rm{m}})$ from that misorientation are smaller than $\rho _{\rm{m}}$ (i.e., segments that fall into the ball of radius $\rho _{\rm{m}}$ centered at the fixed misorientation) are first identified. Then, the distribution is calculated at evenly dispersed directions. Areas of the identified segments whose normals are located at distances $\min (\delta _{\rm{p}})$ not larger than $\rho _{\rm{p}}$ from a given direction (i.e., that fall into the ball of radius $\rho _{\rm{p}}$ in the boundary-plane subspace) are accumulated. In the end, values ascribed to the bins are expressed as multiples of the random distribution: the normalized values obtained from experimental data are divided by the corresponding normalized values obtained from large sets of computer generated random boundaries. Clearly, with the new approach, the averaging over bins is eliminated, and the bins are spherical (with respect to the used metrics) in the subspaces of misorientation and boundary planes. Thus, the bin in the boundary space is a Cartesian product of balls given in the misorientation and boundary-plane subspaces. Bin shapes are also quite regular in the complete space if $\rho _{\rm{p}}$ and $\rho _{\rm{m}}$ are similar.

The benefits of using the metric-based approach are demonstrated for the same test distribution containing $\Sigma 5/(012)$ and $\Sigma 3/(111)$ boundaries as considered above. The volume of $10\,{\rm{deg}}$-bins of the partition is close to that of the distance-based bins when $\rho _{\rm{m}} = 5\,{\rm{deg}} = \rho _{\rm{p}}$. With these radii, peaks in $\Sigma 3$ and $\Sigma 5$ sections of the test distribution are contained in disks with radii equal to the assumed $\rho _{\rm{p}}$ (Figure 1(c)). There is no spread along the $[010]$ direction in the $\Sigma 5$ section of the resulting distributions, and sections for the $[111] / 50\,{\rm{deg}}$ and $[110]/ 57\,{\rm{deg}}$ misorientations are flat with the value of $0$ at all poles.

The volume $v$ of an individual bin, and thus the limiting radii $\rho _{\rm{m}}$ and $\rho _{{\rm{p}}}$, influence the uncertainties of the values of the grain boundary distribution. With $f$ being a value of the distribution in the bin, the minimal number of measurements $n$, required for the relative error defined as (standard deviation of $f$) / $f$ to be smaller than certain $\varepsilon$ is given by $n \approx c/(\varepsilon ^2 v f)$, where $c$ is a coefficient accommodating correlations in the data.[11] With $n$ being the number of distinct grain boundaries (not the number of segments in a reconstructed mesh), the data are only weakly correlated, and hence, $c \approx 1$ can be assumed. With this assumption, the above formula will be used to estimate the relative error $\varepsilon \approx (n v f)^{-1/2}$.

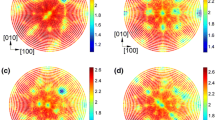
The metric-based approach was applied to experimental data set Small IN100. The set contains three-dimensional microstructural data of Ni-based superalloy IN100. A detailed description of the material and data collection can be found in Reference 2. The data clean-up and reconstruction of boundary surfaces were carried out using DREAM.3D.[12] There were about $13,000$ individual boundaries and about $2.5 \times 10^6$ triangular segments in the mesh of the reconstructed boundary network. Optimal bandwidth selection for the kernel density estimation technique is non-trivial. We have tested a number of values for the parameters $\rho _{\rm{m}}$ and $\rho _{\rm{p}}$. The choice has an impact on the peak height and the errors. To keep the errors at bay, $\rho _{\rm{m}}$ and $\rho _{\rm{p}}$ must be sufficiently large. Since grain reconstruction process decreases the resolution for misorientations, it is reasonable to set the radius $\rho _{\rm{m}}$ at $3\,{\rm{deg}}$. The resolution in the boundary-plane subspace was estimated using coherent twin boundaries; as the standard deviation of the Gaussian function approximating the shape of the $(111)$ peak in the $\Sigma 3$ section of the experimental distribution is close to $7\,{\rm{deg}}$, this value was used as the limiting distance $\rho _{\rm{p}}$. With such radii, the peaks are not excessively spread, while the errors stay at acceptable levels. Sections for the $\Sigma 3$ and $\Sigma 9$ misorientations calculated using the new approach are compared with analogous sections obtained using the partition into $10\,{\rm{deg}}$-bins in Figure 2. The large differences in nominal heights of the peaks obtained by the two methods come partly form the difference in volumes of the $10\,{\rm{deg}}$-bins and the bins limited by $\rho _{\rm{m}}=3\,{\rm{deg}}$ and $\rho _{\rm{p}}=7\,{\rm{deg}}$. Despite the smaller volume, the distribution obtained by the new approach appears to be smoother. The distributions computed using both methods are also compared using one-dimensional sections of the distributions. Figure 3(a) presents the distributions at the $(111)$ pole for misorientations about $[111]$ axis vs the misorientation angle. The curve corresponding to the metric-based approach reveals more details than the piecewise flat graph obtained by the partition-based method. Figure 3(b) shows the profiles of the distribution function along $[1\bar{1}0]$ direction for the $\Sigma 9$ misorientation. Both methods give a relatively strong peak at the $(1\bar{1}4)$ symmetric tilt boundary. The partition into $10\,{\rm{deg}}$-bins leads to an artificial peak near the $(\bar{2}21)$ pole, which disappears when larger $k$ is used; see, e.g., the green line in Figure 3(b). The maxima in the vicinity of the $(\bar{1}15)$ and $(1\bar{1}1)$ poles, clearly visible in the distribution obtained with the new approach are barely discernible in the distribution obtained by the partition-based method. It is worth noting that $(\bar{1}15)$ and $(1\bar{1}1)$ poles correspond to tilt boundaries having multiple tilt axes,[14] the $(\bar{1}15)$ and $(1\bar{1}1)$ planes expressed in the second grain are $(1\bar{1}\bar{1})$ and $(\bar{1}1\bar{5})$, respectively, and—according to Reference 7—minima of grain boundary energy for $\Sigma 9$ are at $(\bar{1}15)$ and $(1\bar{1}1)$.

Summarizing, the metric-based approach to computation of grain boundary distributions allows for elimination of artifacts affecting the distributions obtained by the partition-based method. Weak maxima are better pronounced and distinguishable in the distributions computed using the new method. The control parameters of the new approach can be easily adjusted to experimental resolution, sizes of data sets and errors of distribution functions. Although the reliability of grain boundary distributions depends mainly on the amount and quality of experimental data, it is also important to analyze the data using tools that do not distort the final results. This note is a step toward more effective analysis of experimentally collected sets of grain boundary parameters.

Fig. 2

Distribution of grain boundaries in superalloy IN100. (a) Sections obtained using the partition-based method with $10\,{\rm{deg}}$-bins; the figures are consistent with those in Refs. [7, 13]. (b) Sections computed using the metric-based approach with $\rho _{\rm{m}}=3\,{\rm{deg}}$ and $\rho _{\rm{p}}=7\,{\rm{deg}}$. (c) Error levels for data shown in (b). Left and right columns correspond to the $\Sigma 3$ and $\Sigma 9$ misorientations, respectively

Fig. 3

One-dimensional sections through distributions of grain boundaries in superalloy IN100. (a) Distributions at the $(111)$ pole for $[111]/\alpha$ misorientations computed using the metric-based (disks) and partition-based (circles) methods. (b) Profiles along the $[1\bar{1}0]$ zone (marked by arrows in Fig. 2) for the $\Sigma 9$ misorientation; cf. Fig. 7 of Ref. [6]. Solid lines correspond to the metric-based approach with $\rho _{\rm{m}}=3\,{\rm{deg}}$, $\rho _{\rm{p}}=7\,{\rm{deg}}$ (black) and $\rho _{\rm{m}} = 5\,{\rm{deg}} = \rho _{\rm{p}}$ (red). Dashed lines were obtained by the partition-based method using $10\,{\rm{deg}}$-bins, i.e., $k=9=k'$ (blue), and additionally, using $k=15$, $k'=7$ (green); in the latter case, volumes of the bins are close to those determined by $\rho _{\rm{m}}=3\,{\rm{deg}}$, $\rho _{\rm{p}}=7\,{\rm{deg}}$