On the Calculation of Volume Fraction of Texture Components in AA5754 Sheet Materials

Abstract

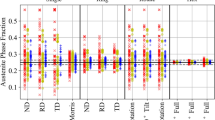
There is currently no general agreement on how to extract the volume fraction of texture components for aluminum alloy sheets based on X-ray diffraction (XRD) and electron backscatter diffraction (EBSD) techniques. In order to clarify this problem, grain orientation data of AA5754 sheet material in the O-temper were acquired using XRD and EBSD. The volume fractions of 10 selected texture components were calculated using the MTM FHM software package for XRD and EDAX-TSL OIM Analysis for EBSD. The measured grain orientation data from EBSD were then processed again using MTM FHM. The results show that there are no significant differences in the constructed pole figures using different measuring techniques when the same analysis system is used. Thus, the differences in volume fractions of texture components are mainly related to the deviation angle used in the two different software packages. The differences in the deviation angle used lead to potential overlaps between the selected texture components. A suitable deviation angle for the volume fraction calculation can be selected using the concept of misorientation.

Appendix

This appendix is written based on Reference 16 to clarify the generation of the model function, f ^m(g), and also to provide M values for all ten selected texture components in the present study.

In order to generate the model function f ^m(g), a Gaussian distribution function f ^m(Φ) for an ideal orientation is defined:

$$ f^{m} {\left( \Phi \right)} = S\exp {\left[ { - {\left( {\Phi \mathord{\left/ {\vphantom {\Phi {\Phi _{0} }}} \right. \kern-\nulldelimiterspace} {\Phi _{0} }} \right)}^{2} } \right]} $$

(A1)

where S = 1/(πΦ₀), Φ is the angular distance to an ideal orientation, and Φ₀ is the spread around it. The latter term is hereafter referred to as the deviation angle. This model function has a maximum value of M.

It must be noted that the Gaussian distribution function f ^m(Φ) in Eq. [A1] is a function of angular distance Φ. In the MTM FHM software, f ^m(Φ) is transformed into a function in the Euler space (f ^m(g ^e)) in the form of C coefficients. The relation of Φ and g ^e = (φ ₁ ,ϕ,φ ₂ ) is as follows:

$$ \Phi = \cos ^{{ - 1}} {\left\{ {\frac{1} {2}{\left[ {{\text{trace}}{\left( {g {\cdot} g^{{ - 1}}_{{TC}} } \right)} - 1} \right]}} \right\}} $$

(A2)

where

$$ g = {\left[ {\begin{array}{*{20}c} {{\cos \varphi _{1} \cos \varphi _{2} - \sin \varphi _{1} \sin \varphi _{2} \cos \phi }} & {{\sin \varphi _{1} \cos \varphi _{2} - \cos \varphi _{1} \sin \varphi _{2} \cos \phi }} & {{\sin \varphi _{2} \sin \phi }} \\ {{ - \cos \varphi _{1} \sin \varphi _{2} - \sin \varphi _{1} \cos \varphi _{2} \cos \phi }} & {{ - \sin \varphi _{1} \sin \varphi _{2} + \cos \varphi _{1} \cos \varphi _{2} \cos \phi }} & {{\cos \varphi _{2} \sin \phi }} \\ {{\sin \varphi _{1} \sin \phi }} & {{ - \cos \varphi _{1} \sin \phi }} & {{\cos \phi }} \\ \end{array} } \right]} $$

The procedure of generating model functions can be completed in the IDEALC program in the MTM-FHM software.

The Gaussian distribution has been chosen to calculate the volume fraction for computational convenience in the MTM FHM software. In Eq. [1], f ^m(g ^e)/M is actually a weighting function that has a value of 1 at the ideal orientation of a texture component (Figure A1). From Figure A1, it is seen that the orientation distribution function f ^x(g ^e) is 100 pct counted in the integral at the ideal orientation. Most of f ^x(g) is counted in the integral within the spread around the orientation, while very little is counted outside the spread away from the ideal orientation.

Fig. A1

Distribution of a model function scaled by its peak value M

The M values of all ten selected texture components with three different spreads (5, 11, and 16.5 deg) are listed in Table AI. From Table AI, it is noted larger M values exist at a smaller spread. This is because the integration of the model function over the full orientation space must be 1. It is also noted that M is different for different texture components. This is due to two reasons. First, the fact that orthorhombic sample symmetry typical for rolling texture is considered when generating a model function. A texture component with lower crystallographic symmetry, e.g., ${\text{S }}{\left( {{\left\langle {{\text{123}}} \right\rangle }{\left\{ {{\text{634}}} \right\}}} \right)}$ component, would have more equivalent orientations and, therefore, smaller M values to satisfy the condition that the integration of the model function over the full orientation space must be 1. Second, Euler space is nonlinear; while, in principle, the nonlinearity is compensated for in the model functions, some variance may occur in the numerical implementation onto linear grids.

Table AI Maximum Value, M, of the Model Functions at Different Spreads