1 Introduction

A high-speed underwater vehicle is a type of stratagem weapon that is essential for naval equipment as, it can be used in deep water and control large areas of sea. The motion of a moving body is a system with the property of unmodeled dynamics and input uncertainty[1,2]. It has a control system that meets the requirements of large distance runs and high-precision tactics, but it is vulnerable to the impact of model input uncertainty.

Recent studies about launched out-of-water tasks give rise to challenging control problems involving cross-media motion process, hydrodynamic parameter uncertainties and external disturbances. The control system should be able to learn and adapt to the changes in the dynamics of highspeed underwater vehicle.

In the past, for nonlinear models of an underwater vehicle with known dynamics, control laws were designed using the Lyapunov stability theory and the pure backstepping design technique[3]. For the control of underwater vehicle models in the presence of uncertainties, sliding mode control was considered[4,5]. Adaptive control laws were also designed for the control of underwater vehicles[6-8]. A discrete-time adaptive sliding mode controller for an underwater vehicle with parameter uncertainties and external disturbance was presented[8]. From the performance evaluation of an exact feedback-linearization controller, it was seen that this method is very sensitive to variation of parameters[9]. The adaptive backstepping control approach in [9–11] is capable of keeping almost all the robustness properties of the unknown uncertainties.

However, by means of these design methods[3-8], the output-generated attitude of the high-speed underwater vehicle out-of-the-water trajectory has a nonlinear and coupled form and hydrodynamic coefficient[12-14]. Therefore, in order to obtain a linearly controlled attitude and keep the robustness of nonlinear sliding mode control, a nonlinear sliding mode control with an adaptive backstepping approach was designed to achieve a high performance attitude tracking of catastrophic course.

The main purpose of this paper is to propose a practicable new control method for the process of getting out of the water. Since the transient dynamics of the high speed underwater vehicle nonlinear system difficult to evaluate by the linear control theory, the model-following control technique is utilized for the proposed control to track a designed linear reference model. Therefore, the transient dynamics of the controlled attitude can be simply designed through a linear reference model. The nonlinear element is considered for the proposed adaptive backstepping control which uses a tuning function to avoid repeated estimates with the same unknown parameters of a pure adaptive backstepping technique.

The proposed hybrid controller for the high-speed underwater vehicle when coming out of the water was shown to be globally asymptotically stable and was proved by the Lyapunov theory. Compared with the other methods, the proposed method has good dynamic performance in attitude state, even in a large bound wave input. It not only takes advantage of nonlinear transformation to simplify the control system design, but also makes use of invariant features of the sliding mode with system perturbation and disturbance. Simultaneously, the proposal is robust in terms of parameter uncertainties and system model errors. The current study focuses on the analysis and simulation of underwater supercavitating characteristics[15,16], but the catastrophic theory and application of course control are less from domestic and foreign public documents.

2 Modeling of catastrophic course

A high-speed underwater vehicle-attack aerial target process is generally experienced in three stages: “in the water”, “air” and “water-gas transition”. The biggest problem is that the features experienced by the missile body in the underwater section are different from those in the air. The buoyancy and added mass are zero after the high-speed underwater vehicle comes out of the water and the mathematical model changes suddenly at the moment. The distribution of the high-speed underwater vehicle’s shape and internal mass are symmetrical about the longitudinal plane, and the symmetrical motion parameters will not have the force and moment asymmetrically.

In order to avoid the control problem of singular attitude angle, a new coordinate system is established to enable the X-axis vertically upward, keep the initial attitude angle as 0, and keep buoyancy, gravity and gravity torque along the o 0 x 0-axis direction.

According to fluid dynamics theory, a nonlinear model of the high-speed underwater vehicle is derived as

$$\begin{array}{*{20}{l}} {(m + {\lambda _{11}}){{\dot \upsilon }_x} + m( - {\upsilon _y}{\omega _z} - {x_c}\omega _x^2) = T - \frac{1}{2}\rho {\upsilon ^2}S{C_{xs}} - \Delta G\;\cos \theta } \\ {(m + {\lambda _{22}}){{\dot \upsilon }_y} + (m{x_c} + {\lambda _{26}}){{\dot \omega }_z} + m{\upsilon _x}{\omega _z} = } \\ {\quad \frac{1}{2}\rho {\upsilon ^2}S(C_y^\alpha \alpha + C_y^\delta {\delta _e} + C_y^{\bar \omega }{{\bar \omega }_z}) - \Delta G\sin \theta } \\ {({J_z} + {\lambda _{66}}){{\dot \omega }_z} + (m{x_c} + {\lambda _{26}}){{\dot \upsilon }_y} + m{x_c}{\upsilon _x}{\omega _z} = } \\ {\quad \frac{1}{2}\rho {\upsilon ^2}SL(m_z^\alpha \alpha + m_z^{{\delta _e}}{\delta _e} + m_z^{{{\bar \omega }_z}}{{\bar \omega }_z}) + G({y_c}\cos \theta + {x_c}\sin \theta )} \end{array}$$
(1)
$$\begin{array}{*{20}{l}} {\dot \theta = {\omega _x}} \\ {{{\dot x}_0} = \upsilon \;\cos (\theta - \alpha )} \\ {{{\dot y}_0} = \upsilon \;\sin (\theta - \alpha )} \\ {\alpha = - \arctan \frac{{{\upsilon _y}}}{{{\upsilon _x}}}} \\ {\upsilon = \sqrt {\upsilon _x^2 + \upsilon _y^2} } \end{array}$$

where \({\dot v_x} = \dot v\;\cos \;\alpha - \dot \alpha v\sin \;\alpha \) and \({\dot v_y} = \dot \alpha v\;\cos \;\alpha - \dot v\sin \;\alpha \).

Successive elimination obtains

$$\begin{array}{*{20}{l}} {\dot \upsilon = \frac{{ - ({J_{zz}} + {\lambda _{66}})m\upsilon \;\cos \alpha \sin \alpha {\omega _z}}}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})]}} + } \\ {\quad \frac{{m{x_c}\upsilon \;\cos \alpha \sin \alpha {\omega _z}}}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})}} + } \\ {\quad \frac{{({J_{zz}} + {\lambda _{66}})({K_{y\alpha }}\alpha + {K_{y\delta }}{\delta _h}){\upsilon ^2}\sin \alpha }}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})]}} + } \\ {\quad \frac{{[({J_{zz}} + {\lambda _{66}}){K_{y\omega }}{\omega _z}\upsilon - ({J_{zz}} + {\lambda _{66}})\Delta G\sin \theta ]\sin \alpha }}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})]}} - } \\ {\quad \frac{{({K_{mz\alpha }}\alpha + {K_{mz\delta }}{\delta _h}){\upsilon ^2}\sin \alpha }}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{26}})}} + } \\ {\quad \frac{{[{K_{mz\omega }}{\omega _z}\upsilon + G({y_c}\cos \theta + {x_c}\sin \theta )]\sin \alpha }}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{26}})}} + } \\ {\quad \frac{{[m( - \upsilon \;\sin \;\alpha {\omega _z} + {x_c}\omega _z^2) + T - {K_x}{\upsilon ^2} - \Delta G\;\cos \theta ]\cos \alpha }}{{(m + {\lambda _{11}})}}} \\ {\dot \alpha = \frac{{ - ({J_{zz}} + {\lambda _{66}})m\;{{\cos }^2}\alpha {\omega _z}}}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})]}} + } \\ {\quad \frac{{m{x_c}{{\cos }^2}\alpha {\omega _z}}}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} - {\lambda _{26}})}} + } \\ {\quad \frac{{({J_{zz}} + {\lambda _{26}})({K_{y\alpha }}\alpha + {K_{y\delta }}{\delta _h})\upsilon \cos \alpha }}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} - {\lambda _{26}})]\alpha }} + } \\ {\quad \frac{{[({J_{zz}} + {\lambda _{66}}){K_{y\omega }}{\omega _z} - \tfrac{1}{\upsilon }({J_{zz}} + {\lambda _{26}})\Delta G\sin \theta ]\cos \alpha }}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} - {\lambda _{26}})]\alpha }} - } \\ {\quad \frac{{({K_{mz\alpha }}\alpha + {K_{mz\delta }}{\delta _h})\upsilon cos\alpha }}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{26}})}} + } \\ {\quad \frac{{[{K_{mz\omega }}{\omega _z} + \tfrac{1}{\upsilon }G({y_c}\cos \theta + {x_c}\sin \theta )]\cos \alpha }}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} - {\lambda _{26}})}} + } \\ {\quad \frac{{[m( - \upsilon \;\sin \;\alpha {\omega _z} + {x_c}\omega _z^2) + T - {K_x}{\upsilon ^2} - \Delta G\;\cos \theta ]{{\cos }^2}\alpha }}{{\upsilon sin\alpha (m + {\lambda _{11}})}} - } \\ {\quad \frac{{m( - \upsilon \;\sin \;\alpha {\omega _z} + {x_c}\omega _z^2) + T - {K_x}{\upsilon ^2} - \Delta G\;\cos \theta }}{{\upsilon sin\alpha (m + {\lambda _{11}})}}} \\ {{{\dot \omega }_{zz}} = \frac{{(m{x_c} + {\lambda _{26}})[m{\upsilon _x}{\omega _x} - ({K_{y\alpha }}\alpha + {K_{y\delta }}{\delta _h}){\upsilon ^2}]}}{{(m + {\lambda _{22}})({J_{zz}} - {\lambda _{26}}) - {{(m{x_c} + {\lambda _{26}})}^2}}} + } \\ {\quad \frac{{(m{x_c} + {\lambda _{26}})( - {K_{y\omega }}{\omega _z}\upsilon + \Delta G\sin \theta )}}{{(m + {\lambda _{22}})({J_{zz}} - {\lambda _{26}}) - {{(m{x_c} + {\lambda _{26}})}^2}}} - } \\ {\quad \frac{{(m + {\lambda _{22}})[m{x_c}{\upsilon _x}{\omega _x} - ({K_{mz\alpha }}\alpha + {K_{mz\delta }}{\delta _h}){\upsilon ^2}]}}{{(m + {\lambda _{22}})({J_{zz}} - {\lambda _{26}}) - {{(m{x_c} + {\lambda _{26}})}^2}}} + } \\ {\quad \frac{{(m + {\lambda _{22}})[{K_{mz\omega }}{\omega _z}\upsilon + G({y_c}cos\theta + {x_c}sin\theta )]}}{{(m + {\lambda _{22}})({J_{zz}} - {\lambda _{26}}) - {{(m{x_c} + {\lambda _{26}})}^2}}}.} \end{array}$$

For the phase of water-gas transition, the reduced acceleration force produced in the process of the high-speed underwater vehicle getting out of the water is caused by fluid added mass, steady state around flow, gravity, buoyancy and surface friction. In the initial impact phase of the out-of-the-water, steady-state resistance, buoyancy and surface friction are small. The momentum equation for the transition phase of out-of-the-water vehicle is derived as (neglecting surface friction) mv 0 − (m + λ)v = \(\int_0^t {{T_0}\operatorname{d} t} + \int_0^t {{B_0}\operatorname{d} t} - mgt - \int_0^t {{C_{ds}}\tfrac{1}{2}\rho S{v^2}\operatorname{d} t} \). The kinetic equation is −(m+λ)\(\dot v - v\dot \lambda \) = T0+B0−mg\( - \tfrac{1}{2}\)CdsρSv2, where S is the cross-section area, m is the mass, G is the weight, J Z is the moment of inertia of the buoyancy center, T 0 and T are the propulsion forces, \(\Delta G = G - \bar B\) is the buoyancy force, C xs and C ds are the resistance coefficients, λ 11, λ 22, λ 26, λ 66 and λ are the incremental masses, \(C_y^\alpha \),\(C_y^\delta \) and \(C_y^{{\omega _z}}\) are the lift force derivatives, \(m_z^\alpha \),\(m_z^{{\delta _e}}\) and \(m_z^\omega \) are the pitching moment derivatives, α is the angle of attack, θ is the pitching angle, ω z is the pitching angular velocity, δ e is the elevator deflection angle, x c and y c are the barycentric coordinates, x0 and y 0 are the center of buoyancy coordinates of the ground coordinate system, v,v x and v y are the velocities of buoyancy center and its components. λ 11, λ 22, λ 26, λ 66, C xs, \(C_y^\alpha \),\(C_y^\delta \),\(C_y^{{\omega _z}}\),\(m_z^{{\alpha}}\),\(m_z^{{\delta _e}}\) and \(m_z^\omega \) are the hydrodynamic parameters within the certain boundary range, \({\bar \omega _z} = \frac{{{\omega _z}L}}{v}\), and L is the length.

The system state vector and input vector for the high-speed underwater vehicle model are chosen as x = [ v α ω z θ ]T , u = δ e .

Therefore, the high-speed underwater vehicle model can be expressed as an affine nonlinear system:

$$\left\{ {\begin{array}{*{20}{l}} {\dot x = f(x) + g(x)u} \\ {y = h(x)} \end{array}} \right.$$
(2)

where

$$\begin{array}{*{20}{l}} {{f_1}(x) = \frac{{({J_{zz}} + {\lambda _{66}})(\Delta G\sin \theta + m{\omega _x}\upsilon \cos \alpha )\sin \alpha }}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})]}} + \frac{{[m{x_c}{\omega _z}\upsilon \cos \alpha - \tfrac{1}{2}\rho {\upsilon ^2}SLm_x^\alpha \alpha + \tfrac{1}{2}\rho \upsilon S{L^2}m_z^{{{\bar \omega }_z}}{\omega _z}]\sin \alpha }}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})}} + \frac{{G({y_c}\cos \theta + {x_c}\sin \theta )\sin \alpha }}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})}} + \frac{{[m( - \upsilon {\omega _z}\sin \alpha + {x_c}\omega _z^2) + T - \tfrac{1}{2}\rho {\upsilon ^2}S{C_{xS}} - \Delta G\cos \theta ]\cos \alpha }}{{(m + {\lambda _{11}})}}} \\ {{f_2}(x) = \frac{{({J_{zz}} + {\lambda _{66}})(\tfrac{1}{2}\rho \upsilon SC_y^\alpha \alpha + \tfrac{1}{2}\rho SLC_y^{{{\bar \omega }_z}}{\omega _z})\cos \alpha }}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})]}} - \frac{{({J_{zz}} + {\lambda _{66}})(\tfrac{1}{\upsilon }\Delta G\sin \theta + m{\omega _x}\cos \alpha )\cos \alpha }}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})]}} + \frac{{(m{x_c}{\omega _z}\cos \alpha - \tfrac{1}{2}\rho \upsilon SLm_z^\alpha \alpha + \tfrac{1}{2}\rho S{L^2}m_y^{{{\bar \omega }_z}}{\omega _z})\cos \alpha }}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})}} + \frac{{\tfrac{1}{\upsilon }\Delta G({y_c}\cos \theta + {x_c}sin\theta )\cos \alpha }}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})}} - \frac{{[m( - \upsilon {\omega _z}\sin \alpha + {x_c}\omega _z^2) + T - \tfrac{1}{2}\rho {\upsilon ^2}S{C_x}S - \Delta G\cos \theta ]{{\sin }^2}\alpha }}{{\upsilon sin\alpha (m + {\lambda _{11}})}}} \\ {{f_3}(x) = \frac{{(m{x_c} + {\lambda _{26}})(m\upsilon {\omega _z}\cos \alpha - \tfrac{1}{2}\rho {\upsilon ^2}SC_y^\alpha \alpha )}}{{(m + {\lambda _{22}})({J_{zz}} + {\lambda _{66}}) - {{(m{x_c} + {\lambda _{26}})}^2}}} + \frac{{(m{x_c} + {\lambda _{26}})( - \tfrac{1}{2}\rho \upsilon SLC_z^{{{\bar \omega }_z}}{\omega _z} + \Delta G\sin \theta )}}{{(m + {\lambda _{22}})({J_{zz}} + {\lambda _{66}}) - {{(m{x_c} + {\lambda _{26}})}^2}}} - \frac{{(m + {\lambda _{22}})(m{x_c}\upsilon {\omega _z}\cos \alpha - \tfrac{1}{2}\rho {\upsilon ^2}SLm_y^\alpha \alpha )}}{{(m + {\lambda _{22}})({J_{zz}} + {\lambda _{66}}) - {{(m{x_c} + {\lambda _{26}})}^2}}} - \frac{{(m + {\lambda _{22}})[\tfrac{1}{2}\rho \upsilon S{L^2}m_y^{{{\bar \omega }_z}}{\omega _z} + G({y_c}\cos \theta + {x_c}sin\theta )]}}{{(m + {\lambda _{22}})({J_{zz}} + {\lambda _{66}}) - {{(m{x_c} + {\lambda _{26}})}^2}}}} \\ {{f_4}(x) = {\omega _z}} \\ {{g_1}(x) = \frac{{({J_{zz}} + {\lambda _{66}})\tfrac{1}{2}\rho S{\upsilon ^2}C_y^{{\delta _e}}}}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})]}}\sin \alpha - \frac{{\tfrac{1}{2}\rho {\upsilon ^2}SLm_x^{{\delta _e}}}}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})}}\sin \alpha } \\ {{g_2}(x) = \frac{{({J_{zz}} + {\lambda _{66}})\tfrac{1}{2}\rho S{\upsilon ^2}C_y^{{\delta _e}}}}{{(m + {\lambda _{22}})[(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})]}}\cos \alpha - \frac{{\tfrac{1}{2}\rho \upsilon SLm_x^{{\delta _e}}}}{{(m{x_c} + {\lambda _{26}}) - ({J_{zz}} + {\lambda _{66}})}}\cos \alpha } \\ {{g_3}(x) = \frac{{(m{x_c} + {\lambda _{26}})\tfrac{1}{2}\rho SC_y^{{\delta _e}}{\upsilon ^2} - (m + {\lambda _{22}})\tfrac{1}{2}\rho SLm_x^{{\delta _e}}{\upsilon ^2}}}{{(m + {\lambda _{22}})({J_{zz}} + {\lambda _{66}}) - {{(m{x_c} + {\lambda _{26}})}^2}}}} \\ {{g_4}(x) = 0.} \end{array}$$

In this paper, the controller is only designed for the former model, whereas the change in dynamics after the highspeed underwater vehicle emerging out of water is treated as modeling uncertainty.

For the purpose of achieving the fast pitching angle dynamics response and operating in the desired dynamic behavior for the beeline or curve trajectory, the attitude control is considered. So, the system output vector is chosen as h(x) = θ.

Based on the input-output feedback-linearization control technique, the following notation is used for the Lie derivative of a function h(x) along a vector field f(x) = (f 1(x),⋯, f„(x )), L f h(x) = \(\frac{{\partial h}}{{\partial x}}\) f(x).

Choose new system states z 1 = h(x),z 2 = \({\dot z_1}\) = L f h.

Then, the model is given in new coordinates by

$$\left( {\begin{array}{*{20}{c}} {{{\dot z}_1}} \\ {{{\dot z}_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{z_2}} \\ {{L_{{f^2}}}h(x)} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{L_g}h} \\ {{L_g}{L_f}h} \end{array}} \right)u$$
(3)

where the Lie derivative functions are given as

$$\begin{array}{*{20}{l}} {{L_g}h(x) = \frac{{\partial h}}{{\partial x}}g(x) = 0} \\ {{L_f}h(x) = \frac{{\partial h}}{{\partial x}}f(x) = {\omega _z}} \\ {{L_g}{L_f}h(x) = \frac{{\partial {L_f}h(x)}}{{\partial x}}g(x) = {g_3}(x)} \\ {{L_{{f^2}}}h(x) = \frac{{\partial {L_f}h(x)}}{{\partial x}}f(x) = {f_3}(x).} \end{array}$$

Furthermore, a nonlinear-state feedback decoupling the control inputs is employed.

Construct the new control inputs as û = L g Lf hu.

Then, system (5) becomes

$$\left( {\begin{array}{*{20}{c}} {{{\dot z}_1}} \\ {{{\dot z}_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{z_2}} \\ {{L_{{f^2}}}h(x)} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)\hat u.$$
(4)

3 Nonlinear sliding mode control

The sliding mode controller design usually consists of two stages. The first stage is to define a sliding surface and the second stage is to develop a controller that satisfies the sliding condition, which dictates that the states remain on the sliding surface. On the sliding surface, the states converge to the desired equilibrium state.

Since (4) is a nonlinear system, the dynamics are hard to regulate by a constant-state feedback gain. So, a model-following nonlinear sliding mode controller is proposed for the dynamic system (4) to track a desired reference model.

From (4), the reference model is introduced as

$$\begin{array}{*{20}{c}} {\dot Z = AZ + B{u_r}} \\ {\left( {\begin{array}{*{20}{c}} {{{\dot z}_1}} \\ {{{\dot z}_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&1 \\ { - {a_1}}&{ - {a_2}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{z_1}} \\ {{z_2}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {{a_2}} \end{array}} \right)\theta } \end{array}$$
(5)

where a 1 and a 2 are the positive constants, and θ is the reference trajectory angle.

Furthermore, we define the tracking errors as e z = [Δz 1,Δz 2]T = [e z 1,e z 2]T. Using (4) and (5), the system error dynamics is obtained as

$${\dot e_x} = A(x) + B(x)\bar u$$
(6)

where \(A(x) = \left( {\begin{array}{*{20}{c}} {{e_{z2}}} \\ {{L_{f2}}h(x)} \end{array}} \right)\),\(B(x) = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)\) ,ū = û + a 1 z 1 + a 2 z 2 −a 2 θ.

According to the system shown in (6), the sliding switching surfaces are chosen as

$$s{e_x} = C{e_x}(x)$$
(7)

where C ∈ R 1×2 is a constant linear matrix, and the inverse of CB(x) must exist for all x, i.e., det(CB(x)) ≠ 0 for all x. Combining (6) and (7) gives

$$\dot s{e_x} = C{\dot e_x}(x) = CA(x) + CB(x)\bar u = - {Q_{sgn}}(s) - Ks$$
(8)

where

$$Q = \left[ {\begin{array}{*{20}{c}} {{q_1}}&0 \\ 0&{{q_2}} \end{array}} \right],\;K = \left[ {\begin{array}{*{20}{c}} {{k_1}}&0 \\ 0&{{k_2}} \end{array}} \right],{q_i},{k_i} > 0,i = 1,2$$

and

$$\operatorname{sgn} (s) = \left\{ {\begin{array}{*{20}{l}} {1,}&{s > 0} \\ { - 1,}&{s < 0.} \end{array}} \right.$$

From (8), and based on Lyapunov theory, the sliding mode controller is obtained as

$$\bar u = - {(CB(x))^{ - 1}}(CA(x) + Q\operatorname{sgn} (s) + Ks).$$
(9)

Using the control law of (9), the reachability of sliding mode control for system (6) is guaranteed.

Theorem 1. With the developed nonlinear sliding mode controller (9) and a stable sliding surface (7), the reaching condition is satisfied, and the controlled system (6) will be stabilized.

Remark 1. Using the model following nonlinear sliding mode control via state-coordinate transformation for a catastrophic course, the transient of pitch angle can be regulated through a linear reference model. In practice, the dynamic model and identification hydrodynamic parameter uncertainties Δk ij, i = 3, j = 1, ⋯, 5 vary in the state or external environment. Therefore, a nonlinear sliding mode controller that makes the course stable and robust against the parameters variations is proposed in the next section.

4 Adaptive sliding mode control

When the high-speed underwater vehicle’s motion state varies or it is influenced by the disturbing sea flow, the parameters of model (1) will give a big change and disturbance. In order to avoid the instability of the control system, the most commonly used method of predicting the motion test data is to extrapolate the trends of identification of hydrodynamic parameters. This gives a basis for boundary prediction of the uncertain moving body and provides seaworthiness conditions to achieve the precision of striking.

Due to the error between the practical measurements and observation data, there exist uncertainties in the hydrodynamic model coefficient. Adaptive backstepping control has a feature which has more than one estimation of each unknown parameter. Due to the advantages of applying the adaptive backstepping control to an unknown uncertainty system, the following design of new control laws is used.

When the system parameters deviate from the nominal value, the tracking error model (6) is re-written in the following form:

$$\begin{array}{*{20}{l}} {{{\dot e}_{z1}} = {e_{z2}} + {\varphi _1}{d_1}(x)} \\ {{{\dot e}_{z2}} = {L_{{f^2}}}h(x) + \bar u + {\varphi _2}{d_2}(x)} \\ {{{\dot e}_z} = [A(x) + \Delta A(x)] + B(x)\bar u} \end{array}$$
(10)

where ϕ i ,i = 1,2, and ΔA(x) denotes the practical uncertainties defined by [ϕ 1 d 1(x), ϕ 2 d 2(x)]T = ΔA(x).

Therefore,

$$\begin{array}{*{20}{l}} {{L_{\Delta f}}h(x) = \frac{{\partial h}}{{\partial x}}\Delta f(x) = \Delta {f_4}(x) = 0} \\ {{L_{\Delta f}}{L_f}h(x) = \frac{{\partial {L_f}h}}{{\partial x}}\Delta f(x) = \Delta {f_3}(x)} \\ {\Delta {f_3}(x) = \Delta {k_{31}}\upsilon {\omega _z}\cos \alpha - \Delta {k_{32}}{\upsilon ^2}\alpha - \Delta {k_{33}}\upsilon {\omega _z} + \Delta {k_{34}}\sin \theta + \Delta {k_{35}}\cos \theta .} \end{array}$$

Assume that |ϕ i | ,i = 1,2 is the unknown and bounded constant. For the first two equations of (10), the derivation of the system errors e z with respect to time t yields

$$\begin{array}{*{20}{l}} {{{\dot e}_{x1}} = {e_{x2}} + {{\hat \varphi }_1}{d_1}(x) - ({{\hat \varphi }_1} - {\varphi _1}){d_1}(x)} \\ {{{\dot e}_{x2}} = {L_{{f^2}}}h(x) + \bar u + {{\hat \varphi }_2}{d_2}(x) - ({{\hat \varphi }_2} - {\varphi _2}){d_2}(x)} \end{array}$$
(11)

where \({\hat \varphi _i}\), i = 1, 2 is the estimate of ϕ i .

It is obvious that the controllers are decoupling with respect to two dynamic models [e z 1,e z 2]. The switch function e z 2 is chosen as ė z 2 = ke z2+ρ•sgn(e z2 ), where k is a positive constant feedback gain.

From (11), the sliding mode control is designed as

$$\bar u = {L_{{f^2}}}h(x) - {\hat \varphi _2}{d_2}(x) - k{e_{x2}} - \rho \cdot \operatorname{sgn} ({e_{x2}})$$
(12)

where ρ is chosen as |(\({\hat \varphi _2}\) − ϕ 2)| × d 2(x) ⩽ ρ × d 2(x). The adaptation law of \({\hat \varphi _2}\) is given by

$${\dot \hat \varphi _2} = \gamma {e_{x2}}{d_2}(x)$$
(13)

where γ is the adaptation gain, ε and k are the constants that are greater than 0, and the sgn(x) is the sign function.

Theorem 2. Using the controller described by (12) and (13), the system is stable and robust subject to the parameters’ unknown uncertainties.

Proof. Define the following Lyapunov function

$${V_1} = \frac{1}{2}\left[ {e_{{x_1}}^2 + e_{{x_2}}^2 + \frac{1}{\gamma }(\hat \varphi _2^2 - \varphi _2^2)} \right].$$
(14)

Using (11), the derivative of (14) with respect to time t is given by

$${\dot V_1} - {e_{x1}}[{\hat \varphi _1}{d_1}(x) - ({\hat \varphi _1} - {\varphi _1}){d_1}(x)] + {e_{x2}}[{L_{{f^2}}}h(x) + \bar u + {\hat \varphi _2}{d_2}(x) - ({\hat \varphi _2} - {\varphi _2}){d_2}(x)] + \frac{1}{{{\gamma _2}}}({\hat \varphi _2} - {\varphi _2}){\dot \hat \varphi _2}.$$
(15)

Applying (12) and (13) to (14) one reduces the equation to \({\dot V_1} = - {k_1}e_{z1}^2 - {k_2}e_{z2}^2 \leqslant 0\). Define the following equations \(L(t) = - {k_1}e_{z1}^2 - {k_2}e_{z2}^2 \leqslant 0\) and \({V_1}(t) = {V_1}(e(0),\hat \varphi (0)) + \int_0^t {{{\dot V}_1}(\tau )\operatorname{d} \tau = } {V_1}(e(0),\hat \varphi (0)) - \int_0^t {L(\tau )\operatorname{d} \tau } \), where e = [e z 1, e z 2]T and . From the definition of the Lyapunov function V 1 ⩾ 0 and the above equation, the following result can be deduced to

$$\mathop {\lim }\limits_{t \to \infty } \int_0^t {L(\tau )\operatorname{d} \tau } \leqslant {V_1}(e(0),\hat \varphi (0)) < \infty .$$

One can deduce that L(t) → 0 as t → ∞, i.e., e z 1 and e z 2 will converge to zero as t → ∞.

Therefore, the proposed controller is stable and robust, even if the parameters’ uncertainties exist.

The sliding mode techniques may generate undesirable chattering, and then a method that makes the function smooth will replace the discontinuous part of the control action[17]. Thus, sgn(s i ) becomes

$$l({s_i}) = \frac{{{s_i}}}{{\left| {{s_i}} \right| + {\delta _i}}}{\delta _i} > 0.$$
(16)

The system structural diagram is shown in Fig. 1.

Fig. 1
figure 1

Block diagram of the control system structure

Full size image

5 Simulation results

A high-speed underwater vehicle launched underwater has vertical orientation or curve attack for the water surface or water-up target under the pitch angle tracking command and adaptive control. The predicted trajectory is programmed in a relatively short period. The pitch angle tracking instructions can be predicted and calculated by the reference model and make a good dynamic performance in the course of an out-of-the-water attack.

After some experiment, good performance was achieved with the following parameters: t = 10 s, the adaptation gain γ in (13) is chosen as 20, ρ = 0.01, δ = 0.05, c = 5, and k = 8. The initial state vector is x(0) = [20m/s 0° 0rad/s 0°], and propulsion force T = 3t. When v = 20m/s, the high-speed underwater vehicle launches out of the water to attack an air target. In the process of mission, its nonlinear model changes simultaneously. But the controller remains the one used before which is designed for the former model.

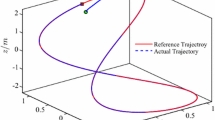
In order to show the high-performance tracking of the proposed attitude control, we choose a 1 = −1, a 2 = −0.3 in model (10) to meet the sine reference input θ = A sin(2πFt), and parameter uncertainty φ 2 = 2 sint. To verify the robustness of the controller, simulation was done with nominal value Δf 3(x) = 0,Δg 3(x) = 0 and parameter uncertainty Δf 3(x) = 3.5, Δg 3(x) = 3.5. The simulated results are shown in Figs. 2 and 3.

Fig. 2
figure 2

The response of system with reference normal model with Δf 3(x) =0,Δg 3(x) = 0

Full size image
Fig. 3
figure 3

The response of system with parameter uncertainties and disturbances with Δf 3(x) = 3.5, Δg 3(x) = 3.5

Full size image

As is evident from the simulation results and experimental analysis, the gentle transition process out of the water at t = 5s ensures the stability of the catastrophic process and tracking accuracy. The integrated errors with constant or parameters of gradual change can be reduced by adapting the controller parameters. Moreover, the system is robust against the uncertainty of model parameters and external interference.

6 Conclusions

It has been shown that the adaptive sliding mode control is simple, and it can guarantee the robustness of the controlled attitude against the parametric uncertainties by using the adaptive backstepping sliding mode control. Further, it can greatly improve the steady-state precision to obtain the transient dynamics of attitude. Since the tracking errors between the state-transformed and reference model converge to 0 asymptotically, the trajectory can be precisely regulated by the linear reference model. Using one nonlinear controller to ensure the process of out-of-the-water security, the variation of motion velocity is round 30 m/s in transition time, and the transition process is smooth and gentle.