Production control of unreliable manufacturing systems with perishable inventory

Abstract

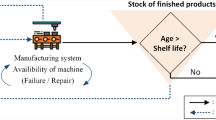
Manufacturing systems with perishable products appears in several industrial branches such as food production, chemical and radioactive material manufacturing, and pharmaceutical industry. Product perishability often results in the disposal of the fraction of products that do not meet the final specifications, after being kept too long within serviceable inventory. The disposal of perishables raises several environmental issues and its minimization together with reduction of other costs related to perishable inventories are most often studied within inventory management framework. The production control problem for the systems with perishable products, especially in case of failure-prone manufacturing facilities, is an important and challenging topic that was only sparsely addressed in the scientific literature. The main difficulty consists in resolving the trade-off between having an inventory level sufficient to fill the demand in case of machine failure, and potential deterioration of products kept too long within inventory. The paper proposes an approach to resolve this trade-off. First, a mathematical model describing the stochastic behavior of such systems is developed. Next, an analytical study of the system is performed, and finally, an optimal production policy that takes the product perishability into account is determined. This policy is shown to be a hedging point-type policy; thus the well-known result about the optimality of hedging point policy (in nonperishable case) is generalized to the class of perishable products with fixed shelf-life. It is shown that under conventional conditions (limited production capacity, Markovian failure/repair processes, constant demand rate), the optimal hedging level does not exceed the cumulative demand along the product shelf-life, and that leads to no disposal of products, known as a zero-waste policy. Numerical simulations allowed to perform the sensitivity analysis and a comparative study of the costs incurred in the systems with and without perishability.

Appendices

Appendix 1. : Conventional discrete equations for the general demand distribution

Equations below are equivalent to those developed in [9], but notation we use is slightly changed in order to allow the unified consideration of backlog y_k,1 < 0

$$ \begin{array}{@{}rcl@{}} y_{k+1,1}&=& min\{y_{k,1},0\} + u_{k} {\varDelta} t - R_{k,N} \end{array} $$

(A1.1)

$$ \begin{array}{@{}rcl@{}} y_{k+1,2}&=& max\{y_{k,1},0\} - D_{k,N} \end{array} $$

(A1.2)

$$ \begin{array}{@{}rcl@{}} y_{k+1,3}&=& y_{k,2} - D_{k,N-1} \end{array} $$

(A1.3)

$$ \begin{array}{@{}rcl@{}} {\dots} &=&{\dots} \\ y_{k+1,N}&=& y_{k,N-1} - D_{k,2} \end{array} $$

(A1.4)

$$ \begin{array}{@{}rcl@{}} {\varDelta} P_{k} =&=& y_{k,N} - D_{k,1} \end{array} $$

(A1.5)

here the conventionally defined functions y⁺ = max{y, 0} and y⁻ = − min{y, 0} are utilized; ΔP_k — indicates the quantity of perished products.

First equation differs form the others: it corresponds to the backlog case and determines the future content of the same (first) inventory layer, since there is no aging for this case; for the same reason the remaining demand R_k,N is not limited by the content of inventory (see formulas (7–9) below), but applied in full. Consecutive equations (3–5) determine the demand action followed by the transfer of remaining inventory into the next age layer. Equation (6), instead of inventory transfer, determines the quantity of perished product, since the age in this case exceeds the shelf-life limit.

To derive these equations, we follow the conventional approach allowing the demand to consume the items from any age layer, but additional priority rule ensures the application of FIFO policy. Thus, the demand depletes first the oldest inventory layer y_⋅,N, then remaining demand (if any) depletes the (N − 1)-th layer and so on. Number of items in any inventory layer except y_⋅,1 must be not negative, first layer may become negative and that corresponds to backlogged demand. This leads to the following equations for demand partitions $D_{k,s}, s=1, \dots , N$ and related quantities $R_{k,s}, s=1, \dots , N$ corresponding to the demand unmet after full depletion of s-th inventory layer.

$$ \begin{array}{@{}rcl@{}} D_{k,1}&=& min\{D {\varDelta} t, y_{k,N}\}, R_{k,1}= D {\varDelta} t-D_{k,1} \end{array} $$

(A1.6)

$$ \begin{array}{@{}rcl@{}} D_{k,2}&=& min\{R_{k,1}, y_{k,N-1}\} , R_{k,2}=R_{k,1} -D_{k,2} \end{array} $$

(A1.7)

$$ \begin{array}{@{}rcl@{}} {\dots} &=&{\dots} \\ D_{k,N}\!&=&\! min\{R_{k,N-1},y_{k,1}\}, R_{k,N} = R_{k,N-1} -D_{k,N} \end{array} $$

(A1.8)

Appendix 2. : Example of demand partitions onto several inventory age layers

Let us consider the system with U = 5,D = 4,T = 4.Δt = 1, and starts from empty inventory x(0) = 0. Let us consider the inventory growth period $u(i)=5 \text { for } i=1,\dots , 15$, then u(16) = 2,u(17) = u(18) = 1. As it is easy to see, we get (according to (1)) the full inventory growing linearly $x(i)=i, \text { for } i=1,\dots , 15$, (since u(i) − D = 1), and by i = 15 the inventory layers are: y_15,1 = y_15,2 = y_15,3 = 5,y_15,4 = 0. Further dynamics of inventory (for all 4 layers) is shown in Table 5.

Table 5 Inventory evolution

As one can see, all inventory layers at i = 19 are $y(19,s)=1, s=1, \dots , 4$ and on the next step demand D = 4 will deplete all layers at once. Inventory evolution along previous time steps $i=1,\dots , 18$ was presented to show the way of building the particular inventory distribution with this property. For all previous steps ($i=1, {\dots } 18$) the demand was acting on either one (for i = 1, 5, 6, 10, 11, 15, 16 ) layer, or on two neighboring layers (for remaining time steps).

Appendix 3. : Proposed discrete model, based on evolution of the oldest portion of inventory

$$ \begin{array}{@{}rcl@{}} y_{k+1,s} \!\!&=&\!\! \left\{ \begin{array}{ll} min\{y_{k,1},0\} + u_{k} {\varDelta} t & \text{ if } s=1 \\ y_{k,s-1}& \text{ if } 2 \leq s \leq r_{k} \end{array} \right. \end{array} $$

(A3.1)

$$ \begin{array}{@{}rcl@{}} r_{k+1}\!\!&=&\!\! \left\{ \begin{array}{ll} r_{k}+1 & \text{if } y_{k,r_{k}} >{\varDelta} D \\ r_{k} & \text{if } {\varDelta} D -y_{k,r_{k}-1} \leq y_{k,r_{k}} \leq {\varDelta} D \\ r_{k} -1 & \text{ otherwise } \end{array} \right. \end{array} $$

(A3.2)

$$ \begin{array}{@{}rcl@{}} y_{k+1,r_{k+1} }\!\!&=&\!\!\left\{ \begin{array}{ll} y_{k,r_{k}}\! - \!{\varDelta} D & \text{if } y_{k,r_{k}} \!>\! {\varDelta} D \\ y_{k,r_{k} \! -\! 1}\!+ \! y_{k,r_{k}}\! -\! \!{\varDelta} D & \text{if } {\varDelta} D\! -\!y_{k,r_{k} \! -\! 1}\! \leq \! y_{k,r_{k}} \! \leq\! {\varDelta} D \\ y_{k,r_{k}-2}\! +\! y_{k,r_{k}-1}\! + \! y_{k,r_{k}} \!\! -\!\! {\varDelta} D & \text{otherwise } \end{array} \right. \end{array} $$

(A3.3)

In equations above, the term ΔD is introduced to unify the formulation for the age layers below and on the limit r_k = N, namely:

$$ \begin{array}{@{}rcl@{}} {\varDelta} D_{k} &=& D {\varDelta} t+ {\varDelta} P_{k}, \text{ where } \end{array} $$

(A3.4)

$$ \begin{array}{@{}rcl@{}} {\varDelta} P_{k} & = & \left\{ \begin{array}{ll} y_{k,N}-D {\varDelta} t & \text{if } y_{k,N}>D_{k}\cdot {\varDelta} t, r_{k}=N\\ 0 & \text{ otherwise } \end{array} \right. \end{array} $$

(A3.5)

An additional equation links whole inventory with age-related components:

$$ x_{k} ={\sum}_{s=0}^{r_{k}} y_{k,s} $$

(A3.6)

Equations (A3.1)–(A3.6) provide the full description of the dynamical system until the shelf-life limit r_k = N is reached. It is worth noticing that for r_k = N first option in Eq. (A3.2) cannot occur (r_k cannot grow) because y_k,N = ΔD_k due to Eqs. (A3.4)–(A3.5).

Appendix 4. : Proofs of propositions and Theorem 2

Proof Proof of Proposition 1

First, it is important to note that each (infinitesimal) inventory layer of the age s at the moment ty(t,s)ds was produced at the moment t − s, therefore y(t,s)ds = u(t − s)ds ≤ Uds. Thus, the whole inventory x(t) can be expressed as an integral of age-related portions y(t,s) over all ages. We can write:

$$ x(t)={{\int}_{0}^{T}} y(t,s)ds ={{\int}_{0}^{T}} u(t-s)ds \leq {{\int}_{0}^{T}} Uds =U\cdot T $$

(A4.1)

This completes the proof because if (any) inventory level is bounded by UT, the optimal level Z^∗ is also bonded by this value. □

Proof Proof of Proposition 2

The proof of the statement is straightforward: since the demand rate is D, the volume that can be potentially consumed along the time T is ${{\int \limits }_{0}^{T}} Ddt =DT$. That will occur if there is enough product within the inventory. Alternatively, some portion of the (cumulative) demand will be backlogged, and actual volume of product consumed during interval [0,T] will be lower. □

Proof Proof of Proposition 3

First, we address the first part of the statement about the non-perishability limit: if inventory exceeds the limit DT — some part of it will be perished and disposed. Let us suppose that at some moment t₁ we have x(t₁) > DT; let us then denote an exceeding inventory by x_e = x(t₁) − DT. According to Proposition 2, the maximal volume that can be consumed along the time interval [t₁,t₁ + T] is DT. Therefore, we can write:

$$ x(t_{1}+T) = x(t_{1})-DT+{\int}_{t_{1}}^{t_{1}+T}u(t)dt \geq x_{e} $$

(A4.2)

In other words, inventory level at t₁ + T is at least x_e (it is exactly x_e if there is no production along t₁,t₁ + T). This exceeding inventory x_e has the age of at least T, as it already existed at time t₁, and, therefore, it has to be disposed as perished. This complete the first part of the proof.

To proof the second part of the statement, let us consider the level Z₁ > DT to be held as a potential hedging level and the corresponding hedging-type policy u₁(⋅) defined according to (16). Let us also define another hedging-type policy u₂(⋅), also defined according to (16) but corresponding to the level Z₂ = DT. Now, let us compare two trajectories of the system generated by these two production policies under assumption, that failures and repairs occur at exactly the same sequence of times $\{\tau _{f}^{(1)},\tau _{r}^{(1)},\tau _{f}^{(2)}, \tau _{r}^{(2)}, \dots , \tau _{f}^{(i)},\tau _{r}^{(i)}, \cdots \}$ for both cases. For simplicity, we also suppose that trajectories start at the same moment t₀ from the corresponding stationary levels (x(t₀) = Z₁) under policy u₁(⋅) (trajectory 1) and (x(t₀) = Z₂) under policy u₂(⋅) (trajectory 2) respectively. Trajectory 1 (Tr1) starts above trajectory 2 (Tr2) and also there will be necessarily some disposal of perishables, since x(t₀) > DT according to the first part of the statement.

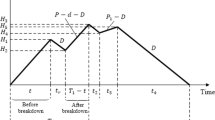
Let us first consider the situation when the machine is up (all the time). As soon as disposal occurs on Tr1, production needs to be increased, to cope with faster decay of inventory at rate D + p(t,r). Tr2, on the contrary, remains disposal-free. Thus incurred cost is higher along Tr1 (higher holding level plus disposal) than it is along Tr2.

Let us now consider the failure case. When the failure occurs (at the same moment for trajectories 1 and 2), both inventories start decreasing, and that continues along the down time (equal for both trajectories). If there is no disposal of perishables, inventories decrease with the same rate and therefore Tr1 remains above Tr2. When disposal of perishables occurs on the Tr1, inventory decreases at higher rate, but it remains above Tr2; two trajectories join when both inventories are consumed: along Tr2 — at demand rate D, along Tr1 — at rate D + p(t,r). Backlog portions of both trajectories coincide. Thus, the overall incurred cost is higher along Tr1 than along Tr2. □

Proof Proof of Proposition 4

Let us consider the disposal event and denote by t_d the moment when it occurs. The condition for the disposal to occur ((p(t_d,r) > 0) according to (11) is r = T,u_d(t_d) > D. The infinitesimal portion of product p(t_d,r)dt disposed at t = t_d was produced at time t_d − T (since its age r = T), and was not consumed (by the demand) along the interval [t_d − T,t_d]. It means that although there were probably some failures along the time interval [t_d − T,t_d], they were short enough for whole inventory gets consumed — at least the portion of products disposed at t_d remained in the inventory. Therefore no backlog occurred along [t_d − T,t_d]. Since the portion of products under study was manufactured at t_d − T we necessarily have u(t_d − T) > 0; therefore, production rate can be slightly reduced to $\tilde {u}(t_{d}-T)= u(t_{d}-T)-\epsilon$ with 𝜖 > 0, such that 𝜖 < u(t_d − T)/2 to guarantee $\tilde {u}(t_{d}-T)>0$ and small enough for not having backlog along the [t_d,T] interval. Let us keep $\tilde {u}(t)=u_{d}(t)$ for t ∈ (t_d − T,t_d]. As it is easy to see, the trajectory corresponding to $\tilde {u}(\cdot )$ is located below the trajectory corresponding to u_d(⋅) (more precisely — the portions of trajectories for t ∈ [t_d − T,t_d]. Since there is no negative inventory (backlog) — the incurred cost is lower for policy $\tilde {u}(\cdot )$ (lower holding cost and lower disposal cost since, both inventory level and volume of disposal at t = t_d are reduced). □

Proof Proof of Theorem 2

Step 1. Let us consider the case x > DT. This may only occur at the initial moment. Namely, u = D at x = Z ∗, and this yields (according to (11)) $\dot {x} \leq 0$, therefore x(t) cannot cross the “barrier” x = Z^∗≤ DT from below. However, it is still possible at the initial moment and requires considerations.

Let us study the evolution of value function v(⋅) along the trajectory Tr(x)starting at x. Since u = 0 for x > DT according to (16), we have $\frac {dx}{dt}<0$. Let us consider a point x_δ on Tr(x) and located at a small time interval δ (ahead) from it. We have v(⋅,x_δ) < v(⋅,x), since there is a positive holding cost accumulated when getting form x_δ to x. While moving in opposite way (from x to x_δ) the “cost to go” (see [32] decreases, therefore $\frac {d v}{dt}<0$ (derivative is computed along T(x)). We may now write:

$$ \frac{dv}{dt}=\frac{\partial v } {\partial x}\cdot \frac{d x}{dt} $$

(A4.3)

As $\frac {d v}{dt}<0$ and $\frac {d x}{dt}<0$, we have $\frac {\partial v }{\partial x}>0$. Therefore, the policy u = 0 satisfies the optimality condition in the form of HJB equations, since min-operation over u ∈Γ for $\frac {\partial v }{\partial x}$ results in $\frac {\partial v }{\partial x}=0$. This completes step 1.

Step 2. Let us suppose that there is such a layer $y(t,\hat {s})ds$ of age $s=\hat {s}$ at the moment t with $y(t,\hat {s})>D$, and it is the oldest one (in other words inventory with age $s>\hat {s}$ are already consumed by the demand). After a time interval $T-\hat {s}$ this layer reaches the end of the buffer. Therefore, (by moving forward in time by $T-\hat {s}$ ) it can be described as $y(T+t-\hat {s},T)ds$, and a portion of it ($y(T+t-\hat {s},T)-D)$ is perished and disposed. Let us move back in time from the moment t to the moment t − s, when this inventory layer has been produced. It can be therefore, described as y(t − s, 0)ds = u^∗(t − s)ds. At that moment of time, inventory volume must be also below DT. Therefore, time T must be sufficient to consume all the inventory at rate D, including the inventory portion under study. This contradicts the assumption that some portion of inventory is perished and disposed, and completes step 2 of the proof. □

Appendix 5. : Inventory evolution under two scenarios

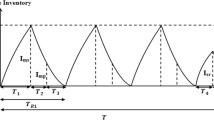
Let us start from zero inventory for both scenarios. If production is set to a maximal rate U, it takes time t₀ = DT/(U − D) to build the level Z^∗ = DT. This leads to the following inventory age distribution

$$ y (t_{0},s)= \left\{ \begin{array}{l} U \text{ if } 0 \leq s \leq DT/U \\ 0 \text{ if } DT/U < s \geq T \end{array} \right. $$

As inventory reaches the critical level x = Z^∗ = DT at time t₀, and here two scenarios diverge.

For the first scenario, the policy switches to on-demand production u = D. This results in keeping inventory level constant, although the age distribution changes: it may be shown that for t ∈ [t₀,t₀ + T] the age distribution evolves in time as follows:

$$ y (t,s)= \left\{ \begin{array}{l} D \text{ if } 0 \leq s \leq t-t_{0} \\ U \text{ if } t-t_{0} < s \geq t-t_{0} +(T+t_{0}-t)D/U) \\ 0 \text{ otherwise } \end{array} \right. $$

It is easy to see from the last equation, that the total inventory is kept at the constant level, and by t₁ = t₀ + T the uniform age distribution y(t₁,s) = D is obtained.

For the second scenario, let us keep production on maximal level for additional (short) time interval τ₁ from t₀ to t₁ = t₀ + τ₁ (u(t) = U for t ∈ [t₀,t₁]). As result, The total inventory becomes X₁ = DT + τ₁(U − D), the inventory age distribution becomes as follows:

$$ y (t_{0},s)= \left\{ \begin{array}{l} U \text{ if } 0 \leq s \leq X_{1}/U \\ 0 \text{ if } X_{1}/U < s \geq T \end{array} \right. $$

The inventory level increases above the threshold DT, it cannot be consumed by the demand during the time interval [t₁,t₁ + T]; thus, some product will inevitably perish and must be disposed. Neither policy can prevent that (it is too late), but idling for some time will minimize the loss. Namely, setting u(t) = 0 for t ∈ [t₁,t₂]) may lead to getting total inventory back to the threshold level. To calculate the value of requiredt₂ we equate the inventory increase during τ₁ to its decrease with rate D and solve an equation τ₁(U − D) = τ₂D. We get τ₂ = τ₁(U − D)/D and t₂ = t₁ + τ₂. Total inventory is down to the threshold level, the age distribution is

$$ y (t_{2},s)= \left\{ \begin{array}{l} 0 \text{ if } 0 \leq s \leq \tau_{2} \\ U \text{ if } \tau_{2} < s \geq \tau_{2} + DT/U \\ 0 \text{ otherwise } \end{array}\right. $$

We suppose that τ₁ is chosen small enough, namely, τ₁ < DT/U. This guarantees that τ₂ + DT/U < T, which means that the age of the oldest inventory layer is below the shelf-life limit, so no disposal is taking place yet. Moreover, setting production to on-demand-rate will keep total inventory constant, but this will not prevent appearance of perishables. Let us set u = D. This will not affect the evolution of inventory “block” initially located between s = τ₂ and s = r = τ₂ + DT/U, which is as follows. Its right edge r moves right with the “speed” (1 − D/U) due to aging and consumption with rate D; its left edge moves to the right with unitary speed due to aging. Therefore this “block” is shortening with the speed (D/U). The time to reach the (right) end of the buffer (s = T) can be calculated as follows:

$$ t_{3} = (T-(\tau_{2} + DT/U))/(1-D/U) = T-\tau_{1}U/D $$

The “length” of the “block” by that time is

$$ DT/U - (D/U)t_{3}=\tau_{1} $$

That means that nonzero inventory portion Uτ₁ has reached the end of the buffer, and perishability process (disposal) starts. Therefore, the inventory will now decrease with the rate U instead of D (consumed with the rate D and disposed with the rate U − D). If only total inventory is monitored, producing new product at rate D, is not sufficient to compensate for the inventory loss due to disposal. This will eventually result in inventory shortage when failures occur.