1 Introduction

Seismic anisotropy observations can provide useful information about the Earth’s interior, such as the material properties and movement patterns, which reflects its inner dynamic processes (Teng et al. 2012). With regard to seismic anisotropy in subduction zones, the geometric relationship between the fast wave polarization direction and the trench strike can be categorized into parallel, oblique, and perpendicular. Ando et al. (1983) were the first to release shear wave splitting data of subduction zones in Honshu, Japan. Since then, various scholars have conducted a series of systematic research on seismic anisotropy in subduction zones. Long and Silver (2008) and Long and Becker (2010) summarized the characteristics of seismic anisotropy for most of the world’s subduction zones. Seismic anisotropy in subduction zones mainly describes the shear wave splitting characteristics of the mantle wedge and mantle beneath the slab. The shear wave splitting characteristics of the mantle wedge are relatively complex, while the fast wave polarization directions of the subslab mantle are mostly parallel to the trench strike (e.g., Long 2013). Long and Silver (2009a, b) compiled shear wave splitting data of 15 subduction zones from previously published literatures and found that only trench migration rate correlates well with the strength of subslab anisotropy in a Pacific hotspot reference frame.

The lattice-preferred orientation (LPO) of olivine, which is the main mineral in the upper mantle, is often considered to explain the seismic anisotropy in subduction zones (e.g., Long and Silver 2008). However, a recent study indicates that hydrated products of peridotite, serpentine, with high anisotropy (about 40 % for v P and 50 % for v S) (Bezacier et al. 2010), may have more important influence on shear wave splitting of subduction zones. Different seismic splitting behavior can simply be inferred from two topotactic relationships between serpentine and olivine (Boudier et al. 2010). Alternative to the complex mixing minerals model of subduction zones, we propose a “pure” crystal model for explaining the fast wave polarization (see Sect. 6.4 for the details).

Subduction zones are the most seismically active areas in the Earth’s surface. The frequent occurrence of earthquakes offers a favorable opportunity for exploring seismic anisotropy in subduction zones. Sykes (1966) discovered the stratified phenomena for earthquakes occurring in the Kuril Islands subduction zones. With the abundance of seismic data and the continuous improvement of earthquake location accuracy, two distinct layers were found from shallow to intermediate and deep earthquakes in global subduction zones, which are known as double seismic zones (DSZs). Kao and Rau (1999) further subdivided DSZs into type I and type II according to the morphological characteristics and focal mechanism of their subducting slabs. Even a triple-layered seismic zone exists in some subduction zones, such as northeastern Japan subduction zone (Kawakatsu and Seno 1983; Igarashi et al. 2001). A significant difference has been found in the stress characteristics of different DSZ types, and this phenomenon is attributed to the dehydration of minerals in subducting slabs (Peacock 2001; Hacker et al. 2003). Recent studies showed that DSZs type is closely related to the temperature and stress field of the subducting plate and other factors (Peacock 2001; Zhang and Wei 2008; Zhang 2010). Similarly, seismic anisotropy in subduction zones is also affected by water content, temperature, and stress characteristics.

Except for some previous studies about identification, classification, and mechanism of DSZs (e.g., Kao and Rau 1999), there were increasing researchers focusing on the seismic anisotropy in subduction zones (e.g., Fouch and Fischer 1996; Polet et al. 2000; Hammond et al. 2010). Song and Kawakatsu (2012) found that fast wave polarization direction changes from trench-parallel under relatively steep subduction zones to trench-normal under shallow subduction zones. Long (2013) provided a detailed review of the subduction geodynamics from seismic anisotropy. Our study is more concerned about the seismic anisotropy within DSZs. With regard to DSZs, the scope of the study area is smaller, the type is clear, and more detailed features of subduction zones can be reflected. Moreover, DSZs widely distributed in the global subduction zones (Brudzinski et al. 2007; Zhang and Wei 2011) can reflect not only local characteristics of subduction zones, but also the general characteristics. Different types of DSZs have different slab stress states, so they represent different subduction condition, such as temperature, pressure, water content, etc. Therefore, we could have insights into subduction process through the exploration of seismic anisotropy in DSZs. In this paper, we collected both seismic anisotropy data and the related parameters of DSZs in subduction zones and statistically analyzed the relationship between seismic anisotropy in subduction zones and the type of DSZs. We attempted to find correlations between them and then used Fresnel polarization ellipsoid to discuss their geodynamical implications and physical mechanism.

2 Subduction zones and DSZs

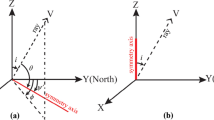
Global subduction zones are mainly classified into Mariana type and Chilean type depending on subduction angles, oceanic plate age, plate thickness, back-arc deformation pattern, and so on (Uyeda and Kanamori 1979; Stern 2002). Mariana-type subduction zones have large subduction angle and strong extension in back-arc, whereas Chilean-type subduction zones have small subduction angle and strong compression in back-arc. By combining previous research results and the stress states of the global earthquake catalogs, DSZs can be roughly divided into two categories: type I or type II DSZs, which are described by the subduction angles α s and α d, respectively (Kawakatsu 1986a; Kao and Rau 1999; Fig. 1). See Sect. 5.1 for details.

Fig. 1
figure 1

Schematic of subduction zones and subduction parameters (after Kawakatsu 1986b; Lallemand et al. 2005). V sub is the absolute velocity of the subducting plate, V t is the trench migration velocity, V up is the overriding plate velocity, V d is the deformation rate in the back-arc region, V c is the convergence velocity, α s is the shallow dip angle, and α d is the deep dip angle

Full size image

Type I DSZs are characterized by the down-dip compression (DDC) and down-dip tension (DDT) of the upper and lower layers, respectively. The layer separation (L) is approximately 20 km to 40 km. This separation decreases with subduction depth and converges fully at 200 km (Hasegawa et al. 1978, 1994). DSZs belonging to this type are mainly distributed in the subduction zones of Kuril-Kamchatka Island arc, Kanto in Japan, northeastern Honshu in Japan, Mariana, and Tonga. Unbending properties are believed to produce this type of DSZ (Kawakatsu 1986b); the slab bends downward during subduction and causes tensile stress to the convex plate. With the increase of subduction depth, the plate becomes straighter and is divided into DDC and DDT stress states by the neutral surface. Deep earthquakes are strongly influenced by temperature and subduction parameters. Other factors may also lead to the formation of deep earthquake DSZs.

Type II DSZs are characterized by a shallow focus depth and smaller layer separation (typically less than 15 km) with the same stress state. Layer separation converges at about 150 km depth and is often accompanied by lateral compression and DDT. The DSZs in the subduction zones of New Zealand’s North Island, northern Chile, northeastern Taiwan, Cascadia, Cook Inlet in Alaska, and New Britain mostly belong to this type (Kao and Rau 1999; Hacker et al. 2003; Yamasaki and Seno 2003). Mineral dehydration can cause changes in pore pressure, leading to a brittle fracture that can result in earthquakes. Dehydration is primarily concentrated in areas above 150 km, which might explain type II DSZs. However, an accurate earthquake location tool has revealed that earthquakes in the subduction zone of northeastern Japan are even distributed in three layers, because of the DSZ extending to a low-angle thrust seismic zone (Kawakatsu and Seno 1983).

Seismic-converted wave and refraction wave method can be employed to determine the upper and lower bounds of DSZs (Hasegawa et al. 1994; Ohmi and Hori 2000; Igarashi et al. 2001). Earthquake catalogs, moment tensors, and other tools can determine the stress state and related parameters of DSZs. Brudzinski et al. (2007) reported the unified standard distribution of 31 DSZs and their parameters were obtained by rotating source coordinates to the direction perpendicular to the subduction direction. They found that the layer separation of DSZs is proportional to the age of the slab. The layer separation can be estimated independently by the well-known plate age (A), thus eliminating observation errors introduced by different locational accuracy and regional networks (Zhang and Wei 2011).

However, Brudzinski et al. (2007) used trench age as the overall age of the subducting slab. Actually, this age could not accurately reflect the physical properties of the subducting slab at different subduction depths. To solve this problem, Zhang and Wei (2011) added eight new DSZs, namely four from Kamchatka, two from Juan de Fuca, and two from Nazca, based on the work of Brudzinski et al. (2007). Combined with the 31 groups of DSZ parameters provided by Brudzinski et al. (2007), totally 39 groups of DSZ parameters in subduction zones were obtained in their work (Fig. 2). Zhang and Wei (2011) comprehensively discussed the relationship between DSZs and subduction geometric, kinematic, and dynamic parameters, and the nature of the overlying plate. Further study showed that the relevant subduction geometric parameters contain slab length, maximum subduction depth, shallow dip angle, and deep dip angle. The layer separation of DSZs is positively correlated with shallow and deep dip angles. The linear relationship is not obvious, and the relationship among layer separation, slab length, and maximum subduction depth is unclear. Slab age, as an independent variable, reflects the characteristics of subduction dynamics. The linear relationship between the independent variable and layer separation is L = 0.15A + 6.55. The observations will be flattened when the plate age is greater than 80 Ma. Considering the general case, the relationship between slab age and layer separation can be expressed as L = 2.44A 1/2 − 2.36 (Zhang and Wei 2012). The layer separation of DSZs is positively correlated with absolute velocity of the subducting plate but is weakly correlated with convergence rate. This implies that the absolute velocity of the subducting plate may play an important role in DSZs.

Fig. 2
figure 2

Distribution of global subduction zones, DSZs, data, and research areas (refer to Zhang and Wei 2011). The rectangles (with thin blue lines) denote the research regions; the regions in light purple are the subduction zones. The plate abbreviations are as follows: AN Antarctic, AU Australia, PH Philippine Sea, PA Pacific, NA North America, SA South America, NZ Nazca, CA Caribbean, and JF Juan de Fuca. The figures are the numbers of the corresponding DSZs. The numbers correspond to the DSZs’ abbreviations in the large rectangle below the main figure. The red circles represent the anisotropy data and the lines represent fast wave polarization direction

Full size image

The subducting plate of type I DSZs generally corresponds to Mariana-type slabs, and layer separation is mainly correlated with age, slab pull, and other dynamic parameters. In contrast, the subducting plate of type II DSZs corresponds mostly to Chilean-type slabs, and layer separation is not only affected by dynamic factors but also related to the local stress state. The nature of the subducting slab determines layer separation in DSZs. However, there are several exceptions within the 39 subduction zones, for example, both NZ1 and NZ2 in southern America are classified as type I DSZs, while HEB in Tonga is classified as type II DSZ, and EA2 cannot be classified as either type I or type II DSZ (Zhang and Wei 2012).

3 Seismic anisotropy data in subduction zones

Schutt and Fouch (2001) and Wüstefeld et al. (2009) collected and compiled seismic anisotropy data from different studies. Several researchers, including Wirth and Long (2010) and Liu et al. (2008), also discussed the quality of the data in their studies. High-quality seismic anisotropy data generally have a high signal-to-noise ratio, a clear waveform, elliptical particle motion, and linear or nearly linear corrected particles. High-quality data require agreement between the rotation-correlation method (Ando et al. 1983) and Silver and Chan’s method (Silver and Chan 1991), namely ±10° for fast wave polarization direction ϕ and ±0.5 s for delay time δt. Fair-quality data require ±20° for ϕ and ±1.0 s for δt, a low-quality waveform, and less linear corrected particle motion. On this basis, Sun and Wei (2013) combined independent collections of global seismic anisotropy data from the recent literatures and obtained a total of 7959 related datasets after filtering and removing duplicate and poor-quality data. Given the fact that most of the anisotropic parameter error estimation for our collected data was not mentioned in the original literature, see Supporting Information attached in this study or the website at http://splitting.gm.univ-montp2.fr/DB/for more detailed information.

It is somewhat difficult for us to directly extract the seismic anisotropy in subduction zones from splitting measurements. However, many previous studies demonstrated that the dominant source of seismic anisotropy appears to be from the upper mantle in the case of teleseismic P-to-S conversions (Savage 1999; Silver 1996). Both the IASP91 model and the global anisotropic structure model by Zhang (2002) showed that seismic anisotropy of the upper mantle is quite strong despite the relatively weaker anisotropy from 300 to 600 km depth (e.g., Bastowa et al. 2015). Apart from the lower transition zone (660–1000 km) and D″ layer, anisotropy of the entire lower mantle is weak (e.g., Savage 1999; Zhang 2002).

This study mainly focuses on seismic anisotropy in DSZs. The seismic anisotropy data used in this study are mostly from SKS (SKKS, PKS etc.). If there exists anisotropy between the core-mantle boundary and the receiving station, SKS wave will be splitted into two subwaves with perpendicular polarization and various velocities. Therefore, SKS splitting could be utilized to sample the seismic anisotropy within the region between the core-mantle boundary and the receiving station (e.g., Silver and Chan 1988). Three obvious advantages of this method are as follows: (1) straightforward anisotropic observation, (2) higher tangential solution, and (3) reliable computation result and rare multiple solutions. SKS splitting has become one of the most popular research methods on the seismic anisotropy. The P-to-S wave converts at core-mantle boundary when it sequentially propagates to a station from the K-to-S wave or P-to-S wave (i.e., line segment BS in Fig. 3). Thus, delay time records the primary part of seismic anisotropy through both the mantle and crust beneath the station regions and reasonably reflects upper mantle (and crust) seismic anisotropy beneath the station areas (i.e., seismic ray path segment CS in Fig. 3) when we neglected relatively weak seismic anisotropy through the lower mantle (i.e., segment BC in Fig. 3). This is consistent with the previous studies on the global pattern of fast SKS splitting anisotropy data by Faccenda et al. (2008). They demonstrated that SKS splitting may primarily reflect seismic anisotropy in the shallow part of the slab due to aligned serpentinized cracks.

Fig. 3
figure 3

Schematic of path of the phase SKS and the anisotropic structure of the Earth, after Garnero. (http://garnero.asu.edu/research_images)

Full size image

4 Oriented statistical analysis and Rayleigh test

The scope of the related subduction zone in this study was also determined according to the starting point using the rule provided by Brudzinski et al. (2007) for the determination of DSZ profiles. The profile is the center, with 2° on both sides, and the rectangular area is the research area. All study areas were obtained from 524 sets of seismic anisotropy data (see the supplementary material for details), which are mainly distributed in 24 out of 39 DSZs. The other 15 DSZs, such as the Philippine Sea DSZs (PH1, PH2) and Hebrides (HEB) DSZs, have no data. These data from the 524 sets mainly show the cited seismic anisotropy in subduction zones from SKS splitting beneath the station areas. We used the data to study the correlations with the DSZs’ related parameters in subduction zones.

A geostatistical method was employed to analyze seismic anisotropy data in each subduction zone. The fast wave polarization direction is similar to stress orientation. Although it is not a vector, we can still apply a resultant vector summation method to deal with in most cases (Coblentz and Richardson 1995). Because the polarization directions are generally recorded in the range of 0° to 180°, measured clockwise from north, we use the double-angle technique suggested by Mardia (1972) to solve the inflating problem of the polarization directions. For example, the fast wave polarization direction 3° and 7° are almost the same orientation, but it represents opposite direction. If we directly use their values in the resultant vector summation, it will give the misleading result.

Spatial orientation data were initially multiplied by 2 and then scaled to a new equivalent unit vector. Their \(X_{i}\) and \(Y_{i}\) components were then obtained in X and Y coordinates, respectively, as follows:

$$X_{i} = \cos 2\phi_{i} ,\quad Y_{i} = \sin 2\phi_{i},$$
(1)

where \(2\phi_{i}\) is the included angle with \(X\) coordinates for the \(i\)th equivalent unit vector. Calculating all the components of the equivalent unit vectors and summing both the sines and cosines of the individual vectors, we obtain

$$X_{\varPhi } = \sum\limits_{i = 1}^{n} {\cos 2\phi_{i} } ,\quad Y_{\varPhi } = \sum\limits_{i = 1}^{n} {\sin 2\phi_{i} },$$
(2)

where \(n\) is the sample size. Mean direction \(\overline{\varPhi }\), which is the angular average of all vectors in a sample, was then obtained.

As an example, fast wave polarization direction is 40°, and its orientation could equally well be recorded as 220°. If we double these angles, we obtain 80° and 440°, which also become (440° − 360°) = 80° coinciding each other. To recover the true mean polarization direction ϕ in the defined subduction zones, we simply divide the calculated mean value \(\overline{\varPhi }\) by two (see also in Fig. 5.23 by Davis 1986).

Let the resultant length, R, be a measure of dispersion by the Pythagorean Theorem as follows:

$$R = \sqrt {X_{\varPhi }^{2} + Y_{\varPhi }^{2} } = \sqrt {\left(\sum\limits_{i = 1}^{n} {\cos 2\phi_{i} } \right)^{2} + \left(\sum\limits_{i = 1}^{n} {\sin 2\phi_{i} }\right)^{2} }.$$
(3)

However, the standardized resultant length is often used in actual statistical analysis and it is defined by

$${\bar{R}} = \frac{R}{n}.$$
(4)

Quantity \({\bar{R}}\), the mean resultant length, ranges from 0 to 1 according to Eq. (4). Large values of \({\bar{R}}\) indicate that the observations are tightly correlated with a small dispersion. We use the Rayleigh test (Mardia 1972, Chap. 6) in this study to estimate polarization direction in subduction zones. The Rayleigh test is simple and involves only the calculation of \({\bar{R}}\). This statistic is compared to a critical value of \({\bar{R}}\) for the desired level of significance. However, if the computed statistic is so large that it exceeds the critical value (Mardia 1972), the null hypothesis must be rejected and the observations might have a preferred orientation. So, the Rayleigh test determines the subduction zones for which the null hypothesis that the polarization directions are random can be rejected. It is based on the assumption that the observations come from a von Mises distribution, which is a circular equivalent of the normal distribution (Mardia 1972). If the orientation data are sampled from other distribution, the test will display misleading results. The critical values of \({\bar{R}}\) for Rayleigh’s test of a preferred trend at various levels of significance (i.e., 95 %, 97.5 %, or 99 %) and numbers of observations were provided by Mardia (1972). If the computed \({\bar{R}}\) exceeds the critical value, the null hypothesis must be rejected and a preferred polarization direction may exist in the subduction zone, which is the mean direction \(\overline{\varPhi }\).

Of all the 24 subduction slabs containing the 524 polarization records, only 20 slabs contain two or more polarization records that can be used in the above Rayleigh test. Five slabs including NZ2 and NIZ in Japan, SIZ in Izu-Bonin, and WA1 and SUM1 in Sumatra-Java failed the Rayleigh test at the 95 % confidence levels and were thus excluded. There are mainly two possible reasons that these 5 DSZs do not pass the Rayleigh test: (1) Measurement methods. Each of them with their own biases, assumptions, preprocessing steps, and error estimation procedures is widely used in researches. (2) Frequency diversity. Different frequency contains different useful information. For example, higher-frequency data for splitting analysis often contain information about near-surface seismic anisotropy (Long and Silver 2009a). These different sources of fast polarization data give random directional distributions, which imply the complex anisotropy patterns of the different splitting wave ray paths. We list their average polarization directions within the other 15 subduction slabs which pass the Rayleigh test (Table 1). Combining with four slabs only containing one polarization direction, 19 subduction slab zones in total with preferred polarization directions are listed in Table 1.

Table 1 Distribution of seismic anisotropy data in global subduction zones
Full size table

5 Statistical analysis of seismic anisotropy in subduction zones

5.1 Mean fast wave polarization direction and DSZs

The subduction angle is an important parameter describing a geodynamical property of DSZ. Lallemand et al. (2005) observed the major change in dip occurring at around 125 km depth. They thus defined a mean shallow dip between 0 and 125 km called α s and a mean deep dip for depths greater than 125 km called α d (Fig. 1). As the Mariana-type subduction zones have much larger dip angle than the Chilean-type ones, and most of the type I DSZs extend to the depth larger than 125 km, while the type II DSZs are mostly distributed shallower than 100 km, the deep angle for Mariana-type subduction zones plays a more significant role in controlling the stress state of the DSZs, and could be more feasible to describe the geometry of type I DSZs. Thus, we uniformly used a DSZ’s angle called α DSZ to define the subduction angle describing both type I and type II DSZs. α DSZ is equal to the deep dip angle α d for type I and the shallow dip angle α s for type II. We excluded one subduction zone of EA2 because it belongs to a special DDT/DDC state of subducting slab and cannot be included as either type I or type II DSZs. Among the rest of the 18 subduction slab zones with preferred polarization directions listed in Table 1, 10 α DSZ angles come from type I of the related DSZs and 8 α DSZ angles from type II DSZs. It is worth noting that we just calculated the related parameters (e.g., average fast direction, angle between trench strike and fast direction) from the data that we collected and without considering error, but it can really reflect the general characteristics. We also listed these 18 subduction angles (α DSZ) in Table 1.

Many DSZs appear to be dominated by either trench-parallel preferred fast directions (e.g., JAV1, CA2, and Kam1) or trench-perpendicular preferred fast directions (e.g., JF1, JF2, and CC1). We defined |ϕ T − ϕ| to describe the included angle between average fast wave polarization direction ϕ and trench strike ϕ T. In this study, we found that the DSZ’s type can be mostly classified by either its subduction angle α DSZ or the |ϕ T − ϕ| angle (Fig. 4a, see also Table 1). In other words, if we used two lines of α DSZ = 45° and |ϕ T − ϕ| = 45° to divide a square into four quadrants, we could find that type I and type II DSZs are preferably located in different quadrants, respectively. When the included angle |ϕ T − ϕ| is less than 45° and subduction angle α DSZ is in the range of 45° to 90°, i.e., the ‘fourth’ quadrant, the corresponding DSZs all belong to type I. Although each of them has only one set of data for Kamchatka (Kam1), Java (JAV1), and Sumatra (SUM1) DSZs, other related researches have also shown that the polarization direction is nearly parallel to trench strike in these areas (Hammond et al. 2010; Peyton et al. 2001). When subduction angle α DSZ is less than 45° and included angle |ϕ T − ϕ| is in the range of 45° to 90°, or in the ‘second’ quadrant, the corresponding DSZs are mostly type II with two type I exceptions of Aleutian (CA1) and Tonga (TON) DSZs. Moreover, the included angle |ϕ T − ϕ| is large for two type I DSZs of TON and SKUR, which are located in the ‘first’ quadrant in Fig. 4a. For example, the included angle |ϕ T − ϕ| in the northeastern Japan (JAP) DSZ is significantly large (54.3°), which may be associated with the complexity of the trench boundary and triple junction. Regardless of the subduction orientation, the statistical results show that most of the average fast wave polarization directions of type I are parallel to trench strike or the included angle is small, whereas the average fast wave polarization direction is trench vertical or nearly vertical for type II.

Fig. 4
figure 4

Relationship between anisotropy and DSZs. a Subduction angle of DSZs and anisotropy. b Relationship between average fast wave polarization direction and trench strike, APM orientation. The type I DSZs are in red, and the type II DSZs are in purple. The red line indicates a linear fit to the data without considering SC1, SMA, TON, and CA1. ϕ T is the trench strike; ϕ is the average fast wave polarization direction; |ϕ T − ϕ| means the intervening angle between trench strike and average fast wave polarization direction

Full size image

We also compared DSZs’ subduction angle α DSZ with included angle |ϕ T − ϕ| (Fig. 4a). Obviously, included angle |ϕ T − ϕ| can be reasonably constrained in the range of 0° to 90° because either ϕ T or ϕ is similar to the fault’s strike changing from 0° to 180°, measured clockwise from north. Regression results show that the included angle |ϕ T − ϕ| decreases with the increase of α DSZ. That is to say that the polarization direction tends to be parallel to the trench strike for large subduction angles, while being perpendicular to the trench strike for small subduction angles, which is consistent with that observed by Song and Kawakatsu (2012). Least squares method was used to obtain the linear relationship between α DSZ and the included angle without considering four DSZs including Mariana (SMA), Tonga (TON), Aleutian (CA1), and Nazca (SC1) DSZs. These four DSZs are located in the ‘first’ and the ‘third’ quadrants in Fig. 4a, and we will discuss them later. The calculated equation is as follows:

$$|\phi_{\text{T}} {-}\phi | = \, - 1.41\alpha_{\text{DSZ}} + \, 99.0.$$
(5)

5.2 Average delay time and DSZs

The average delay time of those 19 global subduction zones with preferred polarization directions is in the range of ~0.2 s to ~1.8 s (Table 1). There are large variations in average delay times for these slab zones, with some zones exhibiting relatively weak seismic anisotropy (e.g., JAP and SMA DSZs) and some others exhibiting delay times up to ~2 s (e.g., JAV1 and KUR DSZs). This is consistent with the complex spatial variations of shear wave splitting patterns in most mantle wedges worldwide concluded by Long and Wirth (2013). The correlations of the average delay time δt with convergence rate V c, as well with DSZ’s subduction angle α DSZ, were analyzed (Fig. 5). The average delay time δt in DSZs decreases gradually with the increase in the convergence rate V c (Fig. 5a). The corresponding relationship between average delay time δt and V c was calculated with the least squares method using the equation: δt = −0.0032V c + 1.23. Excluding Kam1, JAV1, TW, TON, and KUR DSZs (the points in black ellipse), the linear fitting result is described using the following equation:

Fig. 5
figure 5

Relationship between several subduction parameters and average delay time. a Relationship between subduction rate and average delay time. The thin red line indicates a linear fit to the data without considering Kam1, JAV1, TW, TON, and KUR. b Relationship between DSZs’ angle and average delay time; the thin red line indicates a linear fit to all data without JF2. The meanings of the symbols are the same as in Fig. 4

Full size image
$$\delta t = {-}0.015V_{\text{c}} + 1.69.$$
(6)

The value of correlation coefficient is R = −0.7333 for Eq. 6, and it is small for all points, so we can use Eq. 6 to roughly describe the relationship between average delay time δt and convergence rate V c. However, the influence of the average delay time δt is different with subduction angle. We also found a mildly linear relationship (correlation coefficient R = 0.3753) between DSZ’s subduction angle α DSZ and average delay time δt. Average delay time δt increases with DSZ’s subduction angle α DSZ (Fig. 5b), and the equation is as follows:

$$\delta t = 0.016\alpha_{\text{DSZ}} + 0.32.$$
(7)

Although we obtained an equation of DSZs’ subduction angle and delay time, they can only weakly reflect the correlation between them, and it also illustrates the complexity of seismic anisotropy in subduction zones. The relationships among average delay time δt and other related DSZ’s subduction parameters, including layer separation of DSZs, slab age, and maximum subduction depth, were also analyzed in this study. The results show that the relationships among average delay time and these related parameters are difficult to summarize with a linear relationship.

With regard to delay time, \(\delta t = L\delta \overline{\beta } /\beta_{0},\) where L is the path length, \(\beta_{0}\) is the isotropically averaged shear velocity (Silver 1996), and \(\delta \overline{\beta }\) is the dimensionless intrinsic anisotropy. Delay time is obviously associated with anisotropic material and the whole ray path, and is mainly related to the spatial distribution of the anisotropic material. Nevertheless, as we mentioned in Sect. 3, the anisotropy data used in this research mainly record the seismic anisotropy properties beneath the station areas. The statistical results show that seismic anisotropy in DSZs is related to subduction rate or other slab geometrical properties. The average delay time exhibits a linear correlation with V c and DSZ’s subduction angle α DSZ . This possibly reflects the complex geodynamical processing, i.e., different stress regime that corresponds to different types of DSZs in subduction zones.

6 Discussion and conclusions

6.1 Complexities of seismic anisotropy in subduction zones

Figure 4a shows that the included angle |ϕ T − ϕ| decreases with the increasing subduction angle α DSZ of DSZ. However, there are four exceptions to this pattern including SMA in Southern Marianas, SC1 in Southern Chile, TON in Tonga, and CA1 in Central Aleutian, which are excluded from the regression line fitting (Eq. 5). There are 15 seismic anisotropy data records in SMA region and 9 anisotropy data records in SC1 (Fig. 2; Table 1) which show the average fast wave polarization direction as trench-perpendicular (88.6°) and trench-parallel (8.5°), respectively. Both SMA and SC1 are classified as type II DSZs but they correspond to different circumstances. SMA is marked by Mariana-type slabs with large subduction angle and strong extension in back-arc, which is very different from SC1.

On the other hand, both TON and CA1 belong to type I DSZs, and they all have large angles of |ϕ T − ϕ| and subduction angle α DSZ. They exhibit similar slab morphologies but different slab kinematics. For example, we collected 12 seismic anisotropy data records in Tonga (TON) and obtained 64.3° of included angle between average fast wave polarization direction ϕ and trench strike ϕ T, which is quite different with most of the type I DSZs. Recently, a so-called source-side splitting technique has been used to yield stronger constraints on the depth distribution of anisotropy beneath subducting slabs (e.g., Foley and Long 2011; Huang et al. 2011). With this method, they demonstrated that northern Tonga exhibits a well-developed pattern of trench-parallel polarization direction with a weak trend of decreasing δt with focal depth for upper mantle events. This kind of difference thus provides support for the interpretation that the splitting primarily reflects the complexity of seismic anisotropy along the depth distribution beneath the slab.

Many measurements of delay time δt between the fast and slow arrivals of shear wave have been used, especially in the noisy environments that characterize many stations in subduction settings. These methods are mainly used to extract splitting parameters from seismograms as accurately as possible when the δt is much smaller than the characteristic period of the shear wave (e.g., Vecsey et al. 2008; Wüstefeld et al. 2009). Although the well-constrained estimates of δt can be obtained from seismogram records, the complex patterns of seismic anisotropy along a splitting ray path can result in very complicated shear wave (e.g., Silver and Savage 1994; Long 2013; Mohiuddin et al. 2015). Additional complications arise as the splitting parameters are dependent on the frequency content of the shear wave (e.g., Wirth and Long 2010]. The propagation time for each segment of the splitting wave ray path is added to the total δt, which is probably the primary reason for inducing the relatively poor linear relationship between average δt and subduction angle α DSZ (Fig. 5b). On the other hand, the average fast wave polarization direction is mainly dominated by the segment with the strongest seismic anisotropy on a splitting ray path. The part with very weak anisotropy generally decreases the degree of seismic anisotropy rather than changes the last polarization direction of the splitting wave. However, the average seismic anisotropy (δt, ϕ) we obtained in this study mainly represents the statistical mean results reflecting not only in vertical splitting wave ray paths beneath the station regions but also in horizontal area through the whole subduction zone.

In this study, we chose 39 subducting slabs along with the related information about DSZs. These slabs are mostly located around the Pacific Ocean (Fig. 2). However, we only collected approximately 500 seismic anisotropy data records. These records were less than what we expected and were distributed nonuniformly in these subduction zones. For example, these seismic anisotropy data are mainly concentrated in 24 subduction zones. If additional anisotropy data were gathered for the other 15 subduction zones (i.e., ME1, ME2, PE1, etc. in Fig. 2), the equations derived in this study will be more objective to reflect the correlations among seismic anisotropy and the other related parameters describing different types of DSZs. In addition to this, more detailed researches including geodynamical modeling constraints are also necessary to help us understand seismic anisotropy and DSZs’ properties in subduction zones.

6.2 Average seismic anisotropy (δt, ϕ) and the weighted coefficient

In fact, these fast wave polarization direction data are from different studies accompanied by different qualities. Theoretically, the greater the quality of the data is, the larger the weighted coefficient should be when we add it to the oriented statistical analysis. Since we have filtered and removed those poor-quality data having a low signal-to-noise ratio, unclear waveform, and displaying nonelliptical particle motion (Schutt and Fouch 2001; Wüstefeld et al. 2009; Sun and Wei 2013), we use an equal weighting coefficient to all the remaining high-quality and fair-quality polarization data in this study.

The delay time is potentially another factor considered as a weighted coefficient in our analysis. In terms of two defined seismic ray paths with an equal propagation length, there is a positive correlation between the delay time and the degree of seismic anisotropy (e.g., Long 2013). We can therefore put a greater weighted coefficient to the data with larger delay time record. Assuming that there are n anisotropy indicators with the weighted coefficient f i  = δt i for the i-th indicator within a defined subduction zone, the corresponding value R, which is normalized to the range of 0 to 1, can be changed by Eqs. (3) and (4) as follows:

$${\bar{R}} = \frac{1}{W}\sqrt {C^{2} + S^{2} },$$
(8)

where \(W = \sum\nolimits_{i = 1}^{n} {f_{i} }\), \(C = \sum\nolimits_{i = 1}^{n} {f_{i} \cos \theta_{i} }\), \(S = \sum\nolimits_{i = 1}^{n} {f_{i} \sin \theta_{i} }\). We calculated the average fast wave polarization directions (ϕ) of the corresponding 20 DSZs that contain two or more anisotropy indicators (Table 1), which are listed in Table 2. In comparison with Table 1, we found that most directions change no more than 10°. The most prominent change is that the average polarization direction (107.3°) in NIZ (northern Izu of Japan) passes the Rayleigh test now and can be used in the linear regression. The subduction angle α DSZ and the included angle |ϕ T − ϕ| for NIZ in this case are 58.6° and 31°, respectively. Using the least squares method, we calculated the linear equation as |ϕ T − ϕ| = −1.49α DSZ + 103.0 without considering SC1, SMA CA1, and TON as before. This agrees well with Eq. (5) in Sect. 5.

Table 2 Weighted statistical analysis of the DSZs
Full size table

6.3 Seismic anisotropy and absolute plate motions

The statistical analysis method adopted in this study presumes that the observed vectors are sampled from a von Mises distribution. In this case, if the vectors were actually sampled from another type of distribution, the test would provide misleading results. Moreover, the statistical analysis method of directional data was used to study the overall reflection of seismic anisotropy in the research area. However, this method cannot highlight the area’s local characteristics. In terms of the amount of data, seismic anisotropy data cannot cover all of the DSZs. The data distribute unevenly in the DSZs, which affects the statistical result. Another limitation of this study is that we did not consider an original signal for collecting data. We merely filtered available data and did not classify them. Data classification is necessary for a more detailed study in the future.

We use the absolute plate motion (APM) model to calculate plate motion and further compare it with the anisotropy, though the relevance between them is not definitely determined. In some subduction zones, such as the northeastern Japan, the fast wave polarization direction is likely related to the relative plate motion (Nakajima and Hasegawa 2004). Nevertheless, some previous studies have found that the seismic anisotropy is highly relevant to the APM of the Earth’s surface areas, including the subduction zones, the mid-ocean ridge, and the interior of the continental plates (Debayle et al. 2005; Wang et al. 2008). Sun et al. (2013) conducted a statistical analysis to examine the relation among seismic anisotropy, plate motion, and stress orientations. Their results showed that APM is highly correlated with the seismic anisotropy in the interiors of the Arab, Caribbean, Juan de Fuca, North America, Nazca, the Pacific, and South America plates. However, the case of Africa, Antarctica, Australia, Europe, and Asia, including India and Philippine Sea, is weakly related to APM.

We use the APM model HS3-NUVEL-1A (Gripp and Gordon 2002) to determine the direction of subduction and the rate of the subducting plate. The APM directions of the 18 DSZs that contain seismic anisotropy data passing the Rayleigh test are listed in Table 2. These APM-related factors were also analyzed in relation to average delay time and average fast wave polarization direction. However, there is no obvious relationship between these APM-related factors and average delay time or average fast wave polarization direction. For example, the included angle |ϕ T − ϕ| shows a random distribution with the included angle between the direction of absolute plate motion ϕ APM and average fast wave polarization direction ϕ (Fig. 4b). This is somewhat different from the early theory of plate tectonics, in which the upper mantle flows should be consistent with the direction of plate convergence.

6.4 Olivine’s LPO and a possible crystal description of the subducting oceanic lithosphere

DSZs’ subduction angle, one of the important parameters for DSZs, not only describes the type of the subduction zone, but also reflects the different slab morphology. Complex slab morphology has also been invoked to explain the complex splitting patterns in subduction zone (Kneller and van Keken 2007). It is generally agreed that olivine’s LPO makes the primary contribution to mantle anisotropy. High-pressure and high-temperature experiments have shown that many types of LPO in olivine can be determined based on stress, pressure, temperature, and water content (Jung et al. 2006). Katayama and Karato (2006) studied the influence of temperature on the LPO of olivine and found that water-rich, low-stress, or high-temperature conditions produce type C LPO, whereas high-stress or low-temperature conditions produce type B LPO. The DSZ in northeastern Japan (JAP) satisfies the condition of type B LPO and is a cold subduction zone where an old plate is subducted. The DSZ in Juan de Fuca (JF1, JF2) is a warm subduction zone where a young plate is subducted and this DSZ satisfies the condition of type C LPO of olivine (Katayama and Karato 2006). Different types of LPO are often used to explain seismic anisotropy characteristics in subduction zones (e.g., Nakajima and Hasegawa 2004; Long and Silver 2008, 2009a, b).

Statistical results in Sect. 5.1 of this study showed that fast wave polarization direction changes gradually from trench-perpendicular to trench-parallel with the increase of subduction angle, which is similar to the results of Song and Kawakatsu (2012). In this study, we try to propose a possible crystal description of the subducting oceanic lithosphere to explain the above statistical results.

In Fig. 6a, we treat subducting oceanic lithosphere as a large crystal with three mutually orthogonal polarization direction, where the three axes α 1, α 2, and α 3 represent the trench-perpendicular, trench-parallel, and the vertical directions, respectively. We consider it as a Fresnel polarization ellipsoid with three axes of α 1, α 2, and α 3 in Fig. 6b. In this case, the increase of subduction angle is equivalent to the Fresnel polarization ellipsoid rotating around the α 2 axis in the counterclockwise direction. We can thus obtain the velocity and polarization direction of the wave by solving the Christoffel equation (Musgrave 1970) when the elastic constants of the anisotropic crystal medium are known, and then calculate the relationship between subduction angle and fast wave polarization direction in the horizontal plane projection.

Fig. 6
figure 6

Schematic of mechanism. a Schematic of seismic anisotropy in subduction. The three mutually orthogonal axes α 1, α 2, and α 3 represent the trench-perpendicular, trench-parallel, and the vertical directions, respectively, and α 1 > α 2 > α 3 . β is the subduction angle. b The corresponding Fresnel polarization ellipsoid

Full size image

We are more concerned about the fast wave polarization direction in this study. Olivine, as the main mineral of the upper mantle, is generally most easy to deformation and orientation (Mao et al. 2015), which is often considered to be the main source of seismic anisotropy of this layer (e.g., Savage 1999). Therefore, we adopted olivine’s elastic constants provided by Abramson et al. (1997) in calculation, which is similar that of Song and Kawakatsu (2012). Firstly, when α 1 axis is exactly along the trench-perpendicular direction, the theoretical included angle between fast wave polarization direction and trench strike jumps from 90° to 0° when the subduction angle is larger than about 8° (black dotted line in Fig. 7), which may be due to the symmetry of the elastic constants. Nevertheless, it is not consistent with the above statistical results that we obtained. So we let α 1 axis be slightly declined with θ = 2° from the trench-perpendicular direction (Fig. 6a). In this case, the corresponding calculated included angle between fast wave polarization direction and trench strike is not a jump but changes continuously from 90° to 0° with the increase of subduction angle, which is shown as black line in Fig. 7. We can find that it basically reflects the polarization rotation property of the Fresnel ellipsoid although it is quite different from the observed statistical results.

Fig. 7
figure 7

Relationship between subduction angle and fast wave polarization direction. θ is the included angle between fast wave polarization direction (α 1) and normal direction of the trench strike; |ϕ T − ϕ| is the included angle between trench strike and average fast wave polarization direction; α DSZ is the DSZs’ subduction angle. Black dotted line indicates that |ϕ T − ϕ| changes with α DSZ when θ is 0°; Black line indicates that |ϕ T − ϕ| changes with α DSZ when θ is 2°; blue line indicates that |ϕ T − ϕ| changes with α DSZ when θ is 2° after modifying the elastic constants (c23 + 80,c13 + 53). The red line indicates a linear fit to the data without considering SC1, SMA, TON, and CA1

Full size image

Furthermore, we tried to simulate the observed statistical results by modifying the elastic constants of the olivine crystal. We gave a well simulation model shown as blue line in Fig. 7 after a lot of tries, and the corresponding modified elastic constants are listed in Table 3.

Table 3 Modified elastic constants
Full size table

The average fast wave polarization direction is mainly dominated by the oceanic lithosphere segment with the strongest seismic anisotropy on the entire splitting ray path as we discussed in Sect. 6.1, and the modified model describing the subducting oceanic lithosphere may reflect the mixture effect of olivine and other minerals, e.g., serpentine. If we considered the subducting oceanic lithosphere as the modified crystal model, the observed fast wave polarization direction corresponding to different subduction angles in subduction zones can be reasonably explained by rotating the oceanic lithosphere around the trench (or α 2 axis in Fig. 6) in the counterclockwise direction from 0° to 90°. In summary, the average fast wave polarization direction ϕ is strongly dependent on both the trench orientation ϕ T and DSZs’ subduction angle α DSZ (see Eq. 5). When comparing to the previous Olivine’s LPO theory, the Fresnel polarization ellipsoid model describing the subducting oceanic lithosphere in this study can provide a more reasonable explanation to the strong |ϕ T − ϕ| and α DSZ correlation in DSZs.