Introduction

Increase in the energy demand has focused on the alternate energy conversion technologies. Solid oxide fuel cells (SOFCs) offer far more efficiency in conversion of chemical energy in fuels into electricity (65 % for electric power and 85 % efficient for cogeneration). There is worldwide interest in reducing the operating temperature of SOFCs to 500–700 °C for long-term stability and lower cost [1]. This, however, requires increased ionic conductivity of the electrolyte in this temperature range. SOFCs using such electrolytes are called intermediate temperature solid oxide fuel cells (IT-SOFCs).

There is a lot of literature on the improvement of ionic conductivity of solid electrolyte materials, e.g., zirconia, ceria, lanthanum gallate, and bismuth-based oxides [2–6]. Among these materials, ceria doped with aliovalent cations of rare earth and alkaline earth elements has been found to be a promising electrolyte for IT-SOFCs [7–9]. Ionic conductivity of doped ceria resulting from oxygen vacancies depends on the nature and concentration of the dopant [7, 10]. Doped ceria electrolytes such as Ce1 − xGdxO2 − δ (GDC), Ce1 − xSmxO2 − δ (SDC), and Ce1 − xYxO2 − δ (YDC) show high ionic conductivity. Ceria-doped singly with Sm has been reported to exhibit the highest conductivity among the singly doped ceria materials [11, 12]. But, Sm2O3 is very costly. It is important to develop new cost-effective ceria-based electrolyte materials having higher ionic conductivity for IT-SOFCs.

In order to reduce the cost and increase ionic conductivity, co-doping approach has been used and found to be effective. Herle et al. [13] found that co-doping of ceria with rare earth and alkaline earth ions showed significantly higher ionic conductivity than the singly doped materials. Some co-doped ceria electrolytes which have been investigated are Ce1 − x − ySmxCayO2 − δ [14], Ce0.80Sm0.20 − xYxO2 − δ [15], Ce1 − xSm0.15 − xGdxO1.925 [16], Ce0.85Gd0.10 Mg0.05O2 − δ [17], and Ce1 − x − yGdxPryO2 − δ [18]. Yifeng et al. [19] studied electrical properties of Ce0.80Sm0.20 − xMgxO2 − δ samples synthesized by solid state reaction by sintering at 1,550 °C. They found that substitution of Mg for Sm up to 50 mol% increases slightly the conductivity than that of ceria doped with Sm only. Yifeng [19] and Yueming Shi et al. [20] studied the electrical properties of Ce1 − xLax − yCayO2 − δ electrolyte materials and observed that the composition Ce0.85La0.10Ca0.05O2 − δ has the maximum conductivity (3.56 × 10−2 at 700 °C) of all the compositions studied. Cioatera et al. [21] studied the effect of addition of Sr on properties of europium-doped ceria. It was found that an optimum ratio of europium/strontium increased the conductivity, and this increase was mainly due to decrease in the grain boundary resistance. Some other co-doped ceria electrolytes studied are Ce0.80 − xSm0.20SrxO2 − δ [22], Ce0.80 − xGd0.20SrxO2 − δ [23], and Ce0.80Y0.20 − xSrxO2 − δ [24]. An improvement in the conductivity has been found in these systems due to decrease in the grain boundary resistance.

In our previous reports, effect of strontium addition on conductivity of singly La-doped ceria, Ce0.85La0.15O1.925 samples having the same number of oxygen vacancies was studied [25]. In the present work, La and Sr co-doped ceria viz Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} have been prepared to study the effect of increasing oxygen vacancies on the ionic conductivity by changing the concentration of Sr. It was considered worthwhile to study ionic conductivity of these materials because if these have more or comparable conductivity with Sm- or Gd-doped ceria as mentioned above, their use will reduce the cost drastically. A significant improvement in the electrical conductivity has been observed by co-doping ceria with lanthanum and strontium.

Experimental

Sample preparation

A series of samples in the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} (x = 0.0, 0.025, 0.050, and 0.075) have been prepared by citrate-nitrate route using ammonium ceric nitrate (99 % purity, Qualikems, India), lanthanum oxide (99.9 %, Sigma-Aldrich), strontium nitrate (99.5 % purity, Reidel Chemicals, India), and citric acid (99.5 % purity, Loba Chemie, India) as starting materials. La(NO3)3 has been prepared by dissolving required amount of La2O3 in dilute nitric acid followed by heating at 100 °C to dryness water. This gives La(NO3)3 which is then dissolved in distilled water to get an aqueous solution. Solutions of other metal nitrates in distilled water were prepared separately. An aqueous solution of citric acid was added to the mixed solution of nitrates to give a citrate to nitrate ratio, C/N ~0.3 for controlled combustion [26]. The mixed solution was evaporated on a hot plate with constant stirring at approx 200 °C. The solution became viscous and turned into a gel during heating. The gel slowly foamed and finally burnt on its own giving light yellow color ash. Ash was calcined at 800 °C for 4 h. The calcined powder was pressed under a load of 50 kN into cylindrical pellets having ~15 mm diameter and ~2 mm thickness. These pellets were sintered at 1,350 °C for 4 h in air.

Characterization

Powder X-ray diffraction (XRD) patterns were recorded with the help of a Rigaku high resolution powder X-ray diffractometer employing CuKα1 radiation using Ni filter at room temperature. Data were collected in the 2θ range from 20° to 80°. Lattice parameter was determined using nonlinear least square fitting “UnitCell” software [27]. Average crystallite size, D, was determined using Scherrer’s formula:

$$ D=0.9\lambda /\beta cos\theta $$
(1)

where β is the full width at half maxima (FWHM) excluding instrumental broadening, λ is the wavelength of X-rays, and θ is Bragg angle. β is taken for the strongest Bragg’s peak corresponding to (111) reflection for all the samples. For determining instrumental broadening, XRD of a single crystal of Si is done by scanning at a very slow speed around strongest peak of Si which occurs at 2θ = 28.424° corresponding to (111) reflection. The broadening of the peak, β s, corresponding to (111) plane is 0.132° which is taken as instrumental broadening. β is calculated by using the formula:

$$ \beta =\sqrt{\beta_m^2-{\beta}_s^2} $$

where β m is the FWHM of Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} calcined powders determined by XRD. Density of sintered pellets was determined using Archimedes principle. Sintered samples were weighed in air. Samples were then immersed in kerosene in a beaker and kept in a vacuum desiccator for 2 h to ensure that kerosene filled the open pores completely. Then, weights were taken in suspended state in kerosene and after removing from kerosene, wiping out the pellet with a tissue paper (soaked weight). Bulk density was calculated as follows:

$$ Bulk\; Density=\frac{W_d}{W_s-{W}_a}\times Density\; of\; Kerosene $$
(2)

where W d , W s , and W a are the dry weight, soaked weight, and suspended weight of the sample, respectively. Density of kerosene is 0.81 gm/cm3.

Bright field transmission electron micrographs of the calcined powders were taken using Technai-G2 (FEI, Eindhoven, Netherlands) electron microscope equipped with SIS Mega View III CCD camera (FEI, Eindhoven, Netherlands) at 120 KV employing Analysis software (SIS, Muenster, Germany). Samples were dispersed in double distilled water by sonication and dropped on a conventional carbon-coated copper grid. Sintered pellets were polished using emery papers of grade 1/0, 2/0, 3/0, and 4/0 (Sia, Switzerland) followed by polishing on a velvet cloth using diamond paste of grade 1/4-OS-475 (HIFIN). Then, these were etched thermally at 1,250 °C. Micrographs of thermally etched samples were taken using a scanning electron microscope (INSPECT 50 FEI’).

Impedance analysis

Both the surfaces of sintered pellets were polished. Silver paint was applied on both the surfaces. The paint was matured by heating at 700 °C for 15 min. Impedance measurements were made in the temperature range 200–600 °C using a Novocontrol Alpha-A High Performance Frequency Analyzer in the frequency range 1 Hz to 1 MHz by applying 20-mV external ac signal. Data were collected using “Win data” program and fitted to equivalent circuit using ZView software.

Results and discussion

Crystal structure

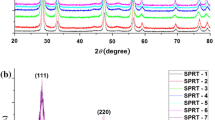
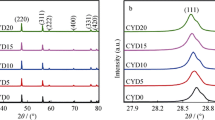
Powder XRD patterns were recorded to check the phase purity of powder and to determine the crystal structure. Figure 1a–d shows powder XRD patterns of all the samples. Diffraction patterns were indexed on the basis of fluorite structure similar to CeO2 using JCPDS file no. 43-1002. It has been observed that (111) and (200) peaks shift toward lower 2θ angle with increasing Sr content (x). This indicates that unit cell of co-doped ceria expands with increasing concentration of dopants. Lattice parameters determined by nonlinear least square fitting of the X-ray data using UnitCell program are given in Table 1. Increase in lattice parameter on substitution of La3+ and Sr2+ is attributed to larger ionic radius of La3+ (1.16 Å) and Sr2+ (1.26 Å) as compared to Ce4+ (0.97 Å) [28]. Variation of lattice parameter with strontium concentration is shown in Fig. 2. It can be seen that lattice parameter increases linearly with increase in Sr content following Vegard’s law [29]. This variation can be represented as

$$ a(x)=0.54557+0.04228 x $$
(3)
Fig. 1
figure 1

Powder X-ray diffraction patterns of the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} for a x = 0.0, b x = 0.025, c x = 0.050, and d x = 0.075

Full size image
Table 1 Crystallite size (determined from the X-ray line broadening), lattice parameter, and % theoretical density of compositions of the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)}
Full size table
Fig. 2
figure 2

Variation of lattice parameter as a function of Sr concentration for the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)}

Full size image

Average crystallite size calculated using Eq. (1) is given in Table 1. Sintered pellets have density more than 95 % of the theoretical values (Table 1).

Microstructure

Typical bright field transmission electron micrographs of the calcined powder of Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} are shown in Fig. 3a, b. These images clearly indicate that some particles are spherical and some are faceting in nature. Some agglomerated particles are also observed. TEM images show that average crystallite size lies in the range 18–30 ± 4 nm. This is in good agreement with the results obtained from XRD data of calcined powders (given in Table 1). Figure 4a–d show scanning electron micrographs of samples thermally etched at 1,250 °C. Micrographs reveal a dense structure and well-defined grains separated by grain boundaries. All the samples have grains of varying size. It is observed that average grain size increases with increasing concentration of Sr. Average grain size determined using linear intercept method is approx 1.0, 2.0, 4.5, and 5 μm for samples with x = 0.0, 0.025, 0.05, and 0.075, respectively.

Fig. 3
figure 3

a BFTEM images of the compositions in the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} with x = 0.0 and 0.025. b BFTEM images of the compositions in the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} with x = 0.05 and 0.075

Full size image
Fig. 4
figure 4

Scanning electron micrographs of the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} for a x = 0.0, b x = 0.025, c x = 0.050, and d x = 0.075 thermally etched at 1,250 °C

Full size image

Electrical conductivity

Electrical conductivity of the samples has been determined using complex plane impedance analysis. Impedance plots for all the compositions at 200 °C are shown in Fig. 5. Typical impedance plots of the composition with x = 0.025 at different temperatures are shown in Fig. 6. At 200 °C, arcs corresponding to grains and grain boundaries are clearly seen. As temperature increases, relaxation frequency of various polarization processes increases leading to shifting of arcs toward higher frequency. Therefore, all the three arcs are not observed at all the temperatures in the limited range of frequency of measurements. Arcs due to grains and grain boundaries are associated with capacitance in the pF and nF range, respectively, determined from the relation 2π f max RC = 1, where f max is the applied frequency at the arc maximum and R is the resistance obtained from the intercept of the arcs on Z′ axis. Impedance spectra were fitted to the equivalent circuits shown in Fig. 6. In equivalent circuits, the terms R1-CPE1 and R2-CPE2 refer to the resistance and constant phase element of the grains and grain boundaries, respectively. Use of a simple capacitor is not sufficient to model the electrical response of these materials due to microstructural inhomogenieties in the sample. A constant phase element (CPE) is, therefore, used to fit the data [30]. CPE is equivalent to a distribution of capacitors in parallel. Total resistance (R t) of the electrolyte is given by the sum of resistance of grains (R g) and grain boundaries (R gb). Conductivity, σ, at different temperatures can be obtained using the formula:

$$ \sigma =\frac{L}{S\times {R}_t} $$
(4)

where L and S represent the thickness and area of the sample, respectively.

Fig. 5
figure 5

Impedance plots of system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} for a x = 0.0, b x = 0.025, c x = 0.050, and d x = 0.075 at 200 °C

Full size image
Fig. 6
figure 6

Impedance plots for the composition with y = 0.025 at temperature a 200 °C, b 300 °C, c 350 °C, and d 600 °C

Full size image

Arrhenius plots for ionic conductivity of grains for all the compositions are shown in Fig. 7. It is clear that conductivity of grains increases for the composition with x = 0.025 followed by a decrease at higher concentration of Sr2+. The enhancement in bulk conductivity is ascribed to an increase in the number of oxygen vacancies and suppression of ordering of oxygen vacancies which leads to a decrease in the activation energy for diffusion of O2− ions [31]. Bulk conductivity decreases at higher concentration of Sr2+. It may be due to increase in the number of neutral associated defect pairs [Sr ′ ′ Ce  − V · · O ]x which reduces free oxygen vacancies leading to a decrease in the conductivity [21].

Fig. 7
figure 7

Ln σ g T versus 1,000/T plots of all the compositions of the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)}

Full size image

It is noted from Fig. 7 that Arrhenius plots of co-doped samples show a change in the slope at 350 °C. It is interpreted as a transition from associated defect pairs (regions where oxygen vacancies are bound to cation defects) to dissociated defects (regions where oxygen vacancies are free). In the low temperature range, activation energy (E a) is equal to sum of migration enthalpy (E M) and association enthalpy (E A), and in the high temperature region, it is equal to migration enthalpy only. At low temperatures, concentration of charge carriers is determined by the thermodynamic equilibrium between the free defects and associated defect pairs viz [La ′ Ce  − V · · O ]· and [Sr ′ ′ Ce  − V · · O ]x [21]. Activation energy of conduction, E g, has been determined using Arrhenius relationship:

$$ {\sigma}_{\mathrm{g}}=\frac{\sigma_{0\mathrm{g}}}{\mathrm{T}}\cdot \exp \left(\frac{-{E}_{\mathrm{g}}}{\mathrm{kT}}\right), $$
(5)

where σ 0g is the pre-exponential factor, k is the Boltzmann constant, and T is absolute temperature. Values of activation energy for bulk ionic conductivity, E g, for all the samples determined by fitting the data in Fig. 7 to Eq. (5) are given in Table 2. Activation energy for bulk conductivity of co-doped samples is lower than that of Ce0.85La0.15O1.925. It can be noted from Table 2 that activation energy is more at low temperature and less at higher temperatures. Value of association energy (E A = E a − E M) has been found to be minimum for the composition with x = 0.025 which is 0.29 eV. It increases with increasing Sr content.

Table 2 Total conductivity at 600 °C, activation energy of grains (E g), grain boundaries (E gb), and total (E t) conductivity of various compositions in the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)}
Full size table

Arrhenius plots for the specific grain boundary conductivity of all the samples are shown in Fig. 8. These plots are linear having single slope. Specific grain boundary conductivity, σ ∗ gb , was calculated using the following equation:

$$ {\sigma}_{g b}^{\ast }=\frac{C_g}{C_{g b}}{\sigma}_{g b} $$
(6)

where C g and C gb are the bulk and grain boundary capacitance. σ gb is the macroscopic grain boundary conductivity calculated from R gb and the macroscopic dimensions of the sample [32]. It can be seen that grain boundary conductivity of co-doped samples is more than that of Ce0.85La0.15O1.925. This clearly shows that doping with Sr has a significant influence on the conductivity of grain boundaries. This may be due to scavenging effect of strontium which removes siliceous impurities present at grain boundaries. Silicon increases the grain boundary resistance due to formation of resistive silicate phases. Sr2+ reacts with silicon present at the grain boundaries to form a second phase. This phase segregates at grain triple point junction rather than being present at the entire grain boundaries. Therefore, majority of grain boundaries become free from the resistive silicate phases. This increases the conductivity of grain boundaries substantially. This mechanism has been reported earlier [8, 33–35]. It has been reported by Gerhardt et al. [36] that grain boundary scavenging effect depends on the concentration and size of dopant. Concentration and size of the dopants control how much Si goes into solid solution and how much is segregated. On the basis of scanning transmission electron microscopy (STEM) combined with energy dispersive X-ray microanalysis (EDXM) and electron energy loss spectroscopy (EELS), Gerhardt et al. [37] reported that in yttrium-doped ceria, there exists an amorphous silica thick layer surrounding the grains. This layer blocks the charge carriers leading to increase in the resistivity of the grain boundaries. They also observed the formation of some silicate phases of yttrium. These phases pocket at the triple point junction leaving clean grain to grain contact area. Therefore, the amount of Si decreases as the concentration of dopants increases, i.e., less amount of Si is available for the formation of thick boundary layer. Similar silicate phases might have formed in the materials under present investigation. The exact compositions, morphology, and distribution of these phases require analytical studies as mentioned above.

Fig. 8
figure 8

Ln σ ∗gb T versus 1,000/T plots of all the compositions of the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)}

Full size image

To confirm the scavenging effect of strontium for grain boundaries, the influence of the grain boundary conductivity on the total conductivity is evaluated through the blocking factor (α R ) proposed by Gerhardt et al. [36]:

$$ {\propto}_R={R}_{g b}/{R}_g+{R}_{g b} $$
(7)

where R g and R gb are the resistance of the grains and grain boundaries. α R gives the fraction of charge carriers being blocked at the impermeable internal surface under measuring conditions with respect to total number of charge carriers in the samples. The lowest blocking factor, 0.29, has been observed in the sample with x = 0.025 at 375 °C which is much less than the value 0.90 [25] obtained for singly La-doped ceria. Therefore, it is concluded that strontium is an effective grain boundary scavenger.

It can also be observed that grain boundary conductivity increases with decreasing average grain size of the co-doped samples. This is because for small grain size, i.e., larger grain boundary area, the finite amount of impurity contained in the sample is not sufficient to form a continuous and uniform glassy phase layer along grain boundaries. This leaves the remaining grain boundary area for clean grain to grain contact [38]. Therefore, the transport of O2− ions becomes faster across the grains through clean grain boundaries.

Activation energy of the conduction for the grain boundaries, E gb, was determined by fitting the data in Fig. 8 to Arrhenius relationship (Table 2):

$$ {\sigma}_{gb}^{\ast }=\frac{\sigma_{0 gb}^{\ast }}{T} exp\left(-\frac{5 gb}{kT}\right) $$
(8)

Values of activation energy for the grain boundary conduction are given in Table 2.

Plots of Ln σ t·T versus 1,000/T for all the compositions along with Ce0.85La0.15O1.925 are shown in Fig. 9. Total conductivity of co-doped samples increases for the composition with x = 0.025 as compared to the sample with x = 0.00. On further increasing concentration of Sr, total conductivity decreases. Values of activation energy of total ionic conductivity, E t, determined by fitting the data points in Fig. 9 to Eq. (9) are given in Table 2.

Fig. 9
figure 9

Ln σ t T versus 1,000/T plots of all the compositions of the system Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)}

Full size image
$$ {\sigma}_t=\frac{\sigma_{0 t}}{T} exp\left(-\frac{E_t}{KT}\right) $$
(9)

Values of total conductivity at 600 °C for all the compositions are given in Table 2. Composition with x = 0.025 exhibits the highest conductivity among all the compositions. Its conductivity at 600 °C is higher than the highest values of conductivity reported for the compositions Ce0.8La0.14Y0.06O1.9 (6.1 × 10−3 S/cm) [39] Ce0.8Sm0.2O1.9 (SDC) (1.20 × 10−2 S/cm) [40], and Ce0.8Gd0.2O1.9 (GDC) (1.29 × 10−2 S/cm) [41] at 600 °C. This may make it a potential candidate as a solid electrolyte for IT-SOFCs. Its cost is definitely much less than the cost of CeO2 singly doped with Sm and Gd as mentioned above. This is because La2O3 is cheaper than Sm2O3 and Gd2O3. Its compatibility with other cell components, however, is necessary for its application in IT-SOFC, and this needs to be checked.

Partial replacement of La with Sr in CeO2 has some opposite effects. It leads to increase in number of oxygen vacancies. Ordering of oxygen vacancies is also suppressed due to co-doping [31]. This leads to decrease in the activation energy for conduction and increases the ionic conductivity. Sr2+ also acts as a grain boundary scavenger. This decreases the grain boundary resistance and hence increases the grain boundary conductivity as well as total conductivity. Number of associated defect pairs and their association energy increase with increasing Sr2+ substitution. This leads to decrease in the ionic conductivity. Deviation of lattice parameter on substituting La3+ and Sr2+ from that of undoped ceria increases the strain in the lattice because ionic radius increases in the order Ce4+ < La3+ < Sr2+ [42]. This increases the activation energy for diffusion of O2− ions. Due to complex interplay of these opposite competing effects, conductivity increases for x = 0.025 followed by a decrease at higher concentration, i.e., x > 0.025.

Conclusions

Co-doped ceria samples with nominal compositions Ce0.85La0.15 − xSrxO{2 − (0.075 + x / 2)} where x = 0.025, 0.050, and 0.075 have been synthesized and studied to compare the conductivity with singly doped ceria. Single-phase solid solution has formed in all the compositions. For x = 0.025 by sintering at 1,350 °C, 98 % theoretical density has been achieved. Composition with x = 0.025 exhibits higher ionic conductivity than that of ceria-doped singly with La and almost equal to the best reported values for Ce0.8Sm0.2O1.9 and Ce0.8Gd0.2O1.9 at 600 °C. This makes it a potential candidate as a solid electrolyte for IT-SOFCs being much cheaper.