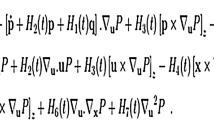Abstract
In this work, the theoretical model explaining the frequency scaling and multi photon effects in metal nanoparticles has been suggested. Its capabilities are demonstrated in relation to the second and third harmonic generation phenomena and the four-wave mixing phenomena as well. The continuum mechanical description of the electron gas of valence electrons underlies the theory. The principal equations of motion are deduced by the Hamilton’s least action principle. The compatibility of the model with the Drude theory is demonstrated in the linear case. On the basis of the proposed model, we investigate the effect of Coulomb interaction in clusters of metal nanoparticles and the resulting motion of particles under the assumption of the compliance of an ambient medium.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bharadwaj P, Deutsch B, Novotny L (2009) Optical antennas. Adv Opt Photon 1:438–483
Lippitz M, van Dijk MA, Orrit M (2005) Third-harmonic generation from single gold nanoparticles. Nano Lett 5(4):799–802
Bachelier G, Butet J, Russier-Antoine I, Jonin C, Benichou E, Brevet PF (2010) Origin of optical second-harmonic generation in spherical gold nanoparticles: local surface and nonlocal bulk contributions. Phys Rev B 82:235403
Slater JC (1967) Insulators, semiconductors and metals. McGraw-Hill, New York
Drachev VP, Chettiar UK, Kildishev AV, Yuan HK, Cai W, Shalaev VM (2008) The Ag dielectric function in plasmonic metamaterials. Opt Express 16(2):1186–1195
Amendola V, Bakr OM, Stellacci F (2010) A study of the surface plasmon resonance of silver nanoparticles by the discrete dipole approximation method: effect of shape, size, structure, and assembly. Plasmonics 5:85–97
Madelung O (1972) Festkorpertheorie I, II. Springer, Berlin
Schrieffer JR (1983) Theory of superconductivity. Benjamin–Cummings, Reading
Clemmow PC, Dougherty JP (1969) Electrodynamics of particles and plasmas. Addison-Wesley, New York
Kohn W (1999) Nobel lecture: electronic structure of matter—wave functions and density functionals. Rev Mod Phys 71(5):1253–1266
Bauer D, Ceccherini F (2001) Time-dependent density functional theory applied to nonsequential multiple ionization of Ne at 800 nm. Opt Express 8(7):377–382
Landau LD, Lifshitz EM (1986) Theoretical physics: hydrodynamics, vol. 6. Nauka, Moscow
Stout B, Auger JC, Devilez A (2008) Recursive T matrix algorithm for resonant multiple scattering: applications to localized plasmon excitations. JOSA A 25:2549–2557
Romero I, Aizpurua J, Bryant GW, de Garcia Abajo FJ (2006) Plasmons in nearly touching metallic nanoparticles: singular response in the limit of touching dimers. Opt Express 14(21):9988–9999
Letnes PA, Simonsen I, Mills DL (2011) Substrate influence on the plasmonic response of clusters of spherical nanoparticles. Phys Rev B 83:075426
Serebrennikov AM (2011) Multipolar resonant particle modes as elementary excitations in chain waveguides: theory, dispersion relations and mathematical modeling. Opt Commun 284(21):5043–5054
Schumacher T et al (2011) Nanoantenna−enhanced ultrafast nonlinear spectroscopy of a single gold nanoparticle. Nat Commun 2:333. doi:10.1038/ncomms1334
Serebrennikov AM (2010) A novel semi-analytic method for the analysis of scattering by dielectric objects immersed in uniform media. Comp Phys Commun 181(6):1087–1095
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Serebrennikov, A.M. On the Nonlinear Mechanoplasmonic Theory of Frequency Scaling and Mixing Effects. Plasmonics 8, 1299–1308 (2013). https://doi.org/10.1007/s11468-013-9522-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11468-013-9522-1