1 Introduction

The problem of the settlement performance of piled foundations has been traditionally investigated under the assumptions of positive (compression) axial loads on piles. The early studies on this subject date back to Poulos [14], Butterfield and Banerjee [2] and Banerjee and Driscoll [1]. Since then, a number of comprehensive works have been published, including well-documented case histories [3, 5, 11]. As a result of this research effort, the available procedure of analysis for settlement prediction of piled foundations can be considered accurate enough [10].

Despite the remarkable achievements in this field and the large demand from energy and communication industry of tall, slender structures, the problem of pile foundations under combined axial–moment loads involving tension (negative) axial load on piles still presents a number of obscure points. One of the plausible reasons for the lack of established procedures of analysis may be detected in the dearth of experimental observations on the rotation of pile foundations under large moment load. As a consequence, a frequent option for the load–settlement analysis under remarkably eccentric load is the use of 3D numerical models. However, care must be taken with this approach, provided that the prediction of the rotation at foundation level is strongly affected by the details of the numerical analysis. For instance, tension axial loads normally imply an upward movement and, consequently, the separation of the pile base from the underlying soil. In addition to this, such an approach usually involves a large volume of supporting and surrounding soil and the adoption of appropriate constitutive laws of soil behavior. Even supposing that the amount and the quality of laboratory and in situ investigations allow a reliable calibration of model parameters, such an approach is not computationally cost-effective for routine design.

The mathematical framework proposed herein is a lumped, physically motivated model based on rational, easily determinable parameters describing the axial response of isolated piles at the macro-scale. It accounts for nonlinearity and irreversibility of the relationship between load and displacement and pile-to-pile interaction. Owing to such ingredients at the pile scale, the model can properly describe the influence of past-load history and the ‘coupling’ between generalized loads and displacements. The load–settlement response of isolated piles can be elastic-perfectly plastic, hyperbolic with truncation, or a user-defined curve so as the behavior from load tests on piles, if any, may be explicitly taken into account.

In the following, the attention is first placed on the details of the mathematical framework underlying the proposed model and then on its prediction capability through a comparison with some rigorous finite element results and an experimental benchmark coming from centrifuge tests on annular shaped pile groups. Finally, the focus is set on the response of this model to load paths in the (Q, M) plane under either constant axial load or constant eccentricity, so as to shed light on how pile-to-pile interaction affects the foundation response.

The proposed model is particularly suited for circumstances where the resultant action at foundation level is almost vertical. This class of problems includes, for example, elevated water tanks, chimneys, silos and tall wind turbines. This last structure is particularly emblematic as the demand of tall turbines from renewable energy industry is relentlessly increasing overall the world. In this case, the resultant action at foundation level is usually slightly inclined, even if remarkably eccentric. For instance, Iovino et al. [9] have documented a case study of a wind farm South of Italy, with 95 m high turbines, where the horizontal load under extreme wind conditions was only 5% of the axial load due to the self-weight of the structure. From an engineering point of view, this problem can be well idealized as a foundation subjected to vertical, eccentric load. On the other hand, the proposed calculation method might be not suited under strongly inclined actions, as in case of quay walls or squatty bridge piers.

2 Mathematical framework

The proposed formulation is based on the interaction factor method and a stepwise incremental approach to account for nonlinear behavior of piles. The main assumptions made to derive the mathematical framework are: (a) piles modeled as uniaxial, nonlinear elements, with load–settlement behavior in compression not necessarily equal to that in uplift; (b) irreversibility of the piles' behavior; (c) piles' connecting cap idealized as a rigid body, clear from the soil; (d) pile-to-pile interaction effects modeled using superposition through the approximate solution by Dobry and Gazetas [8], (e) piles' connections to the raft idealized as hinges. The assumption of rigid cap (c) is a reasonable hypothesis in case of ‘small’ piled rafts as originally defined in Russo and Viggiani [19]. Notably, for ‘large’ piled rafts the load at foundation level is not remarkably eccentric and the response to combined moment–axial loads is a problem of minor concern. With regard to assumption (e), yielding moments at the piles' heads have only a small effect on the failure domain in the (Q, M) plane, as shown in Di Laora et al. [7], so that their contribution can be safely neglected. The same holds for rotational stiffness of individual piles, since this favorable contribution is small compared to the rocking stiffness associated with the axial capacity of piles.

The basic ingredients of the proposed formulation are the failure envelope of the pile group in the (Q, M) (Q = axial load, M = moment) plane and the load–settlement relationship of the piles. With regard to the former point, reference is made to the recent exact solution by Di Laora et al. [7] determined from an application of theorems of limit analysis under the assumptions of piles behaving like uniaxial rigid-plastic elements characterized by two yielding loads, one in compression (Nu) and one in uplift (-Su). In the most general case of unevenly distributed, dissimilar piles, the interaction diagram coming from this approach is an irregular polygon whose coordinates are:

$$\left\{ {\begin{array}{*{20}l} {Q_{ui} = \sum\limits_{j = 1}^{i - 1} {N_{uj} } - \sum\limits_{j = i}^{p} {S_{uj} } } \hfill \\ {M_{ui} = - \sum\limits_{j = 1}^{i - 1} {N_{uj} x_{j} + \sum\limits_{j = i}^{p} {S_{uj} x_{j} } } } \hfill \\ \end{array} \, i = 1, \ldots ,p} \right.$$
(1)
$$\left\{ {\begin{array}{*{20}l} {Q_{uk} = - \sum\limits_{j = 1}^{k - 1} {S_{uj} } + \sum\limits_{j = k}^{p} {N_{uj} } } \hfill \\ {M_{uk} = \sum\limits_{j = 1}^{k - 1} {S_{uj} x_{j} - \sum\limits_{j = k}^{p} {N_{uj} x_{j} } } } \hfill \\ \end{array} \, k = 1, \ldots ,p} \right.$$
(2)

where p is the number of piles and xj is the abscissa of the j-th pile in the reference x-axis, which is supposed to be perpendicular to the direction of the external moment vector. An example application of the above equations to a row of 4 identical, equally spaced piles with Su = 3/4Nu is shown in Fig. 1. In the realm of the upper bound theorem, the vertices of the polygon correspond to plastic mechanisms where the cap displaces by rotation about a point in between two adjacent piles. The conjunction lines also represent subsets of upper bound solutions and correspond to increments of cap rotations about a pile. As outlined by Di Laora et al. [7], the failure envelope in Fig. 1 is also a solution of the lower bound theorem and, thus, an exact solution. As vertices are singularities, a generic load path will never end up in practice on one of them. Hence, an interesting consequence of the foregoing hypotheses is that a pile group always fails by rotating about the head of a pile or a piles' alignment. In this situation, all piles achieve their axial capacity (in compression or uplift) with the exception of those belonging to the rotation axis.

Fig. 1
figure 1

Failure envelope of a row of four identical, equally spaced piles (from [7])

Full size image

Another fundamental ingredient of the proposed mathematical formulation is the assumption on the load–displacement relationship of the isolated pile, which can be of any arbitrary shape. This option may be particularly useful when the results of load tests on piles are already available. For instance, Fig. 2 shows two alternative constitutive assumptions for piles. The curve labeled ‘EPP’ refers to the very simple case of elastic-perfectly plastic elements, while that marked ‘HYP’ to the assumption of a hyperbolic function with a truncation at 90% of the asymptote. In many engineering problems, the foundation is first subjected to the dead load of the structure and then, under constant axial load, to the moment component of the external load vector. The amount of preload on piles (Np) due to the self-weight of the structure (point a in Fig. 2) has usually a paramount effect on the moment–rotation curve of the piled foundation, as shown in the following. Under the application of the moment component of the load vector, some of the piles may undergo a load reversal until the achievement of the uplift capacity (point c in Fig. 2). In particular, the axial stiffness along with the unloading path is taken constant and equal to the initial stiffness in compression (Kc) until the axial load becomes zero (path a-b in Fig. 2). Then, the path corresponding to the load reversal is parallel to the backbone curve (path b-c in Fig. 2) on the side of tension (negative) loads. Notably, the proposed formulation does not account for cyclic or non-monotonic load paths. However, from an engineering standpoint, predicting the foundation rotation at the peak value of the external moment time-history may be appropriate to check serviceability criteria, unless cyclic degradation phenomena are expected to be important.

Fig. 2
figure 2

Constitutive laws of piles

Full size image

Pile-to-pile interaction is modeled using superposition through the closed-form, approximate expression by Dobry and Gazetas [8], in which the ratio between the additional displacement of pile j caused by load Ni on pile i and that of pile j due to its own load Nj is expressed as (for Ni = Nj):

$$\alpha_{ij} \simeq \sqrt {\frac{d}{{2s_{ij} }}}$$
(3)

where d is the pile diameter and sij is the axis-to-axis distance between the two piles. Interaction factors depend mainly on the geometry of the problem at hand and, to a lesser degree, on pile–soil relative stiffness, pile slenderness ratio L/d (L is the pile length) and soil Poisson coefficient [16], while they are very slightly affected by soil stratigraphy [21]. More accurate solutions available in the literature can be adopted, e.g., Randolph and Wroth [17] or Mylonakis and Gazetas [12], in which the above factors are explicitly considered. As outlined by Mylonakis and Gazetas [12], the accuracy of Eq. (3) gradually deteriorates in inhomogeneous soils or piles with small stiffness, while it is fully satisfactory for stiff piles in soft homogeneous soil. After all, the above expression, despite its simplified form, can be considered consistent with the level of complexity of the proposed formulation and is thereby used for the purposes of this work; however, the methodology can account for any expression of interaction factors.

Nonlinearity is concentrated at pile–soil interface and is accounted for by updating at each step of the analysis only the terms of the principal diagonal of the flexibility matrix (Fii = 1/Ki), while the interaction among the piles is assumed to be linear (Fij = αij/Kj,in, where Kj,in the initial stiffness of pile j). As a consequence of this assumption, only the linear component of the displacement of the single pile is amplified, while the nonlinear component is added without amplification. A substantially similar approach has been suggested by Randolph [18], Poulos [15], Mandolini and Viggiani [11] and Russo et al. [20].

The ultimate axial load and moment along with any load path in the (Q, M) plane can be easily determined from the failure envelope of the foundation, allowing the analysis to be performed under load control. Each load step is solved throughout an iterative algorithm (see Appendix A), so as to identify the sequence of piles that progressively achieve their axial capacity in compression or uplift during the loading process. As a final remark, the mathematical model stands for a vertical eccentric force with an assigned eccentricity in both directions, but it cannot predict the response to load paths where the resultant action changes continuously its eccentricity.

3 Validation against numerical and experimental benchmarks

The above procedure is validated against numerical and experimental results. More specifically, the response under axial loads is compared to some numerical results from rigorous Finite Element (FE) analyses, while that under combined axial–moment loading against centrifuge data obtained by the authors.

3.1 Comparison against numerical benchmarks

Reference is made to the rigorous solution by de Sanctis and Mandolini [4] undertaken by FE analyses carried out in undrained conditions using the total stress approach. The parametric study carried out by the authors included square pile groups, ranging between 32 and 72, resting on a clay soil with the undrained shear strength profile, su, shown in Fig. 3. Solid cylindrical piles with a diameter of 1 m, slenderness ratio L/d of 20 or 40, spacing s/d of 4 or 8 and Young’s modulus Ep = 40 GPa were considered. The soil was assumed to behave like an elasto-plastic material with a Tresca yield surface. The undrained Young’s modulus, Eu, was assumed equal to 400su and the Poisson’s ratio ν equal to 0.49. The raft was assumed to be rigid, allowing the analyses to be performed under displacement control. For sake of brevity, the comparison is limited to the subset of pile layouts with slenderness ratio L/d = 20, piles spacing s/d = 4 and number of piles equal to 32 or 52. Also, for the 32 pile group, the solution pertinent to s/d 8 is considered.

Fig. 3
figure 3

(modified from [4])

Soil properties and load–settlement curve of isolated piles in compression

Full size image

Figure 3 illustrates the load–settlement curve of the single pile obtained by an axisymmetric analysis until a vertical displacement equal to 0.25d. The same curve is adopted as the basis of the analyses carried out by the simplified approach proposed in this work. The comparison between the rigorous solution and the simplified method under the assumption of piles behaving like interacting or independent uniaxial elements is shown in Fig. 4. Noticeably, for all the examined pile layouts the rigorous solution falls in between the load-settlement curves determined from the simplified procedure. As a general comment, the assumption of interacting elements yields to a conservative prediction of the foundation settlement over the entire range of axial loads of interest for serviceability limit state analysis. For foundation layouts with a few, closely spaced piles (Fig. 4a), the match between the FE benchmark and the proposed solution is fully satisfactory. By doubling the pile spacing, from 4 to 8d (Fig. 4b), the prediction for interacting piles is significantly softer than the reference curve, and this is presumably due to the oversimplification made about pile-to-pile interaction modeling (Eq. 3). Largely spaced piles behave like independent elements, and in this case it is preferable to adopt the solution with non-interacting piles. Finally, if the number of piles is increased under the same pile spacing, the benchmark curve falls in between the two curves labeled interacting and independent piles (Fig. 4c). Compared to the FE curve, the softer response of the proposed algorithm is mainly due to the assumption of superposition, in which the interaction between any pair of piles is evaluated without considering the ‘stiffening’ effect due to the remaining piles [14]. Notably, all methods in the literature based on superposition have the same conceptual limitation.

Fig. 4
figure 4

Validation against numerical benchmarks: purely axial loads

Full size image

3.2 Comparison against experimental benchmarks

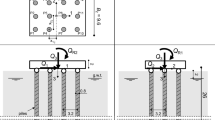
Two series of centrifuge experiments on pile groups under eccentric load have been carried out at the Schofield Centre of the University of Cambridge [6]. The two sets of experiments were performed at an increased gravity of 50 g on annular shaped pile groups consisting of 8 aluminum piles and isolated piles embedded in kaolin clay. For sake of brevity, reference is only made to the first series of experiments, referred to as set A, including a pile group under centered load (A1), a pile group under highly eccentric load (A2) and two isolated piles, one in compression and one in uplift. The arrangement of the model foundations is schematically depicted in Fig. 5.

Fig. 5
figure 5

Plan view and cross section of the model foundations tested in the centrifuge (set A) and soil properties; dimensions (mm) are given at model scale, while dimensions in brackets (m) refer to prototype scale

Full size image

Model piles were 1 mm thick closed-ended hollow cylinders, with an outer diameter of 10 mm and an overall length of 280 mm. They were embedded in a kaolin clay layer for 240 mm, with the exception of the pile tested in uplift whose embedded length was instead 250 mm. The piles belonging to the groups were connected by spherical hinges to a circular raft so that they can carry out only axial loads. Also, they were coated with Houston sand to increase the limiting shear stress at pile–soil interface. Pile group A2 was equipped with a cantilever beam for the application of the eccentric load.

The clay layer was prepared in a cylindrical container and consolidated at 1 g by applying a combination of vertical stress of 70 kPa at the top using a hydraulic press and a suction of 70 kPa at the base by means of a vacuum pump. After removing the container from the hydraulic press, the pile groups and the two isolated piles were driven into the clay until the desired depth. The clay layer was then re-consolidated in the centrifuge under an acceleration of 50 g. At the end of this stage and before the beginning of the loading process, the soil layer had an overconsolidation ratio (OCR) in between 1.58 and 1.68. The undrained shear strength profile obtained from a Cone Penetration Test (CPT) carried out with a miniaturized device during the flight is shown in Fig. 5. The theoretical profile of su calculated from kaolin clay properties using critical state theory is also shown for comparison. Further details can be found in de Sanctis et al. [6].

The recording devices installed to monitor the foundation response are also shown in Fig. 5. As the raft behaves like a rigid body, the settlement distribution was calculated by combining the vertical displacement recorded by the Linear Variable Differential Transformer (LVDT) and the rigid rotations recorded by the Micro-Electro-Mechanical-Systems (MEMS) accelerometers. The external load was applied under displacement control through a miniaturized spherical ball so that it could be idealized as a point load. For each group, the direction of the load path in the (Q, M) plane is known a priori, allowing an easy identification of the collapse load. The axial capacity and initial stiffness in both compression and uplift coming from tests on isolated piles are resumed in Table 1. The two initial stiffnesses were both estimated to be 45 MN/m by considering also loading tests on isolated piles of the second series, referred to as set B. The parameters in Table 1 will be adopted for all subsequent simulations. The failure envelope of the pile group based on the above capacities is illustrated in Fig. 6, where R is the radius of the annular shaped pile group in Fig. 5. The load paths followed in the centrifuge for pile groups A1 and A2 are also shown for comparison. As per the parametric study discussed before, the starting point of any simulation analysis is that corresponding to the weight, W, of the piles. The amount of preload on piles, Qp, is due to the weight of the cap. For pile group A2, this last quantity is slightly eccentric because of the cantilever beam attached to the cap, so as the initial preload on piles vary linearly with the distance along the raft.

Table 1 Axial capacity and axial stiffness in compression and uplift of isolated piles
Full size table
Fig. 6
figure 6

Failure envelope of the pile group and load paths followed in the centrifuge

Full size image

The load–settlement relationship of isolated piles was supposed to be elastic-perfectly plastic (EPP) or hyperbolic with truncation at 90% of the asymptote (HYP), adopting for this last option the following equation:

$$N = \frac{w}{{\frac{1}{{K_{c} }} + \frac{w}{{N_{u} }}}}\,\;\;\;\left( {N = \frac{w}{{\frac{1}{{K_{t} }} + \frac{w}{{ - S_{u} }}}}} \right)$$
(4)

where Kc (Kt) is the initial axial stiffness in compression (uplift).

The axial response determined experimentally from test on pile group A1 is compared to that obtained by the proposed approach in Fig. 7. The prediction of the proposed model with the (HYP) option and interacting elements matches very satisfactorily the observed behavior. The comparison in terms of rotational response is illustrated in Fig. 8a, where θ is the rotation of the rigid cap; since the pile group is tested under constant eccentricity, the external load on the y-axis is also representative of the applied moment M. The load–rotation curve predicted by the approach proposed herein using the hyperbolic formulation compares in a really satisfactory way with that determined from load test on pile group A2. As outlined before, pile-to-pile interaction has only a negligible effect on the foundation rotation. The agreement with the settlements of the foundation center is also satisfactory, as shown in Fig. 8b. Contrary to the linear elastic paradigm, the displacement of the foundation center relies upon both the axial load and the moment component of the external load vector (‘coupled’ behavior). As a final noteworthy point, the elastic-perfectly plastic formulation fails the prediction of the observed behavior under both centered and eccentric load, so as the use of a nonlinear relationship of the behavior of piles is mandatory for a reliable prediction of the foundation performance. Mandolini and Viggiani [11] came to the same conclusion after the interpretation of the experimental data from full scale tests on small pile groups under centered loads carried out for research purposes.

Fig. 7
figure 7

Validation against experimental benchmarks: centered load

Full size image
Fig. 8
figure 8

Validation against experimental benchmarks: eccentric load

Full size image

4 Response to combined axial moment loading

While the proposed algorithm is applicable to pile groups of any shape, the response to combined axial–moment loading is examined herein with reference to the annular shaped foundations of Fig. 9, by taking for simplicity the axial stiffness and capacity of the isolated pile in compression and uplift available from the centrifuge testing program discussed before (i.e., parameters in Table 1). Figure 10 shows the failure envelope of the examined foundation and the load paths selected to investigate the response of the mathematical model. The starting point of any simulation analysis is again the weight of the piles, Wp. Noticeably, the amount of preload is zero only for load path 1, while for the remaining paths this quantity is equal to the weight of the piles' connecting cap, Qp. The response of the proposed model to axial loads only is first examined. The attention is then placed to load paths where the external moment is applied monotonically until failure. For all the examined paths, piles are modeled as: (a) independent, elastic-perfectly plastic elements; (b) independent elements described by a hyperbolic function with truncation at 90% of the asymptote; (c) interacting elements described by the same hyperbola of the preceding case.

Fig. 9
figure 9

Plan view of the reference foundation (B = 6.9 m, R = 3 m, d = 0.5 m)

Full size image

4.1 Centered load

Two simulations are shown to investigate the influence of the axial preload. In the first analysis, the axial load is increased monotonically until the vertical capacity of the foundation, Qu (load path 1 in Fig. 10). In the second one, the load–settlement response is evaluated from the level of preload, Qp (load path 2 in Fig. 10). The corresponding load–settlement curves are plotted in Fig. 11. Under the assumption of elastic-perfectly plastic elements (a), the amount of preload does not affect the initial stiffness of the load–settlement curve (Fig. 11a). On the other hand, when piles are modeled as hyperbolic elements (b), the initial stiffness after the application of the preload diminishes by 22% (Fig. 11b). Finally, pile-to-pile interaction effects lead to a softer response regardless of the constitutive assumption made about the piles' behavior (Fig. 11c).

Fig. 10
figure 10

Load paths in the (Q, M) plane

Full size image
Fig. 11
figure 11

Influence on the load–settlement response of: a axial preload; b constitutive assumption on the behavior of piles; c pile-to-pile interaction

Full size image

4.2 Eccentric load

The response under moment loading is examined along with paths where the moment component is applied monotonically until failure. The moment–rotation curves pertinent to load paths 3–5 in Fig. 10 are illustrated in Fig. 12. Notably, for each plot the rotation at which a piles' alignment achieves a yielding state is identified by a symbol. With regard to model (a), the moment–rotation curve becomes nonlinear only after the outermost pile has achieved its axial capacity, e.g., at the point corresponding to the first symbol. In the nonlinear regime, the moment rotation response relies upon the amount of preload, as it can be argued from the comparison between the curves corresponding to load paths 3 and 4. The initial rotational stiffness is affected by neither the preload nor the slope of the load path. When the load–settlement curve of the isolated piles is a hyperbolic function, the moment–rotation curve becomes nonlinear at the early stage of the loading process, as shown in Fig. 12b.

Fig. 12
figure 12

Influence on the moment-rotation curve of: a axial preload; b constitutive assumption on the behaviour of piles; c pile-to-pile interaction

Full size image

Pile-to-pile interaction has only a negligible effect on the moment rotation response (Fig. 12c). This is not surprising, provided that the interaction mechanism under moment loading differs substantially from that under centered load. In the former case, in fact, tension (negative) axial loads 'compensate' the additional settlement of any pile due to compressive (positive) loads acting on neighboring piles and vice versa, so as the overall effect in terms of foundation rotation becomes negligible. However, such a result relies upon the pile layout. For instance, Fig. 13 illustrates the moment rotation curve obtained by doubling the number of piles within the same foundation. In this case, the compensation between positive and negative axial loads is smaller than before, so that pile-to-pile interaction effects lead to an increase of the foundation rotation. The indication coming from the two pile layouts with 8 and 16 piles may be generalized. The ratio of the axial stiffness, Kv, of the pile group evaluated in linear regime by considering piles' interaction over that calculated under the assumption of independent elements, is plotted in Fig. 14a against the quantity R/d for different values of p. Group effects are always relevant, with the only exception of the ideal layout with 4 piles, for which the ratio of the above quantities does not exceed 2. If the attention is shifted to the rotational stiffness, Kθ, the picture is completely different (Fig. 14b), group effects are much smaller. Also, at low values of p, they lead to an increase of the rotational stiffness. Only at larger values of p and small pile spacing ratios the reduction in rotational stiffness due to pile-to-pile interaction effects may be significant. It follows that, contrary to the established knowledge on pile groups under centered vertical load, interaction effects under the application of highly eccentric loads may increase or decrease foundation stiffness and are, from a general standpoint, less significant.

Fig. 13
figure 13

Effect of number of piles on the moment–rotation response

Full size image
Fig. 14
figure 14

Influence of the pile layout on group effects

Full size image

5 Discussion and conclusions

A simple physically motivated framework has been presented to analyze the problem of pile groups under combined axial–moment loading. The starting point of the proposed model is the failure envelope of the piled foundation in the (Q, M) plane. To this aim, reference is made to the exact solution by Di Laora et al. [7] based on theorems of limit analysis. Pile-to-pile interaction factors are considered using the simple expression by Dobry and Gazetas [8], while the behavior of isolated piles in both compression and uplift may be represented through a user-defined curve. Based on the above assumptions, the proposed model is capable of describing the response of a piled foundation of any shape in terms of settlements and rotations along with a load path under constant axial load or constant eccentricity.

The predicted response of the proposed model matches really satisfactorily that determined form centrifuge tests on annular shaped pile groups under both centered and eccentric load and numerical benchmarks obtained for square groups subjected to purely axial loads.

A parametric study allowed concluding that: (1) an asymmetric backbone curve and a suited unloading–reloading rule are crucial ingredients for a reliable prediction of settlement and rotations of a pile group under monotonic external moment; (2) the moment–rotation response is affected to some extent from the axial preload on piles and the slope of the load path; (3) pile-to-pile interaction effects under moment loading are much less pronounced than those under purely vertical load.

However, it is fair to mention that the mathematical framework developed herein is limited to foundation problems where the resultant action is almost vertical.