Micromechanical inspection of incremental behaviour of crushable soils

Abstract

In granular soils grain crushing reduces dilatancy and stress obliquity enhances crushability. These are well-supported specimen-scale experimental observations. In principle, those observations should reflect some peculiar micromechanism associated with crushing, but which is it? To answer that question the nature of crushing-induced particle-scale interactions is here investigated using an efficient DEM model of crushable soil. Microstructural measures such as the mechanical coordination number and fabric are examined while performing systematic stress probing on the triaxial plane. Numerical techniques such as parallel and the newly introduced sequential probing enable clear separation of the micromechanical mechanisms associated with crushing. Particle crushing is shown to reduce fabric anisotropy during incremental loading and to slow fabric change during continuous shearing. On the other hand, increased fabric anisotropy does take more particles closer to breakage. Shear-enhanced breakage appears then to be a natural consequence of shear-enhanced fabric anisotropy. The particle crushing model employed here makes crushing dependent only on particle and contact properties, without any pre-established influence of particle connectivity. That influence does not emerge, and it is shown how particle connectivity, per se, is not a good indicator of crushing likelihood.

1 Introduction

Grain fragmentation is significant for several important geotechnical problems including side friction on driven piles, railway ballast durability or rockfill dam settlement. To address these problems, granulometric evolution has been incorporated into constitutive models for soils [12, 23, 36, 37, 39, 44, 50, 56, 62]. Such models are inspired by an increasingly large database of laboratory investigations which, despite notable experimental difficulties, document the behaviour of crushable soils [20, 26, 30, 33, 40, 42, 46, 53, 63, 65, 67].

Two well-established observations arising from earlier research are that (a) soil crushability is enhanced by stress obliquity, and (b) plastic deformation in crushable soils is associated with less dilatancy, or, equivalently, that plastic flow is more volumetric when crushing is present. These specimen-scale observations have been reproduced by several DEM models of crushable soils [13, 15, 34]. Specimen-scale responses of soils may be considered as emerging responses, i.e. responses that reflect underlying micromechanical interactions at the grain or element scale. This general principle has not been yet systematically applied to crushable soils, and several aspects of their micromechanics remain relatively obscure.

Laboratory micromechanical investigations of breakable soils are possible [1] but very difficult. On the other hand, DEM simulation offers readily accessible information at the element scale, which may be used to uncover relevant micromechanics. Micromechanical analysis of breakable DEM models has mostly focused on the conditions that lead to particle breakage and the nature of the obtained fragments [27, 29, 38, 55]. Less attention has been paid to the underlying mechanisms that, for instance, may explain the more volumetric nature of crushing-induced plastic flow. This bias is partly due to the use of crushable agglomerates to represent breakable particles in DEM models. When using agglomerates, it is difficult to track inter-granular fabric evolution [19]. Agglomerates may be too compliant [6] or have multiple contact points [64], making fabric measures difficult to interpret. Modelling particles as agglomerates also carries significant computational costs; this limits the number of particles in simulation and, therefore, the robustness of micromechanical statistics. Still, a general observation derived from crushable agglomerate studies [6, 61, 64] is that the development of contact force anisotropy during shear is strongly affected by crushing.

To avoid the problems associated with agglomerates, crushable DEM models based on the splitting particle concept [41] may be used. Zhou et al. [68] used a splitting particle model to study fabric evolution during true-triaxial simulation of breakable particles. However, the study focused on the effects of intermediate principal stress ratio and the connection between breakage and fabric evolution was not investigated.

Ciantia et al. [16] used a DEM model based on the splitting particle concept to explore the incremental response of crushable soils. They showed that grain crushing causes the plastic flow to change direction and that this direction is unique and independent on the loading direction. Crushing-induced plastic flow was observed to be more volumetric than when crushing is inhibited. However, the micromechanics of that response was not investigated.

This study aims to fill that gap, by investigating how particle breakage modifies the micromechanics underlying the incremental stress response of granular specimens. Response envelopes were originally proposed by Gudehus [32] as a means to classify constitutive models. Incremental response envelopes [24, 25, 54] reveal important characteristics soil behaviour such as incremental nonlinearity, associative behaviour, uniqueness of flow rule, etc. Measuring incremental responses in the laboratory is difficult, [21, 22], because of the highly accurate strain measurements required and the need to test several identical samples (one for each probe). For this reason DEM models have been frequently used to study the incremental behaviour of granular materials [3, 7, 11, 47, 58, 60].

Taking advantage of the efficiency of the DEM crushing model of Ciantia et al. [16], results have been obtained from a large number of simulations (> 350). In what follows the DEM model is first described; the methods applied for micromechanical investigation are then introduced before presenting some relevant numerical results. The focus of the paper is to examine the relationship between crushing and the features and evolution of the microstructure. It also aims to explain mesoscale observations such as the enhanced volumetric component of crushing-induced strains, the uniqueness of plastic flow direction and the cascading nature of particle breakage.

2 DEM particle crushing model

The DEM model for crushable soil employed here was described by Ciantia et al. [15]. It was implemented as an user-defined model in the PFC3D code [35] and for completeness an overview is given here. Coulomb friction and the simplified Hertz–Mindlin contact model are used to describe the interaction of spherical elements. Particle rotation was inhibited to give a good match to experimental data without using non-spherical particles. This approach, successfully applied in previous research [2, 8, 9, 59], is equivalent to applying a very large value of rotational resistance at the contacts.

The failure criterion is based on work by Russell and Muir Wood [48] and Russell et al. [49]; a two-parameter material strength criterion is used together with consideration of the elastic stresses induced by point loads on a sphere. A particle subject to a set of external point forces reaches failure when the maximum applied force reaches the following limit condition:

$$F \le \sigma _{\lim } A_{\text{F}}$$

(1)

where σ_lim is the limit strength of the particle and A_F is the contact area. To incorporate the natural material variability into the model, the particle limit strength, σ_lim, is assumed to be normally distributed for a given sphere size. The coefficient of variation of that distribution, var, is taken to be a material parameter. Following McDowell and De Bono [43], the mean strength value for given sphere size, $\bar{\sigma }_{\lim }$, depends on the particle diameter:

$$\bar{\sigma }_{\lim } = \sigma_{\lim 0} f\left( {\text{var} } \right)\left( {\frac{d}{{d_{0} }}} \right)^{ - 3/m}$$

(2)

where $\sigma _{\lim 0}$ is a material constant and f(var) indicates the effect of variability of particle strenght. A_F depends on the contact force and the particle’s elastic properties; applying Hertzian contact theory, the following expression for the breakage criterion is obtained:

$$F \le \left\{ {\sigma_{\lim 0} f\left( {\text{var} } \right)\left( {\frac{d}{{d_{0} }}} \right)^{ - 3/m} \pi \left[ {\frac{3}{4}\frac{{\left( {\frac{{1 - \nu_{1}^{2} }}{{E_{1} }} + \frac{{1 - \nu_{2}^{2} }}{{E_{2} }}} \right)}}{{\left( {\frac{1}{{r_{1} }} + \frac{1}{{r_{2} }}} \right)}}} \right]^{2/3} } \right\}^{3}$$

(3)

where r₁ and r₂ are the radii of the contacting spheres and E_i, ν_i are the Young’s moduli and Poisson’s ratio, respectively. Note that this breakage criterion does not involve exclusively the maximum force on the particle: there is a strong inbuilt dependency on the characteristics of the contacting particles.

Once the limit condition is reached, the spherical particle will split into smaller inscribed tangent spheres. The crushed fragments assume the velocity and material parameters of the original particle apart from the intrinsic strength (σ_lim0) which is randomly assigned sampling its normal distribution. Ciantia et al. [15, 16] concluded that a 14-ball crushed configuration can adequately represent macroscopic behaviour. The capability of this model to capture real test behaviour has been demonstrated by Ciantia et al. [14, 17].

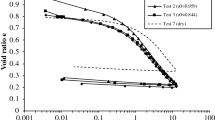
Ciantia et al. [16] calibrated this model to reproduce the observed experimental behaviour of Fontainebleau sand at low pressures (Fig. 1). Particle-scale information, from single particle crushing tests on quartz sands, was also used to select crushing model parameters. The grain size distribution is also close to that of Fontainebleau sand [66]. More recently, Ciantia et al. [17] refined this calibration, using new data to obtain better experimental agreement at very high pressures. The work presented here is not aimed to match laboratory experiments and, for coherence with previous work on response envelopes, the model parameters applied (Table 1) are those of Ciantia et al. [16].

Fig. 1

a DEM model at 5 kPa isotropic compression pressure, b DEM simulation of drained triaxial compression test (cell pressure 100 kPa and experimental data from Seif El Dine et al. [51]), c DEM simulation of oedometric compression (experimental data from Yang et al. [66])

Table 1 Discrete-element method input parameters for simulation

3 Micromechanical inspection methodology

3.1 Numerical specimen

A DEM specimen was created by filling a cube with spheres with particle diameters ranging from 0.1 to 0.4 mm. The cube side lengths of 4 mm (Fig. 1a) contained close to 10,000 particles. This is a representative volumetric element (REV), as small as possible to ease computation, but big enough so that the observed boundary responses do not change with further size increases [16].

Gravity was set to zero in this work. The specimen boundaries were defined using smooth “wall” elements. The cubic REV may then be loaded in true-triaxial space. Rigid boundaries are smooth so that principal axes of stress and strain are coincident with the cube axes. The principal strains are calculated directly from the wall displacements, while the corresponding principal stresses are obtained from the boundary forces. Any compatible stress–strain path may be followed: strain components may be imposed directly as wall motion, whereas stress components are enforced through servo-control. Ciantia et al. [16] examined the spatial distribution of crushing events during incremental probing and showed that the rigid walls induce no localization.

3.2 Stress probing and strain response envelopes

The complete set of simulations carried out in the current study includes some ancillary triaxial tests, but is mostly dedicated to incremental stress probing starting from different initial states on the triaxial plane. For axisymmetric (triaxial) loading, the number of independent stress and strain variables reduces to two, and a convenient graphical representation can be given in a Rendulic plane. Referring to Fig. 2a, in the Rendulic plane of stress increments, the stress probe magnitude is:

$$\left\| {\Delta \sigma } \right\|: = \sqrt {\Delta \sigma \cdot \Delta \sigma } = \sqrt {\left( {\Delta \sigma_{z} } \right)^{2} + \left( {\Delta \sigma_{x} } \right)^{2} + \left( {\Delta \sigma_{y} } \right)^{2} } = \sqrt {2\left( {\Delta \sigma_{x} } \right)^{2} + \left( {\Delta \sigma_{z} } \right)^{2} }$$

(4)

where σ_z is the stress in the z direction and σ_x and σ_y (the stresses in the x and y direction, respectively) are equal due to the axisymmetric conditions. The stress probe magnitude was established as 1% of the mean principal stress value at the corresponding initial state (from which probing is started). The stress probe direction is defined by the angle α_Δσ between the $\sqrt 2 \Delta \sigma_{x}$ axis and the stress increment vector:

$$\alpha_{\Delta \sigma } = \tan^{ - 1} \left( {\frac{{\Delta \sigma_{z} }}{{\sqrt 2 \Delta \sigma_{x} }}} \right)\quad \alpha_{\Delta \sigma } \in \left[ {0;360} \right]$$

(5)

Fig. 2

a Stress probes: IC/E = isotropic compression/expansion, TC/E = “triaxial” (axisymmetric) compression/extension; DC/E = purely deviatoric compression/extension; RE/C = radial extension/compression; EDO = oedometric compression within the range of k₀ developed in the whole simulation. b Representative response envelope to stress probes

At the specimen scale, the response to a set of incremental stress probes is described using an incremental strain response envelope [10, 54]. The strain response envelope is plotted in a Rendulic plane for strain increments, ($\Delta \varepsilon_{z} :\sqrt 2 \Delta \varepsilon_{x}$) (Fig. 2b). The strain increment direction is defined by the angle, α_Δε, between the $\sqrt 2 \Delta \varepsilon_{x}$ axis and the strain increment vector:

$$\alpha_{\Delta \varepsilon } = \tan^{ - 1} \left( {\frac{{\Delta \varepsilon_{z}^{{}} }}{{\sqrt 2 \Delta \varepsilon_{x} }}} \right)\quad \alpha_{\Delta \varepsilon } \in \left[ {0;360} \right]$$

(6)

In Fig. 2b, the strain increment directions corresponding to pure deviatoric strain ($\Delta \varepsilon_{v} = 0$) and pure volumetric strain ($\Delta \varepsilon_{d} = 0$) are also indicated.

The resolution at which the strain envelope should be obtained is dictated by the purpose of the study. Ciantia et al. [16] used only 12 probes for each initial condition; this resolution was appropriate for identifying the main behavioural trends but insufficient to accurately describe the material response. In this work, where the fabric as well as the strain responses are analysed, 108 probes were performed at each probing point (36 incremental directions, spaced at 10 deg α_Δσ, were probed each with 3 parallel probes—see below).

3.3 Fabric descriptors

The mechanical coordination number and fabric tensor were systematically computed as descriptors of specimen fabric in this study. The mechanical coordination number is defined for a collection of particles as [57]:

$$Z^{m} = \frac{{2N_{\text{c}} - N_{1} }}{{N_{\text{p}} - N_{0} - N_{1} }}$$

(7)

where N₁ and N₀ are the number of particles with 1 and 0 contacts, respectively, and N_c and N_p are the number of contacts and particles in the specimen, respectively. As the definition of Z^m cannot be applied to a single particle, when presenting results for single particles we refer to connectivity, defined as the number of contacts per particle.

The fabric tensor ϕ_ij is given by:

$$\phi_{ij} = \frac{1}{{N_{c} }}\sum\limits_{k = 1}^{{N_{c} }} {n_{i}^{k} } n_{j}^{k}$$

(8)

where N_c is the total number of contacts and $n_{i}^{k}$ denotes the unit contact normal for the k-th contact. Fabric anisotropy is quantified using ϕ_d, the second invariant of the deviatoric fabric [4], sometimes referred also as the Von Mises fabric invariant [45]:

$$\phi_{d} = \phi_{1} - \phi_{2}$$

(9)

where ϕ₁ and ϕ₂ are the major and minor principal values of the fabric tensor.

Following Thornton and Zhang [58], for a set of incremental stress probes, it is possible to determine an incremental fabric response envelope. However, in this study, the direction of fabric incremental change remains fixed. This is a consequence of the general condition of null fabric trace change $\Delta \phi_{1} + \Delta \phi_{2} + \Delta \phi_{3} = 0$ and that, for axisymmetric loading, the fabric maintains axial symmetry [57] and $\phi_{2} = \phi_{3}$. In this work, the principal directions 1, 2, 3 coincide with the z, x and y axis directions, respectively, and, for consistency with Eqs. (4)–(6), it follows that (Fig. 3a)

$$\alpha_{\Delta \phi } = \tan^{ - 1} \left( {\frac{{\Delta \phi_{z}^{{}} }}{{\sqrt 2 \Delta \phi_{x} }}} \right) = \tan^{ - 1} \left( { - \frac{2}{\sqrt 2 }} \right) = - \,54.7^{ \circ }$$

(10)

Fig. 3

a Fabric response envelope to triaxial stress probes, b change in fabric as a function of probing direction. IC/E = isotropic compression/expansion, TC/E = “triaxial” (axisymmetric) compression/extension; DC/E = purely deviatoric compression/extension; RE/C = radial extension/compression

Plotting the results in the equivalent Rendulic plane ($\Delta \phi_{z} :\sqrt 2 \Delta \phi_{x}$) will not add any further information to this result. For this reason, the micromechanical interpretation of stress probe results is best illustrated by plotting the change in fabric component magnitudes Δϕ_k against the probe stress loading direction α_Δσ (Fig. 3b).

3.4 Strain and fabric response decomposition: parallel probe approach

The so-called parallel probe approach is a numerical technique that applies the same stress probe to initially identical DEM specimens with differently specified contact properties [54, 60]. As detailed in Ciantia et al. [16], parallel probes may be used to decompose the incremental strain envelope into a reversible (“elastic”) part, Δε^e, and two irreversible (i.e. “plastic”) parts: Δε^pu due to sliding between uncrushable particles, and Δε^pc due to particle crushing, so that

$$\Delta \varepsilon = \Delta \varepsilon^{\text{e}} + \Delta \varepsilon^{\text{pu}} + \Delta \varepsilon^{\text{pc}}$$

(11)

To achieve this decomposition, three simulations were run for each stress probe. The first simulation used the crushable DEM model described above and the measured strain is Δε; this is termed the elasto-plastic-crushable (e-p-c) probe. In the second simulation, all the mechanisms responsible for plasticity (interparticle sliding and particle crushing) are inhibited to give Δε^e; this is taken to be the elastic probe. In the final simulation, only crushing is inhibited and the measured strain is Δε^e + Δε^pu; this is taken to be the elasto-plastic (e-p) probe.

The potential of the parallel probe approach is exploited further in this work. To begin with, the same type of decomposition may be applied to the incremental change in fabric so that:

$$\Delta \phi_{k} = \Delta \phi_{k}^{\text{e}} + \Delta \phi_{k}^{\text{pu}} + \Delta \phi_{k}^{\text{pc}}$$

(12)

where k may represent x, y or z. Furthermore, to study the mechanisms associated with crushing, at every crushing event during an e-p-c stress probe, the micromechanical state (fabric, coordination numbers) was stored. As explained below, this allowed systematic comparison with similar quantities recorded at the same situation in parallel e-p probes and, therefore, isolation of crushing-induced fabric effects.

3.5 Initial states

The three initial states selected for exploration through stress probes (A, B, C; see Fig. 4a) each belong to a p′-constant triaxial compression stress path performed at p′ = 52 MPa. These states are characterized by different degrees of stress obliquity (defined as η = q/p′, where q is the deviatoric stress), with η = 0 at point A; η = 0.5 at B and η = 1 at C. The triaxial response of the crushable model at this stage is ductile and contractive (Fig. 4b). The same stress path was applied with crushing disabled: the response during shear becomes dilatant and slightly brittle (Fig. 4b).

Fig. 4

Initial states for stress probes. a stress paths and grading index contours, b response during triaxial shearing at constant p′ from point A, c compression plane with indication of isotropic compression path and critical state line, d grading index, I_G, evolution with p′

As a reference, Fig. 4a also includes the grading index I_G contours on the triaxial plane, that had been obtained by Ciantia et al. [16]. The grading state index, I_G, was introduced by Muir Wood [44] as a measure of grading evolution and is computed as an area ratio of the current grading to a limit grading in the grain size distribution plot (see [16]. All three probing points are located in a region well above isotropic yield (p′_cr = 40 MPa) (Fig. 4c) in which granular evolution through crushing is already well established. As a reference, Fig. 4c also includes a critical state line (CSL) obtained from several auxiliary triaxial tests, including those used in calibration (Fig. 1). As explained in detail by Ciantia et al. [17], this CSL is that relevant to normally consolidated states such as those considered here. The p′-constant stress path accelerates the crushing-induced evolution with respect to that observed along the isotropic path (Fig. 4d). Therefore, more crushing is expected upon incremental probing at point C than at point B, and more at point B than at point A.

4 Results

4.1 Crushing effect on fabric development

Before examining the incremental responses, it is useful to have a general perspective on how fabric evolves in the triaxial plane as crushing proceeds. To do so, we examine the initial values of Z^m and ϕ_d at the probing points, before incremental loading. To obtain a richer picture, we have extracted relevant data from 12 different initial states attained by following stress paths at fixed stress ratios, η = q/p′, of 0, 0.3 0.75 and 1 (other results from these tests were presented in [16]. To highlight the effect of crushing, the same stress states were also obtained in simulations that inhibited crushing.

Figure 5a, b indicates on the q:p′ plane the values of Z^m for various stress states of the crushable and uncrushable models, respectively. Comparing these values, the most significant effect observed is that Z^m reduces after the onset of crushing. This is clearly visible in Fig. 5c where Z^m is plotted against mean stress p′ normalized by the apparent yield stress on isotropic loading, p′_cr. For values of p′/p′_cr < 1, the Z^m of the crushable and uncrushable samples is practically identical while for p′/p′_cr > 1, Z^m of the crushable samples is significantly lower than the uncrushable ones.

Fig. 5

Stress-plane maps of mechanical coordination number for a crushable, b uncrushable simulations; c mean stress (normalized by isotropic yield stress p′_cr) versus mechanical coordination number, Z^m; d evolution of Z^m during triaxial shearing at constant p′ from point A

There is also an effect of ductility: at the same stress level the crushable material has suffered larger shear strains and is closer to critical state (Fig. 4b). At the critical state (CS), Ciantia et al. [17] observed a practically unique relation between mean stress level and Z^m, that is insensitive to grading. This is again noted here, where the end points (Fig. 5d) are very close for the uncrushable (Z^m = 5.91) and crushable cases (Z^m = 5.66). This implies a rapid fall in Z^m as the CS is approached for the uncrushable material in a dilatant manner. Indeed, such abrupt falls in Z^m for uncrushable particles have been documented before in tests with dilatant responses [31, 45].

Figure 6 presents results related to the Von Mises fabric invariant. For both the crushable (Fig. 6a) and uncrushable (6b) cases fabric anisotropy ϕ_d increases as the stress obliquity η increases. This is in agreement with previous work [57]. Crushing results in a more gradual development of fabric anisotropy as deviatoric stress increases (Fig. 6c); a similar effect had been noted by Xu et al. [64]. However, as it happened with Z^m, the differences reduce as the critical state approaches, with a more abrupt increase of fabric anisotropy in the uncrushable material (Fig. 6c).

Fig. 6

Stress-plane maps of deviatoric fabric, ϕ_d for a crushable, b uncrushable simulations; c effect of normalized mean stress on deviatoric fabric, ϕ_d

4.2 Strain response envelopes and plastic flow

Figure 7 presents the strain response envelopes obtained for the three different initial states, A, B, C. The total strain envelopes obtained with the base model (elasto-plastic-crushable; e-p-c) and the two parallel probe sets (elastic and elasto-plastic; e-p) are presented in the Rendulic plane ($\Delta \varepsilon_{z} :\sqrt 2 \Delta \varepsilon_{x}$). The differences between those envelopes result in the two plastic component envelopes: plastic-uncrushable (pu) and plastic-crushable (pc) also presented in the figure. At each test point, the probe orientation (αΔ_σ) resulting in most crushed particles is noted alongside the number of crushed particles (N_cr). The directions of the previous stress path are also indicated (isotropic compression, IC at point A; constant p′ shear, DC, at points B and C).

Fig. 7

Response envelopes for parallel probes (left) and corresponding plastic components (right) of the three points selected form the p′-constant triaxial compression stress path

As the deviatoric stress level increases, stress probing results in more plastic strain. While the elastic envelope changes little, the e-p-c and e-p strain envelopes increase in size. The uncrushable plastic component is larger than the crushable one at points B and C, but smaller at point A. An isotropic stress path had been followed to point A, and a small amount of crushing takes place along probing directions close to that isotropic loading path (marked IC in Fig. 7a). This memory effect reflecting the previous stress path is also clear in the envelopes at B and C, where the maximum straining is close to, but not coincident with, the previous stress path direction (marked DC in Figs. 7b, c).

For both the crushing-induced and crushing-independent mechanisms, the plastic flow direction is independent of the stress probing direction. Plastic flow tends to a critical state type of flow (i.e. Δε_vol = 0) as η increases, with both plastic flow components becoming more deviatoric as η increases; however, it is clear that the plastic-crushable component is always more volumetric than the plastic-uncrushable one; that was a general feature also noted by Ciantia et al. [16]. Figure 8 details the orientation and magnitude of plastic flow components for all stress probes at point C (η = 1). In Fig. 8, αn_g represents the orientation of the plastic flow direction, while αn_f is the direction of maximum flow magnitude: it is clear that these are not coincident.

Fig. 8

Plastic flow analysis of the stress probe results at point C (η = 1); magnitude (a) and direction (b) of plastic-uncrushable deformations as a function of probing direction. Magnitude (c) and direction (d) of plastic-crushable deformations

Both plastic mechanisms are well described by a cosine shaped curve, although the agreement is better for the crushing-independent plastic mechanism. This is due to the relatively small number of crushing events (46 at maximum) that drive plastic deformation in the crushing-induced mechanism.

4.3 Micromechanical observations on particles that crush

Particle crushing induces a local dynamic instability in the granular network [16] so that crushing events are typically grouped in time and can be described as “cascading” [18, 28]. Cascading means that later crushing events are triggered by the earlier ones, through force redistribution.

Using the parallel probe technique, the connected and cascading nature of different crushing events is easily demonstrated. Results from the probe with largest number of crushing events (α_Δσ = 140 at η = 1) are shown in Fig. 9. For a given particle, we define the critical contact force ratio, $FR_{\text{p}}^{\text{cr}}$ as the maximum of F/F_lim, at its contacts. When crushing is enabled that ratio remains always below 1, but if crushing is disabled it may rise above 1. For instance, Fig. 9a tracks the rise of $FR_{\text{p}}^{\text{cr}}$ during an e-p-c probe on some particles up to their crushing moment, and compares it with the situation of the same particles in a parallel e-p probe, where crushing is disabled. When crushing is disabled, forces on some, but not all, of those particles rise above the crushing limit. The ordering of crushing events is significant in that respect. In Fig. 9b, it is shown that particles that crush earlier in the e-p-c probes are those that experience forces exceeding the crushing limit in the e-p probe, whereas those that crush later in the e-p-c probes remain well below the limit if crushing is disabled.

Fig. 9

The cascading nature of crushing events. Results from two parallel probes with α_Δσ = 140 at η = 1: a evolution of $FR_{\text{p}}^{\text{cr}}$ (for a given particle it’s the maximum of F/F_lim, at its contacts) of several selected particles versus crushing events; lines with symbols correspond to the e-p-c probe, continuous lines denote the parallel e-p probe; b the final $FR_{\text{p}}^{\text{cr}}$ on the e-p probe for all particles crushed during the e-p-c probe

Particles that will break during probing are those at the top of the $FR_{\text{p}}^{\text{cr}}$ distribution (Fig. 10). About 75% of particles are very far from breakage, with $FR_{\text{p}}^{\text{cr}}$ values below 10%. Breakage during probing appears limited to particles that start the probe with $FR_{\text{p}}^{\text{cr}}$ values above 80%. A high critical contact force ratio is not the same as high contact force. Forces acting on particles that go on to crush are not necessarily those at the top of the contact force distribution. Figure 11 represents the cumulative distribution function (CDF) of contact normal forces for different contact subsets. Forces acting on particles that will crush are more narrowly distributed than forces acting on all particles. The difference increases as shear advances and, as a result of crushing, the number of relatively stronger smaller particles is increased.

Fig. 10

Cumulative distribution function of critical contact force ratios before stress probing, for all particles and for particles that will crush

Fig. 11

CDF curves of the contact normal forces for different contacts subsets: all contacts on crushed particles; $FR_{\text{p}}^{\text{cr}}$ contacts on crushed particles; all contacts; $FR_{\text{p}}^{\text{cr}}$ contacts on all particles. For a given particle $FR_{\text{p}}^{\text{cr}}$ is the maximum of F/F_lim, at its contacts

Several models for crushable soils (e.g. Lobo-Guerrero and Vallejo [41]; Ben-Nun and Einav [5]) have included a connectivity-dependent term in their breakage criteria. In contrast, no link to coordination number was prescribed the breakage criteria implemented here. It was then an open question if particle breakage was in any way related to connectivity. To answer this, particle connectivities for particles that are closest to crushing (i.e. those with $FR_{\text{p}}^{\text{cr}}$ values above 80%) are compared with that of all particles in Fig. 12. These data indicate that connectivity is not, per se, a good indicator of crushing likelihood. The main difference is that the CDF of particles that are close to crushing appears—again-somewhat more narrowly distributed (i.e. includes less particles with less than 3 or more than 9 contacts) than the general distribution.

Fig. 12

Connectivity CDF curves for different particle subsets: particles that will crush; particles having a $FR_{\text{p}}^{\text{cr}}$ > 0.8; all particles. For a given particle $FR_{\text{p}}^{\text{cr}}$ is the maximum of F/F_lim, at its contacts

A complementary illustration of this effect is given in Fig. 13, which illustrates the evolution of connectivity on particles that crush during a representative probe (α_Δσ = 140 at η = 0.5, in which the number of crushing events allows a clear plot). Connectivity of particles that crush does not cluster at any particular value and is not much affected by previous crushing events.

Fig. 13

Evolution of the coordination number of particles that crush during a probe. Large dots indicate a crushing event. Results obtained for a probe with α_Δσ = 140 and η = 0.5

Contact fabric data is presented in Fig. 14 for the three initial states before probing. This may be compared with Fig. 15 which is restricted to particle critical contacts, N_c,cr (for a given particle, N_c,cr is the contact closest to crushing, hence the one with the maximum of F/F_lim ratio). As shear progresses force orientation becomes more anisotropic. Critical force contacts (Fig. 15) have a stronger normalized average force magnitude and are more anisotropically oriented that the general contact network. Furthermore, as the shear-induced contact force anisotropy increases, the number of particles whose critical ratio is above a certain threshold also increases (Fig. 16).

Fig. 14

a–c Initial overall contact fabric at the three probing points

Fig. 15

a–c Initial critical contact fabric at the three probing points

Fig. 16

a–c Fabric at the three probing points restricted to contacts where $FR_{\text{p}}^{\text{cr}}$ > 0.2. For a given particle $FR_{\text{p}}^{\text{cr}}$ is the maximum of F/F_lim, at its contacts

4.4 Incremental fabric changes due to crushing

The previous section explored the micromechanical conditions that favour crushing. A separate question is: what is the micromechanical effect of crushing, or, using the terminology introduced previously, what are the mechanisms underlying the plastic-crushable irreversible strain? These plastic strains are due to contact slippage and granular network rearrangement. To identify them, a sequential probe technique was developed.

The sequential probe approach is illustrated in Fig. 17. It comprises several steps:

Fig. 17

Illustration of the sequential probe approach for η = 1, α_Δσ = 140

• 1. From the initial state O an ordinary e-p-c probe (O–B) is performed, to identify the particles that crush during the probe

• 2. From the initial state O an elasto-plastic probe (crushing disabled) was performed (O–A) and final state (point A) was taken as a reference condition

• 3. At the reference condition (point A) particle sliding was inhibited and all the particles that would crush in the corresponding e-p-c probe [determined in (i)] where crushed simultaneously, while maintaining the specimen stress constant. Some very small deformations were observed before equilibrium was restored (point A′). These are due to elastic contact force readjustment in the network.

• 4. Particle sliding (without crushing) was re-enabled. The incremental strain path then moved from A′ to B′. The final strain state obtained (point B′) was close to the e-p-c probe final point (point B) showing that this sequential approach gives a strain response very close to the e-p-c response. The advantage, however, is that this post-crushing sliding step allows to identify the contacts where slip is induced solely by particle crushing.

This sequential probe method was systematically applied to explore the nature of crushing-induced particle slippage. In Fig. 18, rose diagrams of the sliding contacts in the uncrushable step (left) and the crushing-induced step (right) are represented for three representative probes. (For instance, the uncrushable step corresponds to path OA in Fig. 17, while the crushing-induced step corresponds to path A′–B′ in Fig. 17). Each bin in the rose diagram is shaded by the normalized force value for that orientation; (forces are normalized by the overall force mean value, $\bar{f}_{n}$). The dashed red line indicates a preferred (or average) direction, α^ave, for which sliding is maximum. For the uncrushable case this direction is independent of the stress increment direction α_Δσ. For contacts that slip due to particle crushing that preferential direction is not so obvious and sliding contacts are more isotropically distributed.

Fig. 18

Sequential probe results for three probing directions (α_Δσ = 90,150 and 200) starting from test point C (η = 1). Rose diagrams of sliding contacts observed (a) in the uncrushable step (b) the crushing-induced step

The incremental fabric changes due to crushing-induced sliding and to uncrushable sliding are now compared. Results for the strong contact subset network (i.e. network of contacts carrying above-average forces) are presented for both steps of sequential probes in Fig. 19. Restriction to the strong subset network was necessary as incremental fabric changes for the weak contact network were imperceptible (see Sufian et al. [52] for a more general discussion of fractional networks). Figure 19 hence compares the change in vertical strain with the change in the vertical fabric component as function of the probe loading direction. The elastic (e), elasto-plastic (e-p) and elasto-plastic-crush (e-p-c) results are plotted for the three (η = 0, 0.5 and 1) states analysed. The fabric response has a sinusoidal shape that is similar to the vertical deformation response. Even without any sliding there are fabric changes (for the strong contact subset network) during the elastic probe, as contact forces increase and decrease according to the probing direction. For instance, when η = 0 at point A, Δϕ_z = 0 for probing directions (α_Δσ) close to IC and IE, while Δϕ_z is maximum/minimum for a probing direction close to the DC/DE, respectively.

Fig. 19

e, e-p and e-p-c vertical strain (left) and vertical fabric change (right) as a function of probe loading direction $\alpha_{\Delta \sigma }$ at the three probing points. The numbers next to the e-p-c curves represent the number of crushing events

Probing from the isotropic state resulted in very small plastic deformations (Fig. 7a). This is also reflected in Fig. 19a, where the changes in vertical fabric are almost unaffected by activation of the plastic mechanisms. The situation at point B (η = 0.5) is different (Fig. 19b): plastic strains are already significant and are accompanied by perceptible fabric changes. The dominant component is non-crushed induced plastic sliding, which also appears to fully control fabric changes. Although crushing-induced plastic strains are not negligible (see also Fig. 7b) they seem to leave fabric unchanged. When η = 1, at point C (Fig. 19c), the trend towards increased crushing-induced plastic strains is more clear. The effect on fabric of those crushing-induced strains is to reduce the changes that pure frictional sliding will induce, i.e. to reduce the development of anisotropic fabric.

This effect is clearly visible in Fig. 20 which considers only the incremental fabric changes due to plastic-uncrushable strain ($\Delta \phi_{z}^{\text{pu}}$) and plastic-crushable strain ($\Delta \phi_{z}^{\text{pu}}$) for probes starting at η = 1. Each incremental fabric change response is oriented almost identically to the corresponding incremental strains: compare the maximum strain direction in Fig. 8 and that of maximum incremental fabric change in Fig. 20. This directional coincidence is, perhaps, less surprising than the different sign of the fabric change components. It is clear that for the purely frictional, uncrushable mechanism, incremental fabric changes are positive, whereas crushing-induced plastic structural mechanism the change in vertical fabric is negative. This means that, since $\Delta \phi_{z} = - \,2\Delta \phi_{x}$, crushing induces the creation of new strong contacts in the direction perpendicular to the direction of loading and the disappearance of strong contacts parallel to the direction of loading.

Fig. 20

Plastic-uncrushable and plastic-crushable vertical fabric change as a function of probe loading direction $\alpha_{\Delta \sigma }$ of the η = 1 state on the p′-constant triaxial compression stress path

5 Conclusions

This work has examined several aspects of the microscale response of a crushable soil discrete element model. The most significant findings are

• 1. When shearing is accompanied by particle crushing, the evolution of microstructural measures like the mechanical coordination number or Von Mises fabric towards their critical state value is smoothed. A ductile specimen-scale response is accompanied by a slow micromechanical evolution.

• 2. Plastic deformation due to breakage takes place as breakage-induced contact sliding. Sliding due to this mechanism is more isotropically distributed than non-crushable sliding and tends to reduce fabric anisotropy instead of increasing it. The more volumetric nature of crushing-induced plastic flow is thus explained.

• 3. In this model particles that break are those in which one contact force overcomes a breakage limit that depends both on particle and contact properties. There is not a clear connection between particle connectivity and particle breakage. On the other hand, increased fabric anisotropy does take more particles closer to breakage. Shear-enhanced breakage appears then as a consequence of shear-enhanced fabric anisotropy.

Although the third point is clearly dependent on the specification of the breakage model, the second and first points noted above are not. Indeed, breakage smoothing of fabric evolution had been noted in very different discrete breakage models such as those based on aggregates. As the capabilities of experimental micromechanics to address breakable soils improve some or all of the micromechanics uncovered here may be directly verified. In the meantime, performance on mesoscopic simulation would remain the best guide to judge the fitness of discrete models. The role of micromechanics studies, such as this one, is to elucidate the causes underlying a good or a poor performance of the model.