Analytical solutions for organic contaminant diffusion in triple-layer composite liner system considering the effect of degradation

Abstract

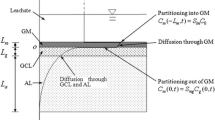
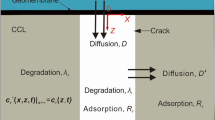
This paper presents analytical solutions for predicting one-dimensional diffusion of an organic contaminant through a triple-layer composite liner system comprising a geomembrane (GM), a geosynthetic clay liner (GCL), and a compacted clay liner (CCL). We consider two different bottom boundary conditions, i.e., fixed-concentration bottom boundary and semi-infinite bottom boundary, for which the methods of separation of variables and Laplace transform, respectively, are used to obtain the analytical solutions. The proposed analytical solutions are then verified against the CST3 numerical model and an analytical solution available in the literature. Using the verified analytical solutions, a series of parametric studies is conducted to investigate the effect of several relevant parameters on contaminant transport through the GM/GCL/CCL liner system. The results indicate that the CCL thickness, the CCL distribution coefficient, and the effective diffusion coefficient of CCL have significant impact on contaminant diffusion in the GM/GCL/CCL liner system, whereas the effective diffusion coefficient of the GCL, the diffusion coefficient of the GM, and the partition coefficient of the GM have negligible effect on contaminant diffusion in the GM/GCL/CCL liner system. The analytical solutions presented herein can be used to aid the design of a triple-layer composite liner system and the verification of other numerical models.

Appendices

Appendix 1

The general solution to the governing Eqs. (1) and (2) can be written as follows:

$$C_{\text{gm}} (z) = A_{1} z + A_{2}$$

(29)

$$C_{\text{gcl}} (z) = B_{1} z + B_{2}$$

(30)

where $A_{1}$ to $B_{2}$ are the parameters to be determined by substituting the above equations into Eqs. (6) to (9) as follows:

$$A_{1} = \frac{{n_{\text{gcl}} D_{\text{gcl}} B_{1} }}{{D_{\text{gm}} }}$$

(31)

$$A_{2} = K_{{d{\text{gm}}}} C_{0} - \frac{{n_{\text{gcl}} D_{\text{gcl}} B_{1} (L_{\text{ccl}} + L_{\text{gcl}} + L_{\text{gm}} )}}{{D_{\text{gm}} }}$$

(32)

$$B_{ 2} = \frac{{K_{{d{\text{gm}}}} C_{0} }}{{K_{{d{\text{gcl}}}} }} - \frac{{n_{\text{gcl}} D_{\text{gcl}} L_{\text{gm}} B_{1} }}{{K_{{d{\text{gcl}}}} D_{\text{gm}} }} - B_{1} (L_{\text{ccl}} + L_{\text{gcl}} )$$

(33)

$$\frac{{K_{{d{\text{gm}}}} C_{0} }}{{K_{{d{\text{gcl}}}} }} - \frac{{n_{\text{gcl}} D_{\text{gcl}} L_{\text{gm}} B_{1} }}{{K_{{d{\text{gcl}}}} D_{\text{gm}} }} - B_{1} L_{\text{gcl}} = \left. {C_{\text{ccl}} (z,t)} \right|_{{z = L_{\text{ccl}} }}$$

(34)

Assume that $C_{\text{ccl}} (z,t)$ is determined by the following equation:

$$C_{\text{ccl}} (z,t) = u_{\text{ccl}} (z,t)\exp ( - \lambda t)$$

(35)

Substituting Eq. (35) into Eq. (3), Eq. (3) can then be expressed as follows:

$$a^{2} \frac{{\partial^{2} u_{\text{ccl}} (z,t)}}{{\partial z^{2} }} = \frac{{\partial u_{\text{ccl}} (z,t)}}{\partial t}$$

(36)

The initial condition of Eq. (36) can be expressed as follows:

$$\left. {u_{\text{ccl}} (z,t)} \right|_{t = 0} = 0$$

(37)

The bottom and top boundary conditions of Eq. (36) can be expressed as follows:

$$\left. {u_{\text{ccl}} (z,t)} \right|_{z = 0} = 0$$

(38)

$$\left. {\frac{{\partial u_{\text{ccl}} (z,t)}}{\partial z}} \right|_{{z = L_{\text{ccl}} }} = \eta B_{1} \exp (\lambda t)$$

(39)

Assume that $u_{\text{ccl}} (z,t)$ is determined by the following equation:

$$u_{\text{ccl}} (z,t) = v(z,t) + w(z,t)$$

(40)

where

$$v(z,t) = \eta B_{1} z\exp (\lambda t)$$

(41)

Substituting Eqs. (40) and (41) into Eqs. (36–39) leads to the governing equation of $w(z,t)$ and the initial and boundary conditions of $w(z,t)$. The $w(z,t)$ is determined by the following equation:

$$a^{2} \frac{{\partial^{2} w(z,t)}}{{\partial z^{2} }} = \frac{\partial w(z,t)}{\partial t} + \eta B_{1} \lambda z\exp (\lambda t)$$

(42)

The initial condition of Eq. (42) can be expressed as follows:

$$\left. {w(z,t)} \right|_{t = 0} = - \eta B_{1} z$$

(43)

The bottom and top boundary conditions of Eq. (42) can be expressed as follows:

$$\left. {w(z,t)} \right|_{z = 0} = 0$$

(44)

$$\left. {\frac{\partial w(z,t)}{\partial z}} \right|_{{z = L_{\text{ccl}} }} = 0$$

(45)

Assume that $w(z,t)$ is determined by the following equation:

$$w(z,t) = w^{\rm I} (z,t) + w^{{{\rm I}{\rm I}}} (z,t)$$

(46)

where $w^{\rm I} (z,t)$ is determined by:

$$a^{2} \frac{{\partial^{2} w^{\rm I} (z,t)}}{{\partial z^{2} }} = \frac{{\partial w^{\rm I} (z,t)}}{\partial t}$$

(47)

The initial condition of Eq. (47) can be expressed as follows:

$$\left. {w^{\rm I} (z,t)} \right|_{t = 0} = - \eta B_{1} z$$

(48)

The bottom and top boundary conditions of Eq. (47) can be expressed as follows:

$$\left. {w^{\rm I} (z,t)} \right|_{z = 0} = 0$$

(49)

$$\left. {\frac{{\partial w^{\rm I} (z,t)}}{\partial z}} \right|_{{z = L_{\text{ccl}} }} = 0$$

(50)

The $w^{{{\rm I}{\rm I}}} (z,t)$ in Eq. (46) is determined by the following equation:

$$a^{2} \frac{{\partial^{2} w^{{{\rm I}{\rm I}}} (z,t)}}{{\partial z^{2} }} = \frac{{\partial w^{{{\rm I}{\rm I}}} (z,t)}}{\partial t} + \eta B_{1} \lambda z\exp (\lambda t)$$

(51)

The initial condition of Eq. (51) can be expressed as follows:

$$\left. {w^{{{\rm I}{\rm I}}} (z,t)} \right|_{t = 0} = 0$$

(52)

The bottom and top boundary conditions of Eq. (51) can be expressed as follows:

$$\left. {w^{{{\rm I}{\rm I}}} (z,t)} \right|_{z = 0} = 0$$

(53)

$$\left. {\frac{{\partial w^{{{\rm I}{\rm I}}} (z,t)}}{\partial z}} \right|_{{z = L_{\text{ccl}} }} = 0$$

(54)

The solution to Eqs. (47) and (51) can be expressed as follows:

$$w^{\rm I} (z,t) = \frac{{2\eta B_{1} }}{{L_{\text{ccl}} }}\sum\limits_{k = 0}^{\infty } {\left\{ {\frac{{( - 1)^{k + 1} }}{{\lambda_{\alpha }^{2} }}\exp ( - \lambda_{\alpha }^{2} a^{2} t)\sin (\lambda_{\alpha } z)} \right\}}$$

(55)

$$\begin{aligned} w^{{{\rm I}{\rm I}}} (z,t) = \frac{{2\eta B_{1} }}{{L_{\text{ccl}} }}\sum\limits_{k = 0}^{\infty } {\left\{ {\frac{{\lambda ( - 1)^{k + 1} }}{{\lambda_{\alpha }^{2} \lambda + a^{2} \lambda_{\alpha }^{4} }}\left[ {\exp (\lambda t) - \exp ( - \lambda_{\alpha }^{2} a^{2} t)} \right]\sin (\lambda_{\alpha } z)} \right\}} \hfill \\ \hfill \\ \end{aligned}$$

(56)

Substituting Eqs. (55) and (56) into Eq. (46) leads to the expression of $w(z,t)$. Substituting the expression of $v(z,t)$ and $w(z,t)$ into Eq. (40) and uniting Eq. (35) leads to the expression of $C_{\text{ccl}} (z,t)$, which can then be substituted into Eq. (34) to obtain the value of $B_{1}$. Then, the values of $A_{1}$, $A_{2}$, and $B_{2}$ can be obtained using Eqs. (31–33).

Appendix 2

The general solution to the governing Eqs. (1) and (2) can be written as follows:

$$C_{\text{gm}} (z) = E_{1} z + E_{2}$$

(57)

$$C_{\text{gcl}} (z) = F_{1} z + F_{2}$$

(58)

where $E_{1}$ to $F_{2}$ are the parameters to be determined by substituting the above equations into Eqs. (6) to (9) as follows:

$$E_{1} = \frac{{n_{\text{gcl}} D_{\text{gcl}} F_{1} }}{{D_{\text{gm}} }}$$

(59)

$$E_{2} = K_{{d{\text{gm}}}} C_{0} - \frac{{n_{\text{gcl}} D_{\text{gcl}} F_{1} (L_{\text{ccl}} + L_{\text{gcl}} + L_{\text{gm}} )}}{{D_{\text{gm}} }}$$

(60)

$$F_{ 2} = \frac{{K_{{d{\text{gm}}}} C_{0} }}{{K_{{d{\text{gcl}}}} }} - \frac{{n_{\text{gcl}} D_{\text{gcl}} L_{\text{gm}} F_{1} }}{{K_{{d{\text{gcl}}}} D_{\text{gm}} }} - F_{1} (L_{\text{ccl}} + L_{\text{gcl}} )$$

(61)

$$F_{1} = \frac{1}{\eta }\left. {\frac{{\partial C_{\text{ccl}} (z,t)}}{\partial z}} \right|_{{z = L_{\text{ccl}} }}$$

(62)

Assume that $C_{\text{ccl}} (z,t)$ is determined by the following equation:

$$C_{\text{ccl}} (z,t) = u_{\text{ccl}} (z,t)\exp ( - \lambda t)$$

(63)

Substituting Eq. (63) into Eq. (3), Eq. (3) can then be expressed as follows:

$$a^{2} \frac{{\partial^{2} u_{\text{ccl}} (z,t)}}{{\partial z^{2} }} = \frac{{\partial u_{\text{ccl}} (z,t)}}{\partial t}$$

(64)

The initial condition of Eq. (64) can be expressed as follows:

$$\left. {u_{\text{ccl}} (z,t)} \right|_{t = 0} = 0$$

(65)

The bottom and top boundary conditions of Eq. (64) can be expressed as follows:

$$\left. {\frac{{\partial u_{\text{ccl}} (z,t)}}{\partial z}} \right|_{z = - \infty } = 0$$

(66)

$$\left. {u_{\text{ccl}} (z,t)} \right|_{{z = L_{\text{ccl}} }} = (F_{1} L_{\text{ccl}} + F_{2} )\exp (\lambda t)$$

(67)

The Laplace transformation technique is used to obtain the solution to Eq. (64), and $\overline{{u_{\text{ccl}} (z,s)}}$ is the Laplace transform of $u_{\text{ccl}} (z,t)$. Equation (64) can then be expressed as follows:

$$a^{2} \frac{{\partial^{2} \overline{{u_{\text{ccl}} (z,s)}} }}{{\partial z^{2} }} - s\overline{{u_{\text{ccl}} (z,s)}} = 0$$

(68)

The Laplace transforms of the boundary conditions considered can be written as follows:

$$\left. {\frac{{\partial \overline{{u_{\text{ccl}} (z,s)}} }}{\partial z}} \right|_{z = - \infty } = 0$$

(69)

$$\left. {\overline{{u_{\text{ccl}} (z,s)}} } \right|_{{z = L_{\text{ccl}} }} = (F_{1} L_{\text{ccl}} + F_{2} )\frac{1}{s - \lambda }$$

(70)

The solution to Eq. (68) can be expressed as follows:

$$\overline{{u_{\text{ccl}} (z,s)}} = \frac{{F_{1} L_{\text{ccl}} + F_{2} }}{s - \lambda }{ \exp }\left[ { - \frac{{(L_{\text{ccl}} - z)\sqrt s }}{a}} \right]$$

(71)

Multiplying the inverse Laplace transform of Eq. (71) by $\exp ( - \lambda t)$ can obtain $C_{\text{ccl}} (z,t)$, which can be expressed as follows:

$$\begin{aligned} C_{\text{ccl}} (z,t) = \frac{{F_{1} L_{\text{ccl}} + F_{2} }}{2}\left\{ {{ \exp }\left[ { - \frac{{(L_{\text{ccl}} - z)\sqrt \lambda }}{a}} \right]{\text{erfc}}\left[ {\frac{{L_{\text{ccl}} - z}}{2a\sqrt t } - \sqrt {\lambda t} } \right] + } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{ \exp }\left[ {\frac{{(L_{\text{ccl}} - z)\sqrt \lambda }}{a}} \right]{\text{erfc}}\left[ {\frac{{L_{\text{ccl}} - z}}{2a\sqrt t } + \sqrt {\lambda t} } \right]} \right\} \hfill \\ \end{aligned}$$

(72)

Substituting Eq. (72) into Eq. (62) and uniting Eqs. (59–61), we can then obtain the values of $E_{1}$ to $F_{2}$.