Analytical solutions for diffusion of organic contaminant through GCL triple-layer composite liner considering degradation in liner

Abstract

Analytical solutions are presented for analyzing diffusion of organic contaminant through a triple-layer composite liner consisting of a geomembrane, a geosynthetic clay liner (GCL) and an attenuation liner (AL). The degradation of organic contaminant in the GCL and AL is considered. Steady-state and full analytical solutions are obtained for two scenarios with zero-concentration or zero-mass-flux boundary conditions at the base of the triple-layer composite liner. The validity and accuracy of the solutions are verified by comparing with an existing analytical solution and a numerical method. Results show that the AL yields major effect to the barrier efficiency of triple-layer composite liner. The contaminant half-life in the GCL has little influence on the mass flux and concentration at the base of triple-layer composite liner. The mass flux and concentration at the base of the triple-layer composite liner decrease with the decrease in contaminant half-life in AL. The steady-state times of bottom mass flux and concentration decrease with the decrease in the contaminant half-life in AL. The mass flux at the base of the triple-layer composite liner decreases with the increase in the thickness or sorption capacity of AL. The steady-state time of bottom mass flux decreases with the decrease in the thickness or sorption capacity of AL. The equivalence between GCL triple-layer composite liner and standard CCL composite liner considering degradation of contaminant is investigated based on the steady-state and full solutions. The analytical solutions can be used for preliminary design of landfill composite liners, verification of complicated numerical methods and evaluation of experimental data.

Appendices

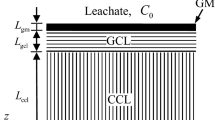
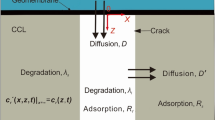
Appendix 1: zero-concentration boundary condition

The solution for the governing equation Eq. (2) can be expressed as

$$C_{\text{m}} \left( {z,t} \right) = A_{1} \left( t \right) + A_{2} \left( t \right)z$$

(94)

where A ₁(t) and A ₂(t) are parameters to be determined. Substituting Eqs. (94) into (1), (3) and (4) results in

$$A_{1} \left( t \right) - A_{2} \left( t \right)L_{\text{m}} = S_{\text{lm}} C_{ 0}$$

(95)

$$A_{1} \left( t \right) = C_{\text{g}} \left( {0,t} \right)S_{\text{mg}}$$

(96)

$$A_{2} \left( t \right) = \frac{{n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{\partial C_{\text{g}} (z,t)}}{\partial z}} \right|_{z = 0}$$

(97)

Substituting Eqs. (96) and (97) into (95) results in

$$C_{\text{g}} \left( {0,t} \right)S_{\text{mg}} - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{\partial C_{\text{g}} (z,t)}}{\partial z}} \right|_{z = 0} = S_{\text{lm}} C_{ 0}$$

(98)

Because of the linear nature of Eqs. (98) and (5)–(16), the C _g(z, t) and C _a(z, t) can be solved by the superposition method (Lee et al. 1992; Chen et al. 2009). The solutions to C _g(z, t) and C _a(z, t) are expressed as follows:

$$C_{\text{g}} (z,t) = u_{\text{g}} (z) + v_{\text{g}} (z,t)$$

(99)

$$C_{\text{a}} (z,t) = u_{\text{a}} (z) + v_{\text{a}} (z,t)$$

(100)

Substitution of Eqs. (99) and (100) into (98) and (5)–(16) yields

$$\frac{{\partial v_{\text{g}} \left( {z,t} \right)}}{\partial t} = \frac{{D_{\text{g}}^{*} }}{{R_{\text{dg}} }}\frac{{\partial^{2} v_{\text{g}} \left( {z,t} \right)}}{{\partial z^{2} }} - \lambda_{\text{g}} v_{\text{g}} \left( {z,t} \right) + \frac{{D_{\text{g}}^{*} }}{{R_{\text{dg}} }}\frac{{{\text{d}}^{2} u_{\text{g}} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{g}} u_{\text{g}} \left( z \right)$$

(101)

$$\frac{{\partial v_{\text{a}} \left( {z,t} \right)}}{\partial t} = \frac{{D_{\text{a}}^{*} }}{{R_{\text{da}} }}\frac{{\partial^{2} v_{\text{a}} \left( {z,t} \right)}}{{\partial z^{2} }} - \lambda_{\text{a}} v_{\text{a}} \left( {z,t} \right) + \frac{{D_{\text{a}}^{*} }}{{R_{\text{da}} }}\frac{{{\text{d}}^{2} u_{\text{a}} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{a}} u_{\text{a}} \left( z \right)$$

(102)

$$v_{\text{g}} \left( {0,t} \right)S_{\text{mg}} - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{\partial v_{\text{g}} (z,t)}}{\partial z}} \right|_{z = 0} = S_{\text{lm}} C_{ 0} - u_{\text{g}} \left( 0 \right)S_{\text{mg}} + \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{{\text{d}}u_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{z = 0}$$

(103)

$$n_{\text{g}} D_{\text{g}}^{*} \left. {\frac{{\partial v_{\text{g}} (z,t)}}{\partial z}} \right|_{{z = L_{\text{g}} }} +\, n_{\text{g}} D_{\text{g}}^{*} \left. {\frac{{{\text{d}}u_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }} = n_{\text{a}} D_{\text{a}}^{*} \left. {\frac{{\partial v_{\text{a}} (z,t)}}{\partial z}} \right|_{{z = L_{\text{g}} }} +\, n_{\text{a}} D_{\text{a}}^{*} \left. {\frac{{{\text{d}}u_{\text{a}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }}$$

(104)

$$v_{\text{g}} \left( {L_{\text{g}} ,t} \right) + u_{\text{g}} \left( {L_{\text{g}} } \right) = v_{\text{a}} \left( {L_{\text{g}} ,t} \right) + u_{\text{a}} \left( {L_{\text{g}} } \right)$$

(105)

$$v_{\text{a}} \left( {L,t} \right) + u_{\text{a}} \left( L \right) = 0$$

(106)

$$v_{\text{g}} \left( {z,0} \right) + u_{\text{g}} \left( z \right) = 0$$

(107)

$$v_{\text{a}} \left( {z,0} \right) + u_{\text{a}} \left( z \right) = 0$$

(108)

In order that the governing equations and boundary conditions of v _g(z, t) and v _a(z, t) become homogeneous, u _g(z) and u _a(z) are set to satisfy

$$\frac{{D_{\text{g}}^{*} }}{{R_{\text{dg}} }}\frac{{{\text{d}}^{2} u_{\text{g}} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{g}} u_{\text{g}} \left( z \right) = 0$$

(109)

$$\frac{{D_{\text{a}}^{*} }}{{R_{\text{da}} }}\frac{{{\text{d}}^{2} u_{\text{a}} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{a}} u_{\text{a}} \left( z \right) = 0$$

(110)

$$u_{\text{g}} \left( 0 \right)S_{\text{mg}} - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{{\text{d}}u_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{z = 0} = S_{\text{lm}} C_{ 0}$$

(111)

$$n_{\text{g}} D_{\text{g}}^{*} \left. {\frac{{{\text{d}}u_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }} = n_{\text{a}} D_{\text{a}}^{*} \left. {\frac{{{\text{d}}u_{\text{a}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }}$$

(112)

$$u_{\text{g}} \left( {L_{\text{g}} } \right) = u_{\text{a}} \left( {L_{\text{g}} } \right)$$

(113)

$$u_{\text{a}} \left( L \right) = 0$$

(114)

u _g(z) and u _a(z) are obtained as

$$u_{\text{g}} \left( z \right) = \frac{{C_{0} S_{\text{lm}} D_{\text{m}} }}{E}\left\{ {n_{\text{g}} D_{\text{g}}^{*} \varepsilon_{\text{g}} \sinh \left( {\varepsilon_{\text{a}} L_{\text{a}} } \right)\cosh \left[ {\varepsilon_{\text{g}} \left( {L_{\text{g}} - z} \right)} \right] + \, n_{\text{a}} D_{\text{a}}^{*} \varepsilon_{\text{a}} \cosh \left( {\varepsilon_{\text{a}} L_{\text{a}} } \right)\sinh \left[ {\varepsilon_{\text{g}} \left( {L_{\text{g}} - z} \right)} \right]} \right\}$$

(115)

$$u_{\text{a}} \left( z \right) = \frac{1}{E}C_{0} S_{\text{lm}} D_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \varepsilon_{\text{g}} \sinh \left[ {\varepsilon_{\text{a}} \left( {L - z} \right)} \right]$$

(116)

where

$$\varepsilon_{\text{g}} = \sqrt {\frac{{R_{\text{dg}} \lambda_{\text{g}} }}{{D_{\text{g}}^{*} }}}$$

(117)

$$\varepsilon_{\text{a}} = \sqrt {\frac{{R_{\text{da}} \lambda_{\text{a}} }}{{D_{\text{a}}^{*} }}}$$

(118)

$$\begin{aligned} E = n_{\text{g}} D_{\text{g}}^{*} \varepsilon_{\text{g}} \sinh \left( {\varepsilon_{\text{a}} L_{\text{a}} } \right)\left[ {S_{\text{mg}} D_{\text{m}} \cosh \left( {\varepsilon_{\text{g}} L_{\text{g}} } \right) + n_{\text{g}} D_{\text{g}}^{*} L_{\text{m}} \varepsilon_{\text{g}} \sinh \left( {\varepsilon_{\text{g}} L_{\text{g}} } \right)} \right] \\ \quad +\, n_{\text{a}} D_{\text{a}}^{*} \varepsilon_{\text{a}} \cosh \left( {\varepsilon_{\text{a}} L_{\text{a}} } \right)\left[ {S_{\text{mg}} D_{\text{m}} \sinh \left( {\varepsilon_{\text{g}} L_{\text{g}} } \right) + n_{\text{g}} D_{\text{g}}^{*} L_{\text{m}} \varepsilon_{\text{g}} \cosh \left( {\varepsilon_{\text{g}} L_{\text{g}} } \right)} \right] \\ \end{aligned}$$

(119)

The governing equations, boundary conditions and initial conditions of v _g(z, t) and v _a(z, t) are as follows:

$$\frac{{\partial v_{\text{g}} \left( {z,t} \right)}}{\partial t} = \frac{{D_{\text{g}}^{*} }}{{R_{\text{dg}} }}\frac{{\partial^{2} v_{\text{g}} \left( {z,t} \right)}}{{\partial z^{2} }} - \lambda_{\text{g}} v_{\text{g}} \left( {z,t} \right)$$

(120)

$$\frac{{\partial v_{\text{a}} \left( {z,t} \right)}}{\partial t} = \frac{{D_{\text{a}}^{*} }}{{R_{\text{da}} }}\frac{{\partial^{2} v_{\text{a}} \left( {z,t} \right)}}{{\partial z^{2} }} - \lambda_{\text{a}} v_{\text{a}} \left( {z,t} \right)$$

(121)

$$v_{\text{g}} \left( {0,t} \right)S_{\text{mg}} - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{\partial v_{\text{g}} (z,t)}}{\partial z}} \right|_{z = 0} = 0$$

(122)

$$n_{\text{g}} D_{\text{g}}^{*} \left. {\frac{{\partial v_{\text{g}} (z,t)}}{\partial z}} \right|_{{z = L_{\text{g}} }} = n_{\text{a}} D_{\text{a}}^{*} \left. {\frac{{\partial v_{\text{a}} (z,t)}}{\partial z}} \right|_{{z = L_{\text{g}} }}$$

(123)

$$v_{\text{g}} \left( {L_{\text{g}} ,t} \right) = v_{\text{a}} \left( {L_{\text{g}} ,t} \right)$$

(124)

$$v_{\text{a}} \left( {L,t} \right) = 0$$

(125)

$$v_{\text{g}} \left( {z,0} \right) = - u_{\text{g}} \left( z \right)$$

(126)

$$v_{\text{a}} \left( {z,0} \right) = - u_{\text{a}} \left( z \right)$$

(127)

The v _g(z, t) and v _a(z, t) can be solved by the method of separation of variables. The solutions to v _g (z, t) and v _a(z, t) are expressed as follows:

$$v_{\text{g}} (z,t) = Z_{\text{g}} (z)T_{\text{g}} (t)$$

(128)

$$v_{\text{a}} (z,t) = Z_{\text{a}} (z)T_{\text{a}} (t)$$

(129)

Substitution of Eqs. (128) and (129) into the governing equations, i.e., Eqs. (120) and (121), yields

$$\frac{{D_{\text{g}}^{*} }}{{R_{\text{dg}} }}\frac{{\frac{{{\text{d}}^{2} Z_{\text{g}} \left( z \right)}}{{{\text{d}}z^{2} }}}}{{Z_{\text{g}} \left( z \right)}} - \lambda_{\text{g}} = \frac{{\frac{{{\text{d}}T_{\text{g}} \left( t \right)}}{{{\text{d}}t}}}}{{T_{\text{g}} \left( t \right)}}$$

(130)

$$\frac{{D_{\text{a}}^{*} }}{{R_{\text{da}} }}\frac{{\frac{{{\text{d}}^{2} Z_{\text{a}} \left( z \right)}}{{{\text{d}}z^{2} }}}}{{Z_{\text{a}} \left( z \right)}} - \lambda_{\text{a}} = \frac{{\frac{{{\text{d}}T_{\text{a}} \left( t \right)}}{{{\text{d}}t}}}}{{T_{\text{a}} \left( t \right)}}$$

(131)

Based on Eqs. (123) and (124), the ratio of T _g(t) and T _a(t) must be constant. This constant can be adjusted to be 1 by an appropriate scaling of Z _g(z) and Z _a(z). Therefore, the following relation can be set as

$$T_{\text{g}} \left( t \right) = T_{\text{a}} \left( t \right)$$

(132)

$$\frac{{\frac{{{\text{d}}T_{\text{g}} \left( t \right)}}{{{\text{d}}t}}}}{{T_{\text{g}} \left( t \right)}} = \frac{{\frac{{{\text{d}}T_{\text{a}} \left( t \right)}}{{{\text{d}}t}}}}{{T_{\text{a}} \left( t \right)}} = - \delta$$

(133)

T _g(t) and T _a(t) are obtained as

$$T_{\text{g}} \left( t \right) = T_{\text{a}} \left( t \right) = e^{ - \delta t}$$

(134)

Z _g(z) and Z _a(z) satisfy

$$\frac{{{\text{d}}^{2} Z_{\text{g}} \left( z \right)}}{{{\text{d}}z^{2} }} + \left( {\delta - \lambda_{\text{g}} } \right)\frac{{R_{\text{dg}} }}{{D_{\text{g}}^{*} }}Z_{\text{g}} \left( z \right) = 0$$

(135)

$$\frac{{{\text{d}}^{2} Z_{\text{a}} \left( z \right)}}{{{\text{d}}z^{2} }} + \left( {\delta - \lambda_{\text{a}} } \right)\frac{{R_{\text{da}} }}{{D_{\text{a}}^{*} }}Z_{\text{a}} \left( z \right) = 0$$

(136)

$$Z_{\text{g}} \left( 0 \right)S_{\text{mg}} - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{{{\text{d}}Z}_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{z = 0} = 0$$

(137)

$$n_{\text{g}} D_{\text{g}}^{*} \left. {\frac{{{{\text{d}}Z}_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }} = n_{\text{a}} D_{\text{a}}^{*} \left. {\frac{{{{\text{d}}Z}_{\text{a}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }}$$

(138)

$$Z_{\text{g}} \left( {L_{\text{g}} } \right) = Z_{\text{a}} \left( {L_{\text{g}} } \right)$$

(139)

$$Z_{\text{a}} \left( L \right) = 0$$

(140)

With the definitions

$$\omega_{\text{g}} = \sqrt {\frac{{R_{\text{dg}} }}{{D_{\text{g}}^{*} }}\left| {\lambda_{\text{g}} - \delta } \right|} \quad {\text{and}}\quad \omega_{\text{a}} = \sqrt {\frac{{R_{\text{da}} }}{{D_{\text{a}}^{*} }}\left| {\lambda_{\text{a}} - \delta } \right|}$$

(141)

the solutions of the differential Eqs. (135) and (136) which obey the boundary condition Eq. (140) are

$$Z_{\text{g}} \left( z \right) = \left\{ {\begin{array}{*{20}c} {a_{{\text{g}}1} \sinh \left( {\omega_{\text{g}} z} \right) + a_{{\text{g}}2} \cosh \left( {\omega_{\text{g}} z} \right) \, \delta < \lambda_{\text{g}} } \\ {a_{{\text{g}}1} z + a_{{\text{g}}2} \, \delta = \lambda_{\text{g}} } \\ {a_{{\text{g}}1} \sin \left( {\omega_{\text{g}} z} \right) + a_{{\text{g}}2} \cos \left( {\omega_{\text{g}} z} \right) \, \delta > \lambda_{\text{g}} } \\ \end{array} } \right.$$

(142)

$$Z_{\text{a}} \left( z \right) = \left\{ {\begin{array}{*{20}c} {a_{\text{a}} \sinh \left[ {\omega_{\text{a}} \left( {L - z} \right)} \right] \, \delta < \lambda_{\text{a}} } \\ {a_{\text{a}} \left( {L - z} \right) \, \delta = \lambda_{\text{a}} } \\ {a_{\text{a}} \sin \left[ {\omega_{\text{a}} \left( {L - z} \right)} \right] \, \delta > \lambda_{\text{a}} } \\ \end{array} } \right.$$

(143)

Substitution of Eqs. (142) and (143) into boundary conditions Eqs. (137)–(139) for any combination δ < λ _g, δ = λ _g, or δ > λ _g and δ < λ _a, δ = λ _a, or δ > λ _a yields a set of three homogeneous equations for the three unknowns a _g1, a _g2 and a _a:

$${\mathbf{M}} \cdot \left( {\begin{array}{*{20}c} {a_{{\text{g}}1} } \\ {a_{{\text{g}}2} } \\ {a_{\text{a}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right)$$

(144)

with M being a 3 × 3 matrix which depends on the characteristic parameters of the barrier system and on δ. Non-trivial solutions of this set of homogeneous equations, i.e., a solution Z _g(z) > 0 and Z _a(z) > 0, only exist if the determinant of the matrix M is zero. Since δ is the only parameter in M which is not yet determined, the equation det M = 0 is the equation which determines the values of δ for which a non-trivial solution of the Eqs. (135)–(139) exists. The equation det M = 0 is the eigenvalue equation for δ.

The direct evaluation of det M for the nine possible combinations δ < λ _g, δ = λ _g, or δ > λ _g and δ < λ _a, δ = λ _a, or δ > λ _a shows that det M is strictly positive for any value of δ except for the following three combinations λ _a < δ < λ _g, λ _g < δ < λ _a and λ _g, λ _a < δ. Therefore, non-trivial solutions can only exist for these three combinations.

The equation det M = 0 for the combination λ _a < δ < λ _g is

$$\begin{aligned} \det \, {\mathbf{M}} &= n_{\text{a}} D_{\text{a}}^{*} \omega_{\text{a}} \cos \left( {\omega_{\text{a}} L_{\text{a}} } \right)\left[ {\sinh \left( {\omega_{\text{g}} L_{\text{g}} } \right) + \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\cosh \left( {\omega_{\text{g}} L_{\text{g}} } \right)} \right] \hfill \\ &\quad + \, n_{\text{g}} D_{\text{g}}^{*} \omega_{\text{g}} \sin \left( {\omega_{\text{a}} L_{\text{a}} } \right)\left[ {\cosh \left( {\omega_{\text{g}} L_{\text{g}} } \right) + \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\sinh \left( {\omega_{\text{g}} L_{\text{g}} } \right)} \right] = 0 \hfill \\ \end{aligned}$$

(145)

Let the eigenvalues be denoted by δ _k and the corresponding eigenfunctions by Z _gk (z) and Z _ak (z). The parameters ω _gk and ω _ak are defined as

$$\omega_{{\text{g}}k} = \sqrt {\frac{{R_{\text{dg}} }}{{D_{\text{g}}^{*} }}\left| {\lambda_{\text{g}} - \delta_{k} } \right|} \quad {\text{and}}\quad \omega_{{\text{a}}k} = \sqrt {\frac{{R_{\text{da}} }}{{D_{\text{a}}^{*} }}\left| {\lambda_{\text{a}} - \delta_{k} } \right|}$$

(146)

Equation (145) may or may not have a solution in the interval (λ _a, λ _g). If a solution δ _k exists, the corresponding eigenfunctions are (with the normalization a _ak  = 1)

$$Z_{{\text{g}}k} \left( z \right) = a_{{\text{g}}1k} \sinh \left( {\omega_{{\text{g}}k} z} \right) + a_{{\text{g}}2k} \cosh \left( {\omega_{{\text{g}}k} z} \right)\quad {\text{if}}\qquad\quad \, \lambda_{\text{a}} < \delta_{k} < \lambda_{\text{g}}$$

(147)

$$Z_{{\text{a}}k} \left( z \right) = \sin \left[ {\omega_{{\text{a}}k} \left( {L - z} \right)} \right]\quad {\text{if}}\quad \lambda_{\text{a}} < \delta_{k} < \lambda_{\text{g}}$$

(148)

with

$$a_{{\text{g}}1k} = D_{\text{m}} S_{\text{mg}} \sin \left( {\omega_{{\text{a}}k} L_{\text{a}} } \right)/\left[ {D_{\text{m}} S_{\text{mg}} \sinh \left( {\omega_{{\text{g}}k} L_{\text{g}} } \right) + \, L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{{\text{g}}k} \cosh \left( {\omega_{{\text{g}}k} L_{\text{g}} } \right)} \right]$$

(149)

$$a_{{\text{g}}2k} = a_{{\text{g}}1k} \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{{\text{g}}k} }}{{D_{\text{m}} S_{\text{mg}} }}$$

(150)

The equation det M = 0 for the combination λ _g, λ _a < δ is

$$\begin{aligned} \det \, {\mathbf{M}} = n_{\text{a}} D_{\text{a}}^{*} \omega_{\text{a}} \cos \left( {\omega_{\text{a}} L_{\text{a}} } \right)\left[ {\sin \left( {\omega_{\text{g}} L_{\text{g}} } \right) + \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\cos \left( {\omega_{\text{g}} L_{\text{g}} } \right)} \right] \hfill \\ + \, n_{\text{g}} D_{\text{g}}^{*} \omega_{\text{g}} \sin \left( {\omega_{\text{a}} L_{\text{a}} } \right)\left[ {\cos \left( {\omega_{\text{g}} L_{\text{g}} } \right) - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\sin \left( {\omega_{\text{g}} L_{\text{g}} } \right)} \right] = 0 \hfill \\ \end{aligned}$$

(151)

Since the interval of the possible solutions is not bounded from above, this equation always has solutions. With the same definition of δ _k , Z _gk (z) and Z _ak (z) as above and the same normalization a _ak  = 1, the eigenfunctions are

$$Z_{{\text{g}}k} \left( z \right) = a_{{\text{g}}1k} \sin \left( {\omega_{{\text{g}}k} z} \right) + a_{{\text{g}}2k} \cos \left( {\omega_{{\text{g}}k} z} \right)\quad {\text{if}}\quad \, \lambda_{\text{a}} ,\lambda_{\text{g}} < \delta_{k}$$

(152)

$$Z_{{\text{a}}k} \left( z \right) = \sin \left[ {\omega_{{\text{a}}k} \left( {L - z} \right)} \right]\quad {\text{if}}\quad \lambda_{\text{a}} ,\lambda_{\text{g}} < \delta_{k}$$

(153)

with

$$a_{{\text{g}}1k} = D_{\text{m}} S_{\text{mg}} \sin \left( {\omega_{{\text{a}}k} L_{\text{a}} } \right)/\left[ {D_{\text{m}} S_{\text{mg}} \sin \left( {\omega_{{\text{g}}k} L_{\text{g}} } \right) +\, L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{{\text{g}}k} \cos \left( {\omega_{{\text{g}}k} L_{\text{g}} } \right)} \right]$$

(154)

$$a_{{\text{g}}2k} = a_{{\text{g}}1k} \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{{\text{g}}k} }}{{D_{\text{m}} S_{\text{mg}} }}$$

(155)

The equation det M = 0 for the combination λ _g < δ < λ _a is

$$\begin{aligned} \det \, {\mathbf{M}} = n_{\text{a}} D_{\text{a}}^{*} \omega_{\text{a}} \cosh \left( {\omega_{\text{a}} L_{\text{a}} } \right)\left[ {\sin \left( {\omega_{\text{g}} L_{\text{g}} } \right) + \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\cos \left( {\omega_{\text{g}} L_{\text{g}} } \right)} \right] \hfill \\ + \, n_{\text{g}} D_{\text{g}}^{*} \omega_{\text{g}} \sinh \left( {\omega_{\text{a}} L_{\text{a}} } \right)\left[ {\cos \left( {\omega_{\text{g}} L_{\text{g}} } \right) - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\sin \left( {\omega_{\text{g}} L_{\text{g}} } \right)} \right] = 0 \hfill \\ \end{aligned}$$

(156)

Equation (156) may or may not have a solution in the interval (λ _g, λ _a). If a solution exists, with the same definition of δ _k , Z _gk (z) and Z _ak (z) as above and the same normalization a _ak  = 1 the eigenfunctions are

$$Z_{{\text{g}}k} \left( z \right) = a_{{\text{g}}1k} \sin \left( {\omega_{{\text{g}}k} z} \right) + a_{{\text{g}}2k} \cos \left( {\omega_{{\text{g}}k} z} \right)\quad {\text{if}}\quad \lambda_{\text{g}} < \delta_{k} < \lambda_{\text{a}}$$

(157)

$$Z_{{\text{a}}k} \left( z \right) = \sin \left[ {\omega_{{\text{a}}k} \left( {L - z} \right)} \right]\quad {\text{if}}\quad \lambda_{\text{g}} < \delta_{k} < \lambda_{\text{a}}$$

(158)

with

$$a_{{\text{g}}1k} = D_{\text{m}} S_{\text{mg}} \sinh \left( {\omega_{{\text{a}}k} L_{\text{a}} } \right)/\left[ {D_{\text{m}} S_{\text{mg}} \sin \left( {\omega_{{\text{g}}k} L_{\text{g}} } \right) +\, L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{{\text{g}}k} \cos \left( {\omega_{{\text{g}}k} L_{\text{g}} } \right)} \right]$$

(159)

$$a_{{\text{g}}2k} = a_{{\text{g}}1k} \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \omega_{{\text{g}}k} }}{{D_{\text{m}} S_{\text{mg}} }}$$

(160)

For each case λ _g < λ _a, λ _g = λ _a and λ _g > λ _a, the solutions of the Eqs. (120)–(127) are

$$v_{\text{g}} \left( {z,t} \right) = \sum\limits_{k = 1}^{\infty } {G_{k} Z_{{\text{g}}k} \left( z \right)} e^{{ - \delta_{k} t}}$$

(161)

$$v_{\text{a}} \left( {z,t} \right) = \sum\limits_{k = 1}^{\infty } {G_{k} Z_{{\text{a}}k} \left( z \right)} e^{{ - \delta_{k} t}}$$

(162)

with δ _k , Z _gk (z) and Z _ak (z) according to Eqs. (145)–(150), (151)–(155) or (156)–(160) depending on the relative size of δ _k , λ _a and λ _g.

The orthogonality of Z _gk (z) (0 < z < L _g) and Z _ak (z) (L _g < z < L) can be shown by considering

$$\begin{aligned} \left( {\delta_{k} - \delta_{\text{m}} } \right)\left[ {n_{\text{g}} R_{\text{dg}} \int_{0}^{{L_{\text{g}} }} {Z_{{\text{g}}k} \left( z \right)Z_{\text{gm}} \left( z \right)} {\text{d}}z + n_{\text{a}} R_{\text{da}} \int_{{L_{\text{g}} }}^{L} {Z_{{\text{a}}k} \left( z \right)Z_{\text{am}} \left( z \right)} {\text{d}}z} \right] \hfill \\ = - n_{\text{g}} R_{\text{dg}} \int_{0}^{{L_{\text{g}} }} {\left( {\frac{{D_{\text{g}}^{*} }}{{R_{\text{dg}} }}\frac{{{\text{d}}^{2} Z_{{\text{g}}k} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{g}} Z_{{\text{g}}k} \left( z \right)} \right)Z_{\text{gm}} \left( z \right)} {\text{d}}z + n_{\text{g}} R_{\text{dg}} \int_{0}^{{L_{\text{g}} }} {Z_{{\text{g}}k} \left( z \right)\left( {\frac{{D_{\text{g}}^{*} }}{{R_{\text{dg}} }}\frac{{{\text{d}}^{2} Z_{\text{gm}} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{g}} Z_{\text{gm}} \left( z \right)} \right)} {\text{d}}z \hfill \\ \quad - n_{\text{a}} R_{\text{da}} \int_{{L_{\text{g}} }}^{L} {\left( {\frac{{D_{\text{a}}^{*} }}{{R_{\text{da}} }}\frac{{{\text{d}}^{2} Z_{{\text{a}}k} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{a}} Z_{{\text{a}}k} \left( z \right)} \right)Z_{\text{am}} \left( z \right)} {\text{d}}z + n_{\text{a}} R_{\text{da}} \int_{{L_{\text{g}} }}^{L} {Z_{{\text{a}}k} \left( z \right)\left( {\frac{{D_{\text{a}}^{*} }}{{R_{\text{da}} }}\frac{{{\text{d}}^{2} Z_{\text{am}} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{a}} Z_{\text{am}} \left( z \right)} \right)} {\text{d}}z \hfill \\ \end{aligned}$$

(163)

If δ _k  ≠ δ _m(k ≠ m), the right-hand side of Eq. (163) is equal to the left-hand side due to Eqs. (135) and (136). With partial integration of the right-hand side and application of the boundary conditions, Eqs. (137)–(140) follow that the right-hand side is zero. Since δ _k  ≠ δ _m, the squared bracket on the left-hand side must be zero.

Using the orthogonality of Z _gk (z) (0 < z < L _g) and Z _ak (z) (L _g < z < L), the following formulation for G _k can be obtained as

$$G_{k} = \frac{1}{{H_{k} }}\left[ {n_{\text{g}} R_{\text{dg}} \int_{0}^{{L_{\text{g}} }} { - u_{\text{g}} \left( z \right)Z_{{\text{g}}k} \left( z \right)} {\text{d}}z + n_{\text{a}} R_{\text{da}} \int_{{L_{\text{g}} }}^{L} { - u_{\text{a}} \left( z \right)Z_{{\text{a}}k} \left( z \right)} {\text{d}}z} \right]$$

(164)

with

$$H_{k} = n_{\text{g}} R_{\text{dg}} \int_{0}^{{L_{\text{g}} }} {Z_{{\text{g}}k}^{2} \left( z \right)} {\text{d}}z + n_{\text{a}} R_{\text{da}} \int_{{L_{\text{g}} }}^{L} {Z_{{\text{a}}k}^{2} \left( z \right)} {\text{d}}z$$

(165)

For each case λ _g < λ _a, λ _g = λ _a and λ _g > λ _a, the solutions of C _g(z, t) and C _a(z, t) are derived as

$$C_{\text{g}} \left( {z,t} \right) = \sum\limits_{k = 1}^{\infty } {G_{k} Z_{{\text{g}}k} \left( z \right)} e^{{ - \delta_{k} t}} + u_{\text{g}} \left( z \right)$$

(166)

$$C_{\text{a}} \left( {z,t} \right) = \sum\limits_{k = 1}^{\infty } {G_{k} Z_{{\text{a}}k} \left( z \right)} e^{{ - \delta_{k} t}} + u_{\text{a}} \left( z \right)$$

(167)

Appendix 2: zero-mass-flux boundary condition

The solution for the governing equation Eq. (2) can be expressed as

$$C_{\text{m}} \left( {z,t} \right) = B_{1} \left( t \right) + B_{2} \left( t \right)z$$

(168)

where B ₁(t) and B ₂(t) are parameters to be determined. Substituting Eqs. (168) into (1), (3) and (4) results in

$$B_{1} \left( t \right) - B_{2} \left( t \right)L_{\text{m}} = S_{\text{lm}} C_{ 0}$$

(169)

$$B_{1} \left( t \right) = C_{\text{g}} \left( {0,t} \right)S_{\text{mg}}$$

(170)

$$B_{2} \left( t \right) = \frac{{n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{\partial C_{\text{g}} (z,t)}}{\partial z}} \right|_{z = 0}$$

(171)

Substituting Eqs. (170) and (171) into (169) results in

$$C_{\text{g}} \left( {0,t} \right)S_{\text{mg}} - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{\partial C_{\text{g}} (z,t)}}{\partial z}} \right|_{z = 0} = S_{\text{lm}} C_{ 0}$$

(172)

Because of the linear nature of Eqs. (172) and (5)–(16), the C _g(z, t) and C _a(z, t) can be solved by the superposition method (Lee et al. 1992; Chen et al. 2009). The solutions to C _g(z, t) and C _a(z, t) are expressed as follows:

$$C_{\text{g}} (z,t) = w_{\text{g}} (z) + y_{\text{g}} (z,t)$$

(173)

$$C_{\text{a}} (z,t) = w_{\text{a}} (z) + y_{\text{a}} (z,t)$$

(174)

In order that the governing equations and boundary conditions of y _g(z, t) and y _a(z, t) become homogeneous, w _g(z) and w _a(z) are set to satisfy

$$\frac{{D_{\text{g}}^{*} }}{{R_{\text{dg}} }}\frac{{{\text{d}}^{2} w_{\text{g}} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{g}} w_{\text{g}} \left( z \right) = 0$$

(175)

$$\frac{{D_{\text{a}}^{*} }}{{R_{\text{da}} }}\frac{{{\text{d}}^{2} w_{\text{a}} \left( z \right)}}{{{\text{d}}z^{2} }} - \lambda_{\text{a}} w_{\text{a}} \left( z \right) = 0$$

(176)

$$w_{\text{g}} \left( 0 \right)S_{\text{mg}} - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{{\text{d}}w_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{z = 0} = S_{\text{lm}} C_{ 0}$$

(177)

$$n_{\text{g}} D_{\text{g}}^{*} \left. {\frac{{{\text{d}}w_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }} = n_{\text{a}} D_{\text{a}}^{*} \left. {\frac{{{\text{d}}w_{\text{a}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }}$$

(178)

$$w_{\text{g}} \left( {L_{\text{g}} } \right) = w_{\text{a}} \left( {L_{\text{g}} } \right)$$

(179)

$$\left. {\frac{{{\text{d}}w_{\text{a}} (z)}}{{\text{d}}z}} \right|_{z = L} = 0$$

(180)

w _g(z) and w _a(z) are obtained as

$$w_{\text{g}} \left( z \right) = \frac{{C_{0} S_{\text{lm}} D_{\text{m}} }}{F}\left\{ {n_{\text{g}} D_{\text{g}}^{*} \varepsilon_{\text{g}} \cosh \left( {\varepsilon_{\text{a}} L_{\text{a}} } \right)\cosh \left[ {\varepsilon_{\text{g}} \left( {L_{\text{g}} - z} \right)} \right] + \, n_{\text{a}} D_{\text{a}}^{*} \varepsilon_{\text{a}} \sinh \left( {\varepsilon_{\text{a}} L_{\text{a}} } \right)\sinh \left[ {\varepsilon_{\text{g}} \left( {L_{\text{g}} - z} \right)} \right]} \right\}$$

(181)

$$w_{\text{a}} \left( z \right) = \frac{1}{F}C_{0} S_{\text{lm}} D_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \varepsilon_{\text{g}} \cosh \left[ {\varepsilon_{\text{a}} \left( {L - z} \right)} \right]$$

(182)

where

$$\varepsilon_{\text{g}} = \sqrt {\frac{{R_{\text{dg}} \lambda_{\text{g}} }}{{D_{\text{g}}^{*} }}}$$

(183)

$$\varepsilon_{\text{a}} = \sqrt {\frac{{R_{\text{da}} \lambda_{\text{a}} }}{{D_{\text{a}}^{*} }}}$$

(184)

$$\begin{aligned} F = n_{\text{g}} D_{\text{g}}^{*} \varepsilon_{\text{g}} \cosh \left( {\varepsilon_{\text{a}} L_{\text{a}} } \right)\left[ {S_{\text{mg}} D_{\text{m}} \cosh \left( {\varepsilon_{\text{g}} L_{\text{g}} } \right) + n_{\text{g}} D_{\text{g}}^{*} L_{\text{m}} \varepsilon_{\text{g}} \sinh \left( {\varepsilon_{\text{g}} L_{\text{g}} } \right)} \right] \\ + \, n_{\text{a}} D_{\text{a}}^{*} \varepsilon_{\text{a}} \sinh \left( {\varepsilon_{\text{a}} L_{\text{a}} } \right)\left[ {S_{\text{mg}} D_{\text{m}} \sinh \left( {\varepsilon_{\text{g}} L_{\text{g}} } \right) + n_{\text{g}} D_{\text{g}}^{*} L_{\text{m}} \varepsilon_{\text{g}} \cosh \left( {\varepsilon_{\text{g}} L_{\text{g}} } \right)} \right] \\ \end{aligned}$$

(185)

The governing equations, boundary conditions and initial conditions of y _g(z, t) and y _a(z, t) are as follows:

$$\frac{{\partial y_{\text{g}} \left( {z,t} \right)}}{\partial t} = \frac{{D_{\text{g}}^{*} }}{{R_{\text{dg}} }}\frac{{\partial^{2} y_{\text{g}} \left( {z,t} \right)}}{{\partial z^{2} }} - \lambda_{\text{g}} y_{\text{g}} \left( {z,t} \right)$$

(186)

$$\frac{{\partial y_{\text{a}} \left( {z,t} \right)}}{\partial t} = \frac{{D_{\text{a}}^{*} }}{{R_{\text{da}} }}\frac{{\partial^{2} y_{\text{a}} \left( {z,t} \right)}}{{\partial z^{2} }} - \lambda_{\text{a}} y_{\text{a}} \left( {z,t} \right)$$

(187)

$$y_{\text{g}} \left( {z,t} \right)\left| {_{z = 0} } \right.S_{\text{mg}} - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{\partial y_{\text{g}} (z,t)}}{\partial z}} \right|_{z = 0} = 0$$

(188)

$$n_{\text{g}} D_{\text{g}}^{*} \left. {\frac{{\partial y_{\text{g}} (z,t)}}{\partial z}} \right|_{{z = L_{\text{g}} }} = n_{\text{a}} D_{\text{a}}^{*} \left. {\frac{{\partial y_{\text{a}} (z,t)}}{\partial z}} \right|_{{z = L_{\text{g}} }}$$

(189)

$$y_{\text{g}} \left( {L_{\text{g}} ,t} \right) = y_{\text{a}} \left( {L_{\text{g}} ,t} \right)$$

(190)

$$\left. {\frac{{\partial y_{\text{a}} (z,t)}}{\partial z}} \right|_{z = L} = 0$$

(191)

$$y_{\text{g}} \left( {z,0} \right) = - w_{\text{g}} \left( z \right)$$

(192)

$$y_{\text{a}} \left( {z,0} \right) = - w_{\text{a}} \left( z \right)$$

(193)

The y _g(z, t) and y _a(z, t) can be solved by the method of separation of variables. The solutions to y _g (z, t) and y _a(z, t) are expressed as follows:

$$y_{\text{g}} (z,t) = Z_{\text{g}} (z)T_{\text{g}} (t)$$

(194)

$$y_{\text{a}} (z,t) = Z_{\text{a}} (z)T_{\text{a}} (t)$$

(195)

T _g(t) and T _a(t) are obtained as

$$T_{\text{g}} \left( t \right) = T_{\text{a}} \left( t \right) = e^{ - \psi t}$$

(196)

Z _g(z) and Z _a(z) satisfy

$$\frac{{{\text{d}}^{2} Z_{\text{g}} \left( z \right)}}{{{\text{d}}z^{2} }} + \left( {\psi - \lambda_{\text{g}} } \right)\frac{{R_{\text{dg}} }}{{D_{\text{g}}^{*} }}Z_{\text{g}} \left( z \right) = 0$$

(197)

$$\frac{{{\text{d}}^{2} Z_{\text{a}} \left( z \right)}}{{{\text{d}}z^{2} }} + \left( {\psi - \lambda_{\text{a}} } \right)\frac{{R_{\text{da}} }}{{D_{\text{a}}^{*} }}Z_{\text{a}} \left( z \right) = 0$$

(198)

$$Z_{\text{g}} \left( 0 \right)S_{\text{mg}} - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} }}{{D_{\text{m}} }}\left. {\frac{{{{\text{d}}Z}_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{z = 0} = 0$$

(199)

$$n_{\text{g}} D_{\text{g}}^{*} \left. {\frac{{{{\text{d}}Z}_{\text{g}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }} = n_{\text{a}} D_{\text{a}}^{*} \left. {\frac{{{{\text{d}}Z}_{\text{a}} \left( z \right)}}{{\text{d}}z}} \right|_{{z = L_{\text{g}} }}$$

(200)

$$Z_{\text{g}} \left( {L_{\text{g}} } \right) = Z_{\text{a}} \left( {L_{\text{g}} } \right)$$

(201)

$$\left. {\frac{{{{\text{d}}Z}_{\text{a}} (z)}}{{\text{d}}z}} \right|_{z = L} = 0$$

(202)

With the definitions

$$\mu_{\text{g}} = \sqrt {\frac{{R_{\text{dg}} }}{{D_{\text{g}}^{*} }}\left| {\lambda_{\text{g}} - \psi } \right|} \quad {\text{and}}\quad \mu_{\text{a}} = \sqrt {\frac{{R_{\text{da}} }}{{D_{\text{a}}^{*} }}\left| {\lambda_{\text{a}} - \psi } \right|}$$

(203)

the solutions of the differential Eqs. (197) and (198) which obey the boundary condition Eq. (202) are

$$Z_{\text{g}} \left( z \right) = \left\{ {\begin{array}{ll} b_{{\text{g}}1} \sinh \left( {\mu_{\text{g}} z} \right) + b_{{\text{g}}2} \cosh \left( {\mu_{\text{g}} z} \right) & \quad \psi lt; \lambda_{\text{g}} \\ b_{{\text{g}}1} z + b_{{\text{g}}2} & \quad \psi = \lambda_{\text{g}} \\ b_{{\text{g}}1} \sinh \left( {\mu_{\text{g}} z} \right) + b_{{\text{g}}2} \cosh \left( {\mu_{\text{g}} z} \right) & \quad \psi > \lambda_{\text{g}} \\ \end{array}} \right.$$

(204)

$$Z_{\text{a}} \left( z \right) = \left\{ \begin{array}{ll} b_{\text{a}} \cosh \left[ {\omega_{\text{a}} \left( {L - z} \right)} \right] & \quad \psi < \lambda_{\text{a}} \\ b_{\text{a}} &\quad \psi = \lambda_{\text{a}} \\ b_{\text{a}} \cos \left[ {\omega_{\text{a}} \left( {L - z} \right)} \right] & \quad \psi > \lambda_{\text{a}} \\ \end{array} \right.$$

(205)

Substitution of Eqs. (204) and (205) into boundary conditions Eqs. (199)–(201) for any combination ψ < λ _g, ψ = λ _g, or ψ > λ _g and ψ < λ _a, ψ = λ _a, or ψ > λ _a yields a set of three homogeneous equations for the three unknowns b _g1, b _g2 and b _a:

$${\mathbf{P}} \cdot \left( {\begin{array}{*{20}c} {b_{{\text{g}}1} } \\ {b_{{\text{g}}2} } \\ {b_{\text{a}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right)$$

(206)

with P being a 3 × 3 matrix which depends on the characteristic parameters of the barrier system and on ψ. Non-trivial solutions of this set of homogeneous equations, i.e., a solution Z _g(z) > 0 and Z _a(z) > 0, only exist if the determinant of the matrix P is zero. Since ψ is the only parameter in P which is not yet determined, the equation det P = 0 is the equation which determines the values of ψ for which a non-trivial solution of Eqs. (197)–(201) exists. The equation det P = 0 is the eigenvalue equation for ψ.

The direct evaluation of det P for the nine possible combinations ψ < λ _g, ψ = λ _g, or ψ > λ _g and ψ < λ _a, ψ = λ _a, or ψ > λ _a shows that det P is strictly positive for any value of ψ except for the following three combinations λ _a < ψ < λ _g, λ _g < ψ < λ _a and λ _g, λ _a < ψ. Therefore, non-trivial solutions can only exist for these three combinations.

The equation det P = 0 for the combination λ _a < ψ < λ _g is

$$\begin{aligned} \det \, {\mathbf{P}}{ \,=\, }n_{\text{a}} D_{\text{a}}^{*} \mu_{\text{a}} \sin \left( {\mu_{\text{a}} L_{\text{a}} } \right)\left[ {\sinh \left( {\mu_{\text{g}} L_{\text{g}} } \right) + \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\cosh \left( {\mu_{\text{g}} L_{\text{g}} } \right)} \right] \hfill \\\qquad\quad - \, n_{\text{g}} D_{\text{g}}^{*} \mu_{\text{g}} \cos \left( {\mu_{\text{a}} L_{\text{a}} } \right)\left[ {\cosh \left( {\mu_{\text{g}} L_{\text{g}} } \right) + \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\sinh \left( {\mu_{\text{g}} L_{\text{g}} } \right)} \right] = 0 \hfill \\ \end{aligned}$$

(207)

Let the eigenvalues be denoted by ψ _i and the corresponding eigenfunctions by Z _gi (z) and Z _ai (z). The parameters μ _gi and μ _ai are defined as

$$\mu_{{\text{g}}i} = \sqrt {\frac{{R_{\text{dg}} }}{{D_{\text{g}}^{*} }}\left| {\lambda_{\text{g}} - \psi_{i} } \right|} \quad {\text{and}}\quad \mu_{{\text{a}}i} = \sqrt {\frac{{R_{\text{da}} }}{{D_{\text{a}}^{*} }}\left| {\lambda_{\text{a}} - \psi_{i} } \right|}$$

(208)

Equation (207) may or may not have a solution in the interval (λ _a, λ _g). If a solution ψ _i exists, the corresponding eigenfunctions are (with the normalization b _ai  = 1)

$$Z_{{\text{g}}i} \left( z \right) = b_{{\text{g}}1i} \sinh \left( {\mu_{{\text{g}}i} z} \right) + b_{{\text{g}}2i} \cosh \left( {\mu_{{\text{g}}i} z} \right)\quad {\text{if}}\quad \lambda_{\text{a}} < \psi_{i} < \lambda_{\text{g}}$$

(209)

$$Z_{{\text{a}}i} \left( z \right) = \cos \left[ {\mu_{{\text{a}}i} \left( {L - z} \right)} \right]\quad {\text{if}}\quad \lambda_{\text{a}} < \psi_{i} < \lambda_{\text{g}}$$

(210)

with

$$b_{{\text{g}}1i} = D_{\text{m}} S_{\text{mg}} \cos \left( {\mu_{{\text{a}}i} L_{\text{a}} } \right)/\left[ {D_{\text{m}} S_{\text{mg}} \sinh \left( {\mu_{{\text{g}}i} L_{\text{g}} } \right) +\, L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{{\text{g}}k} \cosh \left( {\mu_{{\text{g}}i} L_{\text{g}} } \right)} \right]$$

(211)

$$b_{{\text{g}}2i} = b_{{\text{g}}1i} \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{{\text{g}}i} }}{{D_{\text{m}} S_{\text{mg}} }}$$

(212)

The equation det P = 0 for the combination λ _g, λ _a < ψ is

$$\begin{aligned} \det \, {\mathbf{P}}\,{ = }\,n_{\text{a}} D_{\text{a}}^{*} \mu_{\text{a}} \sin \left( {\mu_{\text{a}} L_{\text{a}} } \right)\left[ {\sin \left( {\mu_{\text{g}} L_{\text{g}} } \right) + \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\cos \left( {\mu_{\text{g}} L_{\text{g}} } \right)} \right] \hfill \\ - \, n_{\text{g}} D_{\text{g}}^{*} \mu_{\text{g}} \cos \left( {\mu_{\text{a}} L_{\text{a}} } \right)\left[ {\cos \left( {\mu_{\text{g}} L_{\text{g}} } \right) - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\sin \left( {\mu_{\text{g}} L_{\text{g}} } \right)} \right] = 0 \hfill \\ \end{aligned}$$

(213)

Since the interval of the possible solutions is not bounded from above, this equation always has solutions. With the same definition of ψ _i , Z _gi (z) and Z _ai (z) as above and the same normalization b _ai  = 1, the eigenfunctions are

$$Z_{{\text{g}}i} \left( z \right) = b_{{\text{g}}1i} \sin \left( {\mu_{{\text{g}}i} z} \right) + b_{{\text{g}}2i} \cos \left( {\mu_{{\text{g}}i} z} \right)\quad {\text{if}}\quad \lambda_{\text{a}} ,\lambda_{\text{g}} < \psi_{i}$$

(214)

$$Z_{{\text{a}}i} \left( z \right) = \cos \left[ {\mu_{{\text{a}}i} \left( {L - z} \right)} \right]\quad {\text{if}}\quad \lambda_{\text{a}} ,\lambda_{\text{g}} < \psi_{i}$$

(215)

with

$$b_{{\text{g}}1i} = D_{\text{m}} S_{\text{mg}} \cos \left( {\mu_{{\text{a}}i} L_{\text{a}} } \right)/\left[ {D_{\text{m}} S_{\text{mg}} \sin \left( {\mu_{{\text{g}}i} L_{\text{g}} } \right) + \, L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{{\text{g}}k} \cos \left( {\mu_{{\text{g}}i} L_{\text{g}} } \right)} \right]$$

(216)

$$b_{{\text{g}}2i} = b_{{\text{g}}1i} \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{{\text{g}}i} }}{{D_{\text{m}} S_{\text{mg}} }}$$

(217)

The equation det P = 0 for the combination λ _g < ψ < λ _a is

$$\begin{aligned} \det \, {\mathbf{P}}\,{ = }\,n_{\text{a}} D_{\text{a}}^{*} \mu_{\text{a}} \sinh \left( {\mu_{\text{a}} L_{\text{a}} } \right)\left[ {\sin \left( {\mu_{\text{g}} L_{\text{g}} } \right) + \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\cos \left( {\mu_{\text{g}} L_{\text{g}} } \right)} \right] \hfill \\ + \,n_{\text{g}} D_{\text{g}}^{*} \mu_{\text{g}} \cosh \left( {\mu_{\text{a}} L_{\text{a}} } \right)\left[ {\cos \left( {\mu_{\text{g}} L_{\text{g}} } \right) - \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{\text{g}} }}{{D_{\text{m}} S_{\text{mg}} }}\sin \left( {\mu_{\text{g}} L_{\text{g}} } \right)} \right] = 0 \hfill \\ \end{aligned}$$

(218)

Equation (218) may or may not have a solution in the interval (λ _g, λ _a). If a solution exists, with the same definition of ψ _i , Z _gi (z) and Z _ai (z) as above and the same normalization b _ai  = 1 the eigenfunctions are

$$Z_{{\text{g}}i} \left( z \right) = b_{{\text{g}}1i} \sin \left( {\mu_{{\text{g}}i} z} \right) + b_{{\text{g}}2i} \cos \left( {\mu_{{\text{g}}i} z} \right){\text{ if }}\lambda_{\text{g}} < \psi_{i} < \lambda_{\text{a}}$$

(219)

$$Z_{{\text{a}}i} \left( z \right) = \cosh \left[ {\mu_{{\text{a}}i} \left( {L - z} \right)} \right]\quad {\text{ if }}\lambda_{\text{g}} < \psi_{i} < \lambda_{\text{a}}$$

(220)

with

$$b_{{\text{g}}1i} = D_{\text{m}} S_{\text{mg}} \cosh \left( {\mu_{{\text{a}}i} L_{\text{a}} } \right)/\left[ {D_{\text{m}} S_{\text{mg}} \sin \left( {\mu_{{\text{g}}i} L_{\text{g}} } \right) + \, L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{{\text{g}}k} \cos \left( {\mu_{{\text{g}}i} L_{\text{g}} } \right)} \right]$$

(221)

$$b_{{\text{g}}2i} = b_{{\text{g}}1i} \frac{{L_{\text{m}} n_{\text{g}} D_{\text{g}}^{*} \mu_{{\text{g}}i} }}{{D_{\text{m}} S_{\text{mg}} }}$$

(222)

For each case λ _g < λ _a, λ _g = λ _a and λ _g > λ _a, the solutions of Eqs. (186)–(193) are

$$y_{\text{g}} \left( {z,t} \right) = \sum\limits_{i = 1}^{\infty } {U_{i} Z_{{\text{g}}i} \left( z \right)} e^{{ - \psi_{i} t}}$$

(223)

$$y_{\text{a}} \left( {z,t} \right) = \sum\limits_{k = 1}^{\infty } {U_{i} Z_{{\text{a}}i} \left( z \right)} e^{{ - \psi_{i} t}}$$

(224)

with ψ _i , Z _gi (z) and Z _ai (z) according to Eqs. (207)–(212), (213)–(217) or (218)–(224) depending on the relative size of ψ _i , λ _a and λ _g.

The orthogonality of Z _gi (z) (0 < z < L _g) and Z _ai (z) (L _g < z < L) can be demonstrated by reference to the argumentation presented in Eq. (163). Using the orthogonality of Z _gi (z) (0 < z < L _g) and Z _ai (z) (L _g < z < L), the following formulation for U _i can be obtained as

$$U_{i} = \frac{1}{V}\left[ {n_{\text{g}} R_{\text{dg}} \int_{0}^{{L_{\text{g}} }} { - w_{\text{g}} \left( z \right)Z_{{\text{g}}i} \left( z \right)} {\text{d}}z + n_{\text{a}} R_{\text{da}} \int_{{L_{\text{g}} }}^{L} { - w_{\text{a}} \left( z \right)Z_{{\text{a}}i} \left( z \right)} {\text{d}}z} \right]$$

(225)

with

$$V_{i} = n_{\text{g}} R_{\text{dg}} \int_{0}^{{L_{\text{g}} }} {Z_{{\text{g}}i}^{2} \left( z \right)} {\text{d}}z + n_{\text{a}} R_{\text{da}} \int_{{L_{\text{g}} }}^{L} {Z_{{\text{a}}i}^{2} \left( z \right)} {\text{d}}z$$

(226)

For each case λ _g < λ _a, λ _g = λ _a and λ _g > λ _a, the solutions of C _g(z, t) and C _a(z, t) are derived as

$$C_{\text{g}} \left( {z,t} \right) = \sum\limits_{i = 1}^{\infty } {U_{i} Z_{{\text{g}}i} \left( z \right)} e^{{ - \psi_{i} t}} + w_{\text{g}} \left( z \right)$$

(227)

$$C_{\text{a}} \left( {z,t} \right) = \sum\limits_{i = 1}^{\infty } {U_{i} Z_{{\text{a}}i} \left( z \right)} e^{{ - \psi_{i} t}} + w_{\text{a}} \left( z \right).$$

(228)