Skip to main content
SpringerLink
Log in

Experimental Modal Analysis of Nonlinear Amplified Piezoelectric Actuators by Using Response-Controlled Stepped-Sine Testing

  • Research paper
  • Published:
Experimental Mechanics Aims and scope Submit manuscript

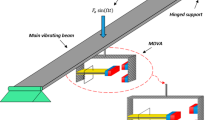
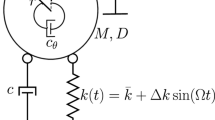Abstract

Background

The nonlinear dynamic behavior of miniature stack-type piezoelectric actuators is not yet fully investigated and is still an open research field.

Objective

The objective of this paper is to determine an accurate dynamical model of an amplified stack-type piezoelectric actuator by using a recently developed nonlinear system identification method, namely Response-Controlled stepped-sine Testing (RCT).

Method

The nonlinear modal identification of a miniature stack-type piezoelectric actuator combined with a rhombus-type compliant mechanism is accomplished by using the RCT method. Several important modifications in the implementation of the RCT method imposed by the miniature nature of the piezo-actuator are successfully achieved for the first time in this study.

Results

Preliminary constant-voltage tests indicate strong softening nonlinearity with jump phenomenon at high voltage levels. In the nonlinear mode of interest, the RCT method quantifies about a 130 Hz change of natural frequency which corresponds to a 3% frequency shift, and a nonlinear modal damping ratio ranging from 1% to 1.5%, corresponding to a 50% change in the amplitude range of interest.

Conclusion

The validity of the single nonlinear mode theory on stack-type piezo-actuators and the quantification of the nonlinear modal damping of this type of actuators are achieved for the first time in this study to the best of the authors’ knowledge. Consequently, an accurate nonlinear modal model is constructed which may help to estimate the parameters of a physical-driven (constitutive) model and therefore gain a better theoretical understanding of the nonlinear behavior of stack-type piezo-actuators. Furthermore, it is shown that the RCT method can be successfully applied for the modal identification of nonlinear miniature electro-mechanical systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Ouyang PR, Tjiptoprodjo RC, Zhang WJ, Yang GS (2008) Micro-motion devices technology: The state of arts review. Int J Adv Manuf Technol 38(5–6):463–478

    Article  Google Scholar 

  2. Claeyssen F, Ducamp A, Barillot F et al (2008) Stepping piezoelectric actuators based on APAs. Proc Actuator 2008:623–626

    Google Scholar 

  3. Jing Z, Xu M, Wu T, Tian Z (2016) Development of a tilt-positioning mechanism driven by flextensional piezoelectric actuators. Rev Sci Instrum 87:8

    Google Scholar 

  4. Claeyssen F, Letty RL, Barillot F, Sosnicki O (2007) Amplified piezoelectric actuators: Static dynamic applications. Ferroelectrics 351(1):3–14

    Article  Google Scholar 

  5. APA35XS (2014) Cedrat Technologies, [Online]. Available: https://www.cedrat-technologies.com/fileadmin/datasheets/APA35XS.pdf. [Accessed: 09 Oct 2021]

  6. Kumar A, DasGupta A (2018) Dynamics of a shell-type amplified piezoelectric actuator. J Vib Acoust 140(4):1–9

    Article  Google Scholar 

  7. Tiersten HF (2013) Linear piezoelectric plate vibrations- elements of the linear theory of piezoelectricity and the vibrations of piezoelectric plates. Springer

  8. Parashar SK, Von Wagner U (2004) Nonlinear longitudinal vibrations of transversally polarized piezoceramics: Experiments and modeling. Nonlinear Dyn 37:51–73

    Article  MATH  Google Scholar 

  9. Shivashankar P, Kandagal SB (2019) Characterization of elastic and electromechanical nonlinearities in piezoceramic plate actuators from vibrations of a piezoelectric-beam. Mech Syst Signal Process 116:624–640

    Article  Google Scholar 

  10. Shivashankar P, Gopalakrishnan S, Kandagal SB (2019) Nonlinear characterization of piezoelectric patches and piezoelectric stacks from vibrations of piezo-actuated structures. Proc SPIE 10967:1–17

    Google Scholar 

  11. Shivashankar P, Gopalakrishnan S, Kandagal SB (2021) Nonlinear modeling of d33-mode piezoelectric actuators using experimental vibration analysis. J Sound Vib 505

  12. Von Wagner U, Hagedorn P (2002) Piezo-beam systems subjected to weak electric field: experiments and modelling of nonlinearities. J Sound Vib 256(5):861–872

    Article  Google Scholar 

  13. Mahmoodi SN, Jalili N (2009) Piezoelectrically actuated microcantilevers: An experimental nonlinear vibration analysis. Sens Actuators A Phys 150(1):131–136

    Article  Google Scholar 

  14. Goldschmidtboeing F, Wischke M, Eichhorn C, Woias P (2009) Nonlinear effects in piezoelectric vibration harvesters with high coupling factors. Proc PowerMEMS 364–367

  15. Stanton SC, Erturk A, Mann BP, Inman DJ (2010) Nonlinear piezoelectricity in electrostatic energy harvesters: modeling and experimental identification. J Appl Phys 108(7)

  16. Stanton SC, Erturk A, Mann BP, Inman DJ (2012) Nonlinear nonconservative behavior and modeling of piezoelectric energy harvesters including proof mass effects. J Intell Mater Syst Struct 23(2):183–199

    Article  Google Scholar 

  17. Leadenham S, Erturk A (2015) Unified nonlinear electroelastic dynamics of a bimorph piezoelectric cantilever for energy harvesting, sensing and actuation. Nonlinear Dyn 79(3):1727–1743

    Article  Google Scholar 

  18. Shahabi P, Ghafarirad H, Tagvaeipour A (2019) Nonlinear vibration analysis of piezoelectric bending actuators: theoretical and experimental studies. Comptes Rendus Mec 347(12):953–966

    Article  Google Scholar 

  19. Karaağaçlı T, Özgüven HN (2021) Experimental modal analysis of nonlinear systems by using response-controlled stepped-sine testing. Mech Syst Signal Process 146

  20. Scheel M, Peter S, Leine RI, Krack M (2018) A phase resonance approach for modal testing of structures with nonlinear dissipation. J Sound Vib 435:56–73

    Article  Google Scholar 

  21. Sherrit S, Trebi-Ollennu A, Bonitz R, Bar-Cohen Y, Yen JT (2010) Compact sensitive piezoelectric mass balance for measurement of unconsolidated materials in space. Sens Smart Struct Technol Civil Mech Aerosp Syst 7647. SPIE

  22. Cabrera MA, Caicedo B, Thorel L (2012) Dynamic actuator for centrifugal modeling of soil-structure interaction. Geotech Test J 35(4)

  23. Yeom T, Simon TW, Zhang M, North MT, Cui T (2012) High frequency, large displacement, and low power consumption piezoelectric translational actuator based on an oval loop sheel. Sens Actuators A Phys 176:99–109

    Article  Google Scholar 

  24. Pages A, Rowe S, Duc S, Sonsnicki O, Jaussaud G, Claeyssen F (2018) Amplified piezo-actuators (APA) enhancement for active vibration control (AVC). ACTUATOR 2018; 16th International Conference on New Actuators, pp. 1–4

  25. Ling M, Zhang X (2021) Coupled dynamic modeling of piezo-actuated compliant mechanisms subjected to external load. Mech Mach Theory 160

  26. Ling M, Yuan L, Luo Z, Huang T, Zhang X (2022) Enhancing dynamic bandwidth of amplified piezoelectric actuators by a hybrid lever and bridge-type compliant mechanism. Actuators 11(5):134

    Article  Google Scholar 

  27. Karaağaçlı T, Özgüven HN (2020) Experimental identification of backbone curves of strongly nonlinear systems by using response-controlled stepped-sine testing (RCT). Vibration 3(3):266–280

    Article  Google Scholar 

  28. Karaağaçlı  T, Özgüven HN (2020) A frequency domain nonparametric identification method for nonlinear structures: Describing surface method. Mech Syst Signal Process 144

  29. Damjanovic D (1997) Logarithmic frequency dependence of the piezoelectric effect due to pinning of ferroelectric-ferroelastic domain walls. Phys Rev B 55(2)

  30. Rosenberg RM (1966) On nonlinear vibrations of systems with many degrees of freedom. Adv Appl Mech 9:155–242

    Article  Google Scholar 

  31. Szemplińska-Stupnicka W (1979) The modified single mode method in the investigations of the resonant vibrations of non-linear systems. J Sound Vib 63(4):475–489

    Article  MATH  Google Scholar 

  32. Setio S, Setio HD, Jezequel L (1992) A method of non-linear modal identification from frequency response tests. J Sound Vib 158(3):497–515

    Article  MATH  Google Scholar 

  33. Gibert C (2003) Fitting measured frequency response using non-linear modes. Mech Syst Signal Process 17(1):211–218

    Article  Google Scholar 

  34. Peeters M, Kerschen G, Golinval JC (2011) Dynamic testing of nonlinear vibrating structures using nonlinear normal modes. J Sound Vib 330(3):486–509

    Article  Google Scholar 

  35. Londoño JM, Neild SA, Cooper JE (2015) Identification of backbone curves of nonlinear systems from resonance decay responses. J Sound Vib 348:224–238

    Article  Google Scholar 

  36. Renson L, Gonzalez-Buelga A, Barton DAW, Neild SA (2016) Robust identification of backbone curves using control-based continuation. J Sound Vib 367:145–158

    Article  Google Scholar 

  37. Peter S, Leine RI (2017) Excitation power quantities in phase resonance testing of nonlinear systems with phase-locked-loop excitation. Mech Syst Signal Process 96:139–158

    Article  Google Scholar 

  38. Krack M (2015) Nonlinear modal analysis of nonconservative systems: extension of the periodic motion concept. Comput Struct 154:59–71

    Article  Google Scholar 

  39. Scheel M, Weigele T, Krack M (2020) Challenging an experimental nonlinear modal analysis method with a new strongly friction-damped structure. J Sound Vib 485

  40. Karaağaçlı T, Özgüven HN (2022) Experimental quantification and validation of modal properties of geometrically nonlinear structures by using response-controlled stepped-sine testing. Exp Mech 62:199–211

    Article  Google Scholar 

  41. Arslan Ö, Özgüven HN (2008) Modal identification of nonlinear structures and the use of modal model in structural dynamic analysis. In Proceedings of the 26th International Modal Analysis Conference (IMAC), Orlando, FL, USA

  42. Link M, Boeswald M, Laborde S, Weiland M, Calvi A (2010) An approach to nonlinear experimental modal analysis. In Proceedings of the 28th International Modal Analysis Conference (IMAC), Jacksonville, FL, USA

  43. Tanrıkulu Ö, Kuran B, Özgüven HN, İmregün M (1993) Forced harmonic response analysis of nonlinear structures. AIAA J 31(7):1313–1320

    Article  MATH  Google Scholar 

  44. Krack M (2021) Extension of the single nonlinear mode theory by linear attachments and application to exciter-structure interaction. J Sound Vib 505

  45. Pacini BR, Kuether RJ, Roettgen DR (2022) Shaker-structure modeling and analysis for nonlinear force appropriation testing. Mech Syst Signal Process 162

  46. Renson L, Shaw AD, Barton DAW, Neild SA (2019) Application of control-based continuation to a nonlinear structure with harmonically coupled modes. Mech Syst Signal Process 120:449–464

    Article  Google Scholar 

  47. Abeloos G, Renson L, Collette C, Kerschen G (2021) Stepped and swept control-based continuation using adaptive filtering. Nonlinear Dyn 104:3793–3808

    Article  Google Scholar 

  48. Instruction Manual optoNCDT 2300 (2021) Micro-epsilon messtechnik GbmH & Co. KG [Online]. Available: http://www.micro-epsilon.de/download/manuals/man--optoNCDT-2300--en.pdf. [Accessed: 09 Oct 2021]

Download references

Acknowledgements

This research was funded by ASELSAN Inc. The financial support is gratefully acknowledged.

Author information

Authors and Affiliations

  1. Middle East Technical University, 06800, Ankara, Turkey

    A. Koyuncu, M. Şahin & H. N. Özgüven

  2. Defense Systems Technologies Business Sector, ASELSAN A.Ş, Ankara, 06172, Turkey

    A. Koyuncu

  3. Defense Industries Research and Development Institute, The Scientific and Technological Research Council of Turkey, TÜBİTAK-SAGE, P.K. 16, 06261, Mamak, Ankara, Turkey

    T. Karaağaçlı

Authors
  1. A. Koyuncu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Karaağaçlı
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Şahin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. H. N. Özgüven
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Koyuncu.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Koyuncu, A., Karaağaçlı, T., Şahin, M. et al. Experimental Modal Analysis of Nonlinear Amplified Piezoelectric Actuators by Using Response-Controlled Stepped-Sine Testing. Exp Mech 62, 1579–1594 (2022). https://doi.org/10.1007/s11340-022-00878-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11340-022-00878-y

Keywords

Search

Navigation