Introduction

Explosion and impact problems have become a very important research issue. Several disciplines are involved in these studies, like physics, material science, computer science, emergency management, but also structural and civil engineering. Nowadays, many structures and infrastructures are considered critical due to their socio-economic relevance in our modern societies; a structural collapse or a decay in their functionality can have a tremendous impact in the life of millions of people. For such reasons critical structures must be adequately protected against terroristic threats and other exceptional scenarios like gas explosion or impacts. In order to build new secure structures or to retrofit existing critical components reliable design methodologies and approaches should be given to the designers. Such tools must be capable of realistically predicting and controlling the mechanical response of structures exposed to blast and impact loading, and this can only be achieved by formulating and incorporating proper models for the materials used, including strain rate effects, and efficient numerical algorithms.

Many different experimental techniques have been developed in the past in order to determine the appropriate constitutive material behaviour at high strain rates [10]: drop weight test [2, 18], Hopkinson and split Hopkinson bar [1, 8], Charpy pendulum [11], etc. When the investigated materials are homogeneous, or have few small imperfections, relatively small samples can be tested in order to check their dynamic properties. However, construction materials, like concrete, present a heterogeneous structure and “size effect” phenomena can play an important role [4, 15, 20]. Thus an adequate sample size, related to the material heterogeneous scale, must be chosen in order to identify the material constitutive behaviour. Especially large heterogeneities can be found in dam concrete, where the maximum aggregate size is usually larger than 50 mm, leading to sample sizes with characteristic dimensions of at least 200 mm.

On the other hand, the size effect defined as the dependence of concrete nominal strength on specimen size, has to be considered. This aspect has been extensively studied in the static regime [3, 13, 17], while scanty information is available on the influence of high strain rate on size effects. This is mainly due to experimental limitations on testing large concrete samples in the dynamic regime. El fahal et al. and Krauthammer et al. [9, 14] have studied the size effect on concrete cylinders (600 mm diameter) subjected to axial impact by means of three large drop weight machines present at Penn State University (USA), National Defense Academy (Japan) and University of British Columbia (Canada) and they have found that the dynamic size effect is different from the known static one.

However, despite the effort and experimental work carried out so far, the data available are still relatively few due to the complexity of the relevant experiments and the fact that these tests are not always directly comparable to each other, even for the simpler compression or tension tests. Moreover, the differences in the data obtained by different experimental techniques can be more marked because of the wave propagation and inertia effects [5]. For these reasons it is important that apparatuses capable of handling the wave propagation be used for the mechanical characterization of concrete at high strain-rates.

The development and some results of innovative equipment, based on Hopkinson bar and optical techniques, for performing dynamic compression tests on large concrete samples is presented in this work. The activity has been centered at the HOPLAB facility (of the Joint Research Centre at Ispra, Italy), which is basically a large-scale split Hopkinson bar. The upgrade of facility has been driven by the needs of a research project focusing on the dynamic characterization of concrete used in dams, whose maximum aggregate size can even be 150 mm. Thus large samples with representative material volumes had to be tested. In the specific case the maximum aggregate size has been chosen as 64 mm, and dynamic compression tests on cylindrical unconfined and confined samples of 200 mm diameter and of up to 400 mm length have been conducted. These are very large samples for Hopkinson bar testing, and, as reported below, a particular setup of two twin bars has been developed in order to apply dynamic compression to the specimen starting from a tensile propagating wave.

Experimental Facility Standard Configuration

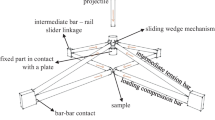
The HOPLAB facility, shown schematically in Fig. 1, is one of the biggest existing Hopkinson bar apparatuses with a length of more than 200 m and a bar diameter of 72 mm made of high strength steel. Different from a classical split Hopkinson bar, where a projectile is used to generate the impact loading pulse, a statically pre-stressed high strength steel cable, which is the physical continuation of the input bar, is used. Through pre-tensioning and suddenly releasing the cable, rectangular force pulses of up to 2 MN, 250 μ s rise time and 40 ms duration can be generated (see Fig. 2) and applied to the specimen [6]. The cable pre-tensioning is effected by means of a hydraulic actuator electronically controlled and placed at one end (“west”), while the instantaneous release of its opposite end is achieved through breaking of a fragile bolt which sustained the pretension load. The fracture in the bolt is induced by a small detonation of explosive inserted in it. The high strength steel cable is 100 m long and has an equivalent diameter of 72 mm. The tensile pulse generated is transmitted to the actual input bar, to the specimen and to the output bar (which is about 90 m long). At the distal end of the output bar a hydraulic damper (“east”) allows to dissipate the remaining energy emanating from the cable and transferred through the specimen to the output bar.

Fig. 1
figure 1

Schematic of the “natural” HOPLAB configuration

Full size image
Fig. 2
figure 2

Force signals vs. time on the input and output bars from a tensile test of a 30 mm-diameter steel specimen in the “natural” Hoplab configuration

Full size image

The configuration described above can be considered as the “natural” one (Fig. 1) and in this configuration HOPLAB can generate tensile pulses in a straight-forward manner. As an example, Fig. 2 shows the high-quality force signals recorded and elaborated from dynamic tensile testing of a 30 mm diameter steel dumb-bell specimen. By modifying the central part of the apparatus it is possible to exploit the tensile wave generated in order to perform different types of tests, as for example compression. The main modifications and features designed and developed for a new experimental configuration able to carry out dynamic compression tests on large samples are described in the next sections.

Dynamic Compression Configuration

Due to the size of the apparatus and the non-modifiable pulse generation mechanism, changing the initial configuration of the HOPLAB in order to perform dynamic compression tests is a complex task; different aspects and parts of the machine have to be re-designed, improved and checked. For this reason an initial preliminary numerical study has been conducted in order to assess the feasibility of the proposed solution, after which a control and adjustment of the various components involved in the HOPLAB were made.

Preliminary Numerical Study

The basic element of the new configuration is the introduction of the twin incident and transmitter bars (see Fig. 3) connected to high strength steel plates at their ends; between the plates a large specimen can be mounted and compressed as represented in Fig. 4. Thanks to this “motion inversion frame” the available tensile pulse can be transformed into a compressive one on the specimen, which is thus compressed dynamically. However, there is a considerable deviation from the standard one-dimensional geometry which is an implicit and important aspect of the Hopkinson bar technique [7, 12].

Fig. 3
figure 3

Schematic of the new HOPLAB configuration

Full size image
Fig. 4
figure 4

Details of the plates mounted at the twin bars ends and the sample

Full size image

This is due to both the distance between the twin bars (270 mm inter-axial distance) and to the flexibility of the steel plates.

For this reason numerical investigations of the new configuration have been performed in order to check all steps of its development. By means of explicit and implicit finite element analysis the geometrical shapes and the distribution of the extra masses have been optimized, thus confirming from a numerical point of view the suitability of the proposed configuration. In particular the deformations of the 30 mm-thick plates for static loads applied over a centered circle of 200 mm diameter (equal to that of the specimen) have been calculated. For a force of 1 MN it is found that the central maximum deflection is equal to about 0.45 mm, and that the average deflection inside the loaded area is 0.3 mm, while the material remains always elastic, Fig. 5. This information on the deformability of the plates is taken into account when determining the net shortening of the specimen in the Hopkinson bar analysis. However, it has not been used in the digital image approaches, which are found superior for calculating in order to compute displacements and deformation, as demonstrated below. The numerical simulations have overall indicated that a Hopkinson bar type testing would be reliably reproduced.

Fig. 5
figure 5

Finite element analysis of compression plate; deflections (mm) for 1 MN static force

Full size image

Mechanical Structure

The developed set-up should be able to perform high strain rate compression tests on large size specimens of concrete. In particular for the dam concrete under consideration, samples are characterized by a diameter equal to 200 mm and a length of 400 mm. This objective has been achieved by means of the set-up proposed and based on a “dynamic inversion frame” that transforms the tensile pulse into a compression load applied to the specimen as Fig. 6 shows. There is a clearance of 5 mm between the sample and the bars. This distance is sufficient in order to perform the actual test without any contact. Then, when the sample is destroyed and the test can be considered practically completed, fragments of the specimen can touch the twin bars. These contacts do not affect the quality of the test results obtained.

Fig. 6
figure 6

Inversion frame with details of mounting of the specimen

Full size image

The inversion frame is composed of two twin bars, which are placed parallel in space at the four vertices of a square. The twin bars are made of high-strength stainless steel and are 6 m long with a diameter of 60 mm. The compressive load is applied to the sample by means of two high-strength steel plates of 30 mm thickness. The plates can transfer the compressive load but are also useful to keep aligned the four bars. Input and output twin bars are rigidly connected to their own plate and can slide in the two plastic bushings of the other plate. Such a configuration leads to a very stiff mechanical structure and to a minimization of the oscillations during the test. Oscillation problems are also avoided by supporting the main and the twin bars with very stiff metallic structures, as shown in Fig. 7.

Fig. 7
figure 7

The single input, the branching and the twin input bars

Full size image

Moreover, to reduce friction all bars slide on Teflon bushings.

Figure 7 shows the input fork that connects the single input bar (72 mm diameter) to the input twin bars.

The design of this “branching” was also aided by numerical investigations in order to prevent excessive spurious reflections and to limit the bending of the twin bars. The connection between the twin bars and the single output bar (72 mm diameter) has been made with mechanical components similar to those previously described for the input elements, in a way that it does not constrain the axial displacement of the single output bar. In this way it is possible to insert an energy absorbing element between the twin and the single bars in order to dissipate part of the energy transmitted from the specimen to the output bar (Fig. 8). Figure 8 shows an aluminum tube used as energy absorber before Fig. 8(a) and after Fig. 8(b) the test. Large amounts of energy can be absorbed in this way by plastic deformation of the aluminum tube (through fold deformation and axial collapse).

Fig. 8
figure 8

The twin and single output bars and the mechanical damper (a) before and (b) after the test

Full size image

Actuators and Dampers

In both the “natural” and the “modified” HOPLAB configurations the input pulse is generated by pretensioning the input cable with a hydraulic jack, which is electronically controlled. The elastic energy stored in the cable can exceed 1 MJ, and clearly the management of this energy is a crucial issue. Part of the energy is consumed in the failure process of the sample, another part is absorbed by the plastic deformation of the aluminum damper described above, but a considerable fraction of it could still end up at the actuators. For this reason the apparatus needs additional energy damping devices at the end of the input and output bars, which would also serve to stop the movement of the bars. It is of course noted that the energy dissipation problem is not acute for the pre-tensioned steel cable because it is self-relaxing after its release.

The absorption of the excess energy present in the system has been assigned to two hydraulic jacks that can work at the same time both as actuators and as dampers. The two cylinders have been developed entirely at the ELSA lab of the JRC and their main features include: piston of 400 mm diameter, 1 m stroke, tubular shaft (external diameter 160 mm, internal diameter 80 mm), maximum static pressure 320 bars.

All mechanical components of the cylinder are made of high-strength steel and the jack is electronically controlled with a proportional valve which connects its two chambers. Moreover, five additional bypasses allow the increase of oil flux between the two chambers when the cylinder is used as a damper.

With the configuration described above, the tasks assigned to the two actuator/dampers are as follows. The “West” cylinder (Figs. 1 and 9) usually works as actuator for stretching the input cable which is rigidly connected to its shaft. Six gas accumulators installed on it, are used in order to allow the compensation of the lack of pressure when the cable is abruptly unloaded.

Fig. 9
figure 9

West cylinder and hydraulic pumping station

Full size image

The “East” cylinder is used as actuator only during the initial preparation phase of the test, when the specimen has to be placed correctly and the output bar should be moved. When a dynamic test is performed all its bypasses are opened in order to use it as a damper and to absorb the energy transmitted by the output bar. To reduce the pressure peaks, six gas accumulators have been installed on each chamber as shown in Fig. 10. A series of Belleville springs are mounted in order to connect elastically the output bar and the jack. The two independent hydraulic power units have been manufactured by Moog, while the control of the two jacks is performed by means of an electronic controller developed in ELSA. This controller allows to impose the pressurisation and displacements in the actuator remotely from the control room.

Fig. 10
figure 10

East cylinder and hydraulic pumping station

Full size image

Instrumentation

Due to the high-strain rates reached during a dynamic test a high sampling-rate transient recorder is needed, moreover this recorder should be capable to acquire electrical signals in three different areas: west end, east end and specimen zone. These requirements have been fulfilled by employing three different transient recorders (Nicolet Multipro with a maximum sampling-rate of 1 MHz) synchronized with the electrical signal that triggers the explosion of the fragile bolt. In addition, in order to study the dynamic behaviour of different parts of the equipment, especially during the development and calibration phases, and of the tested specimens, a high-speed camera, which was synchronized with the transient signals, has been intensively used. The camera is an IDT-Y4 able to perform at 4000 fps with maximum resolution, however the acquired frame-rate can be increased to 200000 fps by reducing substantially one dimension of the recorded image. High speed photo sequences allow full-field displacement measurements to be obtained by applying Digital Imagine Correlation (DIC) techniques. Both east and west actuators have been instrumented with static (WIKA) and dynamic (Kistler) pressure transducers, while displacements are measured by means of static (MTS temposonics) and dynamic (SpaceAge Control wire potentiometers) transducers. In the specimen zone the bar strain histories have been recorded in several positions (see Fig. 11) with strain-gage sensors, in which a full-bridge setup has been adopted to compensate for bending and thermal effects. The recorded signals are conditioned by a high-speed strain gage conditioner (Vishay 2400 with cut-off frequency of 100 kHz). The twin input bars have been instrumented with three measurement points along their length and the output bars with two. At each point two transducers are placed, at orthogonal diameters, in order to eliminate bending phenomena and to have measurement redundancy. In addition, for a few tests piezoelectric force transducers (Piezotech PVDF Shock Gauges) are placed between the specimen and the loading plates in order to measure the local pressure generated at these interfaces.

Fig. 11
figure 11

Schematic of the transducer stations

Full size image

Calibration and Preliminary Tests

In order to check the correct alignment of the equipment and to calibrate all the transducers mounted on the bars a series of tests have been performed. In particular, by using the east and west actuators previously described, a reference load cell was placed between the two loading plates (see Fig. 12) and the full equipment has been put in tension.

Fig. 12
figure 12

Static calibration with an HBM reference cell

Full size image

Comparing the output signals of the reference load cell with the bar strain recordings an accurate calibration has been carried out. It is important to note that no bending phenomena have been noticed even with loads in excess of 1 MN. Figure 13 shows the comparison between the four signals measured through the strain gages placed on the twin input bars close to the plate (station 4 in Fig. 11) and the reference load cell. The four signals completely overlap and non-linear trends, that could be associated to bending phenomena, are absent.

Fig. 13
figure 13

Static calibration of strain transducers

Full size image

When the calibration phase was concluded a series of preliminary tests on the large concrete samples have been performed. The maximum pre-tensioning force reached in these preliminary tests has been about 2 MN, which in turn generates an input pulse of 1 MN amplitude and a plate velocity in the range of 10 m/s to 15 m/s. Figure 14 shows a photo sequence acquired with the high speed camera at 15000 fps during compression of a concrete sample of 200 mm diameter and 200 mm length. The black/white markers placed on the equipment and on the sample allow the determination of the displacements during the test using Digital Image Correlation (DIC) techniques, while irregular patterns on the specimen’s surface are used for determining displacements and strain fields on the specimen, as will be discussed in the next section.

Fig. 14
figure 14

High speed photo sequence of compression test of concrete specimen with length equal to 200 mm

Full size image

Data Analysis and Discussion

The standard equations (equations (1), (2) and (3)), which involve incident ε I , reflected ε R and transmitted ε T strain waves, are used.

$$ \varepsilon(t) = \: -\frac{2C_{0}}{L} \, {{\int}_{0}^{t}}\varepsilon_{R}(t) \, dt $$
(1)
$$ \dot\varepsilon(t) = \: -\frac{2C_{0}}{L} \, \varepsilon_{R}(t) $$
(2)
$$ \sigma(t) = \: E_{0} \, \frac{A_{0}}{A} \, \varepsilon_{T}(t) $$
(3)
$$ \varepsilon_{I} \, + \, \varepsilon_{R} = \: \varepsilon_{T} $$
(4)

In these expressions, L, A, σ and ε are, correspondingly, the length, the cross-sectional area, the stress and the strain of the specimen, A 0 and E 0 are respectively, the total cross-sectional area of the twin output bar and its Young modulus and C 0 is the one-dimensional wave speed in the steel bars. Of course, the application of these equations presupposes the attainment of equilibrium of the specimen during the testing, expressed by equation 4. However, this condition cannot be taken for granted for such long specimens, and in fact its validity is always checked, as shown below.

As in the classical Hopkinson bar tests, the elaboration of the bar strain histories to arrive at the stress-strain diagram of the specimen is not trivial and in order to obtain reliable results some correction algorithms must be applied. Moreover, the non-standard geometry and the large dimensions of the structures and samples tend to compound potential complexities in the data processing.

An example of the bar strain histories is provided in Fig. 15, where the trends of the forces (which are proportional to the strain acquired) in different sections of the bars (see Fig. 11) are represented (for the twin bar sections the sum of the two forces is reported).

Fig. 15
figure 15

Example of signals recorded during a compression test

Full size image

During the tests strain recording at eight measurement points is conducted (Fig. 11): section 1 on the single input bar before the input fork; sections 2, 3 and 4 on the twin input bars; sections 5 and 6 on the twin output bars and sections 7 and 8 on the output single bar after the mechanical energy absorber, previously described. It is immediately noted that the incident and reflected waves that travel in the input bars overlap, since the strain pulse (40 ms) is definitely longer than the traversing time of the input twin bars; such phenomena could occur also in the output twin bars if the specimen does not fail in the first instants of the test. It is also worth considering the signals recorded on the twin output bar (section 5 or 6) and those on the single output bar (section 7 or 8). Their comparison highlights the efficiency of the simple mechanical damper employed. In fact these latter signals represent the excess energy, which is transmitted for absorption to the east actuator damper (Fig. 10).

The separation and re-construction of waves that travel in opposite directions in the bars is the first step of data processing, followed by the equilibrium check at the two specimen ends. In order to compensate eventual distortions due to dispersion phenomena (justified here by the large cross-section of the equipment bars) the procedure proposed by Zhao and Gary [22] has been used during the data processing. Figure 16 shows the separated waves in the twin input bar (the continuous lines represent the incident wave while the dashed ones the reflected wave). Applying next a time shifting and compensating for distortion due to dispersion, as proposed by Tyas and Watson [19], the equilibrium check can be performed at the specimen ends, as shown in Fig. 17.

Fig. 16
figure 16

Separated waves on input twin bars

Full size image
Fig. 17
figure 17

Equilibrium check of specimen

Full size image

It is important to highlight that although the sample is quite long, the two forces corresponding to the “transmitted wave” and “incident + reflected wave” have essentially the same trends and magnitude especially in the central part. As expected, the strain rates reached during the tests, calculated through equation (2) and reported in Fig. 18 are not perfectly constant due to the brittle behaviour of the material investigated. However, the variations are quite small to substantially influence the material behaviour.

Fig. 18
figure 18

Example of strain rate trend

Full size image

The last step of the data processing gives the stress strain curves of the specimen tested, as shown in Fig. 19. In order to obtain this last curve the assumption of uniform stress and strain fields in the sample has been made. Even if the static deflection of the loading plates has been compensated according to the principles presented by Safa and Gary [16], the slope of the rising part of the stress-strain curve is rather small when compared with the static evidence. This is mainly due to the fact that the apparatus, and in general Split Hopkinson Pressure Bar testing, does not produce very accurate results in the small range of strain.

Fig. 19
figure 19

Example of stress vs. strain curve

Full size image

In order to verify the accuracy of the current data-processing, the results obtained with the Hopkinson bar elaboration techniques and the information obtained with the Digital Image Correlation (DIC) algorithms, applied to the high speed photo sequence of the tests, are compared. As introduced in section “Instrumentation“, with DIC it is possible to extract both full-field and local displacement measurements. In Fig. 20 the different targets used for the DIC analyses are highlighted. Specifically, the discrete black and white checker squares, highlighted with the green numbers, have been used to calculate local information, such as displacement and velocity of input and output plates. The targets highlighted with the yellow boxes and placed at the ends of the input and output twin bars have been used to compute the displacements of the bars. Figure 21 presents the comparison of displacements at the end of the bars obtained with the Hopkinson bar and the DIC algorithms.

Fig. 20
figure 20

Example of target distribution used in the DIC analysis

Full size image
Fig. 21
figure 21

Comparison of bar-end displacements computed with Hopkinson and DIC techniques

Full size image

It can be concluded that in this case the results of the two approches are practically indistinguishable.

However, when comparing the average displacements of the input and output plates and the displacements of the twin bar ends (both of them computed through DIC techniques), discrepancies are clearly evident, as shown in Fig. 22, which are due to the plates flexibility.

Fig. 22
figure 22

Comparison of displacements of loading plates and of corresponding bar ends

Full size image

As observed, the two curves differ substantially in the first instants of the test, while their agreement improves later when the level of strain increases and the specimen has practically failed.

In order to elucidate this aspect and produce reliable values for the specimen strains, resorting again to optical DIC techniques was deemed necessary. The potentiality of DIC techniques can be expressed not only through local measures but especially by means of full-field measurements. In fact the introduced DIC algorithms have first been applied to the discrete white markers (joined with the red lines in Fig. 20) on the specimen’s surface for obtaining local information in terms of displacement and velocity. Next, in order to detect and compute the field measures, the sample surfaces have been painted with a random black and white pattern, which is needed in the post processing phase. By means of optical flow algorithms [21] it has been possible to compute displacements and strains on the sample visible surface. Figure 23 shows the comparison of the average strains computed by means of DIC through plates displacements, internal discrete marker displacements (“optical extensometer” indicated with red lines in Fig. 20), full field optical flow techniques and by applying classical Hopkinson bar data analysis.

Fig. 23
figure 23

Comparison of average axial strains of the sample measured applying different techniques

Full size image

As already pointed out, even with the correction procedures adopted, the strains computed by means of Hopkinson bar data processing are overestimated; on the other hand the optical measurements are congruent and the difference among the three procedures used are negligible. This observation would suggest that optical measures with discrete targets are efficient for measuring displacements and strains while full field optical techniques, which are more time consuming, could be performed for more specific analyses, like crack pattern formation.

On the basis of the previous considerations it is possible to synchronize and combine optical strain measures with Hopkinson bar force measures in order to improve the accuracy of the stress vs. strain diagram, where, of course, the assumption of uniform stress and strain fields in the specimen is still employed.

Figure 24 shows the comparison between stress vs. strain curves obtained through Hopkinson bar and the combined Hopkinson bar-optical techniques. Clearly, the applied optical strain correction renders the global material behaviour stiffer and more realistic, its elastic modulus is calculated to be approximately 19.5 GPa. For the sake of comparison, it is reported that the static tests conducted by another laboratory have produced an elastic modulus of 20 GPa and a mean strength of 18 MPa.

Fig. 24
figure 24

Comparison of stress vs. strain curves obtained applying different techniques

Full size image

As introduced above, full field optical techniques, like optical flow, can be employed to evaluate in a qualitative and quantitative way the crack pattern distribution and evolution over the visible surface of the sample during the tests. In Fig. 25 an example of the crack pattern obtained by applying the optical flow algorithm at different time instants is shown. The numerical evaluation is compared with the originally acquired photos, in which the red box delineates the evaluated region.

Fig. 25
figure 25

Example of qualitative crack pattern evolution during a dynamic test (numbers indicate pixels; loading starts at time t=1.93 ms)

Full size image

Conclusions

This study presents a modified Hopkinson bar apparatus designed for studying the response of large size specimens under dynamic conditions. The configuration proposed is characterized by the “motion inversion frame” which is composed of twin incident and transmitter bars and strong plates. The equipment has been carefully designed and calibrated through numerical simulations and experimental tests. Different measurement techniques have been implemented in order to check the reliability of the results produced. The classical Hopkinson bar analysis procedure of the signals, with appropriate corrections, has been conducted and compared with the results of optical measurements. Specifically, Digital Image Correlation has been exploited to check and complete the displacement and strain information coming from the Hopkinson bar analysis. Thus combining DIC and Hopkinson bar analysis it has become possible to enhance the accuracy of the stress vs. strain curves of the material investigated. Moreover, it has also been shown that by means of optical flow algorithms it is possible to follow the evolution of the crack pattern during such dynamic tests.

Preliminary tests have been performed with cylindrical concrete specimens of 200 mm diameter and of up to 400 mm length. The results indicate that the developed experimental equipment represents an accurate and effective tool for testing in dynamic regime large scale samples of heterogeneous materials, with large discontinuities and size effects. As such it can be an important aid in investigating blast and impact behaviour of these materials.