1 Introduction

Hydrodynamic stability problems have been widely analyzed and there are several notable results regarding Newtonian and incompressible fluids. However, the incompressibility assumption is an approximation of the real phenomenon, since perfectly incompressible fluids do not exist in nature. This is the reason why the investigation of compressibility effects in hydrodynamic stability problems is relevant. Therefore, the main goal of this paper is to investigate the compressibility effect on the onset of convection in porous media.

The mathematical models describing the onset of convective motions in horizontal layers of fluids heated from below are well known for both clear fluids and fluid-saturated porous media (see Chandrasekhar 1981; Nield and Bejan 2017 and references therein) and have been widely analyzed under various assumptions: in (Rees 2011; Capone et al. 2021; Capone and Gianfrani 2022a, b; Govender and Vadasz 2007) the authors analyzed the effect of the local thermal non-equilibrium hypothesis on the onset of convection in horizontal porous layers; in Rees (2020) the Darcy-Bénard problem for Bingham fluids has been studied, while in Barletta and Rees (2012) ,Celli and Barletta (2019) the authors examined the onset of convection in an inclined porous layer; convective instabilities in horizontal layers of bi-disperse porous media have been analyzed in Capone and Massa (2021), Capone et al. (2021), Straughan (2009), Capone et al. (2021), Capone et al. (2022), the onset of penetrative convection has been studied in Capone et al. (2011), Arnone and Capone (2022), Capone et al. (2011). In Rana (2014) the onset of thermal convection in an infinite, horizontal, incompressible couple-stress viscoelastic fluid, embedded in a uniform vertical magnetic field, is analyzed. In Rana and Chand (2015), the thermal convection in a rotating nanofluid layer saturating a Darcy-Brinkman porous medium, is investigated. Compressibility effects in hydrodynamic stability problems have been investigated by many authors. In particular, the onset of convection in compressible Walters’ rotating fluid permeated with suspended particles in a Darcy porous medium, is analyzed in Rana and Sharma (2011) and in the case of a uniform rotating layer embedded in a magnetic field in Rana et al. (2012)- Rana et al. (2013), where Brinkman viscosity is considered. However, when the process is not isothermal, the notion of incompressibility is not well defined, see (Gouin and Ruggeri 2012). From a mathematical point of view, the pressure for a compressible fluid is a constitutive function, while the pressure for an incompressible fluid is a Lagrange multiplier that comes from the constraint of incompressibility. To study and compare the mathematical results and solutions of both compressible and incompressible media, we consider the pressure p and the temperature T as thermodynamic variables, therefore \(V=V(p,T)\) and \(\varepsilon =\varepsilon (p,T)\) are the constitutive equations for the specific volume \(V=\frac{1}{\varrho }\) (\(\varrho\) being the fluid density) and the internal energy of the system \(\varepsilon\), see (Ruggeri and Sugiyama 2021).

According to Müller, see (Müller 1985), an incompressible fluid can be defined as a medium whose constitutive equations depend only on temperature T and not on pressure p, in particular:

$$\begin{aligned} \varrho =\varrho (T), \quad \varepsilon =\varepsilon (T). \end{aligned}$$
(1)

Nevertheless, as pointed out by Gouin et al. in Gouin et al. (2012), Müller proved that the definition at (1) is only compatible with the entropy principle if the density is a constant function \(\varrho (T)=\varrho _0\). On assuming constant fluid density, no buoyancy-driven convective instabilities are allowed. However, according to experimental observations, fluids expand when heated and a theoretical assumption, such as the very widely employed Oberbeck-Boussinesq approximation (see Oberbeck 1879; Boussinesq 1879) – which consists in setting constant the density of the fluid in all terms of the governing equations except in the body force term due to gravity – is considered reasonable. Therefore, in order to account for the experimental validity of the problem and its thermodynamic consistency, Gouin et. al in Gouin et al. (2012) defined a new class of fluids, the “quasi-thermal-incompressible fluids”, modifying the constitutive equations (1): a quasi-thermal-incompressible fluid is a medium for which the only equation independent of the pressure p among all the constitutive equations is the fluid density. For such class of fluids, the constitutive equations (1) become:

$$\begin{aligned} \varrho =\varrho (T), \quad \varepsilon =\varepsilon (p,T). \end{aligned}$$
(2)

Using the above definition, the authors proved that a quasi-thermal-incompressible fluid tends to be perfectly incompressible, in the sense of Müller, when the following estimate for the pressure holds:

$$\begin{aligned} p \ll \dfrac{c_p}{\vert V' \vert }=\dfrac{\varrho ^2 c_p}{\vert \varrho ' \vert }, \end{aligned}$$
(3)

where \(c_p\) is the specific heat capacity at constant pressure. In convection problems, there are no sharp temperature variations and, since the temperature variation usually does not exceed 10K, the density variation is of \(1 \%\), see (Chandrasekhar 1981), therefore, the Oberbeck-Boussinesq approximation is coherently employed. When one does not expect large differences in temperature, one may assume that the fluid density in the body force term has a linear dependence on temperature:

$$\begin{aligned} \varrho (T)=\varrho _0 [1-\alpha (T-T_0)], \end{aligned}$$
(4)

where \(\varrho _0\) is the fluid density at the reference temperature \(T_0\), while \(\alpha\) is the thermal expansion coefficient, defined as:

$$\begin{aligned} \alpha =\dfrac{V_T}{V}, \end{aligned}$$

V being the specific volume and \(V_T\) the partial derivative of V with respect to temperature T. When (4) is assumed, the estimate (3) becomes:

$$\begin{aligned} p \ll p_{cr}=\dfrac{c_p \varrho _0}{\alpha } . \end{aligned}$$
(5)

The critical pressure value \(p_{cr}\) gives a limit of validity for the Oberbeck-Boussinesq approximation and from estimate (5), Gouin et. al concluded that a quasi-thermal-incompressible fluid is experimentally similar to a perfectly incompressible fluid.

Later on, with the aim of proposing a more realistic model for fluid dynamics problems, Gouin and Ruggeri (2012) introduced the definition of extended-quasi-thermal-incompressible fluid where they modified the Oberbeck-Boussinesq approximation as follows:

$$\begin{aligned} \varrho (p,T)=\varrho _0 [1-\alpha (T-T_0)+\beta (p-p_0)], \end{aligned}$$
(6)

where \(p_0\) is the reference pressure, while \(\beta\) is the compressibility factor defined as

$$\begin{aligned} \beta =-\dfrac{V_p}{V}, \end{aligned}$$

with \(V_p\) the partial derivative of the volume with respect to the pressure. Moreover, Gouin and Ruggeri (2012) carried out a detailed analysis of the thermodynamic stability, proving that the compressibility factor has a lower bound of:

$$\begin{aligned} \beta> \beta _{cr}=\dfrac{\alpha ^2 TV}{c_p}(>0). \end{aligned}$$
(7)

It is possible to evaluate the order of magnitude of both critical pressure \(p_{cr}\) and compressibility factor \(\beta _{cr}\), (5) and (7), in the case of liquid water (see Lide 2005). Since:

$$\begin{aligned} \begin{aligned}&T_0=293 \ K, \ p_0=10^5 \ Pa, \ V_0=10^{-3} \ m^3/kg, \ \varrho _0=10^3 \ kg/m^3, \\ {}&c_p=4.2 \cdot 10^3 \ J/kg \ K, \ \alpha =207 \cdot 10^{-6} /K, \end{aligned} \end{aligned}$$

one can compute the following values:

$$\begin{aligned} p_{cr}=2 \cdot 10^{10} \ Pa=2 \cdot 10^{5} \ atm \quad \text {and} \quad \beta _{cr}= 3 \cdot 10^{-12} /Pa. \end{aligned}$$

In Passerini and Ruggeri (2014) such an extended approximation was employed for the linear instability analysis of the conduction solution for the classical Bénard problem, and the Authors, via linear instability analysis, proved the destabilizing effect of a dimensionless parameter \(\widehat{\beta }\), proportional to the positive compressibility factor \(\beta\), on the onset of convection.

To the best of our knowledge, there is a lack about investigations on the onset of convective motions in porous media assuming the definition of extended-quasi-thermal-incompressible fluid. This lack motivated the present paper. In Sect. 2 we derive the mathematical model describing the onset of convection for the Darcy-Bénard problem, while in Sect. 3 we perform a linear instability analysis of the thermal conduction solution. Moreover, we analyze the asymptotic behavior of the critical Rayleigh-Darcy number \({\mathcal {R}}\) with respect to the dimensionless compressibility factor \(\widehat{\beta }\), proving the destabilizing effect of \(\widehat{\beta }\) on the onset of convective instabilities. The paper ends with a concluding section that recaps all the results.

2 Mathematical Model

Let us consider a reference frame Oxyz with fundamental unit vectors \(\{ {\textbf {i}},{\textbf {j}},{\textbf {k}}\}\) (\({\textbf {k}}\) pointing vertically upwards) and a horizontal layer \(L={\mathbb {R}}^2 \times [0,d]\) of fluid-saturated porous medium. To derive the governing equations for the seepage velocity \({\textbf {v}}\), the temperature field T and the pressure field p, let us employ the modified Oberbeck-Boussinesq approximation (see Passerini and Ruggeri 2014):

  • the fluid density \(\varrho\) is constant in all terms of the governing equations (i.e., \(\varrho =\varrho _0\)), except in the buoyancy term;

  • in the body force term, the constitutive law for the fluid density is given by

    $$\begin{aligned} \varrho (T)=\varrho _0 [1-\alpha (T-T_0) + \beta (p-p_0)], \end{aligned}$$
    (8)

    with \(\alpha\) and \(\beta\) the thermal expansion coefficient and the compressibility factor, respectively, defined as

    $$\begin{aligned} \alpha =\dfrac{V_T}{V}, \quad \beta =-\dfrac{V_p}{V} \end{aligned}$$

  • \(\nabla \cdot {\textbf {v}}=0\) and \({\textbf {D}} : {\textbf {D}} \approx 0\), being \({\textbf {D}}\) the symmetric part of the gradient of velocity.

Therefore, the mathematical model, according to Darcy’s law, is the following

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\mu }{K} {\textbf {v}}= - \nabla p -\varrho _0 [1-\alpha (T-T_0) + \beta (p-p_0)] g {\textbf {k}} \\ \nabla \cdot {\textbf {v}} = 0 \\ \varrho _0 c_V \Bigl ( \dfrac{\partial T}{\partial t} + {\textbf {v}} \cdot \nabla T \Bigr ) = \chi \Delta T \end{array}\right. } \end{aligned}$$
(9)

where \(\mu , K, \chi , c_V\) are fluid viscosity, permeability of the porous body, thermal conductivity and specific heat at constant volume, respectively.

To system (9) the boundary conditions are appended, i.e.,:

$$\begin{aligned} \begin{aligned}&{\textbf {v}} \cdot {\textbf {k}} =0 \quad \text {on} \ z=0,d \\&\quad T=T_L \quad \text {on} \ z=0 \\&\quad T=T_U \quad \text {on} \ z=d \\&\quad \nabla p \cdot {\textbf {k}} + \varrho _0 d \beta g \ p=0 \quad \text {on} \ z=0,d \end{aligned} \end{aligned}$$
(10)

with \(T_L>T_U\), since the layer is heated from below. Assuming the reference temperature \(T_0=T_L\), system (9)-(10) admits the following stationary conduction solution

$$\begin{aligned} \begin{aligned}&{\textbf {v}}_b={\textbf {0}}, \ T_b(z)=T_L-\dfrac{T_L-T_U}{d} z, \\&p_b(z)=\dfrac{1}{\beta d} + \Bigl [ \dfrac{1}{\beta } - \dfrac{\alpha (T_L-T_U)}{\beta ^2 \varrho _0 g d} \Bigr ] (e^{-\varrho _0 g \beta z} -1) - \dfrac{\alpha (T_L-T_U)}{\beta d} z . \end{aligned} \end{aligned}$$
(11)

Let \(({\textbf {u}},\theta ,\pi )\) be a perturbation to the basic solution, so the equations governing the perturbation fields are

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\mu }{K} {\textbf {u}} = - \nabla \pi + \varrho _0 \alpha g \theta {\textbf {k}} - \varrho _0 \beta g \pi {\textbf {k}} \\ \nabla \cdot {\textbf {u}} = 0 \\ \dfrac{\partial \theta }{\partial t} + {\textbf {u}} \cdot \nabla \theta = \dfrac{T_L-T_U}{d} {\textbf {u}} \cdot {\textbf {k}} + k \Delta \theta \end{array}\right. } \end{aligned}$$
(12)

where \(k=\frac{\chi }{\varrho _0 c_V}\) is the thermal diffusivity. Let us introduce the following scales

$$\begin{aligned} \pi=\,\, & {} P \pi ^*, \quad {\textbf {u}}=U {\textbf {u}}^*, \quad \theta =T^{\#} \theta ^*, \quad t=\tau t^*, \quad x=dx^*,\\ P=\,\, & {} \dfrac{\mu k}{K},\quad U=\dfrac{k}{d},\quad T^\#=T_L-T_U, \quad \tau =\dfrac{d^2}{k}. \end{aligned}$$

Therefore, the corresponding dimensionless system of equations, omitting all the asterisks, is the following:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\textbf {u}}=-\nabla \pi +{\mathcal {R}}\theta {\textbf {k}}-\widehat{\beta }\pi {\textbf {k}}\\ \nabla \cdot {\textbf {u}}=0\\ \dfrac{\partial \theta }{\partial t}+{\textbf {u}}\cdot \nabla \theta =w+\Delta \theta \end{array}\right. } \end{aligned}$$
(13)

where \(u={\textbf {u}} \cdot {\textbf {i}}\) and \(w={\textbf {u}} \cdot {\textbf {k}}\) and

$$\begin{aligned} {\mathcal {R}}=\dfrac{\varrho _0\alpha g d(T_L-T_U)K}{\mu k}, \quad \widehat{\beta }=\varrho _0d g \beta , \end{aligned}$$

are the Rayleigh-Darcy number and the dimensionless compressibility factor, respectively.

To system (13) we add the following boundary and initial conditions

$$\begin{aligned} w=\,\, & {} \theta =\nabla \pi \cdot {\textbf {k}}+\widehat{\beta }\pi =0, \qquad \text {on}\; z=0,1 \end{aligned}$$
(14)
$$\begin{aligned} \textbf{u}(\textbf{x},0)= \,\,& {} \textbf{u}_0(\textbf{x}), \quad \pi (\textbf{x},0)=\pi _0(\textbf{x}), \quad \theta (\textbf{x},0)=\theta _0(\textbf{x}). \end{aligned}$$
(15)

Accounting for (13)\(_2\), taking the divergence of (13)\(_1\), system (13) becomes:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta \pi +\widehat{\beta }\dfrac{\partial \pi }{\partial z}={\mathcal {R}}\dfrac{\partial \theta }{\partial z}\\ {\textbf {u}}=-\nabla \pi +{\mathcal {R}}\theta {\textbf {k}}-\widehat{\beta }\pi {\textbf {k}}\\ \dfrac{\partial \theta }{\partial t}+{\textbf {u}}\cdot \nabla \theta =w+\Delta \theta \end{array}\right. } \end{aligned}$$
(16)

Remark 2.1

In the sequel, we will focus on bi-dimensional perturbations in the plane (x, z) and assume the perturbations fields \(\pi , {\textbf {u}}, \theta\) to be periodic functions in the horizontal direction x with period \(\frac{2 \pi }{a_x}\), \(a_x\) being the wavenumber. Without loss of generality, in the sequel we will assume that the wavelength is 1, so \(\frac{2 \pi }{a_x}=1\) (see Passerini and Ruggeri 2014; Corli and Passerini 2019) and we will consider the periodicity cell \(V=[0,1] \times [0,1]\). Moreover, with \(\Vert \cdot \Vert\) and \(\left\langle \cdot ,\cdot \right\rangle\) we will denote norm and scalar product on \(L^2(V)\), respectively.

3 Linear Instability Analysis

To perform the linear instability analysis of the basic solution, let us consider the linear version of (16):

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta \pi +\widehat{\beta }\dfrac{\partial \pi }{\partial z}={\mathcal {R}}\dfrac{\partial \theta }{\partial z}\\ {\textbf {u}}=-\nabla \pi +{\mathcal {R}}\theta {\textbf {k}}-\widehat{\beta }\pi {\textbf {k}}\\ \dfrac{\partial \theta }{\partial t}=w+\Delta \theta \end{array}\right. } \end{aligned}$$
(17)

together with boundary conditions:

$$\begin{aligned} w=\theta =0\quad \text {and}\quad \dfrac{\partial \pi }{\partial z}=-\widehat{\beta }\pi \qquad \quad \text {on}\; z=0,1. \end{aligned}$$
(18)

By virtue of the Robin boundary condition (18) on the pressure, it is possible to choose:

$$\begin{aligned} \pi =e^{-\widehat{\beta }z}\Pi (x,z,t). \end{aligned}$$
(19)

Therefore equation (17)\(_1\) becomes:

$$\begin{aligned} \Delta \Pi -\widehat{\beta }\dfrac{\partial \Pi }{\partial z}={\mathcal {R}}e^{\widehat{\beta }z} \dfrac{\partial \theta }{\partial z} \end{aligned}$$
(20)

and the Robin boundary conditions \(\dfrac{\partial \pi }{\partial z}=-\widehat{\beta }\pi\) becomes the Neumann condition given by:

$$\begin{aligned} \dfrac{\partial \Pi }{\partial z}=0\qquad z=0,1. \end{aligned}$$
(21)

Introducing the stream function \(\Phi\) such that

$$\begin{aligned} u=-\dfrac{\partial \Phi }{\partial z},\quad w=\dfrac{\partial \Phi }{\partial x} \end{aligned}$$
(22)

and considering the curl of (17)\(_2\) projected on the y-axis, one obtains:

$$\begin{aligned} \Delta \Phi ={\mathcal {R}}\dfrac{\partial \theta }{\partial x}-\widehat{\beta }e^{-\widehat{\beta }z}\dfrac{\partial \Pi }{\partial x}. \end{aligned}$$
(23)

Hence, to perform the linear instability analysis of the conduction solution, we consider the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta \Pi -\widehat{\beta }\dfrac{\partial \Pi }{\partial z}={\mathcal {R}}e^{\widehat{\beta }z} \dfrac{\partial \theta }{\partial z}\\ \Delta \Phi ={\mathcal {R}}\dfrac{\partial \theta }{\partial x}-\widehat{\beta }e^{-\widehat{\beta }z}\dfrac{\partial \Pi }{\partial x}\\ \dfrac{\partial \theta }{\partial t}=\dfrac{\partial \Phi }{\partial x}+\Delta \theta \end{array}\right. } \end{aligned}$$
(24)

to which we add the boundary conditions:

$$\begin{aligned} \theta =\dfrac{\partial \Pi }{\partial z}=\Delta \Phi =0 \qquad \text {on} \ z=0,1. \end{aligned}$$
(25)

By virtue of (25), since system (24) is linear, we assume normal mode solutions:

$$\begin{aligned} \begin{aligned} \theta (x,z,t)&\!= \sum _{m,n=0}^{\infty }[A^1_{mn}(t)\cos (2\pi mx)\sin (\pi nz) \!+\! A^2_{mn}(t)\sin (2\pi mx)\sin (\pi nz)],\\ \Pi (x,z,t)&\!= \sum _{m,n=0}^{\infty }[B^1_{mn}(t)\cos (2\pi mx)\cos (\pi nz) \!+\! B^2_{mn}(t)\sin (2\pi mx)\cos (\pi nz)],\\ \Delta \Phi (x,z,t)&\!= \sum _{m,n=0}^{\infty }[C^1_{mn}(t)\cos (2\pi mx)\sin (\pi nz) \!+\! C^2_{mn}(t)\sin (2\pi mx)\sin (\pi nz)]. \end{aligned} \end{aligned}$$
(26)

In order to get zero mean value on V, we assume \((m,n)\in {\mathbb {N}}\times {\mathbb {N}}_0\). Applying the laplacian operator to (24)\(_3\) and by virtue of (26), one obtains:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \sum _{m,n} [B^1_{mn}\cos (2\pi mx)+B^2_{mn}\sin (2\pi mx)] [-\alpha _{m n} \cos (n \pi z) + \widehat{\beta } n \pi \sin (n \pi z)] \\ \displaystyle \qquad \qquad = {\mathcal {R}}\sum _{m,n} n \pi [A^1_{mn}\cos (2\pi mx)+A^2_{mn}\sin (2\pi mx)] e^{\widehat{\beta } z} \cos (n \pi z) \\ \displaystyle \sum _{m,n} [C^1_{mn}\cos (2\pi mx)+C^2_{mn}\sin (2\pi mx)] \sin (n \pi z) \\ \displaystyle \qquad \qquad = \sum _{m,n=0} 2 \pi m \Bigl \{ {\mathcal {R}}[-A^1_{mn}\sin (2\pi mx)+A^2_{mn}\cos (2\pi mx)] \sin (\pi nz) \\ \displaystyle \qquad \qquad \quad- \widehat{\beta } e^{-\widehat{\beta } z} [-B^1_{mn}\sin (2\pi mx)+B^2_{mn}\cos (2\pi mx)] \cos (n \pi z) \Bigr \} \\ \displaystyle \!\! \sum _{m,n} \! - \! \alpha _{m n} [(\dot{A}^1_{mn} \!\!+\! \alpha _{mn} A^1_{mn}) \cos (2\pi mx) \!+\! (\dot{A}^2_{mn} \!\!+\! \alpha _{mn} A^2_{mn}) \sin (2\pi mx)] \sin (n \pi z) \\ \displaystyle \qquad \qquad = \sum _{m,n} 2 \pi m [-C^1_{mn}\sin (2\pi mx)+C^2_{mn}\cos (2\pi mx)] \sin (n \pi z) \end{array}\right. } \end{aligned}$$
(27)

where \(\alpha _{m n}=(2 \pi m)^2+(\pi n)^2\) and \(\dot{A}^i_{mn}=\dfrac{dA^i_{mn}}{dt}\). From (27)\(_3\), it immediately follows that

$$\begin{aligned} \begin{aligned} C^1_{mn}&= \dfrac{\alpha _{mn}}{2 \pi m} (\dot{A}^2_{mn} + \alpha _{mn} A^2_{mn}), \\ C^2_{mn}&= - \dfrac{\alpha _{mn}}{2 \pi m} (\dot{A}^1_{mn} + \alpha _{mn} A^1_{mn}). \end{aligned} \end{aligned}$$
(28)

Let us multiply (27)\(_1\) by \(\cos (k \pi z)\) and integrate with respect to \(z \in (0,1)\), therefore we get:

$$\begin{aligned} \begin{aligned} \displaystyle&\sum _{m,n} [B^1_{mn}\cos (2\pi mx) \!+\! B^2_{mn}\sin (2\pi mx)] \Bigl [- \alpha _{m n} \!\! \int _0^1 \!\! \cos (n \pi z)\cos (k\pi z) dz \\ {}&\quad + \widehat{\beta } n \pi \!\! \int _0^1 \!\! \sin (n \pi z)\cos (k\pi z) dz \Bigr ] \!\! \\ {}&=\displaystyle \qquad \sum _{m,n} {\mathcal {R}}\ n \pi [A^1_{mn}\cos (2\pi mx)+A^2_{mn}\sin (2\pi mx)] \int _0^1 e^{\widehat{\beta } z} \cos (n \pi z) \cos (k \pi z) dz \end{aligned} \end{aligned}$$
(29)

namely:

$$\begin{aligned} \begin{aligned} \displaystyle&\sum _{m,n} [B^1_{mn}\cos (2\pi mx)+B^2_{mn}\sin (2\pi mx)] \left[ -\dfrac{1}{2}\alpha _{mk}\delta _{nk}+\widehat{\beta } F_{nk} \right] \\ {}&=\displaystyle \qquad \qquad {\mathcal {R}}\sum _{m,n} \ [A^1_{mn}\cos (2\pi mx)+A^2_{mn}\sin (2\pi mx)] \dfrac{\widehat{\beta }}{2} {\mathcal {L}}_{nk}(\widehat{\beta }) \end{aligned} \end{aligned}$$
(30)

with:

$$\begin{aligned} \begin{aligned} F_{nk}&= {\left\{ \begin{array}{ll} 0 \quad &{} \text {if} \ n=k \\ \dfrac{n^2((-1)^{n+k}-1)}{(k-n)(k+n)} \quad &{} \text {if} \ n \ne k \end{array}\right. } \\ {\mathcal {L}}_{nk}(\widehat{\beta })&= n\pi (e^{\widehat{\beta }}(-1)^{k+n}-1)\left( \dfrac{1}{\pi ^2(k+n)^2+\widehat{\beta }^2}+\dfrac{1}{\pi ^2(k-n)^2+\widehat{\beta }^2}\right) . \end{aligned} \end{aligned}$$
(31)

Setting

$$\begin{aligned} {\mathcal {D}}^m_{nk}(\widehat{\beta })=\delta _{nk}+\widehat{\beta }{\left\{ \begin{array}{ll} \dfrac{-2n}{\alpha _{mk}}\left( \dfrac{1}{n-k}+\dfrac{1}{n+k}\right) &{}\quad \text {if}\quad n+k\;\;\text {odd}\\ 0&{}\quad \text {if}\quad n+k\;\;\text {even} \end{array}\right. } \end{aligned}$$
(32)

by virtue of linearity, from (30) one obtains

$$\begin{aligned} \begin{aligned} \displaystyle \sum _{n=0}^{\infty } B^i_{mn} {\mathcal {D}}^m_{nk}(\widehat{\beta }) = -\dfrac{{\mathcal {R}}\widehat{\beta }}{\alpha _{mk}} \sum _{n=0}^{\infty } \ A^i_{mn} {\mathcal {L}}_{nk}(\widehat{\beta }), \qquad i=1,2. \end{aligned} \end{aligned}$$
(33)

Let us remark that the \(N \times N\) matrix \({\mathcal {D}}^m\) is invertible since it is strictly diagonally dominant for small \(\widehat{\beta }\) (see Serre 2010). Moreover, through a fixed point argument, an estimate on the compressibility factor \(\widehat{\beta }\) guaranteeing the invertibility of the matrix \({\mathcal {D}}^m\) for all \(N \in {\mathbb {N}}\) is obtained. The following theorem holds.

Theorem 3.1

If

$$\begin{aligned} \widehat{\beta }<\dfrac{\pi ^2}{2 c} \end{aligned}$$
(34)

with \(c= \dfrac{1}{8} [2 \pi \coth ({2 \pi })+1]\), then the matrix \({\mathcal {D}}^m\) is invertible for all \(N\in {\mathbb {N}}\).

Proof

Let us consider the basis functions:

$$\begin{aligned} \varphi ^i_{mn}(x,z)={\left\{ \begin{array}{ll} \cos (2\pi mx)\cos (n \pi z)&{} \text {if}\;\; i=1\\ \sin (2\pi mx)\cos (n \pi z)&{} \text {if}\;\; i=2 \end{array}\right. } \end{aligned}$$
(35)

which are the eigenfunctions of the Laplace operator:

$$\begin{aligned} \Delta \varphi ^i_{mn}=-\alpha _{mn}\varphi ^i_{mn}, \end{aligned}$$
(36)

\(\alpha _{mn}=4\pi ^2m^2+\pi ^2n^2\) being the eigenvalues. Since:

$$\begin{aligned} b_{mn}:=\Vert \varphi ^i_{mn}\Vert ^2={\left\{ \begin{array}{ll} \dfrac{1}{2}&{}n=0 \\ \dfrac{1}{4}&{}\text {otherwise} \end{array}\right. } \end{aligned}$$
(37)

defining \(\gamma _{mn}=\sqrt{\alpha _{mn}b_{mn}}\), the following normalization can be introduced:

$$\begin{aligned} \psi ^i_{mn}=\dfrac{\varphi _{mn}^i}{\gamma _{mn}}. \end{aligned}$$
(38)

Equation (24)\(_1\) can be written in terms of (38) as:

$$\begin{aligned} -\sum _{\begin{array}{c} i=1,2 \\ m,n \end{array}} B^i_{mn}(-\Delta \psi ^i_{mn})-\widehat{\beta } \sum _{\begin{array}{c} i=1,2 \\ m,n \end{array}}B^i_{mn}\dfrac{\partial \psi ^i_{mn}}{\partial z}= \sum _{\begin{array}{c} i=1,2 \\ m,n \end{array}} e^{\widehat{\beta }z}{\mathcal {R}}A^i_{mn}\dfrac{\partial \psi ^i_{mn}}{\partial z}. \end{aligned}$$
(39)

If we multiply (39) by \(\psi ^j_{lr}\) and integrate on V we obtain:

$$\begin{aligned} -\sum _{\begin{array}{c} i=1,2 \\ m,n \end{array}} B^i_{mn}\left\langle \nabla \psi ^i_{mn},\nabla \psi ^j_{lr}\right\rangle -\widehat{\beta } \sum _{\begin{array}{c} i=1,2 \\ m,n \end{array}}B^i_{mn}\left\langle \dfrac{\partial \psi ^i_{mn}}{\partial z},\psi ^j_{lr}\right\rangle = \sum _{\begin{array}{c} i=1,2 \\ m,n \end{array}} F^{i,j}_{mnlr} \end{aligned}$$
(40)

where:

$$\begin{aligned} F^{i,j}_{mnlr}=e^{\widehat{\beta }z}{\mathcal {R}}A^i_{mn}\left\langle \dfrac{\partial \psi ^i_{mn}}{\partial z},\psi ^j_{lr}\right\rangle . \end{aligned}$$
(41)

From (35) and (38), it follows that:

$$\begin{aligned} \begin{aligned} \left\langle \dfrac{\partial \psi ^i_{mn}}{\partial z},\psi ^j_{lr}\right\rangle&= \dfrac{1}{\gamma _{mn}\gamma _{lr}}\left\langle \dfrac{\partial \varphi ^i_{mn}}{\partial z},\varphi ^j_{lr}\right\rangle \\&=-\dfrac{\delta _{ij}\delta _{ml}}{\gamma _{mn}\,\gamma _{lr}}\dfrac{n}{2}{\left\{ \begin{array}{ll} \frac{1}{n+r}+\frac{1}{n-r} &{} \text {se} \;\; n+r\ge 1 \;\;\text {odd}\\ 0&{} \text {otherwise} \end{array}\right. } \end{aligned} \end{aligned}$$
(42)

and equation (40) becomes:

$$\begin{aligned} -B^j_{lr}+\widehat{\beta }\sum _{\begin{array}{c} i \, \mid \, m,n \\ n+r\ge 1\;\;\text {odd} \end{array}} B^i_{mn}\dfrac{n}{2}\dfrac{\delta _{ij}\delta _{ml}}{\gamma _{mn}\gamma _{lr}}\left( \frac{1}{n+r}+\frac{1}{n-r}\right) -\sum _{i \mid m,n } F^{i,j}_{mnlr}=0. \end{aligned}$$
(43)

Now, let us introduce the following continuous functions:

$$\begin{aligned} \begin{aligned} {\mathcal {P}}&\!:\!B\!\in\! {\mathbb {R}}^N \! \longmapsto \! -B^j_{lr} \!+\! \widehat{\beta }\sum _{\begin{array}{c} i \mid m,n \\ n+r\ge 1\;\;\text {odd} \end{array}} B^i_{mn}\dfrac{n}{2}\dfrac{\delta _{ij}\delta _{ml}}{\gamma _{mn}\gamma _{lr}}\left( \frac{1}{n+r} \!+\! \frac{1}{n-r}\right) - \sum _{i \mid m,n } F^{i,j}_{mnlr} \! \in \! {\mathbb {R}}^N \\ {\mathcal {G}}&:B\in {\mathbb {R}}^N\longmapsto \widehat{\beta }\sum _{\begin{array}{c} i \mid m,n \\ n+r\ge 1\;\;\text {odd} \end{array}} B^i_{mn}\dfrac{n}{2}\dfrac{\delta _{ij}\delta _{ml}}{\gamma _{mn}\gamma _{lr}}\left( \frac{1}{n+r}+\frac{1}{n-r}\right) -\sum _{i \mid m,n } F^{i,j}_{mnlr}\in {\mathbb {R}}^N \end{aligned} \end{aligned}$$
(44)

so the algebraic system (43) - equivalent to system (33) - can be written as \({\mathcal {P}}(B)=0\). Let us observe that the invertibility of \({\mathcal {D}}^m\) is equivalent to prove that system (43) admits a nontrivial solution. Moreover, B is a solution of (43) if and only if B is a fixed point of \({\mathcal {G}}\):

$$\begin{aligned} {\mathcal {P}}(B)=0\quad \Longleftrightarrow \quad {\mathcal {G}}(B)=B. \end{aligned}$$
(45)

The existence of a fixed point for \({\mathcal {G}}\) is guaranteed by the Leray-Schauder theorem, provided that:

$$\begin{aligned} \{ B\in {\mathbb {R}}^N\; \mid \;B=\lambda {\mathcal {G}}(B),\; 0\le \lambda \le 1 \}\subset B_R(0), \end{aligned}$$
(46)

\(B_R(0)\) being a ball of radius \(R>0\) centered in 0, hence:

$$\begin{aligned} \{ B\in {\mathbb {R}}^N\; \mid \;B=\lambda {\mathcal {G}}(B),\; 0\le \lambda \le 1 \}^\complement \supset {\mathscr {B}}:=\{ B\in {\mathbb {R}}^N\; \mid \;B=\lambda {\mathcal {G}}(B),\; \lambda > 1 \}. \end{aligned}$$
(47)

If \(B\in {\mathscr {B}}\), then \(\lambda B+(1-\lambda )B=\lambda {\mathcal {G}}(B)\), i.e., \((1-\lambda )B=\lambda {\mathcal {P}}(B)\), therefore:

$$\begin{aligned} \dfrac{1-\lambda }{\lambda } \vert B \vert ^2={\mathcal {P}}(B)\cdot B \end{aligned}$$
(48)

\(\vert \cdot \vert\) being the standard euclidean norm. Therefore, from (46) and (48) we can state that the proof of the existence of a fixed pointy for \({\mathcal {G}}\) is equivalent to prove that:

$$\begin{aligned} \begin{aligned} {\mathcal {P}}(B)\cdot B =&-\sum _{l,r}(B^j_{lr})^2+\dfrac{\widehat{\beta }}{2} \sum _{\begin{array}{c} i \mid m,n,r \\ n+r\ge 1\;\;\text {odd} \end{array}} B^i_{mn}B^i_{mr}\dfrac{1}{\gamma _{mn}\gamma _{mr}}\left( \frac{n}{n+r}+\frac{n}{n-r}\right) \\ {}&-\sum _{i \mid m,n,l,r } F^{i,j}_{mnlr}B^i_{lr} \end{aligned} \end{aligned}$$
(49)

is negative for \(\vert B \vert >R\). For notational convenience let us set:

$$\begin{aligned} \widetilde{B}^i_{mnr}=\dfrac{B^i_{mn}}{\gamma _{mr}}\qquad \text {and}\qquad \widetilde{B}^i_{mrn}=\dfrac{B^i_{mr}}{\gamma _{mn}} \end{aligned}$$
(50)

and hence, from (49) we have:

$$\begin{aligned} \dfrac{1}{2} \!\!\! \sum _{\begin{array}{c} i \mid m,n,r \\ n+r\ge 1\;\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\left( \frac{n}{n+r}+\frac{n}{n-r}\right) =:I+J. \end{aligned}$$
(51)

Therefore:

$$\begin{aligned} \begin{aligned} I&= \sum _{\begin{array}{c} i \mid m,n,r \\ n+r\ge 1\;\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{n}{n+r}= \sum _{\begin{array}{c} i \mid m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{n}{n+r}+ \sum _{\begin{array}{c} i \mid m \\ n\;\text {odd}, \; r\;\text {even} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{n}{n+r} \\&= \sum _{\begin{array}{c} i \mid m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{n}{n+r} + \sum _{\begin{array}{c} i \mid m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{r}{n+r} = \sum _{\begin{array}{c} i \mid m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn} \end{aligned} \end{aligned}$$
(52)

and similarly with J

$$\begin{aligned} \begin{aligned} J&= \sum _{\begin{array}{c} i \mid m,n,r \\ n+r\ge 1\;\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{n}{n-r} = \sum _{\begin{array}{c} i \mid m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{n}{n-r}+ \sum _{\begin{array}{c} i \mid m \\ n\;\text {odd}, \; r\;\text {even} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{n}{n-r} \\&= \sum _{\begin{array}{c} i \mid m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{n}{n-r} + \sum _{\begin{array}{c} i \mid m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}\frac{r}{n-r}= \sum _{\begin{array}{c} i \mid m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn}. \end{aligned} \end{aligned}$$
(53)

By virtue of (52) and (53), Cauchy-Schwarz and Young inequalities and since \(\gamma ^2_{mn}\ge \tfrac{4\pi ^2+n^2\pi ^2}{4}\), from (51) it follows:

$$\begin{aligned} \begin{aligned}&\sum _{\begin{array}{c} i \mid m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{mnr}\widetilde{B}^i_{mrn} = \sum _{\begin{array}{c} i \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \widetilde{B}^i_{\cdot , nr}\cdot \widetilde{B}^i_{\cdot , rn}\le \sum _{\begin{array}{c} i \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \vert \widetilde{B}^i_{\cdot , nr} \vert \; \vert \widetilde{B}^i_{\cdot , rn} \vert \\&\le \dfrac{1}{2}\left[ \sum _{\begin{array}{c} i \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \vert \widetilde{B}^i_{\cdot , nr} \vert ^2+\sum _{\begin{array}{c} i \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \vert \widetilde{B}^i_{\cdot , rn} \vert ^2 \right] \\&=\dfrac{1}{2}\left[ \sum _{\begin{array}{c} i\; \mid \; m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \dfrac{ \vert {B}^i_{mn} \vert ^2}{\gamma ^2_{mr}} +\sum _{\begin{array}{c} i\; \mid \; m \\ n\;\text {even}, \; r\;\text {odd} \end{array}} \dfrac{\vert {B}^i_{mr} \vert ^2}{\gamma ^2_{mn}} \right] \\&\le 2\left[ \sum _{\begin{array}{c} i\; \mid \; m \\ n\;\text {even} \end{array}} \vert {B}^i_{mn} \vert ^2\sum _{\begin{array}{c} r\;\text {odd} \\ \end{array}} \dfrac{1}{4\pi ^2 \!+\! r^2\pi ^2} \!+ \sum _{\begin{array}{c} i\; \mid \; m \\ r\;\text {odd} \end{array}} \vert {B}^i_{mr} \vert ^2\sum _{\begin{array}{c} n\;\text {even} \\ \end{array}} \dfrac{1}{4\pi ^2 \!+\! n^2\pi ^2} \right] \\&\le \!\! \dfrac{2}{\pi ^2} \!\!\! \left[ \sum _{\begin{array}{c} i\; \mid \; m \\ n\;\text {even} \end{array}} \!\!\!\! \vert {B}^i_{mn} \vert ^2 \!+\! \sum _{\begin{array}{c} i\; \mid \; m \\ r\;\text {odd} \end{array}} \vert {B}^i_{mr} \vert ^2 \right] \sum _{\begin{array}{c} n \\ \end{array}} \dfrac{1}{4+n^2} \!=\! \dfrac{2}{\pi ^2} \vert B \vert ^2\sum _{\begin{array}{c} n \\ \end{array}} \dfrac{1}{4+n^2} \!=\! \dfrac{2}{\pi ^2} \vert B \vert ^2c \end{aligned} \end{aligned}$$
(54)

where \(c=\dfrac{1}{8} [2 \pi \coth ({2 \pi })+1]\). Finally, from (49) and (54) one gets:

$$\begin{aligned} {\mathcal {P}}(B)\cdot B\le -\vert B \vert ^2+\widehat{\beta }c\dfrac{2}{\pi ^2}\vert B \vert ^2+K\vert B \vert \end{aligned}$$
(55)

with \(K=\vert F\vert\). Therefore, for \(\vert B \vert >R := K/(1-\widehat{\beta } c 2 \pi ^{-2})\) and if \(\widehat{\beta }<\tfrac{\pi ^2}{2c}\) it follows \({\mathcal {P}}(B)\cdot B<0\). \(\square\)

Solving system (33), we get component-wise the same relation for the coefficients \(B^1_{mj}\) and \(B^2_{mj}\), i.e., for \(i=1,2\):

$$\begin{aligned} B^i_{mj}=-\dfrac{{\mathcal {R}}\widehat{\beta }}{\alpha _{mk}} \sum _{n,k=0}^{\infty }A^i_{mn}{\mathcal {L}}_{nk}(\widehat{\beta }) [{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj}. \end{aligned}$$
(56)

Now, let us substitute (28) and (56) in (27)\(_2\), obtaining:

$$\begin{aligned} \!\!\!\!\! \begin{aligned} \displaystyle&\sum _{m,j=0}^{\infty } [ \dfrac{\alpha _{mj}}{2 \pi m} (\dot{A}^2_{mj} + \alpha _{mj} A^2_{mj}) \cos (2\pi mx) \\ {}&\qquad \quad - \dfrac{\alpha _{mj}}{2 \pi m} (\dot{A}^1_{mj} + \alpha _{mj} A^1_{mj}) \sin (2\pi mx)] \sin (j \pi z) \\ {}&=\quad \sum _{m,j=0}^{\infty } 2 \pi m \Bigl \{ {\mathcal {R}}[-A^1_{mj}\sin (2\pi mx)+A^2_{mj}\cos (2\pi mx)] \sin (\pi jz) \\ \displaystyle&\qquad \quad - \widehat{\beta } e^{-\widehat{\beta } z} \Bigl [ \dfrac{{\mathcal {R}}\widehat{\beta }}{\alpha _{mj}} \sum _{n,k=0}^{\infty }A^1_{mn}{\mathcal {L}}_{nk}(\widehat{\beta }) [{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj} \sin (2\pi mx) \\ {}&\qquad \qquad \qquad \quad -\dfrac{{\mathcal {R}}\widehat{\beta }}{\alpha _{mj}} \sum _{n,k=0}^{\infty }A^2_{mn}{\mathcal {L}}_{nk}(\widehat{\beta }) [{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj} \cos (2\pi mx)\Bigr ] \cos (j \pi z) \Bigr \}. \end{aligned} \end{aligned}$$
(57)

Let us multiply (57) by \(\sin (h \pi z)\) and integrate with respect to \(z \in (0,1)\), therefore we get:

$$\begin{aligned} \begin{aligned} \displaystyle&\qquad \sum _{m,j=0}^{\infty } \!\! \left[ \dfrac{\alpha _{mj}}{2 \pi m} (\dot{A}^2_{mj} \!+\! \alpha _{mj} A^2_{mj}) \cos (2\pi mx) \!-\! \dfrac{\alpha _{mj}}{2 \pi m} (\dot{A}^1_{mj} \!+\! \alpha _{mj} A^1_{mj}) \sin (2\pi mx) \right] \\& \qquad \qquad \int _0^1 \!\! \sin (j \pi z)\sin (h\pi z)dz \!\! \\ {}&=\qquad \sum _{m,j=0}^{\infty } 2 \pi m \Bigl \{ {\mathcal {R}}[-A^1_{mj}\sin (2\pi mx) \!+\! A^2_{mj}\cos (2\pi mx)] \!\! \int _0^1 \!\! \sin (\pi jz)\sin (h\pi z)dz \\ \displaystyle&\qquad \qquad - \widehat{\beta } \Bigl [\dfrac{{\mathcal {R}}\widehat{\beta }}{\alpha _{mj}} \sum _{n,k=0}^{\infty }A^1_{mn}{\mathcal {L}}_{nk}(\widehat{\beta })[{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj} \sin (2\pi mx)\\&\qquad \qquad -\dfrac{{\mathcal {R}}\widehat{\beta }}{\alpha _{mj}} \sum _{n,k=0}^{\infty }A^2_{mn}{\mathcal {L}}_{nk}(\widehat{\beta })[{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj} \cos (2\pi mx)\Bigr ] \\&\qquad \qquad \int _0^1 \!\!\! e^{\!-\widehat{\beta } z}\cos (j \pi z)\sin (h\pi z)dz \Bigr \} \end{aligned} \end{aligned}$$
(58)

Hence:

$$\begin{aligned} \begin{aligned} \displaystyle&\sum _{m=0}^{\infty } \left[ \dfrac{\alpha _{mh}}{2 \pi m} (\dot{A}^2_{mh} \!+\! \alpha _{mh} A^2_{mh}) \cos (2\pi mx)- \dfrac{\alpha _{mh}}{2 \pi m} (\dot{A}^1_{mh} \!+\! \alpha _{mh} A^1_{mh}) \sin (2\pi mx) \right] \\ {}&\qquad = \sum _{m=0}^{\infty } 2 \pi m {\mathcal {R}}[-A^1_{mh}\sin (2\pi mx)+A^2_{mh}\cos (2\pi mx)] \\ \displaystyle&\qquad - \sum _{m=0}^{\infty } \widehat{\beta }^2 {\mathcal {R}}2 \pi m \sum _{j,n,k=0}^{\infty } \dfrac{1}{\alpha _{mj}} A^1_{mn}{\mathcal {L}}_{nk}(\widehat{\beta })[{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj} {\mathcal {N}}_{jh}(\widehat{\beta }) \sin (2\pi mx) \\ \displaystyle&\qquad + \sum _{m=0}^{\infty } \widehat{\beta }^2 {\mathcal {R}}2 \pi m \sum _{j,n,k=0}^{\infty } \dfrac{1}{\alpha _{mj}} A^2_{mn}{\mathcal {L}}_{nk}(\widehat{\beta }) [{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj} {\mathcal {N}}_{jh}(\widehat{\beta }) \cos (2\pi mx) \end{aligned} \end{aligned}$$
(59)

with

$$\begin{aligned} {\mathcal {N}}_{jh}(\widehat{\beta })=\pi (1-e^{-\widehat{\beta }}(-1)^{h+j})\left( \dfrac{h+j}{\pi ^2(h+j)^2+\widehat{\beta }^2}+\dfrac{h-j}{\pi ^2(h-j)^2+\widehat{\beta }^2}\right) . \end{aligned}$$
(60)

By the linear independence of the sinus and cosinus functions with respect to the variable x, we get, for \(i=1,2\):

$$\begin{aligned} \begin{aligned}\dfrac{\alpha _{mh}}{2\pi m} (\dot{A}^i_{mh} + \alpha _{mh} A^i_{mh})&= 2 \pi m {\mathcal {R}}A^i_{mh} \\ {}&\quad + \widehat{\beta }^2 {\mathcal {R}}2 \pi m \sum _{j,n,k=0}^{\infty } \dfrac{1}{\alpha _{mj}} A^i_{mn}{\mathcal {L}}_{nk}(\widehat{\beta }) [{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj} {\mathcal {N}}_{jh}(\widehat{\beta }). \end{aligned} \end{aligned}$$
(61)

Equations (61) are first order ODEs with respect to time t. To get a unique solution, system (61) decouples and let \(A^i_{mh}\) be the only non-vanishing coefficient, which satisfies the following first-order ordinary differential equation:

$$\begin{aligned} \begin{aligned}\dot{A}^i_{mh} + \alpha _{mh} {A}^i_{mh} &= \dfrac{4\pi ^2 m^2}{\alpha _{mh}} {\mathcal {R}}\ {A}^i_{mh} \\ {}&\qquad + \widehat{\beta }^2 {\mathcal {R}}\dfrac{4\pi ^2 m^2}{\alpha _{mh}} {A}^i_{mh} \sum _{j,k=0}^\infty \dfrac{1}{\alpha _{mj}}{\mathcal {L}}_{hk}(\widehat{\beta })[{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj} {\mathcal {N}}_{jh}(\widehat{\beta }) , \end{aligned} \end{aligned}$$
(62)

together with the initial conditions on \(A^i_{mh}\) that can be derived from (15)\(_3\) and (26)\(_1\). Setting

$$\begin{aligned} {\mathcal {G}}_{mh}(\widehat{\beta })=\dfrac{4\pi ^2 m^2}{\alpha _{mh}}\sum _{j,k=0}^\infty \dfrac{1}{\alpha _{mj}}{\mathcal {L}}_{hk}(\widehat{\beta })[{\mathcal {D}}^m(\widehat{\beta })]^{-1}_{kj} {\mathcal {N}}_{jh}(\widehat{\beta }), \end{aligned}$$
(63)

(62) is equivalent to

$$\begin{aligned} \dot{A}^i_{mh} + A^i_{mh} \Bigl [ \alpha _{mh} - {\mathcal {R}}\dfrac{4\pi ^2 m^2}{\alpha _{mh}} - \widehat{\beta }^2 {\mathcal {R}}\ {\mathcal {G}}_{mh}(\widehat{\beta }) \Bigr ] =0, \end{aligned}$$
(64)

whose solution can be easily computed to be:

$$\begin{aligned} A^i_{mh}(t) = \gamma e^{\left( - \alpha _{mh} + {\mathcal {R}}\frac{4\pi ^2 m^2}{\alpha _{mh}} + \widehat{\beta }^2 {\mathcal {R}}\ {\mathcal {G}}_{mh}(\widehat{\beta }) \right) t}, \end{aligned}$$
(65)

\(\gamma\) being a constant depending on the initial conditions. We obtain that the perturbation fields (26) have an exponential dependence on time t, so let us define the generalized eigenvalue \(\sigma _{mh}\):

$$\begin{aligned} \sigma _{mh} = - \alpha _{mh} + {\mathcal {R}}\dfrac{4\pi ^2 m^2}{\alpha _{mh}} + \widehat{\beta }^2 {\mathcal {R}}\ {\mathcal {G}}_{mh}(\widehat{\beta }). \end{aligned}$$
(66)

Accounting for (66), it arises that the strong principle of exchange of stabilities holds and convection can occur only via stationary motions. Hence, the marginal instability threshold is given setting \(\sigma _{mn}=0\), i.e.,

$$\begin{aligned} {\mathcal {R}}\Bigl ( \dfrac{4\pi ^2 m^2}{\alpha _{mh}} + \widehat{\beta }^2 {\mathcal {G}}_{mh}(\widehat{\beta }) \Bigr ) - \alpha _{mh} =0, \end{aligned}$$
(67)

and the critical Rayleigh-Darcy number for the onset of convection is given by:

$$\begin{aligned} {\mathcal {R}}_L=\inf _{m,h} \dfrac{\alpha _{mh}^2}{4\pi ^2 m^2 + \widehat{\beta }^2 \alpha _{mh} {\mathcal {G}}_{mh}(\widehat{\beta }) }, \end{aligned}$$
(68)

for which, using user-written MATLAB codes, we numerically obtain that function \({\mathcal {G}}_{mh}\) is positive.

In order to compare the obtained results with those ones related to Darcy-Bénard problem when the fluid density constitutive law is given by (4), starting from (66), let us consider the limit case \(\widehat{\beta } \rightarrow 0\) and (66) becomes

$$\begin{aligned} \sigma _{mh}= - \alpha _{mh} + {\mathcal {R}}\dfrac{4\pi ^2 m^2}{\alpha _{mh}}. \end{aligned}$$
(69)

Requiring the eigenvalue \(\sigma _{mh}\) to be positive, we get

$$\begin{aligned} - \alpha _{mh} + {\mathcal {R}}\dfrac{4\pi ^2 m^2}{\alpha _{mh}} >0, \end{aligned}$$
(70)

and one immediately recovers the critical Rayleigh-Darcy number for the onset of convection according to the classical Oberbeck-Boussinesq approximation (see Horton and Rogers 1945; Lapwood 1948; Nield and Bejan 2017):

$$\begin{aligned} {\mathcal {R}}_c =\min _{m,h} \dfrac{[(2 \pi m)^2 + ( h \pi )^2]^2}{4\pi ^2 m^2}=4 \pi ^2. \end{aligned}$$
(71)

Therefore, comparing (68) and (71), we get

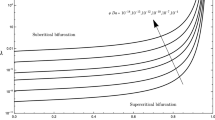
$$\begin{aligned} {\mathcal {R}}_L < {\mathcal {R}}_c(=4 \pi ^2) \qquad \forall \ \widehat{\beta }>0. \end{aligned}$$
(72)

In order to analyze the influence of the dimensionless compressibility factor \(\widehat{\beta }\) on the onset of convection, we numerically solved (68) for quoted values of \(\widehat{\beta }\), under restriction (34) found in Theorem 3.1. In particular, in Fig. 1a–b we choose \(\widehat{\beta }\) in a right neighborhood of 0 (as done in Passerini and Ruggeri (2014)) to emphasize the behaviour of \({\mathcal {R}}\) as a function of \(\widehat{\beta }\). From Fig. 1a–b we can conclude that the dimensionless compressibility factor \(\widehat{\beta }\) has a destabilizing effect on the onset of convective flows: the behaviour of the critical Rayleigh-Darcy number with respect to \(\widehat{\beta }\) is decreasing. This result is coherent with the results for the classical Bénard problem found in Passerini and Ruggeri (2014), where a clear fluid is considered.

Fig. 1
figure 1

a: Critical Rayleigh-Darcy number \({\mathcal {R}}_L\) as function of the compressibility factor \(\hat{\beta }\). b: Neutral curves for quoted values of the compressibility factor \(\hat{\beta }\)

Full size image

4 Conclusions

To the best of our knowledge, in this paper the Darcy-Bénard problem for an extended-quasi-thermal-incompressible fluid was studied for the first time. We determined the instability threshold for the onset of convection via linear instability analysis of the conduction solution: through a closed algebraic form, we showed that the critical Rayleigh-Darcy number depends on the dimensionless compressibility factor \(\widehat{\beta }\) and we rigorously demonstrated that \(\widehat{\beta }\) has a destabilizing effect. Moreover, in the limit case \(\widehat{\beta } \rightarrow 0\) (i.e., according to the classical Oberbeck-Boussinesq approximation), the critical threshold for the Darcy-Bénard problem \(4 \pi ^2\) is recovered. In conclusion, the authors consider the next step in these studies would be to develop the nonlinear stability analysis of the conduction solution (11), in order to compare the linear instability threshold \({\mathcal {R}}_L\) to the nonlinear stability one.