1 Introduction

Natural convection in fluid saturating a porous medium is a research topic of great interest because of its several practical applications in real life and, specifically, in geophysical and engineering field. Most important applications can be found in geothermal energy utilisation, underground contaminant transport, nuclear waste disposal, heat exchangers, thermal insulation, and, more in general, in problems on removal and storage of heat [3].

This paper is intended to investigate the effect of depth-dependent viscosity on the onset of convection in a fluid-saturated porous medium. What motivated this paper is the strong viscosity dependence on temperature and/or depth, for many fluids [2, 4]. In several industrial problems, variations of viscosity with temperature cannot be neglected. Main examples of such problems can be found in geophysical context and in engineering field [1, 2, 5,6,7].

Actually, the correlation between viscosity and temperature deeply depends on which fluid is taken into account. In fact, viscosity of gases increases with temperature, while viscosity of liquids shows the opposite behaviour [3, p. 253]. For example, viscosity of glycerin decreases by three orders of magnitude for a \( 10\,^{\circ }\)C rise in temperature [8], while viscosity of water changes more than 1 order of magnitude between 25 and \(350\,^\circ \)C [9]. Over the same temperature interval, water thermal conductivity exhibits only a \(1 \%\) change [10]. Actually, as stated in [11], for most Newtonian liquids thermal conductivity is essentially constant over the temperature range in which viscosity shows remarkable variations. For this reason, in this paper, we take into account only viscosity variations.

Over the years, thermal convection in variable viscosity fluids has represented a topic of great interest for many researchers. Early studies on thermal convection in clear fluids with temperature-dependent viscosity are those of [2, 12]. Since then, such a problem has been extensively investigated [4, 13,14,15,16,17,18]. In [2], the influence of strongly temperature- and/or depth-dependent viscosity has been studied, with particular attention to convection in Earth’s mantle. In [4], the conditional nonlinear stability is investigated for a clear fluid whose viscosity decreases linearly with temperature. In [15], a global nonlinear stability result is obtained when viscosity shows a maximum. Nonlinear stability results have been obtained also in [16], where viscosity shows exponential dependence on temperature, and in [17] where viscosity is a convex function of temperature.

The problem of thermal convection in variable viscosity fluids saturating a porous medium has been widely investigated, as well [1, 9]. Nonlinear stability results have been determined in [19] and [20]. In [5], linear stability analysis of convection in water-saturated porous medium is performed. The above-cited papers deal with the problem of thermal convection in porous media under the hypothesis of local thermal equilibrium (LTE) between solid and fluid phase, i.e. by employing a single temperature model. Nevertheless, once the fluid velocity is sufficiently high, or as long as the solid thermal conductivity is much different from the fluid one, the assumption of LTE is no longer suitable to describe the physical phenomenon [21]. Applications are numerous and can be found in processes involving quick heat transfer, metal foams, and in everyday technology such as microwave heating [8], tube refrigerators and heat exchangers (see [22] for more details). As a result, the hypothesis of Local Thermal Non Equilibrium (LTNE) is employed to obtain more accurate results. This assumption involves two different temperatures (one for the solid, one for the fluid) so as to take into account heat exchanges between the phases. The problem of thermal convection in porous media in LTNE has been widely studied over the last years, starting from [23, 24], in which both a linear and nonlinear analysis is carried out. Many papers analysed the effect of LTNE on the onset of convection, coupled to rotation and/or anisotropy [25,26,27,28,29], magnetic field [30], vertical throughflow [31, 32], and also in non-horizontal porous layer [33,34,35]. Interesting results are obtained once the assumption of LTNE is combined with the Cattaneo’s law for heat conduction in the solid matrix, since in such a case convection by means of oscillatory motions can occur [36,37,38,39].

At the best of our knowledge, natural convection in depth-dependent viscosity fluids in porous media in LTNE has not received a proper attention so far, that is why we believe this paper may be of great interest. The LTNE model has been employed in [8], where the onset of Darcy-Benard convection is investigated for a temperature-dependent viscosity fluid with quadratic density constitutive equation.

The plan of the paper is the following. Section 2 is devoted to the formulation of the mathematical model describing the motion of a depth-dependent viscosity fluid in presence of an anisotropic porous medium, in LTNE regime. In this Section, the basic steady solution and the dimensionless model governing the evolution of perturbation fields are determined. In Sect. 3, the instability analysis is performed in order to determine the generalised eigenvalue problem which can be solved by means of the Chebyshev-tau method coupled to the QZ algorithm. In Sect. 4, the global nonlinear stability analysis of the conduction solution is carried out by employing the energy method. Finally, in Sect. 5, numerical results are reported, with particular attention devoted to the influence of variable viscosity, mechanical and thermal anisotropy, weighted conductivity ratio, and interaction coefficient on the onset of instability.

2 Mathematical model

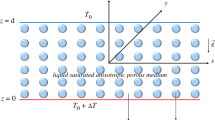
Let us take into account a horizontal porous layer, whose depth is d, saturated by an incompressible fluid \(\mathscr {F}\) initially at rest. We choose a Cartesian frame of reference (x, y, z), being the z-axis vertically upward. A uniform temperature gradient is imposed and maintained across the medium. Let \(T_L\) be the temperature on the lower plane \(z=0\) delimiting the layer, and let \(T_U\) be the temperature on the upper plane \(z=d\). We assume the layer to be heated from below, i.e. \(T_L>T_U\). Moreover, the hypothesis of local thermal non-equilibrium holds for the porous medium at stake, i.e. the heat exchange between solid matrix and fluid is allowed. Based on this assumption, we need to define two different temperatures, one for the fluid phase, another for the solid one.

figure a

Let us denote by \(T_f\) the temperature of the fluid phase and by \(T_s\) the temperature of the solid phase. Then, by virtue of previous considerations,

$$\begin{aligned} T_s=T_f=T_L \qquad \text {on} \quad z=0; \qquad T_s=T_f=T_U \qquad \text {on} \quad z=d, \end{aligned}$$
(1)

with \(T_L>T_U\).

The porous medium exhibits some anisotropic properties. Specifically, permeability and solid thermal conductivity are horizontally isotropic. Let \(\mathcal {K}\) be the permeability tensor and let \(\mathcal {D}_s\) be the solid thermal conductivity one. By assuming that both tensors share the same principal axis (x, y, z), they can be written in diagonal form, i.e.,

$$\begin{aligned}&\mathcal {K} = K_z \mathcal {K}_{*}, \qquad \mathcal {K}_{*} = \begin{pmatrix} \xi &{} \quad 0 &{}\quad 0 \\ 0 &{} \quad \xi &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1 \end{pmatrix}, \qquad \xi = \frac{K_H}{K_z}, \end{aligned}$$
(2.1)
$$\begin{aligned}&\mathcal {D}_s = \kappa _z^s \mathcal {D}^{*}_s, \qquad \mathcal {D}^{*}_s = \begin{pmatrix} \zeta &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad \zeta &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1 \end{pmatrix}, \qquad \zeta = \frac{\kappa _H^s}{\kappa _z^s}. \end{aligned}$$
(2.2)

In addition, we allow viscosity to be strongly dependent on temperature, at least at the steady state where temperature linearly increases with depth [10]. As a consequence, we assume the following behaviour of viscosity with respect to z [1, 2]:

$$\begin{aligned} \mu (z) = \mu _0 f(z), \qquad f(z) = e^{c^\prime (z-\frac{d}{2})} \end{aligned}$$
(3)

being \(\mu _0\) and \(c^\prime \) positive constants.

Under the previous assumptions, by employing the Oberbeck–Boussinesq approximation, the Vadasz–Darcy model is [8]

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _f c_a {\textbf {v}}_{,t} = -\nabla p^\prime + \rho _f \alpha g T_f {\textbf {k}} - \mu (z)\mathcal {K}^{-1} {\textbf {v}}\\ \nabla \cdot {\textbf {v}}=0\\ \varepsilon \rho _f c_f {T_f}_{,t} + \rho _f c_f {\textbf {v}} \cdot \nabla T_f = \varepsilon \kappa _f \Delta T_f + h(T_s - T_f)\\ (1-\varepsilon ) \rho _s c_s {T_s}_{,t} = (1-\varepsilon ) \nabla \cdot (\mathcal {D}_s \nabla T_s) - h(T_s-T_f) \end{array}\right. } \end{aligned}$$
(4)

where \({\textbf {v}}\), \(p^{\prime }\), \(T_f\), and \(T_s\) are (seepage) velocity, pressure, fluid phase temperature, and solid phase temperature, respectively; while \(\mu (z)\) is the fluid viscosity according to (3); \(\kappa _f\), \(\rho _f\), \(\rho _s\), \(c_f\), \( c_s \), g, \(\alpha \), \(c_a\), \(\varepsilon \), h are fluid thermal conductivity, fluid and solid density, specific heat of fluid and solid phase, gravity acceleration, thermal expansion coefficient, acceleration coefficient, porosity, angular velocity and interaction coefficient, respectively.

The following boundary conditions are coupled to (4):

$$\begin{aligned} \begin{aligned}&T_s = T_f = T_L \quad \text {on} \ z=0, \qquad T_s = T_f = T_U \quad \text {on} \ z=d, \\&{\textbf {v}} \cdot {\textbf {n}} = 0 \quad \text {on} \ z=0,d \end{aligned} \end{aligned}$$
(5)

where \( T_L>T_U \) and \({\textbf {n}}\) is the unit outward normal to planes \(z=0,d\).

The basic steady solution of (4) is:

$$\begin{aligned} m_0\!=\!\left\{ {\textbf {v}}_b \!=\! {\textbf {0}}\,, \,\,\,\, {T_s}_b \!=\! {T_f}_b \!=\! -\beta z \!+\! T_L\,, \quad p_b \!=\! -\rho _f g \alpha \beta \frac{z^2}{2}\! +\! \rho _f g \alpha T_L z \!+\! cost\right\} \end{aligned}$$
(6)

where \(\beta =\tfrac{T_L-T_U}{d}(>0)\) is the adverse temperature gradient.

In order to study the stability of \( m_0 \), let us introduce the perturbation fields \( ({\textbf {u}}, \theta , \phi , \pi ) \) to velocity field, fluid temperature field, solid temperature field, and pressure field, respectively.

After introducing perturbations to initial data, the following solution of (4) arises:

$$\begin{aligned} {\textbf {v}} = {\textbf {u}} + {\textbf {v}}_b, \qquad T_f = \theta + {T_f}_b, \qquad T_s = \phi + {T_s}_b, \qquad p^\prime = p + p_b. \end{aligned}$$
(7)

Once the following dimensionless quantities are defined,

$$\begin{aligned} x_i = x_i^* d, \quad t = t^* \dfrac{d^2 \rho _f c_f}{\kappa _f} , \quad p = p^* P, \quad u_i = u^*_i U, \quad \theta = \theta ^* T^{\prime }, \quad \phi = \phi ^* T^{\prime } \end{aligned}$$
(8)

where

$$\begin{aligned} P = \frac{U \mu _0 d}{K_z}\,, \qquad U = \frac{\varepsilon \kappa _f}{\rho _f c_f d}\,, \qquad T^{\prime } = \beta d \sqrt{\frac{\kappa _f \varepsilon \mu _0}{\beta g \alpha K_z \rho _f^2 c_f d^2}}, \end{aligned}$$
(9)

omitting all asterisks, we obtain the following dimensionless model governing the evolution of perturbation fields:

$$\begin{aligned}&\dfrac{1}{V\!a} {\textbf {u}}_{,t} = -\nabla p + R \theta {\textbf {k}} - f(z)\mathcal {K}^{-1} {\textbf {u}},\end{aligned}$$
(10.1)
$$\begin{aligned}&\nabla \cdot {\textbf {u}}=0,\end{aligned}$$
(10.2)
$$\begin{aligned}&{\theta }_{,t} + {\textbf {u}} \cdot \nabla \theta = R w + \Delta \theta + H(\phi - \theta ), \end{aligned}$$
(10.3)
$$\begin{aligned}&A {\phi }_{,t} = \zeta \Delta _1 \phi + \phi _{,zz} - H\gamma (\phi -\theta ), \end{aligned}$$
(10.4)

being \(f(z)=e^{c(z-\frac{1}{2})}\), \( c=c^\prime d \), \(\Delta _1 = \partial _{,xx}+\partial _{,yy}\), and where

$$\begin{aligned}&A= \dfrac{\rho _s c_s \kappa _f}{\rho _f c_f \kappa _z^s}, \quad \gamma =\dfrac{\varepsilon \kappa _f}{(1-\varepsilon ) \kappa _z^s}, \quad H=\dfrac{h d^2}{\varepsilon \kappa _f}, \end{aligned}$$
(11.1--3)
$$\begin{aligned} R^2 = \dfrac{K_z \rho ^2_f c_f d^2 \beta g \alpha }{\mu _0 \varepsilon \kappa _f}, \quad V\!a=\dfrac{c_f d^2 \mu _0}{K_z \kappa _f c_a} \end{aligned}$$
(11.4, 5)

are diffusivity ratio, weighted conductivity ratio, inter-phase heat transfer coefficient, Rayleigh number, and Vadasz number, respectively.

To (10.1), we add the initial conditions:

$$\begin{aligned} {\textbf {u}}({\textbf {x}},0) \! = \!{\textbf {u}}_0({\textbf {x}}) \,,\quad \theta ({\textbf {x}},0)\!=\!\theta _0({\textbf {x}})\,,\quad \phi ({\textbf {x}},0)\!=\!\phi _0({\textbf {x}})\,,\quad p({\textbf {x}},0)\!=\! p_0({\textbf {x}}) \end{aligned}$$
(12)

where \(\nabla \cdot {\textbf {u}}_0=0\), while the boundary conditions are

$$\begin{aligned} w = \theta = \phi = 0 \qquad \text {on} \ z=0,1. \end{aligned}$$
(13)

Let

$$\begin{aligned} V = \bigg [ 0, \dfrac{2\pi }{a_x} \bigg ] \times \bigg [ 0, \dfrac{2\pi }{a_y} \bigg ] \times [0, 1] \end{aligned}$$
(14)

be the periodicity cell and let us define \((\cdot , \cdot )\) and \(\Vert \cdot \Vert \) inner product and norm on \(L^2(V)\), respectively. Perturbations are assumed to be periodic in x and y directions with periods \(\tfrac{2\pi }{a_x}\) and \(\tfrac{2\pi }{a_y}\), respectively. Moreover, \( \forall g \in \{{\textbf {u}}, \theta , \phi , p \},\)

$$\begin{aligned} g \!:\! ({\textbf {x}},t) \!\in \! V \times \mathbb {R}^+ \!\rightarrow \! g({\textbf {x}},t) \!\in \! \mathbb {R}, \ g \!\in \! W^{2,2}(V) \ \forall t \!\in \! \mathbb {R}^+, \end{aligned}$$

and g can be expanded in a Fourier series uniformly convergent in V.

3 Linear instability analysis

In order to perform the linear instability analysis of \( m_0 \), let us consider the linear version of (10.1), i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{1}{V\!a} {{\textbf {u}}}_{,t} = -\nabla p + R \theta {\textbf {k}} - f(z)\mathcal {K}^{-1} {\textbf {u}}\\ \nabla \cdot {\textbf {u}}=0\\ {\theta }_{,t} = R w + \Delta \theta + H(\phi - \theta )\\ A {\phi }_{,t} = \zeta \Delta _1 \phi + \phi _{,zz} - H\gamma (\phi -\theta ) \end{array}\right. } \end{aligned}$$
(15)

that can be written as

$$\begin{aligned} N \frac{\partial }{\partial t} F({\textbf {x}},t) = M F({\textbf {x}},t) \end{aligned}$$
(16)

being \(F= (u,v,w,\pi ,\theta ,\phi )\), N with all zero entries and such that \(diag(N) = \left( \frac{1}{V\!a}, \frac{1}{V\!a}, \frac{1}{V\!a}, 0, 1, \frac{A}{\gamma }\right) \) and

$$\begin{aligned} M = \begin{pmatrix} - \frac{f(z)}{\xi } &{}\quad 0 &{}\quad 0 &{}\quad - \frac{\partial }{\partial x} &{} \quad 0 &{}\quad 0\\ 0 &{}\quad - \frac{f(z)}{\xi } &{}\quad 0 &{}\quad - \frac{\partial }{\partial y} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad -f(z) &{}\quad - \frac{\partial }{\partial z} &{}\quad R &{}\quad 0\\ -\frac{\partial }{\partial x} &{}\quad -\frac{\partial }{\partial y} &{}\quad -\frac{\partial }{\partial z} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad R &{}\quad 0 &{}\quad \Delta -H &{}\quad H\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad H &{}\quad \frac{\zeta }{\gamma }\Delta _1 + \frac{1}{\gamma }. \end{pmatrix}. \end{aligned}$$
(17)

It is straightforward to notice that the spatial operator M related to (15) is symmetric with respect to the \( L^2 \)-scalar product. As a consequence, its spectrum involves only real numbers, and the strong version of the principle of exchange of stabilities holds.

Moreover, system (15) is autonomous. Hence, we can look for solutions such that

$$\begin{aligned} \varphi ^{\prime }({\textbf {x}},t)\!=\! \varphi ({\textbf {x}}) \ e^{\sigma t} \quad \forall \varphi ^{\prime }\! \in \! \{w, \theta , \phi , p\}. \end{aligned}$$
(18)

Substituting (18) into (15), we get

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\sigma }{V\!a} {\textbf {u}} = -\nabla p + R \theta {\textbf {k}} - f(z)\mathcal {K}^{-1} {\textbf {u}}\\ \nabla \cdot {\textbf {u}}=0\\ \sigma \theta = R w + \Delta \theta + H(\phi - \theta )\\ A \sigma \phi = \zeta \Delta _1 \phi + \phi _{,zz} - H\gamma (\phi -\theta ). \end{array}\right. } \end{aligned}$$
(19)

In order to determine the critical threshold of the Rayleigh number for the onset of instability, we focus on the marginal state in (19). Accounting for the principle of exchange of stabilities, we set \(\sigma =0\) in (19), so that

$$\begin{aligned}&0 = -\nabla p + R \theta {\textbf {k}} - f(z)\mathcal {K}^{-1} {\textbf {u}},\end{aligned}$$
(20.1)
$$\begin{aligned}&\nabla \cdot {\textbf {u}}=0,\end{aligned}$$
(20.2)
$$\begin{aligned}&0 = R w + \Delta \theta + H(\phi - \theta ),\end{aligned}$$
(20.3)
$$\begin{aligned}&0 = \zeta \Delta _1 \phi + \phi _{,zz} - H\gamma (\phi -\theta ). \end{aligned}$$
(20.4)

By applying the double curl to (20.1) and retaining only the third component, from (20.1), one gets:

$$\begin{aligned} {\left\{ \begin{array}{ll} \xi R \Delta _1 \theta - f'(z) w_{,z} - f(z) (\xi \Delta _1 w + w_{,zz})=0\\ R w + \Delta \theta + H(\phi - \theta )=0\\ \zeta \Delta _1 \phi + \phi _{,zz} - H\gamma (\phi -\theta )=0 \end{array}\right. } \end{aligned}$$
(21)

where the prime denotes ordinary derivative with respect to z.

Because of periodicity of the perturbations, unknown fields in (21) can be written as:

$$\begin{aligned} \varphi (x,y,z) = \sum _{n=1}^{+\infty } \bar{\varphi }_n(x,y,z) \qquad \forall \varphi \in \{w, \theta , \phi \} \end{aligned}$$
(22)

where

$$\begin{aligned} \Delta _1 \bar{\varphi }_n\! = \!- a^2 \bar{\varphi }_n \end{aligned}$$
(23)

with \(a^2\!=\!a^2_x \!+\! a^2_y\).

Now, let us substitute (22) in (21) and retain only the n-th component. Hence, by denoting \(D \equiv \frac{d}{d z}\) and \(D^2 \equiv \frac{d^2}{d z^2}\), (21) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( D^2 - \xi a^2\right) w_n + c D w_n = - f^{-1}(z)\xi a^2 R \theta _n\\ \left( D^2 - a^2 -H \right) \theta _n = - R w_n - H \phi _n\\ \left( D^2 - \zeta a^2 - H\gamma \right) \phi _n = -H\gamma \theta _n \end{array}\right. } \end{aligned}$$
(24)

which will be solved subject to the boundary conditions

$$\begin{aligned} w = \theta = \phi = 0 \qquad \text {on} \ z=0,1. \end{aligned}$$
(25)

System (24) represents an eigenvalue problem of ordinary differential equations, where R is the eigenvalue. Starting from (24), one can determine the function \( \lambda (a^2) \) which describes how R depends on \( a^2 \). As a consequence, the critical Rayleigh number for the onset of stationary instability is given by

$$\begin{aligned} R_L = \min _{a^2 \in \mathbb {R}^+} \lambda (a^2). \end{aligned}$$
(26)

In order to solve the eigenvalue problem (24), we employ the Chebyshev-tau method coupled with the QZ algorithm. This numerical procedure takes advantage of the orthogonality of Chebyshev polynomials with respect to the scalar product,

$$\begin{aligned} \langle f, g\rangle = \int _{-1}^{1} \frac{f g}{\sqrt{1-z^2}} \hbox {d}z, \qquad f, g \in L^2(-1,1), \end{aligned}$$
(27)

and many of their properties such as a recursive formula for multiplication between two polynomials, i.e.

$$\begin{aligned} 2 T_r T_q = T_{r+q} + T_{|r-q |}. \end{aligned}$$
(28)

We will not go into further details of this numerical method, but we are going to give the main ideas to carry out this procedure. For more details, interested readers can refer to [10, 40,41,42,43].

Let \( T_k \), \( k\in \mathbb {N}\), be the k-th Chebyshev polynomial. The solution of (24) can be expanded as finite series of Chebyshev polynomials, i.e.

$$\begin{aligned} w_n = \sum _{k=0}^{N+2} W_k T_k(z), \quad \theta _n = \sum _{k=0}^{N+2} \Theta _k T_k(z), \quad \phi _n = \sum _{k=0}^{N+2} \Phi _k T_k(z), \end{aligned}$$
(29)

We substitute (29) in (24), and then we take the inner product with \( T_k \), \( k=0, \dots , N \), on the weighted Chebyshev polynomial space. In such a way, we manage to write system (24) as a generalised eigenvalue problem

$$\begin{aligned} A {\textbf {x}} = R B {\textbf {x}} \end{aligned}$$
(30)

where \( {\textbf {x}} = \left( W_0, W_1, \dots , W_N, \Theta _0, \Theta _1, \dots , \Theta _N, \Phi _0, \Phi _1,\dots ,\Phi _N\right) ^T \),

$$\begin{aligned} A= \begin{pmatrix} D^2-\xi a^2 I +c D &{}\qquad 0 &{}\qquad 0 \\ 0 &{}\qquad D^2 - (a^2 +H) I &{}\qquad H I \\ 0 &{}\qquad H\gamma I &{}\qquad D^2 -(\zeta a^2 +H\gamma ) I \end{pmatrix}, \end{aligned}$$
(31)

and

$$\begin{aligned} B =\begin{pmatrix} 0 &{} -\xi a^2F^* &{} 0 \\ -I &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix} \end{aligned}$$
(32)

being \( D^2 \), D the Chebyshev representation of \( \frac{d^2}{d z^2} \) and \( \frac{d}{d z} \), respectively, I the identity matrix, and \( F^* \) the matrix representation of function \( f^{-1}(z) \).

For coding purpose, we work with \( k=1,\dots , N \). Then, the above matrices are \( 3N \times 3N \), and \( F^* \) is \( N\times N \). When the exponential function \( f^{-1}(z) \) can be well approximated by a second-order polynomial, matrix \( F^* \) is computed by means of the following recursive formulas:

$$\begin{aligned} \begin{aligned}&F^*_{i,i} = 1+\frac{c}{2} + \frac{3 c^2}{8}, \quad F^*_{i,i+1}= - \frac{c}{2}\left( 1+\frac{c}{2}\right) , \\&F^*_{i,i+2} = \frac{c^2}{8}, \quad \quad \quad \quad \text {for} \ i=1,\dots ,N-2,\\&F^*_{i,i-1}= - \frac{c}{2}\left( 1+\frac{c}{2}\right) , \quad \text {for} \ i=2,\dots ,N, \\&F^*_{i,i-2} = \frac{c^2}{8}, \quad \text {for} \ i=3,\dots ,N,\\&F^*_{2,1}= - c\left( 1+\frac{c}{2}\right) , \quad F^*_{3,1}=\frac{c^2}{4}, \quad F^*_{2,2}= 1+\frac{c}{2} + \frac{c^2}{2}. \end{aligned} \end{aligned}$$
(33)

The eigenvalue problem (30)–(32) is then solved by the QZ algorithm which provides eigenvalues with no trouble. In Sect. 5, we show numerical results.

4 Nonlinear stability

This Section is devoted to develop a nonlinear stability analysis for the conduction solution \( m_0 \), in order to determine a sufficient condition for its stability.

We perform the scalar multiplication of (10.1) by \( {\textbf {u}} \), (10.3) by \( \theta \) and (10.4) by \( \phi \), and then we integrate over the periodicity cell V. The sum of the resulting equations can be written as

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} E(t) = R I- D \end{aligned}$$
(34)

where

$$\begin{aligned} E(t)= & {} \frac{\Vert {\textbf {u}}\Vert ^2}{2 V\!a} + \frac{\Vert \theta \Vert ^2}{2 } + \frac{A \Vert \phi \Vert ^2}{2 \gamma } \quad \text {Lyapunov Function},\end{aligned}$$
(35.1)
$$\begin{aligned} I(t)= & {} 2(\theta , w) \quad \text {Production term},\end{aligned}$$
(35.2)
$$\begin{aligned} D(t)= & {} \Vert \nabla \theta \Vert ^2 + H \Vert \theta -\phi \Vert ^2 + \frac{\zeta }{\gamma }\Vert \nabla _1 \phi \Vert ^2 + \frac{1}{\gamma } \Vert \phi _{,z}\Vert ^2\nonumber \\&+ \int _V \left( f(z) \frac{u^2}{\xi } + f(z) \frac{v^2}{\xi } + f(z) w^2\right) \hbox {d}V \quad \text {Dissipation term}. \end{aligned}$$
(35.3)

Starting with (34), by defining

$$\begin{aligned} \frac{1}{R_E} = \max _{\mathcal {H}} \frac{I}{D} \end{aligned}$$
(36)

where

$$\begin{aligned} \begin{aligned} \mathcal {H} = \,&\left\{ ({\textbf {u}}, \theta , \phi ) \ : \ w = \theta = \phi =0 \ \text {on} \ z=0,1; \ \text {periodic in} \ x \ \text {and} \ y\text {directions, with period} \ \frac{2 \pi }{a_x},\right. \\&\quad \left. \frac{2 \pi }{a_y} \ \text {respectively}; \ \nabla \cdot {\textbf {u}}=0; \ D< \infty \right\} , \end{aligned} \end{aligned}$$
(37)

we obtain

$$\begin{aligned} \frac{\hbox {d}E}{\hbox {d}t} = - D \left( 1 - R \frac{I}{D}\right) \le - D \left( 1 - \frac{R}{R_E}\right) . \end{aligned}$$
(38)

By employing the Poincaré inequality in (35.3), we get

$$\begin{aligned} D(t) \ge \pi ^2 \Vert \theta \Vert ^2 + \frac{\pi ^2 \zeta ^*}{\gamma }\Vert \phi \Vert ^2 + \xi ^* e^{-\frac{c}{2}} \Vert {\textbf {u}}\Vert ^2 \end{aligned}$$
(39)

being \( \xi ^* = \min \{1,\xi ^{-1}\} \) and \( \zeta ^* = \min \{1,\zeta \} \). Hence, (38), (39) yield the exponential decay of the energy function E(t) . In fact, by virtue of (39), inequality (38) becomes

$$\begin{aligned} \begin{aligned} \frac{\hbox {d}E}{\hbox {d}t}&\le - \left( 1 - \frac{R}{R_E}\right) \left( \pi ^2 \Vert \theta \Vert ^2 + \frac{\pi ^2 \zeta ^*}{\gamma }\Vert \phi \Vert ^2 + \xi ^* e^{-\frac{c}{2}} \Vert {\textbf {u}}\Vert ^2\right) \\&\le - \left( 1 - \frac{R}{R_E}\right) k E(t) \end{aligned} \end{aligned}$$
(40)

where \( k = \min \left\{ 2\pi ^2, \dfrac{2 \pi ^2 \zeta ^*}{A}, 2 \xi ^* e^{-\frac{c}{2}}V\!a\right\} \), from which

$$\begin{aligned} E(t) \le \text {exp }\left\{ - k\left( 1 - \frac{R}{R_E}\right) t \right\} . \end{aligned}$$
(41)

By virtue of (41), as long as \( R< R_E \), perturbation fields on seepage velocity, fluid and solid temperature decay exponentially in time. Thus, we have proved that \( R< R_E \) is a sufficient condition for the global nonlinear and exponential stability of the conduction solution \( m_0 \).

Now, let us proceed to determine the critical threshold \( R_E \). With this aim, we write the Euler–Lagrange equations by solving the variational problem (36), i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} R_E \theta {\textbf {k}} - \left( f\frac{u}{\xi }, f\frac{v}{\xi }, f w \right) = \nabla \omega \\ R_E w + \Delta \theta + H \left( \phi - \theta \right) =0\\ \zeta \Delta _1 \phi + \phi _{,zz} - H\gamma \left( \phi -\theta \right) =0 \end{array}\right. } \end{aligned}$$
(42)

where \( \omega \) is a Lagrange multiplier arising from the incompressibility of \( {\textbf {u}} \). System (42) coincides with (20.1). As a consequence, we manage to obtain the coincidence between the global nonlinear stability threshold \( R_E \) and the linear instability threshold \( R_L \). As a result, condition \( R<R_E \) is not only sufficient, but also necessary for the stability of \( m_0 \).

5 Numerical results

In the present Section, we report results obtained once the generalised eigenvalue problem (30) and the subsequent minimum problem (26) have been solved. Given the coincidence between linear and nonlinear threshold, we denote by \( R^2_c \) the critical Rayleigh number beyond which thermal convection occurs.

The aim of this Section is to highlight the influence of variable viscosity, thermal and mechanical anisotropy, weighted conductivity ratio, and interaction coefficient on the onset of convection. Let us remark that, since the interaction heat transfer coefficient H cannot be easily measured, we set a range in which H can vary. According to the choice done in [29, 44], \( H \in (10^{-2}, 10^6)\). As a consequence, the critical Rayleigh number is plotted as function of H in every picture throughout the Section.

Fig. 1
figure 1

Critical Rayleigh number as function of H for different values of c with \( \xi =1.5, \zeta =5, \gamma =1 \)

Full size image
Table 1 Comparison between the critical wavenumber \(a_c^{2}\) ([1]) and the critical threshold \(R_c^{2}\) ([1]) shown in Table 3 in [1] and the critical wavenumber \(a^{2}_c \) and the rescaled critical threshold \( \frac{R^{2}_c\gamma }{\gamma +1}\) obtained in the present paper when \( H \rightarrow \infty \), \( \gamma =1, \xi =1, \zeta =1 \)
Full size table
Table 2 Comparison between the critical wavenumber \(a_c^{2}\) and the rescaled critical threshold \(\frac{R^{2}_c\gamma }{\gamma +1}\) obtained when \( H \rightarrow \infty \) (i.e. LTE regime) and the critical wavenumber \(a^{2}_c \) and the critical threshold \( R^{2}_c\) obtained when \( H =100 \) (i.e. LTNE regime), with \( \gamma =1, \xi =1, \zeta =1 \)
Full size table

It may be observed that the effect of variable viscosity on the critical Rayleigh number is substantial. As shown in Fig. 1, as c increases, \( R_c^2 \) decreases for every choice of the interaction coefficient H, namely the onset of convection gets easier. This result is physically reasonable and in agreement with what stated in [9], i.e. fluids whose viscosity near the hot boundary is much lower than everywhere else in the layer are more likely to become unstable sooner.

Fig. 2
figure 2

Comparison between neutral stability curve \( R_C \) (black line) obtained via Chebyshev-tau method setting \( c=0 \) and neutral stability curve \( R_A \) (red dashed line) obtained analytically in [45], where \( \xi =1, \zeta =1, H=10^4, \gamma =1 \) (color figure online)

Full size image
Fig. 3
figure 3

Critical Rayleigh number as function of H for different values of \( \xi \) with \( c=1, \zeta =5, \gamma =1 \)

Full size image

Let us remark that, as \( H\rightarrow \infty \), fluid and solid phases can be treated as a single phase since they exchange heat so rapidly that they have nearly identical temperature. As a consequence, we recover the regime of LTE. Whereas, when \( H\rightarrow 0 \), fluid instability is not affected by the properties of the solid matrix. As pointed out in [23], the respective mathematical problems are identical, except for a rescaling of the Rayleigh number. Table 1 shows the coincidence between results delivered in [1] under the assumption of LTE and results obtained in the present paper for \( H \rightarrow \infty \), after rescaling the Rayleigh number. In addition, one can notice that in the first line in Table 1, where \( c=0 \), we recovered the classical Rayleigh number \( 4\pi ^2 \) for the Darcy–Benard problem.

Fig. 4
figure 4

Critical Rayleigh number as function of H for different values of \( \zeta \) with \( c=1, \xi =1.5, \gamma =1 \)

Full size image
Fig. 5
figure 5

Critical Rayleigh number as function of H for different values of \( \gamma \) with \( c=1, \xi =1.5, \zeta =5 \)

Full size image

The decreasing trend of \( R^2_c \) with respect to increasing c, i.e. a higher gradient of viscosity across the layer, depends strongly on H. So, we analyse the behaviour of \( R^2_c \) both for high values of H (for which the LTE regime holds [23]) and for \( H=100 \) (for which the LTNE regime holds). In Table 2, one can notice that the decreasing trend of \( R^2_c \) is less remarkable for \( H \rightarrow \infty \) rather than for \( H=100 \), even though the critical threshold for the LTE case is always lower than the one in LTNE. Such a result suggests that the effect of variable viscosity on the onset of convection is less intense under the assumption of LTE rather than in the case of LTNE. A similar result has been pointed out in [8].

When \( c =0\), function \( f(z)=1 \), i.e. viscosity is constantly equal to \( \mu _0 \), the value assumed in the middle of the layer. In case of isotropic porous medium, by assuming \( c=0 \) we would expect to recover the same results found in [45]. In Fig. 2 we compare results delivered in the present paper by the Chebyshev-tau method with the analytical expression of the critical Rayleigh number found in [45]. The two neutral curves are perfectly overlapped. In fact, one can compute the absolute error, which is \( 1.85 \times 10^{-10} \) at most.

In Fig. 3, the influence of mechanical anisotropy on the critical Rayleigh number is shown. The destabilising effect of increasing permeability on the conduction solution is clear. The Rayleigh number decreases with \( \xi \) for any H, in agreement with findings in [29, 44, 46, 47]. This result is physically admissible. Based on definition (2.1), increasing \( \xi \) is due to an increase in the horizontal permeability \( K_H \), which means that the fluid is allowed to move easier and easier in the horizontal direction. Thus, resistance to fluid motion reduces, and the advective transport enhances [48].

On the other hand, solid thermal conductivity has a stabilising effect on \( m_0 \), delaying the onset of convection. In Fig. 4, such a behaviour is evident, specifically for large values of H. If \( \kappa ^s_H \) grows, the onset of convection is delayed because the solid matrix easily absorbs heat from the fluid. Actually, when H goes to zero, solid thermal conductivity affects weakly the onset of convection. This result is in agreement with what is found in [29], and it is physically reasonable since small values of H imply that the heat exchange between fluid and solid phases occurs so slowly that the solid matrix does not manage to absorb enough heat to cool down the fluid.

The onset of convection is encouraged by increasing values of the weighted conductivity ratio \( \gamma \), as shown in Fig. 5. Increasing values of \( \kappa _f \) lead to an increasing \( \gamma \), which imply a reduction of \( R_c^2 \), i.e. a destabilising effect. This behaviour is expected from a mathematical point of view, since looking at the Rayleigh number definition in (11.4) we can notice that \( R^2 \) is inversely proportional to \( \kappa _f \).

6 Conclusions

A linear and nonlinear stability analysis of the conduction solution of the Vadasz–Darcy model describing the motion of a depth-dependent viscosity fluid in an anisotropic porous medium in LTNE is performed. Linear instability analysis leads to a generalised eigenvalue problem which can be solved by means of the Chebyshev-tau method coupled with the QZ algorithm. Nonlinear stability analysis is carried out by employing the energy method. The optimal result of coincidence between the linear instability threshold and the global nonlinear stability threshold is obtained.

Viscosity decreasing exponentially with depth has a destabilising effect on the onset of convection, leading to lower values of the critical Rayleigh number. In fact, viscosity drag reduces with depth, namely the fluid meets fewer obstacles to its motion. Moreover, comparing results with those ones found under LTE assumption in [1], we can remark that the presence of LTNE makes the influence of variable viscosity more intense. Applications can be found in oil cooling systems in hydraulic units that involve heat exchangers. Within the heat exchanger, maintaining the oil cold is important in order to preserve its characteristics and proper operating conditions. Findings in the paper show that the effect on the onset of convection of replacing a kind of oil with another with a different law of viscosity is larger under the LTNE hypothesis than under the LTE one. A practical example is given by two oils, i.e. SAE 10W-60 and SAE 0W-30, whose values of kinematic viscosity \(\nu \) are shown in the Table (see [49]). If the aim is to inhibit convection, a larger Rayleigh number is achieved if SEA 0W-30 is preferred to SAE 10W-60.

\(T~[^\circ \hbox {C}]\)

\(\nu _{\text {SAE 10W-60}}~[\mathrm{{mm}}^2/\mathrm{{s}}]\)

\(\nu _{\text {SAE 0W-30}}~ [\mathrm{{mm}}^2/\mathrm{{s}}]\)

0

1684.4

550.23

10

831.44

291.93

20

448.10

167.29

40

161.73

66.803

Furthermore, we proved the destabilising effect of both mechanical anisotropy and the weighted conductivity ratio, other than the stabilising effect of thermal anisotropy.