1 Introduction

The study of simultaneous movement of fresh and salt groundwater is generally motivated by practical environmental problems such as seawater intrusion in coastal aquifers, upconing of saltwater under freshwater supply wells and seepage of brackish water in polder areas. An important aspect in such problems is the prediction of the position, and movement of the diffusive/dispersive mixing zone between fresh and salt groundwater in aquifers is required. The interest in fresh–salt groundwater problems dates back to the late nineteenth century, when Ghyben (1888) and Herzberg (1901) independently estimated the thickness of a fresh water lens in a coastal aquifer by considering a stationary fresh/salt interface, see also Verruijt (1980).

Field observations show that in many cases of practical interest the width of the mixing zone between the fluids is small compared to the vertical and horizontal extensions of the aquifer. This allows to disregard the mixing zone, resulting in a sharp interface model. Though relatively straightforward to formulate, fresh–salt interface problems pose many serious mathematical difficulties. The time-dependent case for incompressible fluids yields two-phase free boundary problems for which only partial existence and uniqueness results are known, see, e.g., Duchon and Robert (1985, 1986) and Chan Hong and Hilhorst (1987). One of the main difficulties concerns the regularity of the free boundary. A detailed numerical approach was given by Chan Hong et al. (1989). Many saltwater intrusion problems can be considered stationary. Examples are given in Bear and Verruijt (1987) and by Paster and Dagan (2007, 2008). For stationary problems, rigorous mathematical results are known, see Van Duijn and Alt (1990, 1993) and [17]. Choquet et al. (2015) considers an interesting approach for the time-dependent interface problem, see also Jazar and Monneau (2014). There is extensive engineering literature available. For this, we refer to, e.g., Dawson and Adnan (2015), Oude Essink (2001) and the books of Bear (1979), Bear et al. (1999) and Bear and Verruijt (1987). Recently, there is renewed interest in interface problems related to \(\hbox {CO}_2\)-storage, see Nordbotten and Celia (2012).

Probably the most important simplification in groundwater flow is the so-called Dupuit–Forchheimer approximation, to which we will refer in this paper as the ‘Dupuit approximation,’ see Dupuit (1863) and Forchheimer (1886). The Dupuit approximation, originally formulated for groundwater in an unconfined aquifer with constant density, assumes that the pressure distribution below the groundwater table is hydrostatic, implying that the horizontal component of the specific discharge vector is constant over the depth. The Dupuit approximation reduces the complexity of a hydrogeological problem by reducing the number of space dimensions of the problem by one. The Dupuit formulation of a problem can also be the result of averaging of certain variables in the vertical direction, see, e.g., Strack et al. (2006), Huppert and Woods (1995), Bakker (1989), Strack and Bakker (1995), Danilov and Katz (1980) and in particular Yortsos (1995). More recently, sharp interface models in conjunction with the Dupuit approximation were studied in the framework of geological storage of \(\hbox {CO}_2\), see, e.g., Gasda et al. (2011), Nordbotten and Dahle (2011), and for a rather complete overview the book by Nordbotten and Celia (2012).

Inspired by the unpublished work of the Dutch engineer J.H. Edelman, De Josselin de Jong (1960, 1977, 1969) developed a mathematical formulation for the dynamics of a two-fluid interface, using the stream function as flow variable. In this formulation, one replaces the two different homogeneous fluids by one hypothetical fluid with a distribution of vortices along the interface. The strength of the vortices, resulting from horizontal density gradients, is chosen to obtain the correct discharge field throughout the flow domain. Note that Kidder (1956) addressed a similar problem in an aquifer of finite length using the velocity potential and the method of images to derive a series expansion solution for the evolution of the interface.

In his paper, De Josselin de Jong (1981) [or in the collected papers of De Josselin de Jong (2006)] applied the Dupuit approximation to a sharp fresh–salt interface in an aquifer of infinite horizontal extent. He assumed that the horizontal component of the specific discharge vector \(q_x(x,z,t)\) is constant with respect to the vertical position z in each fluid, with having a jump at the interface. In other words, he assumed that

$$\begin{aligned} q_x(x,z,t) = \left\{ \begin{array}{l} q_{xf}(x,t)\\ q_{xs}(x,t) \end{array} \right. \end{aligned}$$
(1)

where \(q_{xf}(x,t)\) and \(q_{xs}(x,t)\) denote, respectively, the x-component of the specific discharge above (fresh) and below (salt) the interface. By parameterizing the interface along the horizontal coordinate and applying (1), he was able to derive an equation describing the movement of the fresh–salt interface. This equation is a nonlinear doubly degenerate diffusion equation, of which the mathematical properties have been studied in great detail, see, e.g., Van Duijn and Zhang (1988) and Zhang (1988). Note that we explicitly do not consider non-horizontal aquifers. For sake of completeness, we refer to the books of Charny (1963) and Charny et al. (1968) that cover dipping aquifers.

Starting point for this paper is the exact stream function formulation for the flow field in the aquifer as presented in De Josselin de Jong (1981). Using this result, we are able to derive an exact integro-differential equation for the movement of the fresh–salt interface. It is shown that the pointwise (differential) part of the equation is identical to the interface motion equation as derived in De Josselin de Jong (1981) (and which was merely based on the physical intuition of De Josselin de Jong). The integral part of the exact equation can be regarded as the correction term to the approximate Dupuit equation. Our aim is to study the behavior of the integral term in order to give a criterion for the validity of the Dupuit approximation.

In Sect. 2, we formulate the flow problem and give an expression for the specific discharge in terms of an integral along the fresh–slat interface. Next in Sect. 3, we recall the expression for the Dupuit discharge and the related interface motion equation. In Sect. 4, we return to the interface integral and use integration by parts to recover the approximate Dupuit expression as well as a correction term that contains an integral involving a weight function and the second-order spatial derivative of the interface. Then, in Sect. 5, we present a criterion for the validity of the Dupuit approximation by estimating the correction term. The case of flat interfaces, including the explicit Dupuit similarity solution as a rotating interface, is considered in Sect. 6. Finally, Sect. 6.1 summarizes the main conclusion of this work.

2 Problem Formulation

Let the strip

$$\begin{aligned} {\varOmega } = \{(x,z){:}-{\!}\infty<x<+\infty , 0<z<H\}. \end{aligned}$$
(2)

denote a vertical cross section of a horizontally extended aquifer of constant thickness H, which is bounded above and below by impermeable confining layers. The vertical coordinate z is pointing upwards, i.e., opposite to the gravity vector. The aquifer consists of a homogeneous and isotropic porous medium, with intrinsic permeability \(\kappa \) and porosity \(\phi \) , occupied by fresh and salt groundwater. We assume that the scale (H) of the problem is sufficiently large, so that an abrupt change in specific weight \(\gamma \), from freshwater with \(\gamma _f\) to saltwater with \(\gamma _s\), can be assumed. Typical values for seawater intrusion problems are: \(\gamma _f = 1000\,\hbox {N/m}^3\) and \(\gamma _s = 1025\,\hbox {N/m}^3\).

Throughout this paper, we consider the stable case where the heavier saltwater is always below the lighter freshwater. This implies that there exists an interface S between the fluids that can be parameterized as a function of the horizontal coordinate x. In other words, there exists a function \(\zeta {:} \mathbf{R} \rightarrow [0,H]\) such that

$$\begin{aligned} S= \{(x,z)\in {\varOmega }{:}-{\!}\infty<x<+\infty , z= \zeta (x)\}. \end{aligned}$$
(3)

For the specific weight \(\gamma \), this implies

$$\begin{aligned} \gamma = \left\{ \begin{array}{l} \gamma _f \;\;\hbox {in}\;\; \{(x,z)\in {\varOmega }\; {:}\; z>\zeta (x)\},\\ \gamma _s \;\;\hbox {in}\;\; \{(x,z)\in {\varOmega }\; : \; z<\zeta (x)\}, \end{array} \right. \end{aligned}$$
(4)

or

$$\begin{aligned} \gamma (x,z) = (\gamma _s-\gamma _f)H(\zeta (x)-z) +\gamma _f \end{aligned}$$
(5)

for any \((x,z) \in {{\varOmega }}\), where H denotes the Heaviside function,

$$\begin{aligned} H(s) = \left\{ \begin{array}{ll} 1 &{} \hbox {for} \;\;s >0\\ 0 &{} \hbox {for}\;\; s <0 \end{array} \right. \end{aligned}$$
(6)

Finally, we assume that the fluids are incompressible and that they have the same viscosity \(\mu \), see also De Josselin de Jong (1960) and later Verruijt (1980). This generally holds in natural circumstances.

2.1 Flow Equations

Concerning the flow in \({\varOmega }\), we assume here without loss of generality that the fluids are at rest when \(|x|\rightarrow \infty \). Any superimposed flow can easily be incorporated. The simplifying assumptions lead to the following equations:

Continuity

$$\begin{aligned} \hbox {div} \; {\mathbf{q}} = 0\;\; \hbox {in} \;\; {\varOmega }; \end{aligned}$$
(7)

Momentum balance (Darcy’s law)

$$\begin{aligned} \frac{\mu }{\kappa } {\mathbf{q}} +\hbox {grad}\; p + \gamma \; {\mathbf{e}}_z = 0 \;\; \hbox {in}\;\; {\varOmega }; \end{aligned}$$
(8)

Boundary conditions

$$\begin{aligned} {\mathbf{q}}\cdot {\mathbf{n}} = 0 \;\; \hbox {on} \;\; \partial {\varOmega } \;\;\hbox {and} \;\; |{\mathbf{q}}| \rightarrow 0 \;\;\hbox {as}\;\; x\rightarrow \pm \infty \;\;\hbox {for} \;\;z\in (0,H). \end{aligned}$$
(9)

Here, q denotes the specific discharge vector (with components \(q_x\) and \(q_z\)), p the fluid pressure, e \(_z\) the unit vector in the positive z-direction, n the outward unit vector normal to the boundary \(\partial {\varOmega }\) and \(|\cdot |\) the Euclidian norm.

Equation (7) is satisfied if a stream function \({\varPsi }{:}{\varOmega } \rightarrow {\mathbf{R}}\) exists such that

$$\begin{aligned} q_x = -\frac{\partial {\varPsi }}{\partial z} \;\;\hbox {and}\;\; q_z=\frac{\partial {\varPsi }}{\partial x}. \end{aligned}$$
(10)

Taking the two-dimensional curl of Darcy’s law (8) and substituting (10) into the result gives the fundamental equation [see also the pioneering paper of De Josselin de Jong (1960)]

$$\begin{aligned} -{\varDelta } {\varPsi } = \frac{\kappa }{\mu } \frac{\partial \gamma }{\partial x}. \end{aligned}$$
(11)

Using expression (5) in this equation yields

$$\begin{aligned} -{\varDelta } {\varPsi } = {\varGamma } \frac{\partial }{\partial x} \left( H(\zeta (x)-z)\right) ={\varGamma } \int _{{\mathbf{R}}}\frac{d \zeta }{d x}(x_s)\;\delta ({\mathbf{x}}_{\zeta }(x_s)-{\mathbf{x}})\; dx_s \end{aligned}$$
(12)

where

$$\begin{aligned} {\varGamma }= \frac{\kappa }{\mu }(\gamma _s-\gamma _f). \end{aligned}$$
(13)

Here \({\mathbf{x}}_{\zeta }(x_s)=(x_s,\zeta (x_s))\) denotes a point at the interface \(S, {\mathbf{x}}=(x,z)\) a point in the strip \({\varOmega }\) and \(\delta \) is the Dirac delta function in R \(^2\). Equation (12) tells us that the flow (stream function) induced by the fresh–salt interface is equivalent to the flow induced by vortices with strength \({\varGamma } \frac{d \zeta }{d x}(x)\) along the interface. This observation was one of the main results of De Josselin de Jong (1960). From the no-flow conditions (9), we deduce for \({\varPsi }\) the boundary conditions

$$\begin{aligned} {\varPsi }(x,0) = {\varPsi }(x,H) = 0 \;\;\; \hbox {for} \;\;-{\!}\infty<x< +\infty . \end{aligned}$$
(14)

The unique, bounded solution of problem (12), (14) is given by the expression (see Appendix A for details and references)

$$\begin{aligned} {\varPsi }(x,z) = - \frac{{\varGamma }}{4 \pi } \int _{-\infty }^{+\infty } \ln \left\{ \frac{ \cosh ({\tilde{x}}-{\tilde{x}}_{s}) - \cos ({\tilde{z}} -{{\tilde{\zeta }}} (x_{s}))}{\cosh ({\tilde{x}} - {\tilde{x}}_{s} )- \cos ({\tilde{z}} +\tilde{\zeta }(x_{s}))}\right\} {\frac{d \zeta }{d x}}(x_{s})\;dx_{s}. \end{aligned}$$
(15)

where \( \displaystyle { {\tilde{x}} = {\pi x}/{H}}, \; \tilde{z}= {\pi z}/{H} \) and \( \displaystyle { {\tilde{x}}_s = {\pi x_s}/{H}}\). Hence, for a given interface \(\zeta =\zeta (x)\), the induced specific discharge components \(q_x, q_z\) are obtained by differentiating (15) according to (10). Expressing the cosine and hyperbolic cosine in terms of exponentials and introducing complex notation one finds

$$\begin{aligned} q_x-iq_z = \frac{i {\varGamma }}{2H} \int _{- \infty }^{+\infty } \left( \frac{ e^{{\tilde{x}}_{s}+i {{\tilde{\zeta }}}}}{e^{ {\tilde{x}} + i {\tilde{z}}} - e^{{\tilde{x}}_{s}+ i {{\tilde{\zeta }}}}} - \frac{ e^{{\tilde{x}}_{s}-i {{\tilde{\zeta }}}}}{e^{{\tilde{x}}+ i {\tilde{z}}} - e^{{\tilde{x}}_{s} - i {{\tilde{\zeta }}}}} \right) \frac{d \zeta }{d x} (x_{s}) dx_{s}, \end{aligned}$$
(16)

for any point \((x,z)\in {\varOmega }\), provided \((x,z) \not \in S\), i.e., not chosen on the interface. In (16) and in other integrals to come, \(\zeta \) always denotes \(\zeta (x_s) \). To obtain the specific discharge components at a point of the interface, say at \((x_p,\zeta (x_p))\), we first calculate their value at some point \((x_p,z_p)\), with \(z_p > \zeta (x_p)\) or \(z_p < \zeta (x_p)\), and then pass to the limit \(z_p \downarrow \zeta (x_p)\) or \( z_p \uparrow \zeta (x_p) \).

An expression similar to (16) was used by De Josselin de Jong (1981) to compute the discharge for a specific case: a piecewise linear interface. Here, expression (16) is the starting point of the analysis.

3 Dupuit Approximation

A first main result of this paper is that (16) can be written as the sum of local terms and a new integral expression containing the second-order derivative of \(\zeta \). We show this in Sect. 4 by applying integration by parts to (16). For the horizontal discharge \(q_x\), we find, see also (42),

$$\begin{aligned} q_x(x,z)=q_x^D(x,z)+ \hbox {Re} \{ \hbox {Int} (x,z;\zeta )\} \end{aligned}$$
(17)

where

$$\begin{aligned} q_x^D(x,z) = \left\{ \begin{array}{ll} \quad \displaystyle {-\frac{{\varGamma }}{H}(H-\zeta )\frac{\zeta _x}{1+\zeta _x^2}} &{} \hbox {if} \;\;z<\zeta , \\ \quad \displaystyle {+\frac{{\varGamma }}{H}\zeta \frac{\zeta _x}{1+\zeta _x^2}} &{} \hbox {if} \;\;z>\zeta , \end{array} \right. \end{aligned}$$
(18)

and where Int(\(x,z;\zeta )\) denotes the integral given by (44) and \(\zeta _x=\frac{d\zeta }{dx}\). Later, when introducing time dependence, we have \(\zeta =\zeta (x,t)\). Then \(\zeta _x\) denotes the spatial derivative with respect to x: \(\zeta _x=\frac{\partial \zeta }{\partial x}\). For \(q_z(x,z)\) a similar expression is given in (43). The local term in (17) is the Dupuit approximation or Dupuit discharge. Note that it does not depend on the vertical coordinate z in each fluid. This was used by De Josselin de Jong (1981). In that paper, he assumed \(q_x\) to be constant in z in each fluid, as formulated in (1). Using this assumption, he derived (18) from the following argument. The fluid balance

$$\begin{aligned} \int _0^\zeta q_x(x,z)\;dz+ \int _\zeta ^H q_x(x,z)\; dz =0 \end{aligned}$$
(19)

gives

$$\begin{aligned} \zeta q_{sx} + (H-\zeta )q_{fx}=0. \end{aligned}$$
(20)

The shear flow at the interface (as a result of pressure continuity in Darcy’s law) implies

$$\begin{aligned} q_{fx}-q_{sx}={\varGamma } \frac{\zeta _x}{1+\zeta _x^2}. \end{aligned}$$
(21)

Combining (20) and (21) gives the Dupuit expression (18) with the obvious notation \(q_{fx}=q_x^D(z>\zeta )\) and \(q_{sx}=q_x^D(z<\zeta )\).

3.1 Movement of the Interface

So far, we considered stationary discharges resulting from a stationary fresh–salt distribution: \(\zeta =\zeta (x)\) only. We now introduce the time dependence to determine the evolution of the interface, starting from a given initial (say at \(t=0\)) situation. From now on, we write \(\zeta =\zeta (x,t)\) and consequently all derivatives become partial derivatives.

Let

$$\begin{aligned} Q= Q(x,t) = \int _0^{\zeta (x,t)} \;{\mathbf{q}} \cdot {\mathbf{e}}_x \; dz. \end{aligned}$$
(22)

denote the total discharge of saltwater in the positive x-direction. Inserting (17)–(18) gives

$$\begin{aligned} Q=-\frac{{\varGamma }}{H} \zeta (H-\zeta ) \frac{\zeta _x}{1+\zeta _x^2}+\int _0^\zeta \hbox {Re} \{\hbox {Int}(x,z;\zeta )\}\;dz \end{aligned}$$
(23)

Continuity of saltwater requires the balance equation

$$\begin{aligned} \phi \frac{\partial \zeta }{\partial t} +\frac{\partial Q}{\partial x}=0. \end{aligned}$$
(24)

Combining (23) and (24) gives the evolution equation for the interface

$$\begin{aligned} \phi \frac{\partial \zeta }{\partial t}= \frac{{\varGamma }}{H} \frac{\partial }{\partial x} \left( \zeta (H-\zeta )\frac{\zeta _x}{1+\zeta _x^2}\right) +B(x;\zeta ) \end{aligned}$$
(25)

where

$$\begin{aligned} B(x;\zeta ) =- \frac{\partial }{\partial x} \left( \int _0^\zeta \hbox {Re} \{ \hbox {Int}(x,z;\zeta )\} \; dz \right) \end{aligned}$$
(26)

Equation (25) is solved subject to an initial condition

$$\begin{aligned} \zeta (x,0)=\zeta _0(x) \;\;\hbox {for}\;\; -{\!}\infty<x<+\infty \end{aligned}$$
(27)

where \(\zeta _0{:}{\mathbf{R}} \rightarrow [0,H]\) satisfies certain smoothness conditions.

In the absence of the integral term in (17), i.e., the Dupuit case, the term \(B(x;\zeta )\) drops from Eq. (25) and one is left with the nonlinear, doubly degenerate parabolic equation.

$$\begin{aligned} \phi \frac{\partial \zeta }{\partial t}= \frac{{\varGamma }}{H} \frac{\partial }{\partial x} \left( \zeta (H-\zeta )\frac{\zeta _x}{1+\zeta _x^2}\right) . \end{aligned}$$
(28)

This equation received quite some attention in the mathematical literature. Its solutions behave as indicated in Fig. 1. Corresponding to an initial distribution as sketched in Fig. 1a, two free boundaries emerge in the (x, t)-plane, see Fig. 1b.

Fig. 1
figure 1

a Initial interface distribution. b Corresponding free boundaries in the (x, t)-plane

Full size image

One on the left, \(x=S_1(t)\), separating the regions with only freshwater and fresh/saltwater. And one on the right, \(x=S_2(t)\), separating the regions with fresh/saltwater and saltwater only. Existence, uniqueness, asymptotic behavior for large time and regularity and behavior of the free boundaries have been studied, see, for instance, Duijn and Hilhorst (1987), Van Duijn and Zhang (1988) and Bertsch et al. (1992).

A second main result of this paper concerns the validity of the Dupuit approximation, and consequently of Eq. (28). For this, we estimate the integral term in (17) (or in (42)) for \(q_x\) and in (43) for \(q_z\). The results are given in Sect. 5.

4 Recovery of the Dupuit Discharge

The aim of this section is to derive (17) for \(q_x\) and a similar expression for \(q_z\), both from (16). We start the derivation by assuming that for each \(t>0\), the interface \(\zeta (x,t)\) is continuous in x with a piecewise continuous derivative, i.e., \(\zeta (x,t)\) may have kinks.

Let \((x_p,z_p)\) be a fixed point in \({\varOmega }\) which is either in freshwater (\(z_p > \zeta (x_p,t)\)) or in saltwater (\(z_p < \zeta (x_p,t)\)). At this point \((x_p,z_p)\), we want to construct a new expression for the specific discharge which clarifies the role and structure of the interface more explicitly.

Fig. 2
figure 2

Integration by parts along the interface

Full size image

For computational reasons, we introduce a small positive constant \(\beta \), which we later send toward zero, such that \(\zeta (x,t) \not = z_p \) for \(x_p -\beta< x < x_p + \beta \), see Fig. 2. By continuity of \(\zeta (x,t) \) such a \(\beta \) can always be chosen. While in expression (16) the integration stretches from \(-\infty \) to \( +\infty \), we now split the integral into two parts: one where \(x_s\) runs from \(-\infty \) to \( x_p - \beta \) and one where \(x_s\) runs from \(x_p+\beta \) to \(+\infty \). Thus instead of (16) we consider the sum

$$\begin{aligned} \frac{i {\varGamma }}{2H} \int \limits ^{x_{p} - \beta }_{-\infty } (I_{1} - I_{2} ) \frac{\partial \zeta }{\partial x} (x_{s} , t) dx_{s} + \frac{i {\varGamma }}{2H} \int \limits ^{+\infty }_{x_{p}+\beta } (I_{1}-I_{2}) \frac{\partial \zeta }{\partial x} (x_{s},t) dx_{s}, \end{aligned}$$
(29)

where \(I_1\) and \(I_2\) denote the first and second part of the term between brackets in the integrand in (16). Clearly, the sum (29) tends to (16) as \(\beta \rightarrow 0\).

We treat in detail the integration by parts of the term \(I_1\). The other term \(I_2\) can be dealt with in a similar way.

First we write the integrals containing \(I_1\) in the form

$$\begin{aligned} \frac{i {\varGamma }}{2H} \int \limits ^{x_{p}-\beta }_{-\infty } \frac{ e^{{\tilde{x}}_{s} - {\tilde{x}}_{p} + i ({{\tilde{\zeta }}} - z_{p})}}{1-e^{{\tilde{x}}_{s} - {\tilde{x}}_{p} + i({{\tilde{\zeta }}} - {\tilde{z}}_{p})}} \left. \frac{\partial \zeta }{\partial x} \right| _{x_{s}} dx_{s} - \frac{i {\varGamma }}{2H} \int \limits _{x_{p}+ \beta }^{\infty } \frac{1}{1-e^{{\tilde{x}}_{p} - {\tilde{x}}_{s} +i({\tilde{z}}_{p} - {{\tilde{\zeta }}}) }} \left. \frac{\partial \zeta }{\partial x} \right| _{x_{s}} dx_{s},\nonumber \\ \end{aligned}$$
(30)

where we use the notation \(\left. \frac{\partial \zeta }{\partial x}\right| _{x_s} = \frac{\partial \zeta }{\partial x}(x_s,t)\).

Because in the first term \(x_s -x_p < -\beta \) and in the second term \(x_p-x_s < -\beta \), both the integrands can be considered as the limit of a uniformly convergent series. In fact, we have

$$\begin{aligned} \frac{i{\varGamma }}{2H} \int \limits _{-\infty }^{x_p-\beta } \sum _{n=1}^{\infty } e^{n({\tilde{x}}_s - {\tilde{x}}_p + i({{\tilde{\zeta }}} - {\tilde{z}}_p))} \left. \frac{\partial \zeta }{\partial x}\right| _{x_{s}} dx_s - \frac{i{\varGamma }}{2H} \int \limits _{x_p+\beta }^{ \infty } \sum \limits _{n=0}^{\infty } e^{-n({\tilde{x}}_s - {\tilde{x}}_p + i( \tilde{\zeta }- {\tilde{z}}_p))} \left. \frac{\partial \zeta }{\partial x} \right| _{x_{s}} dx_s.\nonumber \\ \end{aligned}$$
(31)

Both integrals in (31) can be integrated by parts. The first integral in (31) yields

$$\begin{aligned}&\displaystyle {\frac{i{\varGamma }}{2\pi } \sum \limits _{n=1}^{\infty } \frac{1}{n} e^{n(-{{\tilde{\beta }}}+i(\tilde{\zeta }(x_p - \beta ,t) - {\tilde{z}}_p))} \cdot \left. \frac{\zeta _x}{1+i \zeta _x} \right| _{x_{p}-\beta } +}\nonumber \\&\quad \displaystyle { -\frac{i{\varGamma }}{2\pi } \int \limits _{-\infty }^{x_p-\beta } \sum \limits _{n=1}^{ \infty } \frac{1}{n} \left( e^{n({\tilde{x}}_s-{\tilde{x}}_p+ i({{\tilde{\zeta }}} - {\tilde{z}}_p))} \right) \cdot \frac{\partial }{\partial x} \left. \left( \frac{\zeta _x}{1+i \zeta _x}\right) \right| _{x_{s}} dx_s }. \end{aligned}$$
(32)

Using

$$\begin{aligned} \ln (1-u) = - \sum \limits _{n=1}^{\infty } \frac{1}{n} u^{n} \;\; \hbox { when } \; \; |u|<1, \end{aligned}$$
(33)

expression (32) becomes

$$\begin{aligned}&\displaystyle { - \frac{i{\varGamma }}{2\pi } \ln \left( 1-e^{-{{\tilde{\beta }}}+i({{\tilde{\zeta }}}(x_p-\beta ,t) -{\tilde{z}}_p)}\right) \cdot \left. \frac{\zeta _x}{1+i\zeta _x} \right| _{x_{p}-\beta }} \nonumber \\&\quad \displaystyle { + \frac{i{\varGamma }}{2 \pi } \int \limits _{-\infty }^{x_p-\beta } \ln \left( 1- e^{{\tilde{x}}_s-{\tilde{x}}_p+i({{\tilde{\zeta }}}-{\tilde{z}}_p)}\right) \cdot \frac{\partial }{ \partial x} \left. \left( \frac{\zeta _x}{1+i\zeta _x} \right) \right| _{x_{s}} dx_s.} \end{aligned}$$
(34)

To apply the same technique to the second integral in (31), we integrate the first term of the series separately, i.e., the term containing \(n=0\). Then we integrate by parts and substitute (33). The result is

$$\begin{aligned}&\displaystyle {-\frac{i{\varGamma }}{2H} \zeta (\infty ,t)+\frac{i{\varGamma }}{2H} \zeta (x_p+\beta ,t) +\frac{i{\varGamma }}{2 \pi } \ln \left( 1-e^{-{{\tilde{\beta }}}-i({{\tilde{\zeta }}}(x_p+\beta ,t)-{\tilde{z}}_p)}\right) \left. \frac{\zeta _x}{1+i\zeta _x} \right| _{x_{p}+\beta } } \nonumber \\&\quad \displaystyle {+\frac{i {\varGamma }}{2 \pi } \int \limits _{x_p+\beta }^{+\infty } \ln \left( 1-e^{-({\tilde{x}}_s - {\tilde{x}}_p+i({{\tilde{\zeta }}} - {\tilde{z}}_p))}\right) \frac{\partial }{\partial x} \left. \left( \frac{\zeta _x}{1+i\zeta _x} \right) \right| _{x_{s}} dx_s}. \end{aligned}$$
(35)

Next, we let \(\beta \rightarrow 0 \) in (34) and (35). Using the identity

$$\begin{aligned} \begin{array}{lll} \displaystyle { \ln (1-e^{\pm i \alpha }) = \ln \left( 2 \left| \sin \frac{1}{2} \alpha \right| \right) \pm i g(\alpha ), }\\ \displaystyle { \hbox { where } \;\;\;g(\alpha ) = \left\{ \begin{array}{ll} \displaystyle {\frac{\alpha }{2}-\frac{\pi }{2} } \;\hbox { if } &{}0< \alpha< 2 \pi \\ \displaystyle {\frac{\alpha }{2}+\frac{\pi }{2} } \;\hbox { if } &{}-2\pi< \alpha < 0, \end{array} \right. } \end{array} \end{aligned}$$
(36)

we find, when adding (34) and (35),

$$\begin{aligned}&\displaystyle {\frac{i{\varGamma }}{2H} ( \zeta (x_p,t) - \zeta (\infty ,t))} \nonumber \\&\quad \displaystyle { +\frac{i {\varGamma }}{2 \pi } \ln \left( 2 \left| \sin \frac{1}{2} ( {{\tilde{\zeta }}}(x_p,t)-{\tilde{z}}_p)\right| \right) \cdot \left( \left. \frac{\zeta _x}{1+i\zeta _x} \right| _{x_{p}^{+}} - \left. \frac{\zeta _x}{1+i\zeta _x} \right| _{x_{p}^{-}} \right) }\nonumber \\&\quad \displaystyle { + \frac{{\varGamma }}{4H} (\zeta (x_p,t) - z_p \pm H) \left( \left. \frac{\zeta _x}{1+i\zeta _x} \right| _{x_{p}^{+}} + \left. \frac{\zeta _x}{1+i\zeta _x} \right| _{x_{p}^{-}} \right) } \nonumber \\&\quad \displaystyle { +\frac{i {\varGamma }}{2 \pi } \;\hbox {PV} \int \limits _{-\infty }^{\infty } G(x_s,x_p,\zeta ,z_p) \frac{\partial }{\partial x} \left( \left. \frac{\zeta _x}{1+i\zeta _x} \right) \right| _{x_{s}} dx_s.} \end{aligned}$$
(37)

where

$$\begin{aligned} G(x_s,x_p,\zeta ,z_p) = \left\{ \begin{array}{lcr} \ln \left( 1- e^{+({\tilde{x}}_s - {\tilde{x}}_p + i ({{\tilde{\zeta }}} - {\tilde{z}}_p))}\right) &{}\hbox {for}&{} x_s<x_p, \\ \ln \left( 1- e^{-({\tilde{x}}_s - {\tilde{x}}_p + i ({{\tilde{\zeta }}} - {\tilde{z}}_p))}\right) &{}\hbox {for}&{} x_s>x_p. \end{array} \right. \end{aligned}$$
(38)

Here \(\zeta _x| _{x_p^\pm } = \lim _{\beta \rightarrow 0} \zeta _x (x_p \pm \beta )\) and PV\(\int \limits _{-\infty }^{\infty } \ldots dx_s\) denotes the principal value of the integral at \(x_p\). In (37), and in other expressions to come, we use the plus-sign (\(+H\)) when \((x_p,z_p)\) is chosen in the freshwater \((z_p > \zeta (x_p,t))\) and we use the minus-sign (\(-H\)) when \((x_p,z_p)\) is chosen in the saltwater \((z_p < \zeta (x_p,t))\).

In a similar fashion, we rewrite the integrals containing the term \(I_2\) in (29). The result is (skipping all details)

$$\begin{aligned}&\displaystyle { \frac{i{\varGamma }}{2H} ( \zeta (x_p,t) - \zeta (\infty ,t))} \nonumber \\&\quad \displaystyle { + \frac{i {\varGamma }}{2 \pi } \ln \left( 2 \left| \sin \frac{1}{2} ( {{\tilde{\zeta }}}(x_p,t)+{\tilde{z}}_p)\right| \right) \cdot \left( \left. \frac{\zeta _x}{1-i\zeta _x} \right| _{x_{p}^{+}} - \left. \frac{\zeta _x}{1-i\zeta _x} \right| _{x_{p}^{-}} \right) }\nonumber \\&\quad \displaystyle {+ \frac{{\varGamma }}{4H} (H-\zeta (x_p,t)-z_p) \left( \left. \frac{\zeta _x}{1-i\zeta _x} \right| _{x_{p}^{+}} + \left. \frac{\zeta _x}{1-i\zeta _x} \right| _{x_{p}^{-}} \right) } \nonumber \\&\quad \displaystyle {+ \frac{i {\varGamma }}{2 \pi }\;\hbox {PV} \int \limits _{-\infty }^{\infty } G(x_s,x_p,-\zeta ,z_p) \frac{\partial }{\partial x} \left( \left. \frac{\zeta _x}{1-i\zeta _x} \right) \right| _{x_{s}} dx_s.} \end{aligned}$$
(39)

The desired expression for the discharge is obtained after subtracting (37) and (39), i.e.,

$$\begin{aligned} (q_x - i q_z)|_{(x_p,z_p)} = (37) - (39). \end{aligned}$$
(40)

Equation (40) is a general expression for the components \({q}_x\) and \({q}_z\) of the specific discharge at an arbitrary point \((x_p,z_p)\) in the aquifer. From this equation, a number of important conclusions can be drawn. First of all, it gives almost directly the shear flow at the interface. This follows from the choice of the sign in (37), as we shall see below. Secondly, it gives explicitly the influence of a jump in the derivative \( \zeta _x \) at \(x=x_p\). Having such a discontinuity, expression (37) shows that at the interface \((z_p \rightarrow \zeta (x_p,t) )\), the components of the specific discharge become infinite, as if the fluids want to smooth out this discontinuity. Thirdly, it shows that the influence of the expressions

$$\begin{aligned} \frac{\partial }{\partial x}\left( \frac{\zeta _x}{1\pm i \zeta _x}\right) , \end{aligned}$$

which are related to the curvature of the interface, is accounted for by multiplying these terms by the weight function G and by integrating the result along the bottom of the aquifer.

At a point \((x_p,z_p)\) where the corresponding \(\zeta (x_p,t)\) is smooth, with \(\displaystyle {\left. \zeta _x \right| _{x_{p}^{+}} = \left. \zeta _x \right| _{x_{p}^{-}}}\), Eq. (40) reduces to

$$\begin{aligned}&\displaystyle {q_x - i q_z } \nonumber \\&\quad \displaystyle {= \frac{{\varGamma }}{2H} (\zeta (x_p,t) - z_p \pm H) \left. \frac{\zeta _x}{1+i\zeta _x} \right| _{x_{p}} + \frac{{\varGamma }}{2H} (\zeta (x_p,t) + z_p - H) \left. \frac{\zeta _x}{1-i\zeta _x} \right| _{x_{p}} } \nonumber \\&\qquad \displaystyle { +\frac{i {\varGamma }}{2 \pi }\;\hbox {PV} \int \limits _{-\infty }^{\infty } G(x_s,x_p,+\zeta ,z_p) \frac{\partial }{\partial x} \left( \left. \frac{\zeta _x}{1+i\zeta _x}\right) \right| _{x_{s}} dx_s } \nonumber \\&\qquad \displaystyle { -\frac{i{\varGamma }}{2\pi }\;\hbox {PV}\int \limits _{-\infty }^{\infty } G(x_s,x_p,-\zeta ,z_p) \frac{\partial }{\partial x} \left( \left. \frac{\zeta _x}{1-i\zeta _x} \right) \right| _{x_{s}} dx_s,} \end{aligned}$$
(41)

which implies for the discharges (dropping the subscript p)

$$\begin{aligned} q_x(x,z)= \pm \frac{{\varGamma }}{2} \frac{\zeta _x}{1+\zeta _x^2} - \frac{{\varGamma }}{2H}(H-2\zeta ) \frac{\zeta _x}{1+\zeta _x^2} + \hbox {Re}\{\hbox {Int}(x,z;\zeta )\}, \end{aligned}$$
(42)

and

$$\begin{aligned} q_z(x,z)= \pm \frac{{\varGamma }}{2}\frac{\zeta _x^2}{1+\zeta _x^2} + \frac{{\varGamma }}{2H}(H-2z) \frac{\zeta _x^2}{1+\zeta _x^2} - \hbox {Im}\{\hbox {Int}(x,z;\zeta )\}. \end{aligned}$$
(43)

where Int(\(x,z;\zeta \)) is given by

$$\begin{aligned} \hbox {Int}(x,z;\zeta )= & {} i\frac{{\varGamma }}{2\pi } \;\hbox {PV}\int _{-\infty }^{+\infty } G(x_s,x,\zeta (x_s,t),z) \frac{\partial }{\partial x} \left. \left( \frac{\zeta _x}{1+i\zeta _x}\right) \right| _{x_s} \; dx_s \nonumber \\&-i\frac{{\varGamma }}{2\pi } \;\hbox {PV}\int _{-\infty }^{+\infty } G(x_s,x,-\zeta (x_s,t),z) \frac{\partial }{\partial x} \left. \left( \frac{\zeta _x}{1-i\zeta _x}\right) \right| _{x_s} \; dx_s. \end{aligned}$$
(44)

Expression (42) is the desired expression that we discussed in Sect. 2, see (17) and (18). The pointwise or local terms are the horizontal Dupuit discharges. Likewise expression (36) is written as

$$\begin{aligned} q_z(x,z)=q_z^D(x,z)-\hbox {Im}\{\hbox {Int}(x,z;\zeta )\}, \end{aligned}$$
(45)

where the vertical Dupuit discharge is given by

$$\begin{aligned} q_z^D(x,z) = \left\{ \begin{array}{ll} \displaystyle {-\frac{{\varGamma }}{H}z \frac{\zeta ^2_x}{1+\zeta _x^2}} &{} \hbox {if} \;\;z<\zeta , \\ \displaystyle {+\frac{{\varGamma }}{H}(H-z) \frac{\zeta ^2_x}{1+\zeta _x^2}} &{} \hbox {if} \;\;z>\zeta . \end{array} \right. \end{aligned}$$
(46)

While div q \(=0\) in \({\varOmega }\), this does not hold for q \(^D\). A straightforward differentiation gives

$$\begin{aligned} \hbox {div }{\mathbf{q}}^D=\left\{ \begin{array}{ll} \displaystyle {-\frac{{\varGamma }}{H} (H-\zeta ) \frac{\partial }{\partial x} \left( \frac{\zeta _x}{1+\zeta _x ^2}\right) } &{} \hbox {if}\;\; z<\zeta ,\\ \displaystyle {+ \frac{{\varGamma }}{H}\zeta \frac{\partial }{\partial x}\left( \frac{\zeta _x}{1+\zeta _x ^2}\right) }&{} \hbox {if} \;\;z>\zeta . \end{array} \right. \end{aligned}$$
(47)

Note that the Dupuit discharges do give the correct shear flow at the interface [see also (21)]. Letting \(z_p\rightarrow \zeta (x_p)\) from above and from below yields the same integral contribution in (37). Hence, at \(z=\zeta (x)\) we find

$$\begin{aligned}{}[q_x] = \left[ q_x^D\right] = q_{fx}^D-q_{sx}^D={\varGamma } \frac{\zeta _x}{1+\zeta _x ^2}, \end{aligned}$$
(48)

and

$$\begin{aligned}{}[q_z] = \left[ q_z^D\right] = q_{fz}^D-q_{sz}^D={\varGamma } \frac{\zeta ^2_x}{1+\zeta _x ^2}. \end{aligned}$$
(49)

At points where \(\zeta _x=0\), for instance when only freshwater is present (\(\zeta =0\)) or when only saltwater is present (\(\zeta =H\)), the local Dupuit terms vanish from (42) and (43). At such points, the discharges are given by the integral terms only, which is in agreement with the findings of De Josselin de Jong (1981).

5 Validity of the Dupuit Discharge

Yortsos (1995) wrote a fundamental paper on the validity of the Dupuit approximation by considering the scaling:

$$\begin{aligned} z{:}=\frac{z}{H}\;\;\hbox {and}\;\; x{:}=\frac{x}{L}, \end{aligned}$$
(50)

where L is a characteristic horizontal length scale. Introducing

$$\begin{aligned} \varepsilon = \frac{H}{L} \end{aligned}$$
(51)

as a small parameter, he was able to recover the Dupuit approximation by applying an asymptotic expansion in terms of \(\varepsilon ^2\). In his paper, Yortsos considered more general cases as we do here.

In expressions (42) and (43) the factor \(1+\zeta _x^2\) appears in the denominator. Applying scaling rules (50) and (51), with

$$\begin{aligned} u{:}=\frac{\zeta }{H} \end{aligned}$$
(52)

gives \(1+\varepsilon ^2 u_x^2\) as denominator. Hence, in the expansion in terms of \(\varepsilon \) (or \(\varepsilon ^2\)), this factor is removed from the expressions. We apply scaling (50)–(52) in Sect. 6 when considering the case of flat interfaces \((\varepsilon<<1)\). In this section, we apply a more subtle approach in which we keep the influence of the denominator. We do this by analyzing (44). We show below in detail how this works for its real part, i.e., for \(q_x\). To obtain the real parts of (44), we first note that

$$\begin{aligned} \displaystyle \hbox {Int}(x,z;\zeta )= & {} +\frac{{\varGamma }}{2\pi } \;\hbox {PV}\int _{-\infty }^{+\infty } G(x_s,x,+\zeta ,z)\frac{\partial }{\partial x} \left( \frac{i\zeta _x+\zeta _x^2}{1+\zeta _x^2}\right) \; dx_s \nonumber \\&\displaystyle -\frac{{\varGamma }}{2\pi } \;\hbox {PV} \int _{-\infty }^{+\infty } G(x_s,x,-\zeta ,z)\frac{\partial }{\partial x} \left( \frac{i\zeta _x-\zeta _x^2}{1+\zeta _x^2}\right) \; dx_s, \end{aligned}$$
(53)

which we write as

$$\begin{aligned} \displaystyle \hbox {Int}(x,z;\zeta )= & {} \frac{i{\varGamma }}{2\pi } \;\hbox {PV}\int _{-\infty }^{+\infty } \omega _-(x_s,x,\zeta ,z)\frac{\partial }{\partial x} \left( \frac{\zeta _x}{1+\zeta _x^2}\right) \; dx_s \nonumber \\&\displaystyle +\frac{{\varGamma }}{2\pi } \;\hbox {PV}\int _{-\infty }^{+\infty } \omega _+(x_s,x,\zeta ,z)\frac{\partial }{\partial x} \left( \frac{\zeta _x^2}{1+\zeta _x^2}\right) \; dx_s, \end{aligned}$$
(54)

where

$$\begin{aligned} \omega _\pm (x_s,x,\zeta ,z)=G(x_s,x,+\zeta ,z)\pm G(x_s,x,-\zeta ,z). \end{aligned}$$
(55)

Hence

$$\begin{aligned} \displaystyle \hbox {Re}\{\hbox {Int}(x,z{:}\zeta )\}= & {} -\frac{{\varGamma }}{2\pi }\;\hbox {PV}\int _{-\infty }^{+\infty }\hbox {Im}\{\omega _-(x_s,x,\zeta ,z)\}\frac{\partial }{\partial x} \left( \frac{\zeta _x}{1+\zeta _x^2}\right) \; dx_s\nonumber \\&\quad \displaystyle + \frac{{\varGamma }}{2\pi }\;\hbox {PV}\int _{-\infty }^{+\infty }\hbox {Re}\{\omega _+(x_s,x,\zeta ,z) \} \frac{\partial }{\partial x} \left( \frac{\zeta _x^2}{1+\zeta _x^2}\right) \; dx_s \nonumber \\=: & {} I_-+I_+. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;. \end{aligned}$$
(56)

We estimate the kernels Im\(\{\omega _-\}\) and Re\(\{\omega _+\}\) in several steps.

Step 1 First consider \(\omega _-\). Using (38) in (55) gives

$$\begin{aligned} \omega _-(x_s,x,\zeta ,z) = \left\{ \begin{array}{l} \displaystyle {\ln \left( \frac{1-e^{+(\tilde{x_s}-\tilde{x})-i\tilde{z}+i{\tilde{\zeta }}}}{1-e^{+(\tilde{x_s}-\tilde{x})-i\tilde{z}-i{\tilde{\zeta }}}}\right) }\;\;\;\;\;\;x_s<x,\\ \displaystyle {\ln \left( \frac{1-e^{-(\tilde{x_s}-\tilde{x})+i\tilde{z}-i{\tilde{\zeta }}}}{1-e^{-(\tilde{x_s}-\tilde{x})+i\tilde{z}+i{\tilde{\zeta }}}}\right) }\;\;\; \;\;\; x_s>x. \end{array} \right. \end{aligned}$$
(57)

Note that, except for the sign of \((\tilde{x_s}-\tilde{x})\), \(\omega _-\) for \(x_s<x\) and for \(x_s>x\) are each other complex conjugate. The structure of \(\omega _-\) is

$$\begin{aligned} \omega _-=\ln \frac{T}{B} =\ln \left| \frac{T}{B}\right| + i\;\hbox {arg}\;\frac{T}{B} \end{aligned}$$

and hence

$$\begin{aligned} \hbox {Im} \{ \omega _- \} =\hbox {arg}\; T-\hbox {arg} \;B. \end{aligned}$$
(58)

Similarly

$$\begin{aligned} \hbox {Re}\{\omega _+\}=\ln (|T|\cdot |B|)=\ln |T|+\ln |B| \end{aligned}$$
(59)

In (58) and (59), we have

$$\begin{aligned} T=\left\{ \begin{array}{l} 1-e^{+({\tilde{x}}_s-{\tilde{x}})-i{\tilde{z}}+i{{\tilde{\zeta }}}}\;\;\;\;\; x_s<x,\\ 1-e^{-({\tilde{x}}_s-{\tilde{x}})+i{\tilde{z}}-i{{\tilde{\zeta }}}}\;\;\;\;\; x_s>x, \end{array} \right. \end{aligned}$$
(60)

and

$$\begin{aligned} B=\left\{ \begin{array}{l} 1-e^{+({\tilde{x}}_s-{\tilde{x}})-i{\tilde{z}}-i{{\tilde{\zeta }}}}\;\;\;\;\; x_s<x,\\ 1-e^{-({\tilde{x}}_s-{\tilde{x}})+i{\tilde{z}}+i{{\tilde{\zeta }}}}\;\;\;\;\; x_s>x, \end{array} \right. \end{aligned}$$
(61)

Step 2 Let \(x_s<x\). Recall that \({\tilde{z}} =\frac{\pi z}{H}\), etc... Let \(a=e^{(\tilde{x_s}-\tilde{x})}\). Clearly \(0<a<1\). Then the expressions for T and B can be written as

$$\begin{aligned} T=1+a \; e^{i(\pi -{\tilde{z}}+{{\tilde{\zeta }}})}\;\;\;\hbox {and}\;\;\; B=1+a \; e^{i(\pi -{\tilde{z}}-{{\tilde{\zeta }}})}. \end{aligned}$$
(62)

In the complex plane, T and B are points on the circle C, see Fig. 3, with radius a and center (1,0). We make use of this figure to estimate Im\(\{\omega _-\}\) and Re\(\{\omega _+\}\).

Fig. 3
figure 3

Points T and B on the circle C in the complex plane

Full size image

-

Step 3 Bound for Im\(\{\omega _-\}\).

With reference to Fig. 3, we observe that the maximum of \(|\hbox {arg} \;T|\) (or \(|\hbox {arg} \;B|\)) is attained when T (or B) is at the points K or M. The same holds for \(x_s>x\) when \(a=e^{-({\tilde{x}}_s-{\tilde{x}})}\). Hence for all \(x, x_s\in \) R we have

$$\begin{aligned} |\hbox {Im}\{\omega _-(x_s,x,\zeta ,z)\}|\le 2 \arctan \frac{a}{\sqrt{1-a^2}}, \end{aligned}$$
(63)

where \(a=e^{-|\tilde{x_s}-\tilde{x}|}\).

Step 4 Bound for Re{\(\omega _+\)}.

Again we use Fig. 3. Clearly

$$\begin{aligned} 1-a\le |T|, |B| \le 1+a. \end{aligned}$$

Using the concavity of \(\ln \), we have

$$\begin{aligned} |\ln |T|,\ln |B||\le |\ln (1-a)|. \end{aligned}$$

Using (59) we obtain for all \(x,x_s\in \) R

$$\begin{aligned} |\hbox { Re}\{\omega _+(x_x,x,\zeta ,z)\}|\le 2|\ln (1-a)|, \end{aligned}$$
(64)

where again \(a=e^{-|\tilde{x_s}-\tilde{x}|}\). Note that estimates (63) and (64) do not depend on the position of the points T and B on the circle C. Therefore, they are uniform in \(z\in [0,H]\) and also uniform with respect to the structure of \(\zeta \).

With \(a=e^{-|\tilde{x_s}-\tilde{x}|}\), let

$$\begin{aligned} f(x_s-x){:}=2 \arctan \frac{a}{\sqrt{1-a^2}} \end{aligned}$$
(65)

and

$$\begin{aligned} g(x_s-x){:}= 2|\ln (1-a)|. \end{aligned}$$
(66)

Then we have obtained the estimate, recall (56) and dropped from now on the PV in the notation,

$$\begin{aligned} \frac{2\pi }{{\varGamma }} |\hbox {Re} \{ \hbox {Int} (x,z;\zeta )\}|\le & {} \int _{-\infty }^{+\infty } f(x_s-x) \left| \frac{\partial }{\partial x} \left( \frac{\zeta _x}{1+\zeta ^2_x}\right) \right| \; dx_s \nonumber \\&+ \int _{-\infty }^{+\infty } g(x_s-x) \left| \frac{\partial }{\partial x} \left( \frac{\zeta _x^2}{1+\zeta ^2_x}\right) \right| \; dx_s \end{aligned}$$
(67)

for all \(x\in {\mathbf{R}}\) and \(0\le z\le H\). The kernels f and g are integrable in R since for each \(x\in \) R

$$\begin{aligned} \int _{-\infty }^{+\infty } f(x_s-x)\; dx_s= & {} 2 \int _{x}^{+\infty }f(x_s-x)\; dx_s\nonumber \\= & {} \frac{4H}{\pi } \int _0^1 \left( \frac{1}{a} \arctan \frac{a}{\sqrt{1-a^2}}\right) \;da \le 2H \end{aligned}$$
(68)

and

$$\begin{aligned} \int _{-\infty }^{+\infty } g(x_s-x)\; dx_s = 2 \int _{x}^{+\infty }g(x_s-x)\; dx_s=\frac{4H}{\pi } \int _0^1 \frac{1}{a} | \ln (1-a)|\;da = \frac{4H}{\pi }c\nonumber \\ \end{aligned}$$
(69)

where c is a positive constant \((0<c<2\ln 2+1)\). Furthermore, both kernels have the same asymptotic behavior for large \(|x_s-x|\). Let \(|x_s-x| \ge H\). Then \(a\le e^{-\pi } \approx \frac{1}{20}\). For such small a, we have

$$\begin{aligned} 2 \arctan \frac{a}{\sqrt{1-a^2}}\approx 2a \;\;\;\rightarrow \;\;\; f(x_s-x) \approx 2 e^{-\frac{\pi }{H}|x_s-x|} \end{aligned}$$
(70)

and

$$\begin{aligned} 2 |\ln (1-a)| \approx 2a \;\;\;\rightarrow \;\;\; g(x_s-x) \approx 2 e^{-\frac{\pi }{H}|x_s-x|} \end{aligned}$$
(71)

Using the properties of f and g in (67), we are able to formulate a criterion with respect to the shape of the interface \(\zeta \) for which the Dupuit approximation holds. The analysis becomes more transparent if we first apply the scaling

$$\begin{aligned} u{:}= \frac{\zeta }{H}, \;\; x{:}= \frac{x}{H}\;\;\hbox {and} \;\; z{:}=\frac{z}{H}. \end{aligned}$$
(72)

Then inequality (67) becomes

$$\begin{aligned} \frac{2\pi }{{\varGamma }} |\hbox {Re} \{ \hbox {Int} (x,z;u)\}|\le & {} \int _{-\infty }^{+\infty } f(x_s-x) \left| \frac{\partial }{\partial x} \left( \frac{u_x}{1+u^2_x}\right) \right| \; dx_s \nonumber \\&+ \int _{-\infty }^{+\infty } g(x_s-x) \left| \frac{\partial }{\partial x} \left( \frac{u_x^2}{1+u^2_x}\right) \right| \; dx_s, \end{aligned}$$
(73)

where in f and g we now have \(a=e^{-\pi |x_s-x|}\).

Claim

Fix \(x_0\in \) R. If

$$\begin{aligned} (\text {i})&\displaystyle \frac{\partial ^2 u}{\partial x^2}\;\;\hbox {is integrable in }{} \mathbf{R}\;\;\left( \hbox {i.e} \int _{-\infty }^{+\infty } \left| \frac{\partial ^2 u}{\partial x^2} \right| \; dx<K \;\hbox {for some} \; K>0\right) ,\nonumber \\ (\text {ii})&\displaystyle \left| \frac{\partial ^2 u}{\partial x^2} \right| \le \delta<<1 \;\; \hbox {for}\;\; |x-x_0|<1, \end{aligned}$$
(74)

then the Dupuit approximation holds at \(x=x_0\).

Demonstration

We first estimate in a straightforward way

$$\begin{aligned} \displaystyle \left| \frac{\partial }{\partial x}\left( \frac{ u_x}{1+u_x^2}\right) \right| , \left| \frac{\partial }{\partial x} \left( \frac{ u^2_x}{1+u_x^2}\right) \right| \le \left| \frac{\partial ^2 u}{\partial x^2} \right| . \end{aligned}$$

Using this in inequality (73), we obtain at \(x=x_0\) and for all \(0 \le z \le 1\)

$$\begin{aligned} \displaystyle \frac{2\pi }{{\varGamma }} |\hbox {Re} \{ \hbox {Int}(x_0,z;u)| \displaystyle\le & {} \int _{-\infty }^{+\infty } f(x_s-x_0) \left| \frac{\partial ^2 u}{\partial x^2} \right| \;dx_s+ \int _{-\infty }^{+\infty } g(x_s-x_0) \left| \frac{\partial ^2 u}{\partial x^2} \right| \;dx_s\nonumber \\&={:}&\hbox {I}_f+\hbox {I}_g \end{aligned}$$
(75)

Writing I\(_f\) as

$$\begin{aligned} \displaystyle \hbox {I}_f = \int _{-\infty }^{x_0-1} f(x_s-x_0) \left| \frac{\partial ^2 u}{\partial x^2} \right| \;dx_s + \int _{x_0-1}^{x_0+1} \cdots \; + \int _{x_0+1}^{+\infty } \cdots \end{aligned}$$

we estimate

$$\begin{aligned} \hbox {I}_f \le f(-1) \int _{-\infty }^{x_0-1}\left| \frac{\partial ^2 u}{\partial x^2} \right| \;dx_s+\delta \int _{x_0-1}^{x_0+1} f(x_s-x)\; dx_s + f(1) \int _{x_0+1}^{+\infty } \left| \frac{\partial ^2 u}{\partial x^2} \right| \;dx_s \end{aligned}$$

where we used (ii) and the monotonicity of \(f(x_s-x_0)\). Since \(f(-1)=f(1)\) we further have

$$\begin{aligned} \hbox {I}_f \le \delta \int _{-\infty }^{+\infty } f(x_s-x)\; dx_s + f(1) \int _{-\infty }^{+\infty } \left| \frac{\partial ^2 u}{\partial x^2} \right| \;dx_s \end{aligned}$$
(76)

Using \(\int _{-\infty }^{+\infty } f(x_s-x)\; dx_s\le 2\) (apply(68) after scaling), \(\int _{-\infty }^{+\infty } \left| \frac{\partial ^2 u}{\partial x^2} \right| \;dx_s \le K\) (see (i) in Claim) and (70) we find

$$\begin{aligned} \hbox {I}_f \le 2\delta +f(1)K \approx 2\delta +2e^{-\pi } K. \end{aligned}$$
(77)

Similarly we find for I\(_g\)

$$\begin{aligned} \hbox {I}_g \le \frac{4c}{\pi }\delta +g(1)K \approx \frac{4c}{\pi }\delta +2e^{-\pi } K. \end{aligned}$$
(78)

Hence

$$\begin{aligned} \frac{1}{{\varGamma }} |\hbox {Re} \{ \hbox {Int} (x,z;u)\}| \displaystyle\le & {} \frac{1}{2\pi }(\hbox {I}_f+\hbox {I}_g)\nonumber \\ \displaystyle\approx & {} \frac{1}{\pi } \left( \left( 1+\frac{2c}{\pi }\right) \delta +2 e^{-\pi } K\right)<<1 \end{aligned}$$
(79)

provided K is not too large. If K is large we need to extend the interval in (ii) of the Claim: \(\left| \frac{\partial ^2 u}{\partial x^2} \right| \le \delta<<1\) for \(|x-x_0| <2\), say. This would give the factor \(e^{-2\pi }\) in estimate (79). The right-hand side of (79) must be compared to the Dupuit discharge \(q^D_x\) from (18) after scaling (72)

$$\begin{aligned} \frac{1}{{\varGamma }} q_x^D = \left\{ \begin{array}{ll} \displaystyle -(1-u) \frac{u_x}{1+u_x^2} &{} \hbox {if} \;\; z<u,\\ \displaystyle u \frac{u^2_x}{1+u_x^2}&{} \hbox {if} \;\; z>u, \end{array}\right. \end{aligned}$$
(80)

which is assumed O(1). This concludes the demonstration.

For the vertical discharge component \(q_z\), one can proceed as above. Similar estimates are obtained and the Claim holds for \(q_z\) as well. Details are omitted.

Example

To clarify the conditions of the claim, we construct the following example. Let \(0<\mu <\frac{1}{2}\), \(\alpha >1\) and drop the time dependence from the interface height : \(u=u(x)\). Then consider

$$\begin{aligned} u(x)=\left\{ \begin{array}{ll} \displaystyle \frac{1}{2} +\frac{1}{\alpha } \left( \frac{1}{2}-\mu \right) x &{} \hbox {for} \;\; 0< x \le \alpha ,\\ \displaystyle 1-\mu e^{-\frac{1}{\alpha \mu }(\frac{1}{2} -\mu )(x-\alpha )} &{} \hbox {for} \;\; x> \alpha , \end{array} \right. \end{aligned}$$
(81)

and

$$\begin{aligned} u(x)=1-u(-x)\;\;\; \hbox {for}\;\;\; x<0, \end{aligned}$$
(82)

see Fig. 4.

Note that \(u\in C^1({\mathbf{R}}), u\) is strictly increasing with \(u(-\infty )=0, u(0)= \frac{1}{2}\) and \(u(+\infty )= 1\), \(\frac{\partial ^2 u}{\partial x^2} \le (\ge )0\) for \(x>(<)0\) and \(\frac{du}{dx} =\frac{1}{\alpha }(\frac{1}{2}-\mu )\) in the interval \((-\alpha ,\alpha )\).

Fig. 4
figure 4

Example interface (81)–(82) satisfying the conditions of the Claim

Full size image

In this example, the conditions of the Claim, and hence the validity of Dupuit, hold for each point in the interval \((\alpha -1,-\alpha +1)\). In the larger interval \((-\alpha ,\alpha )\) we have \(\frac{\partial ^2 u}{\partial x^2}=0\) and

$$\begin{aligned} \int _{-\infty }^{+\infty } \left| \frac{\partial ^2 u}{\partial x^2}\right| \; dx=-2 \int _{0}^{+\infty } \frac{\partial ^2 u}{\partial x^2} \; dx= -2 \int _\alpha ^{+\infty } \frac{\partial ^2 u}{\partial x^2} \; dx= 2\frac{du}{dx}(\alpha )=\frac{1}{\alpha }(1-2\mu )=K \end{aligned}$$

This example also shows that for the Dupuit approximation to hold, it is not necessary to have very flat interfaces. If \(a=\frac{3}{2}\), Dupuit holds in the interval \((-\frac{1}{2}, \frac{1}{2})\) where \(\frac{du}{dx}= \frac{2}{3}(\frac{1}{2}-\mu )\). It is therefore important to keep the factor \(1+\zeta _x^2\) in the denominator of the Dupuit discharges (18), as suggested by de Josselin de Jong. In the next section, we consider the case of flat interfaces.

6 Flat Interfaces

We return to the scaling (50)–(52) introduced by Yortsos (1995). The assumption \(\varepsilon<< 1\) reflects indeed flat interfaces, since

$$\begin{aligned} \frac{\partial \zeta }{\partial x}=\varepsilon \frac{\partial u}{\partial x}. \end{aligned}$$
(83)

In the scaled variables, the Dupuit discharge (2.15) becomes

$$\begin{aligned} \displaystyle \frac{1}{{\varGamma }}q_x^D = \left\{ \begin{array}{lll} \displaystyle { -(1-u)\frac{\varepsilon u_x}{1+\varepsilon ^2u_x^2}}&{}\quad z<u\\ \displaystyle {u\frac{\varepsilon u_x}{1+\varepsilon ^2 u_x^2}}&{}\quad z>u \end{array} \right. \end{aligned}$$
(84)

Note that \(q_x^D/{\varGamma } = O(\varepsilon )\). We show below that in the right-hand side of inequality (67), the f-term is \(O(\varepsilon ^2)\) and the g-term \(O(\varepsilon ^3)\). Applying (50)–(52) to (67) gives for \(x\in {\mathbf{R}}\) and \(0\le z\le 1\)

$$\begin{aligned}&\displaystyle \frac{2\pi }{{\varGamma }}|\hbox {Re}\{\hbox {Int}(x,z;u\}| \nonumber \\&\quad \le \displaystyle {\varepsilon \int _{-\infty }^{+\infty } f_\varepsilon (x_s-x)) \left| \frac{\partial }{\partial x} \left( \frac{ u_x}{1+\varepsilon ^2u_x^2}\right) \right| \; dx_s}\nonumber \\&\qquad +\,\displaystyle {\varepsilon ^2 \int _{-\infty }^{+\infty } g_\varepsilon (x_s-x)) \left| \frac{\partial }{\partial x} \left( \frac{ u^2_x}{1+\varepsilon ^2u_x^2}\right) \right| \; dx_s} \end{aligned}$$
(85)

where \(f_\varepsilon \) is given by (65) and \(g_\varepsilon \) by (66), but where now

$$\begin{aligned} a=e^{-\frac{\pi }{\varepsilon } |x_s-x|}. \end{aligned}$$
(86)

Since

$$\begin{aligned} \left| \frac{\partial }{\partial x} \left( \frac{ u_x}{1+\varepsilon ^2u_x^2}\right) \right| =\left| \frac{(1-\varepsilon ^2 u^2_x)}{(1+\varepsilon ^2u_x^2)^2} \frac{\partial ^2 u}{\partial x^2} \right| \le \left| \frac{\partial ^2 u}{\partial x^2} \right| \end{aligned}$$

and

$$\begin{aligned} \left| \frac{\partial }{\partial x} \left( \frac{ u^2_x}{1+\varepsilon ^2u_x^2}\right) \right| =\left| \frac{2 u_x}{(1+\varepsilon ^2u_x^2)^2} \frac{\partial ^2 u}{\partial x^2} \right| \le 2\left| \frac{\partial u}{\partial x} \frac{\partial ^2 u}{\partial x^2} \right| = \left| \frac{\partial }{\partial x}\left( \frac{\partial u}{\partial x}\right) ^2 \right| , \end{aligned}$$

we find from (85)

$$\begin{aligned} \displaystyle \frac{2\pi }{{\varGamma }}|\hbox {Re}\{\hbox {Int}(x,z;u\}|\le & {} \displaystyle {\varepsilon \int _{-\infty }^{+\infty } f_\varepsilon (x_s-x)) \left| \frac{\partial ^2 u}{\partial x^2} \right| \; dx_s}\nonumber \\&+\displaystyle {\varepsilon ^2 \int _{-\infty }^{+\infty } g_\varepsilon (x_s-x)) \left| \frac{\partial }{\partial x}\left( \frac{\partial u}{\partial x}\right) ^2 \right| \; dx_s}={:}\hbox {I}_{f_\varepsilon } +\hbox {I}_{g_\varepsilon }. \end{aligned}$$
(87)

In the integral, we set

$$\begin{aligned} s=\frac{\pi }{\varepsilon }(x_s-x). \end{aligned}$$
(88)

This gives

$$\begin{aligned} \hbox {I}_{f_\varepsilon }=\frac{\varepsilon ^2}{\pi } \int _{-\infty }^{+\infty } {\tilde{f}}(s) \left| \frac{\partial ^2 u}{\partial x^2}\left( x+\frac{\varepsilon }{\pi }s,t\right) \right| \; ds \end{aligned}$$
(89)

and

$$\begin{aligned} \hbox {I}_{g_\varepsilon }=\frac{\varepsilon ^3}{\pi } \int _{-\infty }^{+\infty } {\tilde{g}}(s) \left| \frac{\partial }{\partial x}\left( \frac{\partial u}{\partial x}\right) ^2 \left( x+\frac{\varepsilon }{\pi }s,t\right) \right| \; ds. \end{aligned}$$
(90)

Here \({\tilde{f}}\) is again given by (65) and \({\tilde{g}}\) by (66), but now with

$$\begin{aligned} a=e^{-|s|}. \end{aligned}$$
(91)

Assuming that the integrals in (89) and (90) are bounded, uniformly in \(\varepsilon >0\), for (x, t) in a subdomain E of the (x, t)-plane, we have

$$\begin{aligned} \hbox {I}_{f_\varepsilon }=O(\varepsilon ^2)\;\;\;\hbox {and}\;\;\; \hbox {I}_{g_\varepsilon }=O(\varepsilon ^3)\;\;\;\hbox {in }{} { E} \end{aligned}$$
(92)

and consequently

$$\begin{aligned} \left| \frac{q_x-q_x^D}{{\varGamma }} \right| = O(\varepsilon ^2)\;\;\;\hbox {in }{} { E} \end{aligned}$$
(93)

as \(\varepsilon \downarrow 0.\) Consistent with the order of approximation, we may simplify \(q_x^D\) in (84) and in (93) by disregarding the term \(\varepsilon ^2u_x^2\) in the denominator. This gives

$$\begin{aligned} \frac{1}{{\varGamma }}q_x^D= \left\{ \begin{array}{ll} -\varepsilon (1-u) u_x &{}\quad z<u,\\ \varepsilon uu_x &{}\quad z>u. \end{array} \right. \end{aligned}$$
(94)

The boundedness of the integrals in (89) and (90) clearly depends on the behavior of the scaled interface \(u=u(x,t)\). Let us investigate this for a particular choice of u. Starting point is the evolution equation for the interface based on the Dupuit approximation (94). Following the procedure as outlined in Sect. 2, one finds the equation, see also 28,

$$\begin{aligned} \frac{\partial u}{\partial t} = D \varepsilon ^2 \frac{\partial }{\partial x} \left( u(1-u) \frac{\partial u}{\partial x}\right) , \end{aligned}$$
(95)

where \(D=\frac{{\varGamma }}{\phi H}\; [s^{-1}]\). Solutions of this equation should approximately describe the motion of the true interface, in particular for flat interfaces (\(\varepsilon<<1\)). Equation (95) has a particular solution, see Van Duijn and Zhang (1988) and De Josselin de Jong (1981), describing the redistribution of fresh and salt groundwater as a rotating line in space. It is given by the similarity solution

$$\begin{aligned} u_s(x,t)= \left\{ \begin{array}{lr} 0 &{} \hbox {for}\;\;x<-\varepsilon \sqrt{Dt},\\ \displaystyle \frac{1}{2} +\frac{x}{2\varepsilon \sqrt{Dt}} &{} \hbox {for}\;\;-\varepsilon \sqrt{Dt}<x<\varepsilon \sqrt{Dt},\\ 1 &{} x> \hbox {for}\;\;\varepsilon \sqrt{Dt}, \end{array} \right. \end{aligned}$$
(96)

with \(t>0\).

To be in the regime of flat interfaces, we need \(\frac{\partial u_s}{\partial x} =O(1)\), see also (83). This requires a large dimensional time in (96). We need \(t=O\left( \frac{1}{\varepsilon ^2}\right) \) and for convenience we write

$$\begin{aligned} t=\frac{T}{D\varepsilon ^2}, \;\; \hbox {with}\;\;T=O(1). \end{aligned}$$
(97)

Using this in (96) gives

$$\begin{aligned} \frac{\partial ^2 u_s}{\partial x^2}(x,T) =\frac{1}{2\sqrt{T}}\left\{ \delta \left( x+\sqrt{T}\right) -\delta \left( x-\sqrt{T}\right) \right\} \end{aligned}$$
(98)

and

$$\begin{aligned} \frac{\partial }{\partial x} \left( \frac{\partial u_s}{\partial x}\right) ^2 (x,T)= \frac{1}{4T}\left\{ \delta \left( x+\sqrt{T}\right) -\delta \left( x-\sqrt{T}\right) \right\} \end{aligned}$$
(99)

Using (98) in (89), together with the symmetry of \({\tilde{f}}\), gives

$$\begin{aligned} \hbox {I}_{f_\varepsilon }= & {} \hbox {I}_{f_\varepsilon }\left( x,T\right) \displaystyle = \frac{\varepsilon ^2}{2\pi \sqrt{T}}\int _{-\infty }^{+\infty } {\tilde{f}}\left( s\right) \left\{ \delta \left( x+\frac{\varepsilon }{\pi }s+\sqrt{T}\right) + \delta \left( x+\frac{\varepsilon }{\pi }s-\sqrt{T}\right) \right\} \; ds \nonumber \\ \displaystyle= & {} \frac{\varepsilon }{2 \sqrt{T}}\left\{ {\tilde{f}} \left( \frac{\pi }{\varepsilon }\left( x+\sqrt{T}\right) \right) +{\tilde{f}} \left( \frac{\pi }{\varepsilon }\left( x-\sqrt{T}\right) \right) \right\} . \end{aligned}$$
(100)

The monotonicity of \({\tilde{f}}\) and again its symmetry yields the estimate

$$\begin{aligned} \hbox {I}_{f_\varepsilon }\left( x,T\right) \le \frac{\varepsilon }{\sqrt{T}}{\tilde{f}} \left( \frac{\pi }{\varepsilon }\left( \sqrt{T}-|x|\right) \right) \end{aligned}$$
(101)

for all \(x\in (-\infty , \infty )\) and \(T>0\). Fixing x such that \(|x|<\sqrt{T}\), i.e., that part of the aquifer where both fresh groundwater and salt groundwater are present with \(\frac{\partial u_s}{\partial x}>0\), we obtain for small \(\varepsilon \) (or for large T)

$$\begin{aligned} \hbox {I}_{f_\varepsilon }(x,T) \le \frac{\varepsilon }{\sqrt{T}}e^{-\frac{\pi }{\varepsilon }\left( \sqrt{T}-|x|\right) }. \end{aligned}$$
(102)

This is sharper than (91) as long as x is in a bounded interval \((-l,l)\) and \(T>l^2\). Using (99) in (90) gives a similar estimate for \(\hbox {I}_{g_\varepsilon }\).

Remark

The rotating line solution (96) is close to the situation of the Claim in Sect. 4, because the second-order derivative of the interface only has a contribution at the toe (where \(u\downarrow 0\)) and at the top (where \(u \uparrow 1\)).

6.1 Explicit Case

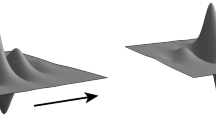
The rotating line similarity solution (96) can be generalized to the ‘non-flat case’ in which we keep the influence of the denominator \(1+\zeta ^2\). In De Josselin de Jong (1981), and later in a generalized stetting in Van Duijn and Zhang (1988), it was shown that the Dupuit interface motion Eq. (28) has a rotating line solution as well. Only the speed of rotation is different. Inspired by this solution, a comparison was made in De Josselin de Jong (1981) between the Dupuit discharge and the exact discharge due to a straight line fresh–salt interface as is shown in Fig. 5. It is instructive to repeat that comparison here because expressions (42), (43) and (54) give directly the result.

Fig. 5
figure 5

Piecewise linear interface

Full size image

For convenience, we drop the time dependence, but keeping the same notation as in Sects. 3 and 4.

In the integral term (54), we use

$$\begin{aligned} \frac{\partial }{\partial x}\left( \frac{\zeta _x^{(1,2)}}{1+\zeta _x^2} \right) = \frac{p^{(1,2)}}{1+p^2}\{ \delta (x-S_1)-\delta (x-S_2)\}, \end{aligned}$$
(103)

where \(p=\tan p\), see Fig. 5.

Fig. 6
figure 6

Upper picture the full (exact) discharge field. Lower picture the Dupuit discharge field [as published in De Josselin de Jong (1981)]

Full size image

This gives for all \(x\in \) R and \(0\le z\le H\)

$$\begin{aligned} \hbox {Int} (x,z;\zeta ) \displaystyle= & {} \frac{i{\varGamma }}{2\pi } \omega _{-}(S_1,x,0,z)\frac{p}{1+p^2}-\frac{i{\varGamma }}{2\pi }\omega _{-}(S_2,x,H,z)\frac{p}{1+p^2}\nonumber \\&+\displaystyle {\frac{{\varGamma }}{2\pi } \omega _{+}(S_1,x,0,z)\frac{p^2}{1+p^2}-\frac{{\varGamma }}{2\pi }\omega _{+}(S_2,x,H,z)\frac{p^2}{1+p^2}}. \end{aligned}$$
(104)

From (57), we immediately see

$$\begin{aligned} \omega _{-}(S_1,x,0,z) = \omega _{-}(S_2,x,H,z)=0. \end{aligned}$$

Hence

$$\begin{aligned} \hbox {Int}(x,z;\zeta ) = \displaystyle {\frac{{\varGamma }}{2\pi } \frac{p^2}{1+p^2} \{\omega _{+}(S_1,x,0,z) -\omega _{+}(S_2,x,H,z)\}}. \end{aligned}$$
(105)

Using the definition (55) of \(\omega _+\), we find

$$\begin{aligned} \hbox {Int} (x,z;\zeta ) =\frac{{\varGamma }}{\pi } \frac{p^2}{1+p^2} \left\{ \begin{array}{llll} \displaystyle \ln \left( \frac{1-e^{-({\tilde{S}}_1-{\tilde{x}})+i{\tilde{z}}}}{1+e^{-({\tilde{S}}_2-{\tilde{x}})+i{\tilde{z}}}}\right) &{} \hbox {for}&{} x<S_1, &{} (a)\\ \displaystyle \ln \left( \frac{1-e^{+({\tilde{S}}_1-{\tilde{x}})-i{\tilde{z}}}}{1+e^{-({\tilde{S}}_2-{\tilde{x}})+i{\tilde{z}}}}\right) &{} \hbox {for}&{} S_1<x<S_2, &{} (b)\\ \displaystyle \ln \left( \frac{1-e^{+({\tilde{S}}_1-{\tilde{x}})-i{\tilde{z}}}}{1+e^{+({\tilde{S}}_2-{\tilde{x}})-i{\tilde{z}}}}\right) &{} \hbox {for}&{} x>S_2. &{} (c) \end{array}\right. \end{aligned}$$
(106)

Using (106) in expressions (42) and (43) gives the exact discharges in the different regions. Fig. 6, which is taken from De Josselin de Jong (1981), shows the discharges as well as the corresponding Dupuit discharges. Note that for \(x<S_1\) (where \( \zeta (x)=0\) and \( \frac{d\zeta }{dx}=0\)) and for \(x<S_2\) (where \( \zeta (x)=H\) and \( \frac{d\zeta }{dx}=0\)), the Dupuit discharges vanish. There the only flow contribution comes from (106a) and (106c).

7 Discussion and Conclusions

In this paper, we revisit the work of de Josselin de Jong on fresh–salt groundwater. In particular, we take his paper De Josselin de Jong (1981) as starting point for our analysis. In that paper, he considered fresh and salt groundwater in a horizontally extended aquifer. The scale of the problem is such that a sharp interface exists between the fluids. Based on earlier work De Josselin de Jong (1977), he constructs an expression for the horizontal and vertical discharge in terms of an integral along the fresh–salt interface. In doing so, he used the stream function formulation form De Josselin de Jong (1977). In this formulation, the stream function (and hence the discharge field) can be obtained for a given interface shape. In De Josselin de Jong (1981), he also considers a Dupuit–Forchheimer type approximation in which it is assumed that the horizontal discharge \(q_x=q_x(x,z)\) does not depend on z in each fluid. He verified this assumption using the stream function for a particular (piecewise linear) interface.

In this paper, we start from (16) as starting point. Applying integration by parts to (15), we recover the Dupuit–Forchheimer discharges as found by De Josselin de Jong (1981), see expressions (42)–(44). Moreover, we are able to give precise mathematical conditions for the validity of approximations (18) and (46). These conditions read as follows: If for some \(t>0\) and \(x_0 \in {\mathbf{R}}\) we have

$$\begin{aligned} \text {i})&\displaystyle \int _{{\mathbf{R}}} \left| \frac{\partial ^2 \zeta }{\partial x^2}(x,t) \right| \; dx < \infty \qquad \hbox {(integrability condition)} \end{aligned}$$
(107)
$$\begin{aligned} \text {ii})&\displaystyle \left| \frac{\partial ^2 \zeta }{\partial x^2}(x,t) \right| \;\;\hbox {is small for } \;\; |x-x_0| <H \quad \hbox {(linearity condition)} \end{aligned}$$
(108)

then the Dupuit approximation holds at \(x=x_0\), with an error that is small and that can be estimated. In other words, if (107) and (108) hold, the integral terms in (42) and (43) are small compared to the local Dupuit discharges (18) and (46). Note that (107) and (108) do not necessarily require flat interfaces. Therefore, the term \(({\partial \zeta }/{\partial x})^2\) in the denominator in (18) and (46) cannot always be disregarded.

In Sect. 5, we use the formulation from Sect. 3 and 4 to consider the case of flat interfaces. By flat we mean that \(\partial \zeta /\partial x = O(\varepsilon )\) and \(\varepsilon<< 1\). We give conditions for which we can estimate the order of convergence in terms of \(\varepsilon \).