The Effect of Microstructure on Models for the Flow of a Bingham Fluid in Porous Media: One-Dimensional Flows

Abstract

The Buckingham–Reiner models for the one-dimensional flow of a Bingham fluid along a uniform pipe or channel are well-known, but are modified here to cover much more general one-dimensional configurations. These include selections of channels with different widths, and five different probability density functions describing distributions of channel widths. It is found that the manner in which breakthrough occurs at the threshold pressure gradient depends very strongly on the type of distribution of pores and that a pseudo-threshold pressure gradient, which might be inferred from measurements of flow at relatively high pressure gradients, may be more than twice the magnitude of the true threshold gradient.

1 Introduction

Many fluids which are used in everyday life and in industry exhibit a yield threshold, by which is meant that the fluid either remains stationary, or else moves as a solid without shear, whenever the shear stress is lower than a threshold value. Fluids which exhibit such a threshold include Casson fluids, Herschel–Bulkley fluids and Bingham fluids. Of these, the Bingham fluid exhibits a linear stress–strain relationship post-threshold. While the literature which is associated with such non-Newtonian fluids is extensive and mature, the research associated with the flow of such fluids through porous media is in the most part relatively small and recent. This short paper, then, is devoted to the task of determining how Darcy’s law, which governs the flow of a Newtonian fluid in a porous medium, is altered when the porous medium is saturated by a Bingham fluid.

Many authors have considered the porous medium to consist either of bundles of tubes or networks of tubes of circular cross section and of various diameters. Flow within such tubes was one of the main considerations in the lengthy work of Bingham (1916), which describes the experimental investigations by Simonis (1905) on the rate of flow of suspensions of fine clay in NaOH solutions through tubes of different radii. Bingham concluded that these suspensions have a yield threshold (i.e. an applied pressure gradient above which the fluid flows) which he called the friction constant, and he stated that the response to the pressure is then linear post-yield. Such a simple piecewise-linear model of the flow dependence on the applied pressure gradient was then assumed to apply for flows in porous media in work by Pascal (1979, 1981, 1983). Bernardiner and Protopapas (1994), in a review of pre-1994 Russian literature, also assume this model; they cite experimental work involving viscoplastic fluids, and Newtonian flows through argillaceous soils, the latter being very similar to Bingham’s suspensions.

Despite Bingham’s stated conclusion that the post-yield flow rate depends linearly on the applied pressure gradient, his Fig. 12 (which was taken from Simonis 1905 and ‘adapted’ by Bingham) shows a well-defined curved section immediately post-yield; this, he concluded, was due to seepage, suggesting implicitly that its presence was an experimental error. In slightly later, and apparently independent papers, Buckingham (1921) and Reiner (1926) derived the now well-known and more recently named Buckingham–Reiner law for flow in cylindrical tubes. This formula, seen later, matches well the shape of Simonis’s curves at least qualitatively, therefore, it might be concluded that Bingham’s supposed reason for the experimental error in the data of Simonis no longer needs to be invoked.

Others have considered different types of channel flow and different aspects of those flows. For example, Daprà and Scarpi (2004) considered unsteady flow in a plane channel, which might be termed a Poiseuille–Bingham flow, and developed a series solution for the start-up flow from rest using the Pascal model. This was extended to pipe flow in Daprà and Scarpi (2005). Muraleva and Muraleva (2011) considered steady flow in an undulating channel using finite difference methods to determine the unyielded regions. Talon et al. (2014) considered more general boundary imperfections for the channel within the lubrication approximation, and they applied their method to periodic and self-affine undulations. The computation of pipe flow in more complicated geometries, such as square cross sections, is hindered by the need to find the yield surfaces numerically. Considerable progress has been made on this aspect, and we refer the reader to the work of Mosolov and Miasnikov (1966), Saramito and Roquet (2001), Huilgol (2006) and Muraleva and Muraleva (2009). It is worth mentioning that Saramito and Roquet (2001) show that the Buckingham–Reiner law for a circular tube may be used with minimal error for a square tube after rescaling. On the other hand, pore networks have also been used to simulate the flow of Bingham fluids in porous media. The paper by Balhoff et al. (2012) reports on some different numerical methods for computing the flow in networks. Flows within a diamond-shaped network were considered by Chevalier and Talon (2015) where the different paths were assigned random thresholds. Attention was then focussed on the numerical simulation on the successive initiation of flow within the different paths from one side of the porous medium to the other. Another analysis of one-dimensional flow within a two-dimensional network was considered by Chen et al. (2005), but this was in the context of imbibition and the displacement of a Bingham fluid by a Newtonian fluid. We would also wish to draw the readers’ attention to the papers by Chevalier et al. (2013, 2014), which report on the experimental determination of a suitable Darcy’s law for Herschel–Bulkley fluids, and the paper by Bleyer and Coussot, which is concerned with the numerical modelling of a Bingham fluid through an array of circular cylinders. Entrance effects have also been considered by Philippou et al. (2016).

The present paper has multiple motivations. One of these is the experimental work of Chase and Dachavijit (2005), which uses a packed column containing spherical glass beads, where it is found that a scaled Buckingham–Reiner equation may be used to model at least this type of particulate porous medium. A second is the analysis of Oukhlev et al. (2014) which shows how a Bingham fluid may be used to determine the pore size distribution within a medium. Their method was tested successfully on a medium consisting of pores which satisfy a Gaussian distribution. An analogous paper by Castro et al. (2014) seeks to determine the pore size distribution by comparing the increased flow rate caused by successive increments in the applied pressure gradient. A third might seem negative, but Coussot (2014) states that network models (a tube bundle being a subset of these) do not provide generic analytical expressions for the velocity/pressure-drop relationship. The present study will show analytically that this relationship does indeed depend quite strongly on the type of distribution of channels/tubes which are present, and therefore Coussot’s view will be confirmed.

Given that this is the centenary of Bingham’s original paper (at the time of submission of the present manuscript, that is), it seems apposite, then, to revisit the simplicity of the one-dimensional channel/tube model of a porous medium in order to show analytically how the Buckingham–Reiner model depends very strongly on the distribution of the channels/tubes. In the main body of the paper, we consider various distributions of channels, both discrete and continuous, while the “Appendix” section lists the equivalent formulae for circular tubes. We find that the manner in which the mean velocity varies with the applied pressure gradient immediately post-threshold takes various power-law forms depending on the distribution of channels/tubes. It is also found that the quantity which we shall term the pseudo-threshold (i.e. the threshold gradient which is given when extrapolating back from flows at high pressure gradients) also varies greatly with the type of distribution of channels/tubes.

2 The plane-Poiseuille flow of a Bingham fluid

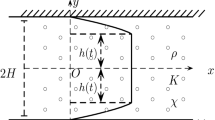
A Bingham fluid is characterised by having a yield stress, but it is otherwise Newtonian, and therefore it flows only when a sufficiently large stress has been imposed. This stress may arise from pressure gradients, moving boundaries or buoyancy forces, for example. The simplest case in which this happens is for Poiseuille flow where we shall take u(y) to be the velocity in the x-direction. For one-dimensional isothermal flow in the x-direction, we have

$$\begin{aligned} 0 = - {\displaystyle \frac{\mathrm{d} p}{\mathrm{d} x}} + {\displaystyle \frac{\mathrm{d} \tau }{\mathrm{d} y}}, \end{aligned}$$

(1)

where $\tau$ is the shear stress. If $\tau _0$ is the yield stress, then the rate of strain is given by

$$\begin{aligned} \begin{aligned} \tau > \tau _0&\Rightarrow \mu {\displaystyle \frac{\mathrm{d} u}{\mathrm{d} y}}=\tau -\tau _0, \\ -\tau _0< \tau< \tau _0&\Rightarrow {\displaystyle \frac{\mathrm{d} u}{\mathrm{d} y}}=0, \\ \tau < -\tau _0&\Rightarrow \mu {\displaystyle \frac{\mathrm{d} u}{\mathrm{d} y}}=\tau +\tau _0. \\ \end{aligned} \end{aligned}$$

(2)

In what follows, we shall work with $\mathcal{G}=-\mathrm{d}p/\mathrm{d}x$, which is the pressure drop per unit length, and therefore a positive value of $\mathcal{G}$ causes the velocity to be positive whenever it is nonzero.

If a uniform channel of width, h, has bounding planes at $y=\pm h/2$, then the velocity profile in the channel takes the form

$$\begin{aligned} \begin{array}{rl} -{\displaystyle \frac{h}{2}} \le y \le -\epsilon {\displaystyle \frac{h}{2}}: &{} \quad \mu u = {\textstyle \frac{1}{8}} \mathcal{G}\left( h^2-4y^2\right) - \tau _0 \left( {\textstyle \frac{1}{2}}h+y\right) \\ &{}\\ -\epsilon {\displaystyle \frac{h}{2}} \le y \le \epsilon {\displaystyle \frac{h}{2}}: &{} \quad \mu u = {\textstyle \frac{1}{8}} \mathcal{G}h^2\left( 1-\epsilon ^2\right) - {\textstyle \frac{1}{2}}\tau _0h(1-\epsilon ) \\ &{}\\ \epsilon {\displaystyle \frac{h}{2}} \le y \le {\displaystyle \frac{h}{2}}: &{} \quad \mu u = {\textstyle \frac{1}{8}} \mathcal{G}\left( h^2-4y^2\right) - \tau _0 \left( {\textstyle \frac{1}{2}}h-y\right) \\ \end{array} \end{aligned}$$

(3)

where the value, $\epsilon$, is given by

$$\begin{aligned} \epsilon = \frac{2\tau _0}{\mathcal{G}h}, \end{aligned}$$

(4)

and where this solution is valid only when $\epsilon <1$. The value of $\epsilon$ is the proportion of the channel which is unyielded, and therefore values which are above unity mean that the whole channel is unyielded and hence $u=0$. It proves to be much more convenient to work with

$$\begin{aligned} \sigma ={\displaystyle \frac{1}{\epsilon }} = {\displaystyle \frac{\mathcal{G}h}{2\tau _0}}, \end{aligned}$$

(5)

because this may be interpreted as a nondimensional pressure gradient, one which is based on the yield stress of the fluid. Thus, the fluid begins to flow once $\sigma$ rises above unity in magnitude, and so $\sigma =1$ is the nondimensional threshold pressure gradient. The velocity profile given by Eq. (3) is parabolic in two outer regions and is a nonzero constant in the middle region where the unyielded fluid forms a plug.

In the context of porous media, it is necessary first to find the mean flow. Therefore, we shall assume in the first instance that the porous medium consists of a periodic array of these channels where the period is H. The porosity of such a medium is then $\phi =h/H$. Within one channel the total volumetric flux, Q, per unit distance in the third coordinate direction (z) is given by

$$\begin{aligned} Q= & {} \int _{-h/2}^{h/2} u\, \mathrm{d}y = \left\{ \begin{array}{cl} {\displaystyle \frac{h^3\mathcal{G}}{12\mu }}\Bigl [ 1 -{\displaystyle \frac{3}{2|\sigma |}}+{\displaystyle \frac{1}{2|\sigma |^3}}\Bigr ] \quad &{} (|\sigma |>1) \\ &{}\\ 0 \quad &{} (|\sigma |<1) \\ \end{array} \right\} \equiv \frac{h^3\mathcal{G}}{12\mu } f(\sigma )\nonumber \\= & {} \Bigl ({\displaystyle \frac{h^2\tau _0}{6\mu }}\Bigr )\sigma f(\sigma ); \end{aligned}$$

(6)

this defines the function $f(\sigma )$ which is the plane-Poiseuille flow equivalent of the widely known Buckingham–Reiner formula for the Hagen–Poiseuille flow of a Bingham fluid; see the “Appendix” section. In the remainder of this paper, we will omit the use of the modulus signs in formulae such as Eq. (6), for simplicity of presentation, and will restrict attention to positive values of $\mathcal{G}$ and hence of $\sigma$.

Given the formula in Eq. (6), the equivalent Darcy velocity for a Bingham fluid, $u_{\mathrm{B}}$, is the mean velocity taken over one period of the pattern of channels. Hence,

$$\begin{aligned} u_{\mathrm{B}}= {\displaystyle \frac{\phi \mathcal{G} h^2}{12\mu }} f(\sigma ) \equiv {\displaystyle \frac{\mathcal{G}K}{\mu }}f(\sigma ), \end{aligned}$$

(7)

where

$$\begin{aligned} K={\displaystyle \frac{\phi h^2}{12}} \qquad \hbox {and} \qquad \phi ={\displaystyle \frac{h}{H}} \end{aligned}$$

(8)

are the permeability and porosity, respectively, of the present porous medium. In what follows, the definitions of K and $\phi$ will depend strongly on the choice of channels which are used to define one period of the porous medium. The general guiding principle will be that the $\sigma \gg 1$ limit, which corresponds to Newtonian flow, should always take the form, $u_{\mathrm{N}}=\mathcal{G}K/\mu$. This means that we have the following comparison between the response of Bingham and Newtonian fluids for the present configuration:

$$\begin{aligned} {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} = f(\sigma ). \end{aligned}$$

(9)

The variation of $f(\sigma )$ is shown in Fig. 1a. While its nature is such that $f(\sigma )\rightarrow 1$ as $\sigma \rightarrow \infty$, its behaviour near to the threshold takes a quadratic form at leading order,

$$\begin{aligned} f(\sigma ) \sim {\textstyle \frac{3}{2}}(\sigma -1)^2 - {\textstyle \frac{7}{2}}(\sigma -1)^3 + \cdots , \qquad (0<(\sigma -1)\ll 1). \end{aligned}$$

(10)

Therefore, the induced velocity first begins to rise from zero in a quadratic manner once the threshold pressure gradient is exceeded; this is precisely the qualitative behaviour found in Fig. 12 of Bingham (1916).

Fig. 1

a The Buckingham–Reiner formulae for plane-Poiseuille flow ($f(\sigma )$, continuous line, Eq. (6)) and for Hagen–Poiseuille flow ($g(\sigma )$, dashed line, Eq. (48)), showing the strength of the flow of a Bingham fluid relative to that of a Newtonian fluid. b The corresponding nondimensional flows, $\sigma f(\sigma )$ and $\sigma g(\sigma )$, together with the large-$\sigma$ behaviours (dotted lines) showing the positions of the pseudo-thresholds

At the opposite extreme of large values of $\sigma$, a Newtonian behaviour is expected. However, the induced flow is equal to $\sigma f(\sigma )$ in nondimensional terms (see Eq. (6)) and this is shown in Fig 1b. The two-term large-$\sigma$ approximation to this flow is given by,

$$\begin{aligned} \sigma f(\sigma ) \sim \sigma - {\textstyle \frac{3}{2}}. \quad (\sigma \gg 1) \end{aligned}$$

(11)

From an experimental point of view, if one were to try to extrapolate back from fairly large values of $\sigma$ to try to find the threshold gradient, then Eq. (11) suggests that the value $\sigma =3/2$ might be found because $\sigma f(\sigma )$ tends quite quickly to the linear behaviour shown in Eq. (11) as $\sigma$ increases above 1; see the dotted line in Fig 1b. We may therefore define a pseudo-threshold value of

$$\begin{aligned} \sigma _\mathrm{pt}={\textstyle \frac{3}{2}} \end{aligned}$$

(12)

for a porous medium consisting of identical channels; this value may also be found in Talon et al. (2014) where it is termed the effective pressure threshold or apparent critical pressure.

The equivalent analysis for Hagen–Poiseuille flow is summarised in the “Appendix” section where the analogous function $g(\sigma )$ is defined and which applies to a circular pore of radius, h. This curve is shown in Fig. 1 as a dashed line; it displays very similar characteristics to that of $f(\sigma )$ with an initial quadratic rise as $\sigma$ increases above 1 and where it tends towards 1 as $\sigma \rightarrow \infty$.

In the rest of the paper, we will use $F(\sigma )$ to denote $u_{\mathrm{B}}/u_{\mathrm{N}}$, the ratio between the flow rate of a Bingham fluid and that of a Newtonian fluid, and therefore the nondimensional Darcy flow is $\sigma F(\sigma )$. The equivalent notations for Hagen–Poiseuille flow in circular channels, which is summarised in the “Appendix” section, are $G(\sigma )$ and $\sigma G(\sigma )$.

2.1 The effect of having two different channel widths

A porous medium will generally be formed of channels with different widths, unless they have been designed otherwise, and therefore we begin a generalisation of the above analysis of the type of Purcell (1949) who considered a porous medium consisting of cylindrical pores with many different diameters. We will now assume that one period of channels will consist of one channel of width, h, and a second narrower channel of width $\gamma h$ where $\gamma <1$. Clearly, if $\sigma =1$ represents the threshold pressure gradient for the wider channel, then $\sigma =1/\gamma$ is the threshold for the narrower channel. Therefore, the total fluid flux through one of each channel is,

$$\begin{aligned} Q = {\displaystyle \frac{\mathcal{G}h^3}{12\mu }} \Bigl [ f(\sigma ) + \gamma ^3 f(\gamma \sigma ) \Bigr ]. \end{aligned}$$

(13)

The corresponding Darcy velocity is now given by,

$$\begin{aligned} u_{\mathrm{B}}= {\displaystyle \frac{\mathcal{G}K}{\mu }} \left[ {\displaystyle \frac{f(\sigma ) + \gamma ^3 f(\gamma \sigma )}{1+\gamma ^3}} \right] , \end{aligned}$$

(14)

or

$$\begin{aligned} {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} = F(\sigma ) = {\displaystyle \frac{f(\sigma ) + \gamma ^3 f(\gamma \sigma )}{1+\gamma ^3}}, \end{aligned}$$

(15)

where the permeability and porosity are given by

$$\begin{aligned} K={\displaystyle \frac{\phi h^2}{12}}{\displaystyle \frac{(1+\gamma ^3)}{(1+\gamma )}} \qquad \hbox {and}\qquad \phi = {\displaystyle \frac{h(1+\gamma )}{H}}. \end{aligned}$$

(16)

The pseudo-threshold value of $\sigma$ is

$$\begin{aligned} \sigma _\mathrm{pt} = {\displaystyle \frac{3(1+\gamma ^2)}{2(1+\gamma ^3)}}. \end{aligned}$$

(17)

Samples of the flow relative to that of a Newtonian fluid are shown in Fig. 2. Attention is focussed on $\gamma =0.25$, 0.5 and 0.75, and the single-channel case, which may be regarded as being perfectly equivalent to either $\gamma =0$ or $\gamma =1$, is included as a reference case. When $\sigma$ takes relatively small values, $F(\sigma )$ appears to decrease as $\gamma$ increases from zero—this may be expected since flow arises in only the wider channel and hence Eq. (15) yields $F(\sigma )=f(\sigma )/(1+\gamma ^2)$—but eventually flow begins in the second channel, we return to the single-channel case as $\gamma \rightarrow 1$, and clearly the variation in $F(\sigma )$ with $\gamma$ cannot be monotonic. Indeed, the $F(\sigma )$ curves for $\gamma =0.5$ and $\gamma =0.75$ close to $\sigma =3.2$.

Fig. 2

The variation of $u_{\mathrm{B}}/u_{\mathrm{N}}$ with $\sigma$ for three two-channel cases, where $\gamma =0.25$, 0.5 and 0.75, and the single-channel case which corresponds to either $\gamma =0$ or $\gamma =1$. The uppermost curve corresponds to $\gamma =0$ in all cases (but also see the main text). Continuous lines correspond to plane-Poiseuille flow, while dashed lines correspond to Hagen–Poiseuille flow

Figure 3 allows us to see more clearly why there is this lack of monotonicity in the variation of $F(\sigma )$ with $\gamma$. Each curve corresponds to a chosen value of $\sigma$ between 1.5 and 100, and each has two symbols. The first (o) shows the value of $\gamma$ above which the narrower channel admits flow. The second ($\bullet$) depicts the smallest value of $F(\sigma )$ as $\gamma$ varies. It is to be expected that, when the permeability is correctly accounted for, the value of $F(\sigma )n$ must be identical in the two cases, $\gamma =0$ and $\gamma =1$, because they describe effectively the same situation, namely that all channels have width, h. We have already seen that the $(1+\gamma ^3)$ scaling factor causes $F(\sigma )$ to decrease as $\gamma$ increases when flow arises only in the wider channels. Once flow begins in the narrower channels, this decrease is attenuated, and given that flow in the narrower channels becomes easier as $\gamma$ increases, $F(\sigma )$ must then achieve a minimum before $\gamma$ eventually rises up to unity.

Fig. 3

The variation of $u_{\mathrm{B}}/u_{\mathrm{N}}$ with $\gamma$ for all two-channel cases, where $\sigma =1.5$, 2, 3, 4, 5 and 10. Continuous lines correspond to plane-Poiseuille flow, while dashed lines correspond to Hagen–Poiseuille flow. Bullets correspond to where $u_{\mathrm{B}}/u_{\mathrm{N}}$ achieves its minimum as $\gamma$ varies and circles to the threshold value of $\gamma$ in the narrow channel

Figure 3 also suggests that the value of $\gamma$ at which $F(\sigma )$ has its minimum tends towards 1 as $\sigma \rightarrow 1^+$. This may be analysed by setting $\sigma =1+\delta _\sigma$ and $\gamma =1-\delta _\gamma$ into Eq. (15) and expanding for small values of both $\delta _\sigma$ and $\delta _\gamma$, both values being assumed to be positive. At leading order, we find that

$$\begin{aligned} F(\sigma ) \sim {\textstyle \frac{3}{4}}\delta _\sigma ^2 + {\textstyle \frac{3}{4}}(\delta _\sigma -\delta _\gamma )^2, \end{aligned}$$

(18)

which shows that, for a fixed value of $\delta _\sigma$, the minimum value of $F(\sigma )$ occurs when $\delta _\gamma =\delta _\sigma$ as $\sigma \rightarrow 1^+$. For Hagen–Poiseuille flow, the equivalent equation is

$$\begin{aligned} G(\sigma ) \sim \delta _\sigma ^2 + (\delta _\sigma -\delta _\gamma )^2, \end{aligned}$$

(19)

which was obtained from Eq. (53), and therefore exactly the same conclusion applies.

2.2 The effect of having many different channel widths

The above two-channel configuration may be generalised further by considering N channels per period. If the widths of the channels are taken to be $\gamma _ih$ for $i=1,\ldots ,N$, and where the channels have been ordered with respect to their widths, then we have

$$\begin{aligned} 1=\gamma _1 \, \ge \,\gamma _2\, \ge \,\gamma _3\, \ge \cdots \ge \gamma _N. \end{aligned}$$

(20)

This definition allows one to define simple ratios of channel widths. For example, if one were to take five channels per period where three have width, h, and the remaining two have width, h / 2, then we may set $\gamma _1=\gamma _2=\gamma _3=1$ and $\gamma _4=\gamma _5={\textstyle \frac{1}{2}}$ with $N=5$.

The Darcy velocity for the general case is now given by

$$\begin{aligned} u_{\mathrm{B}}= {\displaystyle \frac{\mathcal{G}K}{\mu }} \left[ {\displaystyle \frac{\displaystyle \sum \nolimits _{i=1}^N \gamma _i^3f(\gamma _i\sigma )}{\displaystyle \sum \nolimits _{i=1}^N \gamma _i^3}} \right] \qquad \Rightarrow \qquad {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} = F(\sigma ) = {\displaystyle \frac{\displaystyle \sum \nolimits _{i=1}^N \gamma _i^3f(\gamma _i\sigma )}{\displaystyle \sum \nolimits _{i=1}^N \gamma _i^3}}, \end{aligned}$$

(21)

while the permeability and porosity are given by,

$$\begin{aligned} K = {\displaystyle \frac{\phi h^2}{12}} \left[ {\displaystyle \frac{\displaystyle \sum \nolimits _{i=1}^N \gamma _i^3}{\displaystyle \sum \nolimits _{i=1}^N \gamma _i}}\right] \qquad \hbox {and}\qquad \phi =(h/H) {\displaystyle \sum _{i=1}^N \gamma _i}. \end{aligned}$$

(22)

The pseudo-threshold is

$$\begin{aligned} \sigma _\mathrm{pt} ={\displaystyle \frac{\displaystyle 3\sum \nolimits _{i=1}^N \gamma _i^2}{\displaystyle 2\sum \nolimits _{i=1}^N \gamma ^3_i}}. \end{aligned}$$

(23)

Some sample cases of multiple channels are given in Figs. 4 and 5. Figure 4 is concerned with the effect of having different numbers of channels of width, ${\textstyle \frac{1}{2}}h$, in addition to one channel of width, h. We see that the initial curves in the range $1<\sigma <2$ differ from one another and are dependent on the number of smaller channels, despite flow taking place only in the widest channel. In practice, the overall mass flux will be identical, but we are plotting the flow which is obtained relative to that of a Newtonian fluid for which there will be flow in the narrower channels. Mathematically, the reduction in $F(\sigma )$ is due to the presence of the denominator in Eq. (21).

Fig. 4

The variation of $u_{\mathrm{B}}/u_{\mathrm{N}}$ with $\sigma$ for various multi-channel cases consisting of one channel of width, h, and n channels of width, ${\textstyle \frac{1}{2}}h$. The uppermost curve corresponds to the single channel, for reference, labelled $n=0$ here. The remaining cases correspond to $n=1$, $n=4$, $n=9$, $n=16$ and $n=25$ (lowest curve). Continuous lines correspond to plane-Poiseuille flow, while dashed lines correspond to Hagen–Poiseuille flow

Fig. 5

The variation of $u_{\mathrm{B}}/u_{\mathrm{N}}$ with $\sigma$ for various multi-channel cases. This is an attempt to model the uniform distribution case, $a=0$, which is considered later. a (i) Single channel (for reference); (ii) $\gamma =0.2$, 0.4, 0.6, 0.8, 1; (iii) $\gamma =0.1$, 0.2, $\ldots$ 0.9, 1; (iv) $\gamma =0.05$, 0.1, $\ldots$ 0.95, 1; (v) uniform distribution with $a=1$—see Eq. (30). b (i) $\gamma =0.025$, 0.05, $\ldots$ 0.975, 1. (ii) Uniform distribution with $a=1$. Continuous lines correspond to plane-Poiseuille flow, while dashed lines correspond to Hagen–Poiseuille flow

The threshold pressure gradient in the narrower channels is $\sigma =2$, and this only becomes very clearly apparent in the behaviour of the curves when there are a large number of narrower channels; see, for example, when $n=16$ and $n=25$.

Figure 5 shows a selection of cases which approximate a uniform distribution of channels, a case which will be considered in the next section. The general configuration consists of n channels where the values of $\gamma$ take the form, $\gamma _i=i/n$, for $i=1,\ldots ,n$. We show curves which correspond to $n=5$, 10, 20 and 40, and the uniform distribution response given by Eq. (30). The single-channel case, which could be said to be equivalent to $n=0$, is given in Fig. 5a for reference.

In general, the larger the value of n, the smaller is the value of $F(\sigma )$, but the curve representing the variation of $F(\sigma )$ tends monotonically towards that of the uniform distribution, Eq. (30); see Fig. 5a. In particular, the initial $(\sigma -1)^2$ dependence of $F(\sigma )$ which is given in Eq. (10) weakens as n increases as only one out of many channels admits flow followed by another and then others as the pressure gradient increases. The limit as $n\rightarrow \infty$, namely the uniform distribution, then represents an initial cubic dependence on $(\sigma -1)$, as will be shown below. Figure 5b shows that, even for a discrete set of 20 channels with a uniformly distributed set of widths, a continuous uniform distribution of channels may be modelled closely.

3 Random distributions of channels

More likely again is that the porous medium should consist of a distribution of channel widths, and while one may investigate many different types, we shall confine ourselves solely to five, namely a uniform distribution, two different types of linear distributions, a quadratic distribution and a seminormal distribution. We may use the function, $\varPhi (\gamma )$, as the probability density function for the distribution. In general, expressions for the Darcy velocity relative to that of a Newtonian fluid, the permeability and the porosity take the following forms,

$$\begin{aligned} F(\sigma ) \quad =\quad {\displaystyle \frac{\displaystyle \int _0^\infty \gamma ^3 \varPhi (\gamma ) f(\gamma \sigma )\, \mathrm{d}\gamma }{\displaystyle \int _0^\infty \gamma ^3 \varPhi (\gamma ) \, \mathrm{d}\gamma }}, \end{aligned}$$

(24)

where

$$\begin{aligned} K=\Bigl ({\displaystyle \frac{\phi h^2}{12}}\Bigr ) {\displaystyle \frac{\displaystyle \int _0^\infty \gamma ^3 \varPhi (\gamma )\, \mathrm{d}\gamma }{\displaystyle \int _0^\infty \gamma \varPhi (\gamma )\, \mathrm{d}\gamma }} \qquad \hbox {and}\qquad \phi = (h/H) {\displaystyle \int _0^\infty \gamma \varPhi (\gamma )\, \mathrm{d}\gamma }. \end{aligned}$$

(25)

3.1 Uniform distribution

For a uniform distribution of pores in the range, $a\le \gamma \le 1$, the probability density function is, therefore,

$$\begin{aligned} \varPhi (\gamma )=\left\{ \begin{array}{ll} {\displaystyle \frac{1}{1-a}} \quad &{} (a<\gamma <1) \\ &{}\\ 0 \quad &{} (\hbox {otherwise}). \\ \end{array} \right. \end{aligned}$$

(26)

Guided by the above analyses, the Darcy velocity for such a distribution of pores is

$$\begin{aligned} F(\sigma ) \quad =\quad \left\{ \begin{array}{ll} 0 \quad &{} \Bigl (0\le \sigma \le 1\Bigr ) \\ &{}\\ {\displaystyle \frac{ (\sigma -1)^3(\sigma +1) }{(1-a^4)\sigma ^4}} &{} \quad \Bigl (1\le \sigma <{\displaystyle \frac{1}{a}}\Bigr )\\ &{}\\ 1- {\displaystyle \frac{2}{\sigma }} \left[ {\displaystyle \frac{1+a+a^2}{(1+a)(1+a^2)}} \right] + {\displaystyle \frac{2}{\sigma ^3(1+a)(1+a^2)}} &{} \quad \Bigl ({\displaystyle \frac{1}{a}} \le \sigma \Bigr ). \\ \end{array} \right. \end{aligned}$$

(27)

For this case, the permeability and porosity are given by

$$\begin{aligned} K= {\displaystyle \frac{\phi h^2}{12}}\,{\displaystyle \frac{(1+a^2)}{2}} \qquad \hbox {and}\qquad \phi = {\displaystyle \frac{h}{H}}{\displaystyle \frac{(1+a)}{2}}, \end{aligned}$$

(28)

and the pseudo-threshold is

$$\begin{aligned} \sigma _\mathrm{pt}=2{\displaystyle \frac{1+a+a^2}{(1+a)(1+a^2)}}. \end{aligned}$$

(29)

Thus, there are three regimes depending on the value of $\sigma$. The first region is stagnant, while the second (intermediate) regime has flow arising in a proportion of the channels (i.e. those with widths lying between $h/\sigma$ and h), and then the final regime corresponds to flow in all channels.

Figure 6 shows how $F(\sigma )$ varies with $\sigma$ for a selection of values of a. In all the cases where $a\ne 1$, it is important to note that flow starts very weakly as $\sigma$ increases above unity. The formula in Eq. (27) for the intermediate regime shows that the initial increase in the velocity is now proportional to $(\sigma -1)^3$, as opposed to the single-channel case where the increase is quadratic. We also note that, when $a=0$, i.e. when channel widths do not have a lower limit, then the final regime does not exist. In this case, we have the relatively simple relation

$$\begin{aligned} F(\sigma ) \quad =\quad \left\{ \begin{array}{ll} 0 \quad &{} (0\le \sigma \le 1) \\ &{}\\ {\displaystyle \frac{ (\sigma -1)^3(\sigma +1) }{\sigma ^4}} &{} \quad (1\le \sigma ). \\ \end{array} \right. \end{aligned}$$

(30)

In this limit, the pseudo-threshold becomes $\sigma _\mathrm{pt}=2$. This case is difficult to see in Fig. 6 because the curve is almost indistinguishable from that of $a=0.25$.

Fig. 6

The variation of $u_{\mathrm{B}}/u_{\mathrm{N}}$ with $\sigma$ for uniform distributions and for the following values of a: $a=1$ (equivalent to the single-channel case), $a=0.75$, 0.5, 0.25 and 0. Continuous lines correspond to plane-Poiseuille flow, while dashed lines correspond to Hagen–Poiseuille flow

On the other hand, when we formally let $a\rightarrow 1$, which corresponds to almost no variation in the channel widths, the intermediate regime no longer exists, and the formula corresponding to the final regime in Eq. (27) reduces precisely to that given in Eq. (9) for the single channel. Both of these limits are seen in Fig. 6. Similarly, the location of the pseudo-threshold (Eq. (29)) reduces to that for a identical channels; see Eq. (12).

3.2 Linear distributions

We now consider the following two linear distributions of channel widths for which the probability density functions are,

$$\begin{aligned} \hbox {(a)}\,\,\varPhi (\gamma )=2\gamma , \quad \hbox {(b)}\,\,\varPhi (\gamma )=2(1-\gamma ), \quad (0\le \gamma \le 1). \end{aligned}$$

(31)

The first corresponds to situations where very narrow channels are highly unlikely, while the second makes the narrow channels very likely. For case (a), our analysis gives

$$\begin{aligned} F(\sigma ) \quad =\quad {\displaystyle \frac{\displaystyle \int _0^1 \gamma ^3 \varPhi (\gamma ) f(\gamma \sigma )\, \mathrm{d}\gamma }{\displaystyle \int _0^1 \gamma ^3 \varPhi (\gamma ) \, \mathrm{d}\gamma }} \quad =\quad \left\{ \begin{array}{ll} 0 \quad &{} (0\le \sigma \le 1) \\ &{}\\ {\displaystyle \frac{ (\sigma -1)^3(8\sigma ^2+9\sigma +3) }{8\sigma ^5}} \quad &{} (1\le \sigma ),\\ \end{array} \right. \end{aligned}$$

(32)

where the permeability and porosity are given by,

$$\begin{aligned} K= {\displaystyle \frac{3}{5}}\,\Bigl ({\displaystyle \frac{\phi h^2}{12}}\Bigr ) \qquad \hbox {and}\qquad \phi = {\displaystyle \frac{2h}{3H}}. \end{aligned}$$

(33)

The pseudo-threshold is

$$\begin{aligned} \sigma _\mathrm{pt}={\textstyle \frac{15}{8}}. \end{aligned}$$

(34)

For case (b), we have

$$\begin{aligned} F(\sigma ) \quad = \quad \left\{ \begin{array}{ll} 0 \quad &{} (0\le \sigma \le 1) \\ &{}\\ {\displaystyle \frac{ (\sigma -1)^4(2\sigma +3) }{2\sigma ^5}} \qquad &{} (1\le \sigma ),\quad \\ \end{array} \right. \end{aligned}$$

(35)

where

$$\begin{aligned} K= {\displaystyle \frac{1}{10}}\, \Bigl ({\displaystyle \frac{\phi h^2}{12}}\Bigr ) \qquad \hbox {and}\qquad \phi = {\displaystyle \frac{h}{3H}}. \end{aligned}$$

(36)

In each of the two linear cases, we recover a unit scaled velocity as $\sigma \rightarrow \infty$, but the onset of flow near $\sigma =1$ is marked by a different power of $(\sigma -1)$. Thus, for case (b), flow begins very weakly indeed because of the additional lack of availability of channels of width h within which to flow as compared to the uniform distribution case. This also results in an increased value for the pseudo-threshold:

$$\begin{aligned} \sigma _\mathrm{pt}={\textstyle \frac{5}{2}}. \end{aligned}$$

(37)

Both of these conclusions may be seen clearly in Fig. 7 where the increased power of $(\sigma -1)$ near to the true threshold for the second linear distribution means that the strength of the induced flow always remains smaller than that for the first linear distribution and for the uniform distribution.

Fig. 7

Variation of $u_{\mathrm{B}}/u_{\mathrm{N}}$ and $\sigma u_{\mathrm{B}}/u_{\mathrm{N}}$ against $\sigma$ for the plane channels (a, b) and for circular pipes (c, d). In Frame a, the curves correspond to the following distributions: single channel (C1); uniform distribution with $a=0$ (U); the two linear distributions (L1 and L2), the quadratic distribution (Q) and the seminormal distribution (SN). In the three remaining frames, all the curves are in the same order. Also shown as dotted lines are the extrapolations leading to the locations of the pseudo-thresholds

3.3 Quadratic distribution

Given that the initial rise in the flow immediately after $\sigma$ rises above unity is proportional to $(\sigma -1)^3$ in the case of a uniform distribution and is proportional to $(\sigma -1)^4$ for the second linear distribution, we have chosen to consider the following quadratic probability density function,

$$\begin{aligned} \varPhi (\gamma )=3(1-\gamma )^2 \qquad (0\le \gamma \le 1). \end{aligned}$$

(38)

This has been chosen because the powers of $(\sigma -1)$ quoted above seem to be associated with the behaviour of the probability density function at $\gamma =1$. For the uniform distribution, $\varPhi (1)$ is nonzero, while for the second linear distribution it is zero, but the slope is nonzero. The quadratic distribution has been chosen to have a zero value and a zero slope but a nonzero second derivative.

We obtain the following,

$$\begin{aligned} F(\sigma ) = \quad = \quad \left\{ \begin{array}{ll} 0 \quad &{} (0\le \sigma \le 1) \\ &{}\\ {\displaystyle \frac{ (\sigma -1)^5(\sigma +2) }{\sigma ^5}} \qquad &{} (1\le \sigma ),\quad \\ \end{array} \right. \end{aligned}$$

(39)

where

$$\begin{aligned} K= {\displaystyle \frac{1}{20}}\, \Bigl ({\displaystyle \frac{\phi h^2}{12}}\Bigr ) \qquad \hbox {and}\qquad \phi = {\displaystyle \frac{h}{4H}}. \end{aligned}$$

(40)

Clearly, we have obtained an initial velocity which is proportional to $(\sigma -1)^5$ as $\sigma$ rises above unity. This further increased power of $(\sigma -1)$ is evident in Fig. 7. The pseudo-threshold is now

$$\begin{aligned} \sigma _\mathrm{pt}=3, \end{aligned}$$

(41)

which represents another increase over the two linear distribution cases; see Fig. 7b, d.

3.4 Seminormal distribution

We select to use the seminormal distribution which has a mean of unity (and hence a standard deviation which is also unity), and therefore the probability density function is

$$\begin{aligned} \varPhi (\gamma ) = {\displaystyle \frac{2}{\pi }} e^{-\gamma ^2/\pi }. \end{aligned}$$

(42)

Upon following the same ideas as above, we obtain the following expressions for the scaled velocity, permeability and porosity:

$$\begin{aligned}&\displaystyle F(\sigma ) =\Bigl ( 1 - {\displaystyle \frac{1}{2\sigma ^2\pi }} \Bigr ) e^{-1/\sigma ^2\pi } + {\displaystyle \frac{1}{\sigma }} \Bigl ({\displaystyle \frac{1}{2\sigma ^2\pi }}-{\displaystyle \frac{3}{4}}\Bigr ) \hbox {erfc}\Bigl ( {\displaystyle \frac{1}{\sigma \sqrt{\pi }}} \Bigr ), \end{aligned}$$

(43)

$$\begin{aligned}&\displaystyle K = \pi {\displaystyle \frac{\phi h^2}{12}}, \qquad \phi = {\displaystyle \frac{h}{H}}. \end{aligned}$$

(44)

The variation of the scaled velocity with the dimensionless pressure gradient, $\sigma$, is shown in Fig. 7. We have also found the following asymptotic expressions for $F(\sigma )$ for both large and small values of $\sigma$:

$$\begin{aligned} \sigma \gg 1: \quad F(\sigma )= & {} 1 - {\displaystyle \frac{3}{4\sigma }} + O(\sigma ^{-3}), \end{aligned}$$

(45)

$$\begin{aligned} \sigma \ll 1: \quad F(\sigma )\sim & {} {\textstyle \frac{3}{4}}\pi \sigma ^2 e^{-1/\sigma ^2\pi }. \end{aligned}$$

(46)

For this distribution, the pseudo-threshold is

$$\begin{aligned} \sigma _\mathrm{pt} = {\textstyle \frac{3}{4}}. \end{aligned}$$

(47)

This is clearly less than the mean of the probability density function, but it reflects the fact that flow is initiated, albeit weakly, at values of $\sigma$ which are less than unity.

The fact that this is a distribution with a mean of unity tells us that a proportion of the channels have widths which are greater than h and therefore flow may arise when $\sigma <1$. For very small values of $\sigma$, Eq. (46) shows that the strength of the flow is super-exponentially small. When $\sigma =1$, we have $F(\sigma )=0.360539$, at which point all the other distributions which we have considered have just reached their common threshold values of $\sigma$.

4 Conclusions

It has been found that there is a very wide variety of relationships between the Darcy velocity and the applied pressure gradient when a porous medium is composed of distributions of channels or pipes. The chief difference between most of the different configurations of channel which are considered here is the manner in which flow begins once the scaled pressure gradient, $\sigma$, increases past unity. For a finite number of channels comprising a periodic configuration, the initial growth in the strength of the flow is quadratic in $(\sigma -1)$.

Once continuous distributions are encountered, the threshold becomes weaker, and the power of $(\sigma -1)$ which may be expected then depends on the exact nature of the probability density function, $\varPhi (\gamma )$, as $\gamma \rightarrow 1^-$ assuming that $\varPhi (\gamma )=0$ when $\gamma >1$. We have seen two cases which are cubic, and have also obtained both quartic and quintic variations in $(\sigma -1)$. No doubt other distributions could be devised which would yield other types of variation. Specifically, if we restrict ourselves to a distribution, $\varPhi (\gamma )$, where $\varPhi =0$ when $\gamma >1$, then if the limit as $\gamma \rightarrow 1^-$ of the nth derivative of $\varPhi (\gamma )$ is nonzero, but that all other lower derivatives are zero, then the initial rise in $F(\sigma )$ at threshold will be proportional to $(\sigma -1)^{n+2}$. Figure 7 also indicates that the pseudo-threshold displays a tendency to increase as the power of $(\sigma -1)$ increases. For the seminormal distribution, flow begins immediately once $\sigma$ increases from zero, but its strength is super-exponentially small at first.

Therefore, it is clear that the writing down of a definitive Darcy–Bingham model cannot be achieved in general, at least for a bundle of channels or tubes, but that the appropriate model will be specific to the type of porous medium being considered. This conclusion confirms the view of Coussot (2014) stated earlier. While upscaling techniques are often used very successfully in many other situations, the presence of yield surfaces at microscopic lengthscales, and the presence of stagnation in some pores and not others, would therefore seem to militate against the use of traditional upscaling to obtain what might be termed a universal Darcy–Bingham law.

Appendix

The aim of this “Appendix” section is to present a list of formulae for those cases where flow takes place in microchannels of circular cross section, namely Hagen–Poiseuille flow. We will assume that these channels have radius, h, and that H is the period for the underlying pattern of the different channels. Thus, for a single channel in a repeating square ($H\times H$) domain, the porosity is $\phi =\pi h^2/H^2$, for reference. The formula for the fluid flux in a single channel which is analogous to that in Eq. (6) is given by

$$\begin{aligned} Q = \left\{ \begin{array}{cl} {\displaystyle \frac{\pi \mathcal{G}h^4}{8\mu }}\Bigl [ 1 -{\displaystyle \frac{4}{3|\sigma |}}+{\displaystyle \frac{1}{3|\sigma |^4}}\Bigr ] &{} \quad (|\sigma |>1) \\ &{}\\ 0 \quad &{} \quad (|\sigma |<1) \\ \end{array} \right\} \equiv {\displaystyle \frac{\pi \mathcal{G}}{8\mu }} g(\sigma ). \end{aligned}$$

(48)

This formula for $g(\sigma )$ is the classical Buckingham–Reiner formula for the flow of a Bingham fluid relative to that of a Newtonian fluid. Thus, Eqs. (9) and (8) may be replaced by,

$$\begin{aligned} \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}} = g(\sigma ), \end{aligned}$$

(49)

where

$$\begin{aligned} K={\displaystyle \frac{\phi h^2}{8}} \qquad \hbox {and} \qquad \phi =\pi {\displaystyle \frac{h^2}{H^2}}. \end{aligned}$$

(50)

When $\sigma$ is just above unity, we find that

$$\begin{aligned} g(\sigma ) \sim 2(\sigma -1)^2 - {\textstyle \frac{16}{3}}(\sigma -1)^3, \end{aligned}$$

(51)

while the pseudo-threshold value of $\sigma$ is

$$\begin{aligned} \sigma _\mathrm{pt}={\textstyle \frac{4}{3}}. \end{aligned}$$

(52)

For the multi-channel case, Eqs. (21) and (22) are replaced by,

$$\begin{aligned}&\displaystyle {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} = {\displaystyle \frac{\displaystyle \sum \nolimits _{i=1}^N \gamma _i^4g(\gamma _i\sigma )}{\displaystyle \sum \nolimits _{i=1}^N \gamma _i^4}}, \end{aligned}$$

(53)

$$\begin{aligned}&\displaystyle K = \Bigl ({\displaystyle \frac{\phi h^2}{8}}\Bigr ) \left[ {\displaystyle \frac{\displaystyle \sum \nolimits _{i=1}^N \gamma _i^4}{\displaystyle \sum \nolimits _{i=1}^N \gamma _i^2}}\right] \qquad \hbox {and}\qquad \phi =\Bigl (\pi {\displaystyle \frac{h^2}{H^2}}\Bigr ) {\displaystyle \sum _{i=1}^N \gamma _i^2}, \end{aligned}$$

(54)

and the pseudo-threshold is at

$$\begin{aligned} \sigma _\mathrm{pt}= {\displaystyle \frac{\displaystyle 4\sum \nolimits _{i=1}^N \gamma _i^3}{\displaystyle 3\sum \nolimits _{i=1}^N \gamma _i^4}}. \end{aligned}$$

(55)

When channel widths are subject to a probability density function, $\phi (\gamma )$, Eqs. (24) and (25) become

$$\begin{aligned}&\frac{u_{\mathrm{B}}}{u_{\mathrm{N}}} \quad =\quad {\displaystyle \frac{\displaystyle \int _0^\infty \gamma ^4 \phi (\gamma ) g(\gamma \sigma )\, d\gamma }{\displaystyle \int _0^\infty \gamma ^4 \phi (\gamma ) \, \mathrm{d}\gamma }}, \end{aligned}$$

(56)

$$\begin{aligned}&\quad K=\Bigl ({\displaystyle \frac{\phi h^2}{8}}\Bigr ) {\displaystyle \frac{\displaystyle \int _0^\infty \gamma ^4 \phi (\gamma )\, \mathrm{d}\gamma }{\displaystyle \int _0^\infty \gamma ^2 \phi (\gamma )\, \mathrm{d}\gamma }} \qquad \hbox {and}\qquad \phi = \Bigl (\pi {\displaystyle \frac{h^2}{H^2}}\Bigr ) {\displaystyle \int _0^\infty \gamma ^2 \phi (\gamma )\, \mathrm{d}\gamma }. \end{aligned}$$

(57)

For the uniform distribution of pores given by Eq. (26), we find that

$$\begin{aligned} {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} \quad =\quad \left\{ \begin{array}{ll} 0 \quad &{} \Bigl (0\le \sigma \le 1\Bigr ) \\ &{}\\ {\displaystyle \frac{ (\sigma -1)^3(3\sigma ^2+4\sigma +3)}{3(1-a^5)\sigma ^5}} \qquad &{} \Bigl (1\le \sigma <{\displaystyle \frac{1}{a}}\Bigr )\quad \\ &{}\\ 1- {\displaystyle \frac{5}{3\sigma }} \left[ {\displaystyle \frac{(1+a+a^2+a^3)}{(1+a+a^2+a^3+a^4)}} \right] + {\displaystyle \frac{5}{3\sigma ^4(1+a+a^2+a^3+a^4)}} \quad &{} \Bigl ({\displaystyle \frac{1}{a}} \le \sigma \Bigr ), \\ \end{array} \right. \end{aligned}$$

(58)

where

$$\begin{aligned} K= \Bigl ({\displaystyle \frac{\phi h^2}{8}}\Bigr ) {\displaystyle \frac{3(1+a+a^2+a^3+a^4)}{5(1+a+a^2)}} \qquad \hbox {and}\qquad \phi = \Bigl (\pi {\displaystyle \frac{h^2}{H^2}}\Bigr )\,{\displaystyle \frac{(1+a+a^2)}{3}}, \end{aligned}$$

(59)

and where the pseudo-threshold is at

$$\begin{aligned} \sigma _\mathrm{pt} = {\displaystyle \frac{5(1+a+a^2+a^3)}{3(1+a+a^2+a^3+a^4)}}. \end{aligned}$$

(60)

For the first linear distribution, where $\varPhi (\gamma )=2\gamma$ in the range $0\le \gamma \le 1$, we have

$$\begin{aligned} {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} \quad =\quad \left\{ \begin{array}{ll} 0 \quad &{} (0\le \sigma \le 1) \\ &{}\\ {\displaystyle \frac{ (\sigma -1)^3(5\sigma ^3+7\sigma ^2+6\sigma +2)}{5\sigma ^6}} \qquad &{} (1\le \sigma ),\quad \\ \end{array} \qquad \right. \end{aligned}$$

(61)

where

$$\begin{aligned} K= {\displaystyle \frac{2}{3}}\,\Bigl ({\displaystyle \frac{\phi h^2}{8}}\Bigr ) \qquad \hbox {and}\qquad \phi = {\displaystyle \frac{1}{2}}\,\Bigl (\pi {\displaystyle \frac{h^2}{H^2}}\Bigr ). \end{aligned}$$

(62)

The pseudo-threshold is at

$$\begin{aligned} \sigma _\mathrm{pt} = {\textstyle \frac{8}{5}}. \end{aligned}$$

(63)

For the second linear distribution, where $\varPhi (\gamma )=2-2\gamma$ in the range $0\le \gamma \le 1$, we have

$$\begin{aligned} {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} \quad =\quad \left\{ \begin{array}{ll} 0 \quad &{} (0\le \sigma \le 1) \\ &{}\\ {\displaystyle \frac{ (\sigma -1)^4(\sigma ^2+2\sigma +2)}{\sigma ^6}} \qquad &{} (1\le \sigma ),\quad \\ \end{array} \qquad \right. \end{aligned}$$

(64)

where

$$\begin{aligned} K= {\displaystyle \frac{2}{5}}\,\Bigl ({\displaystyle \frac{\phi h^2}{8}}\Bigr ) \qquad \hbox {and}\qquad \phi = {\displaystyle \frac{1}{6}}\,\Bigl (\pi {\displaystyle \frac{h^2}{H^2}}\Bigr ). \end{aligned}$$

(65)

The pseudo-threshold is at

$$\begin{aligned} \sigma _\mathrm{pt} = 2. \end{aligned}$$

(66)

For the quadratic distribution the following may be found.

$$\begin{aligned} {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} \quad =\quad \left\{ \begin{array}{ll} 0 \quad &{} (0\le \sigma \le 1) \\ &{}\\ {\displaystyle \frac{ (\sigma -1)^5(3\sigma ^2+8\sigma +10)}{3\sigma ^7}} \qquad &{} (1\le \sigma ),\quad \\ \end{array} \qquad \right. \end{aligned}$$

(67)

where

$$\begin{aligned} K= {\displaystyle \frac{2}{7}}\,\Bigl ({\displaystyle \frac{\phi h^2}{8}}\Bigr ) \qquad \hbox {and}\qquad \phi = {\displaystyle \frac{1}{10}}\,\Bigl (\pi {\displaystyle \frac{h^2}{H^2}}\Bigr ). \end{aligned}$$

(68)

The pseudo-threshold is at,

$$\begin{aligned} \sigma _\mathrm{pt} = {\textstyle \frac{7}{3}}. \end{aligned}$$

(69)

Finally, for the seminormal distribution, the Darcy velocity is given by

$$\begin{aligned} {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} = {\displaystyle \frac{2}{9\pi \sigma }}\Bigl ( 1 - {\displaystyle \frac{2}{\sigma ^2\pi }} \Bigr ) e^{-1/\sigma ^2\pi } + \Bigl (1 + {\displaystyle \frac{4}{9\sigma ^4\pi ^2}}\Bigr ) \hbox {erfc}\Bigl ( {\displaystyle \frac{1}{\sigma \sqrt{\pi }}} \Bigr ), \end{aligned}$$

(70)

where

$$\begin{aligned} K = {\displaystyle \frac{3\pi ^2}{2}}\, \Bigl ({\displaystyle \frac{\phi h^2}{8}}\Bigr ), \qquad \phi = {\displaystyle \frac{1}{2}}\,\Bigl (\pi {\displaystyle \frac{h^2}{H^2}}\Bigr ). \ \end{aligned}$$

(71)

We may also determine the following asymptotic expressions for Eq. (70):

$$\begin{aligned} \sigma \gg 1: \quad {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} = 1 - {\displaystyle \frac{16}{9\pi \sigma }} + O(\sigma ^{-2}), \qquad \quad \sigma \ll 1: \quad {\displaystyle \frac{u_{\mathrm{B}}}{u_{\mathrm{N}}}} \sim {\textstyle \frac{4}{3}}\sigma e^{-1/\sigma ^2\pi }, \end{aligned}$$

(72)

and therefore the pseudo-threshold is at

$$\begin{aligned} \sigma _\mathrm{pt} = {\displaystyle \frac{16}{9\pi }}. \end{aligned}$$

(73)