Expected discounted utility

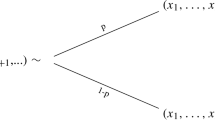
Abstract

Standard axioms of additively separable utility for choice over time and classic axioms of expected utility theory for choice under risk yield a generalized expected additively separable utility representation of risk-time preferences over probability distributions over sure streams of intertemporal outcomes. A dual approach is to use the analogues of the same axioms in a reversed order to obtain a generalized additively separable expected utility representation of time–risk preferences over intertemporal streams of probability distributions over sure outcomes. The paper proposes an additional axiom, which is called risk-time reversal, for obtaining a special case of the two representations—expected discounted utility. The axiom of risk-time reversal postulates that if a risky lottery over streams of sure intertemporal outcomes and an intertemporal stream of risky lotteries yield the same probability distribution of possible outcomes in every point in time then a decision-maker is indifferent between the two. This axiom is similar to assumption 2 “reversal of order in compound lotteries” in Anscombe and Aumann (Ann Math Stat 34(1):199–205, 1963, p. 201).

Appendix

Lemma 1

If Axioms 1–5 hold then the preference relation ≽ satisfies ordinal independence: xPf ≽ xPg implies yPf ≽ yPg for all $x,\;y \in X$; f, g:T\P → X and any time period $P \in \sum$

Proof of Lemma 1

Step 1 If time period P ∈ $\sum$ is null then yPf ≽ xPf and xPg ≽ yPg for all outcomes x, y ∈ X. Thus, if xPf ≽ xPg then we have yPf ≽ xPf ≽ xPg ≽ yPg and Axiom 2 (transitivity) implies that yPf ≽ yPg, i.e. Lemma 1 holds.

Step 2 Note that aPh ≻ bPh implies aPk ≻ bPk for all outcome a, b ∈ X, functions h, k :T\P → X, and a nonnull time period P ∈ $\sum$. Otherwise, if aPk ≻ bPk does not hold, i.e. bPk ≽ aPk, we can then apply Axiom 5 (cardinal independence) as follows: bPk ≽ bPk, bPk ≽ aPk and bPh ≽ bPh imply bPh ≽ aPh; which contradicts aPh ≻ bPh.

Step 3 If x₁Pg ~ xPf and xPf ≻ xPg then Axiom 2 (transitivity) implies that x₁Pg ≻ xPg. By step 2, x₁Pg ≻ xPg implies x₁Pf ≻ xPf (set a = x₁, b = x, h = g and k = f). Since x₁Pf ≻ xPf and xPf ~ x₁Pg then Axiom 2 (transitivity) implies that x₁Pf ≻ x₁Pg.

Step 4 We now prove that xPf ≻ xPg implies yPf ≻ yPg if yPf ≽ xPf and time period P ∈ $\sum$ is nonnull.

If the set {z ∈ X: zPg ≽ xPf} is empty then yPf ≽ xPf implies yPf ≻ yPg (if yPf ≻ yPg does not hold, i.e. yPg ≽ yPf, and yPf ≽ xPf then Axiom 2 (transitivity) implies that yPg ≽ xPf, which contradicts the fact that the set {z ∈ X: zPg ≽ xPf} is empty).

If the set {z ∈ X: zPg ≽ xPf } is nonempty then there exists an outcome z ∈ X such that zPg ≽ xPf. Therefore, we have zPg ≽ xPf ≻ xPg. According to Axiom 3 (solvability), there must then exist an outcome x₁ ∈ X such that x₁Pg ~ xPf.

Since in step 4 we consider only preference yPf ≽ xPf and xPf ~ x₁Pg by our choice of x₁, Axiom 2 then implies that yPf ≽ x₁Pg. Suppose that yPf ≻ yPg does not hold, i.e. yPg ≽ yPf. If yPg ≽ yPf and we just established that yPf ≽ x₁Pg then Axiom 2 implies that yPg ≽ x₁Pg.

If it happens to be so that x₁Pf ≻ yPf then, by step 2 (set a = x₁, b = y, h = f and k = g), we must have x₁Pg ≻ yPg in contradiction to yPg ≽ x₁Pg.

Otherwise, if yPf ≽ x₁Pf (and x₁Pf ≻ x₁Pg by step 3) then we can repeat step 4 from the very beginning with outcome x being replaced by x₁ and choosing outcome x₂ ∈ X such that x₂Pg ~ x₁Pf. By successive iteration, we obtain a so-called standard sequence of outcomes $\{ x_{i} \}_{{i \in {\mathbb{N}}}}$ that is recursively defined by x_iPg ~ x_i−1Pf (with a convention x₀ ≡ x). Axiom 4 implies that the standard sequence $\{ x_{i} \}_{{i \in {\mathbb{N}}}}$ such that yPf ≽ x_iPf is finite. Thus, for some $m \in {\mathbb{N}}$ we must have either

• (a) x_mPf ≻ yPf ≽ x_m−1Pf and we arrive at contradiction by step 2 (x_mPf ≻ yPf implies x_mPg ≻ yPg, which contradicts yPg ≽ x_mPg); or

• (b) yPf ≽ x_m−1Pf and there is no x_m ∈ X such that x_mPg ~ x_m−1Pf. In such a case, the set {z ∈ X: zPg ≽ x_m-1Pf} must be empty. Yet, if yPf ≻ yPg does not hold, i.e. yPg ≽ yPf, and yPf ≽ x_m−1Pf then Axiom 2 implies that yPg ≽ x_m−1Pf and the set {z ∈ X: zPg ≽ x_m−1Pf} cannot be empty. Hence, we must have yPf ≻ yPg in this case as well.

Step 5 If yPg ≻ yPf and yPf ~ y₋₁Pg, then we must have yPg ≻ y₋₁Pg due to Axiom 2. By step 2, yPg ≻ y₋₁Pg implies yPf ≻ y₋₁Pf (set a = y, b = y₋₁, h = g and k = f). Since y₋₁Pg ~ yPf and yPf ≻ y₋₁Pf, Axiom 2 (transitivity) implies that y₋₁Pg ≻ y₋₁Pf.

Step 6 We now prove that yPg ≻ yPf implies xPg ≻ xPf if yPf ≽ xPf and P ∈ $\sum$ is a nonnull time period.

If the set {z ∈ X: yPf ≽ zPg} is empty then we must have xPg ≻ xPf (if xPg ≻ xPf does not hold, i.e. xPf ≽ xPg, and yPf ≽ xPf then we must have yPf ≽ xPg due to Axiom 2, which contradicts the statement that the set {z ∈ X: yPf ≽ zPg} is empty).

If the set {z ∈ X: yPf ≽ zPg} is nonempty then there is z ∈ X such that yPf ≽ zPg. Thus, we have yPg ≻ yPf ≽ zPg. According to Axiom 3 there is then an outcome y₋₁ ∈ X such that y₋₁Pg ~ yPf. If y₋₁Pg ~ yPf and we consider only the case when yPf ≽ xPf then we must have y₋₁Pg ≽ xPf due to Axiom 2. Suppose that xPg ≻ xPf does not hold, i.e. xPf ≽ xPg. Since we already established that y₋₁Pg ≽ xPf and xPf ≽ xPg then we must have y₋₁Pg ≽ xPg due to Axiom 2.

If it happens to be so that xPf ≻ y₋₁Pf then, by step 2 (set a = x, b = y₋₁, h = f and k = g), we must have xPg ≻ y₋₁Pg in contradiction to y₋₁Pg ≽ xPg.

Otherwise, if y₋₁Pf ≽ xPf (and y₋₁Pg ≻ y₋₁Pf by step 5) then we can repeat step 6 from the very beginning with outcome y being replaced by y₋₁ and choosing outcome y₋₂ ∈ X such that y₋₂Pg ~ y₋₁Pf. By iteration, we construct another standard sequence of outcomes $\{ y_{ - i} \}_{{i \in {\mathbb{N}}}}$. Axiom 4 implies that this standard sequence $\{ y_{ - i} \}_{{i \in {\mathbb{N}}}}$ such that y_−iPf ≽ xPf is finite. This implies that for some $n \in {\mathbb{N}}$ we must have either

• (a) y_−nPf ≽ xPf ≻ y_−n−1Pf and we arrive at contradiction by step 2 (xPf ≻ y_−n−1Pf implies xPg ≻ y_−n−1Pg, which contradicts y_−n−1Pg ≽ xPg); or

• (b) y_−nPf ≽ xPf and there is no y_−n−1 ∈ X such that y_−n−1Pg ~ y_−nPf. In such a case the set {z ∈ X: y_−nPf ≽ zPg} must be empty. Yet, if y_−nPf ≽ xPf and xPf ≽ xPg (because we assumed that xPg ≻ xPf does not hold) then we must have y_−nPf ≽ xPg due to Axiom 2 and the set {z ∈ X: y_−nPf ≽ zPg} cannot be empty. Hence, we must have xPg ≻ xPf in this case as well.

Summary If time period P ∈ $\sum$ is null then Lemma 1 holds by step 1. If P ∈ $\sum$ is nonnull then three cases are possible. First, if xPf ≻ xPg and yPf ≽ xPf, then Lemma 1 holds by step 4. Second, if xPf ~ xPg and yPf ≽ xPf, then yPf ≽ yPg (otherwise, if yPg ≻ yPf, then, by step 6, we must have xPg ≻ xPf, which contradicts xPf ~ xPg). Third, if xPf ≽ yPf, then Lemma 1 holds as well. This can be proven by contradiction: suppose that yPf ≽ yPg does not hold, i.e. yPg ≻ yPf. If xPf ≽ yPf then xPg ≽ yPg by step 2 (set a = x, b = y, h = f and k = g). If xPg ≽ yPg and yPg ≻ yPf then xPg ≻ xPf by step 4 (switching x and y as well as f and g in step 4). Yet, xPg ≻ xPf contradicts xPf ≽ xPg.$\square$

Proof of Proposition 1

It is relatively straightforward to show that Axioms 1–5 are necessary. We shall prove only their sufficiency. When all time periods are null, then Proposition 1 holds trivially by setting u(x) = 0 for all $x \in X$ . In this case, constants D(t) ≥ 0 can be chosen arbitrary for all $t \in T$. In the static case when only one time period is nonnull, Lemma II from Debreu (1954, p. 161) or Theorem 2 from Section 2.1 in Krantz et al. (1971)⁵ guarantees the existence of a continuous utility function $u:X \to {\mathbb{R}}$ that represents binary preference relation over outcomes. In this case, we set D(t) = 0 for all null time periods $t \in T$ and D(t) can be an arbitrary positive constant for the remaining nonnull time period $t \in T$.

When exactly two time periods are nonnull, we can set R = P and k = g in Axiom 5 to obtain a so-called Thomsen–Blaschke condition: if xPf ≽ yPg, xPg ≽ zPf, and yPh ≽ xPg then xPh ≽ zPg for all $x,y,z \in X$; f, g, h:T\P → X; and any nonnull time period $P \in \sum$. Preference relation ≽ also satisfies ordinal independence due to Lemma 1 above. Theorem 2 in Section 6.2.4 in Krantz et al. (1971) then establishes that the utility of a stream that yields outcomes f(t) in moments of time $t \in T$ can be written in the weighted utility representation (4), where $u_{t} :X \to {\mathbb{R}}$ is a continuous function that is unique up to a positive affine transformation for all nonnull moments of time t ∈ T.

$$ \mathop \sum \limits_{t \in T } u_{t} \circ f(t). $$

(4)

If more than two time periods are nonnull, we use Lemma 1 above to establish that preference relation ≽ satisfies ordinal independence. Theorem 13 in Section 6.11.1 in Krantz et al. (1971) then guarantees that this preference relation admits the weighted utility representation (4).

If Axiom 5 holds then Theorem 15 in Krantz et al. (1971, Section 6.11.2) establishes that functions u_t(.) in weighted utility representation (4) must be positive affine transformations of each other so that we can write u_t(x) = D(t)u(x) for all x ∈ X, where $D(t) \in {\mathbb{R}}$ for all $t \in T$ and function $u:X \to {\mathbb{R}}$ is continuous and unique up to a positive affine transformation when at least two time periods are nonnull. The constants $D(t) \in {\mathbb{R}}$ must be either all positive or all negative (otherwise Axiom 5 is violated). In the latter case, we can define a new utility function, which is equal to − u(.).$\square$

Proof of Proposition 2

It is relatively straightforward to show that Axioms 1a, 2a, 3–7 are necessary. We shall prove only their sufficiency. If the preference relation ≽ satisfies Axioms 1a, 2a, 6 and 7 then it admits expected utility representation (von Neumann and Morgenstern 1947). In other words, the utility of a risky stream that yields sure streams of intertemporal payoffs $f_{1} , \ldots ,f_{n} \in {\mathcal{F}}$ with respective probabilities $p_{1} , \ldots ,p_{n} \in [0,\;1]$, $p_{1} + \cdots + p_{n} = 1$, $n \in {\mathbb{N}}$, can be written in expected utility form:

$$ \mathop \sum \limits_{i = 1}^{n} p_{i} w(f_{i} ), $$

(5)

where $w:{\mathcal{F}} \to {\mathbb{R}}$. If the preference relation ≽ satisfies Axioms 1–5 then, according to Proposition 1, preferences over sure streams of intertemporal payoffs are represented by additively separable utility (2). Thus, function $w:{\mathcal{F}} \to {\mathbb{R}}$ can be written in the form of a strictly increasing function $v:{\mathbb{R}} \to {\mathbb{R}}$ such that

$$ w(f_{i} ) = v\left( {\mathop \sum \limits_{t \in T } D(t)u \circ f_{i} (t)} \right), $$

(6)

where functions $D:T \to {\mathbb{R}}_{ + }$ and $u:X \to {\mathbb{R}}$ are the same as in Proposition 1.$\square$

Proof of Proposition 3

It is relatively straightforward to show that the analogues of Axioms 1–5 from Sect. 1 on the extended domain $\varPhi$ instead of domain ${\mathcal{F}}$ as well as Axioms 6b and 7b are necessary. We shall prove only their sufficiency.

If a preference relation ≽ on $\varPhi$ satisfies the analogues of Axioms 1–5 from Sect. 1 on the extended domain $\varPhi$ instead of domain ${\mathcal{F}}$ then, according to Proposition 1, preferences over streams of intertemporal lotteries are represented by additively separable utility (2). In other words, the utility of a stream of risky lotteries that yields lottery $L_{t} \in {{\Delta }}(X)$ in moment of time $t \in T$ can be written as

$$ \mathop \sum \limits_{t \in T } D(t)\tilde{w}(L_{t} ), $$

where D(t) ≥ 0 for all $t \in T$ and function $\tilde{w}:\Delta (X) \to {\mathbb{R}}$ is continuous and unique up to a positive affine transformation if at least two time periods are nonnull.

If a preference relation ≽ on $\varPhi$ satisfies the analogues of Axioms 1, 2 from Sect. 1 on the extended domain $\varPhi$ instead of domain ${\mathcal{F}}$ then Axioms 1b and 2b hold as well. If the preference relation ≽ on ${{\Delta }}(X)$ satisfies Axioms 1b, 2b, 6b and 7b then it admits expected utility representation (von Neumann and Morgenstern 1947). In other words, the utility of a static risky lottery $L \in \Delta (X)$ can be written as $\sum\nolimits_{x \in X } {L(x)\tilde{v}(x)} ,$ where $\tilde{v}:X \to {\mathbb{R}}$ is time-invariant Bernoulli utility function. Therefore, function $\tilde{w}:\Delta (X) \to {\mathbb{R}}$ can be written in the form of a strictly increasing function $\tilde{u}:{\mathbb{R}} \to {\mathbb{R}}$ such that

$$ \tilde{w}(L) = \tilde{u}\left( {\mathop \sum \limits_{x \in X } L(x)\tilde{v}(x)} \right) $$

$$ \square $$

Proof of Proposition 4

It is relatively straightforward to show that axioms are necessary. We shall prove only their sufficiency. According to Proposition 2, if a preference relation ≽ on S satisfies Axioms 1a, 2a, 3–7 then the utility of a risky stream $(f_{1} ,\;p_{1} ; \ldots ;f_{n} ,\,p_{n} )$ can be written in a generalized expected additively separable form (2). According to Proposition 3, if a preference relation ≽ on $\varPhi$ satisfies the analogues of Axioms 1–5 from Sect. 1 on the extended domain $\varPhi$ instead of domain ${\mathcal{F}}$ as well as Axioms 6b and 7b, then the utility of an intertemporal stream of risky lotteries $p_{1} f_{1} + \cdots + p_{n} f_{n}$ can be written in a generalized additively separable expected utility form:

$$ U(p_{1} f_{1} + \cdots + p_{n} f_{n} ) = \mathop \sum \limits_{t \in T } D(t)\tilde{u}\left( {\mathop \sum \limits_{i = 1}^{n} p_{i} \tilde{v} \circ f_{i} (t)} \right), $$

(7)

where D(t) ≥ 0 for all $t \in T$; function $\tilde{u}:{\mathbb{R}} \to {\mathbb{R}}$ is continuous and strictly increasing; and $\tilde{v}:X \to {\mathbb{R}}$. If Axiom 8 holds then for all $f_{1} ,\; \ldots ,\;f_{n} \in {\mathcal{F}}$ and $p_{1} ,\; \ldots ,\;p_{n} \in [0,\;1]$, $p_{1} + \cdots + p_{n} = 1$, $n \in {\mathbb{N}}$ the following functional equation must hold:

$$ \mathop \sum \limits_{i = 1}^{n} p_{i} v\left( {\mathop \sum \limits_{t \in T } D(t)u \circ f_{i} (t)} \right) = \mathop \sum \limits_{t \in T } D(t)\tilde{u}\left( {\mathop \sum \limits_{i = 1}^{n} p_{i} \tilde{v} \circ f_{i} (t)} \right). $$

(8)

Setting $p_{i} = 1$ for any $i \in \{ 1, \ldots ,n\}$ in functional Eq. (8) immediately implies that function $v:{\mathbb{R}} \to {\mathbb{R}}$ is linear:

$$ v\left( {\mathop \sum \limits_{t \in T } D(t)u \circ f_{i} (t)} \right) = \mathop \sum \limits_{t \in T } D(t)\tilde{u}(\tilde{v} \circ f_{i} (t)). $$

(9)

$$ \square $$