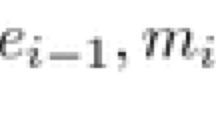Skip to main content
SpringerLink
Log in

The strength of de Finetti’s coherence theorem

  • Published:
Synthese Aims and scope Submit manuscript

Abstract

I show that de Finetti’s coherence theorem is equivalent to the Hahn-Banach theorem and discuss some consequences of this result. First, the result unites two aspects of de Finetti’s thought in a nice way: a corollary of the result is that the coherence theorem implies the existence of a fair countable lottery, which de Finetti appealed to in his arguments against countable additivity. Another corollary of the result is the existence of sets that are not Lebesgue measurable. I offer a subjectivist interpretation of this corollary that is concordant with de Finetti’s views. I conclude by pointing out that my result shows that there is a sense in which de Finetti’s theory of subjective probability is necessarily nonconstructive. This raises questions about whether the coherence theorem can underwrite a legitimate theory of rational belief.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. What I am calling the “coherence theorem” is also known as the “Dutch book theorem.”

  2. See, for example, Joyce (1998).

  3. In mathematics and statistics, countable additivity has reigned since Kolmogorov’s (1950) merger of probability and measure theory. But finitely additive probability theory has found plenty of interesting applications in the work of de Finetti’s followers, e.g. Savage (1954) and Dubins and Savage (1965).

  4. The Hahn-Banach theorem is weaker than the Boolean prime ideal theorem, which is in turn weaker than the axiom of choice (Pincus 1972).

  5. (Freedman and Purves 1969; Heath and Sudderth 1972, 1978; Seidenfeld 2001; Williams 2007).

  6. It is not necessary for my purposes to state the axioms of ZFC formally. Readers can find this information in any reasonably advanced book on set theory, e.g. Jech (2013).

  7. Note that we have already made a number of assumptions that some would reject. For example, our definition of a prevision excludes hyperreal-valued representations (Wenmackers and Horsten 2013). And the fact that previsions take precise values excludes imprecise representations (Augustin et al. 2014).

  8. An unacceptable bet is any function not of the form (1).

  9. Since we appeal to the expected values only of bounded functions of \(\Omega \), we can use an integral for finitely additive measures that is essentially the same as the Lebesgue integral from standard measure theory. Here is a sketch of the details.

    First, define the indicator function \(1_A: \Omega \rightarrow \{0,1\}\) for \(A \subseteq \Omega \) by \(1_A(\omega )=1\) if \(\omega \in A\) and \(1_A(\omega )=0\) if \(\omega \notin A\). Define the expected value of an indicator function \(1_A\) with respect to P as \(E_P(1_A)=P(A)\). For simple functions of the form \(f=\sum _{i=1}^m c_i 1_{A_i}\), \(m \in {\mathbb N}\), \(c_i \in {\mathbb R}\), \(A_i \subseteq \Omega \) define \(E_P(f) = \sum _{i=1}^m c_i E_P(1_{A_i})\). Finally, any \(f \in \ell ^\infty (\Omega )\) can be uniformly approximated by a sequence \((f_n)_{n \in {\mathbb N}}\) of simple functions. Define \(E_P(f) = \lim _{n \rightarrow \infty } E_P(f_n)\). The operator \(E_P: \ell ^\infty (\Omega ) \rightarrow {\mathbb R}\) is then a well-defined positive linear functional that is continuous in the supremum norm. For further details, we refer the reader to Aliprantis and Border (2006) [11.2].

  10. Two clarifications of this formulation of the coherence theorem are in order. First, de Finetti (1974) does not state CT exactly as I have it here. My statement of CT follows more contemporary researchers who view it as “the more transparent way of thinking of coherence” (Berti et al. 2013)[p. 50]. (Heath and Sudderth (1972) and Heath and Sudderth (1978) also adopt the formulation that I use here.) Second, the coherence theorem is usually thought of as a biconditional, whereas I have it as a conditional. For the purposes of investigating the strength of the coherence theorem the converse of CT is not of much interest, for it is easily seen to be a theorem of ZF. Indeed, if P is a finitely additive probability measure for which (3) holds, then the P expected value of any acceptable bet is 0. But this implies that (2) is impossible, which means that \(\phi \) is coherent. Thanks to an anonymous reviewer for pressing me on both of these points.

  11. The other proofs of which I’m aware (Freedman and Purves 1969; Heath and Sudderth 1972, 1978) showing that the Hahn-Banach theorem implies the coherence theorem go by way of the following separating hyperplane theorem:

    SHT:

    If A and B are disjoint nonempty convex subsets of a topological vector space \(\mathcal X\) over the real numbers and B has nonempty interior, then there exists a nonzero continuous linear functional \(\psi : {\mathcal X} \rightarrow {\mathbb R}\) and \(r \in {\mathbb R}\) such that \(\psi (a) \le r\) for all \(a \in A\) and \(\psi (b) \ge r\) for all \(b \in B\).

    For a standard proof that ZF \(+\) HB \(\vdash \) SHT, see Dunford and Schwartz (1958) [p. 417]. For the converse—that is, ZF \(+\) SHT \(\vdash \) HB—see Schechter (1996)[28.4], and, in particular, his HB18. Note that in Schechter’s HB18, the hypothesis that B has nonempty interior is replaced with the hypothesis that B is open. Thus, SHT trivially implies HB18. The converse follows by using HB18 to separate A from the interior of B, then using the fact that the closure of the interior of B is equal to the closure of B (Aliprantis and Border 2006)[5.28], and, finally, using the fact that the separating functional is continuous to show that it separates A from the closure of B, and hence from B.

  12. A sublinear function \(s: {\mathcal X} \rightarrow {\mathbb R}\) satisfies (i) \(s(x + y) \le s(x) + s(y)\) for all \(x,y \in {\mathcal X}\), and (ii) \(\alpha s(x) = s(\alpha x)\) for all \(x \in {\mathcal X}\) and all non-negative \(\alpha \in {\mathbb R}\). To say that s dominates t on V means that \(t(x) \le s(x)\) for all \(x \in V\). A linear extension \(\hat{t}\) of t from V to \({\mathcal X}\) is a linear functional \(\hat{t}: {\mathcal X} \rightarrow {\mathbb R}\) such that \(\hat{t}(x)=t(x)\) for all \(x \in V\). See Luxemburg (1969)[p. 127] or Aliprantis and Border (2006)[5.53].

  13. A proper ideal \({\mathcal I}\) of subsets of \(\Omega \) is a set of subsets of \(\Omega \) that satisfies the following conditions:

    • \(\emptyset \in {\mathcal I}\), \(\Omega \notin {\mathcal I}\);

    • If \(A \in {\mathcal I}\), \(B \subseteq A\), then \(B \in {\mathcal I}\);

    • If \(A, B \in {\mathcal I}\), then \(A \cup B \in {\mathcal I}\).

    A measure m is nontrivial if \(m(\Omega )>0\).

  14. Luxemburg’s Theorem 7.2 says that this statement is equivalent to the statement that there exists a nontrivial finitely additive measure on every Boolean algebra. And his Theorem 7.3 says that the statement that there exists a nontrivial finitely additive measure on every Boolean algebra is equivalent to HB. For different proofs of these results, see Schechter (1996)[23.18, 23.19].

  15. In ZF \(+\) CT, statements about finitely additive measures on Boolean algebras do not follow immediately from statements about finitely additive measures on sets of subsets via Stone’s representation theorem, for Stone’s theorem is strictly stronger than HB and, in fact, equivalent to the Boolean prime ideal theorem (Jech 2013) [p. 81].

  16. Also see Pruss (2014).

  17. For more on fair countable lotteries, see (Schirokauer and Kadane 2007).

  18. Here is a characteristically colorful passage:

    In the finite case, this condition allowed me to choose the probabilities to be all equal, or slightly different, or very different; in short, I could express any opinion whatsoever. Here, on the other hand [...] I am allowed to express them only if they are unbalanced [...] Otherwise, even if I think they are equally probable [...] I am obliged to pick “at random” a convergent series which, however I choose it, is in absolute contrast to what I think. If not, you call me incoherent! In leaving the finite domain, is it I who has ceased to understand anything, or is it you who has gone mad? (de Finetti 1990)[p. 123].

  19. See Howson (2008) for a helpful discussion.

  20. For a proof using Banach limits, see Rao and Rao (1983)[p. 41].

  21. Again, there are some assumptions in play here (footnote 7) that I am not questioning in this paper. Perhaps the tension between totality and symmetry can be resolved by considering hyperreal-valued probabilities, for instance.

  22. More formally, DC says: For any nonempty set X and any function f from X into nonempty subsets of X, there exists a sequence \((x_n)_{n \in {\mathbb N}}\) in X such that \(x_{n+1} \in f(x_n)\). See Schechter (1996) [6.28].

  23. I have adopted this definition from Schechter (1996) [14.77], who uses the term “quasiconstructive.” It must be admitted that this definition does not capture everything that philosophers and mathematicians have meant by “constructive,” but that is not our aim here.

  24. This follows from the fact that there are models of ZF \(+\) DC in which every set of real numbers is Lebesgue measurable (Solovay 1970) and the fact that HB implies the existence of a non-Lebesgue measurable set.

  25. See Pruss (2018) for a reply.

  26. Thanks to two anonymous referees whose comments helped to improve the paper. Thanks also to Al Hájek, Ignacio Ojea Quintana, Katie Steele, Rush Stewart, and the participants in the ANU reading group on the philosophy of probability for discussing these topics with me.

References

  • Aliprantis, C. D., & Border, K. C. (2006). Infinite dimensional analysis: A Hitchhiker’s guide. Berlin: Springer.

    Google Scholar 

  • Augustin, T., Coolen, F. P., De Cooman, G., & Troffaes, M. C. (2014). Introduction to imprecise probabilities. Hoboken: Wiley.

    Book  Google Scholar 

  • Berti, P., Pratelli, L., & Rigo, P. (2013). Finitely additive equivalent martingale measures. Journal of Theoretical Probability, 26(1), 46–57.

    Article  Google Scholar 

  • Buskes, G. (1993). The Hahn-Banach theorem surveyed. Dissertationes Mathematicae 327.

  • de Finetti, B. (1931). Sul significato soggettivo della probabilià. Fundamenta Mathematicae, 17, 298–329.

    Article  Google Scholar 

  • de Finetti, B. (1937). La prevision: ses lois logiques ses sources subjectives. Annales de l’institut Henri Poincaré, 7(1), 1–68.

    Google Scholar 

  • de Finetti, B. (1972). Probability, induction, and statistics. Hoboken: Wiley.

    Google Scholar 

  • de Finetti, B. (1974). Theory of probability (Vol. 1). Hoboken: Wiley.

    Google Scholar 

  • de Finetti, B. (1990). Theory of probability (Vol. 1). Hoboken: Wiley.

    Google Scholar 

  • Dubins, L. E., & Savage, L. J. (1965). How to gamble if you must: Inequalities for stochastic processes. Newyork: Dover Publications.

    Google Scholar 

  • Dunford, N., & Schwartz, J. T. (1958). Linear operators part I: General theory (Vol. 7). New York: Interscience publishers.

    Google Scholar 

  • Easwaran, K. (2014). Regularity and hyperreal credences. Philosophical Review, 123(1), 1–41.

    Article  Google Scholar 

  • Foreman, M., & Wehrung, F. (1991). The Hahn-Banach theorem implies the existence of a non-Lebesgue measurable set. Fundamenta Mathematicae, 138(1), 13–19.

    Article  Google Scholar 

  • Freedman, D. A., & Purves, R. A. (1969). Bayes’ method for bookies. The Annals of Mathematical Statistics, 40(4), 1177–1186.

    Article  Google Scholar 

  • Hájek, A. (2003). What conditional probability could not be. Synthese, 137(3), 273–323.

    Article  Google Scholar 

  • Heath, D., & Sudderth, W. (1978). On finitely additive priors, coherence, and extended admissibility. The Annals of Statistics, 6(2), 333–345.

    Article  Google Scholar 

  • Heath, D. C., & Sudderth, W. D. (1972). On a theorem of de Finetti, oddsmaking, and game theory. The Annals of Mathematical Statistics, 43(6), 2072–2077.

    Article  Google Scholar 

  • Herrlich, H. (2006). Axiom of choice. Berlin: Springer.

    Google Scholar 

  • Howson, C. (2008). De Finetti, countable additivity, consistency and coherence. British Journal for the Philosophy of Science, 59(1), 1–23.

    Article  Google Scholar 

  • Jech, T. (2013). Set theory. Berlin: Springer.

    Google Scholar 

  • Jech, T. J. (1973). The axiom of choice. Amsterdam: North-Holland Publishing Company.

    Google Scholar 

  • Joyce, J. M. (1998). A nonpragmatic vindication of probabilism. Philosophy of Science, 65(4), 575–603.

    Article  Google Scholar 

  • Kolmogorov, A. N. (1950). Foundations of the theory of probability. New York: Chelsea Publishing Company.

    Google Scholar 

  • Lauwers, L. (2016). Why decision theory remains constructively incomplete. Mind, 125(500), 1033–1043.

    Article  Google Scholar 

  • Luxemburg, W. (1969). Reduced powers of the real number system and equivalents of the Hahn-Banach extension theorem. In W. Luxemburg (Ed.), Applications of model theory to algebra, analysis, and probability (pp. 123–137). Toronto: Holt, Rinehart and Winston.

    Google Scholar 

  • Narici, L., & Beckenstein, E. (1997). The Hahn-Banach theorem: the life and times. Topology and its applications, 77(2), 193–211.

    Article  Google Scholar 

  • Pawlikowski, J. (1991). The Hahn-Banach theorem implies the Banach-Tarski paradox. Fundamenta Mathematicae, 138(1), 21–22.

    Article  Google Scholar 

  • Pincus, D. (1972). Independence of the prime ideal theorem from the Hahn-Banach theorem. Bulletin of the American Mathematical Society, 78(5), 766–770.

    Article  Google Scholar 

  • Pincus, D. (1974). The strength of the Hahn-Banach theorem. In Victoria Symposium on Nonstandard Analysis, (pp. 203–248). Springer.

  • Pruss, A. R. (2014). Regular probability comparisons imply the Banach-Tarski paradox. Synthese, 191(15), 3525–3540.

    Article  Google Scholar 

  • Pruss, A. R. (2018). Underdetermination of infinitesimal probabilities. Synthese. https://doi.org/10.1007/s11229-018-02064-x.

  • Ramsey, F. P. (1931). Truth and probability. In R. B. Braithwaite (Ed.), The Foundations of Mathematics and Other Essays (pp. 156–198). London: Kegan, Paul, Trench, Trubner, & Co.

    Google Scholar 

  • Rao, K. B., & Rao, M. B. (1983). Theory of charges: a study of finitely additive measures, Pure and Applied Mathematics (Vol. 109). Cambridge: Academic Press.

    Google Scholar 

  • Savage, L. J. (1954). The foundations of statistics. New York: Wiley.

    Google Scholar 

  • Schechter, E. (1996). Handbook of analysis and its foundations. Cambridge: Academic Press.

    Google Scholar 

  • Schirokauer, O., & Kadane, J. B. (2007). Uniform distributions on the natural numbers. Journal of Theoretical Probability, 20(3), 429–441.

    Article  Google Scholar 

  • Seidenfeld, T. (2001). Remarks on the theory of conditional probability: Some issues of finite versus countable additivity. In V. F. Hendricks, S. A. Pedersen, & K. F. Jørgensen (Eds.), Probability Theory (pp. 167–178). Dordrecht: Klewer.

    Chapter  Google Scholar 

  • Solovay, R. M. (1970). A model of set-theory in which every set of reals is Lebesgue measurable. Annals of Mathematics, 92(1), 1–56.

    Article  Google Scholar 

  • Wenmackers, S., & Horsten, L. (2013). Fair infinite lotteries. Synthese, 190(1), 37–61.

    Article  Google Scholar 

  • Williams, P. (2007). Notes on conditional previsions. International Journal of Approximate Reasoning, 44(3), 366–383.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Philosophy, The University of Sydney, Sydney, Australia

    Michael Nielsen

Authors
  1. Michael Nielsen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael Nielsen.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nielsen, M. The strength of de Finetti’s coherence theorem. Synthese 198, 11713–11724 (2021). https://doi.org/10.1007/s11229-020-02825-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11229-020-02825-7

Keywords

Search

Navigation