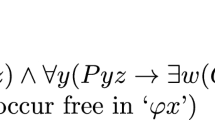Is Weak Supplementation analytic?

Abstract

Mereological principles are often controversial; perhaps the most stark contrast is between those who claim that Weak Supplementation is analytic—constitutive of our notion of proper parthood—and those who argue that the principle is simply false, and subject to many counterexamples. The aim of this paper is to diagnose the source of this dispute. I’ll suggest that the dispute has arisen by participants failing to be sensitive to two different conceptions of proper parthood: the outstripping conception and the non-identity conception. I’ll argue that the outstripping conception (together with a specific set of definitions for other mereological notions), can deliver the analyticity of Weak Supplementation on at least one sense of ‘analyticity’. I’ll also suggest that the non-identity conception cannot do so independently of considerations to do with mereological extensionality.

Philosophy can be strange—perhaps metaphysics especially so. But the dispute over Weak Supplementation is particularly odd. Weak Supplementation is an intuitive mereological decomposition principle governing proper parthood; it is frequently used in the philosophical literature on mereology. The disputants on the one hand seem to think that the principle is so natural that it is analytic; the very meaning of ‘proper parthood’ guarantees its truth. On the other hand, many metaphysicians (both past and present) have argued that Weak Supplementation is false, or endorsed metaphysical theories in clear violation of it, and have supplied an ever-growing list of potential counterexamples. This is strange, since, the dispute over the axiom appears meaningful and substantive; those involved seem semantically competent and don’t appear to be talking past one another.

The aim of this paper is to diagnose the source of the dispute. In Sect. 1, I’ll outline the main lines of the controversy, giving a run-down of most of the types of counterexamples to Weak Supplementation that have been put forward. In Sect. 2, I’ll suggest that the dispute has arisen by participants failing to be sensitive to two different conceptions of proper parthood—the outstripping conception and the non-identity conception. In Sect. 3, I’ll examine a number of different notions of analyticity and I’ll argue that, given the outstripping conception together with a specific set of definitions for other mereological notions, there’s at least one sense of ‘analyticity’ in which Weak Supplementation is indeed analytic. Finally, I’ll suggest that the analyticity of Weak Supplementation on the non-identity conception is deeply entangled with mereological extensionality.

1 The controversy

I’ll use P for the parthood predicate, PP for proper parthood, and O for mereological overlap. How we should understand these notions, and how precisely they should be formally defined, is part of what is at issue in the debate. But to fix ideas, we can think of parthood P as a form of parthood compatible with identity as a limiting case, and mereological overlap O as the relation that holds when things have parts in common. The Weak Supplementation principle (WSP), can be stated as follows:

Weak Supplementation   $\forall x \forall y (PPxy \rightarrow \exists z (Pzy \wedge \lnot Ozx))$

WSP states that whenever an object has a proper part, it has another part that does not overlap—that is mereologically disjoint—from the first. This is a straightforward statement of a basic decomposition intuition, the idea that when a proper part is ‘removed’ from a whole, there must be another ‘supplementing’ disjoint proper part. (This, of course, entails that no composite object can have exactly one proper part.)

Many philosophers have been struck by how natural Weak Supplementation seems, and have suggested that the principle analytically true, that it is partly constitutive of the notion of proper parthood. For example, Varzi (2008, p. 110) claims ‘This principle expresses a minimal requirement which any relation must satisfy (besides reflexivity, antisymmetry and transitivity) if it is to qualify as parthood at all.’ Simons (1987, p. 116) claims that ‘[Weak Supplementation] is indeed analytic—constitutive of the meaning of proper part’.¹

A growing number of metaphysicians have challenged the axiom and endorsed mereologies without Weak Supplementation. It is not difficult to conceive of mereological scenarios that appear to violate WSP. For instance, whoever thinks that a statue and the corresponding lump of clay are part of each other will find WSP unreasonable.² After all, such parts are coextensive; why should we expect anything to be left over when, say, the clay is ‘subtracted’ from the statue (Donnelly 2011, p. 230)?

Cotnoir and Bacon (2012) note that Weak Supplementation is inconsistent with the possibility of proper parthood loops. This is, in part, because WSP entails the irreflexivity of PP in any system where PP is transitive. Suppose PPxx. Then by WSP there must be some z such that Pzx and $\lnot Ozx$, which is impossible. So any purported counterexample to irreflexivity of proper parthood—any self-part—will be thereby serve as a counterexample to Weak Supplementation.

The growing literature surrounding the topic of mereology and time travel has delivered just such examples.³ Effingham offers the following scenario.

Imagine a cube, with each side measuring 10m, made of a homogeneous substance. [...] Not only do we take it back to a time that it previously existed at, but we use a shrinking machine and miniaturize by a factor of 100. We then remove a cube-shaped portion, with edges measuring 10cm, from the earlier, larger version of the cube and replace that portion with the miniaturized future version (which now fits perfectly). The cube is now a proper part of itself at that time. (Effingham 2010, p. 335)

Kearns (2011) has argued against irreflexivity, pointing out that if structured propositions are constructed mereologically, then e.g. the following proposition would appear to be a self-part.⁴

(p) Proposition p is abstract.

For different case, also due to Kearns (2011), self-similar shapes such as fractals might be said to contain themselves as parts in a sense other shapes do not. Indeed, the same could be said of abstract structures more generally. Gödel once claimed:

Nor is it self-contradictory that a proper part should be identical (not merely equal) to the whole, as is seen in the case of structures in the abstract sense. The structure of the series of integers, e.g., contains itself as a proper part and it is easily seen that there exist also structures containing infinitely many different parts, each containing the whole structure as a part. (Gödel 1944, p. 139).

Similarly, suppose one accepts a conception of immanent universals as being ‘wholly present’ wherever they are instantiated. Then it seems perfectly possible that, say, a universal such as whiteness is wholly present in some extended region, r, and also wholly present in subregions of r.

One last example may be drawn from the metaphysics of sets. Suppose we count a set’s members as among its parts;⁵ then non-wellfounded sets, i.e., sets that allow for membership loops (Aczel 1988),⁶ could easily bring about failures of irreflexivity. For instance, in Quine’s alternative set theory, New Foundations (1937), there exist certain self-membered singletons $\{a\} = a$. Such sets, called ‘Quine atoms’, could be considered part of themselves in a non-trivial way.

So much for self-parts. Weak Supplementation also entails the asymmetry of PP in systems where PP is transitive. Suppose that PPxy and PPyx. Then by transitivity we have PPxx which we have just seen is incompatible with WSP. So any purported counterexample to the asymmetry of PP will likewise be a counterexample to Weak Supplementation.

But some have argued for cases of symmetric parts.⁷ Sanford (1993) suggests the Aleph and the earth in a passage from Borges (1967), where the Aleph contains everything as a part, including the earth; and the earth contains the Aleph, since this sits on the cellar stairs in Beatriz Viterbo’s house.⁸ A similar passage appears in the Upanishads that outlines the structural relations between Brahman and persons:

In the center of the castle of Brahman, our own body, there is a small shrine in the form of a lotus-flower, and within can be found a small space. [...] This little space within the heart is as great as this vast universe. The heavens and earth are there, and the sun, and the moon, and the stars; fire and lightning and winds are there; and all that now is and all that is not; for the whole universe is in Him and He dwells within our heart. (Chandogya Upanishad, Sect. 8.1, in Mascaró 1965, p. 120)

Jones (2009, 2010) and Priest (2014a, ch. 11) suggest the same could be said of the ‘Net of Indra’—a net of jewels that stretches infinitely in every direction, but in which each jewel is contained in every other, symbolizing the interconnectedness of the universe. Cotnoir (2017) points out these structures appear in Christian theology, for example in the mutual indwelling of the persons of the Trinity.

Structured propositions, too, have been put forward as counterexamples to asymmetry.⁹

Suppose that the universe exists [...] a thing such that absolutely everything is a part of it. [...] Assuming there is a unique such thing, let’s name it U. According to a popular view of semantic content, ‘U exists’ semantically encodes a singular, structured proposition that has U itself as a constituent as well as the property of existing. By hypothesis, this proposition is a proper part of U. But U is in turn a proper part of the relevant proposition. (Tillman and Fowler 2012, p. 525)

Again this relies on the assumption that constituents of propositions are parts of those propositions.¹⁰

Time travel might call asymmetry into question: consider a case from Kleinschmidt (2011). Clifford is a dog statue which was made partly of other, smaller statues, including Kibble. But Kibble, too, is made partly of other statues, including a time-traveling future version of Clifford himself, suitably reduced in size. As a result, it would seem as though Kibble is a proper part of Clifford that has Clifford as a proper part.

So much for asymmetry. Weak Supplementation also rules out the ‘empty’ or ‘null’ object—an object that is part of everything. Suppose there was such an object n such that for all y, Pny. Then if there is any y distinct from n, we would have PPny and hence by WSP there must be something that is part of y and disjoint from n. But since n is part of everything, nothing is disjoint from it. That means that any metaphysics that accepts the existence of a null individual must reject (or recast) Weak Supplementation.

But metaphysicians have accepted such an object. Some authors have urged that the notion of a null object “is no better or worse than that of the null class” (Martin 1965, pp. 723f). Others have argued that “there is no strong reason for rejecting the empty individual” (Mosterin 1994, p. 521). Even Carnap (1952) thought a null object would be a ‘natural and convenient choice’ for certain purposes (Carnap 1947, p. 37).¹¹ Other philosophers who found it reasonable to posit a mereologically null entity include Bunt (1985) in the context of his ensemble theory, Meixner (1997) for the mereology of states of affairs, Humberstone (2000) in the domain of spatial regions, and Zalta (2016) in connection with the mereology of concepts.¹²

There have also been attempts to offer substantive philosophical interpretations of the notion of a null object. For instance, Giraud (2013) construes it as a Meinongian individual lacking all nuclear properties,¹³ Priest (2014a, b) as a Heideggerian ‘nothing’, and Casati and Fujikawa (2017) as the complement of the fusion of all existing and nonexisting objects, while others have gone as far as construing the null object as the omnipresent devil (Oppy 1997, fn. 19) or, at the opposite extreme, as the ultimate incarnation of divine omnipresent simplicity (Hudson 2006, 2009). Whatever the status of the empty object, it’s clear that disputants in this debate will have to involve a dispute over WSP.

So far our examples have been largely indirect: we find potential counterexamples to WSP by finding potential counterexamples to other (widely held) mereological principles entailed by WSP. But there are plenty of direct putative counterexamples, going back to the beginnings of mereology itself. For example, the theory of extensive connection in Whitehead (1929) according to which no boundary elements are included in the domain of quantification: on this theory, a topologically closed region includes its open interior as a proper part despite there being no boundary elements to distinguish them.¹⁴ Compare Yablo (2016):

A closed sphere of radius 1 properly includes its interior. But its interior has the same volume as the sphere. A difference, if there were to be one, would not take up any space, by additivity of measure. But then there can’t be a difference. (p. 144)

Relatedly, Forrest (2002) argues against WSP on the basis of the possibility of gunk and considerations from measure theory.¹⁵

Other examples are sprinkled throughout the history of metaphysics: consider the view, arguably held by Aquinas, according to which the human person survives physical death along with her soul.¹⁶ On the understanding that persons are hylomorphic composites, and that two things cannot become one, the view implies that upon losing her body a person will continue to exist with only one proper part—the soul.¹⁷ Another case in point is the theory of accidents in Brentano (1981), according to which a mind is a proper part of a thinking mind even though there is nothing to make up for the difference.¹⁸ Similarly, in the theory of qua-objects in Fine (1982), every basic object (e.g. John) qualifies as the only proper part of its incarnations (e.g. John qua philosopher, John qua husband, etc.). A similar counterexample, from the domain of intensive magnitudes, is offered by Geach (1991, p. 254).

Indeed, any case of material coincidence resulting from mereological diminution, as in the Deon and Theon (Sedley 1982) and its modern variant of Tibbles and Tib (Wiggins 1968), would seem to be at odds with WSP: after the diminution, there is nothing that makes up for the difference between what was a proper part and the whole with which it comes to coincide.

Time travel examples (like the above counterexamples to irreflexivity) can pose a direct threat to WSP: if a brick wall may be made entirely of one time-traveling brick, then there won’t be any parts of the wall disjoint from any other parts (Effingham and Robson 2007). Indeed, independent of time travel, multi-location generally can cause trouble for WSP, as argued by Donnelly (2010) and Kleinschmidt (2011).

Sets, too, may directly provide counterexamples to Weak Supplementation. In the context of mereological construals of set theory, Caplan et al. (2010, p. 512) express some sympathy with the rejection of WSP. Interpreting PP as the ancestral of the set membership relation we can find some countermodels: the singleton of the empty set, for instance, or the singleton of any urelement, would have only one proper part on the suggested construal.¹⁹

It is true that WSP has considerable intuitive appeal; some have relied on this intuition in an attempt to discard all of the above theories and scenarios as implausible. But one might also turn things around and regard the plausibility of such theories as a good reason no to accept WSP unrestrictedly, as argued e.g. by Donnelly (2011), Smith (2009), Oderberg (2012), and Lowe (2013). They certainly do pose a challenge to its analyticity.

2 Proper parthood and non-identity

In this section, I want to suggest a possible source of the dispute between those who think Weak Supplementation is analytic, and those who have contended that failures of the principle are not only conceivable, but metaphysically possible, and maybe even actual.

It is useful to outline two distinct conceptions of the notion of proper parthod: what I will call the outstripping conception, and the non-identity conception. I say ‘conceptions’ here because I do not wish to prejudge the issue of whether these distinct ways of thinking about proper parthood correspond to distinct metaphysical relations. In fact, the question of whether or not these conceptions could even correspond to distinct relations is part of what is up for debate.

I’ll begin with the more familiar: the non-identity conception, according to which a proper part is just a part distinct from the whole. Sometimes the proper parthood relation PP is simply defined in such a way.²⁰

Non-Identical Proper Parthood   $PP_{1} :\equiv Pxy \wedge x \ne y$

According to this conception, the salient difference between a proper part and an improper part is simply that a proper part is not identical to the object it is part of, whereas an improper part is identical to the object it is part of. This definition explicitly ties a mereological relation to the relation of numerical identity (or better, numerical distinctness). And if Leibniz’s Law governs the identity relation, then any part which is discernible in any way from the object it is part of will count as a proper part. As such, this conception is explicitly tied to qualitative discernibility.

By contrast, we might rather have in mind the outstripping conception of proper parthood. According to this conception, a part of an object counts as a proper part of that object whenever the object ‘outstrips’ or ‘exceeds’ or ‘isn’t subsumed by’ its part. This intuitive thought can be easier to formulate using the idea of a ‘remainder’. The idea is, roughly, that whenever an object is a proper part of another, then subtracting that part must leave something (or things) of the original object behind—there must be some remainder.

There are some mereological definitions of proper parthood that either explicitly or implicitly appeal to the outstripping conception. Consider, for example the following definition following Goodman (1951).²¹

Strict Proper Parthood   $PP_{2} :\equiv Pxy \wedge \lnot Pyx$

We can read this definition as claiming that x is a proper part of y if it is included in y but does not also include y. The idea that y is not included in x as a part suggests that y outstrips x or ‘exceeds’ x in some way. This definition does not mention identity, and so is not (at least not explicitly) tied to qualitative discernibility.²²

Though $PP_{1}$ does not logically entail $PP_{2}$, it might do so in the presence of other axioms, notably:

Antisymmetry   $Pxy \wedge Pyx \rightarrow x=y$

In particular, whenever P is antisymmetric we will have the equivalence of Non-Identical Proper Parthood and Strict Proper Parthood. But this is unsurprising, since antisymmetry is another principle that explicitly ties parthood to identity. Regardless of whether or not the real parthood relation satisfies this axiom, we can distinguish between the two conceptions.

There are other ways of making the outstripping conception precise. For example, consider the following definition (used by Uzquiano (2011)):

Proper Proper Parthood   $PP_{3}xy :\equiv Pxy \wedge \exists z(Pzy \wedge \lnot Ozx)$

$PP_{3}$ makes the outstripping thought explicit by stating that proper parts are parts-with-remainder. And again, $PP_{1}$ does not logically entail $PP_{3}$ absent other principles, notably Weak Supplementation (with $PP_{1}$ in the antecedent).

There are other versions of the outstripping conception in the literature, too. If we take proper parthood as primitive (and guided by the outstripping conception), then we might agree with Rea (2010) who objects to defining parthood in the usual way:

Parthood 1   $P_{1}xy :\equiv PPxy \vee x = y$

This definition suggests that x is an improper part of y iff $x = y$. But this improperly ties together improper parthood and identity; after all, one might wish to allow for discernible (hence numerically distinct) objects neither of which mereologically outstrips the other. (Think of the statue and the clay.) That is, there might well be a difference which isn’t a mereological difference. Rea offers another definition of P (from Simons (1987, p. 112).

Parthood 2   $P_{2}xy :\equiv (\exists z PPzx \rightarrow \forall$ $z(PPzx \rightarrow PPzy) \wedge (\lnot \exists z PPzx \rightarrow (PPxy \vee x = y))$

This definition is compatible with non-identical improper parts i.e. improper because they do not outstrip.

A final alternative is to define P in terms of mereological overlap (following Goodman (1951)), taking O as primitive.

Parthood 3   $P_{3} xy :\equiv \forall z (Ozx \rightarrow Ozy)$

This definition of parthood allows us to prove reflexivity and transitivity of $P_3$ via logic; but in this case Antisymmetry is equivalent to $\forall z((Ozx \leftrightarrow Ozy) \rightarrow x=y)$, an extensionality principle of overlap. As before $PP_{1}$ will clearly codify the non-identity conception, but now $PP_{2}$ will explicitly correspond to the outstripping conception, as $\lnot Pyx$ just means that y does not include all the x-overlappers.

The outstripping conception of proper parthood most clearly motivates Weak Supplementation; it generates the requisite intuition that there’s a mereological and not merely qualitative difference between an object and its proper part. In fact, this is often how Weak Supplementation is motiviated; e.g. Koslicki (2008, p. 168) explicitly motivates Weak Supplementation using the ‘outstripping’ conception, by appeal to the notion of a remainder when one mereologically ‘subtracts’ a proper part from an object.

In what follows, I want to suggest that the vast majority of the proposed counterexamples to WSP are a result of not clearly distinguishing between these two conceptions of proper parthood. That is, we might use the non-identity conception to generate the ‘it’s a proper part!’ judgement and then show there’s no outstripping going on; or we might use the outstripping conception to generate the ‘it’s a proper part’ judgement and then show it’s a case of identity.

Recall that our purported counterexamples were broadly of four types: (i) self-parts, (ii) mutual parts, (iii) empty objects, and (iv) direct counterexamples. In the case of the self parts, these all clearly use the outstripping conception to generate the judgement that something is a ‘proper part’. Mainly, this relies on the use of non-mereological construals of outstripping.²³ For example, in the case of the time travelling cube, we use spatial extent to generate the ‘outstripping’ intuition. The cube is properly contained in itself! A similar thing happens in the case of immanent universals being instantiated in proper subregions. In the case of fractals, self-similar patterns, and in propositions, it is an object’s position in a structure (or substructure) that generates the outstripping intuition. A proposition is a proper component of itself! A set is a member of itself! The structure of the whole integers is repeated in some of its proper substructures! We judge that something outstrips itself by trading on non-mereological intuitions about ‘position’.

In the case of mutual parts, the reverse story appears to be true. We generate the judgement that ‘it’s a proper part’ by clearly distinguishing between an object and its part. But then show the part fails to outstrip the whole. In the case of the Aleph, it’s clear enough that the Aleph is not identical to say, Beatriz’s house. But because the Aleph is contained in that house, and that house (along with everything else) is contained within the Aleph, neither of these entities can be said to outstrip the other.²⁴ Mutatis mutandis for the lotus flower, the Net of Indra, and the mutual indwelling within the Trinity. A similar story holds for propositions containing the universe as one of its constituents. In this case, we start with the non-identity judgement (‘the universe isn’t a proposition!’), and since the universe is defined to include everything as a part, we get a failure of outstripping. Clifford and Kibbles are distinct, but Kibbles does not outstrip Clifford since it contains Clifford as a part.

As for the counterexamples involving the empty object, these cases are slight different from the above. The empty object may be stipulated to be part of everything, or perhaps that result can be delivered by conceiving of the empty object as the fusion of any unsatisfiable predicate. We then can use the non-identity conception of proper part to get the judgement that, since the empty object isn’t identical to the Eiffel Tower, it must be a proper part of the Eiffel Tower. But then we achieve violations of the outstripping conception when we focus on the ‘remainder’ when the empty element is ‘removed’. If the empty object is really empty, then what is leftover of the Eiffel Tower when it is removed? Clearly, the whole Eiffel Tower itself. There is no prospect of any proper remainder, and this seems to violate the outstripping conception of proper parthood.

Finally, we turn to the direct counterexamples. For the case of topologically closed vs. open regions, the proper parthood judgement is generated by the non-identity conception, and yet if boundaries aren’t real elements of the domain, there is nothing to make up the mereological difference. Exactly parallel considerations apply to the bodiless soul, the thinking mind, qua-objects, singletons, and intensive magnitudes. Similarly, the time-travelling brick qualitatively differs from the wall (as a whole), so is a non-identical proper part, but the wall does not outstrip the brick in the sense that no part of the wall is ‘free from’ some part of the brick. In the case of Deon and Theon, the judgement proceeds temporally: we are forced to their distinctness (by considering their past), and forced to their co-extensiveness (and hence the failure of outstripping) due to their current state of coincidence.

I think all of the purported counterexamples to WSP can be explained as a result of collapsing the two conceptions of proper parthood. Indeed, WSP on the non-identity reading of PP seems to enforce such a collapse. And it is by playing off these differences that we can generate puzzlement.

3 Analyticity

I now want to turn to the purported analyticity of WSP. To adjudicate these claims, it is necessary to be clear on the various notions of analyticity that might be in play.²⁵ For instance, following Boghossian (1996) one can distinguish the following three sense of analyticity:

• Frege Analyticity   Weak Supplementation may be transformed into an logical truth by virtue of substituting synonymous terms.

• Epistemic Analyticity   anyone who understands the concept of proper parthood is in a position to know a priori that Weak Supplementation is true.

• Metaphysical Analyticity   Weak Supplementation is true by virtue of the meaning of the terms that appear in it—principally, the meaning of ‘proper parthood’.

Is WSP analytic in any of these senses? At first blush, WSP doesn’t appear meet the conditions for Frege-analyticity, since given the relatively widespread disagreement over that principle, one cannot plausibly suggest that ‘x is proper part of y’ and ‘there’s a part of y that doesn’t overlap x’ are synonymous at least in common philosophical parlance. Similar considerations apply to epistemic analyticity; disputants in the debate over WSP appear to understand their use of ‘proper part’, and since they disagree on its truth the disputants can’t all be said to know apriori that it is true. Perhaps, disputants don’t really understand the concept, or perhaps that they are in a position to know even if they refuse to believe, etc. Relevant here, of course, is the case for semantic plasticity in Williamson (2007). But still, analytic truths may be (often are) epistemically opaque, which takes us to metaphysical analyticity. It may well be the case that the meaning of ‘proper parthood’ makes WSP true. There are at least two ways in which that might be.

First, PP and the corresponding concept of proper parthood are, after all, technical terms—they are not strictly speaking part of ordinary language, even if they have some philosophical cache. It is clear that, when laying down a set of axioms, one is free to stipulate what one means by PP. In this case, if what one means by PP is ‘whatever satisfies the axioms’, then of course those very axioms will be true of PP by virtue of the meaning of PP. This stipulative definition is a form of metaphysical analyticity: it picks out a precise concept from a range of candidate concepts by laying down a set of axioms for it. But notice in this case, metaphysical analyticity is fairly philosophically thin. None of the other candidate concepts are thereby ruled out as incorrect or philosophically mistaken. It wouldn’t vindicate the view that “denying WSP is not a credible option” (Effingham and Robson 2007, p. 635). A philosopher’s rejection of WSP is simply a strong reason to think that she isn’t using that stipulative definition.

Not all axiomatic projects are stipulative like this. Take for example the Peano axioms for arithmetic. We don’t take them as mere stipulative definitions that precisely pin down one candidate meaning for ‘plus’, leaving other candidate meanings to be philosophically viable. Rather, the Peano axioms are accepted because they correctly identify the arithmetic operations. Rather than being stipulative, such definitions are Socratic. So, a second route to metaphysical analyticity would be to say something similar about proper parthood and PP. Despite the technical nature of these terms, their meanings are not merely stipulated; the axioms and definitions are answerable to the correct metaphysical theory, or perhaps to the ordinary meaning of ‘part’. This is precisely why thought experiments are relevant for testing the truth of such axioms.

Both routes to analyticity face a difficulty, however. Some have argued that some types of definitions cannot be metaphysically analytic—particularly those that are existence entailing. Many philosophers have argued that if the consequent of a conditional is an existence claim, then the conditional can be analytic only if the antecedent makes the same existence claim.²⁶ WSP is a conditional whose consequent is an existence claim.²⁷ Hence, according to the above constraint, WSP cannot be metaphysically analytic unless the antecedent contains the same existence claim.

There are ways out of the difficulty, however. As we have seen there are various ways of making the outstripping conception precise. And on the definition of proper proper parthood—$PP_{3}xy$ does in fact contain an explicit existence claim. And precisely the one needed to validate WSP. So if one takes $PP_{3}$ to be a stipulative definition, then we have a clear case of metaphysical analyticity that does not violate the existence-entailment constraint. In fact, it’s worth noting that if $PP_{3}$ is taken as a stipulative definition, we have a straightforward case for Frege Analyticity. After all, on the $PP_3$ definition, WSP becomes

$$\begin{aligned} (Pxy \wedge \exists z(Pzy \wedge \lnot Ozx)) \rightarrow \exists z(Pzy \wedge \lnot Ozx) \end{aligned}$$

which is a logical truth of the form $A \wedge B \rightarrow A$. Similarly, but less plausibly, if one takes $PP_{3}xy$ to be the correct formal definition of (the oustripping conception of) proper parthood, one could make the case for metaphysical analyticity in a more robust sense.

What about other ways of making the outstripping conception precise? Consider the Weak Supplementation principle for Strict Proper Parthood $PP_{2}xy$.

Strict Supplementation   $\forall x \forall y (PP_{2}xy \rightarrow \exists z (Pzy \wedge \lnot Ozx))$

Now, suppose further we are treating O as primitive and employ the Goodmanian definition of parthood in terms of overlap where $P_{3}xy$ is equivalent to $\forall z (Ozx \rightarrow Ozy)$. Notice that the antecedent of Strict Supplementation is a disguised conjunction, the second conjunct of which is equivalent to $\lnot \forall z(Ozy \rightarrow Ozx)$, i.e. $\exists w (Owy \wedge \lnot Owx)$. This is already fairly close to the implicit existence claim in WSP’s consequent. And given the (uncontentious) concept of overlap O, we know that where Owy, there is some z such that Pzy (and Pzw for that matter), and since $\lnot Owx$ then $\lnot Ozx$ too.

So, we derived the consequent of WSP from nothing but the assumption of its antecedent, together with an appeal to the following principle for O:²⁸

Overlap   $Oxy \leftrightarrow \exists z (Pzx \wedge Pzy)$²⁹

We can say then, that given strict proper parthood, the question of the analyticity of Weak Supplementation boils down to a question of whether Overlap is analytic. There is virtually no controversy over Overlap in the literature; and some of us would be willing to contend that it (not just stipulatively but maybe even Socratically) correctly defines overlap.³⁰

Again, it is worth noting that, in an antisymmetric setting, Strict Supplementation is equivalent to WSP. Yet it is logically weaker.³¹ But the above considerations show, I think, that even for those who reject antisymmetry, there is a plausible case for the analyticity of Strict Supplementation, and by extension the analyticity of Weak Supplementation on the oustripping conception of proper parthood.

What about the non-identity conception of proper parthood? Is there any hope for Weak Supplementation to be considered metaphysically analytic on that definition? Recall that PPxy just means $Pxy \wedge x \ne y$ on the non-identity conception. We know that, by Leibniz’s Law, non-identity implies discernibility; that is, where x and y are distinct, there’s some $\varphi$ such that $\varphi (x) \wedge \lnot \varphi (y)$. This thought doesn’t lead anywhere, however, unless we are willing to assert that distinct objects must be mereologically discernible—that the $\varphi$ in question has to involve our mereological primitive in some ineliminable way.³² But that assumption is tantamount to (the contrapositive of) mereological extensionality—the class of principles that claim mereological indiscernibility implies numerical identity—perhaps the most controversial class of principles in all of mereology.

To make this thought concrete, suppose we are working in a system with O as our mereological primitive. For conditional proof of WSP on the non-identity conception, assume that $PP_{1}xy$. Since $x \ne y$, we might insist that x and y to be O-discernible, to the effect that $\exists z((Ozx \wedge \lnot Ozy)$ or $\exists z(Ozy \wedge \lnot Ozx)$. The former case is ruled out by Pxy, which leaves the latter $\exists z(Ozy \wedge \lnot Ozx)$. But that’s effectively the consequent to WSP. So, it might be argued that proper parthood, on the non-identity conception, contains an implicit existential commitment; and so WSP is metaphysically analytic.

That argument crucially relies on the following hotly contested principle.

Extensionality of Overlap   $\forall x \forall y (\forall z(Ozx \leftrightarrow Ozy) \rightarrow x = y)$

We might have serious doubts about any claims to the analyticity of this. Even if it is true, is it plausibly true simply by virtue of the meaning of ‘overlap’?³³ Crucially: I think these considerations give us grounds for suspicion that those contending for the analyticity of WSP on the non-identity conception are smuggling in a commitment to mereological extensionality.³⁴

By contrast, on the outstripping conception of proper parthood, Weak Supplementation is not tied up with extensionality. Indeed, non-extensionalists can agree that there are genuine senses of ‘analytic’ on which Weak Supplementation counts.³⁵