Introduction

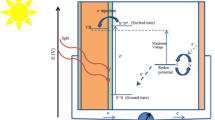
During the past three decades, there have been persistent attempts to find effective alternatives to silicon cells. Dye-sensitized solar cells DSSC [1, 2] are a promising candidate for the next generation of solar cells, owing to their economically, transparency and cheap cost make them attractive as potential candidates for electricity-generating ‘smart window' applications [3,4,5]. In DSSC, a photosensitizing dye, adsorbed onto the surface of a wide bandgap semiconductor such as TiO2, ZnO, or SnO2, absorbs light, followed by injection of the photoelectron from the dye to the conduction band of the semiconductor leaving oxidized dye molecules behind. This injected electron is transported to the counter-electrode, i.e., initiating the electrical current in the solar cell. The dye is restored to its ground state by electron transfer from the electrolyte (typically, I−/I3−) resulting oxidation of I− to I3− ions. The oxidized I3− ions diffuse to the counter-electrode, where they are reduced to I− with the aid of a catalyst that is deposited on the counter-electrode [6].

To enhance the efficiency of photoelectronic conversion in DSSC, dyes must be designed with the following properties in terms of electronic structure. (i) To ensure efficient electron injection into the semiconductor conduction band, the dye molecules must form a strong bond to the surface of the semiconductor through anchoring groups such as carboxylates. (ii) The dye should absorb light over a large spectral range extending from the UV to the near IR region to achieve high light harvesting efficiency. (iii) Correct alignment of the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) energy levels with those of the TiO2 conduction band and the iodide tri-iodide (I−/I−3) red–ox electrolyte, so the LUMO must be slightly higher than the conduction band of the semiconductor to enhance efficient charge injection, and the HOMO must be sufficiently low in energy for efficient regeneration of the oxidized dye by the redox electrolyte. (iv) The electron transport from the dye to the semiconductor must be fast enough to avoid undesirable recombination to the dye’s ground state [7, 8].

Ruthenium (Ru) complexes such as N3, N-719, and black dyes are the most promising dye sensitizers. However, there are significant drawbacks to employing metal-based dyes as sensitizers, including the complexity of the synthesis procedure, the difficulty of purification, and the high cost of the used materials [9]. As a result, metal-free dyes are particularly desirable because to their inexpensive cost, structural versatility, and high molar extinction coefficients which make them as an alternative to Ru-based sensitizers [10]. Highly efficient organic dyes should have special structure of D-π-A (donor–pi–acceptor) configuration with long-alkyl chain to provide better charge separation and to prevent aggregation on the semiconductor’s surface and then reduce the recombination. Upon illumination, electrons are excited and transferred from the donor to the acceptor through the π-conjugated bridge. Electrons are then injected into the semiconductor layer because of the coupling between the Ti-based 3d orbitals and the dye molecules’ LUMO [11, 12].

Among metal-free organic dyes, Coumarin dyes have been developed as photosensitizers in DSSC applications and have reached high conversion efficiencies up to 8% [13]. Coumarin-6 (C6), a chromophore of the highly conjugated coplanar molecule, has been identified and employed as a fluorescent dye for staining organelles or medical materials [14, 15] and as a high-gain medium in tunable and amplifier lasers [16, 17]. Additionally, C6 has generated substantial attention in optoelectronic applications after its successful introduction as an effective dopant in organic light-emitting diodes [18, 19]. C6 is a useful organic material for optoelectronic devices due to its comparatively high melting point of roughly 220 °C, good surface shape stability, and effective light emission [20].

The excited electrons from the dye molecules are injected into the semiconductor conduction band through the acceptor group; hence, the acceptor group plays a critical role in dye anchoring, optical absorption, and electron transfer process. In this regard, modifications to the acceptor moiety of dye sensitizers may significantly alter their electrical and photovoltaic characteristics. Interestingly, several functionalized acids have been successfully used as an efficient acceptor group in the majority of D-π-A dyes, owing to their strong electron-withdrawing characteristics and ability to attach to the semiconductor surface [21, 22].

Prior to conducting experimental testing of dyes in DSSC applications, it is critical to understand the dyes’ molecular characteristics and modifying its structure with potential units. The validity of the new designed dyes as sensitizers can be the theoretical investigated by evaluating many important parameters such as the critical geometrical parameters, photophysical properties, and electronic properties. For this purpose, theoretical calculations based on density functional theory (DFT) and time-dependent DFT (TDDFT) methods has been used to predict the electronic structures, photophysical properties, and other characteristics of dye molecules. Utilizing such a theoretical approach may significantly bring down the cost of developing efficient dyes synthetically.

Based upon the above considerations this work is dedicated, so that two anchoring groups’ Carboxylic acid and Cyanoacrylic acid have been attached to coumarian-6 dye in aim to design new sensitizers dyes C6X and C6N, respectively. Density functional theory (DFT) and time-dependent DFT (TD-DFT) calculations were used to understand the effect of different anchoring groups on the electronic and photophysical properties of C6 dye and hence the photovoltaic performance.

Computational methods

The geometric optimization of the ground-state structures of the studied dyes was performed without any symmetry restriction by DFT calculations combined with the hybrid functional of exchange–correlation B3LYP [23] using the 6-31G (d,p) basis set. Frequency analyses were carried out at the same level of theory to confirm that the optimized structures are true global minima showing the minimum value of the optimal potential energy surface (no imaginary frequency was observed). The optimized ground-state geometries are utilized to calculate the HOMO, LUMO, and band gap energy values and to get the frontier molecular orbitals (FMOs) distribution. TD-DFT calculations were carried out at B3LYP/6–31 G(d,p) level of theory to calculate the UV–vis absorption spectra and to understand the photophysical properties of the dyes such as the vertical excitation energies, oscillator strengths (f), and the contributions of the molecular orbitals responsible for the transition and their percentage of composition. The solvent effect was employed with dichloromethane (DCM) as a solvent by using an integral equation formalism polarizable continuum model (IEF-PCM) [24] to make a reasonable prediction of the experimental outcomes. To investigate the electron injection mechanism from the dye to the semiconductor interface (i.e., dye/TiO2 anatase (101) interface), the (TiO2)9 cluster has been adopted to represent the surface of the TiO2 semiconductor surface. The DFT and TD-DFT calculations of the dye/TiO2 complexes were performed using the B3LYP/6-31G (d,p) method in DCM. All calculations were performed using a suite of the Gaussian 09 packages [25].

Results and discussion

Geometric structures of isolated dyes and dye/TiO2 complexes

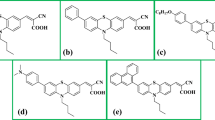
To build the model molecule, a carboxylic acid and cyanoacrylic acid as an anchoring group were attached to Coumarin-6 Dye C6 to design a D–π–A organic dye named as C6X and C6N, respectively, for DSSC application as illustrated in Fig. 1. A diethylamino coumarin moiety represents the donor, benzothiazole moiety as the π spacer, and carboxylic acid or cyanoacrylic acid as anchoring (acceptor) group.

Fig. 1
figure 1

Molecular structure of new designed D-π-A dyes

Full size image

The optimized geometries of the new designed C6X and C6N dyes were obtained using the B3LYP/6-31G(d,p) method in DMC solution and shown in Fig. 2, and Table 1 summarizes some geometrical parameters. It is clear from Table 1 that the dihedral angle φ1 are − 179.79 and − 179.26 for C6X and C6N, respectively. The larger dihedral angle values near to 180° implies that the examined dyes have stronger conjugation effect between π-spacer and acceptor (π-A), indicating significant intramolecular charge transfer (ICT) and successful injection of excited state electrons into the TiO2 conduction band. The values of C–C bond length d1(1.484 Å and 1.448 Å) and d2 (1.459 Å and 1.456 Å), being between that of a single C–C bond (1.54 Å) and a double C = C bond (1.34 Å), implying a fairly strong bond. The shorter value of the length of bridge bonds between π-spacer and acceptor (d1) and between π-spacer and the donor (d2) favored the ICT within the D-π-A dye molecules [26].

Fig. 2
figure 2

Optimized geometries of the studied structures

Full size image
Table 1 Selected bond lengths (d, in Å) and dihedral angles (φ, in degree) of the studied structures
Full size table

The dye adsorbed on the semiconductor surface (dye/TiO2 in this study) was also studied to get more reliable information regarding how the dye adsorbs on the surface of the semiconductor in terms of its electronic structure and optical properties. Figure 2 shows the optimized structure of the dye/TiO2 complexes. In the dye/TiO2 complexes, carboxylic acid binds onto TiO2 surface via different adsorption modes, such as monodentate bridging, bidentate bridging, and bidentate chelating [10, 26].

The adsorption of Coumarin derivatives on the TiO2 anatase (101) surface have been studied using different adsorption modes [26, 27], which concluded that the most stable adsorption mode is, in general, the bidentate chelating configuration. Additionally, this chelating configuration has been reported [28,29,30] to be favorable for dyes with carboxylate groups that are adsorbed on TiO2 anatase surfaces. In the bidentate chelating configuration, O–Ti bonds are formed between the two O atoms of the carboxylic acid in the dye molecules and the 5-bond Ti atom, while the remaining H atom of the carboxylic acid group transferred to a nearby surface O of the (TiO2)9 cluster [21, 31].

The starting geometry of the (TiO2)9 anatase cluster was obtained from the literature [26]; this cluster size is large enough to reproduce properly the electronic and optical properties of some dye/TiO2 complexes [32]. The computed Ti–O bond lengths are in the range of 2.08–2.1 Å, showing that the dye and TiO2 have a strong interaction. The optimized Cartesian coordinates of our studied structures are available in supporting information file.

Frontier molecular orbital and electronic properties

It is known that the intramolecular charge transfer (ICT) is closely related to the frontier molecular orbital energy levels (FMOs) and its distribution. Figure 3 shows the highest occupied molecular orbitals (HOMO) and the lowest unoccupied molecular orbitals (LUMO) energy levels and HOMO–LUMO energy gap (ΔHL) of the studied structures calculated at the B3LYP/6-31G(d,p) level of theory. The energies of the HOMO and LUMO with their calculated energy gap (ΔHL), ELUMO—ECB(TiO2), as well as (I−/I−3)—EHOMO energies barriers (eV) were estimated from the optimized ground-state geometries for the studied structures which are listed in Table 2.

Fig. 3
figure 3

Calculated ground states HOMO and LUMO energy levels (in eV)

Full size image
Table 2 HOMO, LUMO energies, HOMO–LUMO gap (ΔHL), (I−/I−3)—EHOMO and ELUMO—ECB(TiO2) of the studied structures
Full size table

Attaching the anchoring groups to the C6 Dye decreases the HOMO and LUMO values of the C6 Dye. As Fig. 3 demonstrated, the HOMO levels of the C6X and C6N dyes are under the redox potential of I /I3 (− 4.80 eV) [33]. This suggests that the oxidized dye could be restored by getting electrons from electrolyte, resulting an efficient charge separation. The LUMO levels of C6X and C6N dyes are above the TiO2 conduction band (− 4.00 eV) [34], which ensure electron injection from the excited dye into the semiconductor substrate. The values of HOMO and LUMO indicate that the newly designed dyes are good photo-sensitizer candidates and meet the application of DSSCs. Also, the HOMO–LUMO energy gap decreases from 3.29 eV in the case of C6 Dye to 3.14 eV and 2.69 eV by attaching the -COOH and -CN group, respectively, which mean that the newly designed dyes absorb at a higher wavelength. One can notice that C6N dye has the smaller HOMO–LUMO gap which enables the harvesting of more sunlight in the long-wavelength region of the spectrum. After adsorption of the dyes on the TiO2 surface, there is a noticeable drop in the LUMO level of the dye/TiO2 complexes compared to their isolated dyes, while there is no obvious change in the HOMO level.

In sensitizers with push–pull structure containing π-conjugated spacer linking an electron donor (D) to an electron acceptor (A) group, when a photon is absorbed, an electron is transferred from the D part to the A part, resulting in a D+-π-A− excited state. Ideally, the electron completely transfers from the donor (D) and localizes on the acceptor (A) upon excitation. A strong electronic coupling between the excited state of the dye and TiO2 conduction band can be achieved if there is a significant contribution of the acceptor group (A) to the LUMO which is the final state in the charge transition from HOMO to LUMO. Figure 4 shows the computed isodensity surfaces for the HOMO and LUMO of the studied structures.

Fig. 4
figure 4

Contour plots of HOMO and LUMO orbitals for the studied structures

Full size image

As shown in Fig. 4, for the new dyes C6X and C6N, the electron densities of the HOMO were extended to the donor up to the benzothiazole moiety (π spacer), whereas the electron densities of the LUMO is plentifully distributed on π-A part and small amount distributed at donor part.

The electron distribution of the molecular orbitals shown in Fig. 4 demonstrated that electron injection occurred from the donor part to the acceptor part of the dye through the conjugated bridge. In the case of the dye/TiO2 complexes, Fig. 4 shows that, similar to the isolated dyes, the electron densities of the HOMO were distributed from the donor part to the π spacer, while the electron densities of the LUMO were almost entirely concentrated on TiO2, indicating that the LUMO is located close to the acceptor group (carboxylic acid or cyanoacrylic acid) which enhances the orbital overlap with the 3d orbitals of Ti. This allowed the excited electrons to be easily injected into TiO2 via the anchoring unit, resulting in an increase in JSC.

Density of states (DOS)

An essential aspect to consider when determining how the characteristics of the DSSC working electrode impact the photovoltaic performance of DSSC devices is the energy alignment of the interface structure of dye/TiO2 relative to other DSSC material components. Therefore, DFT and TDDFT were employed to model the interface structure and energy alignment. The density of states (DOS) and the projected density of states (PDOS) of C6X/TiO2 and C6N/TiO2 interfaces were computed based on the optimized ground-state structures at the B3LYP/6-31G(d,p) level using GaussSum software [34]. Figure 5a, b shows the density of states (DOS) and projected density of states (PDOS) for C6X/TiO2 and C6N/TiO2 interfaces, where the energy is measured referring to the vacuum energy level.

Fig. 5
figure 5

a Projected density of states (PDOS) of C6X and b C6N adsorbed on TiO2 anatase (101) surface, CBM shifts of c C6X and d C6N absorbed on TiO2 anatase (101) surface

Full size image

All dye/TiO2 models met the required energy alignment criteria for functioning DSSC devices, that is, the dye’s LUMO must be located above and overlapping with the conduction band minimum (CBM) edge of the TiO2 substrate. Thus, the excited dye can be effectively injected into the conductive band (CB) of TiO2. Meanwhile, the HOMO is located in the gap between the conduction band and the valence band (VB) of TiO2, where it is more negative than the iodide/triiodide redox, indicating energetically favorable ground-state dye regeneration.

It is possible to estimate the change in the CBM energy (∆ECB) of TiO2 after dye adsorption by measuring the difference between the intercepts of the fitted lines of TiO2 PDOS and pure TiO2 DOS [35,36,37] with the energy axis as shown in Fig. 5c, d. One can notice that the dye adsorption on the TiO2 surface shifts CBM energy of TiO2 toward the more positive direction compared to pure TiO2, and the values of ∆ECB for C6X and C6N are 0.122 and 0.092 eV, respectively.

Molecular electrostatic potential (MEP)

To further understand the intermolecular interactions (such as nucleophilic and electrophilic attack), the molecular electrostatic potentials (MEPs) of the isolated C6X and C6N dyes and dye/TiO2 complexes were computed at the B3LYP/6-311G(d,p) level, and the results are illustrated in Fig. 6. The different colors on the surface correspond to different electrostatic potential values, with the red and blue areas of the MEP representing electrophilic (electron-rich area) and nucleophilic (electron-deficient area) activity, respectively. In this way, different colors represent various MEP values, which is in increasing order red < orange < yellow < green < blue. It can be noticed that for the two isolated dyes (Fig. 6), the highest nucleophilic potential is located on carboxyl hydrogen atom, and highest electrophilic potential is located on oxygen atoms of the Coumarin moiety and the carboxylic group, in addition to the nitrogen atom of the –CN group in the case of C6N dye. When the dye was adsorbed on the TiO2 surface (Fig. 6), the change was less apparent because the interactions between the dyes and TiO2 rendered the dye molecules more neutral in all areas of the surface. However, the TiO2 cluster’s terminal H atom showed the highest nucleophilic potential.

Fig. 6
figure 6

Molecular electrostatic potential for the studied structures

Full size image

Natural bond orbital (NBO) analysis

A natural bond orbital (NBO) analysis was carried out based on the optimized ground-state structure (S0) derived at the B3LYP/6–31G (d, p) level of theory to investigate the charge distribution and the mechanism of electron transfer from the donor (D) to the acceptor (A) through the π-spacer of the new designed C6X and C6N dyes. The NBO population charges for the electron donor, π-spacer, and electron acceptor are listed in Table 3 with the atomic units. Table 3 shows that the donor moiety in both dyes had a positive NBO value, indicating that they were efficient electron-donating units. In contrast, the π-spacer in C6X dye had a negative NBO value, which indicated that electrons could be trapped in the π-spacer. The negative charge of the electron acceptor moiety in C6X and C6N indicates that it is effective electron-withdrawing units which leading to successfully electron injection from the excited dye to the TiO2 conduction band. The natural charge difference between donor and acceptor is denoted as ∆qD−A. C6N dye exhibited higher ∆qD−A values compared to C6X dye. This indicated that C6N dye could donate more electrons to the anchoring group and hence have the better charge separation compared to the C6X dye [29].

Table 3 The NBO (in a.u) analysis of C6X and C6N dyes in DMC solvent
Full size table

Polarizability and hyperpolarizability

The nonlinear optical (NLO) properties, such as polarizability and hyperpolarizability, determine how a system responds to an intense applied electric field, which in turn determines intramolecular charge delocalization due to the asymmetric polarization caused by electron donor and acceptor groups in D-π-A-conjugated molecules [38]. It is necessary to take into account the nonlinear optical (NLO) properties during the design process of a D-π-A molecules because they characterize the molecule’s tendency to undergo π-electron delocalization and intramolecular charge transfer, which are required for efficient electron injection from the dye to the semiconductor in DSSCs [38]. As a result, good dye molecule candidates for DSSCs should have high polarizabilities (α), first-order hyperpolarizability (βtot) values [39].

The mean molecular isotropic polarizability, α, is defined as the mean value of three diagonal elements of the polarizability tensor and can be represented as follows [40]:

$$\alpha =\frac{1}{3}({\alpha }_{xx}+{\alpha }_{yy}+{\alpha }_{zz})$$
(1)

And the anisotropy of polarizability is given by:

$$\Delta \alpha =\sqrt{\frac{{({\alpha }_{xx}-{\alpha }_{yy})}^{2}+{({\alpha }_{xx}-{\alpha }_{zz})}^{2}+{({\alpha }_{yy}-{\alpha }_{zz})}^{2}}{2}}$$
(2)

where αxx, αyy, and αzz are the tensor components of polarizability. The total first-order hyperpolarizability, βtot, is calculated as:

$${\beta }_{tot}=\sqrt{{({\beta }_{xxx}+{\beta }_{xyy}+{\beta }_{xzz})}^{2}+{({\beta }_{yyy}+{\beta }_{yzz}+{\beta }_{xxy})}^{2}+{({\beta }_{zzz}+{\beta }_{xxz}+{\beta }_{yyz})}^{2}}$$
(3)

where βijk (i,j, k = x,y,z) are tensor components of hyperpolarizability. The polarizability (α), the anisotropy of polarizability (Δα), and total first-order hyperpolarizability (βtot) of the C6X and C6N dyes are calculated using B3LYP/6-31G(d,p) method in DMC solvent, and the calculated values are summarized in Tables 4 and 5.

Table 4 Isotropic polarizabilities (α) of C6X and C6N dyes in DCM solvent
Full size table
Table 5 Hyperpolarizability (β) of C6X and C6N dyes in DCM solvent
Full size table

As shown in Tables 4 and 5, C6N has a higher isotropic polarizability (581.976 a.u) than C6X (459.041 a.u), and also the polarizability anisotropy of the two dyes follows the same order as the isotropic polarizabilities. This shows that C6N would have the most prominent ICT properties. Additionally, C6N has the highest total first hyperpolarizability value, suggesting that it will exhibit a better photocurrent response than C6X dye.

Table 6 Calculated maximum absorption wavelengths (λmax), excitation energy Eex, oscillator strengths (f), light harvesting efficiency LHE, and the orbitals involved in the transitions obtained using TD-DFT/B3YLP/6-31 g(d,p)
Full size table

Absorption spectra

Using the optimized geometry, the TD-DFT calculations in DCM solvent were performed at the same level of calculations B3LYP/6-31G(d,p) to obtain the UV–vis absorption spectra of the investigated structures (presented in Fig. 7) by considering 6 lowest singlet–singlet (S0 to S1) transitions. The optical properties such as the maximum absorption wavelength (λmax), the vertical excitation energy (Ever), the oscillator strengths (f), and transition characters are presented in Table 6. The experimental UV–vis absorbance of C6 Dye in DCM solution shows the absorption maximum (λmax) at 456 nm, while our computational absorption spectrum for C6 Dye in DCM results absorption maximum (λmax) at 416 nm with a high correlation with the experimental value. As shown in Fig. 7, the C6X dye show absorption band range from about 280 to 550 nm, while C6N shows absorption band range from about 300 to 650 nm, indicating that C6N dye has the larger light absorption area.

Fig. 7
figure 7

The simulated absorption spectra of the investigated dyes obtained using TDDFT at the B3LYP/6-31G(d,p) level DCM

Full size image

Attaching the anchoring group to C6 Dye increases the absorption maximum λmax to 437 nm and 515 nm for C6X and C6N dye, respectively. This maximum absorption exhibits in major contribution a HOMO LUMO transition as seen in Table 6, which was assigned to an intramolecular charge transfer (ICT) [12] with a high oscillator strength of 1.363 and 1.177. The UV–visible absorption spectrum of the dye/TiO2 complexes is overall red-shifted, owing to the smaller energy gap. The interaction between the electron anchoring group of the dye and the 3d orbitals of the Ti atom, which led to a decrease in the LUMO energies when compared to the isolated dyes, could be a possible explanation for the red shift of the maximum absorption wavelength of the dye after attaching to TiO2 [28].

Adsorption energy

The adsorption energy (Eads) was obtained from the total energies of the adsorption system by

$${E}_{ads}=E[dye/{\left(Ti{O}_{2}\right)}_{9}]-(E\left[dye\right]+E\left[{\left(Ti{O}_{2}\right)}_{9}\right])$$
(4)

where E[dye], E[(TiO2)9], and E[dye/(TiO2)9] are the energy of the isolated dye, the (TiO2)9 cluster, and the dye/(TiO2)9 complex, respectively. The Eads has a negative value for C6X and C6N dyes as listed in Table 7, indicating a stable adsorption of dye on the TiO2 surface, the larger the Eads value, the more stable adsorption.

Table 7 The calculated excited and ground-state oxidation potential (Edye* and Edye), the adsorption energy (Eads), the electronic vertical transition energy (Ever) associated with the λmax, LHE, ΔGinject, ΔGreg, and open-circuit voltage (VOC) of C6X and C6N dyes
Full size table

Parameters related to the photovoltaic performance of DSSCs

The power conversion efficiency (η) is an important parameter to evaluate DSSCs performance and is defined by the short-circuit photocurrent density (Jsc), the open-circuit photovoltage (Voc), the fill factor (FF), and the incident solar power (Pin):

$$\eta = \frac{{J}_{SC} {V}_{oc}FF}{{P}_{inc}}$$
(5)

For DSSC, the short-circuit current density \({\mathrm{J}}_{\mathrm{sc}}\) can be expressed as [41]:

$${J}_{SC}=\int LHE(\lambda ){\Phi }_{inj}{\eta }_{collect}d\lambda$$
(6)

where \(\mathrm{LHE(\lambda)}\) is the light-harvesting efficiency at a certain wavelength, which is defined as the fraction of light intensity absorbed by the dye molecules and is related to the oscillator strength f by the following relation [42]:

$$LHE=1-{10}^{-f}$$
(7)

\(\Phi_{inj}\) is the electron injection efficiency, and \({\upeta }_{\mathrm{collect}}\) is the charge collection efficiency. It is acceptable to suppose that \(\eta_{collect}\) is constant for the same DSSCs with only different dyes [42]. Therefore, the enhancement of \({\mathrm{J}}_{\mathrm{sc}}\) should focus on improving the LHE and \(\Phi_{inj}\) .

\({\Phi }_{inj}\) is related to the driving force of electron injection (\({\mathrm{\Delta G}}_{\mathrm{inject}}\) t) and is described by the following equation:

$$\Delta {\Phi }_{inj}\propto f({\mathrm{\Delta G}}_{\mathrm{inject}})$$
(8)

As a result, the more negative \({\mathrm{\Delta G}}_{\mathrm{inject}}\) the greater will be the electron injection efficiency. The driving force of electron injection \({\mathrm{\Delta G}}_{\mathrm{inject}}\) can be calculated by [43,44,45]:

$$\Delta {G}^{inject}={E}^{dye*}+{E}_{CB}$$
(9)

where Edye* is the oxidation potential energy in excited state and ECB is energy of the conduction band (CB) of TiO2 (− 4.0 eV) [41]. The oxidation potential energy of the dye in an excited state can be given by the following relation [43]:

$${E}^{dye*}={E}^{dye}-{E}_{ver}$$
(10)

Edye is the ground-state oxidation potential energy (equal to -EHOMO), and Ever represents the vertical excitation energy associated with the wavelength maximum (λmax) obtained from TD-DFT calculations.

The electron regeneration efficiency (ηreg) is defined as the capability of dye to regain electron from the electrolyte after photoexcitation, which is determined by the driving force of dye regeneration (ΔGregen). The dye regeneration energy can be estimated using the following relation [41]:

$${\Delta G}^{reg}={E}^{redox}-{E}^{dye}$$
(11)

\({E}^{redox}\) is the redox potential of tri iodide-iodide (− 4.8 eV) [46].

Table 7 listed the values of LHE, ΔGinject and ΔGreg of the studied two dyes. from the results it can be noticed that LHE values are more than 90% for all the dyes, indicating that C6X and C6N dyes can be able to harvest light to generate electricity and the maximum short circuit current density can be achieved only when the LHE is large [47, 48]. The results also show negative values of ΔGinject and positive values of ΔGreg for the dyes, suggesting that the criteria for the energy level alignments with the semiconductor and electrolyte are satisfactorily met. Scharber et al. [49] proposed an empirical equation to evaluate the open-circuit voltage [50, 51]:

$$V_{oc}=(1/e)[|E_{HOMO}(donor\;or\;dye)|-E_{cb}\;of\;TiO_{2}-0.3]$$
(12)

One of the main parameters influencing the efficiency of charge transfer is the lifetime of the excited state \({\tau }_{e}\), and a dye with a longer excited state lifetime is expected to be more facile for charge transfer and suppress energy loss. The excited state lifetime of a dye can be calculated by the following relation [31]:

$${\tau }_{e}=\frac{1.499}{f\times {E}^{2}}$$
(13)

where E represents the transition energy of the different excited states (E in cm−1 units) and f is the oscillator strength of the electronic state. The first excited lifetime values, corresponding to the lowest excitation energies of C6X and C6N dyes, are given in Table 7. The longer electron lifetime for C6N (3.997 ns) indicates efficient charge transfer and electron injection into the CB of TiO2.

Conclusions

In summary, we have designed two novel dyes (C6X and C6N) based on coumarian-6 dye by attaching two different acceptor groups (-COOH and -CN) to C6 Dye. DFT and TD-DFT calculations were applied to investigate the effect of attaching these groups on the electronic structure, optical and photovoltaic properties, and the use of the new dyes as sensitizers for DSSCs. The bond lengths and dihedral angle values between the (π-A) and (D-π) parts indicated that attaching the anchoring groups improve the coplanarity configuration of the new dyes, thus enhancing the electron delocalization and further intramolecular charge transfer. FMOs show that the values of LUMO and HOMO of C6X and C6N dyes were higher than the TiO2 conduction band and were lower than the redox potential of I−/I3−, indicating efficient dye regeneration and electron injection process. NBO results showed that electrons are successfully transported from D to A by means of the π-conjugated spacer suggesting the feasibility of intermolecular charge transfer. The absorption spectrum of the new dyes is broadened and redshifted due to the decrease in the HOMO–LUMO energy gap. Some parameters related to the photovoltaic performance of DSSCs have been calculated which shows that C6N have higher VOC and τe and the larger absorption spectra, as well as smaller Ever and hence higher PCE efficiency.