Introduction

Intermolecular multiple hydrogen bonding (HB’ing) is of major importance in biochemistry and supramolecular chemistry. It plays a crucial role in formation of the double helix of DNA [1] and in action of artificial receptors used in biochemistry [2, 3]. Hydrogen bonding is the most common non-covalent interaction [2, 4] observed in biosensing, self-complementary aggregation, and non-covalent polymer formation [5–7]. Significance of hydrogen bonding is based on its directionality and reversibility [6]. There are few factors that influence the HB’ed complex stability. These are number of hydrogen bonds, hydrogen bonding pattern [8, 9], secondary interactions [10, 11]. Also the tautomeric equilibrium may be responsible for forming variously stabilized associates. This is due to group and HB’ing pattern changes upon proton transfer.

It is known that secondary interactions result in strengthening of the AAAA/DDDD-type [12] association in comparison with that of ADAD/DADA [13]. The same is true for AAA/DDD [14–17] versus DDA/AAD [18, 19] versus ADA/DAD pairs [7, 8, 20–22]. Although the ADA and the DAD motifs are not self-complementary, their self-association is still possible due to rotamerism (Scheme 1) or tautomerism [23–26]. On the other hand, 2,6-bis(acrylamido)pyridine does not form dimers [27].

Scheme 1
scheme 1

Self-assembly of the DAD motif due to the group rotation resulting in the DADA pattern

Full size image

Steric hindrance [28–31] weakens basicity of 2,6-di-tert-butylpyridine [32]. Thus, the parallel effect should be observed for non-covalent interactions. Also the electronic repulsion is believed to be responsible for weakening of the association of bis(acetylamino)triazine derivatives with imides [33].

The organized structures of 2,6-diacetylaminopyridines with imides were obtained by their aggregation on the Ag surface [34]. Hydrogen bonding in these compounds was studied mainly from the point of view of binding in nucleic bases [35–37], bisurea derivatives [38], structures stabilized by π–π interactions [39], receptors for barbituric acid [40], and fluorine anion [41], enhancement of the fluorescence of conjugated polymeric chain upon complexation [42], cooperative catalyst [43], and potentially drug delivery nanomaterials [44]. Hydrogen bonding and possibility of the complex formation in solution and in solid state between the 2,6-diacetylaminopyridine and enolate derivative of barbituric acid has been shown recently by the X-ray diffraction [45]. Interestingly, conformation of the amide group in N-(pyrimidin-2-yl)pentafluorobenzamide derivatives was found to be of the cis type, especially when the 2,6-diacetylaminopyridine derivative stabilized this form by hydrogen bonding [46].

Feibush have suggests that 2,6-bis(pivaloylamino)pyridine does not form complexes with imides due to steric crowding [47]. On the other hand, stronger hydrogen bonding capability of proton in the NHCOCF3 group (as compared to that in NHCOCH3) is expected to strengthen the complex stability. 2,6-Bis(trifluoromethylcarbonylamino)pyridine has been investigated as a hydrogen bonding counterpart stabilizing the flavin radical anion [48] and as a hydrogen bonding receptor for barbiturate [49]. The acylation of amino moiety, however, not always led to the greater stability of non-covalent associates [33]. It was suggested that this is due to electronic repulsion/secondary repulsive interactions.

Imides are complementary by hydrogen bonding to with 2,6-bis(alkylcarbonylamino)pyridines. The triple hydrogen bonds are expected to strengthen the association especially with the perfluoroalkyl derivatives. Clarification of these interactions between succin- and maleimide, 2,2′-dipyridynamine and 2,6-bis(alkylcarbonylamino)pyridines is the main goal of this article.

Results and discussion

Formulas of 2,6-bis(acylamino)pyridines 1–4 with 2,2′-dipyridylamine (5) and imides (6) and (7) as well as numbering of positions in their molecules are depicted in Fig. 1.

Fig. 1
figure 1

Formulas of the compounds studied and atom numbering

Full size image

NMR

Since NMR chemical shifts of the NH/OH protons are sensitive to the concentration and solvent properties, the 1H NMR spectra of all neat compounds and their 1:1 mixtures were recorded at the same concentration (see “Experimental”). On the other hand, their 13C and 15N spectra were run for the saturated solutions. The chemical shifts are available in the Supporting Information Section (SI, Table S1). H7 protons in 2 and 4 were found to be more acidic than these in 1 and 3. Perfluorination of the alkyl groups results in deshielding of the 1H7 signal by 0.7–0.8 ppm.

The complexation induced shift (CIS) values of the amide protons (δ(H7)) for 1–4 and their 1:1 mixtures with 2,2′-dipyridylamine (5), succinimide (6), and maleimide (7) are collected in Table 1 (see also Table S1).

Table 1 Complexation induced shifts (CIS) [Δδ(H7)/Δδ(H1′)] for the 1:1 mixtures of 2,6-diacetylaminopyridines (1–4) with 2,2′-dipyridylamine (5), succinimide (6), and maleimide (7) and association constants (K assoc)
Full size table

The association constants (Table 1) show that the most stable complexes are 1 + 6 and 3 + 6. It is noteworthy that K assoc obtained now are comparable to these for other triple hydrogen-bonded systems [44, 50–52].

Based on the CIS and K assoc values for mixtures of 1–4 with 5 (Table 1) and δ(H7) for the neat 1–4 (Table S1) one can see that perfluoroalkyl groups increase the hydrogen bond donor properties of H7. This results in increasing stabilities of complexes carrying the electron acceptor groups. Contrary to 1 and 3, negligible effect of complexation of succin- and maleimide was found for perfluoro analogues 2 and 4 implying that their association with those imides is very weak. Such weak complexation was earlier observed in mixture of 2 with flavin [48]. An explanation for the weak association of 2 and 4 with 6 and 7 can be that CF3 and C2F5 groups create electronic repulsions towards the hydrogen bond acceptors, i.e., carbonyl oxygens of the imide. Differing from that in 2,2′-dipyridilamine partial rotation of the pyridine ring around the N1–C2 bond [53] (Fig. 2) causes that this molecule can adopt a geometry that allows complex formation even when substituents show some repulsion with the pyridine rings of 5.

Fig. 2
figure 2

The optimized (M05/6-31G(2d,p) level) structure of 1 + 5 and 1 + 6 complexes

Full size image

Owing to low rotation barrier of the perfluoroalkyl groups around the C–N bond in the amide [46], both the trans and cis forms (Scheme 2) may be expected to be present in the complexes of 2 and 4 with imides 6 and 7. One should keep in mind, however, that electronic repulsion between the carbonyl oxygen of 6 and 7 and fluorine or oxygen atoms of 2 and 4 may destabilize the said complexes (Scheme 3).

Scheme 2
scheme 2

The trans and cis forms of the carbonylamino group

Full size image
Scheme 3
scheme 3

Electronic interactions in the 2 + 6 complex: arrows were used to show repulsions

Full size image

Additional 1H NMR experiments were also run with three component mixtures to clarify what happens in case of competitive binding. The detailed results and discussion can be found in SI.

X-ray structural data

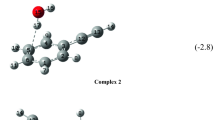
Single crystal structures of 2 and 4 (Fig. 3) show that all the substituent C atoms (except these of CF3 groups in 4) lie almost in the plane of pyridine ring. Although two-dimensional schematic drawings of 2 and 4 indicate these compounds to be symmetrical, there is no crystallographic mirror plane or other symmetry element found along the N1···C4–H4 axis. Despite the amide side chains in 2,6-bis(acylamino)pyridines are slightly twisted with respect to the pyridine ring (Table S12) their geometries are comparable. Figure 2 shows molecular structures of 2 and 4 as the ORTEP-diagrams [54]. Compounds 2 and 4 are held in the crystal phase by a net of the intermolecular hydrogen bonds (Fig. S1, for distances N7···O9 and N(R2)···O(R2) see Table S12).

Fig. 3
figure 3

The ORTEP-diagrams [54] of the compounds 2 (upper) and 4 with thermal ellipsoids drawn at 50% probability level (heteroatoms displayed as octant shaded model)

Full size image

Calculations

Molecular geometries were calculated using the DFT method (M05). It is less time-invasive than, for example, calculations at the MP2 level. The M05 functional is optimized for calculation of many types of non-covalent interactions. This methodology has been previously compared [55] by us with B3LYP and MP2 ones for non-covalent intermolecular interactions in 1,8-naphthyridine derivatives. Detailed geometry data for complexes are collected in SI (Tables S3–S9).

Geometries of the optimized complexes support the results obtained by 1H NMR spectrometry. Substitution of H by F atoms in the acylamino moieties makes H7 protons more acidic. The H7···X3′ distance (X3′ is the nitrogen and oxygen atom in 5 and 6 (and 7), respectively) shows that hydrogen bond is always shorter in the fluorinated derivatives. However, there are some exceptions: H7···X3′ distances in 4 + 6 and in 3 + 6 are practically identical. Moreover, H7 in 4 + 7 is more faraway from X3′ than in 3 + 7. As a result of shortening of the H7···X3′ distance, the H1′···N1 hydrogen bonds in 2 + 5 and 4 + 5 complexes are noticeably shorter than these in 1 + 5 and 3 + 5. The X3′···C8 and X3′···C(R3) distances are noticeably larger in the complexes carrying the CF3 and C2F5 groups. Lower values of C2–N7–C8 angle (Table S7) in fluoroalkyl as compared to these in alkyl derivatives suggest that repulsion between the pyridine ring of 5 or oxygen atoms of imides and fluorine atoms of 2 and 4 takes place. It is noteworthy that energy of the complex formation for fluorinated derivatives 2 and 4 with imides 6 and 7 is ca. 18.4 ± 1 kJ/mol lower than that of 1 and 3 with the same imides (Table S10).

The intermolecular interactions influence electron distribution in each complex. The orbital contours of 1 + 6 and 2 + 6 show the interaction of the hydrogen bond character (exemplified on Fig. 4). Other orbitals (HOMO-20 and HOMO-14, HOMO-27 (no H-bond is visible at this contour level), and HOMO-24, HOMO-29 and HOMO-30, HOMO-35 and HOMO-41, HOMO-36 and HOMO-42) involved in hydrogen bonding in 1 + 6 and 2 + 6 were also considered. There are two orbitals in 2 + 6 (HOMO-38 and HOMO-40) that show the electron repulsion is present. No such orbitals were found for the 1 + 6 complex. Orbital contours are collected in the SI.

Fig. 4
figure 4

Molecular orbitals (HOMO-9) of 1 + 6 and 2 + 6 showing the intermolecular hydrogen bond (continuous electron density along hydrogen bong axis)

Full size image

Conclusions

Complexes of 2,6-bis(alkylcarbonylamino)pyridines with succin- and maleimide as well as with 2,2′-dipyridylamine are stabilized by the triple hydrogen bonds. Substitution of H by F in the alkyl parts of 2,6-bis(alkylcarbonylamino)-pyridines makes the amide protons better hydrogen bond donor. On the other hand, strong intermolecular CO/F electronic repulsion diminishes efficiency of these compounds to associate with imides whereas the conformational flexibility of 2,2′-dipyridilamine enables its association with 2,6-diacylaminopyridines. The association constants of imides and 2,2′-dipyridilamine with 2,6-diacylaminopyridines follow the concept of steric repulsion. The spectra of the double (1 + 4 and 1 + 6) versus triple mixtures (1 + 4 + 6) studied by 1H NMR confirm complexes of imides with 2,6-bis(alkylcarbonylamino)pyridines to be much more stable than these with 2,6-bis(perfluoroalkylcarbonylamino)pyridines, showing the selective binding of imides by non-fluorinated derivatives. The linear dependence between the association constants and the complexation induced shifts enables the latter to be used as a preliminary probe for relative complex stability. The agreement of the computational data (geometry, energy and visualization of molecular orbitals) with experimental one, including the electronic repulsion between oxygen and fluorine, suggests that DFT method is able to describe hydrogen bonding and electronic repulsion reliably.

Experimental

Synthesis

Compounds 1–4 were obtained by refluxing (2 h) of the mixture of 2,6-diaminopyridine (0.2 g, 1.8 mmol) and 2 mL of the appropriate acid anhydride. Excess of the latter compound was decomposed by addition of water (10 mL) and saturated aqueous sodium carbonate solution (5 mL). The obtained mixture was then extracted with chloroform (2 × 15 mL), organic layer dried (Na2SO4), and evaporated to dryness under reduced pressure. The crude products were further purified by recrystallization. Melting points: 1, 199–202 °C (C6H14/AcOEt, white powder) (lit. 202–203 °C [56], 205–206 °C [57]), 2, 154–158 °C (C6H14/AcOEt, pale-yellow needles), 3, 127–128 °C (C6H14/AcOEt, white powder) and 4, 105–107 °C (C6H14/AcOEt, pale-brown crystals). Satisfactory elemental analytical data were obtained for synthesized compounds, i.e., 1 calcd C9H11N3O2 C 55.95, H 5.74, N 21.75, found: C 55.68, H 5.70, N 21.52, 2 calcd C11H15N3O2 C 59.71, H 6.83, N 18.99 found: C 59.54, H 6.76, N 18.69, 3 calcd C9H5F6N3O2 C 35.90, H 1.67, N 13.95 found: C 35.73, H 1.64, N 13.78, 4 calcd C11H5F10N3O2 C 32.93, H 1.26, N 10.47 found: C 32.65, H 1.22, N 10.27. Compounds 5–7 were commercially available and were used as obtained after drying in desiccator.

NMR

1H NMR experiments were run with a Bruker Avance DRX 500 spectrometer equipped with an inverse detection 5-mm diameter probehead with a z-gradient for equimolar CDCl3 solutions at 303 K. 1H and 13C NMR chemical shifts are referenced to an internal TMS (δ = 0.00 ppm). Owing to the limited solubility, 13C and 15N spectra of all compounds are run for their saturated solutions. Acquisition and processing parameters are the same as reported earlier [58]. The 2D pulsed field z-gradient (PFG) selected 1H,13C HMQC, and 1H,13C HMBC experiments were run to assign reliably the 13C NMR spectra [58]. 15N NMR chemical shifts (referenced to an external neat 15N-natural abundance nitromethane, δ = 0.0 ppm) are those obtained with the PFG 1H, 15N HMBC experiments [58].

Association experiments

Equimolar quantities (0.089 mmol) of 1 (17.2 mg), 2 (26.9 mg), 3 (19.7 mg), 4 (35.7 mg), 5 (15.3 mg), 6 (8.8 mg), and 7 (8.6 mg) were dissolved in acetone (10 mL). Solutions of 1–4 (3 mL) were then combined with solutions of 5–7 (3 mL) to obtain the 1 + 5, 1 + 6, 1 + 7, 2 + 5, 2 + 6, 2 + 7, 3 + 5, 3 + 6, and 3 + 7 complexes. Additional 3 mL solutions of compounds 1–7 were kept to prepare the references. Evaporation of the solvent from all solutions prepared and drying of the residue in vacuum desiccator was followed by its dissolving in CDCl3 (0.6 mL). 1H NMR spectra of chloroform solutions of the complexes were recorded within 1 h. The CIS values were obtained by subtraction of the δH7 and/or δH1′ values for the complexes from the chemical shift values of the neat compounds (reference). The NMR titrations were done for the constant concentration of 1–4. Equivalents of the solid titrants added equal to: 0.5–50 for 5, 1–10 for 6, and 1–20 for 7. The titration was continued to obtain the Δδ(H7) smaller than 0.1 ppm upon addition of the next portion. The δH7 (probe) obtained are collected in SI (titration charts). The Benesi–Hildebrandt [59] equation was used to calculate the K assoc.

X-ray

Single crystals of 2 and 4 used in the X-ray crystallographic experiment were obtained by slow evaporation of the solvent (chloroform) from NMR tube. The structural data for these compounds were collected at 123 ± 2 K with a Bruker–Nonius KappaCCD diffractometer equipped with APEXII detector using the graphite monochromatized MoKα radiation (λ = 0.71073 Å). Data were processed with DENZO-SMN [60]. The structures were solved by direct methods, using SIR-2004 [61], and refined on F 2, using SHELXL-97 [61]. The reflections were corrected for Lorenz polarization effects and absorption correction was not used. The H atoms bonded to C atoms were calculated to their idealized positions with isotropic temperature factors (1.2 times the C atom temperature factor) and refined as riding atoms. The H atoms bonded to N atoms were found from electron density map and fixed to distances of 0.88 Å from N atom with isotropic temperature factor (1.2 times the N atom temperature factor). The figures were drawn with ORTEP-3 [54] and MERCURY [62]. Other experimental X-ray data are shown in Table 2. CCDC-763984 (2) and CCDC-763985 (4) contain the supplementary crystallographic data for this article. These data can be obtained free of charge at http://www.ccdc.cam.ac.uk/conts/retrieving.html [or from the Cambridge Crystallographic Data Centre (CCDC), 12, Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033].

Table 2 Selected crystallographic parameters of 2 and 4
Full size table

Calculations

Calculations at the M05/6-31G(2d,p) level for geometry optimizations of all structures studied have been performed in Gaussian [63]. The energy minimum was confirmed by the frequency calculations (all positive frequencies were obtained). Energy of the complex formation was calculated as the difference between energy of the complex and a sum of the energies of its constituents. The basis set superposition error (BSSE) correction was used with default settings. The single-point calculations (MP2/6-31G(2d,p) level) in GAMESS [64] at the geometry taken from M05/6-31G(2d,p) optimizations provided the orbital contours that were drawn with the use of QMView [65].