Abstract
In tenuous plasma the floating potential of sunlit spacecraft reaches tens of volts, positive. The corresponding field disturbs measurements of the ambient plasma by electron and ion sensors and can reduce micro-channel plate lifetime in electron detectors owing to large fluxes of attracted photoelectrons. Also the accuracy of electric field measurements may suffer from a high spacecraft potential. The Active Spacecraft Potential Control (ASPOC) neutralizes the spacecraft potential by releasing positive charge produced by indium ion emitters. The method has been successfully applied on other spacecraft such as Cluster and Double Star. Two ASPOC units are present on each spacecraft. Each unit contains four ion emitters, whereby one emitter per instrument is operated at a time. ASPOC for the Magnetospheric Multiscale (MMS) mission includes new developments in the design of the emitters and the electronics. New features include the use of capillaries instead of needles, new materials for the emitters and their internal thermal insulators, an extended voltage and current range of the electronics, both for ion emission and heating purposes, and a more capable control software. This enables lower spacecraft potentials, higher reliability, and a more uniform potential structure in the spacecraft’s sheath compared to previous missions. Results from on-ground testing demonstrate compliance with requirements. Model calculations confirm the findings from previous applications that the plasma measurements will not be affected by the beam’s space charge. Finally, the various operating modes to adapt to changing boundary conditions are described along with the main data products.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Scientific Objective
The electric surface potential of a body embedded in plasma and under radiation from the Sun is determined by the equilibrium of the various charging currents, the most relevant of them being the photo-emission current, electron and ion currents between plasma and body, and secondary electron currents caused by the impact of primary electrons and ions with higher energy. The plasma environment in the regions of interest to MMS has a density which rarely exceeds tens of particles per cm−3. Moreover, in the lobes in the Earth’s magnetotail, but also in some dayside regions within the magnetopause we find plasma densities well below 0.1 cm−3, in which case a small high-energy tail of the photoelectron distribution may balance the plasma electron current. This interaction results in significantly positive potentials of the spacecraft of several tens of volts, as already shown by Pedersen et al. (1983) for GEOS and ISEE, or Pedersen et al. (2008) for Cluster.
Spacecraft potentials of this magnitude severely disturb measurements of plasma electrons and ions since the particle trajectories and energies undergo significant changes during their passage through the electrostatic sheath around the body. Access of positive ions to the detectors may even be blocked. On the other hand, high positive potentials attract most of the emitted photoelectrons back to the spacecraft and the electron spectrometers where they “pollute” the low-energy part of the data. Disturbances are not limited to particle measurements. Also electric field measurements by probes may suffer from high spacecraft potentials. The high potential well around the spacecraft may lead to inaccuracies of the electric field measurements, which result from exploiting the small voltage difference between opposite probes. An asymmetry of the potential structure, for example in the presence of streaming plasma forming a wake structure, may lead to huge artifact in the data.
The problems associated with spacecraft charging have been recognized very early in the 1970s. A necessary condition to avoid local (differential) charging of spacecraft surfaces particularly near the particle sensors is sufficient electric conductivity of the surface including the solar arrays. Thereafter, the spacecraft potential can be adjusted actively by adding a current from the spacecraft into the plasma in order to change the equilibrium potential in the desired direction. On MMS, this goal is achieved by the emission of positive indium ions at energies of several keV, as detailed in the following sections.
1.2 Science Requirements
ASPOC is a heritage-design instrument that was originally flown for example on ESA’s Cluster spacecraft (Riedler et al. 1997; Torkar et al. 2001), but also on Equator-S (Torkar et al. 1999) and in the Double Star mission (Torkar et al. 2005). The primary objective of active spacecraft potential control (ASPOC) is to ensure the effective and complete measurement of the ambient plasma distribution functions. The ASPOC instrument for MMS emits a beam of positive indium ions at energies of order 4 to 12 keV and variable currents of up to ∼70 μA in order to control the electrical potential of the spacecraft. The total ion current doubles because two instruments are present on each MMS spacecraft. In steady state, a spacecraft will charge to an equilibrium potential where all currents between the spacecraft body and its environment including the ion current generated by the two ASPOCs compensate, resulting in zero net transfer of charge between the spacecraft and the environment. As will be described in more detail in Sect. 3, outside of eclipses and within the regions of interest to MMS mainly photo-emission of electrons drives the spacecraft potential positive relative to the plasma potential. Without active control, spacecraft potentials along the orbit would range from a few volts positive in the solar wind and magnetosheath up to some tens of volts in the plasmasheet and in the magnetospheric lobes. The positive ions emitted by ASPOC have energies above 4 keV and are basically unaffected by the spacecraft potential. They escape into the ambient plasma, and by adjusting their current the equilibrium spacecraft potential can be set to the desired low (a few volts) positive value, as an inverse function of the ion beam current.
Low spacecraft potentials enhance the accuracy of plasma and electric field measurements on-board MMS in several ways.
-
Low potentials ensure less or even negligible modification of energies and trajectories of plasma electrons and ions when they travel through the spacecraft sheath.
-
Low-energy ions will no longer be reflected in the potential barrier around the spacecraft and their complete distribution function can be measured.
-
The calculation of plasma moments including density, and particularly moments calculated on board, becomes more accurate, as opposed to practically useless values obtained especially for electrons at high spacecraft potentials with high photo-electron fluxes into the sensors.
-
Low potentials mitigate the process that re-attracted photo-electrons enter into electron sensors and cause high count rates at low energies which not only makes it difficult if not impossible to detect features of the cold ambient electron population but also accelerate the aging of the micro-channel plates used in the instruments.
-
The size of the sheath around the spacecraft is significantly reduced, thus the accuracy of the electric field measurements by the probes (Spin-Plane Double Probes, SDP and Axial Double Probes, ADP) is enhanced.
Moreover, the cross section of wake structures appearing downstream in flowing plasmas is significantly reduced, making it very unlikely that the measurements will be corrupted by some of the probes being situated inside the wake with its low density plasma and others outside in the undisturbed environment. As an example, Engwall et al. (2006) have pointed out that the plasma upflowing in the polar wind is generally tenuous and cold. Therefore the flow is supersonic, i.e. the condition \(k T_{i} < \frac{m_{i} v_{i}^{2}}{2}\) is fulfilled, and as a consequence a wake is formed the cross section of which being much larger than the spacecraft dimension, namely of the order of the area where the kinetic energy of the ions is too low to allow them to overcome the local electrostatic potential, \(\frac{m_{i} v_{i}^{2}}{2} <e \varPhi\). In this sometimes huge wake region potentials of order kT e /e may occur and produce spin tones in the field data, which are difficult to remove.
The formal requirement on ASPOC on MMS is to ensure spacecraft potentials not higher than +4 V within the region of interest throughout the nominal mission. This value lies conveniently below the lower energy thresholds of the fast plasma instrument (FPI) for electrons and ions, so that the modifications of measured particle trajectories and velocities will be negligible. In addition, precautions shall be in place to turn off the ion emission when the naturally occurring spacecraft potential is already negative. This would happen inside eclipses when the photo-emission current vanishes, but these intervals are predictable and the ion beams can be turned off by command from the ground. Another condition when negative charging may occur is under high fluxes of energetic particles. On-board software shall detect such events and shut down the ion beams accordingly.
The requirement to control the spacecraft potential throughout the mission implies the availability of a sufficient amount of charge material—in our case indium—and its diligent usage. In particular, the beam current should be reduced as soon as the nominal conditions on spacecraft potential are met.
2 Principle of Active Spacecraft Potential Control
The electric potential of a spacecraft results from an equilibrium of currents flowing into and from the ambient plasma. The major drivers in the regions of interest to MMS are photoelectrons created by solar EUV radiation and X-rays and the plasma electron current. Except during heavy magnetospheric substorms or in eclipse the photoelectron current by far exceeds the plasma currents. All other currents such as currents from plasma ions and secondary emission can be neglected for general considerations. The two major currents are predominantly carried by electrons in the energy range between a few eV and hundreds of eV, which is why the electric field around a spacecraft with a potential different from the plasma potential can significantly modify these currents. The equilibrium potential in this normal environment is positive and adjusts itself such that the current of the high-energy tail of the photoelectron distribution escaping from the spacecraft into the plasma is balanced by plasma electrons being accelerated towards the spacecraft.
Flux and energy spectrum of photoelectrons emitted from spacecraft surfaces have been studied by numerous authors for various spacecraft, among them ISEE (Escoubet et al. 1997), Geotail (Nakagawa et al. 2000), and Cluster (Lybekk et al. 2012). It appears as a common feature, as for example stated by Pedersen (1995), that photoelectrons created by solar EUV radiation exist in two regimes, one at energies near 1 eV and another one at 5–15 eV, whereby the flux of the population at lower energy is approximately an order of magnitude higher than that of the latter. The total current is a product of the solar flux and the photo-emission yield of the spacecraft surfaces. In literature one can find saturation current densities (for zero potential) ranging between 30 μA m−2 and 70 μA m−2. Davis et al. (2012) have performed a detailed theoretical study for MMS. They assume an effective cross section (projected surface) of the MMS spacecraft of 4 m2, a photo-emission saturation current density of 70 μA m−2, and the energy spectrum found by Nakagawa et al. (2000) for Geotail. In consequence, the total photo-emission current for MMS under these generalized assumptions becomes 280 μA.
The plasma electron current, which is the major current flowing in direction opposite to the photo-emission current, can be approximated to first order by a Maxwellian. According to the formula by Mott Smith and Langmuir (1926) the random current density, j a0, to a spherical, equipotential surface becomes
The surface area of an MMS spacecraft is about 34 m2, which is equivalent to a sphere with 1.645 m radius. Thus the plasma electron current, I a0, becomes

where I a0 is in μA, n e in electrons cm−3, and kT e in eV. Assuming a typical electron temperature, T e of 1000 eV in the region of interest—except in the solar wind and in the magnetosheath, where T e is of order 10 to 100 eV (Escoubet et al. 1997; Newbury et al. 1998; Schwartz et al. 2011)—an electron density of n e =1 cm−3 is required to make the plasma electron current comparable to the high-energy regime of the photoelectron saturation current (assumed at 10 % of the total photoelectron current). Only in higher plasma density (more than tens of electrons cm−3) will the plasma current increase above 100 μA, and the equilibrium potential will be just a few volts positive, corresponding to the steepest part of the slope in the photoelectron energy spectrum. Due to this slope, the equilibrium potential will vary rather little with the plasma density.
The aim of an active spacecraft potential controller is to achieve such low and stable potentials even in the most tenuous environment. A beam of positive ions with energies sufficiently high so that its acceleration in the spacecraft sheath is negligible, and with a current amounting to a good fraction of the total photo-emission current, will substitute the plasma electron current and achieve a low and stable spacecraft potential. Density variations in the plasma will lead to minor variability of the potential, even if the beam current is constant. In order to suppress these residual potential variations, a control loop can be established between measurements of the potential and the beam current. Thereby a completely constant potential can be achieved, albeit there are practical limitations stemming from unavoidable inaccuracies and time lags in the control loop.
The effect of controlled ion beams with different current levels on the spacecraft potential is illustrated in Fig. 1. Under generalized assumptions (Maxwellian distributions of both the photo and the plasma electrons, non-dimensional calculation, and average solar conditions, i.e. photo-emission) it shows the spacecraft potential as a function of plasma density (assuming a temperature of 100 eV). The curve labeled 0 μA stands for the uncontrolled potential. It compares well with literature, for example Nakagawa et al. (2000) for Geotail and Lybekk et al. (2012) for Cluster. The other thin lines show the effect of ion beams, scaled to a spacecraft with the surface area of MMS. Currents of tens of μA can clamp the potential to low values. Clearly, a current of 40 μA ensures that the spacecraft potential does not exceed the required maximum of 4 V even in the most tenuous plasma. For this reason, a current of 40 μA for both ion beams together (i.e., 20 μA for each beam) has been chosen as the nominal value for instrument development and operations planning purposes. The flatness of the curves indicates that a constant ion current can stabilize the potential to within about 1 V for densities of 1 cm−3 and lower. Around 10 cm−3 the uncontrolled potential becomes lower than 4 V, which means in the framework of MMS requirements that the ion beam can be turned off. Taking into account this requirement, the bold line represents a constant ion beam current mode where the beam is turned off as soon as the potential becomes significantly lower than the required 4 V maximum. In the case that it is desirable to achieve a perfectly constant potential not only for densities below 0.1 cm−3, but below ∼10 cm−3 the beam current has to be varied between 40 μA and 0 μA as can be seen in the dashed line in Fig. 1. The corresponding operation mode is called the feedback mode (see Sect. 5).
Let us look at quantitative assessments of the current-potential relationship for MMS. A charging study has been performed by Davis et al. (2012) using NASCAP 2K. The study is rather detailed but the results for the chassis potential rely on literature values for the photo-emission yield of various materials and results from Geotail for the energy distribution of photoelectrons. They report potentials corresponding to ion beams with 40 μA current of ∼4.5 V in the outer magnetosphere and plasma sheet, ∼4.1 V at the magnetopause, and ∼3.2 V in the solar wind, whereas the uncontrolled potential would rise up to 24 V in the environments under consideration.
An alternative approach of the assessment of the current-potential relationship is to use the results of previous measurements. Since the photoelectrons are correlated with the EUV flux level, it is expected that there will be solar cycle variations in the spacecraft environment. We therefore assess these effects for MMS, which is not taken into account in the current NASCAP 2K approach, by adopting an experimental approach based on the heritage from the Cluster mission. Torkar et al. (2008) studied the spacecraft potential of Cluster under active control over the years 2001 to 2004 and provided histograms of spacecraft potential as a function of ion beam current. As the instruments on Cluster were predominantly operated in low density regions, the results are relevant for these prevailing plasma conditions. Figure 2 shows the maximum occurrences of spacecraft potential, V s , expected for the MMS configuration as explained below and has been adapted from Torkar et al. (2008) as follows. Firstly, the figure by Torkar et al. (2008) showed the raw measurements of the potential of Cluster 3, namely the voltage difference between the spacecraft chassis and the double probes, V s −V p . According to Pedersen et al. (2008), however, the potential of the probes was elevated against the plasma potential, V np , by 0.9 V to 2.2 V in dense and tenuous environments, respectively. The reason for this difference is that the potential control for the probes, achieved by imposing a bias current of −140 nA to them, results in an equilibrium potential for the probes which is driven by the same physics as the spacecraft potential. Hence, in Fig. 2 we add a conservative 2 V to all raw data to obtain the spacecraft potential, V s . Secondly, we scale the ion currents used on Cluster 3 by the ratio of the projected sunlit surfaces of MMS and Cluster, which is 5.9 m2/4.5 m2=1.3, including the areas of the magnetometer booms and the axial and radial electric field booms. The resulting Fig. 2 shows a clear power law between V sc and ion beam current, which is in slight contradiction to the assumption that the energy spectrum of the photoelectrons is a single Maxwellian. With dual or triple Maxwellian photoelectron distributions however, which are quoted by most authors, the dependence of the potential on the ion current would come close to the power law suggested by Fig. 2. Furthermore, one notes a clear downward trend of the potentials over time. The straight lines, which are rms (power law) fits to the data points, have been extrapolated to higher currents than on Cluster, where typically lower ion currents than on MMS have been applied since the requirements on the spacecraft potential for Cluster had been less stringent than for MMS. The slopes of the fitted lines are slightly variable, which is most likely owing to some scatter in the data. It happens, though, that all three intersections of the trend lines for 2002, 2003, and 2004 with a potential V s =4 V coincide with an ion beam current of 40 μA for both beams together (20 μA per beam), which corresponds to the nominal value for MMS (see also Fig. 1). Figure 2 not only confirms the validity of the simplified calculations performed for Fig. 1, but also quantifies the dependence of the spacecraft potential on solar activity.
Maximum occurrences of spacecraft potential, V s , versus ion beam current for Cluster 3, adapted from Torkar et al. (2008) to MMS (see text)
As pointed out by Torkar et al. (2008) and later by Lybekk et al. (2012), the downward trend of the spacecraft potential correlates with solar activity. Looking at the 10.7 cm radio flux progression in the last solar cycle it becomes evident that the period 2001 to 2004 was in the declining phase. The present cycle has so far shown lower activity than the previous one by about a factor 2, and also the current predictions for the time of the MMS nominal mission (from early 2015 onwards) are fairly moderate and comparable to the years 2004 onwards. Hence, it is reasonable to assume similar levels of the photo-emission current.
The correlation between spacecraft potential and solar activity has been further elaborated by Lybekk et al. (2012). These authors studied the photo-emission current escaping from the spacecraft (I phs ) as a function of the spacecraft potential (more exactly, of V s −V p ) for Cluster in the years 2001 to 2006. I phs for a certain potential can be considered as the maximum ion beam current which would have to be emitted to obtain a given potential in the complete absence of ambient plasma currents. Their correlations of I phs for a certain potential with solar EUV radiation are extremely good (r 2=0.99). Thus we conclude that a total of ∼40 μA in current for both beams together will be sufficient to clamp MMS spacecraft potentials to +4 V, and we take these calculations as justification for using this current as the nominal one. The variation of I phs with potential as reported by Lybekk et al. (2012) can be calculated as a factor of 0.8 per volt (based on data between 6 V and 8 V). This factor can be used to estimate the necessary MMS ion beam current to achieve potentials other than 4 V. As an alternative one can use the trend lines in Fig. 2 for this estimation.
3 Instrument
3.1 Overall Configuration
An ASPOC instrument is composed of an electronics box carrying two emitter modules at the top (Fig. 3).
The electronics box consists of three stacked frames (one for each printed circuit board). The rigid top plate of the box supports two cylindrical elements (emitter modules) containing the emitters and a purge connector from which dry nitrogen is routed to both modules. Stiffening rods between the modules and towards the top plate increase the mechanical strength of the assembly. All harness between the electronics box and the emitters is routed outside the structure. The harness includes low voltage harness for the heater elements and external temperature sensors, and high voltage cables. The attachment points for the spacecraft multi-layer insulation (MLI) are located at a plate which is flushed with the top surface of the modules.
3.2 Ion Emitters
As in all previous applications of this instrument, the ion emitters operate based on the principle of field emission by liquid metal ion sources with indium as charge material. Indium has a melting point at 156.6 °C and comes with isotopes of 115 amu and 113 amu to 96 % and 4 %, respectively. These heavy masses lie above the range of the composition analyzer on board. A solid tantalum capillary with an inner diameter of 20 μm near the end is sticking out of a reservoir containing the charge material (see Fig. 4). The reservoir with the capillary is electrically heated to a temperature well above the melting point of indium. Upon applying high voltage between the capillary and an extractor electrode, the electrostatic stress at the surface of the indium at the top of the capillary acts against the surface tension. The liquid forms a sharp tip (the so-called Taylor cone) where the electric field is sufficiently high to initiate field emission. An ion beam of about ±25∘ Half Width Half Maximum is formed at nominal current (20 μA). Higher currents tend to increase the beam width. In the given geometry ignition normally occurs at voltages <8 kV, and operational voltages typically range between 5 kV and 8 kV, depending on the exact condition and shape of the capillary and the indium inside. The high voltage supplies support voltages up to 12 kV in order to cope with potential deviations from the norm.
Figure 4 shows the emitter assembly with the capillary on top, the metallic reservoir in the center, and the heater element based on a PT-100 resistor attached below. The heater is encapsulated in a ceramic tube and thereby electrically isolated from the reservoir which rests at high voltage. The advantages of these sources are not only their small mass and dimensions but also their high electrical efficiency. As little as 1.2 g of indium in a single reservoir can supply charge for several thousand hours of operation at 20 μA current (see detailed assessment further below). Apart from ∼0.8 W required for the heater element, all electrical power goes into the beam.
3.3 Ion Emitter Modules
As shown in Fig. 5, each module contains two inner cylinders, each with an emitter in its center. The emitters lie on a common high voltage supply and are isolated against the housing and the heater elements below. Although high voltage is applied to both emitters, only one emitter is active at a time; the selection of the active emitter is made by liquefying the indium in only one of the reservoirs by its dedicated heater. Each emitter assembly is held in place by a thermal and electrical isolator made out of PEEK. A printed circuit board for the routing of electrical connections and with a few electronic components is located below the emitter assemblies. The extractor electrodes have an integrated baffle which constrains the beam opening angle to ±45∘ even for high currents when the beam spreads. They are connected to the return line of the high voltage supply, but they are electrically floating against structure in order to allow for the monitoring of the net electrical current carried by the emitted ions.
3.4 Lifetime and Redundancy
The analysis and verification of the emitter lifetime was part of the qualification efforts summarized by Torkar and Tajmar (2013). The operating time of an emitter is a function of reservoir size, emitted current, and mass efficiency of the emission process. In addition to ions, liquid metal ion sources emit micro-droplets. The higher the amount of emitted droplets, the lower the emitter efficiency. Increasing the emission current tends to decrease the emission efficiency. For the type of sources used in MMS, a study has been performed by operating the emitter with currents from 10 to 50 μA and intermediate precision weight measurements (Tajmar 2011). The result reproduced in Table 1 indicates strongly decreasing lifetimes with higher emission currents. We obtain a lifetime per emitter of 9112 hours at the nominal current of 20 μA per emitter, which is the expected value for MMS nominal operations.
Let us compare this number to the requirements of the MMS mission which amounts to operating one of the four emitters in each instrument (i.e., to generate two antiparallel ion beams on-board each spacecraft) while the spacecraft pass through the region of interest. The latter covers 50 % of the mission duration of two years, i.e. 8760 h. After adding some margin for tests on the ground and in-orbit commissioning and dividing by four one arrives at an expected utilization time per emitter of 2650 hours. The formal requirement for MMS has been set to twice this number (i.e. 5300 h) in order to obtain significant redundancy. We conclude that the expected lifetime of an emitter at 20 μA current (9112 h) by far exceeds the requirement of 5300 h.
A more detailed account for redundancy is presented in Table 2. We use the photo-emission parameters for the predicted solar activity during the mission as described in Sect. 3, and take into account a nominal statistical variation of plasma density along the orbit and the variable mass efficiency of emitters as reported above. With non-negligible plasma density in some parts of the region of interest it will be possible to operate the instruments at lower currents than 2×20 μA (as illustrated in Fig. 1) and thereby save some indium. Taking all assumptions together, one obtains in the first row of the table an indium margin of 289 % of one emitter, which is to say that from the four emitters per instrument only the indium of 4−2.89=1.11 emitters has been consumed. Conversely, the charge of the remaining 2.89 emitter reservoirs would suffice to cover an additional 580 days (1.6 years) of an extended mission at the nominal operational duty cycle of 50 %.
The second row in the table deals with an assumed loss of one emitter in each of the two instruments on board of one spacecraft. The margin is reduced by about 100 % (by the equivalent of the failed emitter) but remains strongly positive. The difference is slightly higher than 100 % since the table considers all indium including the amount consumed before launch. Even with two emitter failures per instrument (row three) about one emitter remains as a spare.
High solar activity, corresponding to solar maximum, increases the photo-emission current from the spacecraft surfaces and in turn elevates the current requirement for the ion beams by about 20 to 25 % for each increment of 0.5 V in the spacecraft potential. This eats up some of the indium margin, but a single emitter failure per instrument is still in positive territory (41 % remaining reserve). Only the combination of maximum solar activity and two emitter failures per instrument results in a shortage of about 1/2 emitter reservoirs.
The third block (the last three rows) of Table 2 predicts the indium consumption for a slightly relaxed spacecraft potential requirement (4.5 V instead of 4.0 V). In this case the emitted current can be reduced by about 20 to 25 %, which decreases the rate at which indium is consumed, and hence the margin is rising to positive values even for a dual emitter failure. In conclusion, the size of the indium reservoirs and the presence of eight emitters on each spacecraft carries sufficient redundancy to cope with uncertainties of the solar activity and photo-emission along the mission as well as with single or even dual emitter failures.
3.5 Data Processing Unit
The data processing unit (DPU) is located on the lowermost board in the electronics box. The core of the DPU is an FPGA RTAX2000S with sufficient capacity to include an embedded 8085 processor core. This device is a radiation hard FPGA with internal RAM. The need for flexibility of the design and the shortage of radiation hard processors on the market triggered the development of a VHDL implementation of Intel’s 8-bit 8085 microprocessor in an FPGA. The core emulates 243 of the 246 original 8085 instructions which can be selected individually to minimize FPGA resources. It supports all software interrupts, the main hardware interrupts as well as the direct memory access function. Although the operation timing is slightly different for some instructions the maximum core speed is higher than the original 80C85 microprocessor which was limited to 3.12 MHz. In ASPOC, the FPGA is clocked with 8 MHz. The internal RAM of the RTAX2000S provides fast access and is used for the implementation of the FIFO buffers for the telecommand and telemetry interfaces as well as for lookup tables and temporary data buffering. The FPGA is connected to the SpaceWire link interface LVDS drivers and receivers, to the LVTTL drivers and LVDS receiver for the data and command interfaces and to the analog section containing a 12-bit ADC, a Sample & Hold, a 16-channel analog multiplexer, four 16-bit DAC’s and several operational amplifiers. Furthermore a 32k×8-bit RAM is attached to the FPGA.
The main tasks of the DPU include:
-
Communication with the Central Instrument Data Processor (CIDP), the spacecraft potential measurements provided by the FIELDS instrument suite, and the second ASPOC on the same spacecraft. The CIDP is the power, data, and telemetry interface for all MMS payload. As the control loop with the spacecraft potential involves on-board data delivered by the spin-plane double probes (SDP) as part of FIELDS, the DPU has to handle these data as well. Both ASPOCs on board of each spacecraft are independent units. However, in order to respond coherently (i.e., to set the same ion beam current in both units) while operating in feedback mode, communication between the two units is mandatory, which is accomplished by bent-pipe messages exchanged between the ASPOCs.
-
Calculation of the ion beam current in the control loop for the spacecraft potential. There is an approximately semi-logarithmic relation between ion beam current and equilibrium spacecraft potential. The DPU has to carry out the calculations necessary for this control loop.
-
Command decoding and telemetry packet generation.
-
Selection of the active emitter. Based on ground commands, the DPU has to set the control signals for the respective switches.
-
Control of heater power and high voltage for the active emitter including ramp-up and ramp-down.
-
Housekeeping data collection.
-
On-board health and safety monitoring.
3.6 Low Voltage and Emitter Heater Power Converter
The power converters for all secondary low voltages and the heater element in one of the four emitters, as only one heater is active at a time, are located on a board in the center of the electronics box. A half-bridge converter appeared to be the optimum topology for an unregulated power bus and many low output voltages. The low voltage board can be split into four functional blocks:
-
Input Interface, containing the primary side electronics and input bus filtering.
-
Power Stage, a power converter switching cell providing the secondary side DC voltages and the galvanic insulation.
-
Control and protection, a pulse width modulation (PWM) control of the converter and protection circuits.
-
Post-regulation, providing linear post-regulation.
A common mode and differential mode filter is implemented in order to meet the conducted emission requirements. In order to obtain good output voltage regulation performance without using radiation sensitive optocouplers for closing the regulation loop, the PWM controller is located on the secondary side and is supplied by a small auxiliary primary side start-up converter which is switched off during normal operation. The board features several protection functions in order to ensure that the output voltages are not exceeding the specified overvoltage limits and the converter is not damaged by unintentional handling during integration and test. All protection functions lead to a latching shut-down of the converter. The converter can be restarted by cycling the input bus voltage. An output short circuit protection is included in order to switch off the converter in the case of a short circuit at the output.
The heater power supply has to generate a variable output in order to allow the exact setting of the heater power and hence temperature. To keep the control loop simple, a linear relation between the analog control signal from the DPU and temperature is desired. Analysis shows that driving the voltage instead of temperature is sufficiently linear and is therefore the preferred solution because of its simplicity. The heater converter generates an adjustable stabilized output voltage in the range between 0 V and 16 V using a voltage mode controlled buck converter. Additionally, the heater converter provides the selection of one of four ion emitters using latching relays. Analog telemetry signals of the heater current and heater voltage are provided to the DPU. The current monitoring signal is used for the latching overcurrent protection. The converter can be reset by issuing an off–on sequence on the heater converter control input.
3.7 High Voltage Converter
The high voltage converter (HVC) located on the top board includes a current-fed push–pull resonant inverter used for generating the input voltage of the high voltage multiplier which delivers the required voltages between 0 and 12 kV for the ion emitters. According to the operating modes of the instrument, the high voltage converter can operate in several modes:
-
In constant voltage mode it controls the output voltage of the HVC. This mode is utilized during the start-up before the emitter has ignited.
-
In constant current mode it controls the output current of the HVC. This mode is utilized during nominal operations which require the emission of an ion beam current set by the DPU.
-
In voltage limiting mode it limits the output voltage of the HVC. This mode avoids excessive voltages in the case the emitter impedance varies unexpectedly or in case of commanding errors.
-
In current limiting mode it limits the output current of the HVC. This mode protects the system against shorts.
The high voltage converter is supplied from the secondary side output voltages of the DCC and therefore no primary–secondary isolation is required. The power stage consists of a buck converter and of a current-fed resonant push–pull chopper stage. The function of the buck converter is to control the average voltage fed to the resonant push–pull inverter and finally the voltage at the output of the HV multiplier. The multiplier is a 12-stage half wave type powered via a transformer by a sinusoidal voltage at a frequency of 200 kHz. Because of the very wide control range for the high voltage and the emitter current a combination of a linear voltage regulator and a buck converter operating in average current mode has been implemented. If a small output current is commanded, the duty cycle is reduced by the PWM controller, but if the duty cycle becomes smaller than 20 %, the linear voltage regulator starts to reduce the input voltage for the buck regulator. Below a duty cycle of about 7 % the output is controlled only by means of the linear regulator and the duty cycle is held nearly constant. The converter is quasi-resonant and its resonance frequency is defined by the primary and secondary capacitances and the transformer’s magnetization inductance. The limitation of the output voltage to safe values below about 250 V for testing purposes can be enabled or disabled by a disarm signal. Monitoring circuits are in place for:
-
HV output voltage,
-
total high voltage current, and
-
beam current.
The beam current can be measured at the low side through the voltage drop across a current sense resistor between secondary ground and chassis, shown as R1 in Fig. 6. This is possible because the beam current returns in the form of charged particles from the plasma surrounding the spacecraft flowing back to the structure of the spacecraft. This electric current is equal to the emitted ion current and it flows back to the negative terminal of the HV source. A small part of the emitted indium ions, however, hits the extractor electrode and does not escape into space. Also this extractor current flows back to the negative terminal of the HV source. The sum of the beam current and the extractor current is the total current provided by the supply, which is also measured across resistor R2 in the same figure and provided as monitor signal. The output voltage of the HV generator is measured by means of a HV voltage divider. This voltage is equivalent to the energy of the emitted ions, since no further ion optical elements are present in the emitters.
While there is only a single low voltage side of the HVC, each emitter module is supplied by a dedicated high voltage multiplier for redundancy. Thus, each ASPOC unit hosts two multipliers, but only one high voltage output can be activated at a time. A latching relay, controlled by the DPU, is available for this task. In order to keep the size of the multipliers as small as possible, a potted construction has been selected. For the interfaces to the emitters splice blocks have been integrated into the multipliers in order to eliminate the need for heavy high voltage connectors. The multipliers can be operated not only in vacuum but also at ambient pressure.
3.8 Electronics Box
The electronics box consists of three frames with embedded printed circuit boards (PCBs). The interconnection between the boards is made via PCB connectors, and the external connectors are directly mounted to the PCBs. For radiation shielding the mechanical box has a minimum wall thickness of 2 mm. Additional thickness has been given to exposed parts of the box based on a radiation analysis. Therefore the total radiation dose inside does not exceed 10 kRad(Si). The frames are made of stress corrosion resistant aluminum alloy with Alodine surface treatment. The box is black painted with Aeroglaze. The box mounting surface is made flat in order to create a good electrical and thermal conductive exchange to the bracket to which the unit is mounted.
3.9 Heritage and Innovations
The ASPOC instruments have strong heritage from previous missions such as ESA’s Cluster mission (Riedler et al. 1997; Torkar et al. 2001), but also from the Equator-S (Torkar et al. 1999) and Double Star missions (Torkar et al. 2005). The re-design for MMS described in Torkar et al. (2012) was driven by the need for higher emission currents than in the previous missions due to new requirements, by more stringent environmental requirements which affected the ion emitter modules, and by the necessary adaptations of electronics and software to the new interfaces and constraints. In the following we highlight some of the improvements for MMS.
-
The total ion current is split into two beams per spacecraft in order to improve the symmetry of the sheath, and to reduce the ion current from an individual emitter as well as the space charge in the beam.
-
Capillary-type emitters (rather than the previously used needle emitters) were selected because of their higher reliability.
-
The emitter reservoirs have been increased in volume by a factor 2.4 compared to the instruments on-board Cluster, and tantalum has been chosen as the tank material.
-
Thermal isolators made out of glass-fiber reinforced PEEK provide ample mechanical robustness together with acceptably low thermal conductivity.
-
A cylindrical plume shield was implemented on top of the extractor electrode to ensure compliance to the beam width requirement of <±45∘.
-
The high voltage capability of the supply was increased to 12 kV, permitting a higher margin in case of off-nominal emission behavior.
3.10 Block Diagram
Figure 7 shows a block diagram of the electronics indicating the elements discussed in the previous sections.
3.11 Key Technical Parameters
See Table 3.
3.12 Key Responsibilities
The main institutions involved in the development of the ASPOC instruments for MMS are listed in Table 4.
3.13 Accommodation on Spacecraft
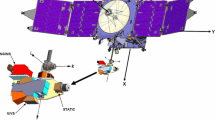
The two ASPOC instruments are mounted at opposite sides of the instrument deck by means of brackets as shown in Fig. 8. The only surfaces exposed to space are the top plates of the emitter modules. The rest of the instrument is covered by multi-layer insulation (MLI, not shown in the figure) and is located inside the spacecraft envelope.
Accommodation of ASPOC on the payload deck of the spacecraft. The acronyms of the scientific payload are written out in Table 5 below
The ion beams of the two ASPOC instruments point in antiparallel directions in order to introduce the least possible asymmetry in the sheath around the spacecraft, as further detailed in Sect. 4. Figure 9 shows a sketch of the ion beam with an assumed width of ±40∘ in relation to the SDP and magnetometer booms. Note that this angle almost represents the possible maximum since a baffle integrated into the emitter system cuts the beam at ±45∘. One can see that the azimuthal angle of the beam center direction has been chosen to be equidistant to the SDP probes in order to minimize any bias introduced to the electric field data. The side lobes of the beams apparently may interfere with the magnetometer booms, but this fact is negligible for the following reasons: The angular distribution of the beam density can be approximated by a cosine function and the current (and charge) density near the edges is low. Furthermore, the beam width for the nominal current of 20 μA is about ±25∘ at half maximum and the current vanishes at angles >32∘, thus the nominal beam is slightly more narrow than shown in the figure, and only in the special condition of higher than nominal beam current a minor fraction of the ion beam will hit the magnetometer boom, but the extent of the interference will be limited to a few atomic layers of added or sputtered layers. The ions hitting the mag boom will not contribute to the spacecraft potential control loop, but again the loss will be negligible due to the small density of the beam at the edges and the minimal geometric cross section of the boom relative to the total cross section of the beam.
4 Expected Performance
4.1 Qualification Results
The qualification process of the instrument and in particular the ion emitters covered all critical aspects and started in 2006 with a long-time storage test of six representative emitters of up to one year under nitrogen purge. Some of the emitters were afterwards stored in clean room conditions for six months. It was concluded that the operating voltages are in almost all cases unaffected by storage either on air or under nitrogen purging.
Several long-term tests were conducted since emitter lifetime assessment was also a key parameter to be tested. Extended testing (1000 hours) was conducted using a breadboard and on four qualification emitters. During such testing the emitter was run in nominal mode, i.e. emitting 20 μA. Although not part of the nominal in-orbit operation, thermal cycles were implemented every 50 hours to investigate any long-term effects on the emitters (none were detected). Following the successful 1000-hour testing, it was decided to investigate the maximum lifetime of an MMS emitter. Subsequently, an emitter test was conducted which was only interrupted for the frequent thermal cycles (every 100 hours) but otherwise left in standard operational mode, i.e. emitting 20 μA (current controlled). The very successful test ran for 8940 hours before its emission ceased. This corresponds very well with an efficiency of 70–71 % as predicted prior to starting this test (see Table 1). Altogether this is to the best knowledge of the authors the longest test of a liquid metal ion source (LMIS) and it shows very well the large operational margin those ion emitters provide to the mission (see Table 2). Figure 10 shows the emitter current and voltage at the outset of the lifetime test. In comparison, Fig. 11 shows the emitter current and voltage at the very end of the test. After nearly 9000 hours of operation and roughly 60 thermal cycles, the emitter ceases to emit. However, prior to its end, the emitter operated at roughly the same voltage as in the very beginning indicating only negligible changes of emission and emitter after such a long time of operation.
The qualification of the emitters was completed by a mechanical strength test and thermal cycling, followed by a 3D X-ray tomographic inspection. Further environmental qualification was performed at instrument level with the usual vibration, shock, and thermal vacuum tests where the emitter modules survived accelerations up to 25 g(rms) and temperatures between −30 °C and +65 °C. An extended report on the qualification of ASPOC has been presented by Torkar and Tajmar (2013).
4.2 Simulation of Plasma Potentials and Plasma Effects
The ion beams reduce the body potential of the spacecraft and the various booms extending up to 60 m from the body. At the same time, the ion beam creates a charge cloud in the environment. The resulting shape of the sheath around the spacecraft is of interest for the proper analysis and interpretation of the plasma and field data. Modeling calculations were carried out at ESA/ESTEC (Clucas and Rodgers 2008). The study involves a particle-in-cell simulation using the SPIS code (http://dev.spis.org/projects/spine/home/spis) in version 3.6. An update using SPIS 4.3 was performed later on. It is noted that simulation work on the Cluster ASPOC instrument has been published for example in Thiébault et al. (2003, 2004), and Cully et al. (2007). The simulation presented in this section is an attempt to look into the differences between the Cluster and MMS missions, being mainly the presence of axial booms on MMS and the division of the active ion emission into two antiparallel plumes, each one carrying about twice the current of the nominal ASPOC beam. The work for MMS takes the following assumptions:
-
Geometry: A simplified geometry is used for the spacecraft. No surface features are present such as payload elements. To aid the complex meshing, the spacecraft is placed within a construction cylinder to allow finer control over the mesh resolution. In addition, to provide a method to easily rotate and position the spacecraft relative to the spin-plane booms, the booms are started from the surface of the cylinder rather than the surface of the spacecraft. This could introduce some uncertainty, but should not be too inaccurate as in this region the spacecraft potential encompasses the starting points of the booms. The spin-plane booms themselves are modeled as “thin wires” within SPIS. For electric field calculations, the wire radius is taken as 0.7 mm, but it length is 58 m, whereby the last 2 m with the pre-amplifier and the probes were excluded from the simulation. Since the role of the probes is to measure the local potential as if they themselves were not present, this is considered an appropriate approach and better than including the probes at a fixed potential. The axial booms are also modeled as thin wires although in reality they consist of a complex ladder-like triangular structure, but modeling this led to difficulties in the SPIS meshing. The gain in accuracy using a more detailed model is expected to be very small.
-
Materials: Default NASCAP material parameters including photo-emission yield were utilized.
-
Plume and particle environment: The ion beams are modeled as In+ currents of 2×20 μA at 5 keV energy. The beam profile was modeled based on laboratory measurements of a representative emitter at that current, with a half width of 35∘. The measured actual composition of the beam comes close to the assumption of a pure In+ beam. A mass efficiency of 100 % was used, but no volume generated species were simulated, such as charge exchange ions. Also other secondary effects such as back sputtering of ions from the residual gas in the operative environment is not taken into account in the simulation. Photo-emission was modeled using PIC and the photoelectrons were tracked fully. The ambient plasma environments considered are representative of a worst case, long Debye length environment (∼700 m).
-
Method: The spacecraft potential has been set to 4 V. The SPIS simulations were run to a point where the ASPOC plumes are fully developed.
Figure 12 shows preliminary PIC simulation results of plasma potentials in the spin plane (top panel) with the Sun in the X direction (vertical in the top panel) and in the plane perpendicular to the Sun direction (bottom panel) under the following conditions: ASPOC is OFF, the plasma environment is such that the spacecraft body and all booms are at +25 V above plasma potential. The signatures of the ∼58 m wire booms are clearly visible, as well as the enhanced potential around the sunlit boom pair.
Figure 13 shows the plasma potentials with ASPOC ON. One can see that the spacecraft body and the booms rest at +4 V above plasma potential. The bottom panel shows that the potentials in the plane through a wire boom pair and perpendicular to the spin plane are slightly enhanced (up to 5.3 V) due to the space charge of the ion beam. In the apex of the beams, immediately in front of the emitters, the plasma potential peaks at about 12.6 V (top panel) but falls off rapidly with increasing distance from the emitters. Overall, the simulation demonstrates that not only the spacecraft body and boom potentials are reduced to +4 V, but also the plasma potential in the vicinity of the spacecraft is reduced from almost 25 V (in the simulation case) to typically 4 to 8 V with the exception of a the small volume directly in front of the emitters where the potential peaks at about 12.6 V.
Mesh-induced uncertainties of the calculated potential were estimated in a reference case with fully symmetric environmental conditions by comparing potentials at symmetric locations. Deviations by less than 5 % were found. Other factors possibly influencing the calculated potential such as different assumptions on the photoelectron spectrum and yield have not been studied. Although these potentials of up to ∼12 V at some distance from the body will have some effect on the plasma and field measurements on the spacecraft, one has to bear in mind that the disturbances by an uncontrolled spacecraft (and boom) potential of ∼50 V (for the same environment conditions) would be much more severe. The residual effect of the controlled, more moderate potential map on the trajectories and energies of the ambient plasma particles has not been modeled and remains open work. It is, however, obvious that shielding of positive ions by positive potential wells as well as acceleration and focusing of ambient electrons will be reduced to a minimum. Departures from gyrotropy of electrons are indicative of demagnetization and hence play an essential role in the detection of reconnection, the prime goal of MMS. The modification of electron trajectories by both charging of the spacecraft body and its various booms and the space charge of ion beam plumes may result in observations of apparent non-gyrotropy where gyrotropy would be expected. Also, variations of the spacecraft potential due to plasma gradients would modify the magnitude of effects on the particles and thus lead to misinterpretations. Scime et al. (1994) have developed a model to correct solar wind observations by the electron spectrometer on Ulysses for non-gyrotropy caused by spherically symmetric equipotentials around the spacecraft. Their method was superior to a simple scalar correction of the particle energy attributed to the spacecraft potential, but it would not work for highly non-symmetric situations caused by booms as for example the numerous booms aboard the MMS spacecraft (magnetometers, spin-plane wire booms, axial booms). In the absence of a controlled spacecraft potential, these booms would carry the said potential far away from the spacecraft body. It is understood that numerical models of the equipotentials and their impact on particle trajectories are important tools to fully reconstruct the undisturbed distribution functions. The modifications introduced by ASPOC are intended to reduce the detrimental effects of body and boom potentials to a minimum while limiting the disturbances by the space charge of the ion beams to moderate levels. Figure 13 indicates that this objective can be achieved.
An earlier study of the photoelectron space charge around a controlled spacecraft has been performed by Zhao et al. (1996) who investigated the effect of a potential barrier created by photoelectrons around a spacecraft with controlled potential. The conditions of this study are also relevant for MMS. They found for currents between 10 and 50 μA that the potential barrier does not exceed 2 V. The magnitude of the positive space charge in the ion beam depends on the current and the beam profile. Thiébault et al. (2003) performed numerical modeling to study the electric potential contours around the ion plume of a 10-μA beam, when the spacecraft is at 7 V in a plasma with a density of 1 cm−3 and an energy of 10 eV. The parameters have been selected to match the Cluster case. They found that the potential distribution in the beam does not exceed values comparable to the potential of the controlled spacecraft body. The potential in most parts of the beam amounts to fractions of a volt. According to the considerations above, the optimum ion current should be in the range between 10 μA and 50 μA. However, the possible influences of ASPOC on particle and field experiments can only be investigated during the commissioning and cross-calibration activities of the experiments in orbit.
4.3 Minimization of Interference
While the main objective of ASPOC is the control of the electric potential for the benefit of on-board plasma measurements, the active emission of ion beams constitutes a potential risk for interferences of various kinds with other measurements. All these risks have been evaluated.
One risk is related to the space charge in the ion beams, which may potentially disturb particle trajectories and electric field measurements by probes. The first step to mitigate these effects was taken by installing two ASPOCs and hence, two ion beams in antiparallel direction. Thereby the charge in each beam is halved. The directions of the beams have been chosen to point into the spin plane in order to be symmetric with respect to the axial electric field probes, and also exactly equidistant to the neighboring radial probes. As shown in Sect. 4.2, some residual space charge is present in the beams, but its effect on particle trajectories is small compared to the influence which an uncontrolled, large spacecraft potential would have.
Other side effects of the ion beams have been analyzed before in the course of previous missions and were found negligible: starting with the giant Larmor radii of the emitted heavy (indium) ions at more than 5 keV energy which prevents them from returning to the spacecraft at any measurable intensity, followed by the negligible amount of backsputtered particles from the residual neutral atmosphere around the spacecraft, and the negligible evaporation of neutral indium which is incapable of covering spacecraft surfaces. On the operational side, as described in Sect. 5, the on-board software ensures smooth variations of the beam current, such that the ambient conditions posed by the ion beams for plasma and field measurements are stable, or in the case of rapid variations of the plasma environment, predictable.
5 Operating Modes
There are several state machines in flight software (FSW) with a small number of operational modes in each. The possible mode transitions are shown in Fig. 14. The most widely used active mode of the instrument will be the constant total current mode (ITOT). It sets a constant output current of the high voltage unit, which includes any losses inside the lens system. Experience has shown that the resulting emission of an almost constant ion current fulfils all requirements for spacecraft potential control in the magnetosphere and the solar wind even without on-board feedback from measurements of the spacecraft potential.
When the fuel save mode option (STOT) is activated, the instrument also listens to the S/C potential message. If the beam is on, and the potential remains below the off-trigger value for more than the trigger delay time, then the instrument switches into hot standby mode. If the beam is off, and the potential remains above the on-trigger value for more than the trigger delay time, then the beam will be turned on and the instrument performs in the same way as in the standard total current mode.
In constant ion current mode (IION) the processor of the instrument reads the monitor of the outgoing beam current and adjusts the output current of the high voltage supply to compensate for any losses in the system.
When the fuel save mode option (SION) is activated, the instrument also listens to the S/C potential message. If the beam is on, and the potential remains below the off-trigger value for more than the trigger delay time, then the instrument switches into hot standby mode. If the beam is off, and the potential remains above the on-trigger value for more than the trigger delay time, then the instrument performs in the same way as in the standard ion current mode.
In the feedback mode (CPOT), a measurement of the spacecraft potential is supplied to ASPOC by the FIELDS Instrument and this information is then used to adjust the beam current in order to maintain a constant value of the potential in a closed-loop scheme. The measurements of the spacecraft potential are updated once every second and sent to ASPOC via dedicated messages (CIDP Bent-Pipe Telemetry).
When the fuel save mode option (SPOT) is activated, the beam is on, and the potential remains below the off-trigger value for more than the trigger delay time, then the instrument switches into hot standby mode. If the beam is off, and the potential remains above the on-trigger value for more than the trigger delay time, then the instrument performs in the same way as in the standard feedback mode.
In slave mode (SLAV), the instrument performs a start-up as in constant ion current mode. As soon as normal operational status is reached (start-up completed), the instrument listens to the beam current and mode information received through the ASPOC status message from the other (master) unit (CIDP Bent-Pipe Telemetry) and follows the master.
When the compensating mode option (COMP) is activated and the beam current of the master is non-zero, the instrument uses a set value for its own control loop twice the set value of the beam current minus the beam current of the master. In this way the sum of both ion beam currents stays at twice the value of the beam current commanded to the compensating slave.
In standby mode (STDB) both the emitters and their heaters are turned off. The standby mode is also the safe mode of the instrument, to which it returns autonomously under certain error conditions. The transition into standby mode also clears all error flags and the emitter selection, and disables high voltage and the heaters.
In order to reduce the time before emission starts, a hot standby mode (HOTS) keeps the indium in a liquid state. This mode can be used to interrupt the ion emission by command, without change of modes or emitters before and after the break. The re-ignition time is reduced to the time required to sweep the high voltage (less than a minute).
A test and commissioning mode (TEST) varies the total ion current in steps of 8 or 16 s with 2 or 4 μA current increments. This mode will be used occasionally to establish the current-voltage characteristics of the spacecraft.
A technical mode (TECH) will be available for low-level commanding during commissioning and re-commissioning of emitters.
Start-up (STUP) is a state of the instrument at the beginning of an active mode when the emitter is being warmed up and ion emission has not yet started. Depending on ambient temperature, emitter condition, and the ramp-up profile of the heater power it takes about 10 to 30 minutes before the indium in the reservoir starts to melt. However, in order to ensure full liquefaction of all indium also inside the capillary, a wait time between 1 and 2 hours is applied before high voltage is ramped up to ignite the ion beam. Within this period the “instrument mode” reported in telemetry will be already the commanded target mode, although there is no ion emission yet.
Once the 8085 processor function has been activated, the code is executed in the program RAM. Even when the processor is activated, the kernel still keeps its supervising function. Time consuming tasks like data block transfers between external and/or internal RAM are implemented as hardware functions in the kernel module and can be initiated by the 8085 program by special control word settings which are polled in the kernel state machine in the background and can force a direct memory access (DMA) request to the 8085 processor. As soon as the kernel receives a DMA acknowledgment the block transfer will be performed and control will be returned to the processor which will continue executing the program where it has been stopped due to the DMA cycle.
The command decoder reads data received from the telecommand receiver buffer (FIFO for first-in, first-out) and forwards these data to a 512×8-bit FPGA internal RAM packet buffer that is accessible by the 8085 core. If the packet error control check is successful, kernel commands will be decoded here and an interrupt request to the kernel unit is generated. In the case of program code up/download commands also the address and length will be decoded.
6 Data Products
ASPOC is an active experiment that modifies the environment of the spacecraft by an energetic ion beam in order to improve measurements of plasma and fields. Detailed knowledge about the operation of ASPOC, its operational status, and of eventual anomalies, is critical for the interpretation of the measurements affected by ASPOC. Short-time variations of the ion beam emitted by ASPOC could be important for a full understanding of plasma, electric field and spacecraft potential data. The operational modes of ASPOC define the method to control the ion beam current. Each method has its own effect on the ion beam. ASPOC therefore provides a data base with full information on the data produced by the ASPOC instruments and on its technical status throughout the mission. Detailed descriptions and specifications of all Level 1/2 data products generated by the Science Data Center (SDC) are given in the Data Products Guide (DPG). While the Level 1 data are generated for each ASPOC separately, Level 2 products will include combined ASPOC1 and ASPOC2 data. No Level 3 products are foreseen at present. Short descriptions on the content of the Level 1 and Level 2 products are given below.
L1 Data Products
ASPOC Level-1 data products contain calibrated raw data at a temporal resolution that corresponds to the data acquisition cycle on-board. The following data products are available (given resolutions are typical values):
-
Ion beam current, energy, ∼1 s resolution
-
Total emitter current, ∼1 s resolution
-
Status and housekeeping, ∼40 s resolution
-
Spacecraft potential as used for control loop, ∼1 s resolution
-
Emitter heater current and voltage, ∼20 s resolution
-
Status flags and parameters, ∼40 s resolution
-
Secondary voltages, ∼60 s resolution
-
Internal temperatures, ∼40 s resolution
L2 Data Products
ASPOC Level-2 products are daily files containing interpolated data at a resolution of 1 second (86400 records per file). For science analysis ASPOC will provide the following data:
-
Ion beam current
individual ASPOC 1 and ASPOC 2 currents and the sum
-
Ion beam energies of individual ASPOCs
-
Data quality information
-
Individual ASPOC 1 and ASPOC 2 modes
-
ASPOC ON/OFF status (ON indicates that at least one ASPOC is emitting ions)
7 Summary
Two ASPOC instruments are part of the payload of each MMS spacecraft. They emit indium ion beams into the spin plane in antiparallel direction in order to control the electric potential of the spacecraft. Beam currents of about 20 μA each are supposed to clamp the potential to values below +4 V, which is beneficial not only for the plasma instrumentation on-board but also improves the conditions for the probe-based electric field measurements. The MMS mission will benefit from an advanced version of the ion emitter instrument ASPOC to control the electric potential of the spacecraft. Compared to previous applications in the ESA Cluster and other missions, longer operation time and higher reliability can be expected.
Abbreviations
- ADC:
-
Analog Digital Converter
- ADP:
-
Axial Double Probes
- ASPOC:
-
Active Spacecraft Potential Control
- CIDP:
-
Central Instrument Data Processor
- DAC:
-
Digital Analog Converter
- DC:
-
Direct Current
- DCC:
-
DC Converter
- DMA:
-
Direct Memory Access
- DPG:
-
Data Products Guide
- DPU:
-
Data Processing Unit
- ESA:
-
European Space Agency
- ESTEC:
-
European Space Research and Technology Centre
- EUV:
-
Extreme Ultra-Violet
- FIFO:
-
First-In First-Out
- FPA:
-
Fast Plasma Instrument
- FPGA:
-
Field Programmable Gate Array
- FSW:
-
Flight Software
- HV:
-
High Voltage
- HVC:
-
High Voltage Converter
- LMIS:
-
Liquid Metal Ion Source
- LVDS:
-
Low Voltage Differential Signal
- LVTTL:
-
Low Voltage Transistor–Transistor Logic
- MLI:
-
Multi-Layer Insulation
- MMS:
-
Magnetospheric Multiscale
- PCB:
-
Printed Circuit Board
- PIC:
-
Particle In Cell
- PWM:
-
Pulse Width Modulation
- RAM:
-
Random Access Memory
- SDC:
-
Science Data Center
- SDP:
-
Spin-Plane Double Probes
- SPIS:
-
Spacecraft Plasma Interaction System
- VHDL:
-
VHSIC Hardware Description Language
- VHSIC:
-
Very High Speed Integrated Circuit
References
S. Clucas, D. Rodgers, Magnetospheric multiscale mission ASPOS plume interactions, in 14th SPINE Workshop, 13–14 November 2008, Noordwijk, The Netherlands. http://dev.spis.org/projects/spine/home/meeting/mxiv/data/Spine08_-_MMS_-_SClucas_pdf
C.M. Cully, R.E. Ergun, A.I. Eriksson, Electrostatic structure around spacecraft in tenuous plasmas. J. Geophys. Res. 112, A09211 (2007). doi:10.1029/2007JA012269, 13 September 2007
V.A. Davis, M.J. Mandell, N.R. Baker, M. Brown-Hayes, G.T. Davis, R.H. Maurer, C. Herrmann, Surface charging analysis of the radiation belt storm probes and magnetospheric multiscale spacecraft. IEEE Trans. Plasma Sci. 40(2), 262–273 (2012)
E. Engwall, A.I. Eriksson, M. André, I. Dandouras, G. Paschmann, J. Quinn, K. Torkar, Low-energy (order 10 eV) ion flow in the magnetotail lobes inferred from spacecraft wake observations. Geophys. Res. Lett. 33 (2006). doi:10.1029/2005GL025179
C.P. Escoubet, A. Pedersen, R. Schmidt, P.A. Lindqvist, Density in the Magnetosphere inferred from ISEE-1 spacecraft potential. J. Geophys. Res. 102, 17595 (1997)
B. Lybekk, A. Pedersen, S. Haaland, K. Svenes, A.N. Fazakerley, A. Masson, M.G.G.T. Taylor, J.-G. Trotignon, Solar cycle variations of the Cluster spacecraft potential and its use for electron density estimations. J. Geophys. Res. 117, A01217 (2012). doi:10.1029/2011JA016969
H. Mott Smith, I. Langmuir, The theory of collectors in gaseous discharges. Phys. Rev. 28, 727 (1926)
T. Nakagawa, T. Ishii, K. Tsuruda, H. Hayakawa, T. Mukai, Net current density of photoelectrons emitted from the surface of the GEOTAIL spacecraft. Earth Planets Space 52(4), 283–292 (2000)
J.A. Newbury, C.T. Russell, J.L. Phillips, S.P. Gary, Electron temperature in the ambient solar wind: typical properties and a lower bound at 1 AU. J. Geophys. Res. 103(A5), 9553–9566 (1998). doi:10.1029/98JA00067
A. Pedersen, Solar wind and magnetosphere plasma diagnostics by spacecraft electrostatic potential measurements. Ann. Geophys. 13, 118–129 (1995)
A. Pedersen, C.R. Chapell, K. Knott, R.C. Olsen, Methods for keeping a conductive spacecraft near the plasma potential, in Spacecraft Plasma Interactions and Their Influence on Field and Particle Measurements, Proceedings of the 17th ESLAB Symposium, ESA SP-198 (1983), pp. 185–190
A. Pedersen, B. Lybekk, M. André, A. Eriksson, A. Masson, F.S. Mozer, P.-A. Lindqvist, P.M.E. Décréau, I. Dandouras, J.-A. Sauvaud, A. Fazakerley, M. Taylor, G. Paschmann, K.R. Svenes, K. Torkar, E. Whipple, Electron density estimations derived from spacecraft potential measurements on cluster in tenuous plasma regions. J. Geophys. Res. 113, A07S33 (2008)
W. Riedler, K. Torkar, F. Rüdenauer, M. Fehringer, A. Pedersen, R. Schmidt, R.J.L. Grard, H. Arends, B.T. Narheim, J. Troim, R. Torbert, R.C. Olsen, E. Whipple, R. Goldstein, N. Valavanoglou, H. Zhao, Active spacecraft potential control. Space Sci. Rev. 79, 271–302 (1997)
S. Schwartz, E. Henley, J. Mitchell, Electron temperature gradient scale at collisionless shocks. Phys. Rev. Lett. 107, 215002 (2011). doi:10.1103/PhysRevLett.107.215002
E.E. Scime, J.L. Phillips, S.J. Bame, Effects of spacecraft potential on three-dimensional electron measurements in the solar wind. J. Geophys. Res. 99, 14769–14776 (1994)
M. Tajmar, Overview of indium LMIS for the NASA-MMS mission and its suitability for an In-FEEP thruster on LISA, in Proceeding of the International Electric Propulsion Conference, IEPC-2011-009 (2011)
B. Thiébault, A. Hilgers, J. Forest, P. Escoubet, M. Fehringer, H. Laakso, Modelling of the photoelectron sheath around an active magnetospheric spacecraft, in Proceedings of the 8th Spacecraft Charging Technology Conference, Huntsville, AL, USA, October 20–24 (2003), NASA/CP-2004-213091
B. Thiébault, A. Hilgers, E. Sasot, H. Laakso, P. Escoubet, V. Génot, J. Forest, Potential barrier in the electrostatic sheath around a magnetospheric spacecraft. J. Geophys. Res. 109, A12207 (2004). doi:10.1029/2004JA010398
K. Torkar, M. Tajmar, Qualification of the liquid metal ion source instruments for the NASA MMS mission. IEEE Trans. Plasma Sci. 41(12), 3512–3519 (2013). doi:10.1109/TPS.2013.2282177
K. Torkar, W. Riedler, M. Fehringer, F. Rüdenauer, C.P. Escoubet, H. Arends, B.T. Narheim, K. Svenes, M.P. McCarthy, K. Parks, R.P. Lin, H. Reme, Spacecraft potential control aboard Equator-S as a test for Cluster-II. Ann. Geophys. 17, 1582–1591 (1999)
K. Torkar, W. Riedler, C.P. Escoubet, M. Fehringer, R. Schmidt, R.J.L. Grard, H. Arends, F. Rüdenauer, W. Steiger, B.T. Narheim, K. Svenes, R. Torbert, M. André, A. Fazakerley, R. Goldstein, R.C. Olsen, A. Pedersen, E. Whipple, H. Zhao, Active spacecraft potential control for cluster—implementation and first results. Ann. Geophys. 19(10/12), 1289–1302 (2001)
K. Torkar, H. Arends, W. Baumjohann, C.P. Escoubet, A. Fazakerley, M. Fehringer, G. Fremuth, H. Jeszenszky, G. Laky, B.T. Narheim, W. Riedler, F. Rüdenauer, W. Steiger, K. Svenes, H. Zhao, Spacecraft potential control for DoubleStar. Ann. Geophys. 23(8), 2813–2823 (2005)
K. Torkar, A.I. Eriksson, P.-A. Lindqvist, W. Steiger, Long-term study of active spacecraft potential control. IEEE Trans. Plasma Sci. 36, 2294–2300 (2008). doi:10.1109/TPS.2008.2003134
K. Torkar, M. Tajmar, C.P. Escoubet, K. Svenes, Active spacecraft potential control for the magnetospheric multiscale mission. IEEE Trans. Plasma Sci. 40(2), 394–401 (2012)
H. Zhao, R. Schmidt, C.P. Escoubet, K. Torkar, W. Riedler, Self-consistent determination of the electrostatic barrier due to photoelectron sheath near a spacecraft. J. Geophys. Res. 101, 15653–15659 (1996)
Acknowledgements
This work was performed under various grants by the Austrian Space Agency through the ESA PRODEX program. The authors thank F. Cipriani (ESA/ESTEC, The Netherlands) for the PIC simulation runs.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Torkar, K., Nakamura, R., Tajmar, M. et al. Active Spacecraft Potential Control Investigation. Space Sci Rev 199, 515–544 (2016). https://doi.org/10.1007/s11214-014-0049-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11214-014-0049-3