Introduction

Doripenem (S-4661) is a new parenteral carbapenem (Fig. 1). Doripenem, similarly to meropenem, ertapenem and biapenem, contains a 1-β-methyl group that prevents degradation caused by renal dehydropeptidase I and therefore does not need to be protected with an inhibitor of this enzyme [1, 2]. Doripenem has a broad spectrum of antimicrobial activity, against both Gram-postitive and Gram-negative bacteria, including Pseudomonas aeruginosa [3–5].

Fig. 1
figure 1

Chemical structure of doripenem

Full size image

Carbapenems are susceptible to degradation during storage and after preparation of parenteral solutions [6–11]. The catalytic effect of citrate, phosphate, acetate, borate and carbonate buffers on the degradation of imipenem has been studied [12]. The components of carbonate buffer do not demonstrate a catalytic effect on the degradation of ertapenem but it was observed that catalysis occurs in the presence of acetate, phosphate and borate buffers [13]. Specific acid–base catalysis of carbapenems involves: (a) hydrolysis of imipenem, meropenem and ertapenem catalyzed by hydrogen ion; (b) spontaneous hydrolysis independent of the charge of imipenem and meropenem or dependent on zwitter ions and dianions of ertapenem under the influence of water and (c) hydrolysis of imipenem, meropenem and ertapenem catalyzed by hydroxide ions [13–15].

The aim of this study was to analyze general and specific acid–base hydrolysis of doripenem in the pH range 0.82–11.56, at 313 K. To determine the reaction rate constants under the influence of buffers, an isocratic HPLC-UV method was used.

Experimental

Material and reagents

Doripenem for injection, DORIBAX™ (Janssen-Cilag International NV), is a white to slightly yellowish sterile crystalline powder. Injection vials contain 500 mg of doripenem monohydrate as an anhydrous basis. The pH of the infusion solution is between 4.5 and 5.5. DORIBAX™ is formulated without any excipients.

Theophylline was used as an internal standard. All other chemicals and solvents were obtained from Merck KGaA (Germany) and were of analytical or high-performance liquid chromatographic grade. High-quality pure water was prepared by using the Millipore purification system (Millipore, Molsheim, France, model Exil SA 67120).

Chromatographic conditions

Chromatographic separation and quantitative determination were performed by using a high performance liquid chromatograph containing a Shimadzu pump, model LC-6A, a UV-VIS detector SPD-6AV (Shimadzu), a Rheodyne 7120 with a 50 μL loop. As the stationary phase, a Lichrospher RP-18, 5 μm particle size, 250 mm × 4 mm (Merck, Darmstadt, Germany) was used. The mobile phase consisted of 4 volumes of acetonitrile and 96 volumes of ammonium acetate, 12 mmol L−1. The flow rate of the mobile phase was 1.2 mL min−1 and the wavelength of the UV-vis detector was set at 298 nm. The HPLC method has been evaluated and validated for the determination of doripenem and biapenem in stability studies [16]. In order to study the effect of buffers on the stability of doripenem, the selectivity was examined for degraded samples in buffers.

Kinetic procedures

The degradation of doripenem in aqueous solutions was studied at 313 K in hydrochloric acid (pH 0.82–2.05), phosphate (pH 2.10–3.38 and 6.36–7.77), acetate (pH 4.23–6.04), borate (pH 7.95–10.49) and carbonate (11.27–11.56) buffers. The pH values of the solutions and those of the buffer standards used to calibrate the pH-meter were measured at reaction temperatures. The pH values of the reaction solutions in HCl were calculated from the equation pH = −log γ HCl [HCl] [17]. The ionic strength of all solutions was adjusted to 0.5 mol L−1 with a solution of sodium chloride (4 mol L−1).

Degradation was initiated by dissolving an accurately weighed 5.0 mg of DORIBAX™ in 25 mL of the solution equilibrated to 313 K in stopped flasks. At specified times, samples of the reaction solutions (1.0 mL) were collected and instantly cooled with a mixture of ice and water, neutralized with 0.8 ml of NaOH solutions of suitable concentrations and assayed. To each sample, 1.0 mL of the internal standard (theophylline 0.1 mg mL−1) was added.

Fig. 2
figure 2

HPLC chromatograms of: solution of doripenem at t = 0 (c = 7.50 × 10−2 mg/mL); solution of doripenem and its degradation products in borate buffer (pH 8.10) after incubation 7.5 min at 313 K (D doripenem, P degradation product, IS internal standard)

Full size image

Results and discussion

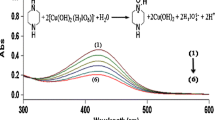
The HPLC method with UV detection used in this study has been found suitable for the determination of doripenem and biapenem under the stress conditions of hydrolysis (acid and base), oxidation, photolysis and thermal degradation [16]. The literature reports the influence of solution pH, temperature and concentration of meropenem, ertapenem and biapenem on the formation of their degradation of products [6, 7, 18]. In this study, the selectivity of this method for the determination of doripenem in the presence of degradation products formed in buffers was confirmed. In the chromatogram, the symmetrical peak of doripenem (tR = 5.8 min) was clearly separated from the peak the of degradation products which formed in the pH range 0.86–11.56 (Fig. 2).

The degradation of doripenem in DORIBAX™ is a pseudo first-order reaction described by the following equation:

$$ \ln ({\text{P}}_{\text{D}} /{\text{P}}_{\text{IS}} ) = \ln ({\text{P}}_{\text{D}} /{\text{P}}_{\text{IS}} )_{0} -{\text{k}}_{\text{obs}} {\text{t}} $$

PD and PIS are the areas of the peaks of doripenem and the internal standard, at time t = 0 and t, respectively. The semi-logarithmic plots ln (PD/PIS) = f(t) were linear and their slopes were equal to the rate constants of the reactions with the negative sign (−kobs).

At a constant pH, ionic strength (0.50 mol L−1) and temperature, the rate constant kobs for the degradation of doripenem increased linearly as the total concentrations of the acetate, phosphate, borate and carbonate buffers increased (Fig. 3). The observed rate constant is a sum of several catalytic rate constants catalyzed by the buffer components and the rate constant at zero buffer concentration. Under the conditions of general acid–base catalysis, kobs was calculated from the following equation:

$$ {\text{k}}_{\text{obs}} = {\text{k}}_{\text{pH}} + {\text{k}}_{\text{B}} [{\text{B}}_{\text{T}} ] $$
(1)

[BT] is the total buffer concentration, kpH the rate constant at zero buffer concentration, kB is the catalytic effect of the buffer components.

Fig. 3
figure 3

Plots of kobs = f(BT) for the degradation of doripenem in acetate (pH 4.23–6.04) and in borate buffers (pH 7.95–10.49) at 313 K

Full size image

The catalytic effect of the acetate buffer was investigated at pH 4.23–6.04. The observed rate constants were calculated from the following equation:

$$ {\text{k}}_{\text{obs}} = {\text{k}}_{\text{pH}} + {\text{k}}_{\text{AcH}} [{\text{AcH}}] + {\text{k}}_{\text{AC}} - [{\text{Ac}}^{ - } ] $$
(2)

AcH is the undissociated acetic acid and Ac− is the acetate ion. The total acetate concentration BT, is:

$$ {\text{B}}_{\text{T}} = [{\text{AcH}}] + [{\text{Ac}}^{ - } ] $$
(3)
$$ {\text{K}}_{\text{a}} = {\frac{{[{\text{H}}^{ + } ][{\text{Ac}}^{ - } ]}}{{[{\text{AcH}}]}}} $$
(4)

The observed rate constant was calculated from the pKa of the acetic acid (4.52) and Eqs. 1 and 2.

$$ k_{obs} = k_{pH} + B_{T} {\frac{{{\text{k}}_{\text{AcH}} [{\text{H}}^{ + } ] + {\text{k}}_{{{\text{AC}}^{ - } }} {\text{K}}_{\text{a}} }}{{[{\text{H}}^{ + } ] + {\text{K}}_{\text{a}} }}} $$
(5)

From the slopes of the plots kobs vs f(BT) for each pH, the buffer catalytic rate constants were calculated (Table 1). The buffer catalytic effect of phosphate (pH 2.10–3.38, pKa = 2.10 and pH 6.36–7.77, pKa = 6.58), borate (pH 7.95–10.49, pKa = 8.90) and carbonate (pH = 11.27–11.56, pKa = 10.02) buffers were calculated from the following equations:

$$ k_{obs} = k_{pH} + B_{T} {\frac{{{\text{k}}_{{{\text{H}}_{3} {\text{PO}}_{4} }} [{\text{H}}^{ + } ] + {\text{k}}_{{H_{2} PO_{4}^{ - } }} {\text{K}}_{\text{a}} }}{{[{\text{H}}^{ + } ] + {\text{K}}_{\text{a}} }}} $$
(6)
$$ k_{obs} = k_{pH} + B_{T} {\frac{{{\text{k}}_{{{\text{H}}_{2} {\text{PO}}_{4}^{ - } }} [{\text{H}}^{ + } ] + {\text{k}}_{{{\text{HPO}}_{4}^{2 - } }} {\text{K}}_{\text{a}} }}{{[{\text{H}}^{ + } ] + {\text{K}}_{\text{a}} }}} $$
(7)
$$ k_{obs} = k_{pH} + B_{T} {\frac{{{\text{k}}_{{{\text{H}}_{3} {\text{BO}}_{4} }} [{\text{H}}^{ + } ] + {\text{k}}_{{{\text{H}}_{2} {\text{BO}}_{3}^{ - } }} {\text{K}}_{\text{a}} }}{{[{\text{H}}^{ + } ] + {\text{K}}_{\text{a}} }}} $$
(8)
$$ k_{obs} = k_{pH} + B_{T} {\frac{{{\text{k}}_{{{\text{HCO}}_{3}^{ - } }} [{\text{H}}^{ + } ] + {\text{k}}_{{{\text{CO}}_{3}^{2 - } }} {\text{K}}_{\text{a}} }}{{[{\text{H}}^{ + } ] + {\text{K}}_{\text{a}} }}} $$
(9)

From Eqs. 5–9, the kpH and the buffer catalytic rate constants of the phosphate, acetate, borate and carbonate buffer components were calculated (Table 1a).

Table 1 Catalytic effect of buffers on the degradation of (a) doripenem, (b) ertapenem and imipenem
Full size table

The kpH rate constants determined in the buffer solutions and calculated from Eq. 1 under the conditions of general acid–base catalysis and in hydrochloric acid (kobs = kpH) were used to calculate the relationship log kpH = f(pH) (Table 2). The relationship log kpH = f(pH) indicates that in aqueous solutions of doripenem at pH 0.86–11.56 the following reactions occur:

Table 2 Observed rate constants of degradation of doripenem in the pH range 0.82–11.56 at 313 K
Full size table

  • degradation of the protonated molecules and zwitter ions of doripenem catalyzed by hydrogen ions (k1 and k2)

  • spontaneous hydrolysis of zwitter ions of doripenem under the influence of water (k3)

  • degradation of zwitter ions and monoanions of doripenem catalyzed by hydroxide ions (k4 and k5)

The total rate of the reaction is equal to the sum of the partial reaction rates:

$$ {\text{k}}_{\text{pH}} = ({\text{k}}_{1} \times {\text{f}}_{1} + {\text{k}}_{2} \times {\text{f}}_{2} ) \times {\text{a}}_{{{\text{H}}^{ + } }} + {\text{k}}_{3} \times {\text{f}}_{2} + {\text{k}}_{4} \times {\text{f}}_{2} \times {\text{a}}_{{{\text{OH}}^{ - } }} + {\text{k}}_{5} \times {\text{a}}_{{{\text{OH}}^{ - } }} \times {\text{f}}_{3} $$
(10)

where \( {\text{a}}_{{{\text{H}}^{ + } }} \) and \( {\text{a}}_{{{\text{OH}}^{ - } }} \) are the hydrogen and hydroxide ion activity, f1–f3 are the fractions of protonated molecules, zwitter ions and monoanions of doripenem. The f1–f3 values were calculated by using the values of pKa of doripenem that were 3.5 and 7.3 at 313 K.

The partial reaction rates (k1 and k2) were calculated by using the values of kpH from the pH range 1.10–4.56. In this pH range f1 + f2 = 1. The plot \( {\text{k}}_{\text{pH}} /{\text{a}}_{{{\text{H}}^{ + } }} = {\text{f}}({\text{f}}_{2} ) \) is linear. The partial reaction rates k1 (1.66 × 10−2 L mol−1 s1) and k2 (1.31 × 10−1 L mol−1 s−1) are equal to the values of \( {\text{k}}_{\text{pH}} /{\text{a}}_{{{\text{H}}^{ + } }} \) for f2 = 0 and f2 = 1, respectively. The partial reaction rates k4 and k5, were calculated by using the values of kpH from the pH range 7.19–11.56. In this pH range, f2 + f3 = 1. The \( {\text{k}}_{\text{pH}} /{\text{a}}_{{{\text{OH}}^{ - } }} = {\text{f}}({\text{f}}_{2} ) \) plot is linear. The reaction rate k4 (11.64 L mol−1 s−1) is equal to the value of \( {\text{k}}_{\text{pH}} /{\text{a}}_{{{\text{OH}}^{ - } }} \) for f2 = 1, while k5 (8.33 × 10−1 L mol−1 s−1) is equal to the value of \( {\text{k}}_{\text{pH}} /{\text{a}}_{{{\text{OH}}^{ - } }} \) for f2 = 0.

The mean value of the partial reaction rate (k3 = 7.87 × 10−7 s−1) was calculated from Eq. 10 by using the kpH values of kpH from the pH range 4.90–6.04:

$$ {\text{k}}_{\text{pH}}^{\prime} = [{\text{k}}_{\text{pH}} - ({\text{k}}_{1} \times {\text{a}}_{{{\text{H}}^{ + } }} \times {\text{f}}_{1} + {\text{k}}_{2} \times {\text{a}}_{{{\text{H}}^{ + } }} \times {\text{f}}_{2} + {\text{k}}_{4} \times {\text{f}}_{2} \times {\text{a}}_{{{\text{OH}}^{ - } }} + {\text{k}}_{5} \times {\text{a}}_{{{\text{OH}}^{ - } }} \times {\text{f}}_{3} )]/{\text{f}}_{2} $$

The correct choice of Eq. 10 was verified by comparing the calculated theoretical profile of log kpH = f(pH) and the experimental results (Fig. 4).

Fig. 4
figure 4

pH-rate profile for the degradation of doripenem at 313 K. The points are determined experimentally. The lines were calculated from Eq. 10

Full size image

The pH-rate profiles of imipenem, ertapenem and doripenem demonstrate that they are the most stable in the pH range 6–7. This is the pH range where the spontaneous hydrolysis of the neutral and ionic molecules of carbapenem occurs. The influence of the catalytic effect of the components of phosphate and acetate buffers on the degradation of these carbapenems is similar. The components of a borate buffer have the greatest catalytic effect on the degradation of imipenem and ertapenem. A comparison of the values of the catalytic rate constants of a carbonate buffer shows that its components have a slight catalytic effect on the degradation of imipenem and do not catalyze the degradation of ertapenem (Table 1b). Therefore, the components of a carbonate buffer can be used in preparations of carbapenems as excipients, e.g. hydrocarbonate sodium in INVANZ and TIENAM and carbonate sodium in MERREM, MERONEM. Doripenem is susceptible to degradation under the influence of the components of common buffers. For that reason, no excipients are present in DORIBAX™.

Conclusions

Doripenem is susceptible to degradation catalyzed by the components of common buffers. Therefore DORIBAX™ contains doripenem without any excipients. The specific acid–base catalysis of doripenem involves: (a) degradation of the protonated molecules and zwitter ions of doripenem catalyzed by hydrogen ions, (b) spontaneous degradation of zwitter ions under the influence of water, (c) degradation of zwitter ions and monoanions catalyzed by hydroxide ions. Doripenem demonstrates the greatest stability at approximately pH 6.0.