1 Introduction

Some interesting papers in the actuarial literature highlight the importance of embedding frailty in the estimation and forecasting of mortality trends (Haberman 2002; Butt and Haberman 2004; Carannante et al. 2023; Olivieri 2006; Vaupel et al. 1979), in order to avoid a material bias in mortality projections. Also in Meyricke and Sherris (2013), the impact of heterogeneity and frailty on the actuarial values of both standard life annuities and underwritten life annuities (i.e., “special rate” life annuities) is investigated. Sherris and Wei (2020) especially focus on the impact of heterogeneity on tail risk and solvency requirements. In Olivieri and Pitacco (2016), the authors suggest adopting a frailty model for risk classification, where the different levels of mortality of the various groups are based on the conditional probability distributions of frailty. To avoid some biases related to adverse selection, a better understanding of heterogeneity is required as in Onchere et al. (2019).

Nevertheless, there is no universal consensus on the definition of frailty, with different knowledge domains using different frailty definitions. In particular, it is noteworthy that, in the actuarial field, frailty represents an unobserved factor including all the sources affecting human mortality other than age. According to the actuarial literature, a cohort consists of a group of heterogeneous individuals in respect of their mortality experience, due to the above-mentioned unobservable factors. The effect of heterogeneity is represented by a positive real number that is frailty level (Pitacco 2019). In the medical field, it is defined as a state of increased vulnerability and reduced ability to recover homeostasis after a stressful event, thereby leading to adverse outcomes, such as falls, disability, delirium, and mortality. Thus, frailty typically results from accumulated impairments in multiple physiological systems and it is suggested in the geriatrics, gerontology and the broader medical literature to be a predictor of functional deterioration and mortality (Strulik 2015; Lacas and Rockwood 2012). Other interesting researches on the concept of frailty applicable also in the actuarial domain represented by the flexible semi-parametric additive frailty hazard model under clustered failure time data, where frailty is assumed to have an additive effect on the hazard function (Liu et al. 2021). The frailty status of an individual, as a process of accumulation of health deficits where ageing is “a consequence of the depletion of redundancy in the human body” (Olshansky et al. 1992), has been well documented in observational studies that reflect real-world clinical practice.

In the present paper, we try to identify the main latent factors explaining the frailty component, in order to clarify its role in the analysis of population mortality trends and projections. We use longitudinal mortality data, to study the effects of the demographic structure and economic aspects on the frailty component that determines the heterogeneity in mortality (Carannante et al. 2023).

Our findings are based on a Random Forest classification algorithm (herein RF) of a longitudinal study of ageing and these lead to an interesting convergence between the actuarial and medical perspectives. We use the metric of variable importance to measure the impact of a predictor variable on predicting the response and this demonstrates that the latent variable frailty is mainly affected by co-morbidities. In other words, the main unspecified factors explaining the frailty (Carannante et al. 2023) consist of the co-morbidities that cause the intrinsic, cumulative, progressive, and deleterious loss of function that eventually culminates in death (Arking 2006). From a mathematical point of view, this result encourages us to introduce the observable component of co-morbidity as a predictor of frailty in a stochastic model for mortality dynamics. In this paper, we propose a frailty-based stochastic model for modelling mortality trends and for projecting mortality in the setting of the seminal Lee–Carter (herein LCA) mortality model. The different models that we investigate encompass time-dependent, and age-dependent frailty factors, forms of interactions of the frailty with the general level of mortality, and finally decomposing the frailty effect across time and by age. We compare these different models, in order to identify the main features, their advantages and shortcomings and to capture the best model choice for including frailty in the estimation of mortality trends. In the context of insurance applications, we consider the risk of relying on too conservative forecasts based on regulatory mortality models (Coulomb et al. 2020).

A comparison of models shows that, although all of the models allow realistic mortality predictions to be made, considering a frailty parameter that includes both the age and time effects leads to improved predictions in comparison with both a basic LCA model and the frailty-based models that consider only one of these effects.

The paper is organized as follows. Section 2 is devoted to a review of the actuarial literature on frailty. Section 3 sets up the mortality models in the Lee–Carter framework by including the frailty component. Section 4 shows the main findings of the empirical investigations that we perform. The final section concludes.

2 Frailty in the actuarial domain

Mortality models are affected by mortality heterogeneity due to observable or non-observable factors. Discrepancies due to the misspecification of the mortality model are known as model risk (Pitacco et al. 2009). Model risk includes shocks caused by period effects that temporarily change the observed mortality.

Frailty is the set of unobservable factors that determines the heterogeneity in mortality. In the actuarial literature, frailty is assumed to be distributed as a non-negative real random variable which represents the individual deviations in mortality from the average behaviour estimated by the model, as analysed by Beard (1971, 2008) and Vaupel et al. (1979).

Let \(Z_x\) be the continuous random frailty at age x, with a probability density function, \(\mu _x(z)\) be the conditional force of mortality for an individual in a population group at age x and with a frailty level z

$$\begin{aligned} \mu _x(z) = \lim _{t \rightarrow 0} \left[ \frac{P(T_x \le t \vert Z_x = z)}{t}\right] \end{aligned}$$
(1)

where \(T_x\) being the remaining lifetime. Note that \(Z_x\) is invariant concerning t. Vaupel et al. (1979) define frailty as a multiplicative factor operating on the force of mortality

$$\begin{aligned} \mu _x(z) = \mu _x \cdot z \end{aligned}$$
(2)

The survival function of an individual at age 0 taking into account the frailty is defined as follows

$$\begin{aligned} S(x,z) = e^{-\int _{0}^{x} \mu _t(Z)dt} = e^{-zH(x)} \end{aligned}$$
(3)

With H(x) being the cumulative standard force of mortality in the interval (0, x).

Improvements in longevity lead to increased mortality heterogeneity due to the onset of co-morbidities (Xu et al. 2019). In much of the actuarial literature, co-morbidities, frailty and disability are often used interchangeably in the identification of the vulnerable elderly (Fried et al. 2001; Jones et al. 2004). The concept of frailty as the onset of a state of health-related vulnerability to mortality is inconsistent with the idea that frailty is invariant over time, as defined in most existing models (i.e., Butt and Haberman 2004; Su and Sherris 2012).

An important milestone in the literature is the paper of Vaupel et al. (1979), which stressed the need to introduce a frailty parameter within mortality models. Frailty was considered difficult to quantify, as it is a latent variable that includes several unspecified factors. This can lead to poor specification of the models, with consequent underestimation or overestimation of the mortality trends.

We propose that the frailty parameter be included in the LCA model, thanks to its desirable properties which include its track record of goodness of fit to historic mortality trends; the ease of interpretation of the key parameters: and the need for a limited number of a priori assumptions. The basic idea of the invariance of frailty over time lies in its definition as an idiosyncratic factor of discrepancy with the general mortality trend. The introduction of an observable and quantifiable frailty parameter pushes us to define it as a latent variable whose value varies over time. For this reason, in the simplest definition of the model, showed in Formula (5), we introduce a time-varying frailty parameter. In other words, considering one or more covariates as significant factors of mortality trends, and no longer a random set of individual and unobservable factors, allows us to build the co-movements of the phenomena over time to explain how they can influence the general trends of mortality.

2.1 The Frailty-based Lee–Carter family models

Let \(\mu _{x,t}\) the force of mortality at age x and time t. A Lee–Carter mortality model (LCA) (Lee and Carter 1992) is defined as follows

$$\begin{aligned} y_{x,t} = \log (\mu _{x,t}) = a_x + b_x k_t + \epsilon _{xt} \end{aligned}$$
(4)

We define the force of mortality conditional on frailty \(\mu _{x,t}\) and the relative model

$$\begin{aligned} y_{x,t} = \log (\mu _{x,t}) = a_x + b_x k_t + z_t + \epsilon _{xt} \end{aligned}$$
(5)

where \(z_t\) is a time-dependent multiplicative coefficient of the force of mortality.

We can express the ordinal least squares optimization for estimating parameters as minimizing the squared sum of errors

$$\begin{aligned} \min _{a_x, b_x, k_t, z_t} \sum _{x,t}^{} \left( y_{x,t,z} - \left( a_x + b_x k_t + z_t \right) \right) ^2 \end{aligned}$$
(6)

so that the objective function is minimised by equating to 0 the first derivatives with respect to \(a_x, b_x, k_t, z_t\).

The updating for the parameters can also be obtained recursively using a normal equation. The required parameters will be obtained numerically according to the following set of equations which can be solved recursively as proposed by Renshaw and Haberman (2003)

$$\begin{aligned} \begin{aligned} a_x = \frac{\sum _{t}^{} D_{xt} \left[ y_{x,t,z} - \hat{b}_x\hat{k}_t - \hat{z}_t \right] }{\sum _{t}^{} D_{xt}} \\ b_x = \frac{\sum _{t}^{} D_{xt}\hat{k}_t \left[ y_{x,t,z} - \hat{a}_x - \hat{z}_t \right] }{\sum _{t}^{} D_{xt}\hat{k}_t^2} \\ k_t = \frac{\sum _{t}^{} D_{xt}\hat{b}_x \left[ y_{x,t,z} - \hat{a}_x - \hat{z}_t \right] }{\sum _{t}^{} D_{xt}\hat{b}_x^2} \\ z_t = \frac{\sum _{t}^{} D_{xt} \left[ y_{x,t,z} - \hat{a}_x - \hat{b}_x\hat{k}_t \right] }{\sum _{t}^{} D_{xt}} \end{aligned} \end{aligned}$$
(7)

As the original LC model, the estimation of \(a_x, b_x, k_t, z_t\) is performed in two stages. The first stage determines the values of the parameters and the second stage involves a re-estimation and matching of the deaths by age x and time t. In this sense, the re-estimation of \(D_{xt}\) at the second stage, could be interpreted as matching observed and modelled deaths allowing for frailty.

To estimate \(z_t\) the definition of a measurable variable of frailty is required. To do this, we perform a RF and we consider the variable importance to determine the main features that affects frailty. On the basis of the results, we build a co-morbidity index (ci) that assigns a frailty score of an individual.

The LCA family of models are based on aggregated data (not individual data) so that we arrange the vector of individual co-morbidity scores in a matrix by age, which we call the Co-morbidity (Aggregated) Matrix CI, in which the rows are the scores for each individual at age x and the columns represent the co-morbidity scores by age from the first observed in the sample, namely 50, to the maximum age \(\omega \).

$$\begin{aligned} CI_t = \begin{pmatrix} ci_{50,1} &{} ci_{50,2} &{} \cdots &{} ci_{50,n} \\ ci_{51,1} &{} ci_{51,2} &{} \cdots &{} ci_{51,n} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ ci_{\omega 1} &{} ci_{\omega 2} &{} \cdots &{} ci_{\omega n} \\ \end{pmatrix} \end{aligned}$$
(8)

where ci is the score of co-morbidity for an individual at age x, each row collects co-morbidity scores of n individuals of a certain age x from 50 to \(\omega \). Being a matrix that collects respondents by age and time, it does not necessarily have the same number of columns per each row. This aspect is not a problem because the matrix representation is only a way to represent the data to be synthesized. Since the co-morbidity score is computed for more than one time according to the waves of a panel survey (see Sect. 3 for a discussion of the data sources), we have \(CI_1, \ldots , CI_T\) co-morbidity matrices that correspond to the calendar years being analysed.

The model is estimated following a similar procedure to the LCA model, which is effectively the application of a singular value decomposition to the matrix of deviances from the \(a_x\) and \(z_t\) parameters.

Let \(\log (m_{x,t})\) the matrix of the log rates by age and time, \(a_x\) the row vector of average age-specific mortality rates and \(z_t\) the column vector of frailty varying by time. We define the matrix \(A_{xt}\) as follows:

$$\begin{aligned} A_{xt} = \log (m_{xt}) - a_x - z_t \end{aligned}$$
(9)

\(A_{xt}\) is the matrix to be factored in to estimate the parameters \(b_x\) and \(k_t\):

$$\begin{aligned} A_{xt} = b_x k_t \end{aligned}$$
(10)

To do this, it is necessary to arrange the co-morbidity matrices \(CI_t\) in a unique matrix age by time. To obtain the input matrix for the models, each co-morbidity matrix \(CI_t\) is aggregated by row, resulting in a series of column vectors representing the average age score for each time t. We consider three measures to aggregate the matrix: the first measure is the average number of co- morbidities. Letting k be a generic individual with age x at time t and \(ci_j\) be a co-morbidity index, that is the number co-morbidities of an individual j, we define the aggregated vectors of the average number of co-morbidities as follows

$$\begin{aligned} C_{ave,t} = \frac{1}{J} \sum _{j=1}^{J} ci_j, t = 1,..., T \end{aligned}$$
(11)

The second measure is the average difference of co-morbidities between age \(x+1\) and age x at time t. Let \(\overline{ci}_j\) the average co-morbidity score for individuals with age x at time t and \(\overline{ci}_{j'}\) the average co-morbidity score for individuals with age \(x+1\) at time t, we define the aggregated vectors of increase of co-morbidity as follows

$$\begin{aligned} C_{inc,t} = \frac{1}{J} \sum _{j' \ne j} \left( \overline{ci}_{j'} - \overline{ci}_j \right) , t = 1,..., T \end{aligned}$$
(12)

And the third measure is the ratio between the deviation from the mean of the co-morbidity score at age x and time t and its mean. Let \(\overline{ci}_j\) be the average co-morbidity score for individuals with age x at time t, we define the aggregated vectors as follows

$$\begin{aligned} C_{rel,t} = \frac{ci_j - \overline{ci}_j}{\overline{ci}_j}, t = 1,\ldots , T \end{aligned}$$
(13)

The indexes in Eqs. (11)–(13) are obtained by fixing time t and aggregating the co-morbidity scores by age x.

The input frailty matrix, namely Z, is obtained by merging the \(C_{t}\) vectors, choosing the best method of aggregation among the three proposed. The time- varying frailty column vector \(z_t\) can be seen as the average values by age of Z matrix

$$\begin{aligned} z_t = \frac{1}{\omega } \sum _{x=1}^{\omega } \zeta _x \end{aligned}$$
(14)

where \(\zeta _x\) are the rows of the Z matrix.

From Equation (5), we define the force of mortality conditional on frailty \(\mu _{x,t}\). The frailty parameter z is included in the different functional forms that we propose for \(y_{x,t} = \log (\mu _{x,t})\), on the basis of the different characteristics being highlighted.

In addition to the model defined by Equation (5), called the Frailty LCA (FLCA) model, we define the Age-dependent Frailty LCA (AFLCA) model, in which a frailty-based average of log-specific mortality rates, \(z_x\) is used as a substitute for the \(a_x\) parameter

$$\begin{aligned} y_{x,t,z} = \log (\mu _{x,t,z}) = b_x k_t + z_x + \epsilon _{xt} \end{aligned}$$
(15)

The idea of this formulation is that frailty is an age-dependent factor that affects the age-specific mortality rate, and represents the mortality effects that the LCA model fails to capture. This aspect is highlighted by the high correlation between \(a_x\) and \(z_x\).

The third model, called the Age and Time Interaction Frailty LCA (IFLCA) model, is formulated to take into account an interaction effect between \(a_x\) and \(z_t\). This model is based on the idea of identifying an effect for both age and time for frailty. However, it has not been possible to use a single parameter \(z_{x,t}\), that is the combined age and time dependent frailty, due to problems related to model convergence.

$$\begin{aligned} y_{x,t,z} = \log (\mu _{x,t,z}) = a_x z_t + b_x k_t + \epsilon _{xt} \end{aligned}$$
(16)

In this formulation, frailty \(z_t\) is a time-varying factor that modifies age- specific mortality rates according to a temporal ageing trend. The fourth model is a generalization of the LCA model proposed by Niu and Melenberg (2014), called the Age-specific and Temporal Frailty LCA (ATFLCA) model, that includes an exogenous trend that affects the mortality trend \(k_t\). In this formulation, \(z_t\) is estimated as a time-varying variable as in Equations (5) and (16), but adding an age-specific coefficient of frailty to be estimated

$$\begin{aligned} y_{x,t,z} = \log (\mu _{x,t,z}) = a_x + g_x z_t + b_x k_t + \epsilon _{xt} \end{aligned}$$
(17)

In this formulation, frailty \(z_t\) is a time-varying factor, independent of the average age- specific mortality rates \(a_x\), but with an age-specific frailty factor \(g_x\) to estimate in combination with \(z_t\).

Table 1 summarises the characteristics of the models proposed in Equations (5) and (15)–(17)

Table 1 Proposed models summary
Full size table

To identify what are the variables that can affect mortality using individual-based data, a Random Forest (RF) algorithm based on classification trees is used. The RF algorithm was introduced by Breiman (2001) and consists of many independent trees grown by recursively performing binary splits on the dataset. Let \(\left[ \left( x_1,\ y_1\right) ,\ldots ,\left( x_n,\ y_n\right) \right] \) the training set. The algorithm predicts the response Y by estimating the regression function \(m\left( x\right) =\mathbb {E}\left[ Y \vert X=x\right] \). The mean-squared generalized error for any numerical predictor h(x) is defined as in the following

$$\begin{aligned} \mathbb {E}_{X,Y} = (Y - h(X))^2 \end{aligned}$$
(18)

where the random forest predictor is the average over \(k = 1, \ldots , n\) trees (Breiman 2001). Breiman (1996) defines bagging as the algorithm to synthesize many trees together generating many bootstrap samples and averaging the predictors. The estimator of the target variable \(\hat{y}_{R_j}\) is the function of the regression tree estimator

$$\begin{aligned} \hat{f}^{tree}(X)=\sum _{j \in J}{\hat{y}_{R_j} 1_{\{X \in R_{j}\}}} \end{aligned}$$
(19)

\(1_{\{.\}}\) being the indicator function and \((R_j)_{j\in J}\) the region of the predictor space which is divided into J distinct and non-overlapping \(R_1, R_2,\ldots , R_J\) and obtained by minimizing the Residual Sum of Squares.

3 Numerical application

3.1 Data description and pre-processing

For our analysis, we refer to two sources of datasets: the Human Mortality Database, used in the mortality model estimation, and the English Longitudinal Study on Ageing (ELSA), used for the detection of determinant factors of frailty and the estimation of the \(z_x\) and \(z_t\) parameters in Eqs. (5) and (15)–(17).

ELSA is a longitudinal household survey dataset for the study of health, economic position, and quality of life among the elderly in England, based on the Health and Retirement Study (HRS) collected in the United States, to facilitate comparisons between the countries (Banks et al. 2021). The dataset is composed of 9 waves from 2002 to 2019, where each wave is a survey carried out every two years in which the same individuals participate until their death and new individuals are introduced to maintain the representativity as the sample ages. The starting sample included 11,050 respondents aged 50 and over on March 1, 2002. The sample is refreshed every two waves, including individuals aged 50 years and over and their partners. The dataset includes any individual interviewed at least once, for a total of 19,802 respondents. Respondents are individuals who were age-eligible at the time of their first interview, while the unit of observations is: the individual, the couple, collecting data relating to the respondent’s partner, and the household.

To perform the Random Forest, we consider only the variable relating to the respondent. To do this, we perform data pre-processing on the original harmonised dataset provided by ELSA. The original dataset is in the form of a cross-sectional data matrix, with the respondent i on the rows and the variables \(x_i\) on the columns, replicating the variables for each wave t. We obtain a panel data matrix, with the respondent and waves on the rows i, t and the variables \(x_{i,t}\) on the columns. To do this, we take the following steps for each respondent i: We detect the first and the last wave in which the respondent participated; We exclude from the dataset those waves where an interviewee’s row is empty because the individual did not enter or left the sample; We find out if the individual responded to all the waves consecutively or skipped some of the waves.

The variables with missing data due to non-response are imputed using the median of the response of the individual in the other waves. Otherwise, missing data are imputed using the median of the respondents. Missing data represent only about 1\(\%\) of the sample.

3.2 Descriptive statistics and variable importance

In both the medical and actuarial literature, frailty is a latent variable linked to population deterioration. To be included in a model, one or more observable features could be identified to find a quantifiable variable that measures frailty. In this sense, we perform a RF to identify the variables relevant to the frailty of individuals. Considering the size of the original matrix, it is necessary to make a qualitative selection of the variables before implementing the model. The target variable is frailty, measured on a scale ranging from 1, indicating excellent status, to 5, indicating poor status.

The feature variables are selected from the following sections of the questionnaire: A: demographics, identifiers, and weights; B: health; C: insurance; F: income and consumption; H: employment history; I: retirement and expectations; L: assistance and care giving; O: end of life planning—which leads to a total of 35 variables.

In particular, features are selected according to the link with frailty and mortality of the individuals. With regard to co-morbidity status, we look for the simultaneous presence of one or more diseases that affect mortality according to the literature, following the approach of the Charlson Co-Morbidity Index (Charlson et al. 1987).

Tables 2, 3, 4, and 5 show the summary statistics of the variables, grouped by theme

Table 2 Summary statistics for socio-demographical variables
Full size table

As can be seen from Table 2, more than half of the sample is made up of women, half have a secondary school qualification and only 16% have tertiary qualifications. In addition, only 5% of the sample has never had a partner, 91% are UK citizens and the average year of birth is 1945.

Table 3 Summary statistics for co-morbidity variables
Full size table

Table 3 shows that the most common pathologies are hypertension, arthritis, heart disease, cataracts, asthma, and diabetes. The other diseases considered are present in less than 10% of the sample. For this reason, we construct a co-morbidity score, in a similar way to the Activities of Daily Living (ADL), a variable of the number of co-morbidities affecting an individual. More than half of the sample has good or very good quality of sight or hearing.

Table 4 Summary statistics for healthy status and habit variables
Full size table

As Table 4 shows, more than 60% of the sample claims to have a good or very good state of health. More than 80% have an ADL score of 0 and only about 2% have a score greater than or equal to 5. Regarding mobility limitations, 47% of the sample have a score of 0 and about 10% have a score greater than or equal to 5. Much of the sample performs physical activity more than once a week, smokes and drinks, while only 30% have active social participation. Less than 1% need care, and the average subjective probability of survival over 10 years is 0.6.

Table 5 Summary statistics for economical variables
Full size table

As Table 5 shows, more than the half of the sample is retired and more than a quarter is employed, only the 13% of the sample has a health insurance policy and only the 34% a life insurance policy.

Variables in Tables 2, 3, 4, and 5 are the feature values used in the RF algorithm, with a categorical variable indicating the death of an individual at the time of interview as the target variable. For this reason, we perform a classification tree RF, with 300 nodes each. The training set is 0.7 of the total dataset. The accuracy of the model, obtained by the average between sensitivity and specificity, is 0.97 in the training set and 0.63 in the test set, with sensitivity of 0.94 and 0.29 and specificity of 0.99 and 0.96 respectively.

Figure 1 shows the variable importance of RF using the mean decrease accuracy and the mean decrease in the Gini coefficient. The Gini coefficient measures the node impurity, that is the probability to be classified incorrectly when selected randomly according to a selected feature. The model is estimated without considering the year of birth, in order to avoid trivial solutions, since the Lee–Carter family of models already consider the calendar year and age.

Fig. 1
figure 1

RF Variable Importance

Full size image

As shown in Fig. 1, for accuracy the most important variable is the co-morbidity score, followed by the mobility score, sight, subjective survival probability, labour and hearing. For the Gini coefficient, the most important variable is income, followed by subjective survival probability, co-morbidity, mobility, hearing and labour. For both criteria, the most important variables concern aspects of self-sufficiency and survival.

Now that we have established that co-morbidity is an aspect that can significantly affect mortality, we will build an indicator that can best represents the phenomenon of frailty, representing the deterioration of the population as it ages.

3.3 Scores of frailty

Figures 2, 3 and 4 show the results relating to the different measures of frailty \(C_{ave,t}\), \(C_{inc,t}\), and \(C_{rel,t}\) defined by Equations (11)–(13). Comparing these measures, we can choose how to aggregate as reliably as possible the \(CI_t\) matrices to obtain the Z matrix to estimate the Lee–Carter family models proposed in the Eqs. (5) and (15)–(17).

Fig. 2
figure 2

Score of frailty as the average number of co-morbidities by age and time (\(C_{ave,t}\))

Full size image

Figure 2 shows that the average number of co-morbidities \(C_{ave,t}\) increases as the age increases for all the years considered. Comparing different years, we can observe that the slope of \(C_{ave,t}\)’s trend is lower for the less recent years and then increases. This suggests that the difference between co-morbidities at the youngest and oldest ages considered becomes more acute over time. Therefore, the incidence of co-morbidities is not constant over time, and moreover the way in which it varies by age tends to be different if we consider its evolution over time.

Fig. 3
figure 3

Score of frailty as the increase of co-morbidities between age x and \(x+1\) (\(C_{inc,t}\))

Full size image

Figure 3 shows that the increase in co-morbidity \(C_{inc,t}\) is oscillating with age, with a slightly increasing trend for older ages. Similarly to \(C_{ave,t}\), different behaviours by time are observed. In particular, we can observe that, for less recent years, the differences between one age and the next tend to be more marked, while in more recent years this phenomenon becomes smaller.

Fig. 4
figure 4

Score of frailty as the relative score of co-morbity by age and time (\(C_{rel,t}\))

Full size image

As shown in Fig. 4, the relative score \(C_{rel,t}\) fluctuates, decreasing with age for the earlier years and slightly increasing with age for other years. Comparing the results by years, we can observe that relative score is higher for the less recent years and than decrease. Note that the increase in co-morbidity and relative score also have zero or negative values.

In order to be able to estimate the LCA-based model, we use an exponential transformation of the data that, being a monotonous transformation, does not cause loss of information.

Once we have determined the measures of frailty, we have estimated the FLCA model, as defined by Eq. (5), using the different scores of frailty and comparing with the LCA estimation. Models are estimated using the Human Mortality Database for England and Wales for the mortality rates and the exposures to risk, and the ELSA dataset for the frailty index. To harmonise the available data between the 2 data sources, we consider the ages from 50 to 90 years and the years 2003, 2005, \(\dots \), 2017, and 2019.

Figures 5, 6, 7 and 8 show the parameters estimates

Fig. 5
figure 5

\(a_x\) parameter comparison for frailty measures

Full size image

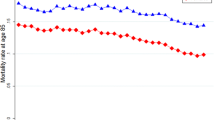
\(a_x\) parameter shown in Fig. 5 represents the average of log-specific mortality rates. Since they do not depend on frailty, they are the same for all the models considered.

Fig. 6
figure 6

\(b_x\) parameter comparison for frailty measures

Full size image

\(b_x\) is the mortality effect due to age. We can observe from Fig. 6 that the parameter changes as the frailty indicator changes. In particular, for the relative score indicator, we observe an inverted functional shape relative to the LCA model, that is an inverted parabola, with lower values for the central ages and higher values for the extreme ages. The increment score indicator has a functional shape similar to the LCA model, with a parabola with slightly lower values at extreme ages and higher values for central ages. Finally, for the average score indicator, the function is similar to LCA but with very small values.

Fig. 7
figure 7

\(k_t\) parameter comparison for frailty measures

Full size image

\(k_t\) is the general trend of mortality. Figure 7 shows that the parameters are very similar across the indicators, and these results are consistent with the general improvement in mortality, which does not depend on frailty, but it is a contributing factor to the secular trends in mortality by age.

Fig. 8
figure 8

\(z_t\) parameter comparison for frailty measures

Full size image

\(z_t\) is the frailty over time. Figure 8 shows that the trend depending on the frailty indicator that is used. With the average indicator \(C_{ave,t}\), the values are higher and have a slightly decreasing trend with age. With the relative indicator \(C_{rel,t}\), the values are decreasing by age, and, finally with the increase indicator \(C_{inc,t}\), the values are around zero and increasing slightly with age.

As shown by Figs. 5, 6, 7 and 8, the use of the frailty parameter \(z_t\) allows us to obtain reliable and unbiased parameter estimates, compared to the LCA model, except for \(b_x\) parameter using the relative \(C_{rel,t}\) score, which we exclude as frailty measure for this reason. Between average \(C_{ave,t}\) and increase \(C_{inc,t}\) measures, we prefer to use the former as it is easier to interpret and to implement in the models.

3.4 Model comparison

Figures 9, 10, 11, 12 and 13 shows the results in terms of parameter estimates for the different models

Fig. 9
figure 9

\(a_x\) parameter comparison for models

Full size image

Figure 9 shows that \(a_x\) is equal for LCA, FLCA, ATFLCA and IFLCA parameters, while for AFLCA the trend is similar, but with a different scale, with only positive values. For all models except ATFLCA, \(a_x\) is calculated in the same way, so the average mortality rates by age are equal. For the model AFLCA, we have replaced the death rates matrix with frailty matrix for calculate the parameter, with consequent different values we have replaced the matrix of mortality rates with the matrix of frailty scores in order to calculate the parameter.

Fig. 10
figure 10

\(b_x\) parameter comparison for models

Full size image

Figure 10 shows that \(b_x\) has a similar age trend for LCA and ATFLCA, with a peak in the mid 70 s. The main difference is that ATFLCA shows lower values in the middle of the age range and higher values for the very old ages. Since bx is an age modulating factor which represents the response of an age to the time trend term \(k_t\), so the ATFLCA model is more optimistic for mortality rates at ages over 80 when \(k_t\) is negative. In contrast, AFLCA and IFLCA have \(b_x\) values which show a decreasing trend by age, that seems an unreliable hypothesis. The age-specific death rate decreases with age. This age pattern is very unusual, compared to the characteristic profile for the LCA model, and implies that mortality would be more responsive to a negative \(k_t\) and a downward time trend at younger ages compared to older ages. We believe that the result is strongly influenced by the measure of the frailty matrix, as these are the two models in which the frailty matrix has greater importance: in the first case, it is used in substitution for the average mortality rates, and in the second case it appears as a product with the the average mortality rates. In these cases, it seems that the models reflect more the age-specific rates of frailty and not age specific mortality rates. The FLCA model shows a similar trend for the parameters to LCA and ATFLCA, but with very small values. We believe that this is a multiplicative effect of frailty that is reflected in the observed values. However, again, the values do not seem to be reliable.

Fig. 11
figure 11

\(k_t\) parameter comparison for models

Full size image

Figure 11 shows that each model shows a similar feature of a downward trend for \(k_t\), with the scale being different for AFLCA. The flattening of curve in 2011–2014 period is a theme studied in actuarial literature (see for instance Djeundje et al. 2022). We believe this aspect is particularly important because it suggests a possible cause-effect relationship between co-morbidity and longevity that the standard Lee–Carter model could not grasp.

Fig. 12
figure 12

\(z_t\) parameter comparison for models

Full size image

Figure 12 shows that the \(z_t\) trend of the variable for the three models is similar, but the values are different, between 0 and 1 for FLCA and IFLCA and between 2.9 and 2.75 for ATFLCA.

Fig. 13
figure 13

\(g_x\) parameter for ATFLCA model

Full size image

Figure 13 shows that the \(g_x\) parameter, which is estimated for ATFLCA model only. As can be seen, \(g_x\) has a parabolic trend by age, with a maximum value around 75 years and with very low values for ages over 84 years. \(g_x\) represents the age-specific response to the trend in frailty values, the main results are that from 50 years to 75 years the sensitivity to the trend in frailty increases and then decreases and for extreme age frailty is lowest and, for extreme ages, the sensitivity to the frailty trend is the lowest.

Table 6 shows the deviance test of frailty models vs LCA model and the information criteria based on deviance. We consider the Akaike Information Criterion (AIC), small-sample corrected AIC (AICc) and Bayesian Information Criterion (BIC)

Table 6 Model information criteria
Full size table

As shown in Table 6, all of the models have a higher deviance with respect to the LCA model. Deviance tests show that the differences, relative to the LCA model, of all models are significant, although marginally for ATFLCA. All the frailty-based models contribute more significantly to the explanation of mortality trend than the LCA model. In addition, the information criteria are lower for all the frailty-based models than for the LCA model. Thus, while ATFLCA is not the best model in terms of goodness-of-fit and computational cost, it still performs better than the LCA model.

Table 7 shows the error measures of the models estimated. We consider Mean absolute error (ME), Mean Square Error (MSE), Mean percentage error (MPE) and Mean absolute percentage error (MAPE)

Table 7 Error measures
Full size table

As shown in Table 7, FLCA, IFLCA and AFLCA, show a lower fitting error with respect to LCA only for some measures, in particular MPE and MAPE for FLCA, ME, MSE and MPE for IFLCA and MSE and MPE for AFLCA. ATFLCA shows a lower fitting error for all of the indeces with respect to LCA and also the other models.

3.5 Forecasting

The five models considered (LCA, FLCA, AFLCA, IFLCA and ATFLCA) were projected for 20 steps ahead, that is 40 years. In order to project the mortality rates, assumptions need to be made about the stochastic processes followed by the time indexes (\(k_t\) in all the models considered, \(z_t\) in the FLCA, IFLCA and ATFLCA models), while the parameters \(a_x\), \(b_x\), \(g_x\) and \(z_x\) are assumed constant over time. For \(k_t\) we have assumed a random walk with drift, as usually adopted in the standard Lee–Carter model, while for \(z_t\) we have adopted the Box-Jenkins method to find the best fitting ARIMA model, also in this case being the random walk with drift. Once we have obtained the ARIMA forecasts, the final projections are computed by adding or multiplying the values of age-dependent parameters, namely \(a_x\), \(b_x\) and, where it is allowed, \(z_x\) and \(g_x\), according to the respective functional forms defined in Eqs. (5) and (15)–(17).

Figure 14 shows the results

Fig. 14
figure 14

Forecasting for 20 steps ahead of models

Full size image

Observing Fig. 14, we notice that the mortality forecasts of FLCA, IFLCA and AFLCA differ from the LCA model, showing a smoother age trend of mortality rates. We also notice, for the IFLCA and AFLCA models only, a greater longevity improvement (in terms of lower mortality rates) for the younger ages than the older ages. In contrast, the ATFLCA model shows mortality forecasts very similar to the LCA model.

Table 8 shows life expectancies at 50 years, obtained by the different models for four selected calendar years

Table 8 Life expectancy projections at age 50
Full size table

Table 8 shows that the values obtained with the IFLCA model are very similar to those obtained with the traditional Lee–Carter model. The values obtained with the AFLCA and ATFLCA models are slightly higher than those of the LCA model (by less than one year in 2059). Finally, the life expectancies of the FLCA model are significantly higher than that of the LCA model (by more than two years in 2059).

The life expectancy results allow us to appreciate how frailty influences the evolution of mortality in the four models that include it. When frailty is considered a time-varying factor, its reduction leads to a decrease in mortality and thus to an increase in life expectancy. In the FLCA model, where an age-specific frailty response coefficient is not included, the effect on mortality of reducing frailty over time is greatest. In models in which an age-specific frailty response coefficient is included, as in the IFLCA and ATFLCA models, the effect on mortality of the decreasing trend in frailty is dampened by the response coefficient. In the AFLCA model, in which frailty is entered as an age dependent factor, the evolution of mortality over time is not influenced by frailty, which only enters the model to represent the age profile of the death probabilities. In this case, the reduction in mortality is only determined by the interaction of the \(k_t\) and \(b_x\) factors. The higher life expectancy obtained with the AFLCA model compared to the LCA model is therefore a consequence of the different age profile of \(b_x\).

Starting from the forecasted models, applying the simulated function, we have produced fan charts showing prediction intervals for mortality rates at ages 50, 70 and 90 for each of the five models considered.

Figure 15 shows the results. Shading in the fan represents prediction intervals at the 50%, 80% and 95% level

Fig. 15
figure 15

Models forecasting at ages 50, 70 and 90

Full size image

Figure 15 represents the uncertainty associated with a model forecast. It can be seen that the LCA model has the narrowest prediction intervals. The introduction of fraity therefore leads to greater volatility in the projections. On the other hand, the greatest uncertainty is observed in those models where frailty is associated with an age dependent response factor (IFLCA and ATFLCA).

The results shown in Table 8 and Fig. 15 are interesting in terms of an actuarial perspective of longevity risk. Actuaries and financial regulators involved in managing pensions and annuities may be interested in a more optimistic assessment of long term trends in life expectancy when fixing prices and capital requirements.

4 Concluding remarks

Forecasting the future mortality trends for a human population is a difficult problems and depends on many factors, for instance, the goodness of the fit to observed data, the robustness of forecasts relative to the sample period used to fit the model and many others factors such as the biological reasonableness of individual stochastic components of the forecasting model (Cairns et al. 2011). The numerous imaginative ‘explanations’ of the functional structures and parameters (Willemse and Kaas 2007) of the mortality models proposed in the literature rely on different hypotheses. In this paper, we try to identify the main latent factors explaining the frailty component, in order to clarify its role in modelling mortality trends and in mortality projections. Our findings based on a machine learning classification of a longitudinal study of ageing lead to recognising co-morbidity as the most important variable determining frailty.

In other words, the main unspecified factors that explain frailty (from a determination of the heterogeneity in mortality outcomes) consist of the co-morbidities that cause the intrinsic, cumulative, progressive, and deleterious loss of function that eventually culminates in death (Arking 2006). From a mathematical point of view, this result encourages the theoretical assumption of embedding, in a stochastic mortality model, the observable component of co-morbidity as a predictor of frailty, to avoid systematic bias in the projections (Vaupel et al. 1979).

In this paper, due to its desirable properties, we propose a frailty-based stochastic model for projecting mortality in the setting of the Lee–Carter family of mortality models. To the best of our knowledge, this is the first proposal to introduce into a mortality model the observable component of co-morbidity as a predictor of frailty. We propose different approaches to including the frailty component into the mortality model by passing from time-dependent, and age-dependent frailty factors and forms of interactions of the frailty with the general level of mortality, leading to decomposing the frailty effect across time and by age. We compare the models that we have developed, and note that each has a good forecasting performance. The analysis of different forms of dependence of mortality on frailty has allowed us to identify the model that seems to capture the phenomenon best. In terms of goodness of fit to the observed data, the model obtaining the best values has turned out to be the ATFLCA, i.e. the model in which frailty is represented by a time-varying factor and an age-specific frailty response coefficient is included. Moreover, our research has pointed out that modelling the observable component of co-morbidity as a predictor of frailty that varies across age and time leads to a superior adjustment to the mortality rate for an individual.

In the projections, the models show how the evolution of frailty contributes to the increase in life expectancy, although in the best performing models this increase is not large (about one year after 40 years of projections). It is also observed that models that include an age-specific frailty response coefficient are characterised by a larger prediction interval.

Further researches will be devoted to the analyses of different datasets in order to verify whether our main numerical findings are specific to the England and Wells experience or have a more general validity. A possible research development could be to investigate the implications of using a model including frailty in the valuation of pension or annuity products and thus measuring the longevity risk faced by an insurance company or pension fund.