Quantum version of Prisoners’ Dilemma under interacting environment

Abstract

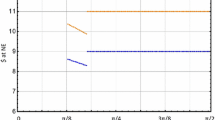
Quantum game theory is a rapidly evolving subject that extends beyond physics. In this research work, a schematic picture of quantum game theory has been provided with the help of the famous game Prisoners’ Dilemma, where both of the prisoners possess an entangled qubit. Increasing the payoffs of the prisoners, quantum theory introduces a new Nash equilibrium. It has been considered that the shared qubits may interact with the environment, which is a bath of simple harmonic oscillators. This interaction introduces decoherence. Calculating the decoherence factor, we have shown that as time increases, the new Nash equilibrium disappears and accordingly the corresponding payoffs reduce. The decoherence factor has been analyzed for different time regions, and a characteristic time scale of decoherence has also been provided. A critical time scale, below which Alice and Bob can use the quantum strategy to achieve a higher payoff, has been described with its connection to the off-diagonal elements of the reduced density matrix of the prisoners. The critical time scale has also been discussed based on whether the decoherence occurred once or twice. A comparative discussion establishes that the process of decoherence is faster when it occurs twice. It needs to be mentioned here that the total time of decoherence is the same in both cases.