Abstract
A mixed lattice vector space is a partially ordered vector space with two partial orderings and certain lattice-type properties. In this paper we first give some fundamental results in mixed lattice groups, and then we investigate the structure theory of mixed lattice vector spaces, which can be viewed as a generalization of the theory of Riesz spaces. More specifically, we study the properties of ideals and bands in mixed lattice spaces, and the related idea of representing a mixed lattice space as a direct sum of disjoint bands. Under certain conditions, these decompositions can also be given in terms of order projections.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The idea of equipping a vector space with two partial orderings plays an important role in classical potential theory [4]. During the 1970 s and early 1980 s, M. Arsove and H. Leutwiler introduced the notion of a mixed lattice semigroup which provides a rather general setting for axiomatic potential theory [2]. The novelty of their theory was that it mixed two partial orderings in a semigroup in such way that the resulting structure is not a lattice, in general, but it has many lattice-type properties, and the interplay between the two partial orderings plays a fundamental role in the theory. Although Arsove and Leutwiler formulated their theory in the semigroup setting, a similar mixed lattice order structure can also be imposed on groups and vector spaces where non-positive elements are present. This gives rise to the notions of mixed lattice groups and mixed lattice vector spaces. In this paper, we are mostly concerned with the latter. A mixed lattice space is a real partially ordered vector space with two partial orderings, where the usual lattice operations (i.e. the supremum and infimum of two elements) are replaced with asymmetric mixed envelopes that are formed with respect to the two partial orderings. As a consequence, the theory of mixed lattice structures is asymmetric in nature. For example, the mixed envelopes do not have commutative or distributive properties, in contrast to the theory of Riesz spaces, where the lattice operations are commutative and distributive. On the other hand, mixed lattice spaces have also many similarities to Riesz spaces. In fact, a Riesz space is just a special case of a mixed lattice vector space, in which the two partial orderings coincide. Early studies of mixed lattice groups were done by Eriksson-Bique [6, 7], and more recently by the authors in [5]. The present paper is a continuation of the research that was commenced in [5,6,7].
Ideals and bands are the main structural components of a Riesz space, and Riesz spaces can be decomposed into order direct sums of disjoint bands. Apart from Riesz spaces, these concepts have recently been studied in more general ordered vector spaces [8, 9], as well as in mixed lattice semigroups in [2]. It is therefore natural to explore these ideas also in the mixed lattice space setting, and this is the main topic of the present paper.
First we give a brief survey of terminology, definitions and basic results that will be needed in the subsequent sections. Section 3 contains some important results on the properties of the mixed envelopes. Many of these results are known in mixed lattice semigroups through the work of Arsove and Leutwiler in [2], but they haven’t been studied in the group setting. The main difficulty here is that many of the results that hold in a mixed lattice semigroup depend on the fact that all the elements are positive. Therefore, some of these properties do not hold in the group setting without some limitations. We also give the mixed lattice version of the fundamental dominated decomposition theorem.
The concept of an ideal in mixed lattice groups and vector spaces was introduced in [5]. Many properties of the most relevant subspaces, including ideals, are determined by their sets of positive elements. In this context, positive cones play a fundamental role and we discuss some properties of mixed lattice cones, which generate mixed lattice subspaces. In Sect. 4 we study the structure of ideals, and we introduce the notion of a band in mixed lattice spaces and give some basic results concerning bands. The two partial orderings give rise to two different types of ideals, called ideals and specific ideals, depending on which partial ordering is considered. Consequently, we also have different notions of a band, depending on the type of the underlying ideal. In addition to these, we introduce an intermediate notion of a quasi-ideal, which plays an important role in the structure theory.
Disjoint complements are introduced in Sect. 5. The disjointness of two positive elements is defined in a similar manner as in Riesz spaces, by requiring that the lower envelope of the two elements is zero. However, the asymmetric nature of the mixed envelopes leads to two distinct one-sided notions of disjointness, the left and right disjointness. The disjoint complements and direct sum decompositions in mixed lattice semigroups were studied by Arsove and Leutwiler in [2], where they showed that the left and right disjoint complements of any non-empty set in a mixed lattice semigroup have certain band-type properties. In mixed lattice vector spaces the situation is a bit more complicated, again due to the existence of non-positive elements. In order to obtain a satisfactory theory, we consider disjointness first for positive elements, and we then define the left and right disjoint complements as the specific ideals and ideals, respectively, generated by certain cones of positive elements that satisfy the disjointness conditions. This approach turns out to be quite natural, and we also find it to be compatible with the existing theory of mixed lattice semigroups. We then investigate the structure and properties of the disjoint complements, such as the band properties and the structure of the sub-cones that generate the disjoint complements. We also introduce the notion of symmetric absolute value in mixed lattice spaces and show that the right disjoint complement can be described in terms of the absolute value. This approach corresponds to the usual definition of the disjoint complement in a Riesz space. Finally, we give some results concerning bands in Archimedean mixed lattice spaces.
In the final section we study decompositions of mixed lattice spaces, where the space can be written as a direct sum of an ideal and a specific ideal that are disjoint complements of each other. The direct sum decompositions give rise to band projections which can be expressed in terms of order projection operators. Of course, these projection properties have their well-known analogues in Riesz space theory. For an account of the theory and terminology of Riesz spaces, we refer to [10] and [11].
2 Preliminaries
The fundamental structure on which most of the theory of mixed lattice groups and vector spaces is based on, is called a mixed lattice semigroup. Let \(S(+,\le )\) be a positive partially ordered abelian semigroup with zero element. The semigroup \(S(+,\le )\) is also assumed to have the cancellation property: \(x+z\le y+z\) implies \(x\le y\) for all \(x,y,z\in S\). The partial order \(\le \) is called the initial order. A second partial ordering \(\preccurlyeq \) (called the specific order) is then defined on S by \(x\preccurlyeq y\) if \(y=x+m\) for some \(m\in S\). Note that this implies that \(x\succcurlyeq 0\) for all \(x\in S\). The semigroup \((S,+,\le ,\preccurlyeq )\) is called a mixed lattice semigroup if, in addition, the mixed lower envelope

and the mixed upper envelope

exist for all \(x,y\in S\), and they satisfy the identity

In the above expressions the minimum and maximum are taken with respect to the initial order \(\le \).
Typical examples of mixed lattice semigroups are constructed by starting with some vector space V and a cone C in V which generates a partial ordering \(\le \). Then a sub-cone S of C is taken as the semigroup in which the specific order \(\preccurlyeq \) is defined as the partial ordering induced by the semigroup S itself, that is, S is taken as the positive cone for the partial ordering \(\preccurlyeq \). This procedure turns S into a mixed lattice semigroup, provided that the conditions in the above definitions are satisfied. Many examples of mixed lattice structures are given in [5].
A mixed lattice group is a partially ordered commutative group \((G,+,\le ,\preccurlyeq )\) with two partial orderings \(\le \) and \(\preccurlyeq \) (called again the initial order and the specific order, respectively) such that the mixed upper and lower envelopes  and
and  , as defined above, exist in G for all \(x,y\in G\). A sub-semigroup S of a mixed lattice group G is called a mixed lattice sub-semigroup of G if
, as defined above, exist in G for all \(x,y\in G\). A sub-semigroup S of a mixed lattice group G is called a mixed lattice sub-semigroup of G if  and
and  belong to S whenever \(x,y\in S\). It should be remarked here that the additional identity (2.1) in the definition of a mixed lattice semigroup is then automatically satisfied because the identity holds in G (see further properties of the mixed envelopes below). A mixed lattice group G is called quasi-regular if the set \(G_{sp}=\{x\in G:x\succcurlyeq 0\}\) is a mixed lattice sub-semigroup of G, and G is called regular if G is quasi-regular and every \(x\in G\) can be written as \(x=u-v\) where \(u,v\in G_{sp}\).
belong to S whenever \(x,y\in S\). It should be remarked here that the additional identity (2.1) in the definition of a mixed lattice semigroup is then automatically satisfied because the identity holds in G (see further properties of the mixed envelopes below). A mixed lattice group G is called quasi-regular if the set \(G_{sp}=\{x\in G:x\succcurlyeq 0\}\) is a mixed lattice sub-semigroup of G, and G is called regular if G is quasi-regular and every \(x\in G\) can be written as \(x=u-v\) where \(u,v\in G_{sp}\).
There are several fundamental rules for the mixed envelopes that hold in quasi-regular mixed lattice groups. These are listed below, and will be used in this paper frequently. For more details concerning these rules and their proofs we refer to [5] and [7].
The following hold for all elements x, y and z in a quasi-regular mixed lattice group G.

We should mention here that (M1)–(M6a) hold more generally in every mixed lattice group. Moreover, quasi-regularity is equivalent to the properties (M8a) and (M8b), and these in turn imply (M7) (but not conversely). A mixed lattice group in which (M7) holds is called pre-regular.
3 Additional properties of mixed lattice groups
In this section we give several further properties of mixed lattice groups. Many of these have been studied in mixed lattice semigroups in [2], but some of them do not carry over to the group setting without some restrictions.
We begin by introducing a useful tool (which is due to M. Arsove and H. Leutwiler, [2]) for studying the properties of the mixed envelopes. For \(x,u\in G\) we define the mapping \(S_x(u)=\min \{w\succcurlyeq 0:u\le w+x\}\), where the minimum is taken with respect to \(\le \). We will first show that the element \(S_x(u)\) exists for all \(x,u\in G\) and it has certain basic properties.
Proposition 3.1
Let G be a quasi-regular mixed lattice group. The mapping \(S_x\) defined above has the following properties.
-
(a)
The element \(S_x(u)=\min \{w\succcurlyeq 0:u\le w+x\}\) exists for all \(x,u\in G\) and it is given by
 .
. -
(b)
If \(x\succcurlyeq 0\) then \(S_x S_y (u)= S_{x+y}(u)\) holds for all \(u,y\in G\). Moreover, if \(x,y\succcurlyeq 0\) then \(S_x S_y (u)=S_y S_x (u)=S_{x+y} (u)\) for all \(u\in G\).
-
(c)
\(S_{x+a}(u+a)=S_x(u)\) for all \(x,u,a\in G\).
-
(d)
If \(u\preccurlyeq v\) then \(S_x(u)=S_{v-u}S_x(v)\) for all \(x\in G\).
Proof
-
(a)
Let \(A=\{w\succcurlyeq 0:u\le w+x\}\). Let
 . The equality
. The equality  follows immediately from (M1). First we note that \(m\succcurlyeq 0\) and
follows immediately from (M1). First we note that \(m\succcurlyeq 0\) and 
and so \(m\in A\). Assume then that \(z\in A\). Then \(u\le z+x\) and since \(z\succcurlyeq 0\), we also have \(u\preccurlyeq z+u\). By (M5) and (M2) it now follows that
 and this implies that
and this implies that  . This shows that \(m=S_x(u)=\min \{w\succcurlyeq 0:u\le w+x\}\).
. This shows that \(m=S_x(u)=\min \{w\succcurlyeq 0:u\le w+x\}\). -
(b)
By part (a) we have
 for all \(y,u\in G\), and similarly \(S_y(u)\le S_x S_y(u) +x\). It follows that \(u\le S_x S_y(u) +x+y\) and by the definition of \(S_x\) we obtain the inequality \(S_{x+y} (u) \le S_x S_y (u)\). Similarly, exchanging the roles of x and y gives \(S_{x+y} (u) \le S_y S_x (u)\). On the other hand, we have \(u\le S_{x+y} (u) +x+y\), and if \(x\succcurlyeq 0\) then \(S_{x+y} (u) +x\succcurlyeq 0\), and it follows again from the definition that \(S_y(u) \le S_{x+y} (u) +x\). Hence, \(S_x S_y (u)\le S_{x+y} (u)\) and so the equality \(S_x S_y (u)= S_{x+y}(u)\) holds for all \(u,y\in G\). If also \(y\succcurlyeq 0\) then we can exchange the roles of x and y above to get \(S_x S_y (u)=S_y S_x (u)= S_{x+y} (u)\) for all \(u\in G\).
for all \(y,u\in G\), and similarly \(S_y(u)\le S_x S_y(u) +x\). It follows that \(u\le S_x S_y(u) +x+y\) and by the definition of \(S_x\) we obtain the inequality \(S_{x+y} (u) \le S_x S_y (u)\). Similarly, exchanging the roles of x and y gives \(S_{x+y} (u) \le S_y S_x (u)\). On the other hand, we have \(u\le S_{x+y} (u) +x+y\), and if \(x\succcurlyeq 0\) then \(S_{x+y} (u) +x\succcurlyeq 0\), and it follows again from the definition that \(S_y(u) \le S_{x+y} (u) +x\). Hence, \(S_x S_y (u)\le S_{x+y} (u)\) and so the equality \(S_x S_y (u)= S_{x+y}(u)\) holds for all \(u,y\in G\). If also \(y\succcurlyeq 0\) then we can exchange the roles of x and y above to get \(S_x S_y (u)=S_y S_x (u)= S_{x+y} (u)\) for all \(u\in G\). -
(c)
The translation invariance property follows immediately from the definition of \(S_x\).
-
(d)
Let \(u\preccurlyeq v\). Then \(a=v-u\succcurlyeq 0\) and using (b) and (c) gives
$$\begin{aligned} S_x(u)=S_{x+a}(u+a)=S_aS_x(u+a)=S_{v-u}S_x(v). \end{aligned}$$
\(\square \)
Using the above results for \(S_x\) we can prove several additional properties of the mixed envelopes. We begin with the following theorem, which gives two important inequalities for the mixed envelopes. They were first studied in mixed lattice semigroups by Arsove and Leutwiler [2, Theorem 3.2]. Later, Eriksson–Bique showed that they hold also in a group extension of a mixed lattice semigroup, and therefore in every regular mixed lattice group [6, Theorem 3.5]. We will now prove that the inequalities hold more generally in every quasi-regular mixed lattice group. Later on, these inequalities will play an important role in the development of the theory.
Theorem 3.2
Let G be a quasi-regular mixed lattice group. If \(x\preccurlyeq y\) then the inequalities

hold for all \(u\in G\).
Proof
First we observe that the first inequality is equivalent to

Now if \(x\preccurlyeq y\) then \(y=a+x\), where \(a=y-x\succcurlyeq 0\). Using the properties of the mapping \(S_x\) we get

and this yields

Hence we have  . Now
. Now  and \(y-x\succcurlyeq 0\), and since G is quasi-regular, it follows by (M8b) that
and \(y-x\succcurlyeq 0\), and since G is quasi-regular, it follows by (M8b) that  . Thus we have shown that
. Thus we have shown that  , or
, or  .
.
The proof of the other inequality is similar. \(\square \)
The next example shows that the assumptions in the last theorem cannot be weakened, that is, the inequalities do not hold if G is not quasi-regular.
Example 3.3
Let \(G=({\mathbb {Z}}\times {\mathbb {Z}},\le ,\preccurlyeq )\) and define partial orders \(\le \) and \(\preccurlyeq \) as follows. If \(x=(x_1,x_2)\) and \(y=(y_1,y_2)\) then \(x\le y\) iff \(x_1\le y_1\) and \(x_2\le y_2\). In addition, \(x\preccurlyeq y\) iff \(x=y\) or \(y_1\ge x_1+1\) and \(y_2\ge x_2+1\). Then G is a mixed lattice group which is pre-regular but not quasi-regular (see [5, Example 2.23]). If \(x=(1,0)\), \(y=(2,1)\) and \(u=(0,0)\) then  and
and  . Now \(x\preccurlyeq y\) but
. Now \(x\preccurlyeq y\) but  does not hold.
does not hold.
The inequalities in Theorem 3.2 have several implications. For example, the following one-sided associative and distributive laws hold for the mixed envelopes. The proof is exactly the same as in the mixed lattice semigroup case, see [2, Theorems 3.3 and 3.5].
Theorem 3.4
If G is a quasi-regular mixed lattice group then the following one-sided associative laws

and one-sided distributive laws

hold for all \(x,y,z\in G\).
In the sequel, \(\sup E\) and \(\inf E\) stand for the supremum and infimum of a subset E with respect to the initial order \(\le \). The supremum and infimum of E with respect to the specific order \(\preccurlyeq \) are denoted by \({{\,\mathrm{sp \,sup}\,}}E\) and \({{\,\mathrm{sp \,inf}\,}}E\), respectively.
The following result is originally due to Boboc and Cornea (see [3, Proposition 2.1.4]). The more general mixed lattice version is given in [2, Theorem 4.2].
Lemma 3.5
Let E be a subset of a quasi-regular mixed lattice group G such that \(u_0=\sup E\) exists in G. If \(w\in G\) is an element such that \(x\preccurlyeq w\) for all \(x\in E\) then \(u_0\preccurlyeq w\). Similarly, if \(v_0=\inf E\) exists and \(w\in G\) is such that \(w\preccurlyeq x\) for all \(x\in E\) then \(w\preccurlyeq v_0\).
Proof
If \(u_0=\sup E\) then \(x\preccurlyeq u_0\) for all \(x\in E\), and so if \(x\preccurlyeq w\) for all \(x\in E\) then by (M5),  for all \(x\in E\). This implies that
for all \(x\in E\). This implies that  . The result concerning the infimum can be proved by a similar argument. \(\square \)
. The result concerning the infimum can be proved by a similar argument. \(\square \)
We obtain stronger results if the supremum and specific supremum of a subset are equal.
Definition 3.6
Let E be a subset of a mixed lattice group G such that \(\sup E\) and \({{\,\mathrm{sp \,sup}\,}}E\) exist in G, and \(u_0=\sup E = {{\,\mathrm{sp \,sup}\,}}E\). The element \(u_0\) is called the strong supremum of E and it is denoted by \(u_0 ={{\,\mathrm{str \,sup}\,}}E\). The strong infimum \(v_0\) of E is defined similarly, and it is denoted by \(v_0={{\,\mathrm{str \,inf}\,}}E\).
The following result can now be proved exactly the same way as in the theory of mixed lattice semigroups (see [2], p. 23). We include the proof here for completeness.
Proposition 3.7
Let E be a subset of a quasi-regular mixed lattice group G such that \(u_0={{\,\mathrm{str \,sup}\,}}E\) exists in G. Then for all \(x\in G\)

Similarly, if \(v_0={{\,\mathrm{str \,inf}\,}}E\) exists then for all \(x\in G\)

Proof
If \(x\in G\) and \(u_0={{\,\mathrm{str \,sup}\,}}E\) then By (M5),  and
and  for all \(u\in E\). Let w be any element such that
for all \(u\in E\). Let w be any element such that  for all \(u\in E\). Then by (M1) we have
for all \(u\in E\). Then by (M1) we have

for all \(u\in E\). Thus  is a \((\le )\)-upper bound of E, and since \(u_0=\sup E\), by (M1) this implies that
is a \((\le )\)-upper bound of E, and since \(u_0=\sup E\), by (M1) this implies that

Hence  , and this shows that
, and this shows that  . On the other hand, by Theorem 3.2 we have
. On the other hand, by Theorem 3.2 we have  for all \(u\in E\). If
for all \(u\in E\). If  for all \(u\in E\) then it follows by Lemma 3.5 that
for all \(u\in E\) then it follows by Lemma 3.5 that  , and so
, and so  . This shows that
. This shows that  . The other identities can be proved in a similar manner. \(\square \)
. The other identities can be proved in a similar manner. \(\square \)
In the sequel, we will use the following notation. The inequalities \(x\preccurlyeq y\) and \(y\le z\) are written more concisely as \(x\preccurlyeq y \le z\). Similarly, the notation \(x\le y \preccurlyeq z\) means that \(x\le y\) and \(y\preccurlyeq z\).
We conclude this section by showing that mixed lattice groups have the dominated decomposition property. We actually have different variants of this property that will be useful.
Theorem 3.8
Let G be a quasi-regular mixed lattice group.
-
(a)
Let \(u\succcurlyeq 0\), \(v_1\ge 0\) and \(v_2\succcurlyeq 0\) be elements of G satisfying \(u\le v_1+v_2\). Then there exist elements \(u_1\) and \(u_2\) such that \(0\le u_1\le v_1\), \(0\preccurlyeq u_2\le v_2\) and \(u=u_1+u_2\). Moreover, if \(v_1\succcurlyeq 0\) then \(u_1 \succcurlyeq 0\), and if \(u\preccurlyeq v_1+v_2\) then \(u_2\preccurlyeq v_2\).
-
(B)
Let \(u\ge 0\), \(v_1\succcurlyeq 0\) and \(v_2\ge 0\) be elements of G satisfying \(u\preccurlyeq v_1+v_2\). Then there exist elements \(u_1\) and \(u_2\) such that \(0\le u_1\preccurlyeq v_1\), \(0\le u_2\le v_2\) and \(u=u_1+u_2\). Moreover, if \(u\succcurlyeq 0\) then \(u_1 \succcurlyeq 0\).
Proof
(a) The element  satisfies \(u_1\le v_1\) and \(u_1\ge 0\) (and \(u_1\succcurlyeq 0\) if \(v_1\succcurlyeq 0\)). Let \(u_2=u-u_1\). Then \(u=u_1+u_2\) and \(u_2\succcurlyeq 0\), since \(u_1\preccurlyeq u\). It remains to show that \(u_2\le v_2\). For this, we note that \(0\preccurlyeq v_2\) and \(u-v_1\le v_2\), and so we have
satisfies \(u_1\le v_1\) and \(u_1\ge 0\) (and \(u_1\succcurlyeq 0\) if \(v_1\succcurlyeq 0\)). Let \(u_2=u-u_1\). Then \(u=u_1+u_2\) and \(u_2\succcurlyeq 0\), since \(u_1\preccurlyeq u\). It remains to show that \(u_2\le v_2\). For this, we note that \(0\preccurlyeq v_2\) and \(u-v_1\le v_2\), and so we have

If \(u\preccurlyeq v_1+v_2\) then \(u-v_1\preccurlyeq v_2\) and we can replace \(\le \) by \(\preccurlyeq \) in the above inequality, by (M8a).
(b) The element  satisfies \(u_1\le u\), \(u_1\preccurlyeq v_1\) and \(u_1\ge 0\) (and \(u_1\succcurlyeq 0\) if \(u\succcurlyeq 0\)). It follows from \(u\preccurlyeq v_1+v_2\) and \(v_1\le v_1+v_2\) that
satisfies \(u_1\le u\), \(u_1\preccurlyeq v_1\) and \(u_1\ge 0\) (and \(u_1\succcurlyeq 0\) if \(u\succcurlyeq 0\)). It follows from \(u\preccurlyeq v_1+v_2\) and \(v_1\le v_1+v_2\) that  , and so if we set \(u_2=u-u_1\) we have \(u_2\ge 0\) and
, and so if we set \(u_2=u-u_1\) we have \(u_2\ge 0\) and

and the proof is complete. \(\square \)
4 Ideals and bands in a mixed lattice vector space
A mixed lattice vector space (or briefly, a mixed lattice space) was defined in [5] as a partially ordered real vector space V with two partial orderings \(\le \) and \(\preccurlyeq \) (called the initial order and the specific order, respectively) such that the mixed upper and lower envelopes  and
and  , as defined in Sect. 2, exist in V for all \(x,y\in V\).
, as defined in Sect. 2, exist in V for all \(x,y\in V\).
We recall that a subset C of a vector space is called a cone if (i) \(\alpha C \subseteq C\) for all \(\alpha \ge 0\), (ii) \(C+C \subseteq C\) and (iii) \(C\cap (-C)=\{0\}\). Cones play an important role in the theory of ordered vector spaces because a partial ordering in a vector space can be given in terms of the corresponding positive cone. For more information about cones and their properties we refer to [1].
Before we proceed, let us introduce some notation. If V is a mixed lattice space then \(V_p=\{x\in V:x\ge 0\}\) and \(V_{sp}=\{x\in V:x\succcurlyeq 0\}\) are the \((\le )\)-positive cone and the \((\preccurlyeq )\)-positive cone of V, respectively. Accordingly, an element \(x\in V_p\) is called positive, and if \(x\in V_{sp}\) then x is said to be specifically positive, or \((\preccurlyeq )\)-positive. In mixed lattice spaces we are particularly interested in cones that are also mixed lattice semigroups.
Definition 4.1
A cone \(C\subseteq V_{sp}\) in a mixed lattice space V is called a mixed lattice cone if  and
and  belong to C whenever \(x,y\in C\).
belong to C whenever \(x,y\in C\).
If E is any subset of V then we define \(E_p=E\cap V_p\) and \(E_{sp}=E\cap V_{sp}\). The notions of regular and quasi-regular mixed lattice space are defined similarly as in mixed lattice groups. Hence, using the notation just introduced, V is quasi-regular if \(V_{sp}\), the positive cone associated with the specific order, is a mixed lattice cone. If C is a cone in a vector space V then \(S=C-C\) is called the subspace generated by C. A mixed lattice space V is regular if \(V_{sp}\) is a generating mixed lattice cone, that is, \(V=V_{sp}-V_{sp}\).
The rules (M1)–(M8) for the mixed envelopes remain valid in quasi-regular mixed lattice spaces. In a mixed lattice space we can add to the list the following rules concerning the scalar multiplication. If V is a mixed lattice space and \(0\le a\in {\mathbb {R}}\) then the following hold for all \(x,y\in V\)

The notions of upper and lower parts of an element and the generalized asymmetrical absolute values were introduced in [5]. If \(x\in V\) then the elements  and
and  are called the upper part and lower part of x, respectively. Similarly, the elements
are called the upper part and lower part of x, respectively. Similarly, the elements  and
and  are called the specific upper part and specific lower part of x, respectively. These play a similar role as the positive and negative parts of an element in a Riesz space. The generalized absolute values of x are then defined as
are called the specific upper part and specific lower part of x, respectively. These play a similar role as the positive and negative parts of an element in a Riesz space. The generalized absolute values of x are then defined as  and
and  . The elements
. The elements  and
and  are distinct, in general, and they are ”asymmetrical” in the sense that
are distinct, in general, and they are ”asymmetrical” in the sense that  for all x.
for all x.
The upper and lower parts and the generalized absolute values have several important basic properties, which were proved in [5]. These properties are given in the next theorem.
Theorem 4.2
Let V be a quasi-regular mixed lattice space and \(x\in V\). Then the following hold.
-
(a)
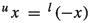 and
and 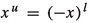 .
. -
(b)
 .
. -
(c)
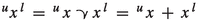 and
and  .
. -
(d)
 .
. -
(e)
 ,
, 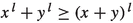 and
and  .
. -
(f)
 ,
,  and
and  .
. -
(g)
 .
. -
(h)

-
(i)
\(x\succcurlyeq 0\) if and only if
 and
and  .
. -
(j)
\(x\ge 0\) if and only if
 and
and  .
. -
(k)
 and
and  . Moreover,
. Moreover,  if and only if \(x=0\).
if and only if \(x=0\). -
(l)
 and
and 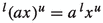 for all \(a\ge 0\).
for all \(a\ge 0\). -
(m)
 and
and  for all \(a<0\).
for all \(a<0\). -
(n)
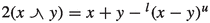 and
and  .
.
The next theorem was also proved in [5], but under more general assumptions. If V is assumed to be quasi-regular then we have a sharper version of the same theorem, as given below. The proof is almost identical to the more general case, see [5, Theorem 3.6].
Theorem 4.3
Let V be a quasi-regular mixed lattice space and \(x\in V\).
-
(a)
If \(x=u-v\) with \(u\succcurlyeq 0\) and \(v\ge 0\), then
 and
and 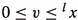 . If also \(v\succcurlyeq 0\) then
. If also \(v\succcurlyeq 0\) then  and
and  .
. -
(b)
Conversely, if \(x=u-v\) with
 then
then  and
and  .
.
For the remainder of this paper, we shall always assume that V is a quasi-regular mixed lattice vector space unless otherwise stated. Due to this convention, we shall drop the term ”quasi-regular”, and henceforth, by a mixed lattice space we mean a quasi-regular mixed lattice space.
The notions of mixed lattice subspaces and ideals were introduced in [5]. A subspace S of a mixed lattice vector space V is called a mixed lattice subspace of V if  and
and  belong to S whenever x and y are in S. A subset \(U\subseteq V\) is called (\(\le \))-order convex, if \(x\le z\le y\) and \(x,y\in U\) imply that \(z\in U\). Similarly, a subset \(U\subseteq V\) is called (\(\preccurlyeq \))-order convex, if \(x\preccurlyeq z\preccurlyeq y\) and \(x,y\in U\) imply that \(z\in U\). A subspace A is (\(\le \))-order convex if and only if \(0\le y\le x\) and \(x\in A\) imply that \(y\in A\). Similarly, a subspace A is (\(\preccurlyeq \))-order convex if and only if \(0\preccurlyeq y\preccurlyeq x\) and \(x\in A\) imply that \(y\in A\). If A is a (\(\le \))-order convex mixed lattice subspace of V then A is called a mixed lattice ideal of V. Similarly, a (\(\preccurlyeq \))-order convex mixed lattice subspace of V is called a specific mixed lattice ideal of V. For brevity, these will be called simply ideals and specific ideals, respectively. This should not cause any confusion as we are mostly dealing with mixed lattice ideals in this paper. If we refer to other type of ideals (such as lattice ideals) then we will emphasize it accordingly.
belong to S whenever x and y are in S. A subset \(U\subseteq V\) is called (\(\le \))-order convex, if \(x\le z\le y\) and \(x,y\in U\) imply that \(z\in U\). Similarly, a subset \(U\subseteq V\) is called (\(\preccurlyeq \))-order convex, if \(x\preccurlyeq z\preccurlyeq y\) and \(x,y\in U\) imply that \(z\in U\). A subspace A is (\(\le \))-order convex if and only if \(0\le y\le x\) and \(x\in A\) imply that \(y\in A\). Similarly, a subspace A is (\(\preccurlyeq \))-order convex if and only if \(0\preccurlyeq y\preccurlyeq x\) and \(x\in A\) imply that \(y\in A\). If A is a (\(\le \))-order convex mixed lattice subspace of V then A is called a mixed lattice ideal of V. Similarly, a (\(\preccurlyeq \))-order convex mixed lattice subspace of V is called a specific mixed lattice ideal of V. For brevity, these will be called simply ideals and specific ideals, respectively. This should not cause any confusion as we are mostly dealing with mixed lattice ideals in this paper. If we refer to other type of ideals (such as lattice ideals) then we will emphasize it accordingly.
To study the relationships between ideals and specific ideals, as well as the structure of mixed lattice spaces in more detail, we introduce the following definitions.
Definition 4.4
-
(i)
A subspace S is called regular, if \(S=S_{sp}-S_{sp}\).
-
(ii)
A subspace S is called positively generated, if \(S=S_p -S_p\).
-
(iii)
A subspace A is called mixed–order convex if \(y\in A\) and \(0\preccurlyeq x\le y\) together imply that \(x\in A\).
-
(iv)
A mixed–order convex mixed lattice subspace is called a quasi-ideal.
-
(v)
A specific ideal A is called a proper specific ideal if A is not a quasi-ideal. Similarly, a quasi-ideal A is called a proper quasi-ideal if A is not an ideal.
Every mixed lattice subspace is positively generated. It is also easy to see that a mixed lattice subspace S is regular if and only if for every \(x\in S\) there exists some \(z\in S_{sp}\) such that \(x\preccurlyeq z\). There are ideals that are not regular (Example 5.15). In many cases, proper specific ideals and proper quasi-ideals are regular, but it is not known whether or not this is true in general.
Before we proceed, we should remark that if A is a subspace of V then, in order to show that A is a mixed lattice subspace it is sufficient to show that  for every \(x\in A\). Indeed, if this holds and \(x,y\in A\) then
for every \(x\in A\). Indeed, if this holds and \(x,y\in A\) then  . Consequently,
. Consequently,  . This observation simplifies many of the proofs that follow.
. This observation simplifies many of the proofs that follow.
Now the following result holds.
Proposition 4.5
Every regular \((\preccurlyeq )\)-order convex subspace is a mixed lattice subspace, and hence a specific ideal.
Proof
If \(x\in A\) then \(x=u-v\) with \(u,v\in A_{sp}\). By Theorem 4.3 we have  and so it follows that
and so it follows that  . Hence, A is a regular \((\preccurlyeq )\)-order convex mixed lattice subspace, by the remark made before the proposition. \(\square \)
. Hence, A is a regular \((\preccurlyeq )\)-order convex mixed lattice subspace, by the remark made before the proposition. \(\square \)
The notion of a mixed-order convex subspace is intermediate between (\(\preccurlyeq \))-order convex and (\(\le \))-order convex subspaces. Every (\(\le \))-order convex subspace is mixed-order convex, and every mixed-order convex subspace is (\(\preccurlyeq \))-order convex. In particular, every ideal is a quasi-ideal, and every quasi-ideal is a specific ideal.
The following simple lemma is useful in the study of mixed-order convex subspaces.
Lemma 4.6
A subspace A is mixed-order convex if and only if \(0\le x\preccurlyeq y\) with \(y\in A\) imply that \(x\in A\).
Proof
Assume that \(0\preccurlyeq x\le y\) with \(y\in A\) implies that \(x\in A\). We observe that if \(0\le u\preccurlyeq v\) with \(v\in A\) then \(0\preccurlyeq v-u\le v\), and this implies that \(v-u\in A\) by assumption. Then \(u=v-(v-u)\in A\) since A is a subspace. The converse implication is similar. \(\square \)
Next we will study some basic properties of mixed lattice cones.
Theorem 4.7
Let V be a mixed lattice space and C a mixed lattice cone in V. Then the subspace generated by C is a mixed lattice subspace. Conversely, if S is a mixed lattice subspace of V then \(S_{sp}\) is a mixed lattice cone in V.
Proof
Let C be a mixed lattice cone. It is clear that \(S=C-C\) is a subspace. If \(x,y\in S\) then \(x=u-v\) and \(y=a-b\) for some \(u,v,a,b\in C\). Then

where  . Also \(v+b\in C\), so
. Also \(v+b\in C\), so  . Similarly
. Similarly  and so S is a mixed lattice subspace.
and so S is a mixed lattice subspace.
Conversely, if S is a mixed lattice subspace then \(S_{sp}\) is clearly a cone. If \(x,y\in S_{sp}\) then  and
and  , by (M8b), and so
, by (M8b), and so  . Similarly,
. Similarly,  , and the identity (2.1) automatically holds, by (M1). Hence \(S_{sp}\) is a mixed lattice cone. \(\square \)
, and the identity (2.1) automatically holds, by (M1). Hence \(S_{sp}\) is a mixed lattice cone. \(\square \)
To gain more information about the structure of specific ideals, we introduce some additional terminology. A mixed lattice cone \(C_1\) is called a mixed lattice sub-cone of another mixed lattice cone \(C_2\) if \(C_1\subseteq C_2\). A sub-cone F of a cone C is called a face of C if \(x + y\in F\) with \(x,y\in C\) imply that \(x,y\in F\).
First we observe that every face of \(V_{sp}\) is a mixed lattice sub-cone.
Proposition 4.8
Every face of \(V_{sp}\) is a mixed lattice sub-cone of \(V_{sp}\).
Proof
Let F be a face of \(V_{sp}\) and \(x,y\in F\). Then  . It follows that
. It follows that  and
and  , and so F is a mixed lattice sub-cone of \(V_{sp}\). \(\square \)
, and so F is a mixed lattice sub-cone of \(V_{sp}\). \(\square \)
The next two results are well-known but we give proofs for completeness.
Lemma 4.9
A sub-cone C of \(V_p\) is (\(\le \))-order convex if and only if \(0\le x\le y\) with \(y\in C\) implies that \(x\in C\). Similarly, a sub-cone C of \(V_{sp}\) is (\(\preccurlyeq \))-order convex if and only if \(0\preccurlyeq x\preccurlyeq y\) with \(y\in C\) implies that \(x\in C\).
Proof
Clearly the given condition is necessary. Assume the condition holds and let \(z\le x\le y\) with \(z,y\in C\). Then \(0\le x-z\le y-z\le y\) which implies that \(x-z\in C\), and since \(z\in C\) and C is a sub-cone, it follows that \(x=(x-z)+z\in C\). The proof of the second statement is essentially the same. \(\square \)
Proposition 4.10
A sub-cone F of \(V_p\) is a face of \(V_{p}\) if and only if F is (\(\le \))-order convex. Similarly, F is a face of \(V_{sp}\) if and only if F is a (\(\preccurlyeq \))-order convex sub-cone of \(V_{sp}\).
Proof
Suppose that F is a face of \(V_p\) and let \(0\le x\le y\) with \(y\in F\). Then \(x\in V_p\), \(0\le y-x\in V_p\) and \((y-x)+x=y\in F\). It follows that \(x\in F\) and this shows that F is (\(\le \))-order convex, by the preceding lemma. Conversely, if F is (\(\le \))-order convex and \(x+y\in F\) then \(0\le x\le x+y\) and \(0\le y\le x+y\) imply that \(x,y\in F\). Hence F is a face. The proof of the second assertion is identical, just replace \(\le \) by \(\preccurlyeq \). \(\square \)
The following result is now an immediate consequence of the preceding results and the definition of a specific ideal.
Corollary 4.11
A mixed lattice subspace A is a specific ideal if and only if \(A_{sp}\) is a face of \(V_{sp}\).
Our next result is important for the theory of ideals. It shows that every ideal contains a quasi-ideal.
Theorem 4.12
If A is an ideal and \(W=A_{sp}-A_{sp}\) then W is a quasi-ideal, and there is no ideal B such that \(W\subseteq B\subseteq A\) and \(B\ne A\). In particular, if W is an ideal then \(W=A\).
Proof
By Theorem 4.7, W is a mixed lattice subspace. Moreover, if \(0\preccurlyeq x \le y\) with \(y\in W\) then \(y\in A\), and A is an ideal, so \(x\in A_{sp}\subseteq W\). This shows that W is mixed-order convex. Let B be any ideal contained in A such that \(W\subseteq B\). Then for every \(x\in A_p\) we have  . This implies that \(x\in B\), so \(B=A\). In particular, if W is an ideal then \(W=A\). \(\square \)
. This implies that \(x\in B\), so \(B=A\). In particular, if W is an ideal then \(W=A\). \(\square \)
We recall that if E is a subset of V then the smallest ideal (with respect to set inclusion) that contains E is called the ideal generated by E. The next result gives a description of ideals generated by a mixed lattice cone.
Theorem 4.13
The ideal A generated by a mixed lattice cone C equals the subspace generated by the cone \(S=\{x\in V: 0\le x\le u \, \text { for some } \,u\in C \}\).
Proof
Since C is a cone, it follows immediately that S is also a cone. Evidently, every ideal that contains C must contain S, so it contains also the subspace \(S-S\). Therefore, it is sufficient to show that the subspace \(S-S\) is an ideal. \(S-S\) is obviously (\(\le \))-order convex, so it remains to show that it is a mixed lattice subspace. Let \(x\in S-S\). Then \(x=x_1-x_2\) with \(x_1,x_2\in S\), and so \(x\le x_1\le u_1\) for some \(u_1\in C\). Since \(C\subseteq V_{sp}\), it follows by Theorem 4.2(i) that  , and so by (M5) we have
, and so by (M5) we have

Thus,  , and so \(S-S\) is a mixed lattice subspace. Hence we have proved that \(S-S\) is a smallest ideal containing C. \(\square \)
, and so \(S-S\) is a mixed lattice subspace. Hence we have proved that \(S-S\) is a smallest ideal containing C. \(\square \)
If A is an ideal then by Theorem 4.7 the set \(A_{sp}\) is a mixed lattice cone, and by Theorem 4.12A is the smallest ideal that contains \(A_{sp}\). Now the two preceding theorems yield the following corollary which tells that ideals are uniquely determined by their sets of \((\preccurlyeq )\)-positive elements.
Corollary 4.14
Every ideal A equals the ideal generated by \(A_{sp}\), that is, the subspace generated by the set \(S=\{x\in V: 0\le x\le u \, \text { for some } \,u\in A_{sp} \}\). In fact, \(S=A_p\). Consequently, if A and B are two ideals such that \(A_{sp}=B_{sp}\) then \(A=B\).
Proof
The only thing that still needs proof is the claim that \(S=A_p\). The inclusion \(S\subseteq A_p\) is clear, and the reverse inclusion holds too, for if \(x\in A_p\) then  . \(\square \)
. \(\square \)
The preceding results have yet another consequence. By Theorem 4.12, if A is an ideal then the subspace \(W=A_{sp}-A_{sp}\) is a regular quasi-ideal. The following gives the converse.
Theorem 4.15
If W is a regular quasi-ideal then there exists an ideal A such that \(W=A_{sp}-A_{sp}\). Hence, W is a regular quasi-ideal if and only if \(W=A_{sp}-A_{sp}\) for some ideal A.
Proof
Let \(W=W_{sp}-W_{sp}\) be a regular quasi-ideal and let A be the ideal generated by \(W_{sp}\). By Theorem 4.7 the set \(W_{sp}\) is a mixed lattice cone, so by Theorem 4.13\(A=S-S\), where \(S=\{x\in V: 0\le x\le u \, \text { for some } \,u\in W_{sp} \}\). Now we only need to show that \(A_{sp}=W_{sp}\). It is clear that \(W_{sp}\subseteq A_{sp}\), so let \(x\in A_{sp}\). Then \(x=y-z\) where \(y,z\in S\), so we have \(0\preccurlyeq x \le y\le u\) for some \(u\in W_{sp}\). But this implies that \(x\in W_{sp}\) since W is a quasi-ideal, so we conclude that \(A_{sp}=W_{sp}\). \(\square \)
Next we will study the properties of algebraic sums of different types of subspaces. For instance, if A and B are quasi-ideals, then what can be said about the sum \(A+B\) ? Another important question is if the sets of positive elements are preserved in these sums, that is, does \((A+B)_{sp}=A_{sp}+B_{sp}\) or \((A+B)_{p}=A_{p}+B_{p}\) hold.
Theorem 4.16
If A is a quasi-ideal and B is a positively generated (\(\le \))-order convex subspace then \(A+B\) is a mixed-order convex subspace. Moreover, if B is an ideal then \(A+B\) is a quasi-ideal, and if, in addition, A is regular then \((A+B)_p=A_p+B_p\).
Proof
It is clear that \(A+B\) is a subspace. Assume first that \(0\preccurlyeq x\le y\) with \(y=y_1+y_2\in A+B\). By assumption, \(y_2=v_1-v_2\) with \(0\le v_1,v_2\in B\), and A is a mixed lattice subspace, so  . Then
. Then  , so we can now apply the dominated decomposition property (Theorem 3.8(a)) and write \(x=x_1+x_2\), where
, so we can now apply the dominated decomposition property (Theorem 3.8(a)) and write \(x=x_1+x_2\), where  and \(0\le x_2 \le v_1\). It follows that \(x_1\in A\) and \(x_2\in B\), so \(x\in A+B\). This shows that \(A+B\) is mixed-order convex.
and \(0\le x_2 \le v_1\). It follows that \(x_1\in A\) and \(x_2\in B\), so \(x\in A+B\). This shows that \(A+B\) is mixed-order convex.
Assume next that B is an ideal and let \(y=y_1+y_2\in A+B\). Then  and, applying Theorem 3.8(a) again we can find elements \(u_1\) and \(u_2\) such that
and, applying Theorem 3.8(a) again we can find elements \(u_1\) and \(u_2\) such that  ,
,  and
and  . This implies that \(u_1\in A\) and \(u_2\in B\), and hence
. This implies that \(u_1\in A\) and \(u_2\in B\), and hence  . This shows that \(A+B\) is a mixed lattice subspace, and hence a quasi-ideal. It is clear that \(A_p+B_p\subseteq (A+B)_p\). Conversely, if \(0\le x\in A+B\) then \(x=x_1+x_2\) with \(x_1\in A\) and \(x_2\in B\). If A is regular, we can choose an element \(0\preccurlyeq v\in A\) such that \(x_1\preccurlyeq v\). Also,
. This shows that \(A+B\) is a mixed lattice subspace, and hence a quasi-ideal. It is clear that \(A_p+B_p\subseteq (A+B)_p\). Conversely, if \(0\le x\in A+B\) then \(x=x_1+x_2\) with \(x_1\in A\) and \(x_2\in B\). If A is regular, we can choose an element \(0\preccurlyeq v\in A\) such that \(x_1\preccurlyeq v\). Also,  , and so we have
, and so we have  . We can now apply Theorem 3.8(b) to find positive elements \(u_1\in A\) and \(u_2\in B\) such that \(x=u_1+u_2\), completing the proof. \(\square \)
. We can now apply Theorem 3.8(b) to find positive elements \(u_1\in A\) and \(u_2\in B\) such that \(x=u_1+u_2\), completing the proof. \(\square \)
Along the same lines we have the following result.
Theorem 4.17
In a mixed lattice space the following hold.
-
(a)
If A and B are quasi-ideals then \((A + B)_{sp}=A_{sp}+B_{sp}\). Moreover, if A and B are regular then \(A + B\) is also a regular quasi-ideal.
-
(b)
If A is a regular specific ideal and B is a regular quasi-ideal then \(A + B\) is a regular specific ideal and \((A + B)_{sp}=A_{sp}+B_{sp}\). The last equality holds, in particular, if B is an ideal.
Proof
(a) If \(x\in (A + B)_{sp}\) then  with
with  and
and  . By Theorem 3.8(a) \(x=a+b\) for some elements a and b such that
. By Theorem 3.8(a) \(x=a+b\) for some elements a and b such that  and
and  . It follows that \(a\in A_{sp}\) and \(b\in B_{sp}\), hence \((A+ B)_{sp}\subseteq A_{sp}+B_{sp}\). The reverse inclusion is obvious. Assume then that \(0\preccurlyeq y \le x\) with \(x\in A+ B\). If A and B are regular it follows that \(A + B\) is also regular, and we may thus assume that \(x\succcurlyeq 0\). Hence, \(0\preccurlyeq y \le x=a+b\) where \(a\in A_{sp}\) and \(b\in B_{sp}\). Now the same argument as above (using Theorem 3.8(a)) shows that \(y\in A + B\), and so \(A + B\) is mixed-order convex. Then \(A + B\) is a mixed lattice subspace, by Proposition 4.5.
. It follows that \(a\in A_{sp}\) and \(b\in B_{sp}\), hence \((A+ B)_{sp}\subseteq A_{sp}+B_{sp}\). The reverse inclusion is obvious. Assume then that \(0\preccurlyeq y \le x\) with \(x\in A+ B\). If A and B are regular it follows that \(A + B\) is also regular, and we may thus assume that \(x\succcurlyeq 0\). Hence, \(0\preccurlyeq y \le x=a+b\) where \(a\in A_{sp}\) and \(b\in B_{sp}\). Now the same argument as above (using Theorem 3.8(a)) shows that \(y\in A + B\), and so \(A + B\) is mixed-order convex. Then \(A + B\) is a mixed lattice subspace, by Proposition 4.5.
(b) If \(x\in (A + B)_{sp}\) then \(x = x_1+x_2\) with \(x_1\in A\) and \(x_2\in B\). Since A and B are regular, there exist elements \(u\in A_{sp}\) and \(v\in B_{sp}\) such that \(x_1\preccurlyeq u\) and \(x_2\preccurlyeq v\). Hence \(0\preccurlyeq x = x_1+x_2\preccurlyeq u+v\), and by Theorem 3.8(a) we have \(x=a+b\) for some elements a and b such that \(0\preccurlyeq a\preccurlyeq u\) and \(0\preccurlyeq b\le v\). It follows that \(a\in A_{sp}\) and \(b\in B_{sp}\), hence \((A+ B)_{sp}\subseteq A_{sp}+B_{sp}\). The reverse inclusion is clear. In particular, if B is an ideal then \(W=B_{sp}-B_{sp}\) is a regular quasi-ideal, and so \(V_{sp}= A_{sp}+W_{sp}=A_{sp}+B_{sp}\). The proof that \(A + B\) is a regular specific ideal is similar to part (a). \(\square \)
Regarding the above theorem we note that by Theorem 4.15 regular quasi-ideals are precisely those subspaces W that \(W=A_{sp}-A_{sp}\) for some ideal A. As with ideals in Riesz spaces, these regular quasi-ideals form a distributive lattice.
Theorem 4.18
Let V be a mixed lattice space and denote by \(\mathcal {R}(V)\) the set of all regular quasi-ideals of V, ordered by inclusion. Then \(\mathcal {R}(V)\) is a distributive lattice where \(A\vee B=A+B\) and \(A\wedge B=A\cap B\). Moreover, \(\mathcal {R}(V)\) has the smallest element \(\{0\}\) and the largest element \(V_{sp}-V_{sp}\).
Proof
If \(A,B\in \mathcal {R}(V)\) then by Theorem 4.17 we have \(A+B\in \mathcal {R}(V)\), and \(A+B\) is clearly the smallest regular quasi-ideal that contains both A and B, hence \(A+B=A\vee B\). It is also clear that \(A\cap B\) is the largest quasi-ideal that is contained in both A and B. To see that \(A\cap B\) is regular, let \(x\in A\cap B\). Since A and B are regular, there exist elements \(u\in A_{sp}\) and \(v\in B_{sp}\) such that \(x\preccurlyeq u\) and \(x\preccurlyeq v\) hold. Then  and the inequalities
and the inequalities  and
and  imply that
imply that  , proving that \(A\cap B\) is regular, and hence \(A\cap B=A\wedge B\). To prove the distributivity, it is sufficient to show that \([(A\cap B)+(A\cap C)]_{sp}= [A\cap (B+C)]_{sp}\), since \((A\cap B)+(A\cap C)\) and \(A\cap (B+C)\) are both regular quasi-ideals. The inclusion \((A\cap B)+(A\cap C)\subseteq A\cap (B+C)\) is rather trivial, so let \(x\in [A\cap (B+C)]_{sp}\). Then \(x\in (B+C)_{sp}\), so \(x=x_1+x_2\) where \(x_1\in B_{sp}\) and \(x_2\in C_{sp}\), by Theorem 4.17. Moreover, \(0\preccurlyeq x_1 \preccurlyeq x \in A\) implies that \(x_1\in A_{sp}\), and similarly, \(x_2\in A_{sp}\). Hence, \(x_1\in (A\cap B)_{sp}\) and \(x_2\in (A\cap C)_{sp}\), and therefore \(x\in [(A\cap B)+(A\cap C)]_{sp}\). This shows that \(\mathcal {R}(V)\) is distributive. Finally, it is clear that \(\{0\}\) is the smallest element in \(\mathcal {R}(V)\), and by Theorem 4.12 the largest element is \(W=V_{sp}-V_{sp}\). \(\square \)
, proving that \(A\cap B\) is regular, and hence \(A\cap B=A\wedge B\). To prove the distributivity, it is sufficient to show that \([(A\cap B)+(A\cap C)]_{sp}= [A\cap (B+C)]_{sp}\), since \((A\cap B)+(A\cap C)\) and \(A\cap (B+C)\) are both regular quasi-ideals. The inclusion \((A\cap B)+(A\cap C)\subseteq A\cap (B+C)\) is rather trivial, so let \(x\in [A\cap (B+C)]_{sp}\). Then \(x\in (B+C)_{sp}\), so \(x=x_1+x_2\) where \(x_1\in B_{sp}\) and \(x_2\in C_{sp}\), by Theorem 4.17. Moreover, \(0\preccurlyeq x_1 \preccurlyeq x \in A\) implies that \(x_1\in A_{sp}\), and similarly, \(x_2\in A_{sp}\). Hence, \(x_1\in (A\cap B)_{sp}\) and \(x_2\in (A\cap C)_{sp}\), and therefore \(x\in [(A\cap B)+(A\cap C)]_{sp}\). This shows that \(\mathcal {R}(V)\) is distributive. Finally, it is clear that \(\{0\}\) is the smallest element in \(\mathcal {R}(V)\), and by Theorem 4.12 the largest element is \(W=V_{sp}-V_{sp}\). \(\square \)
We do not know if the preceding theorem can be stated for regular specific ideals in general. However, in many cases, a mixed lattice space is also a lattice with respect to one (or both) partial orderings. In this case, we obtain stronger results as all the lattice-theoretic tools are available to us. We will now briefly consider this situation. To avoid any confusion, we need to fix some terminology. If \((V,\preccurlyeq )\) is a vector lattice then we will say that V is a \((\preccurlyeq )\)-lattice. If \((V,\preccurlyeq )\) is a vector lattice and A is a lattice ideal in \((V,\preccurlyeq )\), then A is called a \((\preccurlyeq )\)-lattice ideal. We also denote the absolute value and the positive and negative parts of an element x with respect to \(\preccurlyeq \) by \({{\,\textrm{sp}\,}}|x|\), \({{\,\textrm{sp}\,}}(x^+)\) and \({{\,\textrm{sp}\,}}(x^-)\), respectively.
Theorem 4.19
If V is a mixed lattice space such that \((V,\preccurlyeq )\) is a vector lattice then A is a regular specific ideal in V if and only if A is a \((\preccurlyeq )\)-lattice ideal of \((V,\preccurlyeq )\).
Proof
It was proved in [5, Proposition 4.6] that every \((\preccurlyeq )\)-lattice ideal is a specific ideal. Moreover, a \((\preccurlyeq )\)-lattice ideal A is regular (since every \(x\in A\) can be written as \(x={{\,\textrm{sp}\,}}(x^+)-{{\,\textrm{sp}\,}}(x^-)\) where \({{\,\textrm{sp}\,}}(x^+),{{\,\textrm{sp}\,}}(x^+)\in A_{sp}\)), so we only need to prove the converse. Let A be a regular specific ideal. Then A is \((\preccurlyeq )\)-order convex and if \(x\in A\) then also  and
and  . Since A is regular, there is an element \(u\in A_{sp}\) such that
. Since A is regular, there is an element \(u\in A_{sp}\) such that  and
and  . By [5, Proposition 3.16] the absolute value of x formed with respect to \(\preccurlyeq \) is given by
. By [5, Proposition 3.16] the absolute value of x formed with respect to \(\preccurlyeq \) is given by  . Thus we have
. Thus we have  . Since A is \((\preccurlyeq )\)-order convex, it follows that \({{\,\textrm{sp}\,}}|x|\in A\). This shows that A is a \((\preccurlyeq )\)-lattice ideal. \(\square \)
. Since A is \((\preccurlyeq )\)-order convex, it follows that \({{\,\textrm{sp}\,}}|x|\in A\). This shows that A is a \((\preccurlyeq )\)-lattice ideal. \(\square \)
It is well known that the set of lattice ideals in a Riesz space is a distributive lattice. Also, every regular quasi-ideal is a regular specific ideal, so putting all this together with Theorems 4.19 and 4.18 we obtain the following:
Corollary 4.20
Let V be a mixed lattice space that is a lattice with respect to \(\preccurlyeq \), and denote by \(\mathcal {L}(V)\) the set of all regular specific ideals of V, ordered by inclusion. Then \(\mathcal {L}(V)\) is a distributive lattice where \(A\vee B=A+B\) and \(A\wedge B=A\cap B\). Moreover, \(\mathcal {L}(V)\) has the smallest element \(\{0\}\) and the largest element V, and the set \(\mathcal {R}(V)\) of all regular quasi-ideals of V is a sub-lattice of \(\mathcal {L}(V)\).
Now we turn to the discussion of bands in mixed lattice spaces.
Definition 4.21
Let V be a mixed lattice space. A specific ideal A is called a specific band if \({{\,\mathrm{sp \,sup}\,}}E \in A\) whenever E is a non-empty subset of A such that \({{\,\mathrm{sp \,sup}\,}}E\) exists in V. If A is a quasi-ideal with the above property then A is called a quasi-band. An ideal B is called a band if \(\sup E \in A\) whenever E is a non-empty subset of A such that \(\sup E\) exists in V.
It follows from the identity \(\inf E = -\sup (-E)\) that if A is a band and E is a non-empty subset of A such that \(\inf E\) exists in V then \(\inf E \in A\). Similarly, if A is a specific band and \({{\,\mathrm{sp \,inf}\,}}E\) exists in V then \({{\,\mathrm{sp \,inf}\,}}E \in A\).
It is also clear that every quasi-band is a specific band. For the sequel, we need to introduce the following notions.
Definition 4.22
A specific ideal A is called a weak specific band if \({{\,\mathrm{str \,sup}\,}}E \in A\) whenever E is a non-empty subset of A such that \({{\,\mathrm{str \,sup}\,}}E\) exists in V. A quasi-ideal with the above property is called a weak quasi-band, and an ideal with the above property is called a weak band.
Weak bands and weak specific bands in mixed lattice semigroups were introduced by Arsove and Leutwiler [2].
Clearly, every specific band is a weak specific band, every quasi-band is a weak quasi-band and every band is a weak band. Now we can state the following characterization for weak bands and weak specific bands.
Lemma 4.23
If A is a (specific) ideal in V then the following are equivalent.
-
(a)
A is a weak (specific) band.
-
(b)
\({{\,\mathrm{str \,sup}\,}}E\in A\) whenever E is a non-empty subset of \(A_p\) such that \({{\,\mathrm{str \,sup}\,}}E\) exists in V.
-
(c)
\({{\,\mathrm{str \,sup}\,}}E\in A\) whenever E is a non-empty subset of \(A_{sp}\) such that \({{\,\mathrm{str \,sup}\,}}E\) exists in V.
Proof
The implication \((a)\implies (b)\) is clear. Condition (b) obviously implies (c), since \(A_{sp}\subseteq A_p\). Assume that (c) holds and let E be a non-empty subset of A such that \(u_0={{\,\mathrm{str \,sup}\,}}E\) exists in V. Fix an element \(x\in E\) and define  . Then D is a non-empty subset of \(A_{sp}\) and since \(u_0\succcurlyeq x\), by property (M6a) we have
. Then D is a non-empty subset of \(A_{sp}\) and since \(u_0\succcurlyeq x\), by property (M6a) we have  . Using Proposition 3.7 we then have
. Using Proposition 3.7 we then have  , and hence \(u_0=x+(u_0 -x)\in A\). \(\square \)
, and hence \(u_0=x+(u_0 -x)\in A\). \(\square \)
5 Disjoint complements
If \(x,y\in V\) and  then x is said to be left-disjoint with y and y is right-disjoint with x. The reason for this terminology is, of course, the fact that in general
then x is said to be left-disjoint with y and y is right-disjoint with x. The reason for this terminology is, of course, the fact that in general  . Next we will investigate the sets of those elements that are left or right disjoint with each element of a given subspace A. It follows immediately from the inequalities
. Next we will investigate the sets of those elements that are left or right disjoint with each element of a given subspace A. It follows immediately from the inequalities  and
and  that if
that if  then we must have \(x\succcurlyeq 0\) and \(y\ge 0\). Because of this, we will first consider disjointness for positive elements only. As it turns out, these sets of positive disjoint elements are in fact mixed lattice cones. We then define the left and right disjoint complements as the specific ideal and the ideal generated by these cones.
then we must have \(x\succcurlyeq 0\) and \(y\ge 0\). Because of this, we will first consider disjointness for positive elements only. As it turns out, these sets of positive disjoint elements are in fact mixed lattice cones. We then define the left and right disjoint complements as the specific ideal and the ideal generated by these cones.
We begin with the left disjoint complement.
Lemma 5.1
If \(x,y\succcurlyeq 0\) and \(z\ge 0\) with  then
then  . In particular, if also
. In particular, if also  then
then  .
.
Proof
If  and \(x\succcurlyeq 0\) then, using Theorem 3.2 we obtain
and \(x\succcurlyeq 0\) then, using Theorem 3.2 we obtain

On the other hand,  , so we have
, so we have  . The reverse inequality
. The reverse inequality  holds by (M5), and the lemma is proved. \(\square \)
holds by (M5), and the lemma is proved. \(\square \)
We now introduce the set  and study its properties.
and study its properties.
Theorem 5.2
Let V be a mixed lattice space and A a mixed lattice subspace of V. Then the set \(({}^{\perp }A)_{sp}\) defined above is a mixed lattice cone in V.
Proof
Let \(x,y\in ({}^{\perp }A)_{sp}\) and \(z\in A_p\). Then  by the preceding lemma, and hence \(x+y\in ({}^{\perp }A)_{sp}\). If \(0\le \alpha \in {\mathbb {R}}\) and we put \(c=\max \{\alpha , 1\}\), then
by the preceding lemma, and hence \(x+y\in ({}^{\perp }A)_{sp}\). If \(0\le \alpha \in {\mathbb {R}}\) and we put \(c=\max \{\alpha , 1\}\), then  . Thus, \(\alpha x \in ({}^{\perp }A)_{sp}\). This shows that \(({}^{\perp }A)_{sp}\) is a cone in V. Next we note that if
. Thus, \(\alpha x \in ({}^{\perp }A)_{sp}\). This shows that \(({}^{\perp }A)_{sp}\) is a cone in V. Next we note that if  then \(0\preccurlyeq v\preccurlyeq x\) and it follows that for every \(z\in A_p\) we have
then \(0\preccurlyeq v\preccurlyeq x\) and it follows that for every \(z\in A_p\) we have  , and thus
, and thus  . This shows that \(v\in ({}^{\perp }A)_{sp}\). If we set
. This shows that \(v\in ({}^{\perp }A)_{sp}\). If we set  then \(0\preccurlyeq w\preccurlyeq x\), which implies that
then \(0\preccurlyeq w\preccurlyeq x\), which implies that  for all \(z\in A_p\). Thus \(w\in ({}^{\perp }A)_{sp}\), and since \(({}^{\perp }A)_{sp}\) is a cone, we have
for all \(z\in A_p\). Thus \(w\in ({}^{\perp }A)_{sp}\), and since \(({}^{\perp }A)_{sp}\) is a cone, we have  . Hence, \(({}^{\perp }A)_{sp}\) is a mixed lattice cone in V. \(\square \)
. Hence, \(({}^{\perp }A)_{sp}\) is a mixed lattice cone in V. \(\square \)
The preceding result motivates the following definition.
Definition 5.3
Let A a mixed lattice subspace of a mixed lattice space V. The left disjoint complement of A is the specific ideal \({}^{\perp }A\) generated by the cone  .
.
Remark 5.4
We should point out that, more generally, if E is any subset of V such that \(E_p\) is non-empty, then \({}^{\perp }E_p\) is a mixed lattice cone in V. However, for the purposes of the present paper it is sufficient to restrict ourselves to mixed lattice subspaces. By doing so we can avoid some unnecessary complications that arise if one considers non-trivial subspaces S such that \(S_p=\{0\}\). For instance, in such cases the algebraic sum of a subspace and its disjoint complement would not be a direct sum, in general. We will discuss these matters further at the end of this paper.
Theorem 5.5
If E is a subset of \(({}^{\perp }A)_{sp}\) such that \({{\,\mathrm{sp \,sup}\,}}E\) exists in V then \({{\,\mathrm{sp \,sup}\,}}E \in ({}^{\perp }A)_{sp}\). In particular, \({}^{\perp }A\) is a regular weak specific band in V. Moreover, if \({}^{\perp }A\) is an ideal, then it is a weak regular band.
Proof
We will first show that \({}^{\perp }A\) is regular. Let \(W = ({}^{\perp }A)_{sp}- ({}^{\perp }A)_{sp}\). It is clear that W is a subspace and \(W\subseteq {}^{\perp }A\), so we only need to show that W is a specific ideal. It follows from Theorem 5.2 and Theorem 4.7 that W is a mixed lattice subspace in V. Moreover, if \(0\preccurlyeq y\preccurlyeq x\) with \(x\in W\) then for every \(z\in A_p\) we have  , so
, so  and thus \(y\in W\). Hence, W is a regular specific ideal, and so \(W = {}^{\perp }A\).
and thus \(y\in W\). Hence, W is a regular specific ideal, and so \(W = {}^{\perp }A\).
Let E be a non-empty subset of \(({}^{\perp }A)_{sp}\) such that \(u_0={{\,\mathrm{sp \,sup}\,}}E\) exists in V. Then, using (M1) and Theorem 3.2 we have

for all \(u\in E\) and \(z\in A_p\). But  , so the above inequality reduces to
, so the above inequality reduces to  . Thus the element
. Thus the element  is a \((\preccurlyeq )\)-upper bound of the set E, so we have
is a \((\preccurlyeq )\)-upper bound of the set E, so we have  . This implies that
. This implies that  (where the inequality
(where the inequality  follows by (M5), since \(u_0\succcurlyeq 0\) and \(z\ge 0\)), and so
follows by (M5), since \(u_0\succcurlyeq 0\) and \(z\ge 0\)), and so  . Hence, \(u_0 \in ({}^{\perp }A)_{sp}\). In particular, if \(u_0\) is the strong supremum then \({}^{\perp }A\) is a weak specific band, and if \({}^{\perp }A\) is an ideal then \({}^{\perp }A\) is a weak band, by Lemma 4.23. \(\square \)
. Hence, \(u_0 \in ({}^{\perp }A)_{sp}\). In particular, if \(u_0\) is the strong supremum then \({}^{\perp }A\) is a weak specific band, and if \({}^{\perp }A\) is an ideal then \({}^{\perp }A\) is a weak band, by Lemma 4.23. \(\square \)
Next we turn to the right disjoint complement which we define in a similar manner as the left disjoint complement, but the situation is slightly more complicated. Let A be a mixed lattice subspace and consider the set  . It is easy to see that \({\mathcal {S}}(A)\) is closed under multiplication by positive scalars, by using a similar argument as in the proof of Theorem 5.2. However, in general, \({\mathcal {S}}(A)\) is not closed under addition (see Example 5.15).
. It is easy to see that \({\mathcal {S}}(A)\) is closed under multiplication by positive scalars, by using a similar argument as in the proof of Theorem 5.2. However, in general, \({\mathcal {S}}(A)\) is not closed under addition (see Example 5.15).
To get a better understanding of the situation, let us briefly examine the set \({\mathcal {S}}(A)\) more closely. Let \(\mathcal {B}\) be the family of all those subsets of \({\mathcal {S}}(A)\) that are closed under addition. Notice that \(\mathcal {B}\) is non-empty since \(\{0\}\in \mathcal {B}\). Let \(\mathcal {B}\) be ordered by inclusion. If \(\mathcal {C}\) is a totally ordered subset of \(\mathcal {B}\) then \(\bigcup \{C:C\in \mathcal {C}\}\) is an upper bound of \(\mathcal {C}\), and so by Zorn’s lemma \(\mathcal {B}\) has maximal elements. Let us denote by \(\mathcal {M}(A)\) the set of maximal elements of \(\mathcal {B}\), that is, the set of those subsets of \({\mathcal {S}}(A)\) that are maximal with respect to the property of being closed under addition. If \({\mathcal {S}}(A)\) itself is closed under addition then \({\mathcal {S}}(A)\) is the only element of \(\mathcal {M}(A)\). Clearly, \({\mathcal {S}}(A)=\bigcup \{C:C\in \mathcal {M}(A)\}\), and each set in \(\mathcal {M}(A)\) is a \((\le )\)-order convex cone.
Proposition 5.6
The set \({\mathcal {S}}(A)\) is \((\le )\)-order convex, and each \(C\in \mathcal {M}(A)\) is a \((\le )\)-order convex cone.
Proof
We divide the proof into 5 steps.
(1) If \(0\le x\le y\) with \(y\in {\mathcal {S}}(A)\) then  for all \(z\in A_{sp}\), and so
for all \(z\in A_{sp}\), and so  for all \(z\in A_{sp}\), proving that \({\mathcal {S}}(A)\) is \((\le )\)-order convex.
for all \(z\in A_{sp}\), proving that \({\mathcal {S}}(A)\) is \((\le )\)-order convex.
(2) Let \(C\in \mathcal {M}(A)\). Then C is closed under addition by definition.
(3) If \(0\le x \le y\) with \(y\in C\), then \(x\in {\mathcal {S}}(A)\) by step (1). Now, if \(x\notin C\) and \(x+z\in {\mathcal {S}}(A)\) for all \(z\in C\) then \(0\le ax+bz\le (a+b)(x+z) \in {\mathcal {S}}(A)\) for all \(z\in C\) and \(a,b\in {\mathbb {R}}_+\). By step (1) this implies that the set \(D=\{ax+bz: z\in C, \, a,b\in {\mathbb {R}}_+ \}\) is contained in \({\mathcal {S}}(A)\). Clearly, D is closed under addition, and C is contained in D, contradicting the maximality of C. Hence, there exists some \(z\in C\) such that \(x+z\notin {\mathcal {S}}(A)\). But then \(0\le x+z\le y+z\in C\), and by step (1) this implies that \(x+z\in {\mathcal {S}}(A)\), a contradiction. Thus \(x\in C\), and C is \((\le )\)-order convex.
(4) If \(x\in C\) then an inductive argument applied to step (2) shows that \(nx\in C\) for all \(n\in {\mathbb {N}}\). If \(a\in {\mathbb {R}}_+\) then we can find some \(m\in {\mathbb {N}}\) such that \(a\le m\), and so \(0\le ax\le mx\in C\). By step (3) this implies that \(ax\in C\), showing that C is closed with respect to multiplication by positive scalars.
(5) Finally, \(C\cap (-C)=\{0\}\), because the elements of C are positive and \(0\in C\). By steps (2)–(5), C is a \((\le )\)-order convex cone. \(\square \)
Due to the above result, we will call \(\mathcal {M}(A)\) the set of maximal right disjoint cones of A. It was noted above that, in general, the set \({\mathcal {S}}(A)\) is not closed under addition. In this sense, the set \({\mathcal {S}}(A)\) is ”too large”. However, we have the following result which is the analogue of Lemma 5.1.
Lemma 5.7
If \(z,x\succcurlyeq 0\) and \(y\ge 0\) with  then
then  . In particular, if also
. In particular, if also  then
then  .
.
Proof
Let  . Then \(v\le x+y\), so \(v-x\le y\). On the other hand, since \(x\succcurlyeq 0\) we have \(v-x\preccurlyeq v\preccurlyeq z\). Hence,
. Then \(v\le x+y\), so \(v-x\le y\). On the other hand, since \(x\succcurlyeq 0\) we have \(v-x\preccurlyeq v\preccurlyeq z\). Hence,  , and so \(v\le x\). Since we also have \(v\preccurlyeq z\), it follows that
, and so \(v\le x\). Since we also have \(v\preccurlyeq z\), it follows that  . The reverse inequality
. The reverse inequality  holds by (M5), and the desired result follows. \(\square \)
holds by (M5), and the desired result follows. \(\square \)
It is clear that the set  is contained in \({\mathcal {S}}(A)\). The set \(({A}^{\perp })_{sp}\) is in fact a mixed lattice cone.
is contained in \({\mathcal {S}}(A)\). The set \(({A}^{\perp })_{sp}\) is in fact a mixed lattice cone.
Theorem 5.8
If A is a mixed lattice subspace of V then the set \(({A}^{\perp })_{sp}\) defined above is a mixed lattice cone in V.
Proof
The proof of the fact that \(({A}^{\perp })_{sp}\) is a mixed lattice cone is similar to the proof of Theorem 5.2. The only real difference is in showing that the set \(({A}^{\perp })_{sp}\) is closed under addition, and this follows immediately from the preceding lemma. \(\square \)
Definition 5.9
Let V be a mixed lattice space and A a mixed lattice subspace of V. The right disjoint complement of A is the ideal \({A}^{\perp }\) generated by the cone  .
.
Remark 5.10
In the above definition we require A to be a mixed lattice subspace for similar reasons that were explained in Remark 5.4 considering the left disjoint complement. The assumption that A is a mixed lattice subspace guarantees that A contains non-zero specifically positive elements (except, of course, in the trivial case \(A=\{0\}\)).
Theorem 5.11
\(A^{\perp }\) is a weak band and  for all \(0\le x\in A^{\perp }\) and \(z\in A_{sp}\).
for all \(0\le x\in A^{\perp }\) and \(z\in A_{sp}\).
Proof
We will first show that \(({A}^{\perp })_{sp}=\{w\in {A}^{\perp }: w\succcurlyeq 0\}\), that is, the ideal \({A}^{\perp }\) does not contain any \((\preccurlyeq )\)-positive elements that are not in \(({A}^{\perp })_{sp}\). This will also justify the notation used for the set \(({A}^{\perp })_{sp}\) in Definition 5.9. For this, let \(W=({A}^{\perp })_{sp}-({A}^{\perp })_{sp}\) and \(0\preccurlyeq x\le y\in W\). Then \(y=u-v\) for some \(u,v\in ({A}^{\perp })_{sp}\), and so \(0\preccurlyeq x\le u\in ({A}^{\perp })_{sp}\). This implies that  for all \(z\in A_{sp}\), and therefore
for all \(z\in A_{sp}\), and therefore  , so \(x\in ({A}^{\perp })_{sp}\subseteq W\). This shows that W is a regular quasi-ideal, and so by Corollary 4.14 and Theorem 4.15, \(W_{sp}=({A}^{\perp })_{sp}=\{w\in {A}^{\perp }: w\succcurlyeq 0\}\).
, so \(x\in ({A}^{\perp })_{sp}\subseteq W\). This shows that W is a regular quasi-ideal, and so by Corollary 4.14 and Theorem 4.15, \(W_{sp}=({A}^{\perp })_{sp}=\{w\in {A}^{\perp }: w\succcurlyeq 0\}\).
Now, if \(z\in A_{sp}\) and \(0\le x\in A^{\perp }\) then  , so
, so  , which implies that
, which implies that  . Next, let \(E\subseteq (A^{\perp })_{sp}\) be a non-empty set and assume that \(x_0={{\,\mathrm{str \,sup}\,}}E\) exists in V. Then \(x_0\succcurlyeq 0\), and since
. Next, let \(E\subseteq (A^{\perp })_{sp}\) be a non-empty set and assume that \(x_0={{\,\mathrm{str \,sup}\,}}E\) exists in V. Then \(x_0\succcurlyeq 0\), and since  for all \(x\in E\) and \(z\in A_{sp}\), it follows by Proposition 3.7 that
for all \(x\in E\) and \(z\in A_{sp}\), it follows by Proposition 3.7 that  , and hence \(x_0\in (A^{\perp })_{sp}\). By Lemma 4.23 this shows that \(A^{\perp }\) is a weak band. \(\square \)
, and hence \(x_0\in (A^{\perp })_{sp}\). By Lemma 4.23 this shows that \(A^{\perp }\) is a weak band. \(\square \)
The next result provides more information about the relationship between \(A^{\perp }\) and \({\mathcal {S}}(A)\).
Theorem 5.12
If A is a specific ideal then \((A^{\perp })_p \subseteq \bigcap \{C:C\in \mathcal {M}(A)\}\).
Proof
We will first show that that \(({A}^{\perp })_{sp}\subseteq \bigcap \{C:C\in \mathcal {M}(A)\}\). Let A be a specific ideal and \(C\in \mathcal {M}(A)\) with \(x\in C\). Then it follows by Lemma 5.7 that for every \(w\in A_{sp}\) and \(z\in ({A}^{\perp })_{sp}\) we have  , and so \(x+z\in {\mathcal {S}}(A)\). This shows that \(({A}^{\perp })_{sp}+C\subseteq {\mathcal {S}}(A)\). But C is, by definition, a maximal cone in \({\mathcal {S}}(A)\), so we must have \(({A}^{\perp })_{sp}\subseteq C\). This proves that \(({A}^{\perp })_{sp}\subseteq \bigcap \{C:C\in \mathcal {M}(A)\}\).
, and so \(x+z\in {\mathcal {S}}(A)\). This shows that \(({A}^{\perp })_{sp}+C\subseteq {\mathcal {S}}(A)\). But C is, by definition, a maximal cone in \({\mathcal {S}}(A)\), so we must have \(({A}^{\perp })_{sp}\subseteq C\). This proves that \(({A}^{\perp })_{sp}\subseteq \bigcap \{C:C\in \mathcal {M}(A)\}\).
Next, if \(0\le y\in A^{\perp }\) then  . Thus, by what was just proved above, we have
. Thus, by what was just proved above, we have  , and the inequality
, and the inequality  then implies that \(y\in \bigcap \{C:C\in \mathcal {M}(A)\}\), by Proposition 5.6. Hence, \((A^{\perp })_p \subseteq \bigcap \{C:C\in \mathcal {M}(A)\}\). \(\square \)
then implies that \(y\in \bigcap \{C:C\in \mathcal {M}(A)\}\), by Proposition 5.6. Hence, \((A^{\perp })_p \subseteq \bigcap \{C:C\in \mathcal {M}(A)\}\). \(\square \)
In the next theorem we collect some basic properties of the disjoint complements. Some of them are straightforward consequences of the definitions.
Theorem 5.13
If A is a mixed lattice subspace then the following hold.
-
(a)
\(A \cap {}^{\perp }A=\{0\}\) and \(A \cap A^{\perp }=\{0\}\).
-
(b)
\(A\subseteq ({}^{\perp }A)^{\perp }\).
-
(c)
If A is regular then \(A\subseteq {}^{\perp }(A^{\perp })\).
-
(d)
If A is a quasi-ideal then \(({A}^{\perp })_{sp}\subseteq ({}^{\perp }A)_{sp}\).
-
(e)
If A is a quasi-ideal and \({}^{\perp }A\) is quasi-ideal then \(({A}^{\perp })_{sp} = ({}^{\perp }A)_{sp}\). Moreover, if A is a quasi-ideal and \({}^{\perp }A\) is an ideal then \({}^{\perp }A={A}^{\perp }\).
Proof
-
(a)
If \(x\in A \cap {}^{\perp }A\) then also
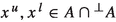 , since A and \({}^{\perp }A\) are mixed lattice subspaces. It follows that
, since A and \({}^{\perp }A\) are mixed lattice subspaces. It follows that  and so \(x\le 0\). Similarly
and so \(x\le 0\). Similarly 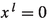 , which implies that \(x\ge 0\). Hence \(x=0\). By a similar argument we have \(A \cap A^{\perp }=\{0\}\).
, which implies that \(x\ge 0\). Hence \(x=0\). By a similar argument we have \(A \cap A^{\perp }=\{0\}\). -
(b)
This follows from the observation that \(A_p \subseteq (({}^{\perp }A)^{\perp })_{p}\). Indeed, it follows from the definitions that \(A_{sp} \subseteq (({}^{\perp }A)^{\perp })_{sp}\). Hence, if \(x\in A_{p}\), we have
 . Since \(({}^{\perp }A)^{\perp }\) is an ideal, it follows from
. Since \(({}^{\perp }A)^{\perp }\) is an ideal, it follows from  that \(x\in (({}^{\perp }A)^{\perp })_{p}\), and so \(A_p \subseteq (({}^{\perp }A)^{\perp })_{p}\).
that \(x\in (({}^{\perp }A)^{\perp })_{p}\), and so \(A_p \subseteq (({}^{\perp }A)^{\perp })_{p}\). -
(c)
It is evident that \(A_{sp} \subseteq {}^{\perp }({A}^{\perp })_{sp}\) and if A is regular then \(A=A_{sp}-A_{sp} \subseteq {}^{\perp }({A}^{\perp })_{sp}- {}^{\perp }({A}^{\perp })_{sp}= {}^{\perp }(A^{\perp })\).
-
(d)
Let \(x\in ({A}^{\perp })_{sp}\) and \(z\in A_{sp}\). Then the inequalities
 and
and  imply that
imply that  , and so \(x\in ({}^{\perp }A)_{sp}\).
, and so \(x\in ({}^{\perp }A)_{sp}\). -
(e)
If \(x\in ({}^{\perp }A)_{sp}\) and \(z\in A_{sp}\) then it follows from
 and
and  that
that  . Hence, \(x\in ({A}^{\perp })_{sp}\) and so \(({}^{\perp }A)_{sp}\subseteq ({A}^{\perp })_{sp}\). The reverse inclusion follows from (e). Then \({}^{\perp }A=({}^{\perp }A)_{sp}-({}^{\perp }A)_{sp}=({A}^{\perp })_{sp}-({A}^{\perp })_{sp}\), by Theorem 5.5, so if \({}^{\perp }A\) is an ideal then the equality \({}^{\perp }A={A}^{\perp }\) follows from Theorem 4.12.
. Hence, \(x\in ({A}^{\perp })_{sp}\) and so \(({}^{\perp }A)_{sp}\subseteq ({A}^{\perp })_{sp}\). The reverse inclusion follows from (e). Then \({}^{\perp }A=({}^{\perp }A)_{sp}-({}^{\perp }A)_{sp}=({A}^{\perp })_{sp}-({A}^{\perp })_{sp}\), by Theorem 5.5, so if \({}^{\perp }A\) is an ideal then the equality \({}^{\perp }A={A}^{\perp }\) follows from Theorem 4.12.
\(\square \)
Remark 5.14
We note that, in particular, \(\{0\}^{\perp }=V\) and \({}^{\perp } V=\{0\}\). Moreover, \(V^{\perp }=\{0\}\) holds always, and \({}^{\perp } \{0\}= V\) holds if and only if V is regular. Indeed, if V is not regular then \({}^{\perp }\{0\}=V_{sp}-V_{sp}\ne V\).
We now give an example to illustrate some of the ideas presented above.
Example 5.15
Let \(V={\mathbb {R}}^3\) where \(\le \) is the standard partial ordering where \((x,y,z)\ge (0,0,0)\) if \(x,y,z\ge 0\). Define \(\preccurlyeq \) to be the partial ordering with the positive cone \(V_{sp}=\{(x,x,z): \, x,z\ge 0\}\). Then V is a quasi-regular mixed lattice space. Consider the following subspaces: \(A=\{(0,0,z):z\in {\mathbb {R}}\}\), \(B=\{(x,y,0):x,y\in {\mathbb {R}}\}\), \(C=\{(x,x,z):x,z\in {\mathbb {R}}\}\), \(D=\{(x,x,0):x\in {\mathbb {R}}\}\), \(E=\{(x,x,x):x\in {\mathbb {R}}\}\). Then A is a regular ideal and B is an ideal (but not regular) such that \(B=A^{\perp }\) and \(A= {}^{\perp }B\). Moreover, \(C=V_{sp}-V_{sp}\) is a quasi-ideal, and it is the largest quasi-ideal in V. Also \(D=B_{sp}-B_{sp}\) is a quasi-ideal, and it is the largest quasi-ideal contained in B. Finally, E is a regular mixed lattice subspace but not a specific ideal.
Next, \(K_1=\{(0,y,z): \, y,z\ge 0\}\) and \(K_2=\{(x,0,z): \, x,z\ge 0\}\) are the maximal right disjoint cones of D and \({\mathcal {S}}(D)=K_1\cup K_2\), which is clearly not closed under addition. Moreover, \((D^{\perp })_{p}=A_{sp}= K_1\cap K_2\) (Theorem 5.12). The inclusion in Theorem 5.12 may be proper. To see this, let us modify the mixed lattice space, and consider \(U={\mathbb {R}}^3\) where \(\le \) is the same as above, and define \(\preccurlyeq \) as the partial ordering with the positive cone \(U_{sp}=\{\alpha (0,0,1)+\beta (0,1,0)+ \gamma (1,1,0): \, \alpha ,\beta ,\gamma \ge 0\}\). Let all the subspaces be the same as above. Then U is a regular mixed lattice space, and \(F=\{(0,y,0):y\in {\mathbb {R}}\}\) is a regular ideal in U. Now \({\mathcal {S}}(F)=K_2\) which is closed under addition, but \((F^{\perp })_{p}=A_{sp}\subseteq K_2\). Note also that A and B are still ideals in U, this time they are both regular, and \(B=A^{\perp }\) and \(A= {}^{\perp }B\) holds.
Our definitions of the left and right disjoint complements differ from the corresponding definition in the theory of Riesz spaces. We recall that if E is a subset of a Riesz space L then the disjoint complement of E is defined as \(E^{\perp }=\{x\in L: |x|\wedge |y|=0 \, \text { for all } y\in E\}\).
In mixed lattice spaces the generalized absolute values exist, and this naturally raises the question whether it is possible to give the definitions of the disjoint complements in terms of the absolute values, like in Riesz spaces. The main difficulty here is that the asymmetric generalized absolute values are not necessarily positive with respect to the specific order. To deal with this issue we introduce the notion of a symmetric absolute value, which is defined in terms of the asymmetric absolute values. It has the advantage of being positive with respect to both partial orderings while retaining most of the other important properties of the absolute value.
Definition 5.16
Let V be a mixed lattice vector space and \(x\in V\). The element  is called the symmetric generalized absolute value of x.
is called the symmetric generalized absolute value of x.
Next we derive some basic properties of the symmetric absolute value. The first item gives useful alternative expressions and the rest of the properties show that, in many ways, the symmetric generalized absolute value behaves like the ordinary absolute value in Riesz spaces.
Theorem 5.17
Let V be a mixed lattice vector space and \(x\in V\). Then the following statements hold.
-
(a)
 .
. -
(b)
\(s(\alpha x)=|\alpha |s(x)\) for all \(\alpha \in {\mathbb {R}}\).
-
(c)
\(s(x)\succcurlyeq 0\) and \(s(x)\ge 0\). Moreover, \(s(x)= 0\) if and only if \(x=0\).
-
(d)
\(x\succcurlyeq 0\) if and only if \(x=s(x)\). In particular, \(s(s(x))=s(x)\).
-
(e)
\(s(x+y)\le s(x)+s(y)\).
-
(f)
 .
.
Proof
-
(a)
All the equalities apart from the first one were given in Theorem 4.2(h). The first equality follows from

where we used Theorem 4.2 (c) and (h).
-
(b)
This follows from Theorem 4.2 (l) and (m).
-
(c)
Since \(x^{u}\succcurlyeq 0\) and \(x^{l}\succcurlyeq 0\) we have \(s(x)=x^{u}+x^{l}\succcurlyeq 0\). Also,
 and
and  imply
imply 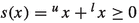 . It is clear that \(x=0\) implies \(s(x)=0\). Assume then that \(s(x)=0\). Now
. It is clear that \(x=0\) implies \(s(x)=0\). Assume then that \(s(x)=0\). Now  , or
, or  . Hence
. Hence  , which implies
, which implies 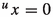 . On the other hand,
. On the other hand,  , or
, or  . So,
. So,  , which in turn implies
, which in turn implies  . Consequently,
. Consequently, 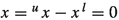 .
. -
(d)
This follows immediately from (a), (c) and Theorem 4.2 (i).
-
(e)
Using (a) together with Theorem 4.2 (e) and (f) we get
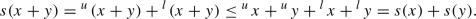
-
(f)
This follows by adding the two identities given in Theorem 4.2 (n).
\(\square \)
We can now characterize ideals in terms of the symmetric absolute value.
Theorem 5.18
Let V be a mixed lattice space and A a subspace of V. The following conditions are equivalent.
-
(a)
A is an ideal.
-
(b)
If \(s(x)\le s(y)\) and \(y\in A\) then \(x\in A\).
Proof
Assume that (a) holds and let \(s(x) \le s(y)\) with \(y\in A\). Then \(s(y)\in A\), and the inequalities  and
and  imply that
imply that  and so
and so  .
.
Conversely, assume that (b) holds and let \(y\in A\). Then by Theorem 5.17 . It follows that
. It follows that  and so A is a mixed lattice subspace. Next, assume that \(0\le x\le y\) with \(y\in A\). Then
and so A is a mixed lattice subspace. Next, assume that \(0\le x\le y\) with \(y\in A\). Then  and so
and so  and
and  . Now the above assumption implies that
. Now the above assumption implies that  . It follows that
. It follows that  and since \(s(x)\le s(s(x))\) by Theorem 5.17(d), we infer that \(x\in A\) and so A is \((\le )\)-order convex, and hence an ideal. \(\square \)
and since \(s(x)\le s(s(x))\) by Theorem 5.17(d), we infer that \(x\in A\) and so A is \((\le )\)-order convex, and hence an ideal. \(\square \)
Next we will show that the right disjoint complement can also be given in terms of the symmetric absolute value, and for Riesz subspaces, the usual Riesz space definition of the disjoint complement can thus be viewed as a special case of the next result.
Theorem 5.19
If A is a mixed lattice subspace then the right disjoint complement is given by  .
.
Proof
Let  . We first note that \(A_{sp}=\{s(z):z\in A\}\) and so
. We first note that \(A_{sp}=\{s(z):z\in A\}\) and so  . Let \(x,y\in X\) and \(z\in A_{sp}\). Since \(s(x)\succcurlyeq 0\) and \(s(y)\succcurlyeq 0\) we have
. Let \(x,y\in X\) and \(z\in A_{sp}\). Since \(s(x)\succcurlyeq 0\) and \(s(y)\succcurlyeq 0\) we have

and so  (here we used Theorem 5.17 and Lemma 5.7). This shows that X is a subspace. To show that X is an ideal, we note that if \(s(x)\le s(y)\) and \(y\in X\) then
(here we used Theorem 5.17 and Lemma 5.7). This shows that X is a subspace. To show that X is an ideal, we note that if \(s(x)\le s(y)\) and \(y\in X\) then  , and so \(x\in X\) and by Theorem 5.18X is an ideal.
, and so \(x\in X\) and by Theorem 5.18X is an ideal.
Clearly, \(A^{\perp }\subseteq X\). If \(x\in X\) then \(s(x)\in A^{\perp }_{sp}\), and it follows from  and
and  that
that  . Hence \(A^{\perp }=X\). \(\square \)
. Hence \(A^{\perp }=X\). \(\square \)
Theorem 5.19 thus gives an alternative (but equivalent) definition of the right disjoint complement by means of the symmetric absolute value. The reason this works is implied by Theorem 5.18, for if A is an ideal then \(x\in A\) if and only if \(s(x)\in A\). However, if A is a specific ideal, then \(x\in A\) implies \(s(x)\in A\), but not conversely in general. This is the fundamental reason why we cannot similarly characterize the left disjoint complement \(^{\perp }A\) in terms of the symmetric absolute value.
In the next section we consider the situation where A is a band such that \(A= ({}^{\perp }A)^{\perp }\). We will now give sufficient conditions for this to hold. The next couple of results have their counterparts in the theory of Riesz spaces, and the methods used in their proofs are also similar. First we recall some terminology. A mixed lattice space V is called \((\le )\)-Archimedean if the condition \(nx\le y\) for all \(n\in {\mathbb {N}}\) implies \(x\le 0\). Similarly, V is called \((\preccurlyeq )\)-Archimedean if the condition \(nx\preccurlyeq y\) for all \(n\in {\mathbb {N}}\) implies \(x\preccurlyeq 0\). It is easy to see that if V is \((\le )\)-Archimedean then it is also \((\preccurlyeq )\)-Archimedean, but the converse is not true as the next example shows.
Example 5.20
Let \(V=({\mathbb {R}}^2,\le ,\preccurlyeq )\), where \(\le \) is the lexicographic ordering defined as
and \(\preccurlyeq \) is the usual coordinatewise ordering \((x_1,x_2)\preccurlyeq (y_1,y_2)\) if \(x_1\le y_1\) and \(x_2\le y_2\). Then V is a mixed lattice space which is \((\preccurlyeq )\)-Archimedean but not \((\le )\)-Archimedean.
Next we will show that in \((\preccurlyeq )\)-Archimedean mixed lattice spaces every band A has the property that \(A= ({}^{\perp }A)^{\perp }\). First we consider the following order-denseness property of quasi-ideals with respect to their second right disjoint complements.
Proposition 5.21
If A is a quasi-ideal and \(x\in ({}^{\perp }A)^{\perp }\) is a non-zero element such that \(x\succcurlyeq 0\), then there exists a non-zero element \(y\in A\) such that \(0\preccurlyeq y\preccurlyeq x\).
Proof
Let \(0\preccurlyeq x\in ({}^{\perp }A)^{\perp }\) be a non-zero element. Then \(x\notin {}^{\perp }A\), and there exists an element \(0\preccurlyeq w\in A\) such that  . Since A is a quasi-ideal, the inequality
. Since A is a quasi-ideal, the inequality  implies that
implies that  . The element
. The element  then satisfies \(0\preccurlyeq y\preccurlyeq x\), as required. \(\square \)
then satisfies \(0\preccurlyeq y\preccurlyeq x\), as required. \(\square \)
Remark 5.22
The above proposition holds also if \(A=\{0\}\), because then \({}^{\perp }A=V_{sp}-V_{sp}\) and \(({}^{\perp }A)^{\perp }=\{0\}\), so there are no non-zero elements in \(({}^{\perp }A)^{\perp }\) which makes the proposition vacuously true.
In \((\preccurlyeq )\)-Archimedean mixed lattice spaces the order-denseness property of the preceding proposition has the following consequence.
Theorem 5.23
Let V be a \((\preccurlyeq )\)-Archimedean mixed lattice space and A a quasi-ideal in V. If \(M_u=\{v\in A: 0\preccurlyeq v\preccurlyeq u\}\) then \(u={{\,\mathrm{sp \,sup}\,}}M_u\) for every \(u\in (({}^{\perp }A)^{\perp })_{sp}\).
Proof
Let \(0\preccurlyeq u\in ({}^{\perp }A)^{\perp }\) and \(M_u=\{v\in A: 0\preccurlyeq v\preccurlyeq u\}\). Clearly, u is a specific upper bound of \(M_u\). Assume that \(u\ne {{\,\mathrm{sp \,sup}\,}}M_u\). Then there exists some specific upper bound \(w_0\) of \(M_u\) such that \(u\preccurlyeq w_0\) does not hold. If we put  then \(0\preccurlyeq w\preccurlyeq u\) holds, and \(w\in ({}^{\perp }A)^{\perp }\), since \(({}^{\perp }A)^{\perp }\) is an ideal. Moreover, \(0\preccurlyeq u-w \in ({}^{\perp }A)^{\perp }\) and so we can apply Proposition 5.21 to find a non-zero element \(z\in A\) such that \(0\preccurlyeq z\preccurlyeq u-w\preccurlyeq u\). In particular, we have \(z\preccurlyeq u\) and \(z\preccurlyeq w_0\), and consequently, \(z\preccurlyeq w\). Hence
then \(0\preccurlyeq w\preccurlyeq u\) holds, and \(w\in ({}^{\perp }A)^{\perp }\), since \(({}^{\perp }A)^{\perp }\) is an ideal. Moreover, \(0\preccurlyeq u-w \in ({}^{\perp }A)^{\perp }\) and so we can apply Proposition 5.21 to find a non-zero element \(z\in A\) such that \(0\preccurlyeq z\preccurlyeq u-w\preccurlyeq u\). In particular, we have \(z\preccurlyeq u\) and \(z\preccurlyeq w_0\), and consequently, \(z\preccurlyeq w\). Hence
and clearly \(2z\in A\), so in fact we have \(2z\in M_u\). Hence, we can repeat the same argument for the element 2z. That is,
and so \(3z\in M_u\). Continuing this way we find that \(nz\in M_u\) for all n, and so \(0\preccurlyeq nz\preccurlyeq u\) for all n. But \(0\preccurlyeq nz\ne 0\), which is impossible since V is \((\preccurlyeq )\)-Archimedean. Hence, \(u={{\,\mathrm{sp \,sup}\,}}M_u\), and the proof is complete. \(\square \)
The following result is now a rather immediate consequence of the preceding theorem.
Corollary 5.24
If V is a \((\preccurlyeq )\)-Archimedean mixed lattice space and A is a quasi-band in V, then \(A_{sp}= (({}^{\perp }A)^{\perp })_{sp}\).
6 Direct sum decompositions and projections
The sum of subspaces A and B of a mixed lattice space V is called a direct sum if \(A\cap B=\{0\}\), and this is denoted by \(A\oplus B\). If V has a direct sum decomposition \(V=A\oplus B\) then each element \(x\in V\) has a unique representation \(x=x_1+x_2\), where \(x_1\in A\) and \(x_2\in B\). The elements \(x_1\) and \(x_2\) are called components of x in A and B, respectively. A vector space can usually be written as a direct sum of subspaces in many ways, but we are mainly concerned with direct sum decompositions that are compatible with the mixed lattice structure in the sense that the order structure of V is determined by its direct sum components.
In this section we give some results concerning direct sum decompositions of a mixed lattice space in terms of ideals and specific ideals. First we show that if a mixed lattice space V can be written as a direct sum of a regular specific ideal A and an ideal B then A and B are necessarily the disjoint complements of each other. Moreover, A has stronger band properties than those implied by Theorem 5.5.
Theorem 6.1
If A is a regular specific ideal and B is an ideal such that \(V=A\oplus B\) then A is a regular specific band and B is a weak band such that \(A= {}^{\perp }B = {}^{\perp }(A^{\perp })\) and \(B= {A}^{\perp } =({}^{\perp }B)^{\perp }\). Moreover, \(V_{sp}=A_{sp}+B_{sp}\).
Proof
Assume that \(V=A\oplus B\), that is, \(A\cap B=\{0\}\). Let \(u\in A\) and \(v\in B\) such that \(u\succcurlyeq 0\) and \(v\ge 0\). Then, since B is an ideal, it follows from  that
that  , and consequently
, and consequently  . On the other hand,
. On the other hand,  and by Theorem 3.2 we have
and by Theorem 3.2 we have

and so  , since A is a specific ideal. Hence, we have
, since A is a specific ideal. Hence, we have  , and so
, and so  . Since
. Since  , this implies that
, this implies that  . Hence, \(A\subseteq {}^{\perp }B\) and \(B\subseteq {A}^{\perp }\).
. Hence, \(A\subseteq {}^{\perp }B\) and \(B\subseteq {A}^{\perp }\).
To prove the reverse inclusions, let \(x\in {}^{\perp }B\). Since \(V=A\oplus B\), the element x has a unique decomposition \(x=x_1+x_2\) with \(x_1\in A\) and \(x_2\in B\). But we showed above that \(A\subseteq {}^{\perp }B\), and so \(x_1\in {}^{\perp }B\). Since \({}^{\perp }B\) is a subspace, we have \(x-x_1=x_2\in {}^{\perp }B\). Thus \(x_2=0\) (by Theorem 5.13) and \(x=x_1\in A\). Hence, \({}^{\perp }B\subseteq A\) and so \(A= {}^{\perp }B\). From this it follows that \(A^{\perp }= ({}^{\perp }B)^{\perp }\) and \(V=A\oplus B={}^{\perp }B \oplus B\). Thus, every \(x\in A^{\perp }=({}^{\perp }B)^{\perp }\) has a unique decomposition \(x=x_1+x_2\) with \(x_1\in {}^{\perp }B\) and \(x_2\in B\subseteq ({}^{\perp }B)^{\perp }\), and so by Theorem 5.13 we have \(x_1=x-x_2 \in ({}^{\perp }B)^{\perp }\). But then \(x_1\in {}^{\perp }B\cap ({}^{\perp }B)^{\perp }= \{0\}\), so we deduce that \(x=x_2\in B\), and therefore \(A^{\perp } \subseteq B\), and so \(A^{\perp }=B\). Hence, we have \(A= {}^{\perp }B = {}^{\perp }(A^{\perp })\) and \(B= A^{\perp }=({}^{\perp }B)^{\perp }\).
The equality \(V_{sp}= A_{sp}+B_{sp}\) holds by Theorem 4.17(b). By Theorem 5.11, B is a weak band, and by Theorem 5.5, A is a weak specific band, but we must show that A is a specific band. For this, let E be a subset of A such that \(w={{\,\mathrm{sp \,sup}\,}}E\) exists in V. Then for any \(x\in E\) we have \(z=w-x\succcurlyeq 0\), and so \(z=z_1+z_2\) with \(z_1\in A_{sp}\) and \(z_2\in B_{sp}\). On the other hand, we have \(w=w_1+w_2\) with \(w_1\in A\) and \(w_2\in B\), and therefore \(z=(w_1-x)+w_2\) where \(w_1-x\in A\). Since the representation of z is unique, we have \(z_1=w_1 -x \in A_{sp}\) and \(z_2=w_2 \in B_{sp}\). Hence, \(x\preccurlyeq w_1 \preccurlyeq w_1+w_2 = w\). Since this holds for any \(x\in E\), it follows that \(w_2 =0\) and \(w=w_1\in A\), and so A is a specific band. \(\square \)
For a regular mixed lattice space we have the following result.
Theorem 6.2
Let A be a regular specific ideal and B an ideal such that \(V=A\oplus B\). Then V is regular if and only if A and B are both regular.
Proof
If A and B are both regular then clearly V is also regular. If V is regular and \(x\in B\) then \(x\preccurlyeq u\) for some \(u\in V_{sp}\). Now by the preceding theorem \(u=u_1+u_2\) with \(u_1\in A_{sp}\) and \(u_2\in B_{sp}\). The inequality \(x\preccurlyeq u_1+u_2\) is equivalent to \(0\preccurlyeq u_1+(u_2-x)\), and, again by Theorem 6.1, we have \(u_2-x\in B_{sp}\). This implies that B is regular. \(\square \)
If there is a weak band A such that \(V={}^{\perp }A\oplus A\) then the components of specifically positive elements in A and \({}^{\perp }A\) are given by the next theorem.
Theorem 6.3
Let A be a weak band such that \(V={}^{\perp }A \oplus A\). Then for every \(x\in V_{sp}\) the elements
exist, and \(x_1\) and \(x_2\) are the components of x in A and \({}^{\perp }A\), respectively.
Proof
Let \(x\in V_{sp}\) have the decomposition \(x=x_1+x_2\) with \(x_1\in A\) and \(x_2\in {}^{\perp }A\). Let \(M=\{v\in A: 0\preccurlyeq v\preccurlyeq x\}\). If \(v\in M\) then the element \(x-v\succcurlyeq 0\) has the unique decomposition \(x-v=(x_1-v)+x_2\) where \(x_1-v\in A_{sp}\) and \(x_2\in ({}^{\perp }A)_{sp}\), by Theorem 6.1. Thus, \(v\preccurlyeq x_1\) and so \(x_1\) is a \((\preccurlyeq )\)-upper bound of M. But we also have \(0\preccurlyeq x_1=x-x_2\preccurlyeq x\), and so \(x_1\in M\). This shows that \(x_1={{\,\mathrm{sp \,sup}\,}}M\). The formula for \(x_2\) is proved similarly. \(\square \)
In accordance with the Riesz space terminology, the components given by the above theorem are called specific projections of x on A and \({}^{\perp }A\). We will return to the discussion of projection elements later.
In the above theorems we considered a direct sum \(V=A\oplus B\) such that \(V_{sp}=A_{sp}+B_{sp}\). If also \(V_{p}=A_{p}+B_{p}\) holds then we obtain stronger results, and this motivates the following definition.
Definition 6.4
Let A and B be subspaces of a mixed lattice space V such that \(V=A\oplus B\). This direct sum is called a mixed-order direct sum if \(V_{sp}=A_{sp}+B_{sp}\) and \(V_p=A_p+B_p\).
Mixed-order direct sums can be characterized as follows.
Theorem 6.5
Let A and B be subspaces of V such that \(V=A\oplus B\). Then the following are equivalent.
-
(a)
\(V=A\oplus B\) is a mixed-order direct sum
-
(b)
A is a regular band and B is a band such that \(A= {}^{\perp }B\) and \(B= {A}^{\perp }\).
Proof
Assuming that \(V=A\oplus B\) is a mixed-order direct sum, we first show that A is \((\le )\)-order convex. Let \(0\le v \le u\) with \(u\in A\). If we put \(w=u-v\) then \(u=v+w\) and \(v,w\ge 0\). Now by assumption v and w have representations \(v=v_1+v_2\) and \(w=w_1+w_2\) where \(v_1,w_1\in A_{p}\) and \(v_2,w_2\in B_p\). Hence, \(u=(v_1+v_2)+(w_1+w_2)\), or \(v_2+w_2=u-(v_1+w_1)\). A and B are subspaces, so \(v_2+w_2\in B\) and \(u-(v_1+w_1)\in A\). But then \(v_2+w_2\in A\cap B =\{0\}\), and it follows that \(v_2=w_2=0\). Thus, \(v=v_1\in A_{p}\) and this shows that A is \((\le )\)-order convex.
Next we need to prove that A is a mixed lattice subspace. By assumption, the elements  and
and  can be written as
can be written as  and
and  where \(a_1\in A_{sp}\), \(b_1\in B_{sp}\) and \(a_2\in A_{p}\), \(b_2\in B_p\). Now
where \(a_1\in A_{sp}\), \(b_1\in B_{sp}\) and \(a_2\in A_{p}\), \(b_2\in B_p\). Now  , so \(b_2-b_1=x-(a_1-a_2)\). Since A and B are subspaces, we have \(b_2-b_1\in B\) and \(x-(a_1-a_2)\in A\). But then \(b_2-b_1\in A\cap B =\{0\}\), and it follows that \(x=a_1-a_2\), and so we have two representations
, so \(b_2-b_1=x-(a_1-a_2)\). Since A and B are subspaces, we have \(b_2-b_1\in B\) and \(x-(a_1-a_2)\in A\). But then \(b_2-b_1\in A\cap B =\{0\}\), and it follows that \(x=a_1-a_2\), and so we have two representations  and \(x=a_1-a_2\) with \(a_1\in A_{sp}\) and \(a_2\in A_p\). By Theorem 4.3 we have
and \(x=a_1-a_2\) with \(a_1\in A_{sp}\) and \(a_2\in A_p\). By Theorem 4.3 we have  and
and  . It follows that
. It follows that  , since A is order-convex. This shows that A is a mixed lattice subspace, and hence an ideal. Similar arguments show that B is also an ideal.
, since A is order-convex. This shows that A is a mixed lattice subspace, and hence an ideal. Similar arguments show that B is also an ideal.
To show that A is regular, we note that  and
and  for all \(x\in A_{sp}\) and \(y\in B_p\), and since A and B are ideals such that \(A\cap B =\{0\}\), it follows that
for all \(x\in A_{sp}\) and \(y\in B_p\), and since A and B are ideals such that \(A\cap B =\{0\}\), it follows that  for all \(x\in A_{sp}\) and \(y\in B_p\). Hence, \(A\subseteq {}^{\perp }B\). Next, let \(0\le z\in {}^{\perp }B\). By assumption we can write \(z=a+b\) where \(a\in A_p\) and \(b\in B_p\). Then \(b=z-a\in {}^{\perp }B\), because \(A\subseteq {}^{\perp }B\) and \({}^{\perp }B\) is a subspace. Thus, \(b\in B\cap {}^{\perp }B=\{0\}\), by Theorem 5.13. Hence, \(z=a\in A\) and so \(A= {}^{\perp }B\), which is a regular weak band by Theorem 5.5. It now follows from Theorem 6.1 that B is a weak band such that \(B= {A}^{\perp }\). To see that B is actually a band, let E be a subset of B such that \(w=\sup E\) exists in V. Then for any \(x\in E\) we have \(z=w-x\ge 0\), and so \(z=z_1+z_2\) with \(z_1\in A_{p}\) and \(z_2\in B_{p}\). On the other hand, \(w=w_1+w_2\) with \(w_1\in A\) and \(w_2\in B\), and so \(z=w_1 + (w_2-x)\) where \(w_2-x\in B\). Since this representation is unique, we have \(z_1=w_1 \in A_{p}\) and \(z_2=w_2-x \in B_{p}\). Hence, \(x\le w_2 \le w_1+w_2 = w\). Since this holds for any \(x\in E\), it follows that \(w_1 =0\) and \(w=w_2\in B\), and so B is a band. A similar argument shows that A is also a band.
for all \(x\in A_{sp}\) and \(y\in B_p\). Hence, \(A\subseteq {}^{\perp }B\). Next, let \(0\le z\in {}^{\perp }B\). By assumption we can write \(z=a+b\) where \(a\in A_p\) and \(b\in B_p\). Then \(b=z-a\in {}^{\perp }B\), because \(A\subseteq {}^{\perp }B\) and \({}^{\perp }B\) is a subspace. Thus, \(b\in B\cap {}^{\perp }B=\{0\}\), by Theorem 5.13. Hence, \(z=a\in A\) and so \(A= {}^{\perp }B\), which is a regular weak band by Theorem 5.5. It now follows from Theorem 6.1 that B is a weak band such that \(B= {A}^{\perp }\). To see that B is actually a band, let E be a subset of B such that \(w=\sup E\) exists in V. Then for any \(x\in E\) we have \(z=w-x\ge 0\), and so \(z=z_1+z_2\) with \(z_1\in A_{p}\) and \(z_2\in B_{p}\). On the other hand, \(w=w_1+w_2\) with \(w_1\in A\) and \(w_2\in B\), and so \(z=w_1 + (w_2-x)\) where \(w_2-x\in B\). Since this representation is unique, we have \(z_1=w_1 \in A_{p}\) and \(z_2=w_2-x \in B_{p}\). Hence, \(x\le w_2 \le w_1+w_2 = w\). Since this holds for any \(x\in E\), it follows that \(w_1 =0\) and \(w=w_2\in B\), and so B is a band. A similar argument shows that A is also a band.
To prove the implication \((b)\Rightarrow (a)\), assume that A is a regular band such that \(V=A\oplus A^{\perp }\). If \(W=({A}^{\perp })_{sp}-({A}^{\perp })_{sp}\) then by Theorem 4.12W is a quasi-ideal, so by Theorem 4.17 we have \(V_{sp}=A_{sp}+(A^{\perp })_{sp}=A_{sp}+W_{sp}\). Then \(V_{p}=A_{p}+(A^{\perp })_{p}\), by Theorem 4.16, and hence \(V=A\oplus A^{\perp }\) is a mixed-order direct sum. \(\square \)
Now, if \(V=A\oplus A^{\perp }\) is a mixed-order direct sum then the left and right disjoint complements of A are very closely related, and they are equal if V is regular.
Theorem 6.6
If \(V=A\oplus A^{\perp }\) is a mixed-order direct sum then \(A= {}^{\perp }(A^{\perp }) = (A^{\perp })^{\perp }\). Moreover, \({}^{\perp }A \subseteq A^{\perp }\), and if \(A^{\perp }\) is regular then \({}^{\perp }A = A^{\perp }\). In this case, \(A= {}^{\perp }(A^{\perp }) = (A^{\perp })^{\perp } = {}^{\perp }({}^{\perp }A) = ({}^{\perp }A)^{\perp }\). In particular, all these equalities hold if V is regular.
Proof
The equality \(A= {}^{\perp }(A^{\perp })\) follows from Theorem 6.5, and since A and \(A^{\perp }\) are both ideals, it then follows from Theorem 5.13(e) that \({}^{\perp }(A^{\perp })=A=(A^{\perp })^{\perp }\). By Theorem 5.13(d) \((A^{\perp })_{sp}\subseteq ({}^{\perp }A)_{sp}\). To prove the reverse inclusion, let \(x\in ({}^{\perp }A)_{sp}\). Then by assumption we can write \(x=x_1+x_2\) where \(x_1\in A_{sp}\) and \(x_2\in (A^{\perp })_{sp}\subseteq ({}^{\perp }A)_{sp}\). Then for every \(z\in A_{sp}\) we have  , and it follows by by Lemma 5.1 that
, and it follows by by Lemma 5.1 that  . Hence \(x_1\in ({}^{\perp }A)_{sp}\), and so \(x_1\in {}^{\perp }A\cap A=\{0\}\). Thus \(x=x_2\in (A^{\perp })_{sp}\), and so \(({}^{\perp }A)_{sp}=(A^{\perp })_{sp}\). Since \({}^{\perp }A=({}^{\perp }A)_{sp}-({}^{\perp }A)_{sp}\), it follows that \({}^{\perp }A\subseteq A^{\perp }\), and if \(A^{\perp }\) is regular then the equality \({}^{\perp }A = A^{\perp }\) holds. In this case we therefore have \(A= {}^{\perp }(A^{\perp }) = (A^{\perp })^{\perp } = {}^{\perp }({}^{\perp }A) = ({}^{\perp }A)^{\perp }\). In particular, this holds if V is regular, by Theorem 6.2. \(\square \)
. Hence \(x_1\in ({}^{\perp }A)_{sp}\), and so \(x_1\in {}^{\perp }A\cap A=\{0\}\). Thus \(x=x_2\in (A^{\perp })_{sp}\), and so \(({}^{\perp }A)_{sp}=(A^{\perp })_{sp}\). Since \({}^{\perp }A=({}^{\perp }A)_{sp}-({}^{\perp }A)_{sp}\), it follows that \({}^{\perp }A\subseteq A^{\perp }\), and if \(A^{\perp }\) is regular then the equality \({}^{\perp }A = A^{\perp }\) holds. In this case we therefore have \(A= {}^{\perp }(A^{\perp }) = (A^{\perp })^{\perp } = {}^{\perp }({}^{\perp }A) = ({}^{\perp }A)^{\perp }\). In particular, this holds if V is regular, by Theorem 6.2. \(\square \)
The next theorem shows that disjoint components of elements in a mixed lattice space have similar properties as in Riesz spaces. In particular, the symmetric absolute value behaves as one would expect.
Theorem 6.7
Let \(V=A\oplus B\) be a mixed-order direct sum. If \(x\in A\) and \(y\in B\) then the following hold.
-
(a)
 and
and 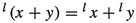 .
. -
(b)
 and
and  .
. -
(c)
 and
and  .
. -
(d)
 .
.
Proof
To prove (a), we start by noting that  . Now
. Now  (by Theorem 4.2) and
(by Theorem 4.2) and  (since
(since  ). Hence, by Lemma 5.7 we have
). Hence, by Lemma 5.7 we have  , and consequently,
, and consequently,  . Now let
. Now let  . Then
. Then  and, since
and, since  , by Theorem 3.2 we also have
, by Theorem 3.2 we also have

This implies that  . Next we note that
. Next we note that  (by Theorem 5.13(d)), and
(by Theorem 5.13(d)), and  , so
, so  . Moreover,
. Moreover,  , so we can use Lemma 5.7 again to obtain
, so we can use Lemma 5.7 again to obtain  . Hence, we have shown that
. Hence, we have shown that  , and consequently, \(w=0\).
, and consequently, \(w=0\).
Since  and
and  , we have
, we have  and
and  , by Theorem 4.3. Similar reasoning proves (b), and adding the equalities in (a) and (b) gives the equalities in (c). Adding the equalities in (c) then gives \(s(x+y)=s(x)+s(y)\). Since this holds for all x and y, we can replace y by \(-y\) to get \(s(x-y)=s(x)+s(-y)=s(x)+s(y)\). The equality \(s(s(x)-s(y))=s(x)+s(y)\) then follows immediately from Theorem 5.17(f) by replacing x with s(x) and y with s(y), and using the fact that
, by Theorem 4.3. Similar reasoning proves (b), and adding the equalities in (a) and (b) gives the equalities in (c). Adding the equalities in (c) then gives \(s(x+y)=s(x)+s(y)\). Since this holds for all x and y, we can replace y by \(-y\) to get \(s(x-y)=s(x)+s(-y)=s(x)+s(y)\). The equality \(s(s(x)-s(y))=s(x)+s(y)\) then follows immediately from Theorem 5.17(f) by replacing x with s(x) and y with s(y), and using the fact that  . Indeed, since \(s(x)\in A_{sp}\) and \(s(y)\in B_{sp}=({A}^{\perp })_{sp}\), then by Theorem 5.13(d) we have \(s(y)\in ({}^{\perp }A)_{sp}\), and so
. Indeed, since \(s(x)\in A_{sp}\) and \(s(y)\in B_{sp}=({A}^{\perp })_{sp}\), then by Theorem 5.13(d) we have \(s(y)\in ({}^{\perp }A)_{sp}\), and so  . Consequently,
. Consequently,  . Here the last equality follows by noting that \(s(x)+s(y)\) is clearly a \((\preccurlyeq )\)-upper bound of \(\{s(x),s(y)\}\), and if \(s(x)\preccurlyeq c\) and \(s(y)\preccurlyeq c\) then
. Here the last equality follows by noting that \(s(x)+s(y)\) is clearly a \((\preccurlyeq )\)-upper bound of \(\{s(x),s(y)\}\), and if \(s(x)\preccurlyeq c\) and \(s(y)\preccurlyeq c\) then  , completing the proof. \(\square \)
, completing the proof. \(\square \)
If C is a mixed lattice cone then the following inequalities hold for all \(x,y,z\in C\). (For the proofs we refer to [2, pp.13] and [2, Theorem 3.6.])


With these inequalities we obtain the following formulae for the mixed envelopes of specifically positive elements.
Proposition 6.8
Let \(V=A\oplus B\) be a mixed-order direct sum. If \(x,y\in V_{sp}\) are elements with components \(x=x_1+x_2\) and \(y=y_1+y_2\) where \(x_1,y_1\in A_{sp}\) and \(x_2,y_2\in B_{sp}\), then

Proof
\(A_{sp}\) and \(B_{sp}\) are mixed lattice cones, so using 6.1 and 6.2 together with the fact that  (where the last equality follows from Theorem 6.6, since \(y_1\in A={}^{\perp }B \subseteq B^{\perp }\)) we get
(where the last equality follows from Theorem 6.6, since \(y_1\in A={}^{\perp }B \subseteq B^{\perp }\)) we get

On the other hand, we have  and
and  , so
, so  , and the first identity follows. Similar reasoning shows that
, and the first identity follows. Similar reasoning shows that  .
.
Substituting these into  gives
gives

\(\square \)
If \(V=A\oplus A^{\perp }\) is a mixed order direct sum then the components of a positive element in A and \(A^{\perp }\) are given by the next theorem, which is proved exactly as Theorem 6.3.
Theorem 6.9
Let A be a band such that \(V=A\oplus A^{\perp }\) is a mixed order direct sum. Then for every \(x\in V_{p}\) the elements
exist, and \(x_1\) and \(x_2\) are the components of x in A and \({A}^{\perp }\), respectively.
As in the theory of Riesz spaces, it turns out that the existence of a mixed order direct sum is equivalent to the existence of the associated order projection. Let \(V=A\oplus A^{\perp }\) be a mixed order direct sum. If \(x\in V\) has the components \(x_1\in A\) and \(x_2\in A^{\perp }\) then we define the mapping \(P_A:V\rightarrow V\) by \(P_A (x)=x_1\). We can immediately see that \(P_A\) has the following properties:
A mapping with these properties is called a mixed order projection and the associated band A is called a projection band. (Note that the specific projection elements in Theorem 6.3 can be given similarly in terms of a specific projection operator that has the properties (P1) and (P3)).
Conversely, if P is a mixed order projection on V then there exists a corresponding mixed order direct sum decomposition of V. Apart from a few minor modifications, the proof is essentially the same as in the case of Riesz spaces (see [11, Theorem 11.4]).
Theorem 6.10
If \(P:V\rightarrow V\) is a mapping with properties (P1)–(P3) then there exists a regular band A such that \(V=A\oplus A^{\perp }\) is a mixed order direct sum and P is the associated projection on A and \(I-P\) is the projection on \(A^{\perp }\).
Proof
Let \(A=\{Px:x\in V\}\) and \(B=\{(I-P)x:x\in V\}\). Then A and B are clearly subspaces of V. If \(x\in A\cap B\) then \(x=Py\) and \(x=(I-P)z\) for some \(y,z\in V\). Using the property (P1) we get
This shows that \(A\cap B=\{0\}\), so \(A\oplus B\) is a direct sum. Moreover, for any \(x\in V\) we have \(x=Px+(x-Px)=Px+(I-P)x\), so \(V=A\oplus B\). It now follows from (P2) that if \(x\ge 0\) then \(Px\ge 0\) and \(0\le x-Px=(I-P)x\). Hence, \(V_p=A_p+B_p\). Similarly, (P3) implies that \(V_{sp}=A_{sp}+B_{sp}\), and so \(V=A\oplus B\) is a mixed order direct sum. It then follows from Theorem 6.5 that A is a regular band and \(B=A^{\perp }\). Clearly, P and \(I-P\) are the projections on A and \(A^{\perp }\), respectively. \(\square \)
If \(x\ge 0\) then by Theorem 6.9 the element \(P_A (x)\) is given by \(P_A (x)=\sup \{v\in A:0\le v\le x\}\). Since every element can be written as a difference of positive elements, we obtain the projection of an arbitrary element.
Theorem 6.11
If \(V=A\oplus A^{\perp }\) is a mixed order direct sum and \(P_A\) and \(P_{A^{\perp }}=I-P_A\) are the associated projections on A and \(A^{\perp }\), respectively, then for any \(x\in V\) we have

or alternatively,

Proof
Every \(x\in V\) can be written as  (or alternatively,
(or alternatively,  , but this case is treated similarly). The elements
, but this case is treated similarly). The elements  and
and  have the components
have the components  and
and  , where \(a,u\in A\) and \(b,v\in A^{\perp }\). On the other hand, \(x=x_1+x_2\) with the components \(x_1\in A\) and \(x_2\in A^{\perp }\). By Theorem 6.7 we have
, where \(a,u\in A\) and \(b,v\in A^{\perp }\). On the other hand, \(x=x_1+x_2\) with the components \(x_1\in A\) and \(x_2\in A^{\perp }\). By Theorem 6.7 we have  and
and  , where
, where  and
and  . Since \(A\cap A^{\perp }=\{0\}\), this implies that
. Since \(A\cap A^{\perp }=\{0\}\), this implies that  ,
,  ,
,  and
and  . These components are the projection elements, and the proof is thus complete. \(\square \)
. These components are the projection elements, and the proof is thus complete. \(\square \)
Next we consider some examples. First it should be noted that there are non-trivial mixed lattice spaces in which non-trivial ideals do not exist, and hence non-trivial mixed lattice decompositions do not always exist either.
Example 6.12
Let \(V={\mathbb {R}}^2\) and define \(\le \) as the partial ordering with the usual positive cone \(V_p=\{(x,y):x\ge 0, y\ge 0\}\). Let \(\preccurlyeq \) to be the partial ordering induced by the positive cone \(V_{sp}=\{\alpha (2,1)+\beta (1,2): \, \alpha ,\beta \ge 0\}\). Then V is a regular mixed lattice space. If \(C_1=\{(x,y):y=\frac{1}{2}x\}\) and \(C_2=\{(x,y):y=2x\}\) then \(C_1\) and \(C_2\) are both specific ideals, but there are no other ideals in V than \(\{0\}\) and V itself.
If we change \(\preccurlyeq \) to be the partial ordering with the positive cone \(V_{sp}=\{\alpha (1,0)+\beta (1,1): \, \alpha ,\beta \ge 0\}\) then V is again a regular mixed lattice space. Let \(A=\{(x,y):y=x\}\) and \(B=\{(x,y):y=0\}\). It is easy to see that A is a regular specific ideal and B is a regular ideal such that \(V=A\oplus B\). The conditions of Theorem 6.1 are thus satisfied and \(A= {}^{\perp }B\) and \(B= {A}^{\perp }\). Moreover, \((A+B)_{sp}=A_{sp} + B_{sp}\) holds. However, this is not a mixed-order direct sum. For instance, the element \(x=(1,2)\) cannot be written as \(x=x_1+x_2\) where \(x_1\in A_{p}\) and \(x_2\in B_p\).
The next one is related to the setting of Theorem 6.1.
Example 6.13
This example is adapted from [2, pp. 34]. See also [5, Example 2.15]. Let \(V=BV([0,1])\) be the set of all functions of bounded variation on the interval [0, 1]. Define the initial order as \(f\le g\) if \(f(x)\le g(x)\) for all \(x\in [0,1]\), and the specific order as \(f\preccurlyeq g\) if \(f\le g\) and \(g-f\) is non-decreasing on [0, 1]. Then V is a regular mixed lattice space.
Now fix some \(c\in (0,1)\) and let A be the subspace consisting of those functions that are constant on the closed interval [c, 1], and let B be the subspace consisting of those functions that vanish on the closed interval [0, c]. Then A is a regular specific ideal and B is a regular ideal such that \(A\cap B=\{0\}\). It is well known that every \(g\in V\) can be written as a difference of two non-decreasing non-negative functions on [0, 1]. Hence, to see that \(V=A\oplus B\) it is sufficient to note that every non-decreasing non-negative function f on [0, 1] can be written as \(f=f_1+f_2\) where \(f_1\in A\) and \(f_2\in B\). Indeed, define \(f_1\) by \(f_1(x)=f(x)\) for all \(x\in [0,c]\), and \(f_1(x)=f(c)\) for all \(x\in [c,1]\). Then define \(f_2\) by \(f_2(x)=0\) for all \(x\in [0,c]\) and \(f_2(x)=f(x)-f(c)\) for all \(x\in [c,1]\). Then \(f_1\in A\), \(f_2\in B\) and \(f=f_1+f_2\), and by Theorem 6.1\(A={}^{\perp }B\) is a specific band and \(B=A^{\perp }\) is a weak band.
If we consider the space W of all continuous functions of bounded variation on [0, 1], and we put \(c=0\) with A and B defined as above, then A is just the set of all constant functions on [0, 1] and \(B=\{g\in W:g(0)=0\}\). Then \(W=A\oplus B\) as above, and B is a weak band by Theorem 6.1, but not a band. This can be seen by choosing \(f(x)=1\) for all \(x\in [0,1]\) and defining \(f_n\) by \(f_n(x)=nx\) for \(x\in [0,1/n]\), and \(f_n(x)=1\) for \(x\in (1/n,1]\). Then \(\{f_n\}\subseteq B\) for all \(n\in {\mathbb {N}}\) and \(\sup \{f_n\}=f\), but \(f\notin B\). Note also, that now f is not the specific supremum (and hence not the strong supremum) of \(\{f_n\}\).
Special cases of mixed-order direct sums are provided by Dedekind complete Riesz spaces, where all bands are projection bands. We give some other examples below.
Example 6.14
Let U be the same mixed lattice space as in Example 5.15, with the subspaces \(C=\{(0,y,z):y,z\in {\mathbb {R}}\}\) and \(D=\{(x,x,0):x\in {\mathbb {R}}\}\). Now C is a regular ideal and D is a regular specific ideal such that \(U=C\oplus D\). Hence, the conditions of Theorem 6.1 are satisfied and we have \(C=D^{\perp }\) and \(D= {}^{\perp }C\). Moreover, \((C+D)_{sp}=C_{sp} + D_{sp}\) but this is not a mixed-order direct sum. If \(A=\{(0,0,z):z\in {\mathbb {R}}\}\) and \(B=\{(x,y,0):x,y\in {\mathbb {R}}\}\) then A and B are both regular ideals such that \(U=A\oplus B\). This is a mixed-order direct sum where \(B=A^{\perp }\) and \(A= {}^{\perp }B\).
Similarly, if V is the same as in Example 5.15, then in V, A is a regular band and B is a band such that \(B=A^{\perp }\), \(A= {}^{\perp }B\) and \(V=A\oplus B\) is a mixed order direct sum.
Example 6.15
Let V be the set of all n-by-n matrices and define \(\le \) as the usual element-wise ordering and define specific order by \(M\succcurlyeq 0\) if \(M\ge 0\) and M is a symmetric matrix. Then V is a quasi-regular mixed lattice space (see [5, Example 2.19]), where the set A consisting of all diagonal matrices is a band and the set B of those matrices with zero diagonal elements is a band such that \(A={}^{\perp }B\), \(B=A^{\perp }\) and \(V=A\oplus B\) is a mixed order direct sum.
As we have seen in Example 6.13, the mixed lattice space of functions of bounded variation has direct sum decompositions of the type described in Theorem 6.1, but it does not possess non-trivial mixed-order direct sum decompositions. The following example is somewhat analogous to the situation in the Riesz space C([0, 1]) of continuous real functions on the interval [0, 1], where non-trivial projection bands do not exist. Before discussing the example we need the following lemma.
Lemma 6.16
The ideal I(u) generated by a single element \(u\in V\) is given by \(I(u)=\{x\in V: s(x)\le n s(u) \text { for some } n\in {\mathbb {N}}\}\).
Proof
We first show that I(u) is a subspace. If \(x,y\in I(u)\) then \(s(x)\le n s(u)\) and \(s(y)\le m s(u)\) for some \(n,m\in {\mathbb {N}}\). Then for all \(a,b\in {\mathbb {R}}\),
where \(p\in {\mathbb {N}}\) is a number such that \(|a|n+|b|m\le p\). Thus, \(ax+ny\in I(u)\). Next, let \(x\in I(u)\) and \(s(y)\le s(x)\). Then \(s(y)\le s(x)\le n s(u)\) for some \(n\in {\mathbb {N}}\) and so \(y\in I(u)\). It follows that I(u) is an ideal, by the condition of Theorem 5.18. To show that I(u) is the smallest ideal that contains u, let J be another ideal such that \(u\in J\). Then also \(ns(u)\in J\) for all \(n\in {\mathbb {N}}\), and if \(x\in I(u)\) the inequality \(s(x)\le ms(u)=s(mu)\) holds for some \(m\in {\mathbb {N}}\). It follows again by Theorem 5.18 that \(x\in J\). Hence, \(I(u)\subseteq J\).
Example 6.17
Consider the regular mixed lattice space \(V=BV([0,1])\), as in Example 6.13. If \(f,g\in V\) then the mixed lower and upper envelopes are given by ([2, Theorem 21.1.])

and

where \(r^+ = \max \{0,r\}\) is the positive part of the real number r.
Now \(V=V \oplus \{0\}\) is the only mixed order direct sum decomposition of V. This can be seen by considering the constant function \(h(x)=1\) for all \(x\in [0,1]\). First we note that the ideal generated by h is V. Indeed, since every \(f\in V\) is bounded, then for any \(f\in V\) there exists some \(n\in {\mathbb {N}}\) such that \(s(f)\le n h =ns(h)\). Hence \(I(h)=V\), by the preceding lemma.
Now if \(V=A\oplus B\) is a mixed order direct sum then h has the components \(f\in A\) and \(g\in B\) such that \(f(x)+g(x)=1\) for all \(x\in [0,1]\) and  . This implies that f and g are positive, so \(0\le f(x)\le 1\) and \(0\le g(x)\le 1\) for all \(x\in [0,1]\). Then the above expression for
. This implies that f and g are positive, so \(0\le f(x)\le 1\) and \(0\le g(x)\le 1\) for all \(x\in [0,1]\). Then the above expression for  gives
gives

If  then we have \(f(u)=\sup \{(f(x)-g(x))^+: x\in [0,u]\}\). In particular, \(f(0)=(f(0)-g(0))^+=(2f(0)-1)^+\). Now, if \(0\le f(0)\le \frac{1}{2}\) then \(f(0)=0\). If \(\frac{1}{2}< f(0)\le 1\) then \(f(0)=2f(0)-1\), or \(f(0)=1\). Hence, we must have either \(f(0)=0\) and \(g(0)=1\), or \(f(0)=1\) and \(g(0)=0\). Since \(h\succcurlyeq 0\) and \(V=A\oplus B\) is a mixed order direct sum then also the components of h satisfy \(f\succcurlyeq 0\) and \(g\succcurlyeq 0\). In other words, f and g are non-decreasing. But this and \(f(x)+g(x)=1\) imply that either \(f(x)=0\) and \(g(x)=1\), or \(f(x)=1\) and \(g(x)=0\) for all \(x\in [0,1]\). This shows that either A or B contains the constant function \(h(x)=1\). Since the ideal generated by h equals V, we must therefore have either \(A=V\) and \(B=\{0\}\), or \(B=V\) and \(A=\{0\}\).
then we have \(f(u)=\sup \{(f(x)-g(x))^+: x\in [0,u]\}\). In particular, \(f(0)=(f(0)-g(0))^+=(2f(0)-1)^+\). Now, if \(0\le f(0)\le \frac{1}{2}\) then \(f(0)=0\). If \(\frac{1}{2}< f(0)\le 1\) then \(f(0)=2f(0)-1\), or \(f(0)=1\). Hence, we must have either \(f(0)=0\) and \(g(0)=1\), or \(f(0)=1\) and \(g(0)=0\). Since \(h\succcurlyeq 0\) and \(V=A\oplus B\) is a mixed order direct sum then also the components of h satisfy \(f\succcurlyeq 0\) and \(g\succcurlyeq 0\). In other words, f and g are non-decreasing. But this and \(f(x)+g(x)=1\) imply that either \(f(x)=0\) and \(g(x)=1\), or \(f(x)=1\) and \(g(x)=0\) for all \(x\in [0,1]\). This shows that either A or B contains the constant function \(h(x)=1\). Since the ideal generated by h equals V, we must therefore have either \(A=V\) and \(B=\{0\}\), or \(B=V\) and \(A=\{0\}\).
A few concluding remarks are in order to further explain and justify our choice of certain definitions. Since we have defined \(A^{\perp }\) to be the ideal generated by the cone \(({A}^{\perp })_{sp}\), one might be inclined to ask why did we define \(^{\perp }A\) as the specific ideal generated by the cone \(({}^{\perp }A)_{sp}\), and not the ideal generated by \(({}^{\perp }A)_{sp}\). The main reason for this stems from the fact that if B is the ideal generated by \(({}^{\perp }A)_{sp}\) then, in general, \(B_{sp}\) is a larger set than \(({}^{\perp }A)_{sp}\). As a consequence, properties such as \(A\cap {}^{\perp }A = \{0\}\) would no longer hold. Moreover (and perhaps most importantly), there is a rather well developed theory of direct sum decompositions in mixed lattice semigroups, as presented in [2]. Indeed, our Theorems 6.1 and 6.5 have their counterparts in the theory of mixed lattice semigroups ([2, Theorems 7.1 and 7.2]). (Note however, that the authors in [2] use different terminology, as they use the potential-theoretic notions of pre-harmonic band and potential band. The corresponding objects in this paper are called specific bands and weak bands, respectively.) Our present definitions of \(A^{\perp }\) and \(^{\perp }A\) are in agreement with the existing theory of mixed lattice semigroups. In fact, if A is an ideal such that \(V= {}^{\perp }A\oplus A\), then the set \(V_{sp}\) is a mixed lattice semigroup in its own right (with the orderings inherited from V), and \(V_{sp}=(^{\perp }A)_{sp} \oplus A_{sp}\) is the corresponding mixed lattice semigroup decomposition of \(V_{sp}\), by Theorem 6.1.
With all these considerations, our definitions of the disjoint complements indeed seem to be the most natural, and also compatible with the theory of mixed lattice semigroups, at least if we restrict ourselves to mixed lattice subspaces, as we have done in this paper. However, the corresponding definitions for more general sets would be more problematic, as pointed out in Remark 5.4.
Data availibility
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Aliprantis, C.D., Tourky, R.: Cones and Duality. American Mathematical Society, Providence (2007)
Arsove, M., Leutwiler, H.: Algebraic Potential Theory. Memoirs of the American Mathematical Society, No. 226 (1980)
Boboc, N., Bucur, G., Cornea, A.: Order and Convexity in Potential Theory: H-Cones. Lecture Notes in Mathematics, vol. 853. Springer-Verlag, Berlin-Heidelberg-New York (1981)
Doob, J.L.: Classical Potential Theory and Its Probablilistic Counterpart. Springer-Verlag, Berlin-Heidelberg (2001)
Eriksson, S.-L., Jokela, J., Paunonen, L.: Generalized absolute values, ideals and homomorphisms in mixed lattice groups. Positivity 25(3), 939–972 (2021). https://doi.org/10.1007/s11117-020-00794-2
Eriksson-Bique, S.-L.: Generalized Riesz spaces. Rev. Roumaine Math. Pures Appl. 36(1–2), 47–69 (1991)
Eriksson-Bique, S.-L.: Mixed lattice groups. Rev. Roumaine Math. Pures Appl. 44(2), 171–180 (1999)
Kalauch, A., Lemmens, B., van Gaans, O.: Bands in partially ordered vector spaces with order unit. Positivity 19, 489–511 (2015). https://doi.org/10.1007/s11117-014-0311-7
Kalauch, A., van Gaans, O.: Ideals and bands in pre-Riesz spaces. Positivity 12(4), 591–611 (2008)
Luxemburg, W.A.J., Zaanen, A.C.: Riesz Spaces, vol. I. North-Holland Publishing Company, Amsterdam (1971)
Zaanen, A.C.: Introduction to Operator Theory in Riesz Spaces. Springer-Verlag, Berlin (1997)
Funding
Open access funding provided by Tampere University including Tampere University Hospital, Tampere University of Applied Sciences (TUNI). The author has no funding to declare.
Author information
Authors and Affiliations
Contributions
The author confirms sole responsibility for the study conception, results, and manuscript preparation.
Corresponding author
Ethics declarations
Conflict of interest
The author has no conflict of interest to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jokela, J. Ideals, bands and direct sum decompositions in mixed lattice vector spaces. Positivity 27, 32 (2023). https://doi.org/10.1007/s11117-023-00985-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11117-023-00985-7




 .
. . The equality
. The equality  follows immediately from (M1). First we note that
follows immediately from (M1). First we note that 
 and this implies that
and this implies that  . This shows that
. This shows that  for all
for all 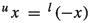 and
and 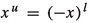 .
. .
.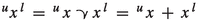 and
and  .
. .
. ,
, 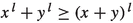 and
and  .
. ,
,  and
and  .
. .
.
 and
and  .
. and
and  .
. and
and  . Moreover,
. Moreover,  if and only if
if and only if  and
and 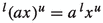 for all
for all  and
and  for all
for all 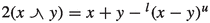 and
and  .
. and
and 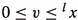 . If also
. If also  and
and  .
. then
then  and
and  .
.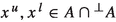 , since A and
, since A and  and so
and so 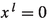 , which implies that
, which implies that  . Since
. Since  that
that  and
and  imply that
imply that  , and so
, and so  and
and  that
that  . Hence,
. Hence,  .
. .
.
 and
and  imply
imply 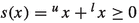 . It is clear that
. It is clear that  , or
, or  . Hence
. Hence  , which implies
, which implies 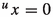 . On the other hand,
. On the other hand,  , or
, or  . So,
. So,  , which in turn implies
, which in turn implies  . Consequently,
. Consequently, 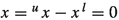 .
.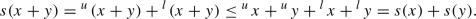
 and
and 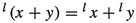 .
. and
and  .
. and
and  .
. .
.