Introduction

Several computational models of chemical reaction networks have been presented in the literature over the years. In some cases, these models showed the appearance and/or further evolution of autocatalytic sets, i.e., collections of molecules and the (catalyzed) chemical reactions between them that, as a whole, can sustain and reproduce themselves from an ambient food source. Such autocatalytic sets are believed to have played an important role in the origin of life (Kauffman 1993; Hordijk 2013), and it has been argued that they may have been the very first units of natural selection, before the appearance of template-based replicators (Vasas et al. 2012).

However, in the various existing computational models of chemical reaction systems, the concept of autocatalytic sets has often been defined in different ways, depending on the particular modeling context. For example, they have been defined as (or even confused with) hypercycles, as cores (connected components) in the catalysis graph, or as viable cores (cores that can sustain themselves from a given food set). Unfortunately, these different definitions do not always translate easily (or at all) between the different modeling contexts. Moreover, they all seem to miss one or more important aspects, or are limited to the particular model to which they were applied.

The goals of this paper are therefore as follows:

  • To suggest a previously developed formal framework known as RAF theory to serve as a standard for defining, detecting, and analyzing autocatalytic sets.

  • To show that this formal framework captures the various other definitions of autocatalytic sets that exist in the literature, and is therefore more general and more complete.

  • To use RAF theory to analyze and highlight the different ways in which autocatalytic sets can emerge and evolve in different computational models of chemical reaction systems.

In the next section, we briefly describe the basics of RAF theory and its main applications and results. We then review four different computational models of chemical reaction networks presented in the literature, and show how they can be described within RAF theory. We then apply this formal framework to analyze some of the main results of these various models, confirming the appearance and evolution of autocatalytic sets as RAF sets, and derive additional conclusions and insights along the way. Finally, we summarize the main conclusions and present some discussion.

Autocatalytic Sets and RAF Theory

The concept of autocatalytic sets was first introduced by Kauffman (1971, 1986, 1993). It was later formalized mathematically and further developed as RAF theory (Steel 2000; Hordijk and Steel 2004; Hordijk 2013). In this section, we briefly review the basics of RAF theory.

First, we define a chemical reaction system (CRS) as a tuple \(Q=\{X,\mathcal {R},C\}\) consisting of a set X of molecule types, a set \(\mathcal {R}\) of chemical reactions, and a catalysis set C indicating which molecule types catalyze which reactions. We also consider the notion of a food set F⊂X, which is a subset of molecule types that are assumed to be directly available from the environment.

The notion of catalysis plays a central role here. A catalyst is a molecule that significantly speeds up the rate at which a chemical reaction happens, without being “used up” in that reaction. Catalysis is ubiquitous in life (Van Santen and Neurock 2006). The majority of organic reactions are catalyzed, and catalysts are essential in determining and regulating the functionality of the chemical reaction networks that support life.

An autocatalytic set, or RAF set, is now defined as a subset \(\mathcal {R}^{\prime } \subseteq \mathcal {R}\) of reactions (and associated molecule types) which is:

  • Reflexively Autocatalytic (RA): each reaction \(r \in \mathcal {R}^{\prime }\) is catalyzed by at least one molecule type involved in \(\mathcal {R}^{\prime }\), and

  • Food-generated (F): all reactants in \(\mathcal {R}^{\prime }\) can be created from the food set F by using a series of reactions only from \(\mathcal {R}^{\prime }\) itself.

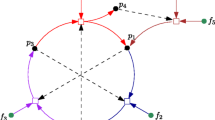
A simple example of a RAF set is presented in Fig. 1. A more formal definition of RAF sets is provided in Hordijk and Steel (2004); Hordijk et al. (2011), including an efficient (polynomial-time) algorithm for finding RAF sets in a general CRS.

Fig. 1
figure 1

An example of a simple RAF set with two reactions. Black dots represent molecule types and white boxes represent reactions. Solid arrows are reactants going into and products coming out of a reaction. Dashed arrows indicate catalysis. The food set consists of the four molecule types at the bottom

Full size image

This RAF algorithm returns the unique maximal RAF set (maxRAF), which is the union of all RAF (sub)sets within a given CRS. If no RAF set exists within a CRS, the RAF algorithm returns the empty set. A maximal RAF set can often be decomposed into several smaller subsets which themselves are RAF sets, i.e., subRAFs (Hordijk et al. 2012). If such a subRAF cannot be reduced any further without losing the RAF property, it is referred to as an irreducible RAF, or irrRAF (Hordijk and Steel 2004).

Note that it is implicitly assumed that reactions can also still happen uncatalyzed, but at a significantly lower rate than catalyzed reactions. In other words, uncatalyzed reactions are possible, but rare. However, such “spontaneous” reactions are often necessary for RAF sets to come into existence in a dynamical sense (given that they exist in the underlying reaction network). For example, in the RAF set in Fig. 1, one of the two reactions will have to happen uncatalyzed as long as there are only food molecules available. But once such a spontaneous reaction has happened the full set can come into existence, and potentially grow exponentially in concentration. As argued elsewhere (and see also below), this requirement for spontaneous reactions is actually a useful property for the potential evolvability of RAF sets (Hordijk and Steel 2014).

RAF theory has been applied extensively to simple polymer-based models of chemical reaction networks, showing that autocatalytic sets are highly likely to exist under a wide variety of model assumptions (Hordijk and Steel 2004; Mossel and Steel 2005; Hordijk et al. 2011; Hordijk et al. 2014b; Smith et al. 2014; Hordijk et al. 2014a). Moreover, these results show that there generally exist many hierarchical levels of subRAFs and irrRAFs in such networks (Hordijk et al. 2012; Hordijk et al. 2015). Finally, the formal RAF framework has also been applied successfully to analyze real chemical and biological networks in terms of autocatalytic sets (Hordijk and Steel 2013; Sousa et al. 2015).

Evolution of Autocatalytic Sets in Chemical Reaction Networks

We now review four computational models of chemical reaction networks that have been presented in the literature. For each model, we show how it can be formally described, analyzed, and interpreted with RAF theory. In all cases, these models clearly show the (potential) evolution of autocatalytic (RAF) sets.

Spontaneous Decay and Information Preservation

Hordijk and Fontanari (2003) present an evolutionary model of a chemical reaction network that was used to study information preservation under spontaneous decay. In particular, a genetic algorithm (GA) was used to evolve reaction networks that are capable of maintaining a certain distribution of longer polymers, while these polymers spontaneously break up into smaller pieces at a rate that is proportional to their length.

The molecules in this model are polymers P i (of a single, unspecified, monomer type), where only their length i is important. These polymers can be of any length i up to 35. The possible chemical reactions are “bonding” (combining two polymers into a longer one: P i + P j →P i + j ) and “breaking” (splitting a polymer into two shorter ones: P i + j →P i + P j ), taking the maximum polymer length into account (i + j≤35). However, only catalyzed reactions are considered. In other words, each bonding or breaking reaction is catalyzed by some (randomly assigned) polymer P k .

Instances of this reaction network model are then created by choosing 100 random bonding and breaking reactions, and assigning a catalyst to each of them, also at random. Starting with an initial polymer distribution of an equal number of polymers up to length nine, the dynamics of such a reaction network is then simulated using the standard Gillespie algorithm (Gillespie 1976, 1977). However, in these simulations an element of spontaneous decay is also included. In particular, each polymer P i breaks down into smaller pieces at a rate that is directly proportional to its length i.

Finally, a genetic algorithm (Goldberg 1989; Mitchell 1996) was used to evolve such reaction networks (each one consisting of 100 catalyzed bonding and breaking reactions). The fitness of a reaction network is determined by comparing its final polymer distribution (after simulating the network dynamics for a certain amount of time) with a pre-specified target distribution. This model set-up was then used to study the evolution of reaction networks, and their capability to preserve a certain amount of information, under various rates of spontaneous decay and target distributions. For full details, see Hordijk and Fontanari (2003).

This model can be formally described within the RAF framework:

$$\begin{array}{lclcl} X & = & \{P_{i} \;|\; i=1,\ldots,35\} \\ \mathcal{R} & = & \{P_{i} + P_{j} \rightarrow P_{i+j}, \; P_{i+j} \rightarrow P_{i} + P_{j} \;|\; i+j \leq 35\}\\ C & = & \{(P_{i},r) \;|\; i=1,\ldots,35, r \in \mathcal{R}\} \\ F & = & \{P_{i} \;|\; i=1,\ldots,9\} \end{array} $$

where each model instance contains a random subset of size 100 of \(\mathcal {R}\) (and, correspondingly, of C).

The main results of this evolutionary model can be summarized as follows:

  1. 1.

    Reaction networks can indeed be evolved to generate a specific polymer distribution from a given initial distribution (even under the “constraint” of spontaneous polymer decay).

  2. 2.

    These evolved reaction networks often contain a small core set of reactions that are responsible for most, if not all, of the network’s behavior.

In Hordijk and Fontanari (2003) Table 1, a set of 13 reactions is presented that forms the core set of one of the best GA-evolved reaction networks. As the authors remark, this core reaction set contains “various hypercycle-like structures”. However, the evolved reaction network, or its core set, was never analyzed in any formal way.

Hypercycles were originally defined as a possible mechanism to build increasing chemical complexity in an origin of life context (Eigen and Schuster 1979). They are indeed autocatalytic cycles, but in a more specific (and restricted) way than autocatalytic sets in general. In particular, each element in a hypercycle is a self-reproducing unit, whereas in an autocatalytic set each element is generally produced from other, different, elements (although some elements could also be self-reproducers). In other words, hypercycles are a restricted subset of, and often show quite different dynamics than, general autocatalytic sets. Unfortunately, the two are still all too often confused (Szathmáry 2013).

Here, we have taken the mentioned core set of 13 reactions and applied the RAF algorithm to it. This results in a (max)RAF set of ten reactions. One of the 13 core reactions is not part of the RAF set, and there are two pairs of identical reactions in the core set, but with different catalysts. Each of these pairs can thus be considered as one reaction, respectively, each one having two possible catalysts. The resulting set of ten reactions, presented in Fig. 2 is, indeed, an actual autocatalytic (RAF) set.

Fig. 2
figure 2

The 10-reaction RAF set that is contained in the 13-reaction core set of a GA-evolved reaction network

Full size image

Note, however, that this RAF set is not a hypercycle, nor does it contain “hypercycle-like structures”, as Hordijk and Fontanari (2003) originally claimed. In fact, none of the elements is a self-reproducing unit. Given their strict requirements, hypercycles are not easy to realize, which is probably why no real examples of a hypercycle exists. However, several autocatalytic (RAF) sets have already been created in the lab (Sievers and Von Kiedrowski 1994; Ashkenasy et al. 2004; Lincoln and Joyce 2009; Vaidya et al. 2012), or observed in living systems (Sousa et al. 2015).

Even though the RAF set of Fig. 2 has only ten reactions, it has a very rich internal structure. Using an extension of the RAF algorithm, it is possible to generate the partially ordered set (poset) of all the possible RAF subsets that are contained within this (maximal) RAF set (Hordijk et al. 2012). This poset is represented as a so-called Hasse diagram in Fig. 3. In this diagram, the 10-reaction maximal RAF is at the top. The row below it contains the nodes representing its 9-reaction RAF subsets, the next row its 8-reaction RAF subsets, and so on, with the irreducible RAF sets at the bottom. There is an arrow from subset \(\mathcal {R}_{i}\) to subset \(\mathcal {R}_{j}\) if \(\mathcal {R}_{j} \subset \mathcal {R}_{i}\) and there is no subset \(\mathcal {R}_{k}\) such that \(\mathcal {R}_{j} \subset \mathcal {R}_{k} \subset \mathcal {R}_{i}\) (Hordijk et al. 2012). In total there are 407 nodes (i.e., possible RAF subsets) in this diagram.

Fig. 3
figure 3

The partially ordered set of all possible RAF subsets of the 10-reaction RAF set of Fig. 2

Full size image

This rich poset structure reflects a high level of modularity in the RAF set. This suggests that there is not just one possible RAF set that can produce the desired functionality (i.e., generate the target polymer distribution), but that there may be multiple (similar) networks that can generate the same kind of dynamical behavior. In other words, evolution probably has a fair chance of finding a good solution for the given problem.

Molecular Cooperation and Network Structure

Jain and Krishna (2001, 2002) present “a simple mathematical model for the evolution of an idealized chemical system to study how a network of cooperative molecular species arises and evolves to become more complex and structured.” In their model, different molecular species i are produced through chemical reactions (although it is not specified how these molecules are produced), and a given species j can be a catalyst for the production of another species i with some small probability p.

An instance of this model can be represented as a so-called “catalysis graph”, where each node represents a molecular species, and there is a directed arrow from node j to node i if species j catalyzes the production of species i. An example is shown in Fig. 4. Such a catalysis graph is completely specified by its adjacency matrix A=(a i j ) where a i j =1 if species j catalyzes the production of species i, and a i j =0 otherwise.

Fig. 4
figure 4

One of the reaction networks, represented as a catalysis graph, during the evolution in the Jain & Krishna model. Reprinted from Jain and Krishna (2002)

Full size image

Given an instance of this model, the dynamics of the system is then simulated for a fixed time T, according to rate equations specified by the adjacency matrix A, and starting from a random initial distribution of species concentrations. At time T, the species with the lowest concentration is replaced with a new species that has random catalytic links with the other species according to the same probability p. The current concentrations are then perturbed by a small random amount, and the dynamics is again simulated for a time T. Once more, the species with the lowest concentration is replaced with a new randomly connected species, and so on. This way, the network, and its dynamic behavior, evolves over time.

Jain and Krishna (2002) performed experiments with this model with 100 species and a given value for the parameter p. They show how the network evolves over time, and forms connected “cores” of mutually catalytic species. Figure 4 shows one such network (represented as a catalysis graph) that appeared at time step 6070 during one of their evolution experiments (reprinted from Jain and Krishna (2002) Fig. 1i). White nodes indicate species that have a concentration of zero. Black nodes indicate the connected cores, and grey nodes the species with non-zero concentrations in the “periphery” of these cores. The existence of such cores can also be derived from a linear algebra analysis of the adjacency matrix A. For complete details, see Jain and Krishna (2002).

This model can also be formally described within the RAF framework:

$$\begin{array}{lclcl} X & = & \{f, i \;|\; i=1,\ldots,100\}\\ \mathcal{R} & = & \{f \rightarrow i \;|\; i=1,\ldots,100\}\\ C & = & \{(i,r) \;|\; i=1,\ldots,100, r \in \mathcal{R}\} \\ F & = & \{f\} \end{array} $$

where f is some generic food molecule (from which all other species are produced), and each model instance contains a random subset of C.

Applying the RAF algorithm to the network shown in Fig. 4 results in a RAF set of size 67, which corresponds exactly to the black and grey nodes in the figure. In other words, the molecular species with a non-zero concentration are exactly those that are part of the (maximal) RAF set. Furthermore, using an extension of the RAF algorithm, the irreducible RAF sets within this maximal RAF set can be found as well (Hordijk and Steel 2004). This results in two irrRAFs, one of size two and one of size five, which correspond exactly with the two cores (connected subsets of black nodes) in Fig. 4.

Note that in this model a generic food set F is implicitly assumed, from which all other molecular species i are produced. In practice, what this means is that the F-generated part in the definition of a RAF set is always (trivially) satisfied for any subset \(\mathcal {R}^{\prime }\) of reactions. In that case, loops, or more generally strongly connected components, in the catalysis graph correspond directly to RAF sets. However, in the more general case where reactions can also have reactants that are not food molecules, this correspondence breaks down, and merely looking for loops or strongly connected components in the catalysis graph of an arbitrary reaction network is not sufficient to identify autocatalytic sets (Hordijk et al. 2014a).

So, the Jain & Krishna model, and their corresponding definition of autocatalytic sets, is rather restrictive in terms of real chemistry. However, it does show interesting behavior in terms of network evolution, and it can be easily described and analyzed within the more general RAF framework. Using this more general framework, it is clear that RAF sets do indeed appear, and can be analyzed in more detail, in the evolved chemical reaction networks in this model.

Units of Selection

Vasas et al. (2012) performed novel experiments to explicitly test for evolvability of autocatalytic sets. They used a polymer model based on the original experiments of Farmer et al. (1986). In this model, molecules consist of polymers made up of two types of monomers, a and b. There are two types of reactions: ligation and cleavage. A ligation reaction combines two polymers into a longer one by simply concatenating them, e.g. aaa + bb →aaabb, while a cleavage reaction breaks a polymer into two smaller ones, e.g., ababab →ab + abab. There is a given (low) probability p that any polymer catalyzes any ligation-cleavage reaction.

The food set consists of a random subset of polymers up to length four, and there is a constant influx of food molecules, and also a constant outflux of all types of molecules. This way, the dynamics of a reaction network within a compartment is modeled, starting with only food molecules, and adding new possible ligation-cleavage reactions and catalysis events to the network as new molecular species are being produced through currently existing reactions. In addition, spontaneous (uncatalyzed) reactions between currently existing polymers can also happen at a low background rate. See Vasas et al. (2012) for a full description of the model.

Evolutionary experiments were then performed by randomly shuffling the current molecular concentrations at given time steps, and also by modeling a population of growing and dividing compartments. One of the main, and important, conclusions of this work is that autocatalytic sets can be evolvable when there are multiple autocatalytic subsets in the underlying reaction network that can (potentially) exist in different combinations within such compartments.

An example of this is shown in Fig. 5, which is reprinted from Vasas et al. (2012) Fig. 4. The reaction network below the blue line shows part of the original chemical network (after randomly selecting the food set and the initial catalysis assignments). The network above the blue line is the additional part that occurred after simulating the network dynamics for a certain number of time steps, and also allowing spontaneous reactions to create novel species.

Fig. 5
figure 5

An example reaction network resulting from the evolutionary model of Vasas et al. (2012)

Full size image

The dotted orange arrows indicate two so-called “viable loops”, sets of molecules (polymers) where each one catalyzes the production of the next one, in a closed loop. In that sense, they are similar to cores in the Jain & Krishna model. However, in addition, viable loops are also self-sustaining in the (non-trivial) sense that their molecular constituents can be built up from the food set by using only reactions that are catalyzed by molecules that are part of the self-sustaining subset of reactions. As the authors then argue, it is exactly these viable loops that could form the units of selection in a pre-template, metabolism-first origin of life scenario (Vasas et al. 2012).

Again, this model can also be formally described within the RAF framework:

$$\begin{array}{lclcl} X & = & \{\textbf{a}, \textbf{b}\}^{\ast} \\ \mathcal{R} & = & \{x_{i} + x_{j} \rightarrow x_{i} \cdot x_{j}, \; x_{i} \cdot x_{j} \rightarrow x_{i} + x_{j} \;|\; x_{i},x_{j} \in X\}\\ C & = & \{(x_{i},r) \;|\; x_{i} \in X, r \in \mathcal{R}\} \\ F & = & \{\textbf{a}, \textbf{b}\}^{\leq 4} \end{array} $$

where each model instance contains random subsets of F and C.

We have taken the reaction network of Fig. 5, which is provided in full detail (48 reactions in total) in the supplementary material of Vasas et al. (2012), and applied the RAF algorithm to it. Not surprisingly, this entire network forms a (maximal) RAF set, as only those polymers will be produced (in the dynamical simulations) that can be formed through a sequence of catalyzed reactions from the food set. More importantly, the viable loops can be easily detected as well.

First, construct the catalysis graph (and its corresponding adjacency matrix, as explained in the previous subsection) of the (maximal) RAF set. In this graph, the nodes represent the molecular species that are part of the RAF set, and there is a directed link from node j to node i if molecule type j catalyzes the production of molecule type i. Next, compute the strongly connected components in this catalysis graph. For the RAF set that is formed by the reaction network in Fig. 5, this results in two components, one of size two and one of size five, which correspond exactly to the two viable loops as indicated by the dotted orange arrows in the figure.

Note that a viable loop in itself is not necessarily a RAF set, as it generally needs other (catalyzed) reactions to build up its constituent molecules from the food set (as is the case in Fig. 5). However, a viable loop is what we have elsewhere termed a “pseudo RAF”, which may not be self-sustaining (Hordijk et al. 2015). Furthermore, as was mentioned in the previous subsection, looking for loops or strongly connected components in the catalysis graph of an arbitrary reaction network is generally not sufficient to identify RAF sets. However, computing the strongly connected components in the catalysis graph of an actual RAF set results in exactly the viable loops contained within it (viable loops, after all, must be part of a RAF set).

The approach of Vasas et al. (2012) seems to be to first identify the loops (or cores) in the catalysis graph of the entire reaction network, and then check for each of these loops whether it is also self-sustaining (i.e., viable). The RAF algorithm, on the other hand, efficiently checks for both of these requirements simultaneously. Furthermore, a RAF set explicitly includes those reactions that are necessary to build up the elements comprising its strongly connected components (i.e., viable loops), whereas in the Vasas et al. (2012) approach these have to be inferred separately. In fact, a viable loop together with the (minimal) set of reactions that make it self-sustaining (given a food set), forms an irreducible RAF, which provides more complete (and indispensable) information.

So, as in the previous examples, the current model can be captured and analyzed efficiently and more completely using RAF theory, which shows that RAF sets have indeed appeared during the evolutionary experiments. Moreover, following the conclusions of Vasas et al. (2012), the existence of multiple RAF (sub)sets (viable cores) in a reaction network is one of the necessary conditions for the possible evolvability of autocatalytic sets. Elsewhere we have shown that, in general, one can indeed expect large numbers of RAF subsets to exist in instances of the binary polymer model (Hordijk et al. 2015).

Multiple RAF Combinations

Wills and Henderson (2000) introduced a similar model consisting of binary polymers, using 0s and 1s as the basic building blocks. However, in this model only single monomers can be added to an already existing polymer, or bit string. More precisely, the set of reactions in this model consists of four categories: (\(\mathcal {R}_{1}\)) ligation of a 0 to a bit string (polymer) ending with a 0, (\(\mathcal {R}_{2}\)) ligation of a 1 to a 0, (\(\mathcal {R}_{3}\)) ligation of a 0 to a 1, and (\(\mathcal {R}_{4}\)) ligation of a 1 to a 1. Catalysts for these reactions are also assigned randomly, but in this model a chosen catalyst will catalyze all reactions in a given reaction category \(\mathcal {R}_{i}\) (rather than just one reaction). Finally, the food set consists of the monomers 0 and 1.

Hordijk and Steel (2014) studied a particular instance of this model in the context of the necessary conditions for evolvability of autocatalytic sets as derived in Vasas et al. (2012). This model instance was already fully described and analyzed using RAF theory in Hordijk and Steel (2014), so here we will only briefly review their main results, and simply include it as yet another computational model in which autocatalytic sets appear and (potentially) evolve.

The instance of the model is as follows:

$$\begin{array}{lclcl} X & = & \{0,1\}^{\leq 3} \\ \mathcal{R} & = & \mathcal{R}_{1} \cup \mathcal{R}_{2} \cup \mathcal{R}_{3} \cup \mathcal{R}_{4} \\ C & = & \{(000,r)|r \in \mathcal{R}_{1}\} \cup \{(010,r)|r \in \mathcal{R}_{2}\} \cup \{(101,r)|r \in \mathcal{R}_{3}\} \cup \{(111,r)|r \in \mathcal{R}_{4}\} \\ F & = & \{0,1\} \end{array} $$

It is then shown, using the RAF algorithm, that this model instance contains three different irreducible RAF sets (irrRAFs), and, through dynamical simulations, that these irrRAFs can emerge and exist in different combinations within a compartment (which satisfies one of the necessary conditions for evolvability of autocatalytic sets). Which particular combination of irrRAFs occurs within a compartment largely depends on random chemical events, given that all three irrRAFs need at least one of their reactions to happen spontaneously (uncatalyzed) before the full set can come into existence. This requirement for spontaneous reactions actually satisfies (part of) a second necessary condition for evolvability: a mechanism for the spontaneous, but rare, gain of new “viable loops”, in the terminology of Vasas et al. (2012).

So, this fourth model can also clearly be described and analyzed within the formal RAF framework, and dynamical simulations show that it satisfies some basic necessary conditions under which autocatalytic sets can be evolvable.

Conclusions and Discussion

We have reviewed four different computational models of chemical reaction networks and corresponding definitions of autocatalytic sets. We found that most definitions fall short, in one way or another, in fully capturing the concept of autocatalytic sets in its most general way, or in a way that is compatible with other models. In particular:

  • Hypercycles are too restrictive to capture the general notion of autocatalytic sets. Furthermore, they are difficult to realize, and do not seem to exist in real chemistry.

  • Cores (connected components) in the catalysis graph are restricted to models in which all elements are directly created from some (implicit) food source. In models where this is not the case, cores are not sufficient to identify true autocatalytic sets (i.e., they may not be self-sustaining).

  • Viable cores include this self-sustaining requirement, and are thus applicable in more general models. However, the reactions that provide the necessary self-sustainability (outside of the core itself) still have to be inferred separately.

On the other hand, we have shown here that these different definitions and models can all be captured and analyzed using RAF theory, which defines the concept of autocatalytic sets in a formal and complete way. Moreover, we have confirmed that in all of these computational models RAF sets do indeed appear and evolve, or at least have the potential to evolve, and that they can be detected and analyzed efficiently using the RAF algorithm. This shows both the versatility as well as the strength of the formal framework, suggesting its use as a standard tool for studying autocatalytic sets in chemical reaction networks.

One criticism one might have is that the computational models reviewed here are rather simplistic, in particular compared to real chemistry. However, as has been shown earlier, many of the main results from RAF theory hold up under a wide variety of chemically more-realistic model assumptions, such as template-based catalysis (Hordijk and Steel 2012), power-law distributed catalysis (Hordijk et al. 2014a), allowing only the longest polymers to be catalysts (Hordijk et al. 2014b), allowing a moderate level of inhibition (Hordijk et al. 2015), using a partitioned polymer model as in, e.g., nucleotides vs. amino acids (Smith et al. 2014), and even in non-polymer systems (Smith et al. 2014).

Perhaps more importantly, autocatalytic sets are not just mathematical or computational constructs. They have been shown to exist in various experimental chemical systems (Sievers and Von Kiedrowski 1994; Ashkenasy et al. 2004; Lincoln and Joyce 2009; Vaidya et al. 2012). In fact, one of these experimental systems, the RNA network of Vaidya et al. (2012), was formally analyzed using RAF theory (Hordijk and Steel 2013). This not only reproduced many of the experimental results, but also provided additional insights that would be hard to obtain from chemical experiments alone. Finally, it was recently shown, also using RAF theory, that the metabolic network of E. coli forms an autocatalytic set (Sousa et al. 2015), indeed a truly evolved one.

In conclusion, autocatalytic sets appear and are able to evolve in various computational models as well as in real chemical and biological reaction networks. Furthermore, this can be formally described and efficiently analyzed using RAF theory. We believe that the ubiquity of autocatalytic sets in all of these real and model systems, together with the availability of a standard and formal analysis tool, could have important implications for a possible metabolism-first origin of life scenario.