Improved Gegenbauer spectral tau algorithms for distributed-order time-fractional telegraph models in multi-dimensions

Abstract

The distributed-order fractional telegraph models are commonly used to describe the phenomenas of diffusion and wave-like anomalous, which can model processes without a power-law scale across the entire temporal domain. To increase the range of implementation of distributed-order fractional telegraph models, there is a need to present effective and accurate numerical algorithms to solve these models, as these models are hard to solve analytically. In this work, a novel matrix representation of the distributed-order fractional derivative based on shifted Gegenbauer (SG) polynomials has been derived. Also, two efficient algorithms based on the aforementioned operatonal matrix and the spectral tau method have been constructed for solving the one- and two-dimensional (1D and 2D) distributed-order time-fractional telegraph models with spatial variable coefficients. Also, a new operational matrix of the multiplication of space vectors has been built to have the ability in applying the tau method in the 2D case. The convergence and error bound analysis of the presented techniques are investigated. Moreover, the presented algorithms are applied on four miscellaneous test examples to illustrate the robustness and effectiveness of these algorithms.

1 Introduction

Single or multi-term fractional differential equations (FDEs) provided by space- and/or time-fractional derivatives have attracted a lot of attention due to there efficiency in modelling many real-world phenomena arising in several fields (see [1,2,3,4,5,6]). Finding analytical or exact solutions of FDEs is difficult to obtain, so several numerical methods are proposed for solving different kinds of FDEs based on the finite difference, B-linear spline, second-order Newton interpolations, spectral method and Bernstein polynomials (see [7,8,9,10,11]). The distributed-order FDEs are a generalisation of the aforementioned two classes of FDEs, in which the fractional derivative order is integrated within a specified range. Subsequently, the distribute-order aggregates the contributions of the model order over the physical domain. As a result, the solutions of the distributed-order FDEs are not mathematically so direct. One of the main reasons for the interest in distributed-order operator is the relationship of this operator to physical processes that lack temporal scaling. Accelerating superdiffusion, random processes subject to Wiener’s processes and decelerating subdiffusion are examples of processes that cannot be handled with fractional operator of specified order and must be modelled in terms of distributed operators [12,13,14].

The earliest results on the general solution for linear differential equations of distributed-order were published by Caputo [15]. The distributed-order time-fractional diffusion equation (DOTFDE) explains a sub-diffusion random mechanism subjugated with the Wiener’s process and has an exponent of decreasing diffusion over time [16]. Atanackovic et al. [17] modeled and analysed waves in a finite length viscoelastic rod by using restricted domain fractional diffusion-wave equations of distributed-order. They acquired stress and displacement in a stress relaxation test by prescribing boundary conditions on displacement. Eab et al. [18] presented the distributed-order Langevin-like equations of fractional order for characterising anomalous diffusion in the absence of scaling exponent or a unique diffusion and applied it for modelling some phenomena. Luchko [19] established the uniqueness of the generalised bounded domains DOTFDE and its continuous sensitivity on initial conditions. Meerschaert et al. [20] introduced stochastic analogues and explicit strong solutions for bounded domains DOTFDE. The fractional telegraph equation has significant for modelling wave-like anomalous and diffusive phenomena. In addition to describe the models of the blood flow under magnetic and vibration mode in a porous tube with thermochemical properties [21], enhancing denoising of image structure of elastic manifolds [22], bimolecular reactions in homogeneous media [23] and anomalous diffusion [24]. So it has many applications in various scientific fields. The single distributed-order time-fractional diffusion-wave equation (DOTFDWE) is generalised to the distributed-order time-fractional telegraph equation (DOTFTE) when the two distinct distributed-order differentiation on the intervals ]1,2] and ]0,1] are presented simultaneously. The DOTFTE can be associated with super/sub-diffusive processes for specific density function choices. Vieira et al. [25] presented the fundamental solution of the DOTFTE in the n-dimensional space by using Fox H-functions via a combination of the Mellin, Fourier and Laplace transforms. Also, the provided techniques are generalisation of approaches for DOTFDWE that have been employed by numerous authors (see [26, 27]).

The approximate solutions of distributed-order FDEs have a growing interest to study the behaviour of these equations while finding the exact analytical solutions of such equations are almost impossible [28,29,30]. In [31], Ye et al. presented a compact difference scheme for the DOTFDWE and proved the convergency and unconditional stability of the presented method. Abbaszadeh and Dehghan [32] developed a meshless method combined the alternative direction implicit procedure with the interpolating element-free Galerkin method for the DOTFDWE. Gao et al. [33] constructed two difference schemes for the 1D time-fractional wave equations of distributed-order where the time fractional derivatives approximated by using a weighted shifted Grünwald formula. Shi et al. [34] developed a completely discrete technique combined a finite element method on an unstructured mesh and the Crank–Nicolson procedure for the multi-term Riesz space and time fractional wave equation of distributed-order. Arianfar et al. [35] established the shifted Legendre collocation approach for the numerical solution of a class of nonlinear fractional boundary value problems of distributed-order with singularity in coefficients where the composite midpoint quadrature rule has been used to discretise the distributed-order time-fractional derivative.

The approximation methods based on spectral techniques and orthogonal functions have become a rigorous tool for solving various fractional dynamical systems [36, 37]. These nonlocal methods are efficient numerical schemes for discretising the nonlocal fractional differential operators [38, 39]. The main benefit of the spectral techniques is their ability to generate accurate approximate results with a few degrees of freedom. The orthogonal functions are often classified into three categories based on their structure: sine-cosine functions; piecewise orthogonal constant functions (block-pulse, hybrid, etc.); and orthogonal polynomials (Gegenbauer, Legendre, Laguerre, etc.). Using orthogonal polynomials as a basis function for the spectral methods gives preferable approximate results [40,41,42]. The main advantage of applying orthogonal functions is that they can be used to convert problems into systems of algebraic equations, substantially simplifying them. As far as we know, the spectral solutions for distributed-order FDEs are rarely discussed. Dehghan and Abbaszadeh [43] proposed the Legendre spectral element technique for simulating the neutral delay distributed-order fractional diffusion-wave equation with damping. Pourbabaee and Saadatmandi [44] presented a spectral method based on operational matrix of shifted Legendre for distributed-order time-FDEs and diffusion equations. Zaky and Machado [45] developed spectral schemes for discretising the multi-dimensional distributed-order time-fractional diffusion equations. Zhang et al. [46] presented a Crank–Nicolson alternating direction implicit (ADI) Galerkin–Legendre spectral technique for the 2D space-Riesz advection–diffusion equation of distributed-order. Zhang et al. [47] proposed a spectral scheme based on ADI Legendre–Laguerre for the 2D-DOTFDWE on a semi-infinite domain. Moreover, the definite integrals of the distributed-order fractional derivatives in aforementioned articles have been discretised by using Gauss quadrature formula or composite Simpson formula or composite trapezoid formula. The Gauss quadrature formula is more stable than the other mentioned formulas and has a higher computational accuracy of order (M⁻ⁿ), where M denotes the used polynomials number and n is a suitable constant.

In the current work, we consider the following 1D and 2D DOTFTE with spatial variable coefficients:

$$ \begin{array}{@{}rcl@{}} \mathcal{D}^{\rho(\eta)}_{t} u(\mathcal{X},t) &+&B_{1}(\mathcal{X}) \mathcal{D}^{\sigma(v)}_{t} u(\mathcal{X},t)+B_{2}(\mathcal{X}) u(\mathcal{X},t)=B(\mathcal{X}) {\Delta}_{\mathcal{X}} u(\mathcal{X},t)\\ &+&f(\mathcal{X},t), (\mathcal{X},t) \in {\Omega} \times {\Lambda}, \end{array} $$

(1.1)

with the initial conditions (ICs) and boundary conditions (BCs):

$$ \begin{array}{ccc} \left\{ \begin{array}{lr} u(\mathcal{X},0)=f_{0}(\mathcal{X}),& \frac{\partial u(\mathcal{X},t)} {\partial t}|_{t=0 }=f_{1}(\mathcal{X}), \mathcal{X} \in {\Omega},\\ u(\mathcal{X},t)|_{\partial {\Omega} }=g(\mathcal{X},t), t \in {\Lambda}, \end{array} \right. \end{array} $$

(1.2)

where $B(\mathcal {X}) {\Delta }_{\mathcal {X}} u(\mathcal {X},t)=B_{3}(x) \frac {\partial ^{2}u(x,t)} {\partial x^{2}}$ for the 1D case and $B(\mathcal {X}) {\Delta }_{\mathcal {X}} u(\mathcal {X},t)=B_{3}(x,y) \frac {\partial ^{2}u(x,y,t)} {\partial x^{2}}+B_{4}(x,y) \frac {\partial ^{2}u(x,y,t)} {\partial y^{2}}$ for the 2D case, Λ = (0,T] represents the time interval and the functions $f(\mathcal {X},t), f_{0}(\mathcal {X}), f_{1}(\mathcal {X})$ and $g(\mathcal {X},t)$ are smooth functions in their domains. $\mathcal {D}^{\rho (\eta )}_{t} u(\mathcal {X},t)$ and $\mathcal {D}^{\sigma (v)}_{t} u(\mathcal {X},t)$ denote the distributed-order time-fractional derivatives which are defined as follows:

$$ D^{\rho(\eta)}_{t} u(\mathcal{X},t)={{\int}_{1}^{2}} \rho(\eta) {\!}^{c}_{0}D^{\eta}_{t} u(\mathcal{X},t) d\eta, D^{\sigma(v)}_{t} u(\mathcal{X},t)={{\int}_{0}^{1}} \sigma(v) {\!}^{c}_{0}{D^{v}_{t}} u(\mathcal{X},t) dv, $$

(1.3)

where the density functions ρ(η) and σ(v) are non-negative functions and satisfy

$$0 < {{\int}_{1}^{2}} \rho(\eta) d\eta < \infty, 0 < {{\int}_{0}^{1}} \sigma(v) dv < \infty,$$

The time-fractional derivatives included in (1.3) are in Caputo sense, which is defined for order 𝜃 by:

$$ \begin{array}{ccc} {\!}^{c}_{0}D^{\theta}_{t} u(\mathcal{X},t) = \left\{ \begin{array}{lr} \frac{1}{\Gamma (n-\theta) }{{\int}_{0}^{t}} (t-\zeta)^{n-\theta-1} \frac{d^{n}}{d\zeta^{n}}u(\mathcal{X},\zeta) d\zeta & n-1< \theta< n, t>0, \\ \frac{\partial^{n}u(\mathcal{X},t)} {\partial t^{n}} & \theta=n. \end{array} \right. \end{array} $$

(1.4)

It is worth to point out that if $B_{2}(\mathcal {X})=0$ and the density function σ(v) = δ(v − 1), where δ(v − 1) is the Dirac delta function, then (1.1) reduces to the distributed-order time-fractional diffusion-wave equation with damping (DOTFDWED). If $B_{1}(\mathcal {X})=B_{2}(\mathcal {X})=0$, then (1.1) reduces to the DOTFDWE. In this paper, we present two efficient spectral algorithms for solving 1D and 2D distributed-order time-fractional telegraph models. We construct a novel SG operational matrix for approximating the fractional derivatives of distributed-order included in these models. Also, a new operational matrix of the multiplication of space vectors has been built to have the ability for completely applying the tau method in the 2D case. The presented spectral algorithms convert the given problem into an algebraic equations system, which is easy to solve. Also, we discuss the convergence and error bound analysis of the presented methods. Some numerical applications are presented to demonstrate the the effectiveness of the presented method.

The paper is arranged as follows: Section 2 introduces mathematical preliminaries of SG polynomials and its using for function approximation. In Section 3, the operational matrix of distributed-order fractional differentiation of the SG polynomials is derived. Section 4 develops two spectral algorithms for solving the 1D and 2D distributed-order models (4.1), (4.2) and (4.13), (4.14). In Section 5, the convergence and error bound analysis of the presented techniques are demonstrated. In Section 6, miscellaneous test examples on the multi-dimensional model (1.1), (1.2) are presented. Section 7 ends the paper with a conclusion.

2 Preliminaries

2.1 SG polynomials

Gegenbauer polynomials $C^{(\alpha )}_{k}(t)$ with degree $k\in \mathbb {Z}^{+}$ and parameter $\alpha >-\frac {1}{2}$ arises as the eigensolution on the interval [− 1,1] for the following singular Sturm–Liouville problem

$$\frac{d}{dt}(1-t^{2})^{\alpha +\frac{1}{2}}\frac{d C^{(\alpha)}_{k}(t)}{dt}+k(k+2 \alpha) (1-t^{2})^{\alpha -\frac{1}{2}} C^{(\alpha)}_{k}(t)=0,$$

and can be generated from the following Rodrigues’ formula

$$ C^{(\alpha)}_{k}(t)=\frac{(-1)^{k} {\Gamma}(k+2 \alpha) {\Gamma}(\alpha +\frac{1}{2})}{2^{k} k! {\Gamma}(k+\alpha+\frac{1}{2}) {\Gamma}(2 \alpha)} (1-t^{2})^{\frac{1}{2}-\alpha} \frac{d^{k}}{dx^{k}} (1-t^{2})^{k+\alpha-\frac{1}{2}}.$$

The Gegenbauer polynomials are standardised in [48] such that $C^{(\alpha )}_{k}(1)=1$ for all non-negative integer k. Moreover, the following recurrence relation defines the standardised Gegenbauer polynomials :

$$ C^{(\alpha)}_{0}(t)=1,C^{(\alpha)}_{1}(t)=t , C^{(\alpha)}_{k+1}(t)=2\frac{k+\alpha}{k+2 \alpha} t C^{(\alpha)}_{k}(t)-\frac{k}{k+2 \alpha}C^{(\alpha)}_{k-1}(t), k> 0, $$

(2.1)

the Gegenbauer polynomials are complete $L_{\omega ^{\alpha }}^{2}[-1,1]$ orthogonal system such that

$$ \langle C^{(\alpha)}_{i}(t) , C^{(\alpha)}_{j}(t) \rangle_{\omega^{\alpha}}={\int}_{-1}^{1} C^{(\alpha)}_{i}(t) C^{(\alpha)}_{j}(t) \omega^{\alpha}(t) dt =h^{(\alpha)}_{i} \delta_{i,j}, $$

(2.2)

where $\omega ^{\alpha }(t) =(1-t^{2})^{\alpha -\frac {1}{2}}$ is the weight function and $h^{(\alpha )}_{i} =\frac {2^{2\alpha -1} i! ({\Gamma }(\alpha +\frac {1}{2}))^{2}}{(i+\alpha ) {\Gamma }(i+2\alpha )}$.

To apply Gegenbauer polynomials on the interval [0,T], the SG polynomials $C^{(\alpha )}_{T,k}(t)$ are defined such that: $C^{(\alpha )}_{T,k}(t)=C^{(\alpha )}_{k}(\frac {2t}{T}-1)$. The SG polynomials are complete $L_{\omega _{T}^{\alpha }}^{2}[0,T]$ orthogonal system such that

$$ \langle C^{(\alpha)}_{T,r}(t) , C^{(\alpha)}_{T,s}(t) \rangle_{\omega^{\alpha}_{T}(t)}={{\int}_{0}^{T}} C^{(\alpha)}_{T,r}(t) C^{(\alpha)}_{T,s}(t) \omega^{\alpha}_{T}(t) dt =J^{(r+1,s+1)}_{\tau}=h^{(\alpha)}_{T,r} \delta_{r,s}, $$

(2.3)

where $\omega ^{\alpha }_{T}(t)=(Tt-t^{2})^{\alpha -\frac {1}{2}}$ and $h^{(\alpha )}_{T,i}=(\frac {T}{2})^{2\alpha } h^{(\alpha )}_{i}$. The SG analytic form is defined by

$$ C^{(\alpha)}_{T,r}(t)=\sum\limits_{k=0}^{r} {\Upsilon}_{r,k} t^{k}, 0<t< T, $$

(2.4)

where

$${\Upsilon}_{r,k}=(-1)^{r-k}\frac{r! {\Gamma}(\alpha +\frac{1}{2}) {\Gamma}(r+k+2\alpha)}{\Gamma(k+\alpha +\frac{1}{2}) {\Gamma}(r+2\alpha) (r-k)! k!T^{k}}.$$

The Caputo fractional derivative of the SG polynomials has the following form [37]

$$ \begin{array}{ccc} D^{\eta}C^{(\alpha)}_{T,r}(t) = \left\{ \begin{array}{lr} {\sum}_{k=\lceil{\eta}\rceil}^{r} {\Upsilon}_{r,k} \frac{\Gamma(k +1)}{\Gamma(k+1-\eta)} t^{k-\eta} & k \ge \lceil{\eta}\rceil,\\ 0 & k < \lceil{\eta}\rceil. \end{array} \right. \end{array} $$

(2.5)

2.2 Functions approximation and fractional derivative operational matrix

∙ The SG polynomials can be used to approximate a function u(t) as follows:

$$ u_{N}(t) \simeq \sum\limits_{k=0}^{N} a_{k} C^{(\alpha)}_{T,k}(t) = \textbf{A}^{\intercal}\phi_{T,N}(t), $$

(2.6)

where $\intercal$ denotes the transpose, the SG expansion coefficients a_k can be calculated from

$$ a_{k} =\frac{1}{ h^{(\alpha)}_{T,k}}\langle u(t) , C^{(\alpha)}_{T,k}(t) \rangle_{\omega^{\alpha}_{T}(t)}=\frac{1}{ h^{(\alpha)}_{T,k}} {{\int}_{0}^{T}} u(t) C^{(\alpha)}_{T,k}(t) \omega^{(\alpha)}_{T}(t) dt, k=0,1,....,N, $$

(2.7)

and

$$ \textbf{A}^{\intercal} \equiv [a_{0},a_{1},.....,a_{N}], \phi_{T,N}(t) \equiv [C^{(\alpha)}_{T,0}(t),C^{(\alpha)}_{T,1}(t),.....,C^{(\alpha)}_{T,N}(t)]^{\intercal}. $$

(2.8)

• The SG polynomials can be used to approximate a function u(x,t) as follows:

  $$ u_{N,M}(x,t)\simeq\sum\limits_{k=0}^{M} \sum\limits_{r=0}^{N}a_{k,r}C^{(\alpha)}_{T,k}(t) C^{(\alpha)}_{L,r}(x)\simeq\phi_{T,M}^{\intercal}(t)\textbf{A}\phi_{L,N}(x), $$

  (2.9)

  here A is an unknown matrix whose entries a_k,r can be calculated from

  $$ \begin{array}{@{}rcl@{}} a_{k,r}&=&\frac{1}{h_{T,k}^{(\alpha)} h_{L,r}^{(\alpha)}} {{\int}_{0}^{T}}{{\int}_{0}^{L}} u(x,t) C^{(\alpha)}_{T,k}(t) C^{(\alpha)}_{L,r}(x) \omega^{(\alpha)}_{T}(t) \omega^{(\alpha)}_{L}(x) dxdt,\\ k&=&0,1,...,M , r=0,1,...,N. \end{array} $$

  (2.10)

• The Kronecker product of a matrix Y of order (p × r) and a matrix Z of order (q × s) is a matrix of order (pq × rs) which has the following block form

  $$ Y \otimes Z=\left( \begin{array}{ccccc} y_{11}Z &y_{12}Z & {\dots} & y_{1r}Z \\ y_{21}Z & y_{22}Z & {\dots} & y_{2r}Z \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ y_{p1}Z & y_{p2}Z & {\dots} & y_{pr}Z \end{array} \right),$$

  where the symbol ⊗ is the Kronecker tensor product. Also, the Kronecker product satisfies the following properties for the matrices W,X,Y and Z

  $$ WX \otimes YZ=(W \otimes Y)(X \otimes Z). $$

  (2.11)

  Accordingly, the function $u(x,y,t)\in {\mathscr{L}}^{2}_{\omega ^{\alpha }}({\Omega } \times {\Lambda })$ can be written with the following structure:

  $$ \begin{array}{@{}rcl@{}} u_{N,P,M}(x,y,t)&=&\sum\limits_{i=0}^{N} \sum\limits_{j=0}^{P} \sum\limits_{k=0}^{M}a_{i,j,k} C^{(\alpha)}_{L,i}(x) C^{(\alpha)}_{l,j}(y) C^{(\alpha)}_{T,k}(t)\\ &=&\phi_{T,M}^{\intercal}(t) \textbf{A} (\phi_{L,N}(x)\otimes\phi_{L,P}(y)), \end{array} $$

  (2.12)

  where the coefficients matrix A is written in the block form as follows:

  $$ \begin{array}{@{}rcl@{}} \textbf{A}&=&[A_{0},A_{1},...,A_{N}], A_{j}=[A_{i,0},A_{i,1},...,A_{i,P}],\\ A_{i,j}&=&[a_{i,j,0},a_{i,j,1},...,a_{i,j,M}]^{\intercal}, \end{array} $$

  (2.13)

  and the coefficients a_i,j,k are calculated by

  $$ \begin{array}{@{}rcl@{}} a_{i,j,k}&=&\frac{1}{h_{T,k}^{(\alpha)} h_{L,i}^{(\alpha)} h_{l,j}^{(\alpha)} } {{\int}_{0}^{l}} {{\int}_{0}^{L}} {{\int}_{0}^{T}} u(x,y,t) C^{(\alpha)}_{T,k}(t) C^{(\alpha)}_{L,i}(x) C^{(\alpha)}_{l,j}(y) \omega^{(\alpha)}_{T}(t) \omega^{(\alpha)}_{L}\\ &&\times (x) \omega^{(\alpha)}_{l}(y) dtdxdy, \end{array} $$

  (2.14)
  $$i=0,1,...,M , j=0,1,...,N, k=0,1,...,p.$$

The following theorem gives the matrix representation of the fractional/integer order derivatives for the SG vector ϕ_T,M(t).

Theorem 2.1 (See 49)

Let ϕ_T,M(t) be given as in (2.8), then the fractional/integer derivative of order (η > 0) in Caputo sense can be expressed as follows:

$$ {\!}^{c}_{0}\mathcal{D}^{\eta}_{t} \phi_{T,M}(t) \simeq \textbf{D}_{T}^{(\eta)}\phi_{T,M}(t), $$

(2.15)

where $\textbf {D}_{T}^{(\eta )}$ is an (N + 1) square matrix defined by

$$ \begin{array}{ccc} \textbf{D}_{T}^{(\eta)} = \left\{ \begin{array}{lr} {\Theta}(k,j,\alpha,\eta) & k \ge \lceil{\eta}\rceil,\\ 0 & k < \lceil{\eta}\rceil, \end{array} \right. \end{array} $$

(2.16)

and

$$ \begin{array}{@{}rcl@{}} {\Theta}(k,j,\alpha,\eta) &=&\sum\limits_{r=\lceil{\eta}\rceil}^{k} {\Upsilon}_{r,k} \frac{r! \tau^{r}}{\Gamma(r+1-\eta)} \sum\limits_{s=0}^{j}\\ &&\times {\Upsilon}_{s,j} \frac{2(j+\alpha) {\Gamma}(j + 2\alpha) {\Gamma}(s+r - \eta+\alpha+\frac{1}{2}) T^{s-\eta}}{ j! {\Gamma}(\alpha + \frac{1}{2}) {\Gamma}(s+r-\eta+2\alpha+1)} . \end{array} $$

(2.17)

3 SG operational matrix of the distributed-order fractional derivative

Assume that $\left \lbrace v^{\beta }_{k}\right \rbrace _{k=0}^{n}$ are the zeroes of $C^{(\beta )}_{n+1}(v)$ and $\left \lbrace \omega ^{\beta }_{k}\right \rbrace _{k=0}^{n}$ are its Christoffel numbers on the interval [− 1,1]. Let $\left \lbrace \tilde {v}^{\beta }_{k}\right \rbrace _{k=0}^{n}$ be the zeroes of SG polynomial $C^{(\beta )}_{\tau ,n+1}(v)$. The integration of a function g(v) on the interval [a,b] can be approximated by (n + 1) −point Gegenbauer–Gauss quadrature rule with β = 0.5 which is equivalent to the Legender Gauss quadrature, as follows:

$$ {{\int}_{a}^{b}} g(v) dv = \frac{b-a}{\tau} {\int}_{0}^{\tau} g(\frac{b-a}{\tau}v+a) dv= \sum\limits_{k=0}^{n} \tilde{\mathcal{W}}^{\beta}_{\tau,k} g(\tilde{\mathcal{T}}^{\beta}_{\tau,k}), $$

(3.1)

where

$$ \tilde{\mathcal{T}}^{\beta}_{\tau,k}=\frac{b-a}{\tau} \tilde{v}^{\beta}_{k}+a , \tilde{\mathcal{W}}^{\beta}_{\tau,k}=\left( \frac{b-a}{\tau}\right) \left( \frac{\tau}{2} \right)^{2 \beta} \omega^{\beta}_{k} , (\omega^{\beta}_{k})^{-1}=\sum\limits_{j=0}^{n} (h_{j}^{\beta})^{-1} (C^{(\beta)}_{j}(v^{\beta}_{k}))^{2}, $$

(3.2)

$\tilde {\mathcal {T}}^{\beta }_{\tau ,k}$ and $\tilde {\mathcal {W}}^{\beta }_{\tau ,k}$ for k = 0,1,...,n; are the SG–Gauss nodes and the weights on the interval [0,τ], respectively.

Lemma 3.1

Let $\tilde {\mathcal {T}}^{\beta }_{\tau ,r}$ and $\tilde {\mathcal {W}}^{\beta }_{\tau ,r}$ be the SG–Gauss quadrature nodes and weights given in (3.2) respectively. then the distributed-order fractional derivative of the SG polynomial satisfies the following relation:

$$ \begin{array}{ccc} D^{\rho(v)}_{t}C^{(\beta)}_{T,i}(t)= \left\{ \begin{array}{lr} {\sum}_{k=\lceil{\tau}\rceil}^{i} {\sum}_{r=0}^{n} \psi_{kr}^{i} t^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}} & i \ge \lceil{\tau}\rceil,\\ 0 & i < \lceil{\tau}\rceil, \end{array} \right. \end{array} $$

(3.3)

where

$$ \psi_{kr}^{i}=\frac{\tilde{\mathcal{W}}^{\beta}_{\tau,r} \rho(\tilde{\mathcal{T}}^{\beta}_{\tau,r}) {\Upsilon}_{i,k} {\Gamma}(k+1)}{\Gamma(k+1-\tilde{\mathcal{T}}^{\beta}_{\tau,r})}. $$

(3.4)

Proof

Applying the SG–Gauss quadrature rule (3.1), (3.2) for (2.5), we get

$$ \begin{aligned} D^{\rho(v)}_{t}C^{(\beta)}_{T,i}(t)&={{\int}_{a}^{b}} \rho(v) {D^{v}_{t}}C^{(\beta)}_{T,k}(t) dv =\sum\limits_{r=0}^{n} \tilde{\mathcal{W}}^{\beta}_{\tau,r} \rho(\tilde{\mathcal{T}}^{\beta}_{\tau,r}) D^{\tilde{\mathcal{T}}^{\beta}_{\tau,r}}_{t}C^{(\beta)}_{T,k}(t)\\ &=\sum\limits_{r=0}^{n} \tilde{\mathcal{W}}^{\beta}_{\tau,r} \rho(\tilde{\mathcal{T}}^{\beta}_{\tau,r}) \sum\limits_{k=\lceil{\tau}\rceil}^{i} {\Upsilon}_{i,k} D^{\tilde{\mathcal{T}}^{\beta}_{\tau,r}}_{t} t^{k}\\ &=\sum\limits_{k=\lceil{\tau}\rceil}^{i} \sum\limits_{r=0}^{n} \frac{\tilde{\mathcal{W}}^{\beta}_{\tau,r} \rho(\tilde{\mathcal{T}}^{\beta}_{\tau,r}) {\Upsilon}_{i,k} {\Gamma}(k+1)}{\Gamma(k+1-\tilde{\mathcal{T}}^{\beta}_{\tau,r})} t^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}}, i=\lceil{\tau}\rceil,...,M, \end{aligned} $$

and

$$D^{\rho(v)}_{t}C^{(\beta)}_{T,i}(t)=0, i=0,1,...,\lceil{\tau}\rceil-1.$$

□

Theorem 3.1

According to the assumptions of Lemma 3.1. The distributed-order fractional derivative of ϕ_T,M(t) is given from

$$ \mathcal{D}^{\rho(v)}_{t} \phi_{T,M}(t) \simeq \textbf{D}^{\rho(v)}_{(a,b)}\phi_{T,M}(t), $$

(3.5)

where $\textbf {D}^{\rho (v)}_{(a,b)}$ is the (M + 1) square SG matrix representation of the distributed-order fractional derivative which has the following form

$$ \textbf{D}^{\rho(v)}_{(a,b)}=\left( \begin{array}{ccccc} 0 & 0 & {\dots} & 0 \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ 0 & 0 & {\dots} & 0 \\ {\Theta}(\lceil{\tau}\rceil,0) & {\Theta}(\lceil{\tau}\rceil,1) & {\dots} & {\Theta}(\lceil{\tau}\rceil,M) \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\Theta}(M,0) & {\Theta}(M,1) & {\dots} & {\Theta}(M,M) \end{array} \right), $$

(3.6)

where

$$ \begin{array}{@{}rcl@{}} {\Theta}(i,j) & = & \frac{2(j+2\beta) {\Gamma}(j+2\beta)}{j! {\Gamma}(\beta +\frac{1}{2})}\sum\limits_{k=\lceil{\tau}\rceil}^{i} \sum\limits_{r=0}^{n}\sum\limits_{p=0}^{j}\\ && \!\times\! \frac{ {\Upsilon}_{i,k} {\Upsilon}_{j,p} T^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p} {\Gamma}(k + 1) {\Gamma}(k - \!\tilde{\mathcal{T}}^{\beta}_{\tau,r}\! + \!p + \beta + \!\frac{1}{2}) \tilde{\mathcal{W}}^{\beta}_{\tau,r} \rho(\tilde{\mathcal{T}}^{\beta}_{\tau,r})}{\Gamma(k + 1 - \tilde{\mathcal{T}}^{\beta}_{\tau,r}) {\Gamma}(k-\tilde{\mathcal{T}}^{\beta}_{\tau,r} + p + 2\beta +1)}. ~~~~~ \end{array} $$

(3.7)

Proof

From Lemma 3.1, we have

$$D^{\rho(v)}_{t}C^{(\beta)}_{T,i}(t)= \sum\limits_{k=\lceil{\tau}\rceil}^{i} \sum\limits_{r=0}^{n} \psi_{kr}^{i} t^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}}, i=\lceil{\tau}\rceil,...,M.$$

By approximating $t^{k-\tilde {\mathcal {T}}^{\beta }_{\tau ,r}}$ as in (2.6)

$$ t^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}} =\sum\limits_{j=0}^{M} a_{j}^{kr} C^{(\beta)}_{T,j}(t). $$

(3.8)

In virtue of (2.6), using the analytic form of SG polynomials (2.4), we get

$$ \begin{aligned} a_{j}^{kr}&=\frac{1}{h_{T,j}^{\beta}} {{\int}_{0}^{T}} t^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}} C^{(\beta)}_{T,j}(t) \omega^{\beta}_{T}(t) dt\\ &=\frac{1}{h_{T,j}^{\beta}} \sum\limits_{p=0}^{j} {\Upsilon}_{j,p} {{\int}_{0}^{T}} t^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}} t^{p} t^{\beta -\frac{1}{2}} (T-t)^{\beta -\frac{1}{2}} dt\\ &=\frac{1}{h_{T,j}^{\beta}} \sum\limits_{p=0}^{j} {\Upsilon}_{j,p} {{\int}_{0}^{T}} t^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p+\beta -\frac{1}{2}} (T-t)^{\beta -\frac{1}{2}} dt, \end{aligned} $$

by making change of the variable $t \rightarrow Tt$, we get

$$ \begin{aligned} a_{j}^{kr}&=\frac{1}{h_{T,j}^{\beta}} \sum\limits_{p=0}^{j} {\Upsilon}_{j,p} T^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p+2\beta} {{\int}_{0}^{1}} t^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p+\beta -\frac{1}{2}} (1-t)^{\beta -\frac{1}{2}} dt\\ &=\frac{\Gamma(\beta +\frac{1}{2})}{h_{T,j}^{\beta}} \sum\limits_{p=0}^{j} \frac{{\Upsilon}_{j,p} T^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p+2\beta} {\Gamma}(k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p+\beta +\frac{1}{2}) }{\Gamma(k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p+2\beta +1)}\\ &=\frac{2(j+2\beta) {\Gamma}(j+2\beta)}{j! {\Gamma}(\beta +\frac{1}{2})} \sum\limits_{p=0}^{j} \frac{{\Upsilon}_{j,p} T^{k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p} {\Gamma}(k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p+\beta +\frac{1}{2}) }{\Gamma(k-\tilde{\mathcal{T}}^{\beta}_{\tau,r}+p+2\beta +1)}. \end{aligned} $$

(3.9)

Now, (3.3), (3.8) and (3.9), yielding

$$ \begin{aligned} D^{\rho(v)}_{t}C^{(\beta)}_{T,i}(t)&= \sum\limits_{k=\lceil{\tau}\rceil}^{i} \sum\limits_{r=0}^{n} \sum\limits_{j=0}^{M} \psi_{kr}^{i} a_{j}^{kr} C^{(\beta)}_{T,j}(t) \\ &=\sum\limits_{j=0}^{M} \left( \sum\limits_{k=\lceil{\tau}\rceil}^{i} \sum\limits_{r=0}^{n} \psi_{kr}^{i} a_{j}^{kr} \right) C^{(\beta)}_{T,j}(t)\\ &=\sum\limits_{j=0}^{M} {\Theta}(i,j) C^{(\beta)}_{T,j}(t), i=\lceil{\tau}\rceil,...,M, \end{aligned} $$

(3.10)

where ${\Theta }(i,j)={\sum }_{k=\lceil {\tau }\rceil }^{i} {\sum }_{r=0}^{n} \psi _{kr}^{i} a_{j}^{kr}$ is given by (3.7). □

4 The proposed methodologies

In this section, the procedures solution of the presented strategies for solving the multi-dimensional DOTFTE models are discussed in details.

4.1 1D-case

Consider the following 1D DOTFTE:

$$ \mathcal{D}^{\rho(\eta)}_{t} u(x,t) +B_{1}(x)\mathcal{D}^{\sigma(v)}_{t} u(x,t)+B_{2}(x) u(x,t) =B_{3}(x) \frac{\partial^{2}u(x,t)} {\partial x^{2}}+f(x,t), $$

(4.1)

with the ICs and BCs:

$$ \begin{array}{cccc} \left\{ \begin{array}{lr} u(x,0)=f_{0}(x), \frac{\partial u(x,t)} {\partial t}|_{t=0 }=f_{1}(x),\\ u(0,t)=g_{0}(t), u(L,t)=g_{1}(t). \end{array} \right. \end{array} $$

(4.2)

We begin the approach by approximate the known functions B_i(x) for i = 1,2,3 and f(x,t),f_j(x),g_j(t) for j = 0,1 as follows:

$$ \begin{array}{ccccccc} \left\{ \begin{array}{lr} B_{1,N}(x)\simeq \textbf{B}_{1}^{\intercal} \phi_{L,N}(x), B_{2,N}(x)\simeq \textbf{B}_{2}^{\intercal} \phi_{L,N}(x), B_{3,N}(x)\simeq \textbf{B}_{3}^{\intercal} \phi_{L,N}(x),\\ f_{N,M}(x,t)\simeq\phi_{T,M}^{\intercal}(t)\textbf{F}\phi_{L,N}(x),\\ f_{0,N,M}(x)\simeq\phi_{T,M}^{\intercal}(0)\textbf{F}_{0}\phi_{L,N}(x), f_{1,N,M}(x)\simeq\phi_{T,M}^{\intercal}(0)\textbf{F}_{1}\phi_{L,N}(x),\\ g_{0,N,M}(t)\simeq\phi_{T,M}^{\intercal}(t)\textbf{G}_{0}\phi_{L,N}(0), g_{1,N,M}(t)\simeq\phi_{T,M}^{\intercal}(t)\textbf{G}_{1}\phi_{L,N}(L), \end{array} \right. \end{array} $$

(4.3)

where B₁,B₂ and B₃ are (N + 1) column matrices whose entries can be calculated similarly as (2.7). Also, F,F₀,F₁,G₀,and G₁ are (M + 1) × (N + 1) known matrices whose entries f_k,r,f_0,k,r,f_1,k,r,g_0,k,r,and g_1,k,r can be calculated similarly as (2.10).

According to [49], consider that $\phi _{L,N}^{\intercal }(x) \textbf {B}$ is the vector form approximation of the smooth and continuous function B(x) with $\textbf {B}=[b_{0},b_{1},...,b_{N}]^{\intercal }$, then the following relation holds:

$$ \phi_{L,N}(x) \phi_{L,N}^{\intercal}(x) \textbf{B}=\textbf{W}^{\intercal} \phi_{L,N}(x), $$

(4.4)

where W is an (N + 1) square matrix defined as follows:

$$ \textbf{W}=\Bigg [\frac{1}{h^{(\alpha)}_{L,i}}\sum\limits_{k=0}^{N} b_{k} {{\int}_{0}^{L}} C^{(\alpha)}_{L,i}(x) C^{(\alpha)}_{L,j}(x) C^{(\alpha)}_{L,k}(x) w^{\alpha}_{L}(x) dx\Bigg]_{i,j=0}^{N}. $$

(4.5)

Now, by employing (2.9), (2.15), (3.5) and (4.4), the following approximations are attained

$$ {{\int}_{1}^{2}} \rho(\eta) \frac{\partial^{\eta}u(x,t)} {\partial t^{\eta}} d\eta = \phi_{T,M}^{\intercal}(t) (\textbf{D}^{\rho(\eta)}_{(1,2)})^{\intercal} \textbf{A} \phi_{L,N}(x), $$

(4.6)

$$ \begin{aligned} B_{1}(x){{\int}_{0}^{1}} \sigma(v) \frac{\partial^{v}u(x,t)} {\partial t^{v}} dv &=\left( \textbf{B}_{1}^{\intercal} \phi_{L,N}(x) \right) \left( \phi_{T,M}^{\intercal}(t) (\textbf{D}^{\sigma(v)}_{(0,1)})^{\intercal} \textbf{A} \phi_{L,N}(x) \right)\\ &= \phi_{T,M}^{\intercal}(t) (\textbf{D}^{\sigma(v)}_{(0,1)})^{\intercal} \textbf{A} \phi_{L,N}(x) \phi^{\intercal}_{L,N}(x) \textbf{B}_{1}\\ &= \phi_{T,M}^{\intercal}(t) (\textbf{D}^{\sigma(v)}_{(0,1)})^{\intercal} \textbf{A} \textbf{W}_{1}\phi_{L,N}(x), \end{aligned} $$

(4.7)

$$ \begin{aligned} B_{2}(x) u(x,t) &=\left( \textbf{B}_{2}^{\intercal} \phi_{L,N}(x) \right) \left( \phi_{T,M}^{\intercal}(t) \textbf{A} \phi_{L,N}(x) \right) = \phi_{T,M}^{\intercal}(t) \textbf{A} \phi_{L,N}(x) \phi^{\intercal}_{L,N}(x) \textbf{B}_{2}\\ &= \phi_{T,M}^{\intercal}(t) \textbf{A} \textbf{W}_{2}\phi_{L,N}(x), \end{aligned} $$

(4.8)

$$ \begin{aligned} B_{3}(x) \frac{\partial^{2}u(x,t)} {\partial x^{2}} &=\left( \textbf{B}_{3}^{\intercal} \phi_{L,N}(x) \right) \left( \phi_{T,M}^{\intercal}(t) \textbf{A} \textbf{D}^{2}_{L} \phi_{L,N}(x) \right)\\ &= \phi_{T,M}^{\intercal}(t) \textbf{A} \textbf{D}^{2}_{L} \phi_{L,N}(x) \phi^{\intercal}_{L,N}(x) \textbf{B}_{3}\\ &= \phi_{T,M}^{\intercal}(t) \textbf{A} \textbf{D}^{2}_{L} \textbf{W}_{3}\phi_{L,N}(x). \end{aligned} $$

(4.9)

Substituting (4.3), (4.6), (4.7), (4.8) and (4.9) into (4.1), we get

$$ \phi_{T,M}^{\intercal}(t) \left( (\textbf{D}^{\rho(\eta)}_{(1,2)})^{\intercal} \textbf{A} +(\textbf{D}^{\sigma(v)}_{(0,1)})^{\intercal} \textbf{A} \textbf{W}_{1}+ \textbf{A} \textbf{W}_{2}- \textbf{A} \textbf{D}^{2}_{L} \textbf{W}_{3}-\textbf{F} \right)\phi_{L,N}(x)=0, $$

(4.10)

by applying the orthogonality relation (2.3) and by using the typical tau method, we can extract an (N − 1) × (M − 1) system of linear algebraic equations in terms of unknown coefficients as follows:

$$ J^{(M-1,M+1)}_{\tau} \left( (\textbf{D}^{\rho(\eta)}_{(1,2)})^{\intercal} \textbf{A} + (\textbf{D}^{\sigma(v)}_{(0,1)})^{\intercal} \textbf{A} \textbf{W}_{1} + \textbf{A} \textbf{W}_{2} - \textbf{A} \textbf{D}^{2}_{L} \textbf{W}_{3}-\textbf{F} \right)J^{(N+1,N-1)}_{L}=0. $$

(4.11)

The 2(M + N) remainder of linear algebraic equations are extracted from ICs and BCs (4.2) as follows:

$$ \begin{aligned} \phi_{T,M}^{\intercal}(0) \Big(\textbf{A}&-\textbf{F}_{0} \Big) J^{(N+1,N-1)}_{L} = 0 ,\\ \phi_{T,M}^{\intercal}(0)\Big((\textbf{D}&_{\tau}^{(1)})^{\intercal} \textbf{A}-\textbf{F}_{1} \Big) J^{(N+1,N-1)}_{L} = 0 ,\\ J^{(M+1,M+1)}_{\tau}&\Big(\textbf{A}-\textbf{G}_{0} \Big) \phi_{L,N}(0) = 0 ,\\ J^{(M+1,M+1)}_{\tau}&\Big(\textbf{A}-\textbf{G}_{1} \Big) \phi_{L,N}(L)= 0. \end{aligned} $$

(4.12)

By solving the algebraic system of (4.11) and (4.12), the unknown coefficients are computed and hence the approximate solution is determined. The main steps of the suggested methodology for solving the 1D DOTFTE are implemented in the following algorithm.

Algorithm 1

1D- DOTFTE.

4.2 2D-case

Consider the following 2D DOTFTE:

$$ \mathcal{D}^{\rho(\eta)}_{t} U +B_{1}(x,y)\mathcal{D}^{\sigma(v)}_{t} U+B_{2}(x,y) U =B_{3}(x,y) \frac{\partial^{2}U} {\partial x^{2}} +B_{4}(x,y) \frac{\partial^{2}U} {\partial y^{2}}+f(x,y,t), $$

(4.13)

where U = u(x,y,t), subject to the ICs and BCs :

$$ \begin{array}{ccc} \left\{ \begin{array}{lr} u(x,y,0)=f_{0}(x,y),& \frac{\partial u(x,y,t)} {\partial t}|_{t=0 }=f_{1}(x,y), (x,y) \in {\Omega},\\ u(0,y,t)=g_{0}(y,t),& u(L,y,t)=g_{1}(y,t), (y,t) \in [0,l] \times {\Lambda}, \\ u(x,0,t)=h_{0}(x,t),& u(x,l,t)=h_{1}(x,t), (x,t) \in [0,L] \times {\Lambda}, \end{array} \right. \end{array} $$

(4.14)

where Ω is the finite rectangular region [0,L] × [0,l] in $\mathbb {R}^{2}$, and Λ = (0,T] represents the time interval.

Firstly, the functions B_i(x,y) for i = 1,2,3,4 can be approximated by the SG polynomials as follows:

$$ B_{i,N,P}(x,y) = \mathcal{P}^{\intercal}_{i} (\phi_{L,N}(x)\otimes\phi_{l,P}(y)), $$

(4.15)

where $\mathcal {P}_{i}$ are column vectors of the following form:

$$ \begin{array}{@{}rcl@{}} \mathcal{P}_{i} \!&=&\! [p_{i,0,0},p_{i,0,1},...,p_{i,0,P},p_{i,1,0},p_{i,1,1},...,p_{i,1,P},\!...,p_{i,N,0},p_{i,N,1},\!...,p_{i,N,P}]^{\intercal},\\ i&=&1,2,3,4. \end{array} $$

(4.16)

where the elements p_i,j,k for i = 1,2,3,4 can be calculated in a similar manner as (2.10).

The functions f(x,y,t),f₀(x,y),f₁(x,y),g₀(y,t),g₁(y,t),h₀(x,t) and h₁(x,t) are approximated by the SG polynomials as follows:

$$ \begin{array}{ccccccc} \left\{ \begin{array}{lr} f_{N,P,M}(x,y,t) \simeq\phi_{T,M}^{\intercal}(t) \textbf{F} (\phi_{L,N}(x)\otimes\phi_{l,P}(y)) ,\\ f_{0,N,P,M}(x,y) \simeq\phi_{T,M}^{\intercal}(0) \textbf{F}_{0} (\phi_{L,N}(x)\otimes\phi_{l,P}(y)) ,\\ f_{1,N,P,M}(x,y) \simeq\phi_{T,M}^{\intercal}(0) \textbf{F}_{1} (\phi_{L,N}(x)\otimes\phi_{l,P}(y)) ,\\ g_{0,N,P,M}(y,t) \simeq\phi_{T,M}^{\intercal}(t) \textbf{G}_{0} (\phi_{L,N}(0)\otimes\phi_{l,P}(y)) ,\\ g_{1,N,P,M}(y,t) \simeq\phi_{T,M}^{\intercal}(t) \textbf{G}_{1} (\phi_{L,N}(L)\otimes\phi_{l,P}(y)) ,\\ h_{0,N,P,M}(x,t) \simeq\phi_{T,M}^{\intercal}(t) \textbf{H}_{0} (\phi_{L,N}(x)\otimes\phi_{l,P}(0)) ,\\ h_{1,N,P,M}(x,t) \simeq\phi_{T,M}^{\intercal}(t) \textbf{H}_{1} (\phi_{L,N}(x)\otimes\phi_{l,P}(l)), \end{array} \right. \end{array} $$

(4.17)

where F,F₀,F₁,G₀,G₁,H₀ and H₁ are known block form matrices written likewise (2.12) and their elements can be calculated likewise (2.14).

The following theorem is substantial to remove the obstacle that facing the use of the tau method for solving the variable coefficients 2D DOTFTE model (4.13):

Theorem 4.1

Let B(x,y) be continuous and smooth function. Therefore, B(x,y) can be approximated by SG polynomials as $B_{N,P}(x,y)= \mathcal {P}^{\intercal }(\phi _{L,N}(x)\otimes \phi _{l,P}(y))$, then there exists an (N + 1)(P + 1) square matrix W satisfying

$$ \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big) \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big)^{\intercal} \mathcal{P} = \textbf{W}^{\intercal} \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big), $$

(4.18)

where

$$ \textbf{W}=\left( \begin{array}{cccccccc} p_{0,0}\mathcal{W}_{0,0,0,0} & p_{0,0}\mathcal{W}_{0,0,0,1} & {\dots} & p_{0,0}\mathcal{W}_{0,0,N,0}& \dots&p_{0,0}\mathcal{W}_{0,0,N,P} \\ p_{0,1}\mathcal{W}_{0,1,0,0} & p_{0,1}\mathcal{W}_{0,1,0,1} & {\dots} & p_{0,1}\mathcal{W}_{0,1,N,0}& \dots&p_{0,1}\mathcal{W}_{0,1,N,P}\\ {\vdots} & {\vdots} & \ddots&\vdots&{\ddots} & {\vdots} \\ p_{0,P}\mathcal{W}_{0,P,0,0} & p_{0,P}\mathcal{W}_{0,P,0,1} & {\dots} & p_{0,P}\mathcal{W}_{0,P,N,0}& \dots&p_{0,P}\mathcal{W}_{0,P,N,P}\\ {\vdots} & {\vdots} & \ddots&\vdots&{\ddots} & {\vdots} \\ p_{N,0}\mathcal{W}_{N,0,0,0} & p_{N,0}\mathcal{W}_{N,0,0,1} & {\dots} & p_{N,0} \mathcal{W}_{0,P,N,0}& \dots&p_{N,0}\mathcal{W}_{N,0,N,P}\\ {\vdots} & {\vdots} & \ddots&\vdots&{\ddots} & {\vdots} \\ p_{N,P}\mathcal{W}_{N,P,0,0} & p_{N,P}\mathcal{W}_{N,P,0,1} & {\dots} & p_{N,P}\mathcal{W}_{N,P,N,0}& \dots&p_{N,P}\mathcal{W}_{N,P,N,P} \end{array} \right), $$

(4.19)

and

$$ \begin{array}{@{}rcl@{}} \mathcal{W}_{i,j,r,s}&=&\frac{1}{ h_{L,p}^{(\alpha)} h_{l,q}^{(\alpha)} } {{\int}_{0}^{l}} {{\int}_{0}^{L}} C^{(\alpha)}_{L,i}(x) C^{(\alpha)}_{l,j}(y) C^{(\alpha)}_{L,r}(x) C^{(\alpha)}_{l,s}(y)\\ &&\times C^{(\alpha)}_{L,p}(x) C^{(\alpha)}_{l,q}(y) \omega^{(\alpha)}_{L}(x) \omega^{(\alpha)}_{l}(y) dxdy. \end{array} $$

(4.20)

Proof

The left hand side of (4.18) can be written as follows:

$$ \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big) \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big)^{\intercal} \mathcal{P} =\sum\limits_{i=0}^{N} \sum\limits_{j=0}^{P} p_{i,j} C^{(\alpha)}_{L,i}(x) C^{(\alpha)}_{l,j}(y) C^{(\alpha)}_{L,r}(x) C^{(\alpha)}_{l,s}(y). $$

(4.21)

By approximating $C^{(\alpha )}_{L,i}(x) C^{(\alpha )}_{l,j}(y) C^{(\alpha )}_{L,r}(x) C^{(\alpha )}_{l,s}(y)$ for r = 0,1,...,N and s = 0,1,...,P as

$$ \begin{array}{@{}rcl@{}} C^{(\alpha)}_{L,i}(x) C^{(\alpha)}_{l,j}(y) C^{(\alpha)}_{L,r}(x) C^{(\alpha)}_{l,s}(y)&=&\sum\limits_{p=0}^{N} \sum\limits_{q=0}^{P} \chi^{i,j,r,s}_{p,q}C^{(\alpha)}_{L,p}(x) C^{(\alpha)}_{l,q}(y)\\ &=&\mathcal{W}_{i,j,r,s}\Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big), \end{array} $$

(4.22)

where

$$\mathcal{W}_{i,j,r,s} = [\chi^{i,j,r,s}_{0,0},\chi^{i,j,r,s}_{0,1},...,\chi^{i,j,r,s}_{0,P},\chi^{i,j,r,s}_{1,0},\chi^{i,j,r,s}_{1,1},..., \chi^{i,j,r,s}_{1,P},...,\chi^{i,j,r,s}_{N,0},\chi^{i,j,r,s}_{N,1},...,\chi^{i,j,r,s}_{N,P}]^{\intercal},$$

and

$$\mathcal{W}_{i,j,r,s}=\frac{1}{ h_{L,p}^{(\alpha)} h_{l,q}^{(\alpha)} } {{\int}_{0}^{l}} {{\int}_{0}^{L}} C^{(\alpha)}_{L,i}(x) C^{(\alpha)}_{l,j}(y) C^{(\alpha)}_{L,r}(x) C^{(\alpha)}_{l,s}(y) C^{(\alpha)}_{L,p}(x) C^{(\alpha)}_{l,q}(y) \omega^{(\alpha)}_{L}(x) \omega^{(\alpha)}_{l}(y) dxdy. $$

From (4.21) and (4.22), we have

$$ \begin{aligned} \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big) \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big)^{\intercal} \mathcal{P}&=\sum\limits_{i=0}^{N} \sum\limits_{j=0}^{P} p_{i,j} \sum\limits_{p=0}^{N} \sum\limits_{q=0}^{P} \chi^{i,j,r,s}_{p,q}C^{(\alpha)}_{L,p}(x) C^{(\alpha)}_{l,q}(y)\\ &= \sum\limits_{p=0}^{N} \sum\limits_{q=0}^{P} C^{(\alpha)}_{L,p}(x) C^{(\alpha)}_{l,q}(y) \sum\limits_{i=0}^{N} \sum\limits_{j=0}^{P} p_{i,j} \chi^{i,j,r,s}_{p,q}\\ &=\Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big)^{\intercal} \mathcal{Z}_{r,s}\\ &=\mathcal{Z}_{r,s}^{\intercal} \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big), \end{aligned} $$

(4.23)

where

$$ \mathcal{Z}_{r,s} = [\mathcal{W}_{0,0,r,s},\mathcal{W}_{0,1,r,s},...,\mathcal{W}_{0,P,r,s},\mathcal{W}_{1,0,r,s},\mathcal{W}_{1,1,r,s},...,\mathcal{W}_{1,P,r,s},...,\mathcal{W}_{N,0,r,s},\mathcal{W}_{N,1,r,s},...,\mathcal{W}_{N,P,r,s}] \mathcal{P},$$

and the (N + 1)(P + 1) square matrix W in (4.18) can be defined as follows:

$$ \textbf{W}=[\mathcal{Z}_{0,0},\mathcal{Z}_{0,1},...,\mathcal{Z}_{0,P},\mathcal{Z}_{1,0},\mathcal{Z}_{1,1},...,\mathcal{Z}_{1,P},...,\mathcal{Z}_{N,0},\mathcal{Z}_{N,1},...,\mathcal{Z}_{N,P}], $$

(4.24)

which completes the proof. □

Now, by employing (2.11), (2.12), (2.15), (3.5) and (4.18) for approximating (4.13), the following approximations are given

$$ {}\mathcal{D}^{\rho(\eta)}_{t} U =\phi_{T,M}^{\intercal}(t) (\textbf{D}_{(1,2)}^{\rho(\eta)})^{\intercal} \textbf{A} (\phi_{L,N}(x)\otimes\phi_{l,P}(y)), $$

(4.25)

$$ \begin{aligned} B_{1}(x,y) \mathcal{D}^{\sigma(v)}_{t} U &=\Big(\mathcal{P}^{\intercal}_{1} (\phi_{L,N}(x)\otimes\phi_{l,P}(y))\Big) \Big(\phi_{T,M}^{\intercal}(t) (\textbf{D}_{(1,2)}^{\sigma(v)})^{\intercal} \textbf{A} (\phi_{L,N}(x)\otimes\phi_{l,P}(y))\Big)\\ &= \phi_{T,M}^{\intercal}(t) (\textbf{D}_{(1,2)}^{\sigma(v)})^{\intercal} \textbf{A} \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big) \Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big)^{\intercal} \mathcal{P}_{1}\\ &= \phi_{T,M}^{\intercal}(t) (\textbf{D}_{(1,2)}^{\sigma(v)})^{\intercal} \textbf{A} \textbf{W}^{\intercal}_{1} \Big(\phi_{L,N}(x) \otimes\phi_{l,P}(y) \Big), \end{aligned} $$

(4.26)

$$ \begin{aligned} B_{2}(x,y) U &=\Big(\mathcal{P}^{\intercal}_{2} (\phi_{L,N}(x)\otimes\phi_{l,P}(y))\Big) \Big(\phi_{T,M}^{\intercal}(t) \textbf{A} (\phi_{L,N}(x)\otimes\phi_{l,P}(y))\Big)\\ &= \phi_{T,M}^{\intercal}(t) \textbf{A} \textbf{W}^{\intercal}_{2} \Big(\phi_{L,N}(x) \otimes\phi_{l,P}(y) \Big), \end{aligned} $$

(4.27)

$$ \begin{aligned} B_{3}(x,y) \frac{\partial^{2} U} {\partial x^{2}} &= \Big(\mathcal{P}^{\intercal}_{3} (\phi_{L,N}(x)\otimes\phi_{l,P}(y))\Big) \Big(\phi_{T,M}^{\intercal}(t) \textbf{A} (\textbf{D}_{L}^{(2)} \phi_{L,N}(x) \otimes\phi_{l,P}(y) )\Big)\\ &= \Big(\mathcal{P}^{\intercal}_{1} (\phi_{L,N}(x)\otimes\phi_{l,P}(y))\Big) \Big(\phi_{T,M}^{\intercal}(t) \textbf{A} (\textbf{D}_{L}^{(2)} \otimes I_{P+1} ) (\phi_{L,N}(x) \otimes\phi_{l,P}(y))\Big)\\ &= \phi_{T,M}^{\intercal}(t) \textbf{A} \Big(\textbf{D}_{L}^{(2)} \otimes I_{P+1} \Big) \Big(\phi_{L,N}(x) \otimes\phi_{l,P}(y) \Big)\Big(\phi_{L,N}(x)\otimes\phi_{l,P}(y)\Big)^{\intercal} \mathcal{P}_{3}\\ &= \phi_{T,M}^{\intercal}(t) \textbf{A} \Big(\textbf{D}_{L}^{(2)} \otimes I_{P+1} \Big) \textbf{W}_{3}^{\intercal}\Big(\phi_{L,N}(x) \otimes\phi_{l,P}(y) \Big), \end{aligned} $$

(4.28)

in a similar manner as (4.28), we get

$$ B_{4}(x,y) \frac{\partial^{2} U} {\partial y^{2}} \simeq \phi_{T,M}^{\intercal}(t) \textbf{A} \Big(I_{N+1} \otimes \textbf{D}_{l}^{(2)} \Big) \textbf{W}_{4}^{\intercal}\Big(\phi_{L,N}(x) \otimes\phi_{l,P}(y) \Big). $$

(4.29)

By substituting (4.17), (4.25), (4.26), (4.27), (4.28) and (4.29) into (4.13), we get

$$ \phi_{T,M}^{\intercal}(t) \textbf{E} (\phi_{L,N}(x)\otimes\phi_{l,P}(y))=0, $$

(4.30)

where

$$ \begin{array}{@{}rcl@{}} \textbf{E}&=&(\textbf{D}_{(1,2)}^{\rho(\eta)})^{\intercal} \textbf{A} +2 (\textbf{D}_{(0,1)}^{\sigma(v)})^{\intercal} \textbf{A} \textbf{W}^{\intercal}_{1}+ \textbf{A} \textbf{W}^{\intercal}_{2}\\ &&- \textbf{A} \Big(\textbf{D}_{L}^{(2)} \otimes I_{P+1} \Big) \textbf{W}_{3}^{\intercal} - \textbf{A} \Big(I_{N+1} \otimes \textbf{D}_{l}^{(2)} \Big) \textbf{W}_{4}^{\intercal} - \textbf{F}. \end{array} $$

(4.31)

By applying the orthogonality relation (2.3) for (4.30) and by using the typical tau method, we can extract an (M − 1) × (N − 1) × (P − 1) algebraic system of linear equations in terms of unknown coefficients as follows:

$$ J^{(M-1,M+1)}_{\tau} \textbf{E} (J^{(N+1,N-1)}_{L} \otimes J^{(P+1,P-1)}_{l} )=0. $$

(4.32)

The 2(N − 1) × (P − 1) + 2P(M + 1) + 2N(M − 1) remainder of linear algebraic equations are extracted from ICs and BCs (4.14) as follows:

$$ \begin{aligned} \phi_{T,M}^{\intercal}(0) \Big(\textbf{A}&-\textbf{F}_{0} \Big)(J^{(N+1,N-1)}_{L} \otimes J^{(P+1,P-1)}_{l}) = 0 ,\\ \phi_{T,M}^{\intercal}(0)\Big((\textbf{D}&_{\tau}^{(1)})^{\intercal} \textbf{A}-\textbf{F}_{1} \Big)(J^{(N+1,N-1)}_{L} \otimes J^{(P+1,P-1)}_{l}) = 0 ,\\ J^{(M+1,M+1)}_{\tau}&\Big(\textbf{A}-\textbf{G}_{0} \Big) (\phi_{L,N}(0) \otimes J^{(P+1,P)}_{l})= 0 ,\\ J^{(M+1,M+1)}_{\tau}&\Big(\textbf{A}-\textbf{G}_{1} \Big) (\phi_{L,N}(L)\otimes J^{(P+1,P)}_{l})= 0 ,\\ J^{(M+1,M+1)}_{\tau}&\Big(\textbf{A}-\textbf{H}_{0} \Big) (J^{(N+1,N)}_{L} \otimes\phi_{l,P}(0)) = 0 ,\\ J^{(M+1,M+1)}_{\tau}& \Big(\textbf{A}-\textbf{H}_{1} \Big) (J^{(N+1,N)}_{L} \otimes\phi_{l,P}(l)) = 0. \end{aligned} $$

(4.33)

By solving the algebraic system of (4.32) and (4.33) for the unknowns coefficients. As a result, the approximate solution is determined easily. The main steps of the suggested methodology for solving the 2D DOTFTE are implemented in the following algorithm.

Algorithm 2

2D DOTFTE.

5 Convergence and error estimation

This section focuses on the convergence and error bound analysis of the proposed numerical technique in the weighted ${\mathscr{L}}^{\text {2}}$-norm.

5.1 1D-case

Consider the polynomials space of NM-degree $\mathcal {S}_{N,M}=\text {span}\langle C_{L,i}^{(\alpha )}(x) C_{T,j}^{(\alpha )}(t)\rangle |_{i,j=0}^{N,M}$. Let Ω = (0,L) × (0,T). We define the weighted norm and inner product as follows:

$$ \left\Vert u\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})}^{2}=\langle u,u \rangle_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}}=\iint\limits_{\Omega} u^{2}(x,t) ~\omega^{\alpha}_{LT}~ dxdt, \forall u \in \mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega}), $$

where $\omega ^{\alpha }_{LT}=\omega ^{\alpha }_{L}(x)\omega ^{\alpha }_{T}(t)$. The generalised Taylor’s expansion [50] of finite terms has the form

$$ \mathcal{G}^{\theta,\zeta}_{N,M}(x,t)= \sum\limits_{i=0}^{N} \sum\limits_{j=0}^{M} \frac{x^{i \theta } t^{j \zeta}}{\Gamma{(i\theta+1)} {\Gamma}{(j\zeta+1)}} {\!}^{c}_{0}D^{i\theta}_{x}({\!}^{c}_{0}D^{j\zeta}_{t} u(x,t))|_{(0,0)}. $$

(5.1)

In this subsection, we will consider the following notations before introducing the main theorems:

$$i=0,1,..,N;~~ j=0,1,..,M;~~ N^{\prime}=N+1,~~ M^{\prime}=M+1,$$

$$\mathcal{H}= \sup_{(x,t) \in {\Omega}}| {\!}^{c}_{0}D^{N^{\prime}\theta}_{x}({\!}^{c}_{0}D^{M^{\prime}\zeta}_{t} u(x,t))|, \mathcal{J}= \sup_{(x,t) \in {\Omega}}| {\!}^{c}_{0}D^{N^{\prime}\theta}_{x}({\!}^{c}_{0}D^{M^{\prime}\zeta+\eta}_{t} u(x,t))|,$$

$$\mathcal{K}= \sup_{(x,t) \in {\Omega}}| {\!}^{c}_{0}D^{N^{\prime}\theta}_{x}({\!}^{c}_{0}D^{M^{\prime}\zeta+v}_{t} u(x,t))|, \mathcal{B}= \sup_{(x,t) \in {\Omega}}| {\!}^{c}_{0}D^{N^{\prime}\theta+2}_{x}({\!}^{c}_{0}D^{M^{\prime}\zeta}_{t} u(x,t))|,$$

$$\mathcal{R}_{N,M}=\frac{ {\Gamma}{(\alpha+\frac{1}{2})}}{\Gamma{(N^{\prime}\theta+1)} {\Gamma}{(M^{\prime}\zeta+1)}} \sqrt{\frac{L^{\prime} T^{\prime} {\Gamma}{(2 N^{\prime}\theta+\alpha+\frac{1}{2}}) {\Gamma}{(2M^{\prime}\zeta+\alpha+\frac{1}{2}}).}{\Gamma{(2N^{\prime}\theta+2\alpha+1)} {\Gamma}{(2M^{\prime}\zeta+2\alpha+1)}}}$$

Theorem 5.1

Let ${\!}^{c}_{0}D^{i\theta }_{x}({\!}^{c}_{0}D^{j\zeta }_{t} u(x,t)) \in \mathcal {C}({\Omega })$. If u_N,M(x,t) is the best approximation to u(x,t) in $\mathcal {S}_{N,M}$, then for $L^{\prime }=L^{2N^{\prime }\theta +2\alpha }$ and $T^{\prime }=T^{2M^{\prime }\zeta +2\alpha }$ the following estimation holds

$$ \left\Vert u(x,t)-u_{N,M}(x,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{L\tau}}({\Omega})} \le \mathcal{H} ~\mathcal{R}_{N,M}. $$

(5.2)

Proof

From the generalised Taylor expansion (5.1) and knowing that u_N,M(x,t) is the best approximation of u(x,t) in $\mathcal {S}_{N,M}$, we have

$$ \left\vert u(x,t)-u_{N,M}(x,t)\right\vert \le \left\vert u(x,t)-\mathcal{G}^{\theta,\zeta}_{N,M}(x,t)\right\vert \le \frac{ x^{N^{\prime} \theta } t^{M^{\prime} \zeta}}{\Gamma{(N^{\prime}\theta+1)} {\Gamma}{(M^{\prime}\zeta+1)}} \mathcal{H}. $$

(5.3)

By applying the ${\mathscr{L}}^{2}_{\omega ^{\alpha }_{LT}}({\Omega })$-norm on inequality (5.3), we get

$$ \left\Vert u(x,t)-u_{N,M}(x,t)\right\Vert^{2}_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} \le \frac{\mathcal{H}^{2} }{({\Gamma}{(N^{\prime}\theta+1)} {\Gamma}{(M^{\prime}\zeta+1)})^{2}} {{\int}_{0}^{T}} {{\int}_{0}^{L}} x^{2N^{\prime} \theta } t^{2M^{\prime} \zeta} \omega^{\alpha}_{L}(x) \omega^{\alpha}_{T}(t) dx dt. $$

(5.4)

The double integration of (5.4) can be estimated as follows:

$$ \begin{array}{@{}rcl@{}} I&=&{{\int}_{0}^{T}} {{\int}_{0}^{L}} x^{2N^{\prime} \theta } t^{2M^{\prime} \zeta} \omega^{\alpha}_{L}(x) \omega^{\alpha}_{T}(t) dx dt\\ &=& {{\int}_{0}^{T}} {{\int}_{0}^{L}} x^{2N^{\prime} \theta+\alpha-\frac{1}{2} } t^{2M^{\prime} \zeta+\alpha-\frac{1}{2}} (L-x)^{\alpha-\frac{1}{2}} (T-t)^{\alpha-\frac{1}{2}} dx dt, \end{array} $$

by making change of variables $x \rightarrow Lx$ and $t \rightarrow Tt$, we get

$$ \begin{aligned} I&= L^{\prime} T^{\prime} {{\int}_{0}^{1}} {{\int}_{0}^{1}} x^{2N^{\prime} \theta+\alpha-\frac{1}{2} } t^{2M^{\prime} \zeta+\alpha-\frac{1}{2}} (1-x)^{\alpha-\frac{1}{2}} (1-t)^{\alpha-\frac{1}{2}} dx dt\\ &= \frac{L^{\prime} T^{\prime} {\Gamma}{(2N^{\prime} \theta+\alpha+\frac{1}{2})} {\Gamma}{(2M^{\prime} \zeta+\alpha+\frac{1}{2})} ({\Gamma}{(\alpha+\frac{1}{2})})^{2}}{\Gamma{(2N^{\prime} \theta+2\alpha+1)} {\Gamma}{(2M^{\prime} \zeta+2\alpha+1)}}. \end{aligned} $$

(5.5)

Now, by substituting from (5.5) in (5.4) then the square root of the resulting equation completes the proof. □

The following corollaries 5.1, 5.2 and 5.3 can be proved by using the same procedure as in Theorem 5.1.

Corollary 5.1

Let ${\!}^{c}_{0}D^{i\theta }_{x}({\!}^{c}_{0}D^{j\zeta +\eta }_{t} u(x,t)) \in \mathcal {C}({\Omega })$. If $({\!}^{c}_{0}D^{\eta }_{t}u)_{N,M}(x,t)$ is the best approximation to ${\!}^{c}_{0}D^{\eta }_{t}u(x,t)$in $\mathcal {S}_{N,M}$, then for $L^{\prime }=L^{2N^{\prime }\theta +2\alpha }$ and $T^{\prime }=T^{2M^{\prime }\zeta +2\alpha }$ the following error estimation holds

$$ \left\Vert{\!}^{c}_{0}D^{\eta}_{t} u(x,t)-({\!}^{c}_{0}D^{\eta}_{t}u)_{N,M}(x,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} \le \mathcal{J} ~\mathcal{R}_{N,M}. $$

(5.6)

Corollary 5.2

According to assumptions of Corollary 5.1 for η = v, we have:

$$ \left\Vert{\!}^{c}_{0}{D^{v}_{t}} u(x,t)-({\!}^{c}_{0}{D^{v}_{t}}u)_{N,M}(x,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} \le \mathcal{K} ~\mathcal{R}_{N,M}. $$

(5.7)

Corollary 5.3

Let ${\!}^{c}_{0}D^{i\theta +2}_{x}({\!}^{c}_{0}D^{j\zeta }_{t} u(x,t)) \in \mathcal {C}({\Omega })$. If $({\!}^{c}_{0}{D^{2}_{x}}u)_{N,M}(x,t)$ is the best approximation to ${\!}^{c}_{0}{D^{2}_{x}}u(x,t)$in $\mathcal {S}_{N,M}$, then for $L^{\prime }=L^{2N^{\prime }\theta +2\alpha }$ and $T^{\prime }=T^{2M^{\prime }\zeta +2\alpha }$, we have:

$$ \left\Vert{\!}^{c}_{0}{D^{2}_{x}} u(x,t)-({\!}^{c}_{0}{D^{2}_{x}}u)_{N,M}(x,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} \le \mathcal{B} ~\mathcal{R}_{N,M}. $$

(5.8)

Theorem 5.2

According to assumptions of Theorem 5.1 and Corollaries 5.1–5.3. Also, consider that the functions B_i(x) are bounded on the interval [0,L] with bounds $\mathcal {A}_{i}$ for i = 1,2,3 respectively, then the error of the proposed method in the ${\mathscr{L}}^{2}_{\omega ^{\alpha }_{L\tau }}({\Omega })$ with $\left \Vert \rho (\eta )\right \Vert \le \lambda$ and $\left \Vert \sigma (v)\right \Vert \le \mu$ is given by

$$ \left\Vert\mathcal{E}_{N,M}\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} \le (\lambda\mathcal{J}+\mu \mathcal{A}_{1}\mathcal{K}+\mathcal{A}_{2}\mathcal{H}+\mathcal{A}_{3}\mathcal{B}) \mathcal{R}_{N,M}. $$

(5.9)

Proof

We know that

$$\begin{aligned} \left\Vert\mathcal{E}_{N,M}\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} &= \Big|\Big|{{\int}_{1}^{2}} \rho(\eta) ({\!}^{c}_{0}D^{\eta}_{t} u)_{N,M}(x,t) d\eta \\ &\quad+B_{1}(x){{\int}_{0}^{1}} \sigma(v) ({\!}^{c}_{0}{D^{v}_{t}} u)_{N,M}(x,t) dv\\ &\quad+B_{2}(x) u_{N,M}(x,t) -B_{3}(x) (\frac{\partial^{2}} {\partial x^{2}}u)_{N,M}(x,t) - f(x,t)\Big|\Big|_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})}\\ &=\Big|\Big|{{\int}_{1}^{2}} \rho(\eta) ({\!}^{c}_{0}D^{\eta}_{t} u)_{N,M}(x,t) d\eta\\ &\quad+B_{1}(x){{\int}_{0}^{1}} \sigma(v) ({\!}^{c}_{0}{D^{v}_{t}} u)_{N,M}(x,t) dv+B_{2}(x) u_{N,M}(x,t)\\ &-B_{3}(x) (\frac{\partial^{2}} {\partial x^{2}}u)_{N,M}(x,t)-{{\int}_{1}^{2}} \rho(\eta) {\!}^{c}_{0}D^{\eta}_{t} u(x,t) d\eta\\ &\quad-B_{1}(x){{\int}_{0}^{1}} \sigma(v) {\!}^{c}_{0}{D^{v}_{t}} u(x,t) dv-B_{2}(x) u(x,t) \\ &\quad+B_{3}(x) \frac{\partial^{2}} {\partial x^{2}}u(x,t)\Big|\Big|_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} \\ & \quad\le {{\int}_{1}^{2}} \left\Vert\rho(\eta)\right\Vert \left\Vert{\!}^{c}_{0}D^{\eta}_{t} u(x,t)-({\!}^{c}_{0}D^{\eta}_{t} u)_{N,M}(x,t))\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} d\eta\\ &\quad+\left\vert{B_{1}(x)}\right\vert {{\int}_{0}^{1}} \left\Vert{\sigma(v)}\right\Vert \left\Vert{{\!}^{c}_{0}{D^{v}_{t}} u(x,t) - ({\!}^{c}_{0}{D^{v}_{t}} u)_{N,M}(x,t))}\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} dv\\ &\quad+\left\vert{B_{2}(x)}\right\vert \left\Vert{u(x,t)-(u_{N,M})(x,t)}\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} \\ &\quad+\left\vert B_{3}(x)\right\vert \left\Vert\frac{\partial^{2}} {\partial x^{2}}u(x,t)-(\frac{\partial^{2}} {\partial x^{2}}u)_{N,M}(x,t))\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LT}}({\Omega})} \end{aligned} $$

$$ \begin{aligned} & \le (\lambda\mathcal{J}+\mu \mathcal{A}_{1}\mathcal{K}+\mathcal{A}_{2}\mathcal{H}+\mathcal{A}_{3}\mathcal{B}) \mathcal{R}_{N,M}. \end{aligned} $$

(5.10)

Therefore, for enough large values of M;N, we get $\left \Vert \mathcal {E}_{N,M}\right \Vert _{{\mathscr{L}}^{2}_{\omega ^{\alpha }_{LT}}({\Omega })} \rightarrow 0$. □

5.2 2D-case

Consider the polynomials space of NMP-degree $\mathcal {S}_{N,M,P}=\text {span}\langle C_{L,i}^{(\alpha )}(x) C_{l,j}^{(\alpha )}(y)$ $C_{T,k}^{(\alpha )}(t)\rangle |_{i,j,k=0}^{N,P,M}$. Let $\tilde {\Omega } =(0,L) \times (0,l) \times (0,T)$. We define the weighted norm and inner product as follows:

$$ \left\Vert u\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})}^{2}=\langle u,u \rangle_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})}^{2}=\iiint\limits_{\tilde{\Omega}} u^{2}(x,t)~ \omega^{\alpha}_{LlT}~ dxdydt, \forall u \in \mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega}), $$

where $\omega ^{\alpha }_{LlT}=\omega ^{\alpha }_{L}(x) \omega ^{\alpha }_{l}(y) \omega ^{\alpha }_{T}(t)$. The generalised Taylor’s expansion [50] of finite terms can be defined as follows:

$$ \mathcal{G}^{\theta,\xi,\zeta}_{N,P,M}(x,y,t) = \sum\limits_{i=0}^{N} \sum\limits_{j=0}^{P} \sum\limits_{k=0}^{M} \frac{x^{i \theta} y^{j \xi} t^{k \zeta}}{\Gamma{(i\theta+1)} {\Gamma}{(j\xi + 1)} {\Gamma}{(k\zeta+1)}} {\!}^{c}_{0}D^{i\theta}_{x}({\!}^{c}_{0}D^{j\xi}_{y}({\!}^{c}_{0}D^{k\zeta}_{t} u(x,y,t)))|_{(0,0,0)}. $$

(5.11)

In this subsection, we will consider the following notations before introducing the main theorems:

$$i=0,1,...,N;~~ j=0,1,...,P;~~ k=0,1,...,M;~~ N^{\prime}=N+1,~~ P^{\prime}=P+1,~~ M^{\prime}=M+1 $$

$$\tilde{\mathcal{H}}= \sup_{(x,y,t) \in \tilde{\Omega}}| {\!}^{c}_{0}D^{N^{\prime}\theta}_{x}({\!}^{c}_{0}D^{P^{\prime}\xi}_{y}({\!}^{c}_{0}D^{M^{\prime}\zeta}_{t} u(x,y,t)))|, \tilde{\mathcal{J}}= \sup_{(x,y,t) \in \tilde{\Omega}}| {\!}^{c}_{0}D^{N^{\prime}\theta}_{x}({\!}^{c}_{0}D^{P^{\prime}\xi}_{y}({\!}^{c}_{0}D^{M^{\prime}\zeta+\eta}_{t} u(x,y,t)))|, $$

$$\tilde{\mathcal{K}}= \sup_{(x,y,t) \in \tilde{\Omega}}| {\!}^{c}_{0}D^{N^{\prime}\theta}_{x}({\!}^{c}_{0}D^{P^{\prime}\xi}_{y}({\!}^{c}_{0}D^{M^{\prime}\zeta+v}_{t} u(x,y,t)))|, \tilde{\mathcal{B}}= \sup_{(x,y,t) \in \tilde{\Omega}}| {\!}^{c}_{0}D^{N^{\prime}\theta+2}_{x}({\!}^{c}_{0}D^{P^{\prime}\xi}_{y}({\!}^{c}_{0}D^{M^{\prime}\zeta}_{t} u(x,y,t)))| $$

$${}\tilde{\mathcal{F}}= \sup_{(x,y,t) \in \tilde{\Omega}}| {\!}^{c}_{0}D^{N^{\prime}\theta}_{x}({\!}^{c}_{0}D^{P^{\prime}\xi+2}_{y}({\!}^{c}_{0}D^{M^{\prime}\zeta}_{t} u(x,y,t)))|.$$

$$\tilde{\mathcal{R}}_{N,P,M}= \frac{\Gamma{(\alpha+\frac{1}{2})} \sqrt{\frac{L^{\prime} l^{\prime} T^{\prime} {\Gamma}{(2 N^{\prime}\theta+\alpha+\frac{1}{2}}) {\Gamma}{(2 P^{\prime}\xi+\alpha+\frac{1}{2}}) {\Gamma}{(2M^{\prime}\zeta+\alpha+\frac{1}{2}}) {\Gamma}{(\alpha+\frac{1}{2})}}{\Gamma{(2N^{\prime}\theta+2\alpha+1)} {\Gamma}{(2P^{\prime}\xi+2\alpha+1)} {\Gamma}{(2M^{\prime}\zeta+2\alpha+1)}}}}{\Gamma{(N^{\prime}\theta+1)} {\Gamma}{(P^{\prime}\xi+1)} {\Gamma}{(M^{\prime}\zeta+1)}} .$$

Theorem 5.3

Let ${\!}^{c}_{0}D^{i\theta }_{x}({\!}^{c}_{0}D^{j\xi }_{y}({\!}^{c}_{0}D^{k\zeta }_{t} u(x,y,t))) \in \mathcal {C}(\tilde {\Omega })$. If u_N,P,M(x,y,t) is the best approximation to u(x,y,t)in $\mathcal {S}_{N,P,M}$, then for $L^{\prime }=L^{2N^{\prime }\theta +2\alpha }, l^{\prime }=l^{2P^{\prime }\xi +2\alpha }$ and $T^{\prime }=T^{2M^{\prime }\zeta +2\alpha }$, the following error estimation holds

$$ \left\Vert u(x,y,t)-u_{N,P,M}(x,y,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} \le \mathcal{\tilde{H}} ~\tilde{\mathcal{R}}_{N,P,M}. $$

(5.12)

Proof

From the generalised Taylor expansion and knowing that u_N,P,M(x,y,t) is the best approximation of u(x,y,t) in $\mathcal {S}_{N,P,M}$, we have

$$ \begin{array}{@{}rcl@{}} \left\vert u(x,y,t)-u_{N,P,M}(x,y,t)\right\vert &\!\le\!& \left\vert u(x,y,t)-\mathcal{G}^{\theta,\xi,\zeta}_{N,P,M}(x,y,t)\right\vert\\ &\!\le\!& \frac{ x^{N^{\prime} \theta } y^{P^{\prime} \xi } t^{M^{\prime} \zeta}}{\Gamma{(N^{\prime}\theta + 1)} {\Gamma}{(P^{\prime}\xi + 1)} {\Gamma}{(M^{\prime}\zeta + 1)}} \mathcal{\tilde{H}}. \end{array} $$

(5.13)

By applying the ${\mathscr{L}}^{2}_{\omega ^{\alpha }_{LlT}}(\tilde {\Omega })$-norm on inequality (5.13), we get

$$ \begin{aligned} &\left\Vert u(x,y,t)-u_{N,P,M}(x,y,t)\right\Vert^{2}_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})}\\ &\le \frac{\mathcal{\tilde{H}}^{2} }{({\Gamma}{(N^{\prime}\theta + 1)} {\Gamma}{(P^{\prime}\xi+1)} {\Gamma}{(M^{\prime}\zeta+1)})^{2}} {{\int}_{0}^{T}} {{\int}_{0}^{l}} {{\int}_{0}^{L}} x^{2N^{\prime} \theta} y^{2P^{\prime} \xi} t^{2M^{\prime} \zeta} \omega^{\alpha}_{L}(x) \omega^{\alpha}_{l}(y) \omega^{\alpha}_{T}(t) dx dy dt. \end{aligned} $$

(5.14)

The triple integration of (5.14) can be estimated as follows:

$${}I={{\int}_{0}^{T}} {{\int}_{0}^{l}} {{\int}_{0}^{L}} x^{2N^{\prime} \theta } y^{2P^{\prime} \xi } t^{2M^{\prime} \zeta} \omega^{\alpha}_{L}(x) \omega^{\alpha}_{l}(y) \omega^{\alpha}_{T}(t) dx dy dt$$

$$= {{\int}_{0}^{L}} {{\int}_{0}^{l}} {{\int}_{0}^{T}} x^{2N^{\prime} \theta+\alpha-\frac{1}{2} } y^{2P^{\prime} \xi+\alpha-\frac{1}{2} } t^{2M^{\prime} \zeta+\alpha-\frac{1}{2}} \Big((L-x) (l-y) (T-t)\Big)^{\alpha-\frac{1}{2}} dx dy dt,$$

by making change of variables $x \rightarrow Lx, y \rightarrow ly$ and $t \rightarrow Tt$, we get

$$ \begin{aligned} I&= L^{\prime} l^{\prime} T^{\prime} {{\int}_{0}^{1}} {{\int}_{0}^{1}} {{\int}_{0}^{1}} x^{2N^{\prime} \theta+\alpha-\frac{1}{2}} y^{2P^{\prime} \xi+\alpha-\frac{1}{2} } T^{2M^{\prime} \zeta+\alpha-\frac{1}{2}} \Big((1-x) (1-y) (1-t)\Big)^{\alpha-\frac{1}{2}} dx dy dt\\ &= \frac{L^{\prime} l^{\prime} T^{\prime} {\Gamma}{(2N^{\prime} \theta+\alpha+\frac{1}{2})} {\Gamma}{(2P^{\prime} \xi+\alpha+\frac{1}{2})} {\Gamma}{(2M^{\prime} \zeta+\alpha+\frac{1}{2})} ({\Gamma}{(\alpha+\frac{1}{2})})^{3}}{\Gamma{(2N^{\prime} \theta+2\alpha+1)} {\Gamma}{(2P^{\prime} \xi+2\alpha+1)} {\Gamma}{(2M^{\prime} \zeta+2\alpha+1)}}. \end{aligned} $$

(5.15)

Now, by substituting from (5.15) in (5.14), then the square root of the resulting equation completes the proof. □

The following corollaries 5.4, 5.5, 5.6 and 5.7 can be proved by using the same procedure as in Theorem 5.3.

Corollary 5.4

Let ${\!}^{c}_{0}D^{i\theta }_{x}({\!}^{c}_{0}D^{j\xi }_{y}({\!}^{c}_{0}D^{k\zeta +\eta }_{t} u(x,y,t))) \in \mathcal {C}(\tilde {\Omega })$. If $({\!}^{c}_{0}D^{\eta }_{t}u)_{N,P,M}(x,y,t)$ is the best approximation to ${\!}^{c}_{0}D^{\eta }_{t}u(x,y,t)$in $\mathcal {S}_{N,P,M}$, then for $L^{\prime }=L^{2N^{\prime }\theta +2\alpha }, l^{\prime }=l^{2P^{\prime }\xi +2\alpha }$ and $T^{\prime }=T^{2M^{\prime }\zeta +2\alpha }$, the following error estimate holds

$$ \left\Vert{\!}^{c}_{0}D^{\eta}_{t} u(x,y,t)-({\!}^{c}_{0}D^{\eta}_{t}u)_{N,P,M}(x,y,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} \le \mathcal{\tilde{J}} ~\mathcal{\tilde{R}}_{N,P,M}. $$

(5.16)

Corollary 5.5

According to assumptions of Corollary 5.4 for η = v, we have:

$$ \left\Vert{\!}^{c}_{0}{D^{v}_{t}} u(x,y,t)-({\!}^{c}_{0}{D^{v}_{t}}u)_{N,P,M}(x,y,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} \le \mathcal{\tilde{K}} ~\mathcal{\tilde{R}}_{N,P,M}. $$

(5.17)

Corollary 5.6

Let ${\!}^{c}_{0}D^{i\theta +2}_{x}({\!}^{c}_{0}D^{j\xi }_{y}({\!}^{c}_{0}D^{k\zeta }_{t} u(x,y,t))) \in \mathcal {C}(\tilde {\Omega })$. If $({\!}^{c}_{0}{D^{2}_{x}}u)_{N,P,M}(x,y,t)$ is the best approximation to ${\!}^{c}_{0}{D^{2}_{x}}u(x,y,t)$in $\mathcal {S}_{N,P,M}$, then for $L^{\prime }=L^{2N^{\prime }\theta +2\alpha }, l^{\prime }=l^{2P^{\prime }\xi +2\alpha }$ and $T^{\prime }=T^{2M^{\prime }\zeta +2\alpha }$, we have:

$$ \left\Vert{\!}^{c}_{0}{D^{2}_{x}} u(x,y,t)-({\!}^{c}_{0}{D^{2}_{x}}u)_{N,P,M}(x,y,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} \le \mathcal{\tilde{B}} ~\mathcal{\tilde{R}}_{N,P,M}. $$

(5.18)

Corollary 5.7

Let ${\!}^{c}_{0}D^{i\theta }_{x}({\!}^{c}_{0}D^{j\xi +2}_{y}({\!}^{c}_{0}D^{k\zeta }_{t} u(x,y,t))) \in \mathcal {C}(\tilde {\Omega })$. If $({\!}^{c}_{0}{D^{2}_{y}}u)_{N,P,M}(x,y,t)$ is the best approximation to ${\!}^{c}_{0}{D^{2}_{y}}u(x,y,t)$in $\mathcal {S}_{N,P,M}$, then for $L^{\prime }=L^{2N^{\prime }\theta +2\alpha }, l^{\prime }=l^{2P^{\prime }\xi +2\alpha }$ and $T^{\prime }=T^{2M^{\prime }\zeta +2\alpha }$, we have:

$$ \left\Vert{\!}^{c}_{0}{D^{2}_{y}} u(x,y,t)-({\!}^{c}_{0}{D^{2}_{y}}u)_{N,P,M}(x,y,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} \le \mathcal{\tilde{F}} ~\mathcal{\tilde{R}}_{N,P,M}. $$

(5.19)

Theorem 5.4

According to assumptions of Theorem 5.3 and Corollaries 5.4–5.7. Also, consider that the functions B_i(x,y) are bounded on the interval [0,L] × [0,l] with bounds $\mathcal {\tilde {A}}_{i}$ for i = 1,2,3,4; respectively, then the error of the proposed method in the ${\mathscr{L}}^{2}_{\omega ^{\alpha }_{LlT}}(\tilde {\Omega })$ with $\left \Vert \rho (\eta )\right \Vert \le \lambda$ and $\left \Vert \sigma (v)\right \Vert \le \mu$ is given by

$$ \left\Vert\mathcal{E}_{N,P,M}\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} \le (\lambda\mathcal{\tilde{J}}+\mu \mathcal{\tilde{A}}_{1}\mathcal{\tilde{K}}+\mathcal{\tilde{A}}_{2}\mathcal{\tilde{H}}+\mathcal{\tilde{A}}_{3}\mathcal{\tilde{B}}+\mathcal{\tilde{A}}_{4}\mathcal{\tilde{F}}) \mathcal{\tilde{R}}_{N,P,M}. $$

(5.20)

Proof

We know that

$$\begin{aligned} \left\Vert\mathcal{E}_{N,P,M}\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} &=\Big|\Big|{{\int}_{1}^{2}} \rho(\eta) ({\!}^{c}_{0}D^{\eta}_{t} u)_{N,P,M}(x,y,t) d\eta\\ &\quad+B_{1}(x,y){{\int}_{0}^{1}} \sigma(v) ({\!}^{c}_{0}{D^{v}_{t}} u)_{N,P,M}(x,y,t) dv\\ &\quad+B_{2}(x,y) u_{N,P,M}(x,y,t) -B_{3}(x,y) (\frac{\partial^{2}} {\partial x^{2}}u)_{N,P,M}(x,y,t)\\ &\quad-B_{4}(x,y) (\frac{\partial^{2}} {\partial y^{2}}u)_{N,P,M}(x,y,t)-f(x,y,t)\Big|\Big|_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})}\\ &=\Big|\Big|{{\int}_{1}^{2}} \rho(\eta) ({\!}^{c}_{0}D^{\eta}_{t} u)_{N,P,M}(x,y,t) d\eta\\ &\quad+B_{1}(x,y){{\int}_{0}^{1}} \sigma(v) ({\!}^{c}_{0}{D^{v}_{t}} u)_{N,P,M}(x,y,t) dv\\ &\quad+B_{2}(x,y) u_{N,P,M}(x,y,t)-B_{3}(x,y) (\frac{\partial^{2}} {\partial x^{2}}u)_{N,P,M}(x,y,t) \end{aligned} $$

$$\begin{aligned} &\quad-B_{4}(x,y) (\frac{\partial^{2}} {\partial y^{2}}u)_{N,P,M}(x,y,t) -{{\int}_{1}^{2}} \rho(\eta) {\!}^{c}_{0}D^{\eta}_{t} u(x,y,t) d\eta\\ &\quad-B_{1}(x,y){{\int}_{0}^{1}} \sigma(v) {\!}^{c}_{0}{D^{v}_{t}} u(x,y,t) dv-B_{2}(x,y) u(x,y,t)\\ &\quad+B_{3}(x,y) \frac{\partial^{2}} {\partial x^{2}}u(x,y,t)+B_{4}(x,y) \frac{\partial^{2}} {\partial y^{2}}u(x,y,t)\Big|\Big|_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} \end{aligned} $$

$$ \begin{aligned} & \le {{\int}_{1}^{2}} \left\Vert\rho(\eta)\right\Vert \left\Vert{\!}^{c}_{0}D^{\eta}_{t} u(x,y,t)-({\!}^{c}_{0}D^{\eta}_{t} u)_{N,P,M}(x,y,t))\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} d\eta\\ &+\left\vert{B_{1}(x,y)}\right\vert{{\int}_{0}^{1}} \left\Vert{\sigma(v)}\right\Vert \left\Vert{{\!}^{c}_{0}{D^{v}_{t}} u(x,y,t)-({\!}^{c}_{0}{D^{v}_{t}} u)_{N,P,M}(x,y,t))}\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})} dv\\ &+\left\vert B_{2}(x,y)\right\vert \left\Vert u(x,y,t)-(u_{N,P,M})(x,y,t)\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})}\\ &+\left\vert B_{3}(x,y)\right\vert \left\Vert\frac{\partial^{2}} {\partial x^{2}}u(x,y,t)-(\frac{\partial^{2}} {\partial x^{2}}u)_{N,P,M}(x,y,t))\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})}\\ &+\left\vert B_{4}(x,y)\right\vert \left\Vert\frac{\partial^{2}} {\partial y^{2}}u(x,y,t)-(\frac{\partial^{2}} {\partial y^{2}}u)_{N,P,M}(x,y,t))\right\Vert_{\mathcal{L}^{2}_{\omega^{\alpha}_{LlT}}(\tilde{\Omega})}\\ & \le (\lambda\mathcal{\tilde{J}}+\mu \mathcal{\tilde{A}}_{1}\mathcal{\tilde{K}}+\mathcal{\tilde{A}}_{2}\mathcal{\tilde{H}}+\mathcal{\tilde{A}}_{3}\mathcal{\tilde{B}}+\mathcal{\tilde{A}}_{4}\mathcal{\tilde{F}}) \mathcal{\tilde{R}}_{N,P,M}. \end{aligned} $$

(5.21)

Therefore, for enough large values of M;N;P, we get $\left \Vert \mathcal {E}_{N,P,M}\right \Vert _{{\mathscr{L}}^{2}_{\omega ^{\alpha }_{LlT}}(\tilde {\Omega })} \rightarrow 0$. □

6 Illustrative examples

In this section, four numerical examples represent the 1D and 2D DOTFTE models are presented to manifest the high accuracy of the proposed algorithms and illustrate the agreement of the theoretical analysis with numerical results. All computations are carried out by using Mathematica 12.2, on a DESKTOP-2L1UJVK with the processor: Intel(R) Core(TM) i3-6100 CPU, 3.70GHz and 8.00G RAM, with 64 bit operating system.

Let us define the maximum absolute error (MAE) as follows:

$$\underset{(x,t)\in {\Omega}}{\max} |u(x,t)-u_{N,M}(x,t)|, \underset{(x,y,t)\in {\Omega} \times {\Lambda}}{\max} |u(x,y,t)-u_{N,P,M}(x,y,t)|.$$

Example 1

Consider the following 1D DOTFTE:

$$ {{\int}_{1}^{2}} {\Gamma}(6-\eta) {\!}^{c}_{0}D^{\eta}_{t} u(x,t) d\eta+ B_{1}{{\int}_{0}^{1}} \sigma(v) {\!}^{c}_{0}{D^{v}_{t}} u(x,t) dv+B_{2} u(x,t)= B_{3}\frac{\partial^{2}u(x,t)} {\partial x^{2}}+f(x,t), $$

(6.1)

where the source term is

$$f(x,t)= \Big[\frac{120 (t-1) }{\ln(t)}+120 B_{1} t^{2}{{\int}_{0}^{1}} \frac{\sigma(v) t^{-v}}{\Gamma(6-v)}dv+(B_{2}+B_{3})t^{2}\Big] t^{3} \sin(x),$$

with L = 1,τ = 0.5 and the ICs and BCs are given from the exact solution $u(x,t)=t^{5} \sin \limits (x)$.

Table 1 displays the MAEs of the 1D multi-case model given by example 1 at various choice of coefficients, values of N=M and weight functions σ(v) with α = 0.5. Cases 1 and 2 represent the 1D DOTFTE with variable and constant coefficients, respectively. Cases 3 and 4 represent the 1D DOTFDWE with variable and constant coefficients respectively. Cases 5 and 6 stand for the 1D DOTFDWED with variable and constant coefficients, respectively. The absolute errors of case 1 with α = 0.00001 and 1 are plotted in Fig. 1.

Table 1 MAEs with α = 0.5 and M=N for example 1

Fig. 1

The surfaces of the absolute errors of case 1 with N = M = 8 for example 1

Example 2

Consider the following 1D DOTFDWE [31]:

$$ {{\int}_{1}^{2}} \mu^{\eta}~ {\!}^{c}_{0}D^{\eta}_{t} u(x,t) d\eta=\frac{\partial^{2}u(x,t)} {\partial x^{2}}, 0<x<1, 0<t \le 0.5 , $$

(6.2)

with the ICs and BCs:

$$ \begin{array}{cccc} \left\{ \begin{array}{lr} u(x,0)=x^{2}(1-x^{2}), \frac{\partial u(x,t)}{\partial t}|_{t=0 }=0, 0 \le x \le 1,\\ u(0,t)=0, u(1,t)=0, 0 \le t \le 0.5. \end{array} \right. \end{array} $$

(6.3)

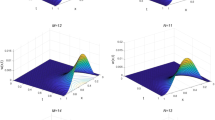
The weight function of example 2 has the form ρ(η) = μ^η where the parameter μ > 0 physically represents the relaxation time. Figure 2 demonstrates the effect of μ on the behaviour of the wave. It is noted that, with gradually increase of μ, the wave becomes higher. The graphical representation of our obtained results is in good agreement with the known results.

Fig. 2

The approximate solution of example 2 for μ = 1.5,3,4.5,6, respectively

Example 3

Consider the following 2D DOTFTE:

$$ \begin{aligned} {{\int}_{1}^{2}} {\Gamma}(\lambda +1-\eta)~ {\!}^{c}_{0}D^{\eta}_{t} u(x,y,t) d\eta&+2 e^{(x+y)}{{\int}_{0}^{1}} {\Gamma}(\lambda +1-v)~ {\!}^{c}_{0}{D^{v}_{t}} u(x,y,t) dv\\ &+\sin^{2}(x+y)u(x,y,t)=(1+x^{2})\frac{\partial^{2}u(x,y,t)} {\partial x^{2}}\\ &+(1+y^{2})\frac{\partial^{2}u(x,y,t)} {\partial y^{2}}\\ &+f(x,y,t), 0<x,y<1,~~ 0<t \le 0.5 , \end{aligned} $$

(6.4)

where

$$ f(x,y,t)=16\Big[\frac{\Gamma(\lambda +1 )(t-1) t^{\lambda-2}}{\ln(t)}(1+2te^{(x+y)})+t^{\lambda}(\sin^{2}(x+y)-x^{2}-y^{2}-2)\Big]e^{(-x-y)}, $$

and the ICs and BCs can be defined from the exact solution u(x,y,t) = 16t^λe^(−x−y).

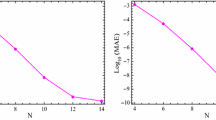
The MAEs for various values of λ are presented in Table 2. The obtained MAEs show the accuracy of the proposed method for smooth and non-smooth solutions.

Table 2 MAEs with α = 0.5 and M=N=P for example 3

Example 4

Consider the following multi-cases 2D distributed-order equation:

$$ \begin{aligned} {{\int}_{1}^{2}} {\Gamma}(5-\eta)~ {\!}^{c}_{0}D^{\eta}_{t} u(x,y,t) d\eta&+B_{1} \frac{\partial u(x,y,t)} {\partial t} =B_{2}\frac{\partial^{2}u(x,y,t)} {\partial x^{2}}\\ &+B_{3}\frac{\partial^{2}u(x,y,t)} {\partial y^{2}}+f(x,y,t). \end{aligned} $$

(6.5)

where

$$ f(x,y,t)=\Big[\frac{24 (t-1) }{\ln(t)}+4t B_{1}+\pi^{2} t^{2}(B_{2}+B_{3})\Big] t^{2}\sin(\pi x)\sin(\pi y).$$

The ICs and BCs can be obtained from the exact solution $u(x,y,t)=t^{4}\sin \limits (\pi x)\sin \limits (\pi y)$.

• Case 1 (variable coefficients 2D DOTFDWED): B₁ = 2xy,B₂ = x²,B₃ = y².

• Case 2 (variable coefficients 2D DOTFDWE): B₁ = 0,B₂ = x²,B₃(x,y) = y².

• Case 3 (constant coefficients 2D DOTFDWED): B₁ = B₂ = B₃ = 1.

• Case 4 (constant coefficients 2D DOTFDWE): B₁ = 0,B₂ = B₃ = 1.

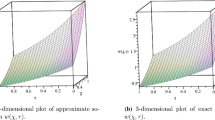
The MAEs at various time levels of cases 1 and 2 of example 4 are listed in Table 3 with M = 4, N = P and α = 0.5. Figure 3 shows the approximate solution and absolute error surfaces of case 3 at time level t = 0.5 with M = 4, N = P and α = 0.5. In Table 4, the MAEs of case 4 with (α = − 0.49, n= 10) and (α = 1, n=N) for M = 4,N = P are listed and compared with the element-free Galerkin method [32] based on Gauss-Legendre quadrature with (h^− 1 = 20, n= 25) and (n= 0.5τ^− 1 with random points) for various time step size τ where h is the computational domain size and n denotes the number of nodes. The numerical results demonstrate the effectiveness and the accuracy of our proposed method in comparison with the results [32].

Table 3 MAEs with M = 4 and N = P for case 1 and case 2 of example 4

Fig. 3

The approximate solution and absolute error with M= 4, N=P= 10 at t = 0.5 for case 3 of example 4

Table 4 Comparison of MAEs with M = 4 and N = P for case 4 of example 4

7 Conclusion

In this paper, the DOTFTEs in multi-dimensions were considered where the distributed-order over the intervals ]1,2] and ]0,1] are existed simultaneously. The certain choices of the density function and the coefficients can give the so-called DOTFDWED and DOTFDWE which are relevant to sub/super-diffusive processes; therefore, the existence of the accurate solutions of these equations is required.

The main objective of this paper was to offer improved and accurate spectral tau algorithms for numerical solutions of the aforementioned equations in multi-dimensions with constant and variable space coefficients based on a novel operational matrix of distributed-order fractional derivative of SG polynomials. A new operational matrix of the multiplication of space vectors has been built to have the ability in applying the tau method in the 2D DOTFTE. The convergence analysis of the presented algorithms has been discussed. The numerical solutions obtained by the proposed spectral tau algorithms have high accuracy with a small number of basis functions for smooth and non-smooth solutions as shown from the test examples. For non-smooth solutions, we used a smooth transformation by using SG polynomials to avoid the convergence deteriorated.