1 Introduction

Understanding the mechanisms which influence chaotic movement and nonlinear dynamics of gas bubbles in a liquid is a scientific as well as engineering issue. It is due to a wide range of applications because they are found in chemical engineering, the nuclear industry, the pharmaceutical industry and others [1,2,3]. Moreover, currently conducted research is aimed at a better understanding of the impact of the methane bubbles flow in underwater environments on the global balance of greenhouse gases [4, 5]. Therefore, it is necessary to understand the processes of bubble formation, bubble flow and its stability. The experimentally and numerically investigations of the bubble formation [1, 6], bubble coalescence [7, 8], gas bubble trajectories [9, 10] or chaotic bubble behaviours [11,12,13] are still conducted.

The bubble departure frequency can be divided into two periods: waiting time and growth time. The growth time is the period of time between bubble formation and departure following after growth at the nozzle [1, 5], while waiting time is the moment after the bubble departures and a new bubble appears in the nozzle [14]. The evolution of a bubble from its beginning to departure is called bubble dynamics. Many efforts indicate that the character of bubble dynamics is nonlinear [15].

The interest in nonlinear analysis of bubble dynamics has increased, and some experimental and theoretical papers have been created. Tritton and Egdell [16] in their experimental study analysed beaker on bubbling from an upwardly pointing vertical tub of an internal diameter of 1.2 mm in which the working fluid was a water–glycerol mixture of 24% by volume of water. Authors noticed chaotic behaviour in the inter-pulse return mass period-doubling sequence, which caused a period-doubling sequence. To the analysis, they used the signal from a hot-film anemometer probe. Those results were confirmed by Mittoni et al. [17], they conducted the experiment with a slightly broader range of the injection nozzle diameter (0.8, 1.0, 1.2 and 1.4 mm) and gas injection flow rates (0.3, 0.42, 0.52 and 0.65 l/min). However, the dynamics bubbling for chamber volume dynamics influence only at gas flow rates lower than 0.65 l/min. In the study of Ruzicka et al. [18], the chaotic features of bubbling from a submerged nozzle above the chamber were detected. It has been shown that Kolmogorov entropy and correlation dimension of the attractor have been qualified as indicators of hydrodynamic regime transitions.

In addition, the nonlinear analyses of bubble departure from the orifice or nozzle have been summarized in papers [19,20,21,22,23,24,25,26,27]. The above works indicate that the behaviour of bubble formations [20, 23, 26, 27] and the processes taking place in the gas supply system during bubble departures [19, 21, 22, 24] are responsible for the appearance of chaotic bubble departure.

As shown in the paper [28], chaotic systems can be synchronized because they have positive Lyapunov exponents. The use of the Lyapunov exponent in the papers [29,30,31] allowed authors to control and test the synchronization of spacecraft, nuclear spin generator and finance modelling. In our previous work [22], we proposed the cross-recurrence plot (CRP) method to identify the mutual relationships between pressure fluctuations and the depth of liquid penetrations into the nozzle. It has been shown that the chaotic bubbles departure occurs when the correlation between pressure fluctuations and the depth of liquid penetration into the nozzle decreases. CRP method was used to assess the synchronization between the two mentioned time series. The applied analysis has not completely answer the question, whose processes are accompanied for the periodic and chaotic bubble departures (gas supply system or liquid flow inside the nozzle). This involves the use of different types of signals (generated by various physical systems) in the CRP method. The recurrence occurring in the analysed signals is related to the bubble departures. Therefore, to understand which process is responsible for initiating non-periodic bubble departures, the recurrence synchronization must be considered. Such an analysis can be performed using the joint recurrence plot (JRP) [32,33,34].

This article presents the novel approaches to the analysis of the behaviour of the synchronization between the air pressure fluctuations and the depth of liquid penetrations into the nozzle using JRP.

The structure of the thesis is as follows: the experimental set-up and data characteristics are presented in Chapter 2, Chapter 3 contains the methodology of nonlinear data analysis, the results of data analysis are described in Chapter 4, and discussion is included in Chapter 5. The final conclusion is made in the last chapter.

2 Experimental set-up and data characteristics

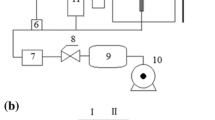
Experimental set-up used to investigate the bubble departure under constant conditions is shown in Fig. 1. During the experiment, a square glass tank (300 mm × 150 mm × 700 mm) was filled with distilled water. The air bubbles were generated through a glass nozzle located at the bottom of the central section of the tank. The length of the nozzle was equal to 75 mm, and the inner diameter of the nozzle was equal to 1 mm. The water temperature was equal to 20 ± 0.1 °C and was measured with the Maxim DS18B20 digital thermometer (with an accuracy of 0.1 °C). The Bronkhorst flow meter was used to measure the air volume flow rate (q) which was considered in two cases at q = 0.023 l/min and q = 0.026 l/min. The range of the air volume flow rate (q) was selected so that the process of liquid penetration into the nozzle was visible. (It is not clearly visible for the other air volume flow rates.) The gas to the nozzle was supplied by an air pump. The pressure in the air tank (p) was set by proportional pressure reducing valve Metalwork Regtronic. The adjustable range of pressure was from 0.05 to 10 bar, with accuracy of 0.5%. The air pressure was set at 0.3 bar. Air pressure fluctuations were measured using the MPX12DP silicon pressure sensor with a sensitivity of 5.5 mV/kPa.

Fig. 1
figure 1

Scheme of experimental set-up: 1—glass tank (300 × 150 x 700 mm), 2—nozzle, 3—pressure sensor, 4—flow meter, 5—air valve, 6—air tank, 7—pressure regulator, 8—air pump, 9—high-speed camera, 10—screen, 11—light source, 12—phototransistor, 13—laser, 14—data acquisition system

Full size image

Time series of air pressure changes were recorded using the data acquisition system (Data Translation DT9804) with a sampling frequency of 1 kHz and a resolution of 16 bits. These time series were resampled using linear interpolation method with a sampling frequency of 5 kHz.

The phenomenon was recorded using a high-speed digital video camera (Phantom v1600) at the rate of 5000 fps. The duration of each video was 15 s. Images contained 512 × 768 pixels displaying grayscale. In order to conduct analyses, videos of the liquid penetration into the nozzle were divided into frames. Examples of the obtained time series of liquid penetration into the nozzle (h) are shown in Fig. 2.

Fig. 2
figure 2

Time series of the depth of liquid penetration into the glass nozzle for studied air volume flow rates, a q = 0.023 l/min, b q = 0.026 l/min

Full size image

Fluctuations in the maximum depth of liquid penetration into the nozzle indicate the character of bubble departures. When the maximum depth of the liquid penetration into the nozzle changes slightly, it means that the liquid penetration occurs almost periodically. Significant changes in the maximum depth of liquid penetration into the nozzle indicate the chaotic nature of this process. The analysis of changes of the maximum depth of liquid penetration over time determines the time periods in which this process is chaotic or almost periodic.

The periods in which the liquid penetration into the nozzle is almost periodic are marked with the symbol I. During this period, the amplitude of fluctuations of maximum depth of liquid penetration is less than 5% and the largest Lyapunov exponent is in the range of 0.86 bit/s to 1.94 bit/s (Table 1). Periods in which liquid penetration into the nozzle is chaotic are marked with symbol II, and the values of the largest Lyapunov exponent are equal to 16.27 bit/s, 10.77 bit/s and 14.62 bit/s. The deviation of liquid penetration into the nozzle (less or more than 5%) was estimated based on the mean value of liquid penetration in the analysed time series. The mean value of liquid penetration for q = 0.023 l/min was about 5.65 mm and for q = 0.026 l/min was about 5.15 mm.

Table 1 Time delay (τ) and the largest Lyapunov exponent (λ) for periods marked I and II in Fig. 2
Full size table

The largest Lyapunov exponent was calculated according to the following formula [35]:

$$ L = \frac{1}{t}\mathop \sum \limits_{j = 1}^m {\log_2}\frac{{d\left( {{x_{j + 1}}} \right)}}{{d\left( {x_j} \right)}}$$
(1)

where m is the number of examined points, t—time of evolution, d(xj)—distance between points at t = 0, and d(xj)—distance between points at t = te.

The shape evolution of the bubbles over time during the process of bubble departure in the liquid is shown in Fig. 3. The presence of water inside the nozzle is marked by pixels with the higher brightness.

Fig. 3
figure 3

Video frames of liquid penetration into the nozzle, air volume flow rate was equal to 0.023 l/min, the single cycle of bubble departure was recorded on 478 frames

Full size image

An example of the time series of the pressure changes in the gas supply system is shown in Fig. 4.

Fig. 4
figure 4

Time series of pressure changes in the gas supply system for studied air volume flow rates, a q = 0.023 l/min, b q = 0.026 l/min

Full size image

In Fig. 4, the time periods (I, II) are the same as in Fig. 2. We can notice that in all time periods the pressure changes in the gas supply system are chaotic. To confirm our statement in Table 2, the values of time delay (τ) and the largest Lyapunov exponent (λ) are presented. For each case, the largest Lyapunov exponent remains positive.

Table 2 Time delay (τ) and the largest Lyapunov exponent (λ) for periods marked I and II in Fig. 4
Full size table

The bubble departure is identified by the minimum value of air pressure fluctuations. Such a minimum will occur almost periodically when the time series of pressure fluctuations in the gas supply system is synchronized with the nearly periodic time series of the depth of liquid penetration into the nozzle.

Because pressure changes are chaotic, the synchronization will never be complete. One of the methods which can be used to analyse the degree of synchronization of chaotic systems is the JRP method [36].

3 Methodology of nonlinear data analysis

The recurrence plot (RP) is a tool developed by Eckmann et al. [37] to visualize and analyse the behaviour of the dynamic system. RP is the square matrix (NxN) representing states of the system embedding in the m-dimensional phase space. From the formal point of view, RP is described by the following relation:

$$ R_{{i,j}} = \theta \left( {\varepsilon - \left\| {x_{i} - x_{j} } \right\|} \right),\,x_{i} \in \mathbb{R}^{m} ,i,j - 1...N, $$
(2)

where N is the number of states under consideration, \(\varepsilon\) is a threshold distance, || || is a norm, θ (·) is the Heaviside function, ℝ is a set of real numbers and i, j is a number of points.

The first step to obtain the RP is the attractor reconstruction. The proper attractor reconstruction requires the time delay (τ) estimation. The method which is used to determine τ is the mutual information method [38, 39], in which the first minimum of the following function is treated as the proper value of τ:

$$ I\left( {x_{i} ,x_{i + \tau } } \right) = \mathop \sum \limits_{{x_{i + \tau } }} \mathop \sum \limits_{{x_{i} }} p\left[ {x_{i} ,x_{i + \tau } } \right]{\text{log}}\left\{ {\frac{{p\left[ {x_{i} ,x_{i + \tau } } \right]}}{{p\left[ {x_{i} } \right],p\left[ {x_{i + \tau } } \right]}}} \right\} $$
(3)

where \(p\left[ {x_{i} ,x_{i + \tau } } \right]\) is the joint probability function of \(\left\{ {x_{i} } \right\}\) and\(\left\{{x}_{i+\tau }\right\}\), \( p\left[ {x_{i} } \right] \) and \(p\left[{x}_{i+\tau }\right]\) which are the marginal probability distribution functions of \(\{{x}_{i}\}\) and\(\left\{{x}_{i+\tau }\right\}\).

In order to calculate the proper embedding dimension (m) of the attractor, the false nearest neighbours (FNN) algorithm is used [40]. The main idea of this method is to determine how the number of adjacent points in the embedding space changes with the increase in the embedding dimension. Points which disappear with the embedding dimension increase are called false neighbours. The dimension for which the fraction of false neighbours is zero is treated as the proper embedding dimension.

The number of recurrence points on the RP is related to the value of threshold (ε) [40]. The algorithm of calculating the proper value of the ε has been considered by many authors [41,42,43]. We chose that the value of ε is equal to 10% of the maximum attractor diameter [43].

The points of the RP create structures of various shapes, which are related to the character of system dynamics. The structures of points on the RP are characterized by recurrence quantification analysis method (RQA) [43].

The joint recurrence plot (JRP) is an expanded recurrence plot which is used to visualize the dynamics properties of two time series. The JRP analysis is carried out with the use of RP created separately for the two analysed systems. On the JRP remains the points which belong to both RP. From the formal point of view, JRP is described by the following formula [33]:

$$ JRP_{{i,j}} = \theta \left( {\varepsilon _{x} - \left\| {x_{i} - x_{j} } \right\|} \right) \cdot \theta \left( {\varepsilon _{y} - \left\| {y_{i} - y_{j} } \right\|} \right),\,x_{i} \in \mathbb{R}^{m} ,\,y_{i} \in R^{m} ,i,j = 1,...,N $$
(4)

When the systems are synchronized, their recurrence appears at the same time. In the synchronization theory, one of the systems is called the master and the other the slave [36]. The “stronger” system (master) directs the “weaker” system (slave)—the slave system adapts to the behaviour of the master system. The measure of the synchronization is the synchronization error which is the difference between the parameters describing the same feature of the synchronized systems [36, 44]. The following types of synchronization are defined [36, 44, 45]: complete synchronization, partial synchronization, practical synchronization, exact synchronization and almost synchronization.

The number of JRP points is a measure of the recurrence similarity. The measure of the number of points in the JRP is the recurrence rate (RR) coefficient which is calculated using the JRQA method [32, 34]. RR is the percentage measure of the number of JRP points [33]:

$$ {\text{RR}} = \frac{1}{{N^{2} }}\mathop \sum \limits_{i,j = 0}^{N} R_{i,j} $$
(5)

4 Results of nonlinear data analysis

In the windowed JRQA method, JRQA is calculated for subsequent time windows with constant length which are shifted by a constant number of samples. The windowed JRQA coefficients and the parameters of τ, m and ɛ were calculated in each moving window containing 5000 samples (1 s). The window was shifted by 1250 samples (0.25 s). The length of the analysed time series was equal to 20 000 samples (4 s).

Examples of the RPs of the pressure changes in gas supply system signals and the depth of the liquid penetration into the nozzle for air volume flow rate 0.023 l/min are shown in Fig. 5.

Fig. 5
figure 5

RPs for the time series of the liquid penetration into the nozzle and the air pressure in the gas supply system for the air volume flow rate q = 0.023 l/min. a Time series of pressure in the gas supply system, b time series of the liquid penetration inside the nozzle. The values of m were calculated using the FNN algorithm, τ were calculated using a mutual information method, and ε was calculated as 10% of attractor diameter in m-dimensional space

Full size image

An example of the JRP for the air volume flow rate equal to 0.023 l/min is shown in Fig. 6.

Fig. 6
figure 6

JRP for time series of the depth of liquid penetration into the nozzle (horizontal) and the pressure changes in the gas supply system for air volume flow rate of q = 0.023 l/min

Full size image

On the RPs and JRP (Figs. 5 and 6) occur diagonal lines with single recurrence points and solid diagonal lines. The dashed diagonal lines are typical for chaotic processes, whereas the solid diagonal lines are typical for periodic processes. The RPs show that longer periods of stable process occur for the depth of liquid penetration into the nozzle (Fig. 5 b) than for the pressure changes in the gas supply system (Fig. 5 a). Comparing both RPs, the distance between the diagonal lines is similar; hence, the frequencies of pressure changes and liquid penetration changes slightly differ. The obtained JRP shows that during the bubble departure from the nozzle we observed synchronization (the occurrence of solid diagonal line) and desynchronization (the occurrence of dashed diagonal line) of processes of liquid penetration into the nozzle and pressure changes. The distance between the diagonal lines is not constant, which means that the synchronization periods change chaotically. The windowed JRQA method was used to explain the phenomenon of synchronization of liquid penetration into the nozzle and pressure changes processes.

In Figs. 7 and 8, the changes of τ and RR for depth of liquid penetration into the nozzle and air pressure fluctuations are shown for two analysed air volume flow rates—q = 0.023 l/min and q = 0.026 l/min. The results shown in Figs. 7a and 8a indicate that the value of τ is greater for changes in the depth of liquid penetration into the nozzle compared to τ obtained for air pressure fluctuations. Moreover, it can be seen that the RR coefficient (Figs. 7b and 8b) for the depth of liquid penetration changes monotonically (increase or decrease), while the RR coefficient for the air pressure fluctuations changes chaotically. Differences in τ and RR coefficient changes for the liquid penetration into the nozzle and the air pressure fluctuations mean that the air pressure fluctuations are more chaotic than changes of the depth of liquid penetration into the nozzle.

Fig. 7
figure 7

The parameters of τ and RR of windowed JRQA (black solid line) for time series of the depth of liquid penetration into the nozzle (grey solid line) and the air pressure fluctuations (grey dashed line) for air volume flow rate of q = 0.023 l/min (1250 samples). a Time delay (τ), b RR. (Color figure online)

Full size image
Fig. 8
figure 8

The parameters of τ and RR of windowed RQA and JRQA (black solid line) for time series of depth of liquid penetration into the nozzle (grey solid line) and air pressure fluctuations in gas supply system (grey dashed line) for air volume flow rate of q = 0.026 l/min (1250 samples). a) Time delay (τ), b RR. (Color figure online)

Full size image

5 Discussion

In order to identify mechanisms allowing for stabilization of periodic bubble departure, the numerical simulations of liquid penetration into the nozzle were used. The liquid movement inside the nozzle is described by the following equation [3, 6]:

$$ \frac{d}{dt}\left\{ {\left[ {\frac{4}{3}\rho_{l} \pi r_{n}^{2} x_{l} + \rho_{l} \frac{4}{3}\pi \left( {2r_{n} } \right)^{3} } \right]\frac{{dx_{l} }}{dt}} \right\} = F_{1} - F_{2} $$
(6)

The force F1 is related to the pressure difference that occurs in the system [3, 6]:

$$ F_{1} = - s\Delta p = - \pi r_{n}^{2} \left[ {p_{c} \left( t \right) - \left( {p_{h} + \rho_{l} g\left( {2x_{l} } \right) + 2\frac{\sigma }{{r_{n} }} - \frac{{\rho v_{pp} \left| {v_{pp} } \right|}}{2}} \right)} \right] $$
(7)

The force F2 is related to the resistance of the movement of the liquid in the nozzle and is described by the following formula [3, 6]:

$$ F_{2} = 8C_{o} \pi \mu_{l} x_{l} \frac{{{\text{d}}x_{l} }}{{{\text{d}}t}} $$
(8)

where rn is the nozzle diameter (m), xl is the depth of the liquid penetration into the nozzle (m), σ is the surface tension (N/m), ρl is the liquid density (kg/m3), μl is the liquid viscosity (kg/ms), s is the cross-sectional area of the nozzle (m2), pc is the gas pressure in the plenum chamber (Pa), ph is the hydrostatic pressure, vpp is the velocity of the liquid around the growing bubble (m/s), and Co = 2 drag coefficient of moving water inside the capillary [3, 6].

A criterion for the end of the liquid movement is xl = 0.

According to experimental investigations of periodic bubble departures described in the paper Dzienis and Mosdorf [21], it can be assumed that the transition between chaotic and periodic processes is preceded by significant changes of minimum and maximum pressure values. The minimum value of pressure was modified by liquid velocity above the nozzle, generated by the departing bubbles. The changes in pmin cause the changes in Δp and its effects on pmax [46]. The character of changes of liquid velocity is nonlinear. Therefore, in the numerical simulation the values of the minimum pressure in the gas supply system were changed. Those values were selected based on experimental investigations and were changed in the range 5200–5900 Pa, with the step equal to 100 kPa. The air volume flow rate supplied to the nozzle was constant and was equal to 0.020 l/min. The depth of liquid penetration inside the nozzle and pressure changes for one cycle of bubble departure were simulated.

In Fig. 9, the numerical results of liquid movement inside the nozzle and pressure changes for one cycle of bubble departures—pmin = 5200 Pa and pmin = 5900 Pa—are shown.

Fig. 9
figure 9

Liquid movement inside nozzle and pressure changes for one cycle of bubble departures—pmin = 5200 Pa and pmin = 5900 Pa. a Liquid movement inside nozzle, b pressure changes

Full size image

The force F1 (Eq. 7) and F2 (Eq. 8) affect the depth of liquid penetration into the nozzle. The increase in force F1 reduces in the depth of liquid penetration into the nozzle. The force F1 depends on the hydrostatic pressure, pressure in the gas supply system and liquid velocity above the nozzle. In our numerical studies, the initial values of the hydrostatic pressure and the liquid velocity into the nozzle were constant, so the changes in F1 are caused by the pressure changes in the gas supply system. When the pressure in the gas supply system is higher, the liquid penetration into the nozzle is lower because the higher pressure causes more resistance to the liquid as it penetrates the nozzle. It causes the less volume of water which is involved in the liquid penetration process. Consequently, time of liquid penetration decreases. The decrease in time of liquid penetration caused a decrease in pmax.

In Fig. 10, the dimensionless time between appearance of maximum value of liquid penetration into the nozzle and appearance of maximum value of pressure (pmax) versus the pmin, for air volume flow rates—0.23 l/min and 0.26 l/min—is shown.

Fig. 10
figure 10

The dimensionless time between appearance of maximum value of liquid penetration into the nozzle and appearance of maximum value of pressure (pmax) vs the initial value of pmin, for air volume flow rates—0.23 l/min and 0.26 l/min

Full size image

The dimensionless time between appearance of maximum value of liquid penetration into the nozzle and appearance of maximum value of pressure was estimated according to the following formula:

$$ t_{d } = \frac{{t_{{h{\text{max}}}} - t_{{p{\text{max}}}} }}{{t_{w} }} $$
(9)

where thmax is the time in which the depth of flooding reaches its maximum value, tpmax is the time in which the pressure in the gas supply system reaches its maximum value and twis the time of liquid penetration into the nozzle.

The increase in pmin causes an increase in dimensionless time. The loss of stability of bubble departures is preceded by an increase in pmin, which causes an increase in the time between extremes. It can be concluded that the chaotic bubble departures due to desynchronization between pressure changes in the gas supply system and liquid movement inside the glass nozzle. Moreover, the return to periodic bubble departure is preceded by a decrease in pmin, which is associated with a decrease in time between extremes.

This dimensionless time increase can be treated as the decrease in level of synchronization between liquid depth of the liquid penetration and pressure changes. Such phenomenon decreases the value of RR coefficient which is shown in Figs. 7 and 8. We can conclude that the stabilization of periodic bubble departures is preceded by a decrease in pmin. The similar results of decrease or increase in pmin were obtained in the paper [3]. The obtained results also confirm that the JRQA method can be used for synchronization analysis.

6 Conclusions

In the presented paper, the synchronization between the air pressure fluctuations and the depth of liquid penetration into the nozzle during bubble departures was investigated. The recurrence rate coefficient of the windowing joint recurrence quantification analysis is treated as the synchronization measure.

In the system under consideration, the periodic movement of an incompressible liquid (water) leads to non-periodic oscillations of gas pressure (due to gas compressibility). This situation is visible in period I—in Figs. 2 and  4. The calculated time delay (Figs. 7a and 8a) of the considered time series indicates that the pressure fluctuations are more chaotic in comparison with the changes of the depth of liquid penetration into the nozzle.

It can be seen that the RR coefficient for the depth of liquid penetration changes monotonically (increase or decrease) (Figs. 7b and 8b), while the RR coefficient for the pressure fluctuations changes chaotically (Figs. 7b and 8b). The RR coefficient for the JRP is determined by the RP properties for changes of the depth of liquid penetration into the nozzle. Because the RR coefficient in JRQA is a measure of the synchronization of two chaotic signals under consideration, finally we can conclude that the synchronization of the pressure changes and the depth of liquid penetration appears in the system when the periodic changes of the depth of liquid penetration occur in long period of time.

The simulations of the liquid penetration into the nozzle, pressure changes in the gas supply system, the dimensionless time between appearance of maximum value of liquid penetration into the nozzle and appearance of maximum value of pressure were calculated. It has been shown that the increase in pmin caused an increase in the dimensionless time. Comparison between simulation results and results of experimental data analysis shows that the loss of stability of periodic bubble departures is preceded by an increase in pmin.

The obtained results confirm the hypothesis proposed in the paper [22] in which it was postulated that the synchronization of pressure fluctuations and changes of the depth of liquid penetration into the nozzle is determined by the initial velocity of the liquid above the nozzle. When the velocity varies slightly for subsequent bubbles, bubbles depart periodically. When periodic bubbles departures occur in a long period of time, pressure fluctuations become almost periodic.

In future research, the presented method of JRQA can be used to analyse the stability of pressure changes in the gas supply system during the alternative bubble departures from two neighbouring nozzles.