The loss of synchronization between air pressure fluctuations and liquid flow inside the nozzle during the chaotic bubble departures

Abstract

The paper investigates the dynamics of bubble departures from a glass nozzle submerged in a tank filled with distilled water. Air pressure and liquid flow inside the nozzle are simultaneously recorded using a data acquisition system and a high speed camera. The recurrence plot and cross recurrence plot methods are used to identify the loss of synchronization between air pressure fluctuations and the depth of liquid flow inside the nozzle during chaotic bubble departures. We claim that the synchronization between pressure fluctuations and the depth of liquid penetration inside the nozzle is suppressed during chaotic bubble departures. The experimental results show agreement with the numerical findings. The results demonstrate that the non-linearities of processes occurring during liquid penetration inside the nozzle have a significant impact on the synchronization between the time histories of pressure and the corresponding depths of liquid penetration inside the nozzle.

1 Introduction

Synchronization and chaotic behaviour are fundamental properties of nonlinear systems [1–4]. These properties stem from the competitions of multiple solutions present in a multidimensional nonlinear system. The corresponding basin of attraction distributions together as well as their dimensions change with the system’s parameters, leading to different system responses through intermittencies, synchronizations, and bifurcations. The nonlinear dynamics of bubble departures from a glass nozzle submerged in a tank filled with fluid has been recently studied both experimentally and theoretically [5–8]. The experiments have found that the periodic bubble departures are often interrupted by a sequence of chaotically departing bubbles. The frequency of appearance of chaotic bubbles departure depends on the system’s conditions including a volume of plenum chamber [5] and air volume flow rate [6–8] (see the schematic plot in Fig. 1a). Consequently, during the chaotic bubble departures the duration and the depth of the liquid penetration into the nozzle showed also nonperiodic behaviour. Furthermore, the particular bubble sizes and paths were correlated with the depth of liquid penetration into the nozzle [5].

Fig. 1

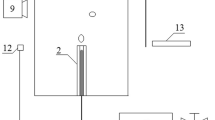
Experimental setup and the liquid (distilled water) penetration inside the nozzle. a Experimental setup: 1 glass tank, 2 light source, 3 camera, 4 data acquisition system, 5 glass nozzle, 6 pressure sensor, 7 flow meter, 8 air valve, 9 air tank, 10 air pumps; 11 plenum chamber with adjustable volume. b Examples of frames recorded by high speed camera illustrating liquid penetration inside the nozzle

On the other hand, there are models of bubble growth and liquid movement inside the nozzle that were proposed by Ruzicka et al. [9, 10]. It has also been found that the non-linear character of the pressure growth during the liquid penetration inside the nozzle amplifies the disturbance of initial condition of liquid penetration inside the nozzle. The non-linear behaviours of the bubbling process have been reported, among others in [6, 8, 9, 11–18]. Furthermore, the non-linear behaviours of bubbles flow in the liquid have also been discussed in [11, 19–26]. The effect of plate thickness, surface tension, liquid viscosity and the height of liquid column on the depth of liquid penetration into the nozzle has also been reported in [9, 12, 17, 26, 27].

In the present paper, we will analyze the synchronization between the plenum pressure fluctuations and the depth of liquid penetration into the nozzle. The nature of such synchronization is a measure of interactions between the air supply system and the ability of a liquid to transfer the air supplied (during this transfer the process of bubbles formation occurs).

To illustrate and identify the loss of synchronization between air pressure fluctuations and liquid flow inside the nozzle during the chaotic bubble departures, the wavelet, recurrence plot and cross recurrence plot methods colorblue are used in the present paper. Finally, the model of liquid flow inside the nozzle is also presented and the simulation results have been compared with the experimental findings.

2 Experimental setup and measurement techniques

In the experiment, bubbles were generated in a tank (300 mm $\times$ 150 mm $\times$ 700 mm) that was filled with distilled water by using a glass nozzle with an inner diameter of 1 mm. The length of the nozzle was 70 mm. The schematic design of the experimental setup is shown in Fig. 1a.

The distance between the nozzle and the plenum chamber was set to 100 mm. The volume of the plenum chamber could be adjusted in the range from 0 to 10 ml, but the volume of air supply system (pipes without the chamber) was 0.45ml. Consequently, the volume of gas supply system was regulated in the range from 0.45 to 10.45 ml. The volume of the connecting pipes (between the nozzle and the plenum chamber) was equal to 314 $\hbox {mm}^3$, while its length was 100 mm and its inner diameter was 1 mm.

In the analyzed case, the air volume flow rate was maintained constants at $q\,=\,0.00632\pm 0.00032$ l/min and the volume of air supply system was $V\,=\,0.45000\pm 0.00012$ ml. The air pressure fluctuations were measured with the use of a silicon pressure sensor, MPX12DP, with a sensitivity of 5.5 mV/kPa. The air volume flow rate, q, was measured by using the flow meter (MEDSON s.cSho-Rate-Europe Rev D, P10412A). The accuracy of the flow meter was equal to 5%. The air pressure was recorded by using a data acquisition system DT9804 with a sampling frequency of 2 kHz and 16 bits of resolution. The motion of liquid inside the nozzle was recorded with a high speed camera, the CASIO EX FX 1.

The measurements were conducted for different air volumes flow rates and different volume of air supply systems - the total number of measurements was equal to 50. The influence of these parameters on chaotic bubble departures was presented in the works [5, 7]. The same processes of loss of synchronization between the air pressure fluctuations and liquid flow inside the nozzle during the chaotic bubble departures were observed for all cases of measurements. The error of estimate of liquid position (distribution) inside the nozzle was equal to 1 pixel (about 0.158 mm).

The data and video images were recorded when the system was in a steady state by the system (approximately 15 min after changing in the air volume flow rate). The frames of the video illustrating the liquid penetration inside the nozzle are shown in Fig. 1b. The time period between the frames marked as “I” and “II” was 0.017s. The depth of the liquid penetration inside the nozzle was measured by using a computer program for analysing subsequent frames, which involved counting the number of pixels that had a brightness of greater than a certain brightness threshold on the each frame, along the nozzle wall. The threshold was adjusted for each video by comparing the results of the computer calculations with visual observations of the depth of liquid penetration into the nozzle as recorded in the video. The depth of liquid penetration inside the nozzle and the air pressure changes were recorded with different sampling frequencies, ranging from 600 Hz (for video) and 2 kHz (pressure measurement). The accuracy of the synchronisation was less than the time between the subsequent video frames (i.e., 1.666 ms). More detailed information about the experimental setup and experimental results is given in the works [5, 7]. Examples of the recorded time series of the changes in the depth of the liquid penetration inside the nozzle and the pressure fluctuations in the plenum chamber are shown in Fig. 2.

Fig. 2

Time series of the depth of the liquid penetration inside the nozzle $x_l$ and the air pressure in the plenum chamber p for air volume flow rate of $q\,=\,0.00632$ l/min and volume of plenum chamber of $V\,=\,0.45$ ml. In the horizontal axis, the label n denotes time expressed in the sampling units of $\delta t\,=\,0.0017\,\hbox {s}$, while $x_l$ was measured in pixels using a the digital camera and expressed in millimeters (1pixel $\approx 0.158$ mm)

The results confirm that there is a certain correlation of the liquid penetration, $x_l$, and the air pressure, p. The relationship between these quantities is the main subject of investigation in the subsequent sections of this paper.

3 Periodic and chaotic bubble departures

The impact of chamber volume and the height of the liquid over the orifice outlet on the frequency of bubble departures was studied in [27]. In particular, it was found the increase in the height of the liquid over the orifice outlet leads to an increase in the time period between subsequent bubbles [17]. Time period between departing bubbles decreases, when the number of gas–liquid interface oscillations inside the orifice decreases [8]. The phenomena of liquid movement inside the orifice or nozzle have been experimentally investigated and modelled by many researchers [10, 12, 27]. The works [5, 7] demonstrate that there are correlations between the flow of bubbles in the liquid over the nozzle outlet, gas and liquid flow inside the nozzle, the dynamics of gas pressure changes in the system supplying air to the nozzle (plenum chamber), the dynamics of bubble growth, its size and departure velocity.

It is worth observing that the pressure drop and its growth for subsequent bubble departures were predominantly studied phenomenologically [5, 7]. However, the main results indicated that the liquid penetration inside the nozzle was obviously affected by non-linear phenomena of the two phase flow [19, 28]. The explanation of the nature of the chaotic bubble departures requires taking account of the interactions between phenomena occurring in the plenum chamber and during the flow of bubbles in the liquid over the nozzle outlet. The dynamics of bubble growth is correlated with plenum pressure changes. The increasing plenum pressure decreases the depth of liquid penetration into the nozzle. Such an increase in the pressure also causes an increase in bubble growth velocity. This, in turn, leads to an increase in plenum pressure drop after the bubble departure, which causes an increase in the depth of liquid penetration into the nozzle.

4 Wavelet analysis

A wavelet is a small wave with a compact support. The wavelet analysis is a method which can be applied to follow the dynamics of studied phenomena simultaneously in two domains: time and frequency. The continuous wavelet transform (CWT) of a function (or corresponding time series) x(t) with respect to a mother wavelet $\psi (t)$ is defined as a convolution [29, 30]:

Fig. 3

Wavelet power spectra showing the liquid penetration inside the nozzle (a) and the air pressure in the plenum chamber (b) for the time series given in Fig. 2. Note, colours are assigned in the logarithmic scale (periods and sampling time were expressed in sampling time steps, $\delta t\,=\,0.0017\,\hbox {s}$)

$$\begin{aligned} W(s, \eta )\,=\,\int _{-\infty }^{\infty } x(t) \psi ^*_{s,\eta } (t) \mathrm{d} t, \end{aligned}$$

(1)

where

$$\begin{aligned} \psi ^*_{s,\eta } (t) \,=\, \frac{1}{\sqrt{s}} \psi \left( \frac{t-\eta }{s} \right) \end{aligned}$$

(2)

is a scaled and translated version of the mother wavelet $\psi (t)$, and the asterisk * on denotes its complex conjugate. The symbols s and $\eta$ are called a scale parameter and a translation parameter, respectively. The scale parameter controls the dilation ($s > 1$) and contraction ($s < 1$) of the wavelet, whereas the translation parameter, $\eta$, indicates the location of the wavelet in time. The wavelet power spectrum (WPS) of the signal representing the energy at scale s is defined as the squared modulus of the CWT:

$$\begin{aligned} P(s,\eta )\,=\,|W(s,\eta )|^2. \end{aligned}$$

(3)

In the present calculations we used a complex mother wavelet

$$\begin{aligned} \psi (y) \,=\, \pi ^{-1/4} \mathrm{e}^{i\omega _0y} \mathrm{e}^{-y^2/2}, \end{aligned}$$

(4)

where $\omega _0\,=\,6$ is the center frequency, also referred to the order of the wavelet.

Using a continuous wavelet transform we have analyzed the variations of pressure inside the plenum chamber and the corresponding volume (Fig. 2). The results are shown in Fig. 3a, b, respectively. Intermediate and short-term periodicities positions and their time evolution have been identified from the wavelet power spectrum of the pressure signal. Note that both diagrams (Fig. 3a, b) show a similar intermittency in bubbles dynamics. The characteristic periods coincide in the examined cases.

5 Non-linear data analysis

Generally, in non-linear analysis, involves performing reconstruction of dynamical attractor in certain embedding dimension, spanned on measured and reconstructed coordinates. Such an analysis provides information about properties such as system complexity and its stability.

In the present section we use the delayed coordinates method. The subsequent coordinates of attractor points are calculated basing on the sampling points of time series, between which the distance is equal to the time delay, $\tau$. Thus the subsequent coordinates defines the state vector, x, in the corresponding embedding phase space are as follows [31]:

$$\begin{aligned} \mathrm{\mathbf{x}}(t)\,=\, \left\{ x(t),x(t+\tau ),..., x(t+(n-1)\tau ) \right\} , \end{aligned}$$

(5)

where x corresponds to the measured time series and n is the dimension of the embedding space. The collection of x(t) defines the attractor.

In Fig. 4 we show the 3D attractor reconstructed from the time series of the pressure fluctuations and the depth of the liquid penetration inside the nozzle using different time delays, $\tau$.

Fig. 4

The attractor reconstructed from time series of the depth of the liquid penetration inside the nozzle and the air pressure in the plenum chamber for gas with a volume flow rate of $q\,=\,0.00632$ l/min and $V\,=\,0.45$ ml. a Pressure changes attractor with the time delay $\tau \,=\,47~\delta t$. b Attractor of the liquid penetration depth into the nozzle with the time delay $\tau \,=\,60~\delta t$. The sampling step, $\delta t$, was 0.0017 s

Usually, the dynamical attractor in n-dimensional space depends on time delay. For instance, if the time delay is too small, the attractor becomes flattened, which makes further analysis of its structure problematic. On the other hand this time delay cannot be too long as we can neglect some important time scale for the examined system dynamics. Fortunately, the mutual information between the time series: x(t) and $x(t+\tau )$ can be used to determine proper time delay for attractors reconstruction [31, 32]. The mutual information, I, can be defined as [33]:

$$\begin{aligned} I(x(t), x(t + \tau )) \,=\, \sum _{x(t+\tau )} \sum _{x(t)} p[x(t), x(t + \tau )]\log _2 \left\{ \frac{p[x(t),x(t+\tau )]}{p[x(t)]p[x(t+\tau )]} \right\} , \end{aligned}$$

(6)

where $p[x(t),x(t+\tau )]$ is the joint probability distribution function of x(t) and $x(t+\tau )$, and p[x(t)] and $p[x(t+\tau )]$ are the marginal probability distribution functions of x(t) and $x(t+\tau )$. Usually, as $\tau$ increases, the mutual information decreases, then it usually rises again. Note that the mutual information is equal to zero if x(t) and $x(t+\tau )$ are independent variables in a deterministic system. For the system effected by noise, it reaches a minimum value. The desired time delay, $\tau$, for the phase space reconstruction, could be fixed for the first minimum of I as a function of $\tau$.

Fig. 5

The mutual information for the time series of the depth of the liquid penetration inside the nozzle and the air pressure in the plenum chamber for gas with a volume flow rate of $q\,=\,$0.00632 l/min and $V\,=\,$0.45 ml. a Results for time series of pressure changes. b Results for time series of depth of the liquid penetration into the nozzle. The delay time, $\tau$ was measured in sampling time steps, $\delta t\,=\,0.0017$ s

Figure 5 shows the mutual information functions versus time delay (here, the number of sampling points) for the time series of the depth of the liquid penetration inside the nozzle and the air pressure in the plenum chamber. After careful examination these results, we report that for the time series of pressure fluctuations, the first minimum is reached for the time delay (the number of samples) amounting to 47, while for the time series of the depth of the liquid penetration inside the nozzle the time delay is equal to 60. Note that these values of time delay are used for attractors reconstructions which shown in Fig. 4. In the next step the false nearest neighbour algorithm [33, 34] was used to estimate the proper embedding dimension of estimated attractors. In this method the changes of the number of neighbours of points in the embedding space with increasing the embedding dimension are considered. For each sampled point, $x_i\,=\,x(t_i)$, the Euclidean distances to its nearest neighbour, $x_j$, are calculated, in m and in $m+1$ dimensional space. The point is treated as a false neighbour when the distance between points (i, j) becomes substantially larger with increasing the space dimension. Otherwise, the embedding dimension (see Eq. 5) is $n\,=\,m$. The number of false neighbours is calculated for the whole time series and for several dimensions until the fraction of false points reaches zero, or at least it becomes sufficiently small (in practice, lower than 1%). Such a dimension is treated as a proper embedding dimension for attractor reconstruction. Figure 6 shows the changes of fraction of the number of false neighbours versus the embedding dimension are shown. The results indicate that ($n\,=\,3$) and at the same time they demonstrate that the 3D reconstructed attractors presented in Fig. 4 are proper for the examined time series.

The recurrence plot is a technique of visualizing the recurrence of states $x_i$ in a n- dimensional phase space. The recurrence of states at the time i and at a different time j is marked within black dots in the 2D plot, where both axes are time axes. The recurrence plot is defined as [35]:

$$\begin{aligned} R_{i,j} \,=\, \Theta (\varepsilon - \parallel \mathrm{\mathbf x}_i - \mathrm{\mathbf x}_j \parallel ), \quad \mathrm{\mathbf x}_i \in {\mathfrak {R}}^n,\quad i,j \,=\, 1 ... N, \end{aligned}$$

(7)

where N is the number of considered states x $_i$, $\varepsilon$ is a threshold distance for states (expressed in the units of the standard deviation $\sigma _x$) which are identified as the same, $\parallel \cdot \parallel$ a norm and $\Theta ( \cdot )$ the Heaviside function.

Fig. 6

The changes of number of false nearest neighbours points for the time series of the depth of liquid penetration into the nozzle and the air pressure in the plenum chamber for gas with a volume flow rate of $q\,=\,$0.00632 l/min and $V\,=\,$0.45 ml

Fig. 7

Recurrence plot for the time series of the depth of the liquid penetration inside the nozzle and the air pressure in the plenum chamber for gas with a volume flow rate of $q\,=\,$0.00632 l/min and $V\,=\,$0.45 ml. j, and i on the axes denote the sampling time. a Time series of pressure changes, $n\,=\,$3, $\varepsilon \,=\,$ 0.8, $\tau \,=\,47~\delta t$. b Time series of the depth of liquid penetration into the nozzle, $n\,=\,$3, $\varepsilon \,=\,$ 1.5, $\tau \,=\,60~\delta t$ (sampling step, $\delta t\,=\,$0.0017 s). The calculations were made using the Matlab Toolbox [36]

A line parallel to the main diagonal line occurs when a segment of the trajectory runs parallel to another segment and the distance between trajectories is less than $\varepsilon$. The length of this diagonal line is determined by the duration interval of this phenomenon. On the other hand, a vertical (horizontal) line indicates a time in which a state either does not change or changes very slowly. The diagonal lines (structures) periodically occurring in the recurrence plot are characteristic of the periodic system. For quasi-periodic systems, the distances between the diagonal lines vary in time. Figure 7 shows the recurrence plots of pressure fluctuations and the depth of liquid penetrations liquid inside the nozzle. In the both recurrence plots one can observe the diagonal structures. The distance between them indicates the time period between subsequently departing bubbles. Note that this distance is not constant, which implies modulations. Such modulations occur as a result of the superimposed dynamical response characterized by an additional time scale [37]. In Fig. 7a it has been shown the three intervals marked by “I” and “II”. In the interval “I” the bubbles departed periodically. In this case, the recurrence plots reveal the presence of point structures parallel to the main diagonal lines. The distances between these point structures are the same. In turn, when the bubbles depart chaotically then the distances between the points structures and diagonal lines change in time. For a small depth of liquid penetration inside the nozzle the distances decreases. In this case, the frequency of bubble departures increases. On the border between the intervals “I” and “II” the distance between points structures and diagonal lines become larger than those observed in periodic bubble departures. The characteristic block pattern of the recurrence plots implies intermittent behaviour. Interestingly, the type of intermittency can be examined by more sophisticated statistics of multiple points appearance in the given square region [37, 39]. The recurrence rate, RR, is a measure of the percentage of recurrence points in the recurrence plot. It is defined as follows:

$$\begin{aligned} RR \,=\, \frac{1}{N(N-1)} \sum _{i,j\,=\,0}^N R_{i,j}, \end{aligned}$$

(8)

for $i \ne j$. The value of RR corresponds to the correlation sum [35].

Fig. 8

Recurrence rate, RR, versus $\varepsilon$ for the time series of the depth of liquid penetration into the nozzle and the air pressure in the plenum chamber for gas with a volume flow rate of $q\,=\,$0.00632 l/min and $V\,=\,$ 0.45 ml, for $n\,=\,$ 3, and $\tau \,=\,$ 60. As the RR tolerance criterion for $\varepsilon$ choice we proposed the smallest value for a linear slope part. The calculations have been made using the Matlab Toolbox [36]

Fig. 9

Recurrence rate, RR, vs. $\varepsilon$ for the CRP of time series of the depth of liquid penetration into the nozzle and the air pressure in the plenum chamber for gas with a volume flow rate of $q\,=\,0.00632$ l/min and $V\,=\,0.45\,\hbox {ml}$. Embedding and threshold parameters: $m\,=\,$3, $\varepsilon \,=\,$0.8, $\tau \,=\,$ 60. The calculations have been made using the Matlab Toolbox [36]

Fig. 10

The CRP of time series of the depth of liquid penetration into the nozzle (horizontal axis-black in the upper panel) and the air pressure (vertical axis-red in the upper panel) in the plenum chamber for gas with a volume flow rate of $q\,=\,0.00632$ l/min and $V\,=\,0.45\,\hbox {ml}$. In the upper panel, the air pressure line (in red) is slightly ahead the depth of liquid penetration line (in black). Embedding and threshold parameters: $m\,=\,$ 3, $\varepsilon \,=\,$ 0.8, $\tau \,=\,$ 60. The calculations have been made using the Matlab Toolbox [36]. The axes of the CRP correspond to the time in the sapling units. (Colour figure online)

Fig. 11

Recurrence rate of windowed CRP (200 samples) of time series of the depth of liquid penetration into the nozzle and the air pressure in the plenum chamber for gas with a volume flow rate of $q\,=\,$0.00632 l/min. System and recurrence parameters: a $V\,=\,0.45\,\hbox {ml}$. $m\,=\,3$, $\varepsilon \,=\,0.8$, $\tau \,=\,60$; (b) $V\,=\,2.95\,\hbox { ml}$, $m\,=\,3$, $\varepsilon \,=\,$0.8, $\tau \,=\,$80. The horizontal axis shows time expressed the sampling units of $\delta t\,=\,0.0017$ s

The number of points appears in the recurrence plot depends on the threshold value $\varepsilon$. Furthermore, the recurrence rate is a non-linear function of $\varepsilon$. Figure 8 shows the function $RR(\varepsilon )$ obtained for two time series under considerations. A strong nonlinearity of the function $RR(\varepsilon )$ is visible for the small and high values of $\varepsilon$ (the time series ware normalised, $x' \,=\, (x - \overline{x} )/\sigma _x$ by the averaged $\overline{x}$ and standard deviation $\sigma _x$). In the middle part of $RR(\varepsilon$), the nonlinearity becomes smaller. We assumed that the lower value of $\varepsilon$ in the middle (fairly linear increase) part of the function $RR(\varepsilon )$ is the proper value of the threshold value to prepare of the corresponding recurrence plot. For the time series of pressure fluctuations $\varepsilon \,=\,$0.8 while for the depth of liquid penetration inside the nozzle $\varepsilon \,=\,1.5$ (Fig. 7).

To identify the mutual relationships between pressure fluctuations and the depth of liquid penetrations into the nozzle a cross recurrence plot was used. The cross recurrence plot (CRP) is an extension of recurrence plot and it is used for analyze the dependencies between two different systems. For two dynamical systems, $x_i$ and $y_i$, in an n-dimensional phase space the cross recurrence plot is defined as [35]:

$$\begin{aligned} CR_{i,j} \,=\, \Theta (\varepsilon - \parallel \mathrm{\mathbf x}_i - \mathrm{\mathbf y}_j \parallel ),\quad \mathrm{\mathbf x}_i, \mathrm{\mathbf y}_i \in {\mathfrak {R}}^n,\quad i,j \,=\, 1 ... N. \end{aligned}$$

(9)

In order to identify the proper value of $\varepsilon$, we used the same method as in the case of recurrence plots. Figure 9 illustrates the function $RR(\varepsilon )$ defined for a cross recurrence plot in the form:

$$\begin{aligned} CRR\,=\, \frac{1}{N(N-1)} \sum _{i,j\,=\,0}^N CR_{i,j}. \end{aligned}$$

(10)

Here we assumed that the proper value of $\varepsilon$ was equal to 0.8.

In general, the CRP does not contain the main diagonal line, however if the time series under consideration, are similar then in the CRP we can observe a structure resembling a distorted or shifted main diagonal line. This structure contains information about the similarity of time series under consideration—it describes the relationship between the systems in the time domain.

Fig. 10 shows the ’large’ CRP (Fig. 10b) prepared for the whole time series under consideration and six ’small’ CRPs (Figs. 10c–h) prepared for six parts of time series with their length equal to 200 sampling events. These six small CRPs are the magnifications of six parts of the large CRP which are marked by small squares. These magnifications show the actual shape of the structure of points of the CRP around the diagonal lines. Figure 10a illustrates the two time series under consideration after rescaling the values. The structures of recurrence points close to the diagonal lines show that at the beginning and at the end part of the time series, when the bubbles depart fairly periodically, a similar form (Figs. 10c, h). These structures show agreement of similar groups of recurrence points. This means that the relationships between the pressure fluctuations and the depth of liquid penetration inside the nozzle do not change for subsequent departing bubbles. The opposite situation appeared in the middle part of large CRP (Fig. 10b) when the bubbles departed chaotically (Figs. 10d–g). In this case the shape of points of CRP near the diagonal line changing for subsequent bubbles. It means that the relationships between pressure fluctuations and depth of liquid penetration inside the nozzle are modified for subsequently departing bubbles. The larger square clusters separated by white stripes indicate intermittencies [37, 39]. In order to estimate the changes of the shapes of point structures near the diagonal lines, the CRR factor was calculated for a moving window of length of 200 samples. For each window the CRP has been constructed and a value of the CRR has been calculated. The results for the time series recorder for two volumes of the plenum chamber are presented in Fig. 11.

For the plenum chamber $V\,=\,$0.45 ml (Fig. 11a) the nature of CRR changes in case for periodic bubble departures is similar in the beginning and in the end part of the time series. The changes in CRR are similar to those in the periodic function. On the other hand, during the chaotic bubble departures the nature of changes in CRR significantly differs. This confirms that during the chaotic bubble departures the relationships between the fluctuations of air pressure in the plenum chamber and the depth of liquid penetration inside the nozzle change with time. Consequently, these time series become less correlated. The results obtained for $V\,=\,$2.95 ml also show that chaotic bubble departures are accompanied by large amplitude fluctuations in CRR, which identify the significant changes of correlation between the two examined time series. But the nature of changes in the CRR is different from the that observed for the two cases presented in Fig. 11 Therefore the values the CRR cannot be treated as a direct measure of synchronization between the two examined time series. In contrast, the changes of the amplitude of its fluctuations identify the changes in synchronization between the examined time series. The chaotic bubble departures naturally decrease the correlation between pressure fluctuations and the depth of liquid penetrations inside the nozzle.

6 Modelling the synchronization between the pressure changes and depth of liquid penetration inside the nozzle

To explain the relationships between the pressure fluctuations and the depth of liquid penetrations inside the nozzle we use a model of subsequent bubble departures. The proposed model describes the bubble growth and liquid penetration inside the nozzle. Originally, the model of bubble growth and liquid penetration inside the nozzle was proposed by Ruzicka et al. [9, 10]. Recently, a modified version of this model was discussed [5]. In addition to the previous models which only enabled examining a single cycle of bubble growth accompanied by the corresponding liquid movement inside the nozzle, the new model [5] can be adjusted and applied for simulations of subsequent bubbles departures. The forces responsible for bubble growth and liquid movement inside the nozzle are considered as the functions of the liquid velocity around the nozzle outlet. For simplicity, an isothermal process was considered while the bubble growth was described by the Rayleigh–Plesset equation [5, 10]:

$$\begin{aligned} r \left( \frac{\mathrm{d}^2 r}{\mathrm{d}t^2} \right) - \frac{3}{2} \left( \frac{\mathrm{d}r}{\mathrm{d} t} \right) ^2 \,=\, \frac{1}{\rho _l} \left( p_b-p_h - \frac{2\sigma }{r_n} -\frac{4 \mu _l}{r} \frac{\mathrm{d} r}{\mathrm{d} t} \right) , \end{aligned}$$

(11)

where: r is a radius of bubble (m), $p_h$ is hydrostatic pressure (Pa), $\sigma$ is surface tension (N/m), $\rho _l$ is liquid density (kg/m$^3$), $p_b$ is the pressure of air inside the bubble (Pa), $\mu _l$ dynamic viscosity of gas (kg/ms), $r_n$ radius of the nozzle (m). The air volume flow rate supplied to the bubble through the nozzle was determined by the Hagen–Poiseuille equation [10]: and pressure changes in the bubble are described by the following equation:

$$\begin{aligned} \frac{\mathrm{d} p_b}{\mathrm{d} t} \,=\, \frac{p_b}{V_b} \left[ \frac{\pi r_n^4}{8 \mu _g l} (p_c-p_b) - \frac{\mathrm{d} V_b}{\mathrm{d} t} \right] , \end{aligned}$$

(12)

where $V_b$ denotes the volume of bubble (m$^3$), $\mu _g$ is the dynamic viscosity of gas (kg/ms), l is nozzle height (m), $p_c$ denotes the air pressure in the plenum chamber (Pa). Pressure changes in the air supply system are described by the following equation [10]:

$$\begin{aligned} \frac{\mathrm{d} p_c}{\mathrm{d} t} \,=\, \frac{k_c p_c}{V_c} \left[ q- \frac{\pi r_n^4}{8 \mu _g l} (p_c-p_b) \right] \end{aligned}$$

(13)

where: q is the air flow rate (m$^3$/s), $V_c$ is the plenum chamber volume (m$^3$), The following forces acting on the bubble are considered: buoyancy force, $F_B$, gas momentum force, $F_M$, maximum value of the surface tension force, $F_{\sigma }$, drag force, $F_D$, and added mass force, $F_AM$. The added mass force and drag forces are considered as a function of the liquid velocity around the nozzle outlet:

$$\begin{aligned} F_{AM}& \,=\, \rho \frac{\mathrm{d}}{\mathrm{d} t} \left[ C_M V_b \left( \frac{\mathrm{d} x_c}{\mathrm{d} t} - v_{pp} \right) \right] , \end{aligned}$$

(14)

$$\begin{aligned} F_D& \,=\, 0.5 C_d \rho _l \pi r^2 \left( \frac{\mathrm{d} x_c}{\mathrm{d} t} - v_{pp} \right) \left| \frac{\mathrm{d} x_c}{\mathrm{d} t} - v_{pp} \right| . \end{aligned}$$

(15)

The bubble departure occurs when the resulting force $F_B+F_M+F_{AM} -F_{\sigma } -F_D$ exceeds the nodal value. In this case the bubble is connected with the nozzle with a thin neck. The increase in the bubble radius is further defined by the Rayleigh - Plesset equation but the motion of the bubble mass centre is determined by Newton’s second law written as:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t} \left[ \left( \rho _g + C_b \rho _l \right) V_b \left( \frac{\mathrm{d} x_c}{\mathrm{d} t} - v_{pp} \right) \right] \,=\, F_B+F_M+F_{AM} -F_{\sigma } -F_D. \end{aligned}$$

(16)

When $x_c \ge\,r + 2r_n$, the bubble departs and the liquid starts to penetrate the nozzle. This liquid flow inside the nozzle following the bubble departure is modelled by the equation of motion of the liquid mass centre [5, 10]:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t} \left\{ \frac{3}{4} \rho _l \pi r_n^2 \left[ x_l + 8 r_n \right] \frac{{\mathrm{d}} x_l}{{\mathrm{d}}t} \right\} \,=\, F_1-F_2, \end{aligned}$$

(17)

where the force $F_1$ is related to the pressure difference that occurs in the system [5, 10]:

$$\begin{aligned} F_1\,=\,-s \Delta p \,=\, - \pi r_n^2 \left[ p_c - \left( p_h +2\rho _l g x_l + 2 \frac{\sigma }{r_n} \right) \right] , \end{aligned}$$

(18)

while the force $F_2$ is related to the resistance of the movement of the liquid in the nozzle [5, 10]:

$$\begin{aligned} F_2\,=\,8C \pi \mu _l x_l \frac{\mathrm{d} x_l}{\mathrm{d} t}. \end{aligned}$$

(19)

The corresponding pressure changes in the air supply system are described by the following equation:

$$\begin{aligned} \frac{\mathrm{d} p_c}{\mathrm{d} t} \,=\, \frac{p_c}{V_c} \left( q+ \pi r_n^2 \frac{\mathrm{d} x_l}{\mathrm{d} t} \right) . \end{aligned}$$

(20)

The system of Eqs. (11–16), describing the growth of the bubbles contains the following independent variables: $p_b$, r, v, $p_c$, $x_c$, $v_c$, and parameter $v_{pp}$. The equations describing the liquid motion (Eqs. 17–20) involved in the flooding the nozzle, contain the following independent variables: $x_l$, $p_c$, $v_l\,=\,\mathrm{d} x_l /\mathrm{d} t$, and the parameter $v_{pp}$. It has been assumed [5] that the initial value of gas pressure ($p_b$) in the bubble and in the gas supply system ($p_c$), is equal to gas pressure in the plenum chamber at the end of liquid movement.

The initial velocity of bubble growth (v) is equal to the liquid velocity at the end of liquid movement ($v_c$). The liquid velocity around the nozzle outlet is equal to the previous bubble departure velocity. The initial value of gas pressure in the gas supply system $p_c$ for liquid flow inside the nozzle is equal to the gas pressure $p_c$ at the last stage of bubble growth. The initial value of liquid flow velocity, $v_l$ (liquid which takes part in liquid movement inside the nozzle) and initial value of liquid flow over the nozzle outlet, $v_{pp}$, is equal to the value of bubble departure velocity. Fig. 12 shows an example of changes in in the depth of liquid movement inside the nozzle, pressure fluctuations in gas supply system and liquid velocity over the nozzle. Here, the air volume flow rate, q, was set to 0.0078 l/min, the volume of gas supply system, V, was set to 0.5105 ml.

Fig. 12

Changes in the depth of liquid movement inside the nozzle, pressure fluctuations in the gas supply system and liquid velocity over the nozzle for $q\,=\,0.0078$ l/min, $V\,=\,0.5105\,\hbox { ml}$. a Depth of liquid movement inside the nozzle. b Pressure fluctuations in gas supply system. c Liquid velocity over the nozzle outlet

Fig. 12 illustrates the changes of liquid velocity over the nozzle outlet ($v_l$) accompanied by changes of depth of liquid movement inside the nozzle (Fig. 12a) and pressure in gas supply system (Fig. 12b) during the chaotic bubble departures. The relationship between liquid flow over the nozzle outlet $v_{pp}$ versus time is shown in Fig. 12c. The above results point to significant oscillations of liquid velocity over the nozzle outlet during bubble departures.

Fig. 13

CRR for a single cycle of liquid flow inside the nozzle for a time series of liquid penetration depth inside the nozzle and air pressure in chamber versus initial liquid velocity. The corresponding pictures of CRP for two border values of $v_l$ are given above the chart

To illustrate the correlations between the pressure and the depth of liquid penetration into the nozzle the process of liquid movement inside the nozzle with respect to the liquid velocity, over the nozzle outlet, we show the changes in the CRR parameter versus initial liquid velocity, $v_{l}$, calculated for a single cycle of liquid movement inside the nozzle (Fig. 13).

Furthermore, the two examples of CRPs for two different $v_l$ are given. The number of points in the CRP (CRR parameter) is a non-linear function of $v_l$. The initial liquid velocity modifies the maximum value of depth of liquid penetration inside the nozzle. During the chaotic bubble departures, the depth of liquid penetration for subsequent bubbles varies. This process changes the relation between pressure in the plenum chamber and the depth of liquid penetration inside the nozzle as shown in Fig. 12. A similar process was observed during the analysis of experimental data. The obtained results show that the changes of liquid velocity, $v_l$, during the liquid penetration modify the relationship between pressure, $p_c$, and depth of liquid penetration, $x_l$.

7 Conclusions

It has been found that the synchronization between pressure fluctuations and the depth of liquid penetration inside the nozzle is governed by intermittent dynamics of bubble departures. Such a dynamical schema gives rise to chaotic behaviour. In this region, the correlation between pressure fluctuations and the depth of liquid penetrations inside the nozzle decreases substantially. These results are confirmed by results obtained using mathematical model simulations, which points to the important role of system nonlinearities. Furthermore, the simulation results also show that the synchronization of the variations in plenum pressure and the depth of liquid penetration inside the nozzle can be modified by the initial liquid velocity conditions. The obtained results can be treated as a manifestation of the self-organising dynamical structure of bubble departures [8]. Chaotic bubble departures (when the correlation between pressure fluctuations and the depth of liquid penetrations inside the nozzle becomes weaker) introduce substantial changes into the hydrodynamic condition of the nozzle by modifying subsequent bubble occurrences. This leads to a desynchronization of departures and depths of liquid penetration inside the nozzle. This study can help to reveal the complex dynamics of multiphase flow from the experimental data [40]. The results could be important for applications in microchannel technology [41].