1 Introduction

Brain functions are sometimes emulated using some analog integrated circuits based on the organizational principle of natural neural networks (NNN). Neuromorphic engineering is the research branch devoted to the study and realization of such circuits with striking features [1]. Some of these circuits are obtained from some mathematical models of the neurons that have been developed. Hodgkin–Huxley neuron [2], Izhikevich neuron [3], Morris–Lecar neuron [4], 2-D Hindmarsh–Rose (HR), 3-D-HR model [5, 6], FitzHugh–Nagumo (FN) model [7], Hopfield neural network model [8,9,10,11], Chay model [12], and the Rulkov model [13], just to name a few, are among those neurons. Recall that in brain dynamics, neurons have a significant role in the brain's recording, selection, storage, learning, thinking, and data transfer processes. From the work addressed to a single neuron, it has been found that it can exhibit resting dynamics, spiking, and bursting dynamics [14]. Numerous studies on neuron dynamics have looked at single neurons, two-coupled neurons, and neural networks. Considering the case of single neurons, several studies have been done. Among others, [15] introduced a novel equilibrium-free HR model using memristive electromagnetic induction. During their investigations, the authors found that the proposed model of the neuron was to exhibit the phenomena of hidden homogeneous extreme multistability. That phenomenon is characterized by the simultaneous existence of an infinite number of firing activities of the same shape but at different positions. In [16], the authors studied in an extended model of a 4D HR neuron model the phenomenon of coexistence of firing patterns. The investigations revealed that the model could exhibit several types of complex phenomena, including symmetry breaking, period doubling, reverse period-doubling, and crisis scenarios. Hou et al. [17] estimated the neuron's electrical activity in a depolarization field. In their investigation, they detected a spike in the firing interval of the neuron when the stimulus strength increased. In addition, the neuron-firing pattern was able to switch from a single burst to an intermittent multimodal burst in the presence of an electric field as the amplitude and frequency of the electric field increased.

Kafraj et al. [18] proposed and studied a modified Izhikevich model to characterize the activity of neurons in the presence of electromagnetic induction and noise. Their study revealed several complex phenomena in the proposed model. They also found that the firing activities of the neuron were caused by an outer field, whereas it was at rest without the effect of that outer field.

Some intriguing works on neurons have also designed models that take into account natural phenomena such as the effect of light [19], temperature [20], and sound [21]. Very recently, Xu et al. introduced and investigated a memristor-based novel model of non-autonomous Rulkov neuron. Afterward, the results of their numerical simulations, as well as experimental investigations, revealed that the proposed memristive model was able to exhibit extreme multistable behavior [13].

Concerning coupled neurons or networks, Pisarchik et al. [22] have explored the dynamics of two identical coupled 3D HR neurons. The model is built by exploiting a bidirectional asymmetric electrical synapse. Njitacke et al. investigated successively the bidirectional coupling between two non-identical 2D HR neurons in the absence and the presence of electromagnetic radiation [23, 24]. Karthikeyan et al. [25] have introduced a modified Hindmarsh–Rose neuron model having a fractional-order threshold magnetic flux. Their investigations were conducted considering the effect of a magnetic field. Besides, the development of the spiral waves in the suggested network was explored. The variation of the parameters of the proposed network enabled them to see how they affected the birth and death of spiral waves.

Baran et al. [26] investigated the phenomenon of spike-timing-dependent-plasticity (STDP) learning using chemical and memristive synapses on two coupled HR neurons. Their results were obtained based on numerical simulation, and they showed that in neuromorphic studies of nonlinear processes like chaos and hyperchaos, the memristive device might be employed as an alternative synapse. In [27], using a sigmoid function as the recovery variable, the authors investigated the complex dynamics of a set of coupled FitzHugh–Nagumo neurons. The coupling connection was obtained using electromagnetic flux coupling. Their analyses revealed that for higher magnetic coupling strengths, spiral waves were destroyed, giving birth to the periodic regimes in the individual nodes. The synchronization process and chimera state were analyzed and addressed in a set of FitzHugh–Nagumo neurons under the photosensitive effect [28]. These chimera states were also demonstrated in a thermosensitive FitzHugh–Nagumo neuronal network [29]. In [30], considering the effects of electrical synapses and autapses, the authors have explored the behaviors of the considered network of Hindmarsh–Rose neurons. Using numerical simulations, they were able to show the occurrence of the chimera states in the considered network. More interestingly, traveling chimera patterns have been demonstrated in a 2-D HR neuronal network by Simo et al. [31]. A set of 3D HR neurons under an electric field has been investigated in [32]. As a result, traveling chimera states and multicluster oscillating breathers could be found in the absence of the field, whereas chimera states, multichimera states, alternating chimera states, and multicluster traveling chimeras could be found in the presence of the field.

In all of these works that address neurons, two-coupled neurons, or networks of neurons, energy is required for each firing activity as well as the transition between electrical activities. Indeed, during the metabolic process of the neuronal system or biological system, energy is consumed so that neurons can save normal and continuous electric activity [33]. The liberation and storage of energy of neuron models can be estimated. Then, it is interesting to determine the amount of energy released during transitions between the electric activity of neurons and neuron networks [31, 34]. In several works focused on the dynamics of neurons, using Helmholtz's theorem, a Hamilton's function is derived and used to calculate energy consumption. The previously mentioned energy can also be used to explain biological processes like bursting regimes, spiking states, and synchronization states [31, 34]. This discussion on energy is generally focused on a single neuron or homogeneous neural network. Recall that this Hamiltonian method has been widely used by Ma and collaborators to estimate the energy released by neurons during electrical activity [34,35,36].

So, from all the above-mentioned work, it is obvious that several scientific contributions have been devoted to the research and study of a large number of models of neurons or neural networks, taking into account environmental effects. Among them, we have the effect of external current [22, 23], the magnetic field effect [37,38,39], the electric field effect [32, 40], photosensitive effect [19], piezoelectric ceramics or auditory effect [21, 35], and thermosensitive effect [20], just to name a few.

It is well known that the nervous system consists of a multitude of neurons. Some of them have specific biological functions and structures. Most works on coupled neurons or neural network models only considers identical neurons with a single biological function [17, 23, 39, 41,42,43]. Then, from the previous literature, it is obvious that many research efforts have been devoted to the study of the behaviors of coupled neurons. These coupled neurons are built with either identical or non-identical neurons described by the same physical equation. In contrast, previous research has rarely studied the dynamic behavior of coupled neurons, as described by different mathematical models [44]. Therefore, more diverse neural network models, as well as memristive neural networks, must be constructed based on neurons with different mathematical models [45].

This is why, in this contribution, we propose and investigate the complex behavior of a small heterogeneous network of three neurons. That small network is constructed by coupling two traditional 2D HR neurons through a 2D FN neuron. Using the well-known Helmholtz theorem, the energy of the network is estimated to justify the nonlinear behaviors found during the analysis of the proposed model. So the remaining part of this work is structured as follows: In Sect. 2, the mathematical model of the proposed small network is established and its Hamilton energy is calculated. In Sect. 3, numerical simulations are used to investigate the nonlinear behavior of the coupled network. In Sect. 4, a PSPICE circuit of the network of three neurons is realized. Lastly, in Sect. 5, we summarize the paper.

2 Design and analysis of the proposed network

2.1 Presentation of the model

The brain as a nonlinear system is made up of an interconnection of several types of neurons with several functions. These various types of neurons, as well as neuron networks, are explored based on their mathematical models. The Hodgkin–Huxley neuron [30], the Hindmarsh–Rose (HR) neuron [31], the Morris–Lecar neuron [17], the FitzHugh–Nagumo neuron [32], the Izhikevich neuron [33], and the Hopfield neural networks [34,35,36,37] are among the mathematical models. In addition to the preceding research, the complicated functioning of the brain has been examined using homogeneous coupling (the pairing of similar neurons) between several of these quoted neuron models. However, a practical brain model is made of the interconnection of neurons with different functions and different mathematical models. Those neurons can also be subjected to perturbations induced by fields (magnetic or electric), temperature, light, and sound. This is why, in this contribution, the small network in Fig. 1 is proposed. It is made up of the bidirectional coupling between two HR neurons connected through a FN neuron.

Fig. 1
figure 1

The topological configuration of the small network of three neurons used for this study

Full size image

Based on that coupling scheme in Fig. 1, the mathematical model of that small network is given in Eq. (1).

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = y_{1} - a_{1} x_{1}^{3} + b_{1} x_{1}^{2} + i_{1} + m_{{12}} \left( {x_{2} - x_{1} } \right)} \hfill \\ {\dot{y}_{1} = c_{1} - d_{1} x_{1}^{2} - y_{1} } \hfill \\ {\dot{x}_{2} = x_{2} - b_{2} x_{2}^{3} - y_{2} + i_{2} + m_{{21}} \left( {x_{1} - x_{2} } \right) + m_{{23}} \left( {x_{3} - x_{2} } \right)} \hfill \\ {\dot{y}_{2} = 1/\varepsilon \left( {a_{2} + x_{2} - c_{2} y_{2} } \right)} \hfill \\ {\dot{x}_{3} = y_{3} - a_{3} x_{3}^{3} + b_{3} x_{3}^{2} + i_{3} + m_{{32}} \left( {x_{2} - x_{3} } \right)} \hfill \\ {\dot{y}_{3} = c_{3} - d_{3} x_{3}^{2} - y_{3} } \hfill \\ \end{array} } \right. $$
(1)

Here \(x_{i}\) are the potentials of the membrane in HR neuron and FN neuron, respectively, \(y_{i}\) are retrieval variables related to a fast current of either \(Na^{ + }\) or \(K^{ + }\), \(i_{i}\) represent exterior input currents and \(m_{ij}\) indicate the strengths of electrical coupling utilized to connect neurons together \(\left( {i = 1, \cdots ,3} \right)\) and \(\left( {j = 1, \cdots ,3} \right)\). Let us stress that in the considerations of this model the parameters are all positive and defined as: \(a_{1} = 1\), \(b_{1} = 3.0\), \(c_{1} = 1\),\(d_{1} = 5\), \(i_{1} = 0.5\),\(a_{2} = 0.77\), \(b_{2} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}\), \(c_{2} = 0.8\)\(\varepsilon = 13\), \(i_{2} = 0\); \(a_{3} = 1\), \(b_{3} = 3.0\), \(c_{3} = 1\),\(d_{3} = 5\), \(i_{3} = 0.5\), and \(m_{12} {, }m_{21} ,m_{23} , \, m_{32} {\text{ are}}\,{\text{tuneable}}\).

2.2 Rest points of the network

The rest points are very important for the analysis of the stability of the considered network. As a result, they allow justification if the dynamics of the considered network are self-excited or hidden. We recall that self-excited dynamics is associated with a system having unstable rest points, whereas hidden dynamics is associated with a system without rest point or with stable rests point generally. To determine the rest points of the considered network, let us consider \(\dot{x}_{i} = \dot{y}_{i} = 0\) and then, Eq. (2) is obtained.

$$\left\{ {\begin{array}{*{20}l} {y_{1} - a_{1} x_{1}^{3} + b_{1} x_{1}^{2} + i_{1} + m_{{12}} \left( {x_{2} - x_{1} } \right) = 0} \hfill \\ {c_{1} - d_{1} x_{1}^{2} - y_{1} = 0} \hfill \\ {x_{2} - b_{2} x_{2}^{3} - y_{2} + i_{2} + m_{{21}} \left( {x_{1} - x_{2} } \right) + m_{{23}} \left( {x_{3} - x_{2} } \right) = 0} \hfill \\ {1/\varepsilon \left( {a_{2} + x_{2} - c_{2} y_{2} } \right) = 0} \hfill \\ {y_{3} - a_{3} x_{3}^{3} + b_{3} x_{3}^{2} + i_{3} + m_{{32}} \left( {x_{2} - x_{3} } \right) = 0} \hfill \\ {c_{3} - d_{3} x_{3}^{2} - y_{3} = 0} \hfill \\ \end{array} } \right. $$
(2)

After computing the equilibrium of each state variable of the coupled neurons with the software Maple 18, we discover that they are in the form \(\alpha + j\beta\), which is a complex number (two cases are shown in the appendix), implying that this small network has a hidden dynamics.

2.3 The energy needed for firing activities.

The energy produced during the transition of electrical activity is very important and has been estimated in neural dynamics [46]. Given the lack of an accurate method for determining energy consumption and supply, Hamilton energy based on Helmholtz's theorem is commonly used to identify the appurtenance of state on energy in the context of a neuron or networks of neurons [47]. To determine the energy of our small network made of three neurons \(F\left( x \right)\), let us express its dynamical equations by Eq. (3) [48, 49].

$$ F\left( x \right) = F_{c} \left( x \right) + F_{d} \left( x \right) = \left[ {J\left( x \right) + R\left( x \right)} \right]\nabla H $$
(3)

In Eq. (3) \(F_{c} \left( x \right)\) and \(F_{d} \left( x \right)\) stand for the conservative component and the dissipative component. \(\nabla H\) stands for the gradient matrix of the energy/Hamilton function \(H\left( x \right)\). \(J\left( x \right)\) Indicates a skew-symmetric matrix and \(R\left( x \right)\) is a symmetric matrix. The Hamilton function is obtained by:

$$ \left\{ {\begin{array}{*{20}l} {\dot{H} = \nabla H^{T} R\left( x \right)\nabla H = \nabla H^{T} F_{d} \left( x \right)} \hfill \\ {\nabla H^{T} J\left( x \right)\nabla H = \nabla H^{T} F_{c} \left( x \right) = 0} \hfill \\ \end{array} } \right. $$
(4)

For the small network of Eq. (1), the conservative component and the dissipative component can be expressed as:

$$F_{c} = \left[ {\begin{array}{*{20}l} {y_{1} + i_{1} + m_{{12}} x_{2} } \hfill \\ {c_{1} - d_{1} x_{1}^{2} } \hfill \\ { - y_{2} + i_{2} + m_{{21}} x_{1} + m_{{23}} x_{3} } \hfill \\ {\frac{1}{\varepsilon }\left( {a_{2} + x_{2} } \right)} \hfill \\ {y_{3} + i_{3} + m_{{32}} x_{2} } \hfill \\ {c_{3} - d_{3} x_{3}^{2} } \hfill \\ \end{array} } \right] $$
(5)
$$ F_{d} = \left[ {\begin{array}{*{20}l} { - a_{1} x_{1}^{3} + b_{1} x_{1}^{2} - m_{{12}} x_{1} } \hfill \\ { - y_{1} } \hfill \\ {x_{2} - b_{2} x_{2}^{3} - m_{{21}} x_{2} - m_{{23}} x_{2} } \hfill \\ { - \frac{{c_{2} }}{\varepsilon }y_{2} } \hfill \\ { - a_{3} x_{3}^{3} + b_{3} x_{3}^{2} - m_{{32}} x_{3} } \hfill \\ { - y_{3} } \hfill \\ \end{array} } \right] $$
(6)

Using Eqs. (5) and (6), the energy \(H\left( {x_{1} ,y_{1} ,x_{2} ,y_{2} ,x_{3} ,y_{3} } \right)\) of the small neuron of three neurons will verify the following equation:

$$ \begin{gathered} \left( {y_{1} + i_{1} + m_{12} x_{2} } \right)\frac{\partial H}{{\partial x_{1} }} + \left( {c_{1} - d_{1} x_{1}^{2} } \right)\frac{\partial H}{{\partial y_{1} }} + \left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)\frac{\partial H}{{\partial x_{2} }} + \frac{1}{\varepsilon }\left( {a_{2} + x_{2} } \right)\frac{\partial H}{{\partial y_{2} }} + \hfill \\ \left( {y_{3} + i_{3} + m_{32} x_{2} } \right)\frac{\partial H}{{\partial x_{3} }} + \left( {c_{3} - d_{3} x_{3}^{2} } \right)\frac{\partial H}{{\partial y_{3} }} = 0 \hfill \\ \end{gathered} $$
(7)

The general solution of Eq. (7) can be expressed as:

$$ \begin{gathered} H = \frac{{ - 2d_{1} }}{{3m_{12} m_{23} }}x_{1}^{3} + \frac{{2c_{1} }}{{m_{12} m_{23} }}x_{1} + \frac{{ - 2d_{3} }}{{3m_{32} m_{21} }}x_{3}^{3} + \frac{{2c_{3} }}{{m_{32} m_{21} }}x_{3} + \frac{1}{{\varepsilon m_{21} m_{23} }}\left( {a_{2} + x_{2} } \right)^{2} - \hfill \\ \frac{1}{{m_{12} m_{23} }}\left( {y_{1} + i_{1} + m_{12} x_{2} } \right)^{2} - \frac{1}{{m_{32} m_{21} }}\left( {y_{3} + i_{3} + m_{32} x_{2} } \right)^{2} + \frac{1}{{m_{21} m_{23} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)^{2} \hfill \\ \end{gathered} $$
(8)

The Hamilton energy function’s derivative with respect to time is denoted by

$$ \begin{gathered} \frac{{{\text{d}}H}}{{{\text{d}}t}} = \dot{x}_{1} \left( {\frac{{ - 2d_{1} }}{{m_{12} m_{23} }}x_{1}^{2} + \frac{{2c_{1} }}{{m_{12} m_{23} }} + \frac{2}{{m_{23} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)} \right) + \dot{y}_{1} \left( {\frac{ - 2}{{m_{12} m_{23} }}\left( {y_{1} + i_{1} + m_{12} x_{2} } \right)} \right) \hfill \\ +\, \dot{x}_{2} \left( {\frac{2}{{\varepsilon m_{21} m_{23} }}\left( {a_{2} + x_{2} } \right) - \frac{2}{{m_{23} }}\left( {y_{1} + i_{1} + m_{12} x_{2} } \right) - \frac{2}{{m_{21} }}\left( {y_{3} + i_{3} + m_{32} x_{2} } \right)} \right) \hfill \\ +\, \dot{y}_{2} \left( {\frac{ - 2}{{m_{21} m_{23} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)} \right) \hfill \\ +\, \dot{x}_{3} \left( {\frac{{ - 2d_{3} }}{{m_{32} m_{21} }}x_{3}^{2} + \frac{{2c_{3} }}{{m_{32} m_{21} }} + \frac{2}{{m_{21} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)} \right) + \dot{y}_{3} \left( {\frac{ - 2}{{m_{32} m_{21} }}\left( {y_{3} + i_{3} + m_{32} x_{2} } \right)} \right) \hfill \\ \end{gathered} $$
(9)

It is simple to demonstrate that after some algebraic manipulation,

$$ \begin{gathered} \frac{{{\text{d}}H}}{{{\text{d}}t}} = \left( {\frac{{ - 2d_{1} }}{{m_{12} m_{23} }}x_{1}^{2} + \frac{{2c_{1} }}{{m_{12} m_{23} }} + \frac{2}{{m_{23} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)} \right)\left( { - a_{1} x_{1}^{3} + b_{1} x_{1}^{2} - m_{12} x_{1} } \right) \hfill \\ +\, \left( {\frac{ - 2}{{m_{12} m_{23} }}\left( {y_{1} + i_{1} + m_{12} x_{2} } \right)} \right)\left( { - y_{1} } \right) \hfill \\ +\, \left( {\frac{2}{{\varepsilon m_{21} m_{23} }}\left( {a_{2} + x_{2} } \right) - \frac{2}{{m_{23} }}\left( {y_{1} + i_{1} + m_{12} x_{2} } \right) - \frac{2}{{m_{21} }}\left( {y_{3} + i_{3} + m_{32} x_{2} } \right)} \right)\left( {x_{2} - b_{2} x_{2}^{3} - m_{21} x_{2} - m_{23} x_{2} } \right) \hfill \\ +\, \left( {\frac{ - 2}{{m_{21} m_{23} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)} \right)\left( { - \frac{{c_{2} }}{\varepsilon }y_{2} } \right) \hfill \\ +\, \left( {\frac{{ - 2d_{3} }}{{m_{32} m_{21} }}x_{3}^{2} + \frac{{2c_{3} }}{{m_{32} m_{21} }} + \frac{2}{{m_{21} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)} \right)\left( { - a_{3} x_{3}^{3} + b_{3} x_{3}^{2} - m_{32} x_{3} } \right) \hfill \\ +\, \left( {\frac{ - 2}{{m_{32} m_{21} }}\left( {y_{3} + i_{3} + m_{32} x_{2} } \right)} \right)\left( { - y_{3} } \right) \hfill \\ \end{gathered} $$
(10)

Remark that Eq. (10) is also equal to \(\nabla H^{T} F_{d}\) since

$$ \nabla H^{T} F_{d} = \left[ {\begin{array}{*{20}c} {\gamma_{1} } & {\gamma_{2} } & {\gamma_{3} } & {\gamma_{4} } & {\gamma_{5} } & {\gamma_{6} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \begin{gathered} - a_{1} x_{1}^{3} + b_{1} x_{1}^{2} - m_{12} x_{1} \hfill \\ \, - y_{1} \hfill \\ x_{2} - b_{2} x_{2}^{3} - m_{21} x_{2} - m_{23} x_{2} \hfill \\ \end{gathered} \\ { - \frac{{c_{2} }}{\varepsilon }y_{2} } \\ { - a_{3} x_{3}^{3} + b_{3} x_{3}^{2} - m_{32} x_{3} } \\ { - y_{3} } \\ \end{array} } \right] $$
(11)

with

$$ \begin{aligned} \gamma_{1} &= \left( {\frac{{ - 2d_{1} }}{{m_{12} m_{23} }}x_{1}^{2} + \frac{{2c_{1} }}{{m_{12} m_{23} }} + \frac{2}{{m_{23} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)} \right), \, \gamma_{2} = \left( {\frac{ - 2}{{m_{12} m_{23} }}\left( {y_{1} + i_{1} + m_{12} x_{2} } \right)} \right) \hfill \\ \gamma_{3} &= \left( {\frac{2}{{\varepsilon m_{21} m_{23} }}\left( {a_{2} + x_{2} } \right) - \frac{2}{{m_{23} }}\left( {y_{1} + i_{1} + m_{12} x_{2} } \right) - \frac{2}{{m_{21} }}\left( {y_{3} + i_{3} + m_{32} x_{2} } \right)} \right){, }\gamma_{4} { = }\left( {\frac{ - 2}{{m_{21} m_{23} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)} \right) \, \hfill \\ \gamma_{5} &= \left( {\frac{{ - 2d_{3} }}{{m_{32} m_{21} }}x_{3}^{2} + \frac{{2c_{3} }}{{m_{32} m_{21} }} + \frac{2}{{m_{21} }}\left( { - y_{2} + i_{2} + m_{21} x_{1} + m_{23} x_{3} } \right)} \right),\gamma_{6} = \left( {\frac{ - 2}{{m_{32} m_{21} }}\left( {y_{3} + i_{3} + m_{32} x_{2} } \right)} \right) \, \hfill \\ \end{aligned} $$
(12)

From (10) to (12), it can be concluded that \(\frac{{{\text{d}}H}}{{{\text{d}}t}} = \nabla H^{T} F_{d} \left( x \right)\) which reinforces the selection of the energy function. Regarding Eq. (8), it is evident that the Hamilton energy of the small network of neurons is a function of all state variables and all parameters. Even more fascinating, it is clear that the energy function defined in Eq. (8) is clearly dependent on all the external currents \(i_{i}\) as suggested in [48, 49]. As a result, there will be enough energy to sustain continuous electrical activity in the small network of neurons under consideration.

3 Numerical analysis

In this section, our main objective is to investigate the global dynamics of the proposed network of three neurons using the fourth-order Runge–Kutta algorithm with a fixed step time of \(5 \times 10^{ - 3}\). The parameters as well as the electrical coupling weight of the network are selected in the extended precision mode for better accuracy of the calculations. Nonlinear analysis tools such as two-parameter Lyapunov exponent graphs, the graph of the Hamiltonian energies, bifurcation diagrams, phase portraits; time series as well as the basin of attractions are used to characterize the complex dynamics of the network.

3.1 Global dynamics of the network

To investigate the global dynamics of the proposed network, electrical coupling weights will be used as bifurcation control parameters. Based on those electrical coupling weights, some two-parameter Lyapunov exponent graphs are provided in Fig. 2. These diagrams have been computed when increasing (left side) and decreasing (right side) both parameters. This computational technique represents a nice way to cover a wide range of the parameters and highlight hysteretic dynamics. From Fig. 2(a) and (b), the two-parameter diagrams on the left- and right-hand sides are almost the same, which excludes the possibility of hysteretic dynamics.

Fig. 2
figure 2

Two parameter Lyapunov exponent diagrams showing the largest LE in the \(\left( {m_{12} - m_{21} } \right)\), \(\left( {m_{23} - m_{32} } \right)\) and \(\left( {m_{12} - m_{32} } \right)\) spaces helping to characterize the variety of the behaviors exhibited by the coupled neurons. The parameters varying, respectively, in range: a \(0.1 \le m_{12} \le 8\) and \(0.1 \le m_{21} \le 8\) for \(m_{32} = 0.52\), \(m_{23} = 0.2\) b \(0.1 \le m_{23} \le 1.6\) and \(0.1 \le m_{32} \le 1.6\) for \(m_{21} = 4\), \(m_{14} = 4\) and c \(0.1 \le m_{12} \le 4\) and \(0.1 \le m_{32} \le 1.6\) for \(m_{21} = 4\), \(m_{23} = 1.6\). Initial conditions are \(\left( { - 2,0,0,0,0,0.1} \right)\)

Full size image

In contrast, from Fig. 2(c), a large region of discrepancy is observed between both diagrams. That discrepancy is justified by the hysteretic nature of the network for the set of the electrical coupling weights used for the investigations. As it can be seen on those two-parameter Lyapunov exponents, the dynamics of the proposed network is able to vary from periodic firing activities \(\left( {\lambda_{\max } = 0} \right)\) to chaotic firing activities \(\left( {\lambda_{\max } > 0} \right)\) based on the sign of the maximum Lyapunov exponent. Remark that for each firing activity observed in those diagrams, energy, also called Hamiltonian, is consumed. So the Hamilton energy associated with each electrical activity on the left-hand side of Fig. 2 is provided in Fig. 3. That energy is obtained by varying two electrical synaptic weights simultaneously and recoding the equivalent energy function as given in Eq. (8). From those diagrams in Fig. 3, it is clear the energy of that proposed small network of three neurons strongly depends on the values of the various electrical synaptic weights that enable it to couple neurons.

Fig. 3
figure 3

3D projection showing the evolution of the Hamilton energy (left-hand side) its corresponding absolute value (right-hand side) of the small network when two electrical coupling weights are both varied. Parameters are those of Fig. 2

Full size image

To see which type of firing activity can occur during the transition between electrical activities, the bifurcation diagrams of Fig. 4 and its corresponding graph of the maximum Lyapunov exponent have been computed when varying \(m_{32}\). As it can be seen in those diagrams, the dynamics of the small network of three neurons varies from periodic to periodic firing activities through several windows of chaotic firing activities. Recall that the bifurcation diagram is computed by varying a control parameter (electrical coupling weight) and recording the maxima of the membrane potential of any neuron at each iteration of the control parameter. It can also be obtained by superimposing two diagrams when increasing or decreasing the control parameter. For this computational method, the final states of the network for an iteration are used as initial conditions for the next iteration. For some discrete values of the electrical coupling weight \(m_{32}\), phase portraits are displayed in Fig. 5, showing the phenomenon of the period-doubling bifurcation exhibited by the considered network.

Fig. 4
figure 4

a Bifurcation diagrams showing local maximum of the coordinate \(x_{3}\) versus \(m_{32}\) computed for forward (black) and backward (red) values of \(m_{32}\) in the range of \(0.2 \le m_{32} \le 1.2\). b the corresponding largest exponent Lyapunov for the parameters: \(i_{1} = i_{3} = 0.5\), \(m_{12} = 0.1\), \(m_{21} = 0.52\), and \(m_{23} = 0.52\). Initial conditions are \(\left( { - 2,0,0,0,0,0.1} \right)\)

Full size image
Fig. 5
figure 5

Phase portraits showing the transient to chaos by doubling period in \(\left( {y_{1} ,x_{2} } \right)\) plan for discrete value of m32: a \(m_{32} = 1\) is a limit cycle of period-1, b \(m_{32} = 0.95\) is a limit cycle of period-2, c \(m_{32} 0.923\) is a limit cycle of period-4 and d \(m_{32} )0.868\) is chaotic attractor

Full size image

3.2 Multistable behavior of the small network

Previously, it has been obtained from Fig. 2(c) that the network of three neurons considered in this work was able to display hysteretic dynamics. That phenomenon is characterized by the coexistence of several firing activities for the same set of electrical coupling weights, but using different initials for the membrane potentials as well as retrieval variables. This phenomenon of multistability involving the coexistence of bifurcations is analyzed in this work using the bifurcation diagrams of Fig. 6. From these diagrams, three sets of data, namely blue, red, and black, associated with the coexistence of the firing activities are found. The details of the choice of the initial conditions and sweeping direction used to compute these diagrams are given in Table 1.

Fig. 6
figure 6

a Bifurcation diagrams showing local maximum of the coordinate \(x_{3}\) versus. Three set of data are superimposed when \(m_{32}\) is varied in the range \(0.9 \le m_{32} \le 1.15\) and the computational technique provided in Table 1. b An enlargement of the bifurcation diagrams displayed in (a). The parameters are \(i_{1} = 0.4\), \(i_{3} = 0.6\), \(m_{12} = 0.785\), \(m_{21} = 0.52\), and \(m_{23} = 0.2\)

Full size image
Table 1 Procedures exploited to capture coexisting bifurcations when varying \(m_{32}\) (see Fig. 6). The rest of the parameters are fixed as in Fig. 6
Full size table

For a discrete value of the electrical coupling weight \(m_{32} = 0.994\), three types of coexisting firing activities are reported in Fig. 7 using the state variables of all the neurons in our proposed network. Among the three coexisting firing activities, two are periodic, while one is chaotic. The bursting nature of that chaotic coexisting activity is supported using the time series of Fig. 8. From those time series, it is obvious that the membrane potential of the first and third neurons evolves as the fast variables, whereas the membrane potential of the second neuron evolves as the slow variable. Remember that bursting neuron activity occurs when the activity of neurons swaps between a resting regime and redundant spiking [14]. Originally, that phenomenon was exploited to characterize the electrical activity of neurons. When the model is divided into two subsystems with two different time scales, these burstings in neurons or coupled neurons may occur.

Fig. 7
figure 7

Coexistence of three different electrical activities for the value of the coupling strength \(m_{32} = 0.994\) with the initial conditions \(\left( { - 2,0,0,0,x_{3} \left( 0 \right),0.1} \right)\). Chaotic firing activity is obtained \(x_{3} \left( 0 \right) = 1.12\); period-5 for \(x_{3} \left( 0 \right) = 1.2\); and period-1 for \(x_{3} \left( 0 \right) = 1.56\)

Full size image
Fig. 8
figure 8

Time evolution of the chaotic firing pattern of Fig. 7 showing bursting behavior of our coupled neurons considered in this work

Full size image

The fast subsystem contains fast variables, and the slow subsystem contains slow variables. Then, the model can display two time scales. Initial conditions are very important for the analysis of neuronal systems. In nature, the initial conditions of those neuronal systems, including each category of neurons or coupled neurons, can be influenced by the effects of light, temperature or fields that can be either electrical or magnetic. So, when varying the initial conditions of the small network of three neurons considered in this work, the basins of attraction in Fig. 9 are obtained. These basins of attraction are separated by colors that correspond to the set of the initial conditions that enable us to obtain each coexisting firing activity in Fig. 7. From those attraction basins, it is obvious that one of the chaotic firing activities (bursting oscillations) is less than the other one of the two periodic firing activities.

Fig. 9
figure 9

Basins of attraction showing the distribution of the initial conditions that enable to obtain each of the coexisting attractors of Fig. 7 in the plane \(\left( {x_{1} \left( 0 \right),y_{1} \left( 0 \right)} \right)\), \(\left( {x_{2} \left( 0 \right),y_{2} \left( 0 \right)} \right)\), \(\left( {x_{2} \left( 0 \right),y_{2} \left( 0 \right)} \right)\), respectively, when all the other initial states are fixed at zero

Full size image

4 Circuit realization of the proposed small network

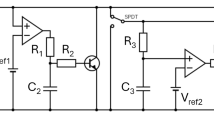
In this section, the objective is to confirm the hidden behavior of the small network of three neurons proposed in this work. To achieve this goal, an analog circuit based on operational amplifiers TL082, analog multipliers AD633JN, resistors, and capacitors is built as presented in Fig. 10. The power supply of the operational amplifiers is \(\pm 15V\) symmetric. Remember that the original goal of neuromorphic engineering was to create analog integrated circuits based on the natural neuronal network (NNN) organizational principle to mimic some of the brain's functions. [1]. Using the well-known Kirchhoff’s electrical circuit law, the circuit equations of the proposed network are given as:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{C_{1} {\text{d}}X_{1} }}{{{\text{d}}t}} = \frac{1}{R}Y_{1} - \frac{1}{{R_{{a_{1} }} }}X_{1}^{3} + \frac{1}{{R_{{b_{1} }} }}X_{1}^{2} + \frac{1}{{R_{8} }}E_{1} + \frac{1}{{R_{{m_{{12}} }} }}\left( {X_{2} - X_{1} } \right)} \hfill \\ {\frac{{C_{2} {\text{d}}Y_{1} }}{{{\text{d}}t}} = \frac{1}{{R_{5} }}c_{1} - \frac{1}{{R_{{d_{1} }} }}X_{1}^{2} - \frac{1}{R}Y_{1} } \hfill \\ {\frac{{C_{3} {\text{d}}X_{2} }}{{{\text{d}}t}} = \frac{1}{R}X_{2} - \frac{1}{{R_{{b_{2} }} }}X_{2}^{3} - \frac{1}{R}Y_{2} + \frac{1}{{R_{{27}} }}E_{2} + \frac{1}{{R_{{m_{{21}} }} }}\left( {X_{1} - X_{2} } \right) + \frac{1}{{R_{{m_{{23}} }} }}\left( {X_{3} - X_{2} } \right)} \hfill \\ {\frac{{C_{4} {\text{d}}Y_{2} }}{{{\text{d}}t}} = \frac{{A_{2} }}{{R_{{28}} }}a_{2} + \frac{1}{{R_{{d_{2} }} }}X_{2} - \frac{1}{{R_{{c_{2} }} }}Y_{2} } \hfill \\ {\frac{{C_{5} {\text{d}}X_{3} }}{{{\text{d}}t}} = \frac{1}{R}Y_{3} - \frac{1}{{R_{{a_{3} }} }}X_{3}^{3} + \frac{1}{{R_{{b_{3} }} }}X_{3}^{2} + \frac{1}{{R_{{39}} }}E_{3} + \frac{1}{{R_{{m_{{32}} }} }}\left( {X_{2} - X_{3} } \right)} \hfill \\ {\frac{{C_{6} {\text{d}}Y_{3} }}{{{\text{d}}t}} = \frac{1}{{R_{{40}} }}c_{3} - \frac{1}{{R_{{d_{3} }} }}X_{3}^{2} - \frac{1}{R}Y_{3} } \hfill \\ \end{array} } \right. $$
(13)
Fig. 10
figure 10

PSPICE circuit of the small network of three neurons

Full size image

In the set of the nonlinear differential equations obtained in Eq. (13), \(X_{i}\) and \(Y_{i}\) represent the state evolution of the membrane potential and the recovery variable, respectively. Considering \(RC = 10nF \times 10K\Omega = 100us\), \(V_{0} = \, 1V\),\(x_{i} = \frac{{X_{i} }}{{V_{0} }}\), \(y_{i} = \frac{{Y_{i} }}{{V_{0} }}\), the comparison between Eqs. (13) and (1) yields:

\(\begin{gathered} R_{{a_{1} }} = \frac{R}{{a_{1} }} = 10k\Omega ,R_{{b_{1} }} = \frac{R}{{b_{1} }} = 3.333k\Omega ,C\__{1} = \frac{{R_{5} }}{R}c_{1} = 1V,R_{{d_{1} }} = \frac{R}{{d_{1} }} = 2k\Omega ,R_{{b_{2} }} = \frac{R}{{b_{2} }} = 30k\Omega ,E_{2} = \frac{{R_{27} }}{R}i_{2} = 0V, \hfill \\ A_{2} = \frac{{a_{2} R_{28} }}{\varepsilon R} = 0.0592V,R_{{c_{2} }} = \frac{\varepsilon R}{{c_{2} }} = 162.5k\Omega ,R_{{d_{2} }} = \frac{\varepsilon R}{{d_{2} }} = 130k\Omega ,R_{{a_{3} }} = \frac{R}{{a_{3} }} = 10k\Omega ,R_{{b_{3} }} = \frac{R}{{b_{3} }} = 3.333k\Omega , \hfill \\ C\__{3} = \frac{{R_{40} }}{R} = 1V,c_{3} ,R_{{d_{3} }} = \frac{R}{{d_{3} }} = 2k\Omega ,E_{1} = \frac{{R_{8} }}{R}i_{1} = {\text{tuneable}},R_{{m_{12} }} = \frac{R}{{m_{12} }} = {\text{tuneable}},R_{{m_{21} }} = \frac{R}{{m_{21} }} = {\text{tuneable}}, \hfill \\ R_{{m_{23} }} = \frac{R}{{m_{23} }} = {\text{tuneable}},E_{3} = \frac{{R_{39} }}{R}i_{3} = {\text{tuneable}},R_{{m_{32} }} = \frac{R}{{m_{32} }} = {\text{tuneable}} \hfill \\ \end{gathered}\)with \(t = \tau RC\),\(C_{1} = C_{2} = C_{3} = C_{4} = C_{5} = C_{6} = C\) and \( \, R_{8} = R_{5} = R_{20} = R_{27} = R_{28} = R_{39} = R_{40} = R\).

\(R = 10K\Omega\), \(C_{i} = 10nF\).

When performing PSPICE simulations, the phenomenon of the period-doubling bifurcation route to the chaos was also obtained for some discrete values of the control parameter \(R_{{m_{32} }}\). For example, period-1 limit cycle was obtained for \(R_{{m_{32} }} = 10k\Omega\), and period-2 limit cycle was obtained for \(R_{{m_{32} }} = 10.52k\Omega\). The period-4 limit cycle was obtained for \(R_{{m_{32} }} = 10.83k\Omega\) and finally a chaotic attractor for \(R_{{m_{32} }} = 11.52k\Omega\) as its shown in Fig. 11. The coexisting behaviors found in the previous section have been also reported. Figure 12 shows the phase portraits of the three coexisting stable states exhibited by each neuron of the proposed small network using three different initial conditions. Finally, the chaotic bursting behavior found among the coexisting stable states has been further supported using the time series of Fig. 13. There, it is obvious that state variables \(V\left( {X1} \right)\) and \(V\left( {X3} \right)\) stand for the fast subsystem with state variable \(V\left( {X2} \right)\) denoting the slow subsystem. Good accordance is observed between the results of MATLAB simulations and those obtained from PSPICE. So we can conclude that the neuromorphic circuit built in this work can perfectly reproduce the dynamic of the proposed network of three neurons.

Fig. 11
figure 11

PSPICE simulation showing period doubling bifurcation route to chaos for \(E_{1} = 0.5V,R_{{m_{12} }} = 100k\Omega ,R_{{m_{21} }} = 19.23k\Omega ,R_{{m_{23} }} = 19.23k\Omega ,E_{3} = 0.5V,R_{{m_{32} }} = \frac{R}{{m_{32} }} = {\text{tuneable}}\). Initial conditions are \(\left( { - 2V,0V,0V,0V,1.2V,0.1V} \right)\)

Full size image
Fig. 12
figure 12

PSPICE simulation of the coexisting attractors for \(R_{{m_{12} }} = 12.738k\Omega ,\) \(R_{{m_{21} }} = 19.23k\Omega ,\)\(R_{{m_{23} }} = 50k\Omega ,E_{3} = 0.6V,R_{{m_{32} }} = 10.05k\Omega\) with the initial condition, respectively \(\left( {0V,0V,0V,0V, - 1V,0.1V} \right)\), \(\left( { - 2V,0V,0V,0V,1.2V,0.1V} \right)\) and \(\left( { - 2V,0V,0V,0V,1.56V,0.1V} \right)\), for the first, second, and the third columns of the coexisting attractors

Full size image
Fig. 13
figure 13

PSPICE simulation showing time evolution of the chaotic firing pattern of Fig. 12 corresponding to bursting behavior of our coupled neurons considered in this work

Full size image

5 Conclusion

In this contribution, the complex behavior of a new small network of three neurons has been investigated. The numerical computation of the equilibria of the proposed network revealed that they are all complex numbers, which implies the possibility for the network to exhibit hidden dynamics. Using the famous Helmholtz theorem, the Hamilton energy of the coupled neurons has been determined. That quantity corresponds to the amount of energy released by the coupled neurons during each electrical activity. It has also been found during the numerical investigation of the model that it is able to exhibit the phenomenon of the period-doubling bifurcation. It has been found that the proposed network was also able to show hysteretic dynamics characterized by the coexistence of three different firing actives for the same set of electrical coupling weights but using different initial conditions. All the numerical results presented in this work use nonlinear analysis tools such as the two-parameter Lyapunov exponent, bifurcation diagrams, the graph of the largest Lyapunov exponent, phase portraits, time series, and the basin of attractions. Finally, an electronic circuit for the proposed network has been designed and investigated in the PSPICE simulation environment. That circuit of the network was able to reproduce all the behaviors of the mathematical model.