Construction and application of new high-order polynomial chaotic maps

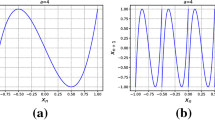
Abstract

Generating pseudorandom numbers with good statistical performance based on chaotic maps has become a topic of interest in chaotic cryptography. Several high-order polynomial chaotic maps with special forms are proposed by the Li–Yorke theorem in this paper, and chaotic conditions and intervals are given. The dynamical behaviors of chaotic maps satisfying the chaotic conditions are numerically analyzed, such as the bifurcation and Lyapunov exponent, the analysis results show the correctness of the related chaos criterion theorems. Chaotic maps are essential for the design of pseudorandom number generator and are widely used in many applications. Based on the superposition of chaotic maps, a pseudorandom number generator is designed, and the available chaotic parameters of the pseudorandom number generator are increased through the superposition of chaotic maps. This paper tests and analyses the performance of pseudorandom sequences produced by the pseudorandom number generator, and the analysis results show that pseudorandom sequences produced by pseudorandom number generator have good randomness, uniformity, complexity, and sensitivity to the initial parameters. Performance analyses show that the pseudorandom number generator in this paper can generate sequences with high quality. Several high-order polynomial chaotic maps we constructed based on the Li–Yorke theorem enrich the chaotic map and provide the possibility for its application in the field of cryptography.

Appendix

1.1 Examples of several polynomial chaotic maps with other forms

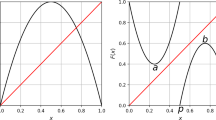
Example 1. For Theorem 3 in Table 1, let $n = 2$, $H(x) = x(qx^{4} + b)$.

The image of the maps $g_{3} \left( \mu \right)$ and $g_{4} (b)$ are given in Fig. 

Fig. 7

a Image of the relationship between $g_{3} (\mu )$ and $\mu$; b image of the relationship between $g_{4} (b)$ and $b$

7.

The solution of $g_{3} \left( \mu \right) = 0$ in $({1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-\nulldelimiterspace} 5},1)$ is

$$ \mu^{ * } = 0.75885235323, $$

The solution of $g_{4} \left( b \right) = 0$ in $({5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-\nulldelimiterspace} 4},5)$ is

$$ b^{ * } = 2.063286489, $$

Therefore, if

$$ 1.74458380 \approx \sqrt[4]{{{{\mu^{ * } \cdot 5^{5} } \mathord{\left/ {\vphantom {{\mu^{ * } \cdot 5^{5} } {4^{4} }}} \right. \kern-\nulldelimiterspace} {4^{4} }}}} \le b \le b^{ * } \approx 2.063286489, $$

then $H(x)$ is chaotic.

Example 2. For Theorem 4 in Table 1, let $n = 3$, $G(x) = x(ax^{5} + b)$.

The image of the map $g_{5} \left( \mu \right)$ is shown in Fig. 

Fig. 8

Image of the relationship between $g_{5} (\mu )$ and $\mu$

8.

The solution of $g_{5} \left( \mu \right) = 0$ in $({1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-\nulldelimiterspace} 6},1)$ is

$$ \mu^{ * } = 0.7016902434 $$

Therefore, if

$$ 1.59970751 \approx \sqrt[5]{{{{\mu^{ * } } \mathord{\left/ {\vphantom {{\mu^{ * } } k}} \right. \kern-\nulldelimiterspace} k}}} \le b \le \sqrt[5]{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-\nulldelimiterspace} k}}} = \frac{{6^{\frac{6}{5}} }}{5} \approx 1.71716290 $$

then $G(x)$ is chaotic.

Example 3. For Theorem 5 in Table 1, let $n = 2$, $f(x) = x(x^{2} - 4)(x^{2} - 9)$, $b > 0$, we can obtain

$$ Q(x) = bx(x^{2} - 4)(x^{2} - 9), $$

From $f(x)$, we can obtain maximum $f\left( {\frac{{\sqrt {390 - 30\sqrt {89} } }}{10}} \right) \approx 24.03436770$ in $(0,2)$, the maximum is the largest maximum on $(0,3)$.

From $Q(x)$, we can obtain

$$ b \in \left[ {\frac{2}{{f\left( {\frac{{\sqrt {390 - 30\sqrt {89} } }}{10}} \right)}},\frac{3}{{f\left( {\frac{{\sqrt {390 - 30\sqrt {89} } }}{10}} \right)}}} \right],\;\;b_{1} = \frac{2}{{f\left( {\frac{{\sqrt {390 - 30\sqrt {89} } }}{10}} \right)}} \approx 0.08321417,\;\;b_{2} = \frac{3}{{f\left( {\frac{{\sqrt {390 - 30\sqrt {89} } }}{10}} \right)}} \approx 0.12482126. $$

Then $Q(x)$ is chaotic in $[ - 3,3]$.

Example 4. For Theorem 6 in Table 1, let $n = 2$, $R(x) = (ax^{2} + bx)(x + \frac{b}{2a})^{4}$.

Then $t_{2} = \frac{{ - (n + 1) - \sqrt {n(n + 1)} }}{2(n + 1)} = \frac{ - 3 - \sqrt 6 }{6}$,

$$ \frac{{(t_{2}^{2} + t_{2} )(2t_{2} + 1)^{2n} }}{{2^{2n - 1} }} \le - \frac{{a^{2n} }}{{b^{2n + 1} }} \le \frac{{(t_{2}^{2} + t_{2} )(2t_{2} + 1)^{2n} }}{{2^{2n} }} $$

$$ \Rightarrow - 0.00462962 \le - \frac{{a^{4} }}{{b^{5} }} \le - 0.00231482. $$

Therefore, when

$$ - 0.00462962 \le - \frac{{a^{4} }}{{b^{5} }} \le - 0.00231482(a < 0) $$

or

$$ - 0.00462962 \le - \frac{{a^{4} }}{{b^{5} }} \le - 0.00231482(a > 0), $$

then $R(x)$ is chaotic.

1.2 The numerical simulation of dynamical behaviors

For example 1, $H(x) = x(qx^{4} + b)$, we can obtain

$$ 1.74458380 \approx \sqrt[4]{{{{\mu^{ * } \cdot 5^{5} } \mathord{\left/ {\vphantom {{\mu^{ * } \cdot 5^{5} } {4^{4} }}} \right. \kern-\nulldelimiterspace} {4^{4} }}}} \le b \le b^{ * } \approx 2.063286489, $$

Let $q = - 1$, $x_{0} = 0.1$, the bifurcation graph and Lyapunov exponent spectrum are given in Fig. 

Fig. 9

a Bifurcation graph of b in example 1; b Lyapunov exponent of b in example 1

9. As can be seen from Fig. 9, this system is in a state of chaos when $b \in \left[ {1.74458380,2.063286489} \right]$. The Lyapunov exponent is close to 1 and reaches the maximum when $b$ is about $2.0632$ in Fig. 9, which means that the system has the best chaotic behavior.

For example 2, $G(x) = x(ax^{5} + b)$, we can obtain

$$ 1.59970751 \approx \sqrt[5]{{{{\mu^{ * } } \mathord{\left/ {\vphantom {{\mu^{ * } } {m_{2} }}} \right. \kern-\nulldelimiterspace} {m_{2} }}}} \le b \le \sqrt[5]{{{1 \mathord{\left/ {\vphantom {1 {m_{2} }}} \right. \kern-\nulldelimiterspace} {m_{2} }}}} = \frac{{6^{\frac{6}{5}} }}{5} \approx 1.71716290, $$

Let $a = - 1$, $x_{0} = 0.1$, the bifurcation graph and Lyapunov exponent spectrum are shown in Fig. 

Fig. 10

a Bifurcation graph of b in example 2; b Lyapunov exponent of b in example 2

10. As can be seen from Fig. 10, this system is in a state of chaos when $b \in \left[ {1.59970751,1.71716290} \right]$. The Lyapunov exponent is greater than 0.6 and reaches the maximum when $b$ is about $1.7171$ in Fig. 10, which means that the system has the best chaotic behavior.

For example 3, $f(x) = x(x^{2} - 4)(x^{2} - 9)$, $Q(x) = bx(x^{2} - 4)(x^{2} - 9)$, $b > 0$, we can obtain $0.08321417 \le b \le 0.12482126$, let $x_{0} = 0.1$, the bifurcation graph and Lyapunov exponent spectrum are given in Fig. 

Fig. 11

a Bifurcation graph of b in example 3; b Lyapunov exponent of b in example 3

11. As can be seen from Fig. 11, this system is in a state of chaos when $b \in \left[ {0.08321417,0.12482126} \right]$. The Lyapunov exponent is greater than 1 and reaches the maximum when $b$ is about $0.132$ in Fig. 11, which means that the system has the best chaotic behavior.

For example 4, $R(x) = (ax^{2} + bx)\left( {x + \frac{b}{2a}} \right)^{4}$, let $b = 1$, we can obtain

$$ - 0.26084729 \le a \le - 0.21934580, $$

Let $x_{0} = 0.1$, the bifurcation graph and Lyapunov exponent spectrum are shown in Fig. 

Fig. 12

a Bifurcation graph of a in example 4; b Lyapunov exponent of a in example 4

12. As can be seen from Fig. 12, this system is in a state of chaos when $b \in \left[ { - 0.26084729, - 0.21934580} \right]$. The Lyapunov exponent is greater than 1 and reaches the maximum when $b$ is about $- 0.2194$ in Fig. 12, which means that the system has the best chaotic behavior.

Let $a = \pm 1$, we can obtain $2.93015727 \le b \le 3.36586392$, let $x_{0} = 0.1$, the bifurcation graph and Lyapunov exponent spectrum are given in Fig. 

Fig. 13

a Bifurcation graph of b in example 4; b Lyapunov exponent of b in example 4

13. As can be seen from Fig. 13, this system is in a state of chaos when $b \in \left[ {2.93015727,3.36586392} \right]$. The Lyapunov exponent is greater than 1 and reaches the maximum when $b$ is about $3.3658$ in Fig. 13, which means that the system has the best chaotic behavior. The changing trend of the Lyapunov exponent of example 4 is similar while parameters $a$ and $b$ vary.

From example 1 to example 4, the Lyapunov exponents of these systems are between 0 and 1.5. Their Lyapunov exponents are about the same when example 3 and example 4 are at their best chaotic behavior, respectively. It can be concluded from the above analysis, the best chaotic behaviors of example 3 and example 4 are better than the best chaotic behavior of example 1, the best chaotic behavior of example 1 is better than the best chaotic behavior of example 2.