Skip to main content
SpringerLink
Log in

A novel reduction approach to obtain \({\varvec{N}}\)-soliton solutions of a nonlocal nonlinear Schrödinger equation of reverse-time type

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

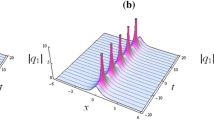
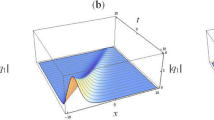
In this paper, a novel reduction approach is reported for a physically meaningful nonlocal nonlinear Schrödinger (NLS) equation of reverse-time type to obtain its N-soliton solutions. Firstly, single-soliton solutions of the nonlocal NLS equation are obtained by reducing those of the local NLS equation. Secondly, inspired by the form of single-soliton solutions, N-soliton representations of the nonlocal NLS equation are conjectured and then verified via an algebraic proof. Thirdly, to demonstrate the features of the soliton solutions, some special soliton dynamics are theoretically explored and graphically illustrated. The reduction approach proposed in this paper has the merit that it is purely algebraic which does not need to perform complicated spectral analysis of the corresponding Lax pair.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Ablowitz, M.J., Musslimani, Z.H.: Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 110, 064105 (2013)

    Article  Google Scholar 

  2. Ablowitz, M.J., Musslimani, Z.H.: Integrable nonlocal nonlinear equations. Stud. Appl. Math. 139, 7 (2017)

    Article  MathSciNet  Google Scholar 

  3. Ablowitz, M.J., Musslimani, Z.H.: Inverse scattering transform for the integrable nonlocal nonlinear Schrödinger equation. Nonlinearity 29, 915 (2016)

    Article  MathSciNet  Google Scholar 

  4. Zhou, Z.X.: Darboux transformations and global solutions for a nonlocal derivative nonlinear Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 62, 480 (2018)

    Article  MathSciNet  Google Scholar 

  5. Lou, S.Y., Huang, F.: Alice-Bob physics: coherent solutions of nonlocal KdV systems. Sci. Rep. 7, 869 (2017)

    Article  Google Scholar 

  6. Gürses, M., Pekcan, A.: Nonlocal KdV equations. Phys. Lett. A 384, 126894 (2020)

    Article  MathSciNet  Google Scholar 

  7. Fokas, A.S.: Integrable multidimensional versions of the nonlocal nonlinear Schrödinger equation. Nonlinearity 29, 319 (2016)

  8. Ma, W.X.: Inverse scattering and soliton solutions of nonlocal reverse-spacetime nonlinear Schrödinger equations. Proc. Amer. Math. Soc. 149, 251 (2021)

    Article  MathSciNet  Google Scholar 

  9. Ma, W.X.: Riemann-Hilbert problems and soliton solutions of nonlocal real reverse-spacetime mKdV equations. J. Math. Anal. Appl. 498, 124980 (2021)

    Article  MathSciNet  Google Scholar 

  10. Stalin, S., Senthilvelan, M., Lakshmanan, M.: Degenerate soliton solutions and their dynamics in the nonlocal Manakov system: I symmetry preserving and symmetry breaking solutions. Nonlinear Dyn. 95, 343 (2019)

    Article  Google Scholar 

  11. Stalin, S., Senthilvelan, M., Lakshmanan, M.: Energy sharing collisions and the dynamics of degenerate solitons in the nonlocal Manakov system. Nonlinear Dyn. 95, 1767 (2019)

    Article  Google Scholar 

  12. Sinha, D., Ghosh, P.K.: Integrable nonlocal vector nonlinear Schrödinger equation with self-induced parity-time-symmetric potential. Phys. Lett. A 381, 124 (2017)

    Article  MathSciNet  Google Scholar 

  13. Ablowitz, M.J., Musslimani, Z.H.: Integrable discrete \({\cal{PT}}\) symmetric model. Phys. Rev. E 90, 032912 (2014)

    Article  Google Scholar 

  14. Yang, J.K.: Physically significant nonlocal nonlinear Schrödinger equation and its soliton solutions. Phys. Rev. E 98, 042202 (2018)

    Article  MathSciNet  Google Scholar 

  15. Manakov, S.V.: On the theory of two-dimensional stationary self-focusing of electromagnetic waves. Sov. Phys. JETP 38, 248 (1974)

    Google Scholar 

  16. Yang, J.K.: General \(N\)-solitons and their dynamics in several nonlocal nonlinear Schrödinger equations. Phys. Lett. A 383, 328 (2019)

    Article  MathSciNet  Google Scholar 

  17. Chen, J.C., Yan, Q.X.: Bright soliton solutions to a nonlocal nonlinear Schrödinger equation of reverse-time type. Nonlinear Dyn. 100, 2807 (2020)

    Article  Google Scholar 

  18. Yang, J.K.: Nonlinear Waves in Integrable and Nonintegrable Systems. SIAM, Philadelphia (2010)

    Book  Google Scholar 

Download references

Acknowledgements

The author is very grateful to the editor and the anonymous referees for their valuable suggestions. The author would also like to thank the support by the Collaborative Innovation Center for Aviation Economy Development of Henan Province.

Author information

Authors and Affiliations

  1. School of Science, Zhengzhou University of Aeronautics, Zhengzhou, Henan, 450046, People’s Republic of China

    Jianping Wu

Authors
  1. Jianping Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Ethics declarations

Conflict of interest

The author declares that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, J. A novel reduction approach to obtain \({\varvec{N}}\)-soliton solutions of a nonlocal nonlinear Schrödinger equation of reverse-time type. Nonlinear Dyn 106, 775–781 (2021). https://doi.org/10.1007/s11071-021-06813-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-021-06813-5

Keywords

Search

Navigation