Skip to main content
SpringerLink
Log in

Degenerate soliton solutions and their dynamics in the nonlocal Manakov system: I symmetry preserving and symmetry breaking solutions

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

In this paper, we construct degenerate soliton solutions (which preserve \(\mathscr {PT}\)-symmetry/break \(\mathscr {PT}\)-symmetry) to the nonlocal Manakov system through a nonstandard bilinear procedure. Here, by degenerate we mean the solitons that are present in both the modes which propagate with same velocity. The degenerate nonlocal soliton solution is constructed after briefly indicating the form of nondegenerate one-soliton solution. To derive these soliton solutions, we simultaneously solve the nonlocal Manakov equation and a pair of coupled equations that arise from the zero curvature condition. The latter consideration yields general soliton solution which agrees with the solutions that are already reported in the literature under certain specific parametric choice. We also discuss the salient features associated with the obtained degenerate soliton solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Suchkov, S.V., Sukhorukov, A.A., Huang, J., Dmitriev, S.V., Lee, C., Kivshar, Y.S.: Nonlinear switching and solitons in \(\mathscr {PT}\)-symmetric photonic systems. Laser Photonics Rev. 10, 177 (2016)

    Article  Google Scholar 

  2. Konotop, V.V., Yang, J., Zezyulin, D.A.: Nonlinear waves in \(\mathscr {PT}\)-symmetric systems. Rev. Mod. Phys. 88, 035002 (2016)

    Article  Google Scholar 

  3. Ablowitz, M.J., Musslimani, Z.H.: Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 110, 064105 (2013)

    Article  Google Scholar 

  4. Ablowitz, M.J., Musslimani, Z.H.: Inverse scattering transform for the integrable nonlocal nonlinear Schrödinger equation. Nonlinearity 29, 915 (2016)

    Article  MathSciNet  Google Scholar 

  5. Gerdjikov, V.S., Saxena, A.: Complete integrability of nonlocal nonlinear Schrödinger equation. J. Math. Phys. 58, 013502 (2017)

    Article  MathSciNet  Google Scholar 

  6. Olver, P.J.: Applications of Lie Groups to Differential Equations, 2nd edn. Springer, New York (1993)

    Book  Google Scholar 

  7. Bluman, G.W., Kumei, S.: Symmetries and Differential Equations. Springer, New York (1989)

    Book  Google Scholar 

  8. Ovsiannikov, L.V.: Group Analysis of Differential Equations. Academic Press, New York (1982)

    MATH  Google Scholar 

  9. Bender, C.M., Boettcher, S.: Real spectra in non-Hermitian hamiltonians having \(\mathscr {PT}\)-symmetry. Phys. Rev. Lett. 80, 5243 (1998)

    Article  MathSciNet  Google Scholar 

  10. Sarma, A.K., Miri, M.A., Musslimani, Z.H., Christodoulides, D.N.: Continuous and discrete Schrödinger systems with parity-time-symmetric nonlinearities. Phys. Rev. E 89, 052918 (2014)

    Article  Google Scholar 

  11. Gadzhimuradov, T.A., Agalarov, A.M.: Towards a gauge-equivalent magnetic structure of the nonlocal nonlinear Schrödinger equation. Phys. Rev. A 93, 062124 (2016)

    Article  Google Scholar 

  12. Lakshmanan, M.: Continuum spin system as an exactly solvable dynamical system. Phys. Lett. A 61, 53 (1977)

    Article  Google Scholar 

  13. Khare, A., Saxena, A.: Periodic and hyperbolic soliton solutions of a number of nonlocal nonlinear equations. J. Math. Phys. 56, 032104 (2015)

    Article  MathSciNet  Google Scholar 

  14. Li, M., Xu, T.: Dark and antidark soliton interactions in the nonlocal nonlinear Schrödinger equation with the self-induced parity-time-symmetric potential. Phys. Rev. E 91, 033202 (2015)

    Article  MathSciNet  Google Scholar 

  15. Huang, X., Ling, L.: Soliton solutions for the nonlocal nonlinear Schrödinger equation. Eur. Phys. J. Plus 131, 148 (2016)

    Article  Google Scholar 

  16. Wen, X.Y., Yan, Z., Yang, Y.: Dynamics of higher-order rational solitons for the nonlocal nonlinear Schrödinger equation with the self-induced parity-time-symmetric potential. Chaos 26, 063123 (2016)

    Article  MathSciNet  Google Scholar 

  17. Stalin, S., Senthilvelan, M., Lakshmanan, M.: Nonstandard bilinearization of \(\mathscr {PT}\)-invariant nonlocal nonlinear Schrödinger equation: Bright soliton solutions. Phys. Lett. A 381, 2380 (2017)

    Article  MathSciNet  Google Scholar 

  18. Stalin, S., Senthilvelan, M., Lakshmanan, M.: A critique on the soliton solutions of \(\mathscr {PT}\)-invariant reverse space nonlocal nonlinear Schrödinger equation. arXiv:1709.00733 (2018)

  19. Ablowitz, M.J., Musslimani, Z.H.: Integrable discrete \(\mathscr {PT}\)-symmetric model. Phys. Rev. E 90, 032912 (2014)

    Article  Google Scholar 

  20. Fokas, A.S.: Integrable multidimensional versions of the nonlocal nonlinear Schrödinger equation. Nonlinearity 29, 319 (2016)

    Article  MathSciNet  Google Scholar 

  21. Lou, S.Y., Huang, F.: Alice-Bob Physics: Coherent Solutions of Nonlocal KdV Systems. Sci. Rep. 7, 869 (2017)

    Article  Google Scholar 

  22. Rao, J., Cheng, Y., He, J.: Rational and semirational solutions of the nonlocal Davey–Stewartson equations. Stud. Appl. Math 139, 568 (2017)

    Article  MathSciNet  Google Scholar 

  23. Liu, Y., Mihalache, D., He, J.: Families of rational solutions of the y-nonlocal Davey–Stewartson II equation. Nonlinear Dyn. 90, 2445 (2017)

    Article  MathSciNet  Google Scholar 

  24. Xu, Z.X., Chow, K.W.: Breathers and rogue waves for a third order nonlocal partial differential equation by a bilinear transformation. Appl. Math. Lett. 56, 72 (2016)

    Article  MathSciNet  Google Scholar 

  25. Li, M., Xu, T., Meng, D.: Reverse space-time nonlocal Sasa–Satsuma equation and its solutions. J. Phys. Soc. Jpn. 85, 124001 (2016)

    Article  Google Scholar 

  26. Ma, L.Y., Zhu, Z.N.: \(N\)-soliton solution for an integrable nonlocal discrete focusing nonlinear Schrödinger equation. Appl. Math. Lett. 59, 115 (2016)

    Article  MathSciNet  Google Scholar 

  27. Ji, J.L., Zhu, Z.N.: On a nonlocal modified Korteweg-de Vries equation: integrability, Darboux transformation and soliton solutions. Commun. Nonlinear Sci. Numer. Simul. 42, 699 (2017)

    Article  MathSciNet  Google Scholar 

  28. Ma, L.Y., Zhu, Z.N.: Nonlocal nonlinear Schrödinger equation and its discrete version: soliton solutions and gauge equivalence. J. Math. Phys. 57, 083507 (2016)

    Article  MathSciNet  Google Scholar 

  29. Zhang, H.Q., Zhang, M.Y., Hu, R.: Darboux transformation and soliton solutions in the parity-time-symmetric nonlocal vector nonlinear Schrödinger equation. Appl. Math. Lett. 76, 170 (2018)

    Article  MathSciNet  Google Scholar 

  30. Wen, Z., Yan, Z.: Solitons and their stability in the nonlocal nonlinear Schrödinger equation with \(\mathscr {PT}\)-symmetric potentials. Chaos 27, 053105 (2017)

    Article  MathSciNet  Google Scholar 

  31. Zhang, G., Yan, Z.: Multi-rational and semi-rational solitons and interactions for the nonlocal coupled nonlinear Schrödinger equations. Eur. Phys. Lett. 118, 60004 (2017)

    Article  Google Scholar 

  32. Chen, K., Zhang, D.J.: Solutions of the nonlocal nonlinear Schrödinger hierarchy via reduction. Appl. Math. Lett. 75, 82 (2018)

    Article  MathSciNet  Google Scholar 

  33. Chen, K., Deng, X., Lou, S., Zhan, D.J.: Solutions of nonlocal equations reduced from the AKNS hierarchy. Stud. Appl. Math. 00, 1 (2018)

    MathSciNet  Google Scholar 

  34. Liu, W., Li, X.: General soliton solutions to a (\(2+1\))-dimensional nonlocal nonlinear Schrödinger equation with zero and nonzero boundary conditions. Nonlinear Dyn. 93, 721 (2018)

    Article  Google Scholar 

  35. Tang, X.Y., Liang, Z.F.: A general nonlocal nonlinear Schrödinger equation with shifted parity, charge-conjugate and delayed time reversal. Nonlinear Dyn. 92, 815 (2018)

    Article  Google Scholar 

  36. Zhang, Y., Liu, Y., Tang, X.: A general integrable three-component coupled nonlocal nonlinear Schrödinger equation. Nonlinear Dyn. 89, 2729 (2017)

    Article  Google Scholar 

  37. Sun, B.: General soliton solutions to a nonlocal long-wave-short-wave resonance interaction equation with nonzero boundary condition. Nonlinear Dyn. 92, 1369 (2018)

    Article  Google Scholar 

  38. Ma, L.Y., Zhao, H.Q., Gu, H.: Integrability and gauge equivalence of the reverse space-time nonlocal Sasa–Satsuma equation. Nonlinear Dyn. 91, 1909 (2018)

    Article  Google Scholar 

  39. Radhakrishnan, R., Lakshmanan, M., Hietarinta, J.: Inelastic collision and switching of coupled bright solitons in optical fibers. Phys. Rev. E 56, 2213 (1997)

    Article  Google Scholar 

  40. Kanna, T., Lakshmanan, M.: Exact soliton solutions, shape changing collisions, and partially coherent solitons in coupled nonlinear Schrödinger equations. Phys. Rev. Lett. 86, 5043 (2001)

    Article  Google Scholar 

  41. Radhakrishnan, R., Lakshmanan, M.: Bright and dark soliton solutions to coupled nonlinear Schrödinger equations. J. Phys. A. Math. Theor. 28, 2683 (1995)

    MATH  Google Scholar 

  42. Sheppard, A.P., Kivshar, Y.S.: Polarized dark solitons in isotropic Kerr media. Phys. Rev. E 55, 4773 (1997)

    Article  MathSciNet  Google Scholar 

  43. Kanna, T., Lakshmanan, M.: Exact soliton solutions of coupled nonlinear Schrödinger equations: shape-changing collisions, logic gates, and partially coherent solitons. Phys. Rev. E 67, 046617 (2003)

    Article  Google Scholar 

  44. Vijayajayanthi, M., Kanna, T., Lakshmanan, M.: Bright-dark solitons and their collisions in mixed \(N\)-coupled nonlinear Schrödinger equations. Phys. Rev. A 77, 013820 (2008)

    Article  Google Scholar 

  45. Kanna, T., Lakshmanan, M., Dinda, P.T., Akhmediev, N.: Soliton collisions with shape change by intensity redistribution in mixed coupled nonlinear Schrödinger equations. Phys. Rev. E 73, 026604 (2006)

    Article  MathSciNet  Google Scholar 

  46. Ohta, Y., Wang, D.S., Yang, J.: General \(N\) dark-dark solitons in the coupled nonlinear Schrödinger equations. Stud. Appl. Math. 127, 345 (2011)

    Article  MathSciNet  Google Scholar 

  47. Sinha, D., Ghosh, P.K.: Integrable nonlocal vector nonlinear Schrödinger equation with self-induced parity-time-symmetric potential. Phys. Lett. A 381, 124 (2017)

    Article  MathSciNet  Google Scholar 

  48. Gilson, C., Hietarinta, J., Nimmo, J., Ohta, Y.: Sasa-Satsuma higher-order nonlinear Schrödinger equation and its bilinearization and multisoliton solutions. Phys. Rev. E 68, 016614 (2003)

    Article  MathSciNet  Google Scholar 

  49. Kanna, T., Vijayajayanthi, M., Lakshmanan, M.: Coherently coupled bright optical solitons and their collisions. J. Phys. A: Math. Theor. 43, 434018 (2010)

    Article  MathSciNet  Google Scholar 

  50. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  Google Scholar 

  51. Correa, F., Fring, A.: Regularized degenerate multi-solitons. JHEP 9, 8 (2016)

    Article  MathSciNet  Google Scholar 

  52. Li, S., Biondini, G., Schiebold, C.: On the degenerate soliton solutions of the focusing nonlinear Schrödinger equation. J. Math. Phys. 58, 033507 (2017)

    Article  MathSciNet  Google Scholar 

  53. Cen, J., Correa, F., Fring, A.: Degenerate multi-solitons in the sine-Gordon equation. J. Phys. A: Math. Theor. 50, 435201 (2017)

    Article  MathSciNet  Google Scholar 

  54. Hu, W., Deng, Z., Han, S., Zhang, W.: Generalized multi-symplectic integrators for a class of Hamiltonian nonlinear wave PDEs. J. Comput. Phys. 235, 394 (2013)

    Article  MathSciNet  Google Scholar 

  55. Hu, W., Deng, Z., Yin, T.: Almost structure-preserving analysis for weakly linear damping nonlinear Schrödinger equation with periodic perturbation. Commun. Nonlinear Sci. Numer. Simul. 42, 298 (2017)

    Article  MathSciNet  Google Scholar 

  56. Hu, W., Song, M., Deng, Z., Yin, T., Wei, B.: Axial dynamic buckling analysis of embedded single-walled carbon nanotube by complex structure-preserving method. Appl. Math. Model. 52, 15 (2017)

    Article  MathSciNet  Google Scholar 

  57. Hu, W., Deng, Z., Wang, B., Ouyang, H.: Chaos in an embedded single-walled carbon nanotube. Nonlinear Dyn. 72, 389 (2013)

    Article  MathSciNet  Google Scholar 

  58. Hu, W., Deng, Z.: Chaos in embedded fluid-conveying single-walled carbon nanotube under transverse harmonic load series. Nonlinear Dyn. 79, 325 (2015)

    Article  Google Scholar 

  59. Hu, W., Song, M., Yin, T., Wei, B., Deng, Z.: Energy dissipation of damping cantilevered single-walled carbon nanotube oscillator. Nonlinear Dyn. 91, 767 (2018)

    Article  Google Scholar 

  60. Stalin, S., Senthilvelan, Lakshmanan, M.: Energy sharing collisions and the dynamics of degenerate solitons in the nonlocal Manakov system. Nonlinear Dyn. arXiv:1806.06735 (2018)

Download references

Acknowledgements

The work of MS forms part of a research project sponsored by DST-SERB, Government of India, under the Grant No. EMR/2016/001818. The research work of ML is supported by a SERB Distinguished Fellowship and also forms part of the DAE-NBHM research project (2/48 (5)/2015/NBHM (R.P.)/R&D-II/14127).

Author information

Authors and Affiliations

  1. Centre for Nonlinear Dynamics, School of Physics, Bharathidasan University, Tiruchirappalli, Tamil Nadu, 620 024, India

    S. Stalin, M. Senthilvelan & M. Lakshmanan

Authors
  1. S. Stalin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Senthilvelan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Lakshmanan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Senthilvelan.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Appendices

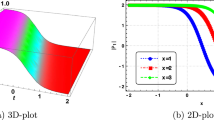
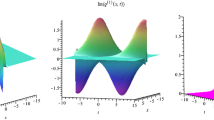
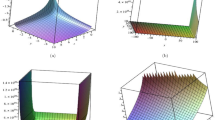
Appendix

A. The constants which appear in the nondegenerate one-soliton solution (10a)–(10b)

The constants which appear in the nondegenerate one-soliton solution (10a)–(10b) have the explicit forms,

$$\begin{aligned}&\text{ e }^{\varDelta _1^{(j)}}=\frac{(-1)^j(\bar{k}_1^{(1)}-\bar{k}_1^{(2)})\alpha _1^{(1)}\alpha _1^{(2)}\beta _1^{(3-j)}}{(\bar{k}_1^{(j)}+k_1^{(3-j)})(k_1^{(3-j)}+\bar{k}_1^{(3-j)})^2}, \end{aligned}$$
(26)
$$\begin{aligned}&\text{ e }^{\gamma _1^{(j)}}=\frac{(-1)^j(k_1^{(1)}-k_1^{(2)})\alpha _1^{(3-j)}\beta _1^{(1)}\beta _1^{(2)}}{(k_1^{(j)}+\bar{k}_1^{(3-j)})(k_1^{(3-j)}+\bar{k}_1^{(3-j)})^2},\nonumber \\&\quad ~ j=1,2, \end{aligned}$$
(27)
$$\begin{aligned}&\text{ e }^{\delta _1}=\frac{-\alpha _1^{(1)}\beta _1^{(1)}}{(k_1^{(1)}+\bar{k}_1^{(1)})^2},~\text{ e }^{\delta _2}=\frac{-\alpha _1^{(2)}\beta _1^{(2)}}{(k_1^{(2)}+\bar{k}_1^{(2)})^2}, \end{aligned}$$
(28)
$$\begin{aligned}&\text{ e }^{\delta _3}=\frac{\alpha _1^{(1)}\alpha _1^{(2)}\beta _1^{(1)}\beta _1^{(2)}(k_1^{(1)}-k_1^{(2)})(\bar{k}_1^{(1)}-\bar{k}_1^{(2)})}{(k_1^{(1)}+\bar{k}_1^{(1)})^2(\bar{k}_1^{(1)}+k_1^{(2)})(k_1^{(1)}+\bar{k}_1^{(2)})(k_1^{(2)}+\bar{k}_1^{(2)})^2}.\nonumber \\ \end{aligned}$$
(29)

B. The constants which appear in the reduced form of general two-soliton solution (21a)–(21b)

The following constants appear in the two-soliton solution (21a)–(21b)

$$\begin{aligned} \text{ e }^{\varDelta _1^{(j)}}= & {} \bar{\varrho }_{12}(-1)^{3-j}k_1\beta _1^{(3-j)}\nu _1+\bar{k}_2\alpha _2^{(j)}\varGamma _{11}\\&-\,\bar{k}_1\alpha _1^{(j)}\varGamma _{21}]/\kappa _{11}\kappa _{12}, \end{aligned}$$
$$\begin{aligned} \text{ e }^{\varDelta _2^{(j)}}= & {} \bar{\varrho }_{12}[(-1)^{3-j}k_2\beta _2^{(3-j)}\nu _1+\bar{k}_2\alpha _2^{(j)}\varGamma _{12}\\&-\,\bar{k}_1\alpha _1^{(j)}\varGamma _{22}]/\kappa _{21}\kappa _{22},\\ \text{ e }^{\gamma _1^{(j)}}= & {} \varrho _{12}[k_2\beta _2^{(j)}\varGamma _{11}-k_1\beta _1^{(j)}\varGamma _{12}\\&+\,(-1)^{(j)}\bar{k}_1\alpha _1^{(3-j)}\nu _2]/\kappa _{11}\kappa _{21},\\ \text{ e }^{\gamma _2^{(j)}}= & {} \varrho _{12}[k_2\beta _2^{(j)}\varGamma _{21}-k_1\beta _1^{(j)}\varGamma _{22}\\&+\,(-1)^{(j)}\bar{k}_2\alpha _2^{(3-j)}\nu _2]/\kappa _{12}\kappa _{22},\\ \text{ e }^{\delta _{1}}= & {} -\frac{\varGamma _{11}}{\kappa _{11}},~\text{ e }^{\delta _{2}}=-\frac{\varGamma _{21}}{\kappa _{12}},\\ ~\text{ e }^{\delta _{3}}= & {} -\frac{\varGamma _{12}}{\kappa _{21}},~\text{ e }^{\delta _{4}}=-\frac{\varGamma _{22}}{\kappa _{22}}, \\ \text{ e }^{\delta _{5}}= & {} \varrho _{12}\bar{\varrho }_{12}(\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2\\&-\,\varrho _{3}\varGamma _{21}\varGamma _{12})/\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}. \end{aligned}$$

Correspondingly in the \(\mathscr {PT}\)-symmetry preserving two-soliton solution (23), the form of various constants can be given as follows.

$$\begin{aligned} \text{ e }^{\delta _1}= & {} \frac{2(l_1+\bar{l}_2)(l_2+\bar{l}_1)}{(l_1-l_2)(\bar{l}_1-\bar{l}_2)}\text{ e }^{i(\theta _{12}+\varphi _{12})},\\ \text{ e }^{\delta _2}= & {} \frac{-2(l_1+\bar{l}_1)(l_2+\bar{l}_2)}{(l_1-l_2)(\bar{l}_1-\bar{l}_2)}\text{ e }^{i(\theta _{22}+\varphi _{12})},\\ \text{ e }^{\delta _3}= & {} \frac{-2(l_1+\bar{l}_1)(l_2+\bar{l}_2)}{(l_1-l_2)(\bar{l}_1-\bar{l}_2)}\text{ e }^{i(\theta _{12}+\varphi _{22})},\\ \text{ e }^{\delta _4}= & {} \frac{2(l_1+\bar{l}_2)(l_2+\bar{l}_1)}{(l_1-l_2)(\bar{l}_1-\bar{l}_2)}\text{ e }^{i(\theta _{22}+\varphi _{22})},\\ \text{ e }^{\varDelta _1^{(j)}}= & {} -\frac{2(l_1+\bar{l}_2)(l_2+\bar{l}_2)}{(\bar{l}_1-\bar{l}_2)}\text{ e }^{i(\theta _{12}+\varphi _{12}+\theta _{2j})},\\ \text{ e }^{\delta _5}= & {} 4\text{ e }^{i(\theta _{12}+\theta _{22}+\varphi _{12}+\varphi _{22})},\\ \text{ e }^{\varDelta _2^{(j)}}= & {} \frac{2(l_1+\bar{l}_1)(l_2+\bar{l}_1)}{(\bar{l}_1-\bar{l}_2)}\text{ e }^{i(\theta _{12}+\varphi _{22}+\theta _{2j})}, ~j=1,2. \end{aligned}$$

C. The unfactored degenerate two-soliton solution

A general unfactored degenerate two-soliton solution can be deduced by considering the following forms of seed solution for the functions \(g_1^{(j)}(x,t)\) and \(g_1^{(j)*}(-x,t)\), for Eq. (8) that is

$$\begin{aligned}&g^{(j)}_1(x,t)=\alpha _{1}^{(j)}\text{ e }^{\bar{\xi }_1}+\alpha _{2}^{(j)}\text{ e }^{\bar{\xi }_2},~\bar{\xi _j}=i \bar{k_{j}}x+i\bar{k_{j}^{2}}t , \end{aligned}$$
(30a)
$$\begin{aligned}&g^{(j)*}_1(-x,t)=\beta _{1}^{(j)}\text{ e }^{\xi _1}+\beta _{2}^{(j)}\text{ e }^{\xi _2},\nonumber \\&\quad \xi _{j}=i k_{j}x-ik_{j}^{2}t, ~j=1,2 . \end{aligned}$$
(30b)

The above form of seed solutions truncates the series expansions (7a)–(7c) at in 7-th order in \(g^{(j)}(x,t)\) and \(g^{(j)*}(-x,t)\), at 8-th order in f(x, t) and \(f^{*}(-x,t)\) and 6-th order in \(s^{(1)}(-x,t)\) and \(s^{(2)}(-x,t)\). By solving the resultant equations that arise at each order of \(\epsilon \), we have obtained the following expressions for the unknown functions \(g^{(j)}(x,t)\), \(g^{(j)*}(-x,t)\) and f(x, t),

$$\begin{aligned} g^{(j)}(x,t)= & {} \alpha _{1}^{(j)}\text{ e }^{\bar{\xi }_1}+\alpha _{2}^{(j)}\text{ e }^{\bar{\xi }_2}+\text{ e }^{\xi _{1}+2\bar{\xi }_1+\varDelta _{1}^{(j)}}\nonumber \\&+\,\text{ e }^{\xi _{2}+2\bar{\xi _1}+\varDelta _{2}^{(j)}}+\text{ e }^{\xi _{1}+2\bar{\xi _2}+\varDelta _{3}^{(j)}}\nonumber \\&+\,\text{ e }^{\xi _{2}+2\bar{\xi _2}+\varDelta _{4}^{(j)}} +\text{ e }^{\xi _{1}+\bar{\xi _1}+\bar{\xi _2}+\varDelta _{5}^{(j)}}\nonumber \\&+\,\text{ e }^{\xi _{2}+\bar{\xi _1}+\bar{\xi _2}+\varDelta _{6}^{(j)}}+\text{ e }^{2\xi _{1}+2\bar{\xi _1}+\bar{\xi _2}+\,\varDelta _{7}^{(j)}}\nonumber \\&+\,\text{ e }^{2\xi _{1}+\bar{\xi _1}+2\bar{\xi _2}+\varDelta _{8}^{(j)}}+\text{ e }^{2\xi _{2}+2\bar{\xi _1}+\bar{\xi _2}+\varDelta _{9}^{(j)}}\nonumber \\&+\,\text{ e }^{2\xi _{2}+\bar{\xi _1}+2\bar{\xi _2}+\mu _{1}^{(j)}}+\text{ e }^{\xi _{1}+\bar{\xi _1}+\xi _2+2\bar{\xi _2}+\mu _{2}^{(j)}}\nonumber \\&+\,\text{ e }^{\xi _{1}+2\bar{\xi _1}+\xi _2+\bar{\xi _2}+\mu _{3}^{(j)}}\nonumber \\&+\,\text{ e }^{2\xi _{1}+2\bar{\xi _1}+\xi _{2}+2\bar{\xi _2}+\mu _{4}^{(j)}}\nonumber \\&+\,\text{ e }^{2\bar{\xi _1}+2\bar{\xi _2}+\xi _{1}+2\xi _{2}+\mu _{5}^{(j)}}\end{aligned}$$
(31a)
$$\begin{aligned} g^{(j)*}(-x,t)= & {} \beta _{1}^{(j)}\text{ e }^{\xi _{1}}+\beta _{2}^{(j)}\text{ e }^{\xi _{2}}+\text{ e }^{2\xi _{1}+\bar{\xi _1}+\gamma _{1}^{(j)}}\nonumber \\&+\,\text{ e }^{2\xi _{1}+\bar{\xi _2}+\gamma _{2}^{(j)}}+\text{ e }^{2\xi _{2}+\bar{\xi _1}+\gamma _{3}^{(j)}}\nonumber \\&+\,\text{ e }^{2\xi _{2}+\bar{\xi _2}+\gamma _{4}^{(j)}}+\text{ e }^{\xi _{1}+\bar{\xi _1}+\xi _{2}+\gamma _{5}^{(j)}}\nonumber \\&+\,\text{ e }^{\xi _{1}+\xi _{2}+\bar{\xi _2}+\gamma _{6}^{(j)}}+\text{ e }^{2\xi _{1}+2\bar{\xi _1}+\xi _{2}+\gamma _{7}^{(j)}}\nonumber \\&+\,\text{ e }^{\xi _{1}+2\bar{\xi _1}+2\xi _{2}+\gamma _{8}^{(j)}}+\text{ e }^{2\xi _{1}+2\bar{\xi _2}+\xi _{2}+\gamma _{9}^{(j)}}\nonumber \\&+\,\text{ e }^{2\xi _{2}+2\bar{\xi _2}+\xi _{1}+\varphi _{1}^{(j)}}+\text{ e }^{2\xi _{1}+\bar{\xi _1}+\xi _{2}+\bar{\xi _2}+\varphi _{2}^{(j)}}\nonumber \\&+\,\text{ e }^{\xi _{1}+\bar{\xi _1}+2\xi _{2}+\bar{\xi _2}+\varphi _{3}^{(j)}}\nonumber \\&+\,\text{ e }^{2\xi _{1}+2\bar{\xi _1}+2\xi _{2}+\bar{\xi _2}+\varphi _{4}^{(j)}}\nonumber \\&+\,\text{ e }^{2\xi _{1}+\bar{\xi _1}+2\xi _{2}+2\bar{\xi _2}+\varphi _{5}^{(j)}}\end{aligned}$$
(31b)
$$\begin{aligned} f(x,t)= & {} 1+\text{ e }^{\xi _{1}+\bar{\xi _1}+\delta _1}+\text{ e }^{\xi _{2}+\bar{\xi _1}+\delta _2}+\text{ e }^{\xi _{1}+\bar{\xi _2}+\delta _3}\nonumber \\&+\,\text{ e }^{\xi _{2}+\bar{\xi _2}+\delta _4}+\text{ e }^{2(\xi _{1}+\bar{\xi _1})+\delta _{11}}\nonumber \\&+\,\text{ e }^{2(\xi _{2}+\bar{\xi _1})+\delta _{12}}+\text{ e }^{2(\xi _{1}+\bar{\xi _2})+\delta _{13}}\nonumber \\&+\,\text{ e }^{2(\xi _{2}+\bar{\xi _2})+\delta _{14}}+\text{ e }^{2\bar{\xi _1}+\xi _{1}+\xi _{2}+\delta _{15}}\nonumber \\&+\,\text{ e }^{2\bar{\xi _2}+\xi _{1}+\xi _{2}+\delta _{16}}+\text{ e }^{2\xi _{1}+\bar{\xi _1}+\bar{\xi _2}+\delta _{17}}\nonumber \\&+\,\text{ e }^{2\xi _{2}+\bar{\xi _1}+\bar{\xi _2}+\delta _{18}}+\text{ e }^{\xi _{1}+\bar{\xi _1}+\xi _{2}+\bar{\xi _2}+\delta _{19}}\nonumber \\&+\,\text{ e }^{2\xi _{1}+2\bar{\xi _1}+\xi _{2}+\bar{\xi _2}+\delta _{21}}\nonumber \\&+\,\text{ e }^{2\xi _{1}+\bar{\xi _1}+\xi _{2}+2\bar{\xi _2}+\delta _{22}}\nonumber \\&+\,\text{ e }^{\xi _{1}+2\bar{\xi _1}+2\xi _{2}+\bar{\xi _2}+\delta _{23}}\nonumber \\&+\,\text{ e }^{\xi _{1}+\bar{\xi _1}+2\xi _{2}+2\bar{\xi _2}+\delta _{24}}\nonumber \\&+\,\text{ e }^{2(\xi _{1}+\bar{\xi _1}+\xi _{2}+\bar{\xi _2})+\delta _{31}}\equiv f^{*}(-x,t). \nonumber \\ \end{aligned}$$
(31c)

The explicit expression of all the constants that appear in two-soliton solution is given as

$$\begin{aligned} \text{ e }^{\delta _{1}}= & {} -2\frac{\varGamma _{11}}{\kappa _{11}},~\text{ e }^{\delta _{2}}=-2\frac{\varGamma _{12}}{\kappa _{21}},\\&\text{ e }^{\delta _{3}}=-2\frac{\varGamma _{21}}{\kappa _{12}},~\text{ e }^{\delta _{4}}=-2\frac{\varGamma _{22}}{\kappa _{22}},\\ \varGamma _{11}= & {} \left( \alpha ^{(1)}_1\beta ^{(1)}_1+\alpha ^{(2)}_1\beta ^{(2)}_1\right) ,\\ \varGamma _{12}= & {} \left( \alpha ^{(1)}_1\beta ^{(1)}_2+\alpha ^{(2)}_1\beta ^{(2)}_2\right) ,\\ \varGamma _{21}= & {} \left( \alpha ^{(1)}_2\beta ^{(1)}_1+\alpha ^{(2)}_2\beta ^{(2)}_1\right) ,\\ \varGamma _{22}= & {} \left( \alpha ^{(1)}_2\beta ^{(1)}_2+\alpha ^{(2)}_2\beta ^{(2)}_2\right) ,\\ \kappa _{lm}= & {} (k_l+\bar{k}_m)^2 ,~l,m=1,2.\\ \text{ e }^{\varDelta _{1}^{(j)}}= & {} -\frac{\alpha _1^{(j)}\varGamma _{11}}{\kappa _{11}},~\text{ e }^{\varDelta _{2}^{(j)}}=-\frac{\alpha _1^{(j)}\varGamma _{12}}{\kappa _{21}},\\ \text{ e }^{\varDelta _{3}^{(j)}}= & {} -\frac{\alpha _2^{(j)}\varGamma _{21}}{\kappa _{12}},~\text{ e }^{\varDelta _{4}^{(j)}}=-\frac{\alpha _2^{(j)}\varGamma _{22}}{\kappa _{22}}, \\ \text{ e }^{\varDelta _{5}^{(j)}}= & {} -\bigg (\alpha _1^{(j)}\varGamma _{21}(k_1+\bar{k}_1)(k_1+2\bar{k}_1-\bar{k}_2)\\&+\,\alpha _2^{(j)}\varGamma _{11}(k_1+\bar{k}_2)(k_1+2\bar{k}_2-\bar{k}_1)\bigg )/\kappa _{11}\kappa _{12},~\\ \text{ e }^{\varDelta _{6}^{(j)}}= & {} -\bigg (\alpha _1^{(j)}\varGamma _{22}(k_2+\bar{k}_1)(k_2+2\bar{k}_1-\bar{k}_2)\\&+\,\alpha _2^{(j)}\varGamma _{12}(k_2+\bar{k}_2)(k_2+2\bar{k}_2-\bar{k}_1)\bigg )/ \kappa _{21}\kappa _{22},\\ \text{ e }^{\gamma _{1}^{(j)}}= & {} -\frac{\beta _1^{(j)}\varGamma _{11}}{\kappa _{11}},~\text{ e }^{\gamma _{2}^{(j)}}=-\frac{\beta _1^{(j)}\varGamma _{21}}{\kappa _{12}},\\ \text{ e }^{\gamma _{3}^{(j)}}= & {} -\frac{\beta _2^{(j)}\varGamma _{12}}{\kappa _{21}},~\text{ e }^{\gamma _{4}^{(j)}}=-\frac{\beta _2^{(j)}\varGamma _{22}}{\kappa _{22}},\\ \text{ e }^{\gamma _{5}^{(j)}}= & {} -\bigg (\beta _1^{(j)}\varGamma _{12}(k_1+\bar{k}_1)(\bar{k}_1+2k_1-k_2)\\&+\,\beta _2^{(j)}\varGamma _{11}(k_2+\bar{k}_1)(\bar{k}_1+2k_2-k_1)\bigg )/\kappa _{11}\kappa _{21},\\ \text{ e }^{\gamma _{6}^{(j)}}= & {} -\bigg (\beta _1^{(j)}\varGamma _{22}(k_1+\bar{k}_2)(\bar{k}_2+2k_1-k_2)\\&+\,\beta _2^{(j)}\varGamma _{21}(k_2+\bar{k}_2)(\bar{k}_2+2k_2-k_1)\bigg )/\kappa _{12}\kappa _{22}. \end{aligned}$$
$$\begin{aligned} \text{ e }^{\delta _{11}}= & {} \frac{\varGamma _{11}^2}{\kappa _{11}^2},~\text{ e }^{\delta _{12}}=\frac{\varGamma _{12}^2}{\kappa _{21}^2},~\text{ e }^{\delta _{13}}=\frac{\varGamma _{21}^2}{\kappa _{12}^2},\\ \text{ e }^{\delta _{14}}= & {} \frac{\varGamma _{22}^2}{\kappa _{22}^2},~\text{ e }^{\delta _{15}}=\frac{2\varGamma _{11}\varGamma _{12}}{\kappa _{11}\kappa _{21}},\\ \text{ e }^{\delta _{16}}= & {} \frac{2\varGamma _{21}\varGamma _{22}}{\kappa _{12}\kappa _{22}},~\text{ e }^{\delta _{17}}=\frac{2\varGamma _{11}\varGamma _{21}}{\kappa _{11}\kappa _{12}},~\text{ e }^{\delta _{18}}=\frac{2\varGamma _{12}\varGamma _{22}}{\kappa _{21}\kappa _{22}},\\ \text{ e }^{\delta _{19}}= & {} \frac{2(\kappa _{21}\kappa _{12})^{\frac{1}{2}}\varLambda _3+2(\kappa _{11}\kappa _{22})^{\frac{1}{2}}\varLambda _4+4\varLambda _5}{\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}},\\ \varLambda _3= & {} (k_1(2\bar{k}_1+k_2-\bar{k}_2)+2k_2\bar{k}_2+\bar{k}_1(\bar{k}_2-k_2))\\&(\alpha _1^{(1)}\beta _1^{(1)}\alpha _2^{(2)}\beta _2^{(2)}+\alpha _1^{(1)}\beta _1^{(2)}\alpha _2^{(1)}\beta _2^{(1)}),\\ \varLambda _4= & {} (-k_2\bar{k}_2+\bar{k}_1(2k_2+\bar{k}_2)+k_1(2\bar{k}_2-\bar{k}_1+k_2))\\&(\alpha _1^{(2)}\beta _1^{(1)}\alpha _2^{(1)}\beta _2^{(2)}+\alpha _1^{(1)}\beta _1^{(2)}\alpha _2^{(2)}\beta _2^{(1)}),\\ \varLambda _5= & {} (k_2^2\bar{k}_2^2+k_2\bar{k}_1\bar{k}_2(\bar{k}_2-k_2)\\&+\,\bar{k}_1^2(k_2^2+k_2\bar{k}_2+\bar{k}_2^2)+k_1^2(\bar{k}_1^2+k_2^2\\&+\,\bar{k}_1(k_2-\bar{k}_2)+k_2\bar{k}_2\\&+\,\bar{k}_2^2)+k_1[k_2\bar{k}_2(k_2-\bar{k}_2)+\bar{k}_1^2(\bar{k}_2-k_2)\\&+\,\bar{k}_1(k_2^2+5k_2\bar{k}_2+\bar{k}_2^2)])\\&(\alpha _1^{(2)}\beta _1^{(2)}\alpha _2^{(2)}\beta _2^{(2)}+\alpha _1^{(1)}\beta _1^{(1)}\alpha _2^{(1)}\beta _2^{(1)}).\\ \text{ e }^{\varDelta _{7}^{(j)}}= & {} \bar{\varrho }_{12}\varGamma _{11}\bigg ((-1)^{j}k_1\beta _1^{(3-j)}\nu _1\\&-\,\bar{k}_2\alpha _2^{(j)}\varGamma _{11}+\bar{k}_1\alpha _1^{(j)}\varGamma _{21}\bigg )/\kappa _{11}^2\kappa _{12},\\ \text{ e }^{\varDelta _{8}^{(j)}}= & {} \bar{\varrho }_{12}\varGamma _{21}\bigg ((-1)^{j}k_1\beta _1^{(3-j)}\nu _1\\&-\,\bar{k}_2\alpha _2^{(j)}\varGamma _{11}+\bar{k}_1\alpha _1^{(j)}\varGamma _{21}\bigg )/\kappa _{11}\kappa _{12}^2,\\ \text{ e }^{\varDelta _{9}^{(j)}}= & {} \bar{\varrho }_{12}\varGamma _{12}\bigg ((-1)^{j}k_2\beta _2^{(3-j)}\nu _1\\&-\,\bar{k}_2\alpha _2^{(j)}\varGamma _{12}+\bar{k}_1\alpha _1^{(j)}\varGamma _{22}\bigg )/\kappa _{21}^2\kappa _{22},\\ \text{ e }^{\mu _{1}^{(j)}}= & {} \bar{\varrho }_{12}\varGamma _{22}\bigg ((-1)^{j}k_2\beta _2^{(3-j)}\nu _1\\&-\,\bar{k}_2\alpha _2^{(j)}\varGamma _{12}+\bar{k}_1\alpha _1^{(j)}\varGamma _{22}\bigg )/\kappa _{21}\kappa _{22}^2,\\ \end{aligned}$$
$$\begin{aligned} \text{ e }^{\gamma _{7}^{(j)}}= & {} \varrho _{12}\varGamma _{11}\bigg (-k_2\beta _2^{(j)}\varGamma _{11}\\&+\,k_1\beta _1^{(j)}\varGamma _{12}+(-1)^{(3-j)}\bar{k}_1\alpha _1^{(3-j)}\nu _2\bigg )/\kappa _{11}^2\kappa _{21},\\ \text{ e }^{\gamma _{8}^{(j)}}= & {} \varrho _{12}\varGamma _{12}\bigg (-k_2\beta _2^{(j)}\varGamma _{11}\\&+\,k_1\beta _1^{(j)}\varGamma _{12}+(-1)^{(3-j)}\bar{k}_1\alpha _1^{(3-j)}\nu _2\bigg )/\kappa _{11}\kappa _{21}^2,\\ \text{ e }^{\gamma _{9}^{(j)}}= & {} \varrho _{12}\varGamma _{21}\bigg (-k_2\beta _2^{(j)}\varGamma _{21}\\&+\,k_1\beta _1^{(j)}\varGamma _{22}+(-1)^{(3-j)}\bar{k}_2\alpha _2^{(3-j)}\nu _2\bigg )/\kappa _{12}^2\kappa _{22},\\ \text{ e }^{\varphi _{1}^{(j)}}= & {} \varrho _{12}\varGamma _{22}\bigg (-k_2\beta _2^{(j)}\varGamma _{21}\\&+\,k_1\beta _1^{(j)}\varGamma _{22}+(-1)^{(3-j)}\bar{k}_2\alpha _2^{(3-j)}\nu _2\bigg )/\kappa _{12}\kappa _{22}^2,\\ \text{ e }^{\mu _2^{(j)}}= & {} \frac{\bar{\varrho }_{12}\varLambda _6}{\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}},~\text{ e }^{\mu _3^{(j)}}=\frac{\bar{\varrho }_{12}\varLambda _7}{\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}},\\ \text{ e }^{\varphi _2^{(j)}}= & {} \frac{\varrho _{12}\varLambda _8}{\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}},~ \text{ e }^{\varphi _3^{(j)}}=\frac{\varrho _{12}\varLambda _9}{\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}},\\ \varLambda _6= & {} \left( -2k_2^2\bar{k}_2\alpha _2^{(j)}\varGamma _{11}\varGamma _{22}+2\bar{k}_1^3\alpha _1^{(j)}\varGamma _{21}\varGamma _{22}\right. \\&+\,k_1^2\left[ -2\bar{k}_2\alpha _2^{(j)}\varGamma _{21}\varGamma _{12}+\bar{k}_1(\alpha _2^{(j)}\varGamma _{11}\right. \\&+\,\alpha _1^{(j)}\varGamma _{21})\varGamma _{22}+k_2\nu _1(-\alpha _2^{(j)}\nu _2\\&\left. +\beta _2^{(3-j)}(-1)^j\varGamma _{21})\right] +\bar{k}_1k_2[k_2\varGamma _{21}(\alpha _1^{(j)}\varGamma _{22}+\alpha _2^{(j)}\\&\varGamma _{12})+\bar{k}_2\alpha _2^{(j)}(\alpha _1^{(1)}(-2\beta _1^{(1)}\varGamma _{22}-\alpha _2^{(2)}\nu _2)\\&+\,\alpha _1^{(2)}(-2\beta _1^{(2)}\varGamma _{22}+\alpha _2^{(1)}\nu _2))]\\&+\,\bar{k}_1^2[k_2\varGamma _{21}(2\alpha _1^{(j)}\varGamma _{22}+(-1)^j\beta _2^{(3-j)}\nu _1)\\&-\,\bar{k}_2\alpha _2^{(j)}(\alpha _1^{(1)}(\beta _2^{(1)}\varGamma _{21}+\beta _1^{(1)}\varGamma _{22})+\alpha _1^{(2)}\\&(\beta _1^{(2)}\varGamma _{22}+\beta _2^{(2)}\varGamma _{21}))]+k_1\left[ \bar{k}_1^2\varGamma _{22}(2\alpha _1^{(j)}\varGamma _{21}\right. \\&+\,(-1)^j\beta _1^{(3-j)}\nu _1)+k_2(k_2\nu _1(-1)^j((-1)^j\\&\alpha _2^{(j)}\nu _2+\beta _1^{(3-j)}\varGamma _{22})+\bar{k}_2\alpha _2^{(j)}(\varGamma _{11}\varGamma _{22}+\varGamma _{21}\varGamma _{12}))\\&+\,\bar{k}_1\left[ \bar{k}_2\alpha _2^{(j)}\big (\alpha _1^{(1)}(-2\beta _2^{(1)}\varGamma _{21}\right. \\&+\,\alpha _2^{(2)}\nu _2)+\alpha _1^{(2)}(-\alpha _2^{(1)}\nu _2-2\beta _2^{(2)}\varGamma _{21})\big )\\&+\,k_2\big (-3\alpha _1^{(3-j)}\alpha _2^{(j)}(\beta _2^{(3-j)}\varGamma _{21}+\beta _1^{(3-j)}\varGamma _{22})\\&+\,\alpha _1^{(j)}\big (\alpha _2^{(3-j)}\beta _1^{(3-j)}\varGamma _{22}+\alpha _2^{(3-j)}\beta _2^{(3-j)}\varGamma _{21}\\&\left. \left. \left. +2\alpha _2^{(j)2}\beta _1^{(3-j)}\beta _2^{(3-j)}-2\alpha _2^{(j)2}\beta _1^{(j)}\beta _2^{(j)}\big )\big )\right] \right] \right) , \end{aligned}$$
$$\begin{aligned} \varLambda _7= & {} \bigg (-k_2\varGamma _{11}[2\bar{k}_2^2\alpha _2^{(j)}\varGamma _{12}+k_2\bar{k}_2(2\alpha _2^{(j)}\varGamma _{12}\\&+\,(-1)^{(3-j)}\beta _2^{(3-j)}\nu _1)+k_2^2(\alpha _1^{(j)}\varGamma _{22}+\alpha _2^{(j)}\\&\varGamma _{12})]+k_1^2[-\bar{k}_2(\alpha _1^{(j)}\varGamma _{21}+\alpha _2^{(j)}\varGamma _{11})\varGamma _{12}\\&+\,2\bar{k}_1\alpha _1^{(j)}\varGamma _{11}\varGamma _{22}+(-1)^jk_2\nu _1((-1)^{(3-j)}\alpha _1^{(j)}\\&\nu _2+\beta _2^{(3-j)}\varGamma _{11})]+\bar{k}_1\alpha _1^{(j)}[2k_2^2\varGamma _{21}\varGamma _{12}\\&+\,\bar{k}_2^2\big (\alpha _1^{(1)}(\beta _2^{(1)}\varGamma _{21}+\beta _1^{(1)}\varGamma _{22})+\alpha _1^{(2)}(\beta _1^{(2)}\varGamma _{22}\\&+\,\beta _2^{(2)}\varGamma _{21})\big )+k_2\bar{k}_2\big (\alpha _1^{(1)}(2\beta _2^{(1)}\varGamma _{21}-\alpha _2^{(2)}\nu _2)\\&+\,\alpha _1^{(2)}(2\beta _2^{(2)}\varGamma _{21}+\alpha _2^{(1)}\nu _2)\big )]-k_1\\&[\bar{k}_2^2(2\alpha _2^{(j)}\varGamma _{11}+(-1)^{(3-j)}\beta _1^{(3-j)}\nu _1)\varGamma _{12}\\&+\,(-1)^{(3-j)}k_2^2\nu _1((-1)^j\alpha _1^{(j)}\nu _2+\beta _1^{(3-j)}\varGamma _{12})\\&+\,k_2\bar{k}_2\big ((-1)^{(3-j)}\beta _1^{(3-j)}\varGamma _{12}\nu _1\\&+\,(-1)^{(3-j)}\beta _2^{(3-j)}\varGamma _{11}\nu _1-2\alpha _1^{(j)}\alpha _2^{(3-j)}(\beta _1^{(3-j)}\\&\varGamma _{12}+\beta _2^{(3-j)}\varGamma _{11})+2\alpha _1^{(3-j)2}\alpha _2^{(j)}\beta _1^{(3-j)}\beta _{2}^{(3-j)}\\&-\,2\alpha _1^{(j)2}\alpha _2^{(j)}\beta _1^{(j)}\beta _2^{(j)}\big )+\bar{k}_1\alpha _1^{(j)}\big (\bar{k}_2\\&(-2\varGamma _{11}\varGamma _{22}+\nu _1\nu _2)+k_2(\varGamma _{11}\varGamma _{22}+\varGamma _{12}\varGamma _{21})\big )]\bigg ),\\ \varLambda _8= & {} \bigg (-\bar{k}_1^2[\bar{k}_2(\beta _1^{(j)}\nu _1+(-1)^j\alpha _2^{(3-j)}\varGamma _{11})\nu _2\\&+\,k_2\varGamma _{21}(\beta _2^{(j)}\varGamma _{11}+\beta _1^{(j)}\varGamma _{12})]-k_2\varGamma _{11}\\&[2k_2^2\varGamma _{21}\beta _2^{(j)}+\bar{k}_2^2(\beta _2^{(j)}\varGamma _{21}+\beta _1^{(j)}\varGamma _{22})\\&+\,k_2\bar{k}_2(2\beta _2^{(j)}\varGamma _{21}+(-1)^j\alpha _2^{(3-j)}\nu _2)]\\&+\,k_1\beta _1^{(j)}[2\bar{k}_2^2\varGamma _{12}\varGamma _{21}+2\bar{k}_1^2\varGamma _{11}\varGamma _{22}\\&+\,k_2\bar{k}_2(2\varGamma _{21}\varGamma _{12}+\nu _1\nu _2)+k_2^2(\varGamma _{12}\varGamma _{21}+\varGamma _{11}\varGamma _{22})\\&+\,\bar{k}_1\big (-\bar{k}_2(\varGamma _{12}\varGamma _{21}+\varGamma _{11}\varGamma _{22})\\&+\,k_2(2\varGamma _{11}\varGamma _{22}-\nu _2\nu _2)\big )]+\bar{k}_1[(-1)^{(3-j)}\bar{k}_2^2\nu _2\\&((-1)^{(3-j)}\beta _1^{(j)}\nu _1+\alpha _1^{(3-j)}\varGamma _{21})-k_2^2\varGamma _{21}(2\beta _2^{(j)}\\ \end{aligned}$$
$$\begin{aligned}&\varGamma _{11}+(-1)^{(j)}\alpha _1^{(3-j)}\nu _2)+k_2\bar{k}_2\\&\big (\alpha _1^{(j)}\beta _1^{(j)}(2\beta _1^{(j)}\varGamma _{22}+(-1)^{(3-j)}\alpha _2^{(3-j)}\nu _2)\\&+\alpha _1^{(3-j)}((-1)^{(3-j)}\varGamma _{21}\nu _2+2\beta _1^{(j)}\beta _2^{(3-j)}\\&\varGamma _{21}+3(-1)^{(3-j)}\alpha _2^{(3-j)}\beta _1^{(3-j)}\nu _2)\big )]\bigg ),\\ \varLambda _9= & {} \bigg (-2k_2\bar{k}_2^2\varGamma _{11}\varGamma _{22}\beta _2^{(j)}+2k_1^3\beta _1^{(j)}\varGamma _{12}\varGamma _{22}\\&+\,\bar{k}_1^2(-1)^j[(-1)^{(3-j)}2k_2\varGamma _{21}\beta _2^{(j)}+(-1)^{(3-j)}\\&\bar{k}_2\nu _2(\nu _1\beta _2^{(j)}+(-1)^{(j)}\alpha _2^{(3-j)}\varGamma _{12})]\\&+\,k_1^2[\bar{k}_1\varGamma _{22}(2\beta _1^{(j)}\varGamma _{12}+(-1)^{(3-j)}\alpha _1^{(3-j)}\nu _2)\\&+\,\bar{k}_2\varGamma _{12}(2\beta _1^{(j)}\varGamma _{22}+(-1)^{(3-j)}\alpha _2^{(3-j)}\nu _2)\\&-\,k_2\beta _2^{(j)}(\varGamma _{11}\varGamma _{22}+\varGamma _{12}\varGamma _{21})]+\bar{k}_1\bar{k}_2[(-1)^{(3-j)}\bar{k}_2\\&\nu _2(\alpha _1^{(3-j)}\varGamma _{22}+(-1)^{(3-j)}\beta _2^{(j)}\nu _1)\\&+\,k_2\beta _2^{(j)}\big (\alpha _1^{(1)}(\beta _2^{(1)}\varGamma _{21}+\beta _1^{(1)}\varGamma _{22})+\alpha _1^{(2)}\\&(\beta _1^{(2)}\varGamma _{22}+\beta _2^{(2)}\varGamma _{21})\big )]\\&+\,k_1[\bar{k}_1^2\varGamma _{22}(\beta _2^{(j)}\varGamma _{11}+\beta _1^{(j)}\varGamma _{12})\\&+\,\bar{k}_2\big (\bar{k}_2\varGamma _{12}(\beta _1^{(j)}\varGamma _{22}+\beta _2^{(j)}\varGamma _{21})+k_2\beta _2^{(j)}\\&(-2\varGamma _{11}\varGamma _{22}+\nu _1\nu _2)\big )\\&+\,\bar{k}_1\big (k_2\beta _2^{(j)}[\alpha _1^{(1)}(-2\beta _2^{(1)}\varGamma _{21}+\alpha _2^{(2)}\nu _2)\\&+\,(-2\beta _2^{(2)}\varGamma _{21}-\alpha _2^{(1)}\nu _2)]\\&+\,\bar{k}_2[\alpha _1^{(j)}\beta _2^{(j)}(-2\beta _2^{(j)}\varGamma _{21}+(-1)^{(3-j)}\alpha _2^{(3-j)}\nu _2)\\&+\,\alpha _1^{(3-j)}(-2\beta _1^{(j)}\beta _2^{(j)}\varGamma _{22}+(-1)^{(3-j)}\nu _2\\&\varGamma _{22}+3(-1)^{(3-j)}\alpha _2^{(3-j)}\beta _2^{(j)}\nu _2)]\big )]\bigg ),\\ \nu _1= & {} \alpha _1^{(2)}\alpha _2^{(1)}-\alpha _1^{(1)}\alpha _2^{(2)},~\nu _2=\beta _1^{(1)}\beta _2^{(2)}-\beta _1^{(2)}\beta _2^{(1)},\\ \varrho _{12}= & {} (k_1-k_2),~\bar{\varrho }_{12}=(\bar{k}_1-\bar{k}_2), \\ \text{ e }^{\delta _{21}}= & {} -2\varrho _{12}\bar{\varrho }_{12}\varGamma _{11}\bigg (\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2\\&-\,\varrho _{3}\varGamma _{21}\varGamma _{12}\bigg )/\kappa _{11}^2\kappa _{12}\kappa _{21}\kappa _{22},\\ \text{ e }^{\delta _{22}}= & {} -2\varrho _{12}\bar{\varrho }_{12}\varGamma _{21}\bigg (\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2\\&-\,\varrho _{3}\varGamma _{21}\varGamma _{12}\bigg )/\kappa _{11}\kappa _{12}^2\kappa _{21}\kappa _{22}, \end{aligned}$$
$$\begin{aligned} \text{ e }^{\delta _{23}}= & {} -\,2\varrho _{12}\bar{\varrho }_{12}\varGamma _{12}\bigg (\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2\\&-\,\varrho _{3}\varGamma _{21}\varGamma _{12}\bigg )/\kappa _{11}\kappa _{12}\kappa _{21}^2\kappa _{22},\\ \text{ e }^{\delta _{24}}= & {} -\,2\varrho _{12}\bar{\varrho }_{12}\varGamma _{22}\bigg (\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2\\&-\,\varrho _{3}\varGamma _{21}\varGamma _{12}\bigg )/\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}^2,\\ \varrho _{1}= & {} (k_2\bar{k}_2+k_1\bar{k}_1),~\varrho _{2}=(k_1k_2+\bar{k}_1\bar{k}_2),\\ \varrho _{3}= & {} (k_1\bar{k}_2+k_2\bar{k}_1).\\ \text{ e }^{\mu _{4}^{(j)}}= & {} -\varrho _{12}\bar{\varrho }_{12}^2\bigg ((-1)^{j}k_1\beta _1^{(3-j)}\nu _1\\&-\,\bar{k}_2\alpha _2^{(j)}\varGamma _{11}+\bar{k}_1\alpha _1^{(j)}\varGamma _{21}\bigg )\\&\bigg (\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2-\varrho _{3}\varGamma _{21}\varGamma _{12}\bigg )\bigg /\kappa \kappa _{11}\kappa _{12} ,\\ \text{ e }^{\mu _{5}^{(j)}}= & {} -\varrho _{12}\bar{\varrho }_{12}^2\bigg ((-1)^{j}k_2\beta _2^{(3-j)}\nu _1\\&-\,\bar{k}_2\alpha _2^{(j)}\varGamma _{12}+\bar{k}_1\alpha _1^{(j)}\varGamma _{22}\bigg )\\&\bigg (\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2-\varrho _{3}\varGamma _{21}\varGamma _{12}\bigg )\bigg /\kappa \kappa _{21}\kappa _{22} \\ \text{ e }^{\varphi _{4}^{(j)}}= & {} -\varrho _{12}^2\bar{\varrho }_{12}\bigg (-k_2\beta _2^{(j)}\varGamma _{11}\\&+\,k_1\beta _1^{(j)}\varGamma _{12}+(-1)^{(3-j)}\bar{k}_1\alpha _1^{(3-j)}\nu _2\bigg )\\&\bigg (\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2-\varrho _{3}\varGamma _{21}\varGamma _{12}\bigg )/\kappa \kappa _{11}\kappa _{21},\\ \text{ e }^{\varphi _{5}^{(j)}}= & {} -\varrho _{12}^2\bar{\varrho }_{12}\bigg (-k_2\beta _2^{(j)}\varGamma _{21}\\&+\,k_1\beta _1^{(j)}\varGamma _{22}+(-1)^{(3-j)}\bar{k}_2\alpha _2^{(3-j)}\nu _2\bigg )\\&\bigg (\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2-\varrho _{3}\varGamma _{21}\varGamma _{12}\bigg )/\kappa \kappa _{12}\kappa _{22},\\ \text{ e }^{\delta _{31}}= & {} \varrho _{12}^2\bar{\varrho }_{12}^2\bigg (\varrho _{1}\varGamma _{11}\varGamma _{22}-\varrho _{2}\nu _1\nu _2\\&-\,\varrho _{3}\varGamma _{21}\varGamma _{12}\bigg )^2\bigg /\kappa _{11}^2\kappa _{12}^2\kappa _{21}^2\kappa _{22}^2,\\ \kappa= & {} \kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}. \end{aligned}$$

We arrive at the degenerate two-soliton solution by substituting the expression given in (31a)–(31c) in Eq. (4). The auxiliary functions are found to be

$$\begin{aligned}&s^{(1)}(-x,t)=s^{(2)}(-x,t)=\varGamma _{11}\text{ e }^{\xi _1+\bar{\xi }_1}+\varGamma _{21}\text{ e }^{\xi _1+\bar{\xi }_2}\\&\quad +\,\varGamma _{12}\text{ e }^{\bar{\xi }_1+\xi _2}+\varGamma _{22}\text{ e }^{\xi _2+\bar{\xi }_2}\\&\quad +\,\text{ e }^{\xi _1+2\bar{\xi }_1+\xi _2+\phi _1}+e^{2\xi _1+\bar{\xi }_1+\bar{\xi }_2+\phi _2}\\&\quad +\,\text{ e }^{\xi _1+\xi _2+2\bar{\xi }_2+\phi _3}+\text{ e }^{2\xi _2+\bar{\xi }_1+\bar{\xi }_2+\phi _4}\\&\quad +\,\text{ e }^{\xi _1+\bar{\xi }_1+\xi _2+\bar{\xi }_2+\phi _5}+\text{ e }^{2\xi _1+2\bar{\xi }_1+\xi _2+\bar{\xi }_2+\phi _{11}}\\&\quad +\,\text{ e }^{\xi _1+2\bar{\xi }_1+2\xi _2+\bar{\xi }_2+\phi _{12}}+\text{ e }^{2\xi _1+\bar{\xi }_1+\xi _2+2\bar{\xi }_2+\phi _{13}}\\&\quad +\,\text{ e }^{\xi _1+\bar{\xi }_1+2\xi _2+2\bar{\xi }_2+\phi _{14}} \end{aligned}$$

where the constants are obtained as

$$\begin{aligned} \text{ e }^{\phi _{1}}= & {} \frac{-\varrho _{12}^2\varGamma _{11}\varGamma _{12}}{\kappa _{11}\kappa _{21}},~\text{ e }^{\phi _{2}}=\frac{-\bar{\varrho }_{12}^2\varGamma _{11}\varGamma _{21}}{\kappa _{11}\kappa _{12}},\\ \text{ e }^{\phi _{3}}= & {} \frac{-\varrho _{12}^2\varGamma _{21}\varGamma _{22}}{\kappa _{12}\kappa _{22}},~\text{ e }^{\phi _{4}}=\frac{-\bar{\varrho }_{12}^2\varGamma _{12}\varGamma _{22}}{\kappa _{21}\kappa _{22}},\\ \text{ e }^{\phi _5}= & {} \frac{\varGamma _{11}\varGamma _{22}(\kappa _{12}\kappa _{21})^{1/2}\varLambda _1+\varGamma _{12}\varGamma _{21}(\kappa _{11}\kappa _{22})^{1/2}\varLambda _2}{\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}}, \end{aligned}$$
$$\begin{aligned} \varLambda _1= & {} (2\kappa _{11}(\kappa _{21}\kappa _{12})^{\frac{1}{2}}-\kappa _{11}\kappa _{12}^{\frac{1}{2}}(2\bar{k}_1+k_2-\bar{k}_2)\\&-\,\kappa _{11}\kappa _{21}^{\frac{1}{2}}(2k_1-k_2+\bar{k}_2)\\&+\,\kappa _{21}^{\frac{1}{2}}\kappa _{22}(-k_1+\bar{k}_1-2\bar{k}_2)\\&+\,(k_1-\bar{k}_1-2k_2)\kappa _{12}+2(\kappa _{12}\kappa _{21})^{\frac{1}{2}}\kappa _{22}),\\ \varLambda _2= & {} \left( \kappa _{11}^{\frac{1}{2}}(k_1-2k_2-\bar{k}_2)\kappa _{21}\right. \\&+\,\kappa _{11}^{\frac{1}{2}}\kappa _{12}(\bar{k}_1-k_2-2\bar{k}_2)\\&+\,2(\kappa _{11}\kappa _{22})^{\frac{1}{2}}\kappa _{21}-\kappa _{21}\kappa _{22}^{\frac{1}{2}}(k_1+2\bar{k}_1-\bar{k}_2)\\&\left. +\,2\kappa _{12}\kappa _{22}\kappa _{11}^{\frac{1}{2}}-(2k_1+\bar{k}_1-k_2)\kappa _{12}\kappa _{22}^{\frac{1}{2}}\right) ,\\ \text{ e }^{\phi _{11}}= & {} \frac{\varrho _{12}\bar{\varrho }_{12}\varGamma _{11}\psi }{\kappa _{11}^2\kappa _{21}\kappa _{12}},~\text{ e }^{\phi _{12}}=\frac{\varrho _{12}\bar{\varrho }_{12}\varGamma _{12}\psi }{\kappa _{11}\kappa _{21}^2\kappa _{22}},\\ \text{ e }^{\phi _{13}}= & {} \frac{\varrho _{12}\bar{\varrho }_{12}\varGamma _{21}\psi }{\kappa _{11}\kappa _{12}^2\kappa _{22}},~\text{ e }^{\phi _{14}}=\frac{\varrho _{12}\bar{\varrho }_{12}\varGamma _{22}\psi }{\kappa _{21}\kappa _{12}\kappa _{22}^2},\\ \psi= & {} \bigg (k_2\bar{k}_2\varGamma _{11}\varGamma _{22}+k_1(-\bar{k}_2\varGamma _{21}\varGamma _{12}\\&+\,\bar{k}_1\varGamma _{11}\varGamma _{22}-k_2\nu _1\nu _2)-\bar{k}_1(k_2\varGamma _{21}\varGamma _{12}+\bar{k}_2\nu _1\nu _2)\bigg ), \end{aligned}$$

D. The constants which appear in the degenerate three-soliton solution (24a)–(24c)

The constants which appear in factorized degenerate three-soliton solution (24a)–(24c) have the explicit forms,

$$\begin{aligned} \text{ e }^{\varDelta _1^{(j)}}= & {} \bar{\varrho }_{12}[(-1)^{3-j}k_1\beta _1^{(3-j)}\nu _1^{(1)}+\bar{k}_2\alpha _2^{(j)}\varGamma _{11}\\&-\,\bar{k}_1\alpha _1^{(j)}\varGamma _{21}]/\kappa _{11}\kappa _{12},\\ \text{ e }^{\varDelta _2^{(j)}}= & {} \bar{\varrho }_{13}[(-1)^{3-j}k_1\beta _1^{(3-j)}\nu _2^{(1)}+\bar{k}_3\alpha _3^{(j)}\varGamma _{11}\\&-\,\bar{k}_1\alpha _1^{(j)}\varGamma _{31}]/\kappa _{11}\kappa _{13},\\ \text{ e }^{\varDelta _3^{(j)}}= & {} \bar{\varrho }_{23}[(-1)^{3-j}k_1\beta _1^{(3-j)}\nu _3^{(1)}+\bar{k}_3\alpha _3^{(j)}\varGamma _{21}\\&-\,\bar{k}_2\alpha _2^{(j)}\varGamma _{31}]/\kappa _{12}\kappa _{13},\\ \text{ e }^{\varDelta _4^{(j)}}= & {} \bar{\varrho }_{12}[(-1)^{3-j}k_2\beta _2^{(3-j)}\nu _1^{(1)}+\bar{k}_2\alpha _2^{(j)}\varGamma _{12}\\&-\,\bar{k}_1\alpha _1^{(j)}\varGamma _{22}]/\kappa _{21}\kappa _{22},\\ \text{ e }^{\varDelta _5^{(j)}}= & {} \bar{\varrho }_{13}[(-1)^{3-j}k_2\beta _2^{(3-j)}\nu _2^{(1)}+\bar{k}_3\alpha _3^{(j)}\varGamma _{12}\\&-\,\bar{k}_1\alpha _1^{(j)}\varGamma _{32}]/\kappa _{21}\kappa _{23},\\ \text{ e }^{\varDelta _6^{(j)}}= & {} \bar{\varrho }_{23}[(-1)^{3-j}k_2\beta _2^{(3-j)}\nu _3^{(1)}+\bar{k}_3\alpha _3^{(j)}\varGamma _{22}\\&-\,\bar{k}_2\alpha _2^{(j)}\varGamma _{32}]/\kappa _{22}\kappa _{23},\\ \text{ e }^{\varDelta _7^{(j)}}= & {} \bar{\varrho }_{12}[(-1)^{3-j}k_3\beta _3^{(3-j)}\nu _1^{(1)}+\bar{k}_2\alpha _2^{(j)}\varGamma _{13}\\&-\,\bar{k}_1\alpha _1^{(j)}\varGamma _{23}]/\kappa _{31}\kappa _{32},\\ \end{aligned}$$
$$\begin{aligned} \text{ e }^{\varDelta _8^{(j)}}= & {} \bar{\varrho }_{13}[(-1)^{3-j}k_3\beta _3^{(3-j)}\nu _2^{(1)}+\bar{k}_3\alpha _3^{(j)}\varGamma _{13}\\&-\,\bar{k}_1\alpha _1^{(j)}\varGamma _{33}]/\kappa _{31}\kappa _{33},\\ \text{ e }^{\varDelta _9^{(j)}}= & {} \bar{\varrho }_{23}[(-1)^{3-j}k_3\beta _3^{(3-j)}\nu _3^{(1)}+\bar{k}_3\alpha _3^{(j)}\varGamma _{23}\\&-\,\bar{k}_2\alpha _2^{(j)}\varGamma _{33}]/\kappa _{32}\kappa _{33},\\ \text{ e }^{\gamma _1^{(j)}}= & {} \varrho _{12}[k_2\beta _2^{(j)}\varGamma _{11}-k_1\beta _1^{(j)}\varGamma _{12}\\&+\,(-1)^{(j)}\bar{k}_1\alpha _1^{(3-j)}\nu _1^{(2)}]/\kappa _{11}\kappa _{21},\\ \text{ e }^{\gamma _2^{(j)}}= & {} \varrho _{13}[k_3\beta _3^{(j)}\varGamma _{11}-k_1\beta _1^{(j)}\varGamma _{13}\\&+\,(-1)^{(j)}\bar{k}_1\alpha _1^{(3-j)}\nu _2^{(2)}]/\kappa _{11}\kappa _{31},\\ \text{ e }^{\gamma _3^{(j)}}= & {} \varrho _{23}[k_3\beta _3^{(j)}\varGamma _{12}-k_2\beta _2^{(j)}\varGamma _{13}\\&+\,(-1)^{(j)}\bar{k}_1\alpha _1^{(3-j)}\nu _3^{(2)}]/\kappa _{21}\kappa _{31},\\ \text{ e }^{\gamma _4^{(j)}}= & {} \varrho _{12}[k_2\beta _2^{(j)}\varGamma _{21}-k_1\beta _1^{(j)}\varGamma _{22}\\&+\,(-1)^{(j)}\bar{k}_2\alpha _2^{(3-j)}\nu _1^{(2)}]/\kappa _{12}\kappa _{22},\\ \text{ e }^{\gamma _5^{(j)}}= & {} \varrho _{13}[k_3\beta _3^{(j)}\varGamma _{21}-k_1\beta _1^{(j)}\varGamma _{23}\\&+\,(-1)^{(j)}\bar{k}_2\alpha _2^{(3-j)}\nu _2^{(2)}]/\kappa _{12}\kappa _{32},\\ \text{ e }^{\gamma _6^{(j)}}= & {} \varrho _{23}[k_3\beta _3^{(j)}\varGamma _{22}-k_2\beta _2^{(j)}\varGamma _{23}\\&+\,(-1)^{(j)}\bar{k}_2\alpha _2^{(3-j)}\nu _3^{(2)}]/\kappa _{22}\kappa _{32},\\ \text{ e }^{\gamma _7^{(j)}}= & {} \varrho _{12}[k_2\beta _2^{(j)}\varGamma _{31}-k_1\beta _1^{(j)}\varGamma _{32}\\&+\,(-1)^{(j)}\bar{k}_3\alpha _3^{(3-j)}\nu _1^{(2)}]/\kappa _{13}\kappa _{23}, \end{aligned}$$
$$\begin{aligned} \text{ e }^{\gamma _8^{(j)}}= & {} \varrho _{13}[k_3\beta _3^{(j)}\varGamma _{31}-k_1\beta _1^{(j)}\varGamma _{33}\\&+\,(-1)^{(j)}\bar{k}_3\alpha _3^{(3-j)}\nu _2^{(2)}]/\kappa _{13}\kappa _{33},\\ \text{ e }^{\gamma _9^{(j)}}= & {} \varrho _{23}[k_3\beta _3^{(j)}\varGamma _{32}-k_2\beta _2^{(j)}\varGamma _{33}\\&+\,(-1)^{(j)}\bar{k}_3\alpha _3^{(3-j)}\nu _3^{(2)}]/\kappa _{23}\kappa _{33},\\ \text{ e }^{\delta _{1}}= & {} -\frac{\varGamma _{11}}{\kappa _{11}},~\text{ e }^{\delta _{2}}=-\frac{\varGamma _{21}}{\kappa _{12}},~\text{ e }^{\delta _{3}}=-\frac{\varGamma _{31}}{\kappa _{13}},\\ \text{ e }^{\delta _{4}}= & {} -\frac{\varGamma _{12}}{\kappa _{21}},~\text{ e }^{\delta _{5}}=-\frac{\varGamma _{13}}{\kappa _{31}},\\ \text{ e }^{\delta _{6}}= & {} -\frac{\varGamma _{22}}{\kappa _{22}},~\text{ e }^{\delta _{7}}=-\frac{\varGamma _{32}}{\kappa _{23}}, \\ \text{ e }^{\delta _{8}}= & {} -\frac{\varGamma _{23}}{\kappa _{32}},~\text{ e }^{\delta _{9}}=-\frac{\varGamma _{33}}{\kappa _{33}},\\ \text{ e }^{\delta _{11}}= & {} \varrho _{12}\bar{\varrho }_{12}(\varrho _{1}\varGamma _{11}\varGamma _{22}\\&-\,\varrho _{2}\nu _1^{(1)}\nu _2^{(2)}-\varrho _{3}\varGamma _{21}\varGamma _{12})/\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22},\\ \text{ e }^{\delta _{12}}= & {} \varrho _{12}\bar{\varrho }_{13}(\varrho _{4}\varGamma _{11}\varGamma _{32}\\&-\,\varrho _{6}\nu _2^{(1)}\nu _1^{(2)}-\varrho _{5}\varGamma _{31}\varGamma _{12})/\kappa _{11}\kappa _{21}\kappa _{13}\kappa _{23},\\ \text{ e }^{\delta _{13}}= & {} \varrho _{12}\bar{\varrho }_{23}(\varrho _{9}\varGamma _{1}\varGamma _{32}\\&-\,\varrho _{7}\nu _3^{(1)}\nu _1^{(2)}-\varrho _{8}\varGamma _{31}\varGamma _{22})/\kappa _{12}\kappa _{22}\kappa _{13}\kappa _{23},\\ \text{ e }^{\delta _{14}}= & {} \varrho _{13}\bar{\varrho }_{12}(\varrho _{10}\varGamma _{11}\varGamma _{23}\\&-\,\varrho _{12}\nu _1^{(1)}\nu _2^{(2)}-\varrho _{11}\varGamma _{21}\varGamma _{13})/\kappa _{11}\kappa _{12}\kappa _{31}\kappa _{32},\\ \text{ e }^{\delta _{15}}= & {} \varrho _{23}\bar{\varrho }_{12}(\varrho _{13}\varGamma _{12}\varGamma _{23}\\&-\,\varrho _{15}\nu _1^{(1)}\nu _3^{(2)}-\varrho _{14}\varGamma _{22}\varGamma _{13})/\kappa _{21}\kappa _{22}\kappa _{31}\kappa _{32},\\ \text{ e }^{\delta _{16}}= & {} \varrho _{13}\bar{\varrho }_{13}(\varrho _{16}\varGamma _{11}\varGamma _{33}\\&-\,\varrho _{18}\nu _2^{(1)}\nu _2^{(2)}-\varrho _{17}\varGamma _{31}\varGamma _{13})/\kappa _{11}\kappa _{31}\kappa _{13}\kappa _{33},\\ \text{ e }^{\delta _{17}}= & {} \varrho _{23}\bar{\varrho }_{13}(\varrho _{19}\varGamma _{12}\varGamma _{33}\\&-\,\varrho _{21}\nu _2^{(1)}\nu _3^{(2)}-\varrho _{20}\varGamma _{32}\varGamma _{13})/\kappa _{21}\kappa _{31}\kappa _{23}\kappa _{33},\\ \text{ e }^{\delta _{18}}= & {} \varrho _{13}\bar{\varrho }_{23}(\varrho _{22}\varGamma _{21}\varGamma _{33}\\&-\,\varrho _{24}\nu _3^{(1)}\nu _2^{(2)}-\varrho _{23}\varGamma _{31}\varGamma _{23})/\kappa _{12}\kappa _{32}\kappa _{13}\kappa _{33},\\ \text{ e }^{\delta _{19}}= & {} \varrho _{23}\bar{\varrho }_{23}(\varrho _{25}\varGamma _{22}\varGamma _{33}\\&-\,\varrho _{27}\nu _3^{(1)}\nu _3^{(2)}-\varrho _{26}\varGamma _{32}\varGamma _{23})/\kappa _{22}\kappa _{32}\kappa _{23}\kappa _{33},\\ \end{aligned}$$
$$\begin{aligned} \text{ e }^{\chi _1^{(j)}}= & {} \frac{\varrho _{12}\bar{\varrho }_{12}\bar{\varrho }_{13}\bar{\varrho }_{23}\varLambda _1^{(j)}}{\kappa _{11}\kappa _{12}\kappa _{21}\kappa _{22}\kappa _{13}\kappa _{23}},~\text{ e }^{\chi _2^{(j)}}=\frac{\varrho _{13}\bar{\varrho }_{12}\bar{\varrho }_{13}\bar{\varrho }_{23}\varLambda _2^{(j)}}{\kappa _{11}\kappa _{12}\kappa _{31}\kappa _{32}\kappa _{13}\kappa _{33}},\\ \text{ e }^{\chi _3^{(j)}}= & {} \frac{\varrho _{23}\bar{\varrho }_{12}\bar{\varrho }_{13}\bar{\varrho }_{23}\varLambda _3^{(j)}}{\kappa _{21}\kappa _{22}\kappa _{31}\kappa _{32}\kappa _{23}\kappa _{33}},~\text{ e }^{\varphi _1^{(j)}}=\frac{\bar{\varrho }_{12}\varrho _{12}\varrho _{13}\varrho _{23}\varLambda _4^{(j)}}{\kappa _{11}\kappa _{21}\kappa _{12}\kappa _{22}\kappa _{31}\kappa _{32}},\\ \text{ e }^{\varphi _2^{(j)}}= & {} \frac{\bar{\varrho }_{13}\varrho _{12}\varrho _{13}\varrho _{23}\varLambda _5^{(j)}}{\kappa _{11}\kappa _{21}\kappa _{31}\kappa _{13}\kappa _{23}\kappa _{33}},~\text{ e }^{\varphi _3^{(j)}}=\frac{\bar{\varrho }_{23}\varrho _{12}\varrho _{13}\varrho _{23}\varLambda _6^{(j)}}{\kappa _{12}\kappa _{22}\kappa _{32}\kappa _{13}\kappa _{23}\kappa _{33}},\\ \varLambda _1^{(j)}= & {} (-1)^{(3-j)}k_2\bar{k}_2\bar{k}_3\varGamma _{11}\big [(-1)^{j}k_2\beta _2^{(3-j)}\nu _3^{(1)}\\&-\,\bar{k}_3\alpha _3^{(j)}\varGamma _{22}+\bar{k}_2\alpha _2^{(j)}\varGamma _{32}\big ]\\&+\,\bar{k}_1\big [k_2^2\beta _2^{(3-j)}\big (\bar{k}_3\nu _2^{(1)}\varGamma _{21}-\bar{k}_2\nu _1^{(1)}\varGamma _{11}\big )\\&+\,(-1)^jk_2\varGamma _{12}\big (-\bar{k}_3^2\alpha _3^{(j)}\varGamma _{21}+\bar{k}_2^2\alpha _2^{(j)}\varGamma _{31}\big )\\&+\,(-1)^j\bar{k}_2\bar{k}_3\nu _1^{(2)}\big (-\bar{k}_3\nu _1^{(1)}\alpha _3^{(j)}+\bar{k}_2\alpha _2^{(j)}\nu _2^{(1)}\big )\big ]\\&+\,k_1^2\beta _1^{(3-j)}\big [\bar{k}_2\bar{k}_3\nu _3^{(1)}\varGamma _{12}+\bar{k}_1\big (-k_2\nu _3^{(1)} \varGamma _{12}\\&-\,\bar{k}_3\nu _2^{(1)}\varGamma _{22}+\bar{k}_2\nu _1^{(1)}\varGamma _{32} \big )+k_2\big (\bar{k}_2\nu _2^{(1)}\varGamma _{22}\\&-\,\bar{k}_3\nu _1^{(1)}\varGamma _{32}\big )\big ]+\bar{k}_1^2\alpha _1^{(j)}\big [(-1)^{(3-j)}\bar{k}_2\bar{k}_3\nu _3^{(1)}\\&\nu _1^{(2)}+(-1)^{(3-j)}k_2\big (\bar{k}_2\varGamma _{31}\varGamma _{22}-\bar{k}_3\varGamma _{21}\varGamma _{32}\big )\big ]\\&+\,k_1\big [\bar{k}_2\varGamma _{21}\big (-k_2^2\nu _2^{(1)}\beta _2^{(3-j)}+(-1)^{(3-j)}\bar{k}_3^2\alpha _3^{(j)}\varGamma _{12}\big )\\&+\,\bar{k}_1\varGamma _{11}\big (k_2^2\nu _3^{(1)}\beta _2^{(3-j)}+(-1)^{(j)}\bar{k}_3^2\alpha _3^{(j)}\varGamma _{22}\\&+\,(-1)^{(3-j)}\bar{k}_2^2\alpha _2^{(j)}\varGamma _{32}\big )+(-1)^{(j)}\bar{k}_2^2\alpha _2^{(j)}\big (\bar{k}_3\varGamma _{31}\varGamma _{12}\\&+\,k_2\nu _2^{(1)}\nu _1^{(2)}\big )+(-1)^{(3-j)}\bar{k}_1^2\alpha _1^{(j)}\big (\bar{k}_3\varGamma _{31}\varGamma _{22}\\&+\,\bar{k}_2\varGamma _{21}\varGamma _{32}+k_2\nu _3^{(1)}\nu _1^{(2)}\big )\\&+\,k_2\bar{k}_3\nu _1^{(1)}\big (k_2\varGamma _{31}\beta _2^{3-(j)}+(-1)^{(3-j)}\bar{k}_3\alpha _3^{(j)}\nu _1^{(2)}\big )\big ], \end{aligned}$$
$$\begin{aligned} \varLambda _2^{(j)}= & {} -\,\bar{k}_2k_3\bar{k}_3\varGamma _{11}\big [(-1)^{(j)}k_3\nu _3^{(1)}\beta _3^{(3-j)}\\&-\,\bar{k}_3\alpha _3^{(j)}\varGamma _{23}+\bar{k}_2\alpha _2^{(j)}\varGamma _{33}\big ]\\&+\,k_1^2\beta _1^{(3-j)}\big [(-1)^{(3-j)}k_3\bar{k}_3\nu _1^{(1)}\varGamma _{33}\\&+\,(-1)^{(j)}\bar{k}_2\big (\bar{k}_3\nu _3^{(1)}\varGamma _{13}+k_3\\&\nu _2^{(1)}\varGamma _{23}\big )+(-1)^{(3-j)}\bar{k}_1\big (k_3\nu _3^{(1)}\varGamma _{13}\\&+\,\bar{k}_3\nu _2^{(1)}\varGamma _{23}+(-1)^{(j)}\bar{k}_2\nu _1^{(1)}\\&\varGamma _{33}\big )\big ]+\bar{k}_1\big [(-1)^{(j)}k_3\bar{k}_3\varGamma _{21}\big (k_3\nu _2^{(1)}\beta _3^{(3-j)}\\&+\,(-1)^{(3-j)}\bar{k}_3\alpha _3^{(j)}\varGamma _{13}\big )+\bar{k}_2^2\alpha _2^{(j)}\big (k_3\varGamma _{13}\varGamma _{31}\\&+\,\bar{k}_3\nu _2^{(1)}\nu _2^{(2)}\big )+(-1)^{(3-j)}\big (k_3^2\varGamma _{31}\beta _3^{(3-j)}\\&+\,(-1)^{(3-j)}\alpha _3^{(j)}\nu _2^{(2)}\big )\big ]\nonumber \\&+\,\bar{k}_1^2\alpha _1^{(j)}\big [k_3\bar{k}_3\varGamma _{21}\varGamma _{33}-\bar{k}_2\big (k_3\varGamma _{31}\varGamma _{23}+\bar{k}_3\nu _3^{(1)}\nu _2^{(2)}\big )\big ]\\&+\,k_1\big [-\bar{k}_2\varGamma _{21}\big ((-1)^{(j)}k_3^2\nu _2^{(1)}\beta _3^{(3-j)}+\bar{k}_3^2\alpha _3^{(j)}\varGamma _{13}\big )\\&+\,\bar{k}_1\varGamma _{11}\big ((-1)^{(j)}k_3^2\nu _3^{(1)}\beta _3^{(3-j)}+\bar{k}_3^2\alpha _3^{(j)}\varGamma _{23}\\&-\,\bar{k}_2^2\alpha _2^{(j)}\varGamma _{33}\big )+(-1)^{(j)}k_3\\&\bar{k}_3\nu _1^{(1)}\big (k_3\varGamma _{31}\beta _3^{(3-j)}+(-1)^{(3-j)}\bar{k}_3\alpha _3^{(j)}\nu _2^{(2)}\big )\\&+\,\bar{k}_2\alpha _2^{(j)} \big (\bar{k}_3\varGamma _{31}\varGamma _{13}+k_3\nu _2^{(1)}\nu _1^{(2)}\big )\\&+\,\bar{k}_1^2\alpha _1^{(j)}\big (-\bar{k}_3\varGamma _{31}\varGamma _{23}+\bar{k}_2\varGamma _{21}\varGamma _{33}\\&-\,k_3\nu _3^{(1)}\nu _2^{(2)}\big )\big ],\\ \varLambda _3^{(j)}= & {} -\,\bar{k}_2k_3\bar{k}_3\varGamma _{12}\big [(-1)^{(j)}k_3\nu _3^{(1)}\beta _3^{(3-j)}\\&-\,\bar{k}_3\alpha _3^{(j)}\varGamma _{23}+\bar{k}_2\alpha _2^{(j)}\varGamma _{33}\big ]\\&+\,k_2^2\beta _2^{(3-j)}\big [(-1)^{(3-j)}k_3\bar{k}_3\nu _1^{(1)}\varGamma _{33}\\&+\,\bar{k}_2\big ((-1)^{(j)}\bar{k}_3\nu _3^{(1)}\varGamma _{13}+(-1)^{(j)}k_3\nu _2^{(1)}\varGamma _{23}\big )\big ]\\&+\,\bar{k}_1\big [(-1)^{(j)}k_3\bar{k}_3\varGamma _{22}\big (k_3\nu _2^{(1)}\beta _3^{(3-j)}+(-1)^{(3-j)}\\&\bar{k}_3\alpha _3^{(j)}\varGamma _{13}\big )+k_2\varGamma _{12}\big ((-1)^{(j)}k_3^2\nu _3^{(1)}\beta _3^{(3-j)}\\&+\,\bar{k}_3^2\alpha _3^{(j)}\varGamma _{23}-\bar{k}_2^2\alpha _2^{(j)}\varGamma _{33}\big )\\ \end{aligned}$$
$$\begin{aligned}&+\,k_2^2\beta _2^{(3-j)}\big ((-1)^{(3-j)}k_3\nu _3^{(1)}\varGamma _{13}\\&+\,(-1)^{(3-j)}\bar{k}_3\nu _2^{(1)}\varGamma _{23}+(-1)^{(j)}\\&\bar{k}_2\nu _1^{(1)}\varGamma _{33}\big )+(-1)^{(3-j)}\bar{k}_2\nu _1^{(1)}\big (k_3^2\varGamma _{32}\beta _3^{(3-j)}\\&+\,(-1)^{(j)}\bar{k}_3^2\alpha _3^{(j)}\nu _3^{(2)}\big )\\&+\,\bar{k}_2^2\alpha _2^{(j)}\big (k_3\varGamma _{32}\varGamma _{13}+\bar{k}_3\nu _2^{(1)}\nu _3^{(2)}\big )\big ]\\&+\,\bar{k}_1^2\alpha _1^{(j)}\big [k_3\bar{k}_3\varGamma _{22}\varGamma _{33}+k_2\big (-\bar{k}_3\\&\varGamma _{32}\varGamma _{23}+\bar{k}_2\varGamma _{22}\varGamma _{33}-k_3\nu _3^{(1)}\nu _3^{(2)}\big )\\&-\,\bar{k}_2\big (k_3\varGamma _{32}\varGamma _{23}+\bar{k}_3\nu _3^{(1)}\nu _3^{(2)}\big )\big ]\\&+\,k_2\big [-\bar{k}_2\varGamma _{22}\big ((-1)^{(j)}k_3^2\nu _2^{(1)}\beta _3^{(3-j)}\\&+\,\bar{k}_3^2\alpha _3^{(j)}\varGamma _{13}\big )+(-1)^{(j)}k_3\bar{k}_3\nu _1^{(1)}\\&\big (k_3\varGamma _{32}\beta _3^{(3-j)}+\bar{k}_3\alpha _3^{(j)}\nu _3^{(2)}\big )\\&+\,\bar{k}_2^2\alpha _2^{(j)}\big (\bar{k}_3\varGamma _{32}\varGamma _{13}+k_3\nu _2^{(1)}\nu _3^{(2)}\big )\big ],\\ \varLambda _4^{(j)}= & {} -\,k_2\bar{k}_2k_3\varGamma _{11}\big [-k_3\varGamma _{22}\beta _3^{(j)}\\&+\,k_2\beta _2^{(j)}\varGamma _{23}+(-1)^{(3-j)}\alpha _2^{(3-j)}\bar{k}_2\nu _3^{(2)}\big ]\\&+\,\bar{k}_1\big [(-1)^{(3-j)}\bar{k}_2k_3\nu _1^{(2)}\big ((-1)^{(j)}k_3\nu _1^{(1)}\beta _3^{(j)}\\&+\,\bar{k}_2\alpha _2^{(j)}\varGamma _{13}\big )+k_2^2\\&\beta _2^{(j)}\big (k_3\varGamma _{21}\varGamma _{13}+\bar{k}_2\nu _1^{(1)}\nu _1^{(2)}\big )\\&-\,k_2\varGamma _{12}\big (k_3^2\varGamma _{21}\beta _3^{(j)}+(-1)^{(3-j)}\\&\bar{k}_2^2\alpha _2^{(3-j)}\nu _2^{(2)}\big )\big ]+k_1^2\beta _1^{(j)}\big [\bar{k}_2k_3\varGamma _{12}\varGamma _{23}\\&+\,\bar{k}_1\big (-k_3\varGamma _{22}\varGamma _{13}+k_2\varGamma _{12}\varGamma _{23}\\&-\,\bar{k}_2\nu _1^{(1)}\nu _3^{(2)}\big )-k_2\big (\bar{k}_2\varGamma _{22}\varGamma _{13}\\&+\,k_3\nu _1^{(1)}\nu _3^{(2)}\big )\big ]+\bar{k}_1^2\alpha _1^{(3-j)}\big [(-1)^{(j)}\bar{k}_2k_3\\&\nu _1^{(2}\varGamma _{23}+(-1)^{(3-j)}k_2\big (\bar{k}_2\varGamma _{22}\nu _2^{(2)}\\&+\,k_3\varGamma _{21}\nu _3^{(2)}\big )\big ]+k_1\big [(-1)^{(j)}k_2\nu _1^{(2)}\\&\big ((-1)^{(3-j)}k_3^2\nu _1^{(1)}\beta _3^{(j)}+\bar{k}_2^2\alpha _2^{(3-j)}\varGamma _{13}\big )\\&-\,\bar{k}_2k_3\varGamma _{12}\big (k_3\varGamma _{21}\beta _3^{(j)}+(-1)^{(j)}\\&\bar{k}_2\alpha _2^{(j)}\nu _2^{(2)}\big )+k_2^2\beta _2^{(j)}\big (\bar{k}_2\varGamma _{21}\varGamma _{13}\\&+\,k_3\nu _1^{(1)}\nu _2^{(2)}\big )+\bar{k}_1^2\alpha _1^{(3-j)}\big ((-1)^{(3-j)}\\&k_2\nu _1^{(2)}\varGamma _{23}+(-1)^{(j)}k_3\varGamma _{22}\nu _3^{(2)}\\&+\,(-1)^{(j)}\bar{k}_2\varGamma _{21}\nu _3^{(2)}\big )+\bar{k}_1\varGamma _{11}\big (k_3^2\varGamma _{22}\\&\beta _3^{(j)}-k_2^2\beta _2^{(j)}\varGamma _{23}+(-1)^{(3-j)}\bar{k}_2^2\alpha _2^{(3-j)}\nu _3^{(2)}\big )\big ], \end{aligned}$$
$$\begin{aligned} \varLambda _5^{(j)}= & {} -\,k_2\bar{k}_3k_3\varGamma _{11}\big [-k_3\varGamma _{32}\beta _3^{(j)}+k_2^{(j)}\beta _2^{(j)}\varGamma _{33}\\&-\bar{k}_3\alpha _3^{(3-j)}\nu _3^{(2)}\big ]+\bar{k}_1\big [-k_3\bar{k}_3\\&\nu _1^{(2)}\big (k_3\beta _3^{(j)}\nu _2^{(1)}+(-1)^{(j)}\bar{k}_3\alpha _3^{(3-j)}\varGamma _{13}\big )\\&+\,k_2^2\beta _2^{(j)}\big (k_3\varGamma _{31}\varGamma _{13}+\bar{k}_3\nu _2^{(1)}\nu _2^{(2)}\big )\\&-\,k_2\varGamma _{12}\big (k_3^2\varGamma _{31}\beta _3^{(j)}+(-1)^{(3-j)}\bar{k}_3^2\alpha _3^{(3-j)}\nu _2^{(2)}\big )\big ]\\&+\,k_1^2\beta _1^{(j)}\big [k_3\bar{k}_3\varGamma _{12}\varGamma _{33}\\&-\,k_2\big (\bar{k}_3\varGamma _{32}\varGamma _{13}+k_3\nu _2^{(1)}\nu _3^{(2)}\big )+\bar{k}\big (-k_3\varGamma _{32}\varGamma _{13}\\&+\,k_2\varGamma _{12}\varGamma _{33}-\bar{k}_3\nu _2^{(1)}\nu _3^{(2)}\big )\big ]\\&+\,\bar{k}_1^2\alpha _1^{(3-j)}\big [(-1)^{(j)}k_3\bar{k}_3\nu _1^{(2)}\varGamma _{33}\\&+\,k_2\big ((-1)^{(3-j)}\bar{k}_3\varGamma _{32}\nu _2^{(2)}+(-1)^{(j)}k_3\varGamma _{31}\\&\nu _3^{(2)}\big )\big ]+k_1\big [(-1)^{(j)}k_2\nu _1^{(2)}\big ((-1)^{(3-j)}k_3^2\nu _2^{(1)}\beta _3^{(j)}\\&+\,\bar{k}_3^2\alpha _3^{(3-j)}\varGamma _{13}\big )-k_3\bar{k}_3\varGamma _{12}\\&\big (k_3\varGamma _{31}\beta _3^{(j)}+(-1)^{(j)}\bar{k}_3\alpha _3^{(3-j)}\nu _2^{(2)}\big )\\&+\,k_2^2\beta _2^{(j)}\big (\bar{k}_3\varGamma _{31}\varGamma _{13}+k_3\nu _2^{(1)}\nu _2^{(2)}\big )\\&+\,\bar{k}_1^2\alpha _1^{(3-j)}\big ((-1)^{(3-j)}k_2\nu _1^{(2)}\varGamma _{33}\\&+\,(-1)^{(j)}k_3\varGamma _{32}\nu _2^{(2)}+(-1)^{(j)}\bar{k}_3\varGamma _{31}\nu _3^{(2)}\big )\\&+\,\bar{k}_1\varGamma _{11}\big (k_3^2\varGamma _{32}\beta _3^{(j)}-k_2^2\beta _2^{(j)}\varGamma _{33}\\&+\,(-1)^{(3-j)}\bar{k}_3^2\alpha _3^{(3-j)}\nu _3^{(2)}\big )\big ],\\ \varLambda _6^{(j)}= & {} (-1)^{(j)}\bar{k}_2\bar{k}_3k_3\nu _1^{(2)}\big [(-1)^{(3-j)}k_3\nu _3^{(1)}\beta _3^{(j)}\\&-\,\bar{k}_3\alpha _3^{(3-j)}\varGamma _{23}+\bar{k}_2\alpha _2^{(3-j)}\varGamma _{33}\big ]\\&+\,k_2^2\beta _2^{(j)}\big [-k_3\bar{k}_3\varGamma _{21}\varGamma _{33}+\bar{k}_2\big (k_3\varGamma _{31}\varGamma _{23}\\&+\,\bar{k}_3\nu _3^{(1)}\nu _2^{(2)}\big )\big ]+k_1^2\beta _1^{(j)}\big [k_3\bar{k}_3\varGamma _{22}\\&\varGamma _{33}+k_2\big (-\bar{k}_3\varGamma _{32}\varGamma _{23}+\bar{k}_2\varGamma _{22}\varGamma _{33}-\,k_3\nu _3^{(1)}\nu _3^{(2)}\big )\\&-\,\bar{k}_2\big (k_3\varGamma _{32}\varGamma _{23}+\bar{k}_3\nu _3^{(1)}\\&\nu _3^{(2)}\big )\big ]+k_1\big [-k_2\nu _1^{(2)}\big (k_3^2\nu _3^{(1)}\beta _3^{(j)}\\&+\,(-1)^{(3-j)}\bar{k}_3^2\alpha _3^{(3-j)}\varGamma _{23}+(-1)^{(j)}\\ \end{aligned}$$
$$\begin{aligned}&\bar{k}_2^2\alpha _2^{(3-j)}\varGamma _{33}\big )-k_3\bar{k}_3\varGamma _{22}\big (k_3\varGamma _{31}\beta _3^{(3-j)}\\&+\,(-1)^{(j)}\bar{k}_3\alpha _3^{(3-j)}\nu _2^{(2)}\big )+k_2^2\beta _2^{(j)}\\&\big (\bar{k}_3\varGamma _{31}\varGamma _{23}-\bar{k}_2\varGamma _{21}\varGamma _{33}+k_3\nu _3^{(1)}\nu _2^{(2)}\big )\\&+\,\bar{k}_2^2\alpha _2^{(3-j)}\big ((-1)^{(j)}k_3\varGamma _{32}\nu _2^{(2)}\\&+\,(-1)^{(j)}\bar{k}_3\varGamma _{31}\nu _3^{(2)}\big )+\bar{k}_2\varGamma _{21}\big (k_3^2\varGamma _{32}\beta _3^{(j)}\\&+\,(-1)^{(3-j)}\bar{k}_3^2\alpha _3^{(3-j)}\nu _3^{(2)}\big )\big ]\\&+\,k_2\big [-\bar{k}_2\varGamma _{22}\big (k_3^2\varGamma _{31}\beta _3^{(j)}\\&+\,(-1)^{(3-j)}\bar{k}_3^2\alpha _3^{(3-j)}\nu _2^{(2)}\big )+k_3\bar{k}_3\varGamma _{21}\big (k_3\varGamma _{32}\\&\beta _3^{(j)}+(-1)^{(j)}\bar{k}_3\alpha _3^{(3-j)}\nu _3^{(2)}\big )\\&+\,\bar{k}_2^2\alpha _2^{(3-j)}\big ((-1)^{(3-j)}\bar{k}_3\varGamma _{32}\nu _2^{(2)}\\&+\,(-1)^{(3-j)}k_3\varGamma _{31}\nu _3^{(2)}\big )\big ],\\ \text{ e }^{\delta _{20}}= & {} \frac{-\varLambda _{71}}{(k_1+\bar{k}_1+k_2+\bar{k}_2+k_3+\bar{k}_3)^2},\\ \varLambda _{71}= & {} (-k_1-\bar{k}_1+k_2+\bar{k}_2+k_3+\bar{k}_3)^2\text{ e }^{\delta _{19}+\delta _1}\\&+\,(-k_1+\bar{k}_1+k_2-\bar{k}_2+k_3+\bar{k}_3)^2\\&\text{ e }^{\delta _{17}+\delta _2}+(-k_1+\bar{k}_1+k_2+\bar{k}_2+k_3\\&-\,\bar{k}_3)^2\text{ e }^{\delta _3+\delta _{15}}+\text{ e }^{\delta _4+\delta _{18}}\\&(k_1-\bar{k}_1-k_2+\bar{k}_2+k_3+\bar{k}_3)^2+\text{ e }^{\delta _5+\delta _{13}}\\&(k_1-\bar{k}_1+k_2+\bar{k}_2-k_3+\bar{k}_3)^2\\&+\,(k_1+\bar{k}_1-k_2-\bar{k}_2+k_3+\bar{k}_3)^2\text{ e }^{\delta _6+\delta _{16}}\\&+\,(k_1+\bar{k}_1-k_2+\bar{k}_2+k_3-\bar{k}_3)^2\\&\text{ e }^{\delta _7+\delta _{14}}+(k_1+\bar{k}_1+k_2-\bar{k}_2-k_3\\&+\,\bar{k}_3)^2\text{ e }^{\delta _8+\delta _{12}}+\text{ e }^{\delta _9+\delta _{11}}\\&(k_1+\bar{k}_1+k_2+\bar{k}_2-k_3-\bar{k}_3)^2+\text{ e }^{\gamma _9^{(1)}+\varDelta _1^{(1)}}\\&+\,\text{ e }^{\gamma _9^{(2)}+\varDelta _1^{(2)}}+\text{ e }^{\gamma _6^{(1)}+\varDelta _2^{(1)}}\\&+\,\text{ e }^{\gamma _6^{(2)}+\varDelta _2^{(2)}}+\text{ e }^{\gamma _3^{(1)}+\varDelta _3^{(1)}}+\text{ e }^{\gamma _3^{(2)}+\varDelta _3^{(2)}}\\&+\,\text{ e }^{\gamma _8^{(1)}+\varDelta _4^{(1)}}+\text{ e }^{\gamma _8^{(2)}+\varDelta _4^{(2)}}\\&+\,\text{ e }^{\gamma _5^{(1)}+\varDelta _5^{(1)}}+\text{ e }^{\gamma _5^{(2)}+\varDelta _5^{(2)}}++\text{ e }^{\gamma _2^{(1)}+\varDelta _6^{(1)}}\\&+\,\text{ e }^{\gamma _2^{(2)}+\varDelta _6^{(2)}}++\text{ e }^{\gamma _7^{(1)}+\varDelta _7^{(1)}}\\&+\,\text{ e }^{\gamma _7^{(2)}+\varDelta _7^{(2)}}+\text{ e }^{\gamma _4^{(1)}+\varDelta _8^{(1)}}+\text{ e }^{\gamma _4^{(2)}+\varDelta _8^{(2)}}\\&+\,e^{\gamma _1^{(1)}+\varDelta _9^{(1)}}+\text{ e }^{\gamma _1^{(2)}+\varDelta _9^{(2)}}\\&+\,\sum _{j=1}^{2}\alpha _3^{(j)}\text{ e }^{\varphi _1^{(j)}}+\sum _{j=1}^{2}\alpha _2^{(j)}\text{ e }^{\varphi _2^{(j)}}\\&+\,\sum _{j=1}^{2}\alpha _1^{(j)}\text{ e }^{\varphi _3^{(j)}}+\sum _{j=1}^{2}\beta _3^{(j)}\text{ e }^{\chi _1^{(j)}}\\&+\,\sum _{j=1}^{2}\beta _2^{(j)}\text{ e }^{\chi _2^{(j)}}+\sum _{j=1}^{2}\beta _1^{(j)}\text{ e }^{\chi _3^{(j)}},\\ \end{aligned}$$
$$\begin{aligned} \varGamma _{nm}= & {} (\alpha _n^{(1)}\beta _{m}^{(1)}\!+\!\alpha _n^{(2)}\beta _{m}^{(2)}),\kappa _{nm}\!=\!(k_n\!+\! \bar{k}_m)^2,~n\!=\!m\!=\!1,2,3,\\ \nu _1^{(1)}= & {} \alpha _1^{(2)}\alpha _2^{(1)}-\alpha _1^{(1)}\alpha _2^{(2)},~\nu _2^{(1)}=\alpha _1^{(2)}\alpha _3^{(1)}-\alpha _1^{(1)}\alpha _3^{(2)},\\ \nu _3^{(1)}= & {} \alpha _2^{(2)}\alpha _3^{(1)}-\alpha _2^{(1)}\alpha _3^{(2)},~\nu _1^{(2)}=\beta _1^{(1)}\beta _2^{(2)}-\beta _1^{(2)}\beta _2^{(1)},\\ \nu _2^{(2)}= & {} \beta _1^{(1)}\beta _3^{(2)}-\beta _1^{(2)}\beta _3^{(1)},~\nu _3^{(2)}=\beta _2^{(1)}\beta _3^{(2)}-\beta _2^{(2)}\beta _2^{(1)},\\ \varrho _1= & {} k_1\bar{k}_1+k_2\bar{k}_2,~\varrho _2=k_1k_2+\bar{k_1}\bar{k}_2,\\ \varrho _3= & {} k_1\bar{k}_2+k_2\bar{k}_1,~\varrho _4=k_2\bar{k}_3+k_1\bar{k}_1,\\ \varrho _5= & {} k_1\bar{k}_3+k_2\bar{k}_1,~\varrho _6=k_1k_2+\bar{k}_1\bar{k}_3,\\ \varrho _7= & {} k_1k_2+\bar{k}_2\bar{k}_3,~\varrho _8=k_2\bar{k}_2+k_1\bar{k}_3,\\ \varrho _9= & {} k_2\bar{k}_3+k_1\bar{k}_2,~\varrho _{10}=k_3\bar{k}_2+k_1\bar{k}_1,\\ \varrho _{11}= & {} k_3\bar{k}_1+k_1\bar{k}_2,~\varrho _{12}=k_3k_1+\bar{k}_2\bar{k}_1,\\ \varrho _{13}= & {} k_3\bar{k}_2+k_2\bar{k}_1,~\varrho _{14}=k_3\bar{k}_1+k_2\bar{k}_2,\\ \varrho _{15}= & {} \bar{k}_1\bar{k}_2+k_2k_3,~\varrho _{16}=k_3\bar{k}_3+k_1\bar{k}_1,\\ \varrho _{17}= & {} k_1\bar{k}_3+k_3\bar{k}_1,~\varrho _{18}=k_3k_1+\bar{k}_1\bar{k}_1,\\ \varrho _{19}= & {} k_3\bar{k}_3+k_2\bar{k}_1,~\varrho _{20}=k_2\bar{k}_3+k_3\bar{k}_1,\\ \varrho _{21}= & {} k_2k_3+\bar{k}_3\bar{k}_1,~\varrho _{22}=k_3\bar{k}_3+k_1\bar{k}_2,\\ \varrho _{23}= & {} k_1\bar{k}_3+k_3\bar{k}_2,~\varrho _{24}=k_3k_1+\bar{k}_2\bar{k}_3,\\ \varrho _{25}= & {} k_3\bar{k}_3+k_2\bar{k}_2,~\varrho _{26}=k_2\bar{k}_3+k_3\bar{k}_2,\\ \varrho _{27}= & {} k_2k_3+\bar{k}_2\bar{k}_3,\\ \varrho _{12}= & {} (k_1-k_2),~\varrho _{13}=(k_1-k_3),\\ \varrho _{23}= & {} (k_2-k_3),~\bar{\varrho }_{12}=(\bar{k}_1-\bar{k}_2),\\ \bar{\varrho }_{13}= & {} (\bar{k}_1-\bar{k}_3),~\bar{\varrho }_{23}=(\bar{k}_2-\bar{k}_3). \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Stalin, S., Senthilvelan, M. & Lakshmanan, M. Degenerate soliton solutions and their dynamics in the nonlocal Manakov system: I symmetry preserving and symmetry breaking solutions. Nonlinear Dyn 95, 343–360 (2019). https://doi.org/10.1007/s11071-018-4567-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4567-5

Keywords

Search

Navigation