Nonlocal elasticity in shape memory alloys modeled using peridynamics for solving dynamic problems

Abstract

The work is primarily devoted to the peridynamic model elaborated for a solid body made of shape memory alloys (SMAs). The superelasticity effect is taken into consideration as well as its practical applications. Hence, the numerical simulations, making use of the phenomena of superelasticity, are carried out for the model of an SMA wire to investigate mechanical energy dissipation. The nonlocal peridynamic model of an SMA component is derived based on the theory proposed by Lagoudas—introduced to describe the phenomenon of solid phase transitions that occur in SMA. The results of the conducted experimental work are applied by the authors to validate the elaborated model. Moreover, an alternative verification of the peridynamic model is also performed using other numerical tool—the finite element code based on the analytical approach for modeling SMA, developed by Auricchio. The hysteretic character of the stress–strain relationship for the modeled SMA component, which undergoes the superelasticity effect, is shown using quasi-static peridynamic simulations. Finally, the capability of energy dissipation when cyclic loading for the elaborated nonlocal model is investigated via dynamic simulations. The numerical results obtained for the studied case are discussed to show the applicability of the presented modeling approach in the field of structural dynamics. A particular focus is placed on the available structural stiffness control functionality in mechanical systems equipped with SMA and efficiency of energy dissipation in SMA-based dampers, which may be effectively applied to suppress mechanical vibrations. Both mentioned application areas for SMA are of the authors’ special concern in the designing process of the nonlinear supporting structure in gas foil bearings, which is also discussed in the final part of the paper to highlight the practical aspects of the conducted research.

1 Introduction

Nonlocal modeling applied to both analytical problem formulations in mechanics and numerical applications within the frame of computational mechanics has been successfully used for many decades. The idea of nonlocality was first employed in the sixties of the previous century to describe and understand the material behavior observed during experiments. The breakthrough works of Kröner, Kunin, Eringen and Edelen [1,2,3] showed realistic links between experimental outcomes and the nonlocality proposed to be considered when modeling internal interactions found in the investigated materials. In other words, nonlocality has arisen as a sort of remedy for the identified deficiencies of modeling methods. This fact is also of particular importance in dynamics since nonlocal modeling enables efficient control of the dispersion properties of the modeled medium [4].

Classically, continuum mechanics refers to locally formulated governing equations. This means that only local relationships between strains and stresses are taken into account when dealing with a solid body. Despite undeniable popularity of local elasticity, this approach, however, exhibits several drawbacks. As already referred to, it is basically incapable of completely describing and, therefore, predicting a real behavior of a deformable material. This applies especially when considering various physical phenomena revealing themselves at consecutive geometric scales (lengthscales). In this case, various material properties should be defined at these lengthscales as well, which is not allowed in a local formulation explicitly. However, the unique formulation of a nonlocal elasticity leads to the demanded capability of introducing the required specific lengthscales referring to the range of nonlocal interactions within the modeled body [5]. In fact, both micro- and macrostructure characteristics may contribute in the resultant nonlocal model [6,7,8].

The most known phenomena that require nonlocal elasticity, to allow for more physical description, are wave dispersion and shear bands observed during stretching [3, 8, 9]. Other examples explaining the need of nonlocality are provided in [10]. As reported in the cited works, the observed lack of convergence between experiments and theories may be effectively addressed via nonlocal interactions introduced in a modeled body. As far as dynamics is of concern, the use of nonlocal approaches enables more accurate simulations of the phenomenon of wave propagation. Nonlocal elasticity leads to lower requirements for model mesh density with its spatial domain discretization. On the one hand, it helps to mitigate numerical dispersion, which emerges for crude meshes [11,12,13,14,15]. This behavior is observed when the distances between nodes in a numerical model are comparable with the wavelengths. Moreover, nonlocal elasticity, via long-range interactions, introduces the means for relatively easy formulation of arbitrary shapes for physical dispersion relationships [14, 16].

Up to now, nonlocal elasticity has been widely used for various physical domains, materials and research fields. First, various types of geometric discontinuities (e.g., cracks), that, in general, stand for challenging modeling issues for the classically formulated local elasticity—due to gradient-based equations—can be effectively addressed by nonlocal approaches. It should be noted that various types of geometric discontinuities, including those ones originating from material nonlinearities and boundary conditions, may result in ambiguity regarding calculations of derivatives. Nonlocality allows for introduction of integral-based expressions that help to reduce or even eliminate the above-mentioned inconvenience. Moreover, via nonlocality, more physical behavior of the models may be assured for growing cracks [17,18,19]. In fact, more spontaneous crack’s growth is achievable for numerical simulations [20]. The other applications of nonlocality deal with vibro-acoustic interaction [21], model upscaling [22], regularization of boundary value problems [23], impact loading [24], viscoplasticity [25], thermal diffusion [26], thermoelasticity, including both the earliest and recent papers [27,28,29,30] and piezoelectricity [31, 32]. The theory of generalized continua proposed for granular media, which is valid at various geometric scales, makes use of nonlocally formulated material properties [33]. Moreover, nonlocal elasticity has been successfully applied to model graphene [34, 35] and shape memory alloys (SMAs) [36,37,38].

The only two disadvantages of nonlocal modeling tools, that are worth to be mentioned, are the computational costs required and parameters identification for nonlocal models. Indeed, more reliable material description may need both greater number of interactions between pieces of a modeled body and more complicated material models with the coefficients defying long-range interactions. The former issue refers to more populated global system matrices that need higher computational effort for their processing. The latter, in turn, results in more demanding and comprehensive experiments to be performed for material data identification. Nowadays, the use of parallel computing in GPU may help to solve the problems partially. However, it should be noted that, whenever required and feasible, the coupling between local and nonlocal models may be performed to take advantages of both modeling approaches [39].

Due to the well-recognized advantages of the computational techniques based on nonlocal elasticity, the authors of the present paper have attempted to apply one of these theories, namely peridynamics, for modeling the phenomenon of superelasticity in SMA. Having introduced the theoretical part of the work, the numerical outcomes obtained for the elaborated one-dimensional (1-D) model of an SMA wire are presented giving an exemplary practical application of the developed approach in the field of structural dynamics.

In detail, the following sections contribute to the paper. After presenting introductory Sect. 1, which is devoted to the applications of nonlocal approaches in computational mechanics, the next three sections provide the fundamentals regarding peridynamics (Sect. 2), SMA (Sect. 3) and the analytical description proposed by Lagoudas to model superelasticity in SMA (Sect. 4). Complementarily, other selected known modeling techniques used for SMA are also shortly discussed by the authors. A peridynamic model proposed by the authors of the present work to simulate the phenomenon of superelasticity in SMA is described in Sect. 5. Next, in Sect. 6, the results of experiments conducted for an SMA sample are presented to validate the elaborated peridynamic model. Moreover, an additional verification of the peridynamic model is also addressed using an alternative numerical tool—the finite element (FE) code based on the analytical approach for modeling SMA provided by Auricchio. Section 7 presents and discusses the results of the numerical simulations performed for the peridynamic model of a damper made of an SMA wire. Based on the obtained results, practical aspects of the theoretical part of the work are also discussed in Sect. 7, including the issues of structural stiffness control functionality available in mechanical systems equipped with SMA and efficiency of energy dissipation in SMA-based dampers applied for reduction in mechanical vibrations. A special authors’ attention is paid on the capability of efficient change of the properties of nonlinear supporting structure in gas foil bearings (GFBs), which may be achieved via superelasticity phenomenon, applying the proposed nonlocal modeling tools. The last Sect. 8 summarizes the paper and draws final conclusions.

2 Fundamentals of peridynamics

Peridynamics is a type of nonlocal modeling approach proposed quite recently by Silling in 2000 [40]. It assumes coexistence of the pieces in a modeled body (named as particles in the theory of peridynamics), which are linked via both local and nonlocal interactions. In case of the so-called bond-based peridynamics, the resultant force acting on an actual central particle (localized at the position $\mathbf{x})$ is found based on integration of the contributing interaction forces $\mathbf{f}$ over the specified region—the horizon H, as shown in Fig. 1.

Fig. 1

Interactions in a nonlocal peridynamic model specified within a horizon defined for an actual central particle

The peridynamic governing equation takes the following general form with the spatial component consisting of an integral expression

$$\begin{aligned} \rho {\ddot{\mathbf{u}}}\left( {{\mathbf{x}},t} \right)= & {} \int _H {\mathbf{f}}\left( {{\mathbf{u}}\left( {\hat{\mathbf{x}},t} \right) - {\mathbf{u}}\left( {{\mathbf{x}},t} \right) ,\hat{\mathbf{x}}- {\mathbf{x}}} \right) \mathrm{d}V_{\hat{\mathbf{x}}} \nonumber \\&+\, {\mathbf{b}}\left( {{\mathbf{x}},t} \right) \end{aligned}$$

(1)

With reference to graphical interpretation given in Fig. 1, the following parameters are used in Eq. (1): $\mathbf{x}$, $\hat{\mathbf{x}}$—position vectors for central and neighboring particles, $\mathbf{u}\left( {\mathbf{x},t} \right)$, $\mathbf{u}\left( {\hat{\mathbf{x}} ,t} \right)$—displacement vectors for central and neighboring particles, $\mathbf{b}\left( {\mathbf{x},t} \right)$—external body force volumetric density considered for the current central particle, $\rho$—mass density of the central particle, $\mathrm{d}V_{\hat{\mathbf{x}}}$—fraction of the neighboring particle’s volume which is covered by the horizon H and therefore they are considered when calculations of the interaction forces $\mathbf{f}$. As already referenced, the function $\mathbf{f}$ defines the pairwise interaction force determining the force links between central and neighboring particles observed within the horizon H.

For further explanation, it is convenient to introduce the vectors $\varvec{\upxi }$ and $\varvec{\upeta }$ defying the relative particles’ position and displacement, respectively, where:

$$\begin{aligned} \varvec{\upxi }= & {} \hat{\mathbf{x}} -\mathbf{x} \end{aligned}$$

(2)

$$\begin{aligned} \varvec{\upeta }= & {} \mathbf{u}\left( {\hat{\mathbf{x}} ,t} \right) -\mathbf{u}\left( {\mathbf{x},t} \right) \end{aligned}$$

(3)

By definition, the pairwise force $\mathbf{f}=\mathbf{f}\left( {\varvec{\upxi },\varvec{\upeta }} \right)$ can be conditionally defined as follows [40, 41]:

$$\begin{aligned} \mathbf{f}\left( {\varvec{\upxi },\varvec{\upeta }} \right) =\left\{ \begin{array}{l@{\quad }l} \mathbf{e}\left( {\varvec{\upxi },\varvec{\upeta }} \right) c\left( \varvec{\upxi } \right) s\left( {\varvec{\upxi },\varvec{\upeta }} \right) ,&{} \hbox {if}\,\Vert \varvec{\upxi }\Vert \le \delta \\ 0,&{} \hbox {otherwise} \\ \end{array}\right. \end{aligned}$$

(4)

where $\mathbf{e}$—unit vector pointing the direction of the interaction force $\mathbf{f}$, c—the so-called micromodulus function, which defines elastic properties of the modeled material, s—strain, $\delta$—radius of the horizon H. As demanded, nonzero forces may appear only if the condition $\Vert \varvec{\upxi }\Vert \le \delta$ is satisfied, which means that the force interactions localized within the horizon H are taken into account merely.

A very specific and useful property of peridynamics is its ability to direct use of macroscale, i.e., engineering, properties of the materials—applying the definition of the micromodulus function c—e.g., Young’s moduli, irrespectively from the lengthscales considered. Hence, resultant material properties may be introduced to carry out calculations for various geometric scales providing efficient tools for multiscale studies [22].

In case of a two-dimensional (2-D) model built with a homogeneous and isotropic material, an exemplary form of the definition for micromodulus function c may be as follows:

$$\begin{aligned} c=\frac{6E}{\pi \delta ^{3}\left( {1-\nu } \right) T} \end{aligned}$$

(5)

where the elastic properties of the material are: E—Young’s modulus and $\nu$—Poisson’s ratio. The parameter T declares the thickness of the model.

As shown, the integral-based formulation of governing equation used in peridynamics requires a number of interactions to be taken into account over the defined horizon. This fact inevitably leads to the increased computational effort comparing to the locally formulated approaches. However, the issue of peridynamic models’ convergence was already subject to studies. The relationships between particles’ distances and horizon diameters as well as their absolute values were already proposed for various modeling cases [41]. Even though natural consequence of an application of the peridynamic approach is the introduction nonlocal interactions, a locally formulated solution of a given problem may be easily found as well. A gradual decrease in the horizon radius $\delta$ allows for the expected convergence.

Since peridynamics makes use of an integral description regarding spatial domain, it can relatively easily solve the problems involving various types of geometric discontinuities, e.g., fatigue cracks (considering the research field of damage modeling in general), boundaries of grains, interconnection layers and interfaces with considerable impedance mismatches. All the above-mentioned cases, if improperly handled, may cause significant numerical issues. The overview on various applications of peridynamics may be found in [19,20,21, 35, 42,43,44]. Hence, the present work should be considered as the extension of the previous investigations made on peridynamic capabilities, in which the phenomenon of superelasticity in SMA is of particular concern.

3 Fundamentals of SMA

SMA is one of the most popular and widely applied groups of smart materials exhibiting extraordinary physical properties. These properties result from the thermomechanical phenomena observed for phase transformations (phase transitions) in SMA. SMA characterizes reversible transformations of their crystal structures, i.e., they exhibit solid-state phase changes at nanoscale, which specifically allow to memorize arbitrarily given geometric shapes at macroscale as well as withstand relatively high elastic deformations [45]. The former capability of memorizing either one or two geometric shapes originates from the two-way martensitic phase transition, i.e., martensite–austenite phase transition. The latter functionality of SMA, in turn, reflects the phenomenon of superelasticity (also known as pseudoelasticity).

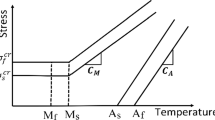
In case of shape memory property, the applied thermal activation—via either cooling or heating—leads to forward and backward transitions of the martensitic phase, respectively, as demanded. This phenomenon is illustrated in Fig. 2, where the changing contribution of austenite phase for varying temperatures is presented. As shown, SMA is characterized by four specific temperatures. These temperatures, i.e., $A_{s}$, $A_{f}$, $M_{s}$ and $M_{f}$, are the material properties being dependent on the alloy’s ingredients used. They, respectively, stand for the temperatures at which solid phases, austenite and martensite, are generated via mutual transitions. The indexes ‘s’ and ‘f’ denote begin and finish of the respective transition, which means either forward or backward martensitic phase transition. It must be mentioned that the four characteristic temperatures depend on the applied mechanical stress. These dependencies are not linear, which is particularly seen for the temperatures $A_{s}$ and $A_{f}$ for small stresses.

Fig. 2

Contribution of austenite in an SMA sample for temperature-activated reversible martensitic phase transition—exemplary plot for hysteretic behavior

Activation of martensitic phase transitions leads to the demanded rebuilding of the crystal structure, which is required for changes in the geometric shapes observable at macroscale. Depending on the capabilities achieved via shape training procedures, SMA may exhibit either the so-called one- or two-way memory effects. These effects reflect the capabilities of remembering either one or two different geometric shapes, respectively.

It should be noted that martensitic phase transitions are spontaneous and subject to hysteretic behavior. In fact, the number of possible intermediate geometric shapes achieved by evolving SMA sample is infinite, even though the demanded, i.e., memorized, geometries finally appear. Thermal loads lead to the specific, unrepeatable gradual changes of the crystal structure while phase transitions occurs that may be considered as random at macroscale.

For the sake of clarity, the phenomenon of one-way memory effect is briefly described in the following. Consecutive solid phase transitions are illustrated in Fig. 3. As shown, the effect of memorizing a geometric shape in SMA reflects the existence of the two different types of crystal structures for the considered austenite and martensite solid phases. There coexist the cubic crystal structure for austenite and the rhomboidal one for martensite. Additionally, the rhomboidal structure may take two forms, namely either undeformed or deformed one, depending on the external load application history.

Fig. 3

Exemplary course of solid phase transitions and shape recovery in an SMA sample during temperature-activated one-way memory effect

The one-way memory effect can be observed within a repeatable cycle, which contains the following steps (enumerated in Fig. 3): (1) mechanical deformation of an SMA sample at constant temperature when rhomboidal crystal structures in martensite exhibit deformation, (2) stress release while keeping the deformed shape of SMA, (3) recovery of the memorized shape via thermal load at zero stress when austenite phase generation is activated, (4) cooling down of an SMA sample leading to the undeformed martensite phase present for a memorized shape.

The second type of the unique phenomena experimentally observed in SMA, i.e., superelasticity, is manifested via significant elastic deformations, not present in other metallic materials. Typically, allowable strains in SMA are within the range 6–8%, which is approximately ten times greater than the values of the respective quantities for steel, aluminum, titanium and copper. Due to the attempted scope of the present work, superelasticity is of the special authors’ concern, and it is addressed in detail in the following Sect. 4.

The extraordinary physical characteristics of SMA enable many practical applications. Both memory effects and superelasticity are very attractive properties. They have opened new perspectives for applications of SMA in the structures exhibiting quite rigorous requirements regarding movable components, available space and biocompatibility. Hence, SMA is used in such distant applications as medicine and aerospace [46].

The surprising fact is that there is still significant deficiency of reliable models of SMA. This motivated the authors of the present work to look for some alternative modeling methods, especially the ones based on nonlocal elasticity, to allow for new capabilities when reflecting the experimental results, as already referenced in Sects. 1 and 2. Even though many papers address SMA modeling, there are still several unsolved problems, which have appeared in experiments [47]. Some of the observed phenomena are not studied yet sufficiently to allow for a reliable theoretical description. Providing with an example, it should be highlighted that the influence of boundary conditions on the behavior of SMA and spontaneity of the martensitic phase transition is still a missing part [48]. The physics of SMA seems complex, which explains why so many attempts have been made so far toward the development of new reliable and accurate models [47].

4 Analytical description of superelasticity in SMA

The scope of the present study deals with modeling of the phenomenon of superelasticity in SMA. Therefore, more detailed characterization of this effect is provided in the following. The analytical description of the problem constitutes the main part of this section, since it is crucial to understand the fundamentals of the developed peridynamic model.

As stated before, superelasticity reflects significant elastic deformations present in SMA after external stresses are applied. This phenomenon may be observed at a constant temperature; however, the austenite phase is required to be maintained at the ambient temperature before any mechanical load is considered. This means that the temperature during experiment should exceed the quantity $A_{f}$, as shown in Fig. 4.

Fig. 4

Superelasticity effect in SMA—reversible solid phase transitions observed at a constant temperature. Note that four auxiliary solid lines symbolically depict the relationships between stress and characteristic temperatures. In fact, as already mentioned in Sect. 3, these relationships are monotonic but not linear

In the presence of gradually increasing mechanical load, an SMA sample experiences solid phase transitions. This behavior results from the fact that all four characteristic temperatures $A\left( M \right) _{f\left( s \right) }$ undergo a monotonic growth when the applied stress increases, which is symbolically visualized in Fig. 4 by auxiliary four parallel lines. In fact, a complete phase change within the entire body of SMA may be achieved under the condition that sufficient level of the externally imposed stresses is assured. The increase in the stresses induces spontaneous austenite to martensite phase change. The superelasticity effect is reversible, and the austenite phase is instantly recreated when the loads are released. However, different stress–strain paths are observed for the two phase transition directions, as visualized in Fig. 5. This dependency upon the transition direction is represented by a hysteretic behavior of SMA [49].

Fig. 5

Hysteretic character for the stress–strain paths observed for superelasticity effect in SMA

Two plateau regions appear in the stress–strain plot. They represent the processes of gradual and spontaneous rebuilding crystal structures in SMA observed during phase transitions in both directions. As a result, when the contributing solid phases swap, the stresses remain nearly constant, whereas the strains change dramatically. This unique behavior allows for building the SMA-based structures exhibiting nearly constant reaction force generation for relatively wide ranges of elastic deflections. The most known practical applications making use of both extraordinary strains allowed in SMA and their functionality of constant force generation are stents, medical staples and dental braces [50]. Finally, the ability of effective energy dissipation, while performing consecutive cycles within the hysteresis loop, leads to the applications of superelasticity in mechanical dampers [51, 52].

When investigating the shape of the hysteresis plot shown in Fig. 5, it should be highlighted that significant strains allowed in SMA have basically two sources. The main reason for that is instantaneous creation of the deformed variants of martensite phase, i.e., deformed rhomboidal structure, while the stresses increase. The minor reason originates from the fact that the Young’s modulus for the martensite phase is less than the respective elastic quantity for austenite.

Having introduced the theory given by Lagoudas in the work [53], the following analytical description for superelasticity is provided as the required background for the developed peridynamic model of SMA.

First, a definition for the total specific Gibbs free energy (the total Gibbs free energy per unit mass) G should be defined for a polycrystalline SMA. An SMA sample is assumed to consist of a mixture of the two contributing martensite and austenite phases. The quantity G equals

$$\begin{aligned} G\left( {\bar{\bar{\varvec{\upsigma }}} ,T,\xi ,\bar{\bar{\varvec{\upvarepsilon }^{\mathbf{t}}}}} \right)= & {} -\frac{1}{2\rho }{} \mathbf{C}_{\mathbf{ijkl}} {\varvec{\upsigma }}_{\mathbf{ij}} {\varvec{\upsigma }}_{\mathbf{kl}} \nonumber \\&-\,\frac{1}{\rho }{\varvec{\upsigma }}_{\mathbf{ij}} \left[ {{\varvec{\upalpha }}_{\mathbf{ij}} \left( {T-T_0 } \right) +\bar{\bar{\varvec{\upvarepsilon }^{\mathbf{t}}}}} \right] \nonumber \\&+\,c\left[ {\left( {T-T_0 } \right) -T\hbox {ln}\left( {\frac{T}{T_0 }} \right) } \right] \nonumber \\&-\,s_0 T+u_0 +\frac{1}{\rho }f\left( \xi \right) \end{aligned}$$

(6)

The arguments of the parameter G are: $\bar{\bar{\varvec{\upsigma }}}$—second-order Cauchy stress tensor, T—temperature, $\xi$—martensitic volume fraction and $\overline{\overline{\varvec{\upvarepsilon }^{\mathbf{t}}}}$—second-order transformation strain tensor. The dimensionless parameter $\xi \in \left[ {0,1} \right]$ defines the contribution of both solid phases, where the value 0 refers to the structure entirely made of austenite, and 1 declares the martensite phase as the only existing one in a model of SMA. An alternative symbolic description for the stress tensor $\bar{\bar{\varvec{\upsigma }}}$ is introduced in Eq. (6) using the quantities ${\varvec{\upsigma }}_{\mathbf{ij}}$ and ${\varvec{\upsigma }}_{\mathbf{kl}}$ that follow the Einstein summation notation. It is used whenever unambiguous definition for the tensor calculations must be provided. The remaining parameters used in Eq. (6) are: $\rho$—the mass density, $\mathbf{C}_{\mathbf{ijkl}}$—fourth-order elastic compliance tensor, ${\varvec{\upalpha }}_{\mathbf{ij}}$—second-order thermal expansion coefficient tensor, $T_0$—reference (ambient) temperature, c—specific heat, $s_0$—specific entropy at the reference state, $u_0$—specific internal energy at the reference state, $f\left( \xi \right)$—the transformation hardening function. The function $f\left( \xi \right)$ stands for elastic strain energy related to the interactions present between various variants of martensitic phase and the surrounding phase as well as the interactions observed within the martensitic phase.

Since the phenomenon of superelasticity is of the authors’ concern, Eq. (6) may be rewritten in the following form:

$$\begin{aligned} G\left( \bar{\bar{\varvec{\upsigma }}} ,T,\xi ,\bar{\bar{\varvec{\upvarepsilon }^{\mathbf{t}}}} \right)= & {} -\frac{1}{2\rho }{} \mathbf{C}_{\mathbf{ijkl}} {\varvec{\upsigma }}_{\mathbf{ij}} {\varvec{\upsigma }}_{\mathbf{kl}}\nonumber \\&-\,\frac{1}{\rho }{\varvec{\upsigma }}_{\mathbf{ij}} \bar{\bar{\varvec{\upvarepsilon }^{\mathbf{t}}}}-s_0 T_0 +u_0 +\frac{1}{\rho }f\left( \xi \right) \nonumber \\ \end{aligned}$$

(7)

where the temperature effects are neglected. It is assumed in Eq. (7) that the case of isothermal phase transitions is considered, i.e., when $T=T_0$. In an ideal case, phase transitions are activated by mechanical loads only, and with reference, no influential temperature variation is observed. As experimentally proven by the authors, formula (7) can be successfully used in analytical/numerical simulations for SMA as long as the phase transitions’ speed is limited adequately to follow the physical behavior of the tested SMA. More specifically, the experimentally identified limited scale of the phenomenon of spontaneous phase changes, which is found at the limited phase transitions’ speed, allows for a reliable linear approximation of the stress–strain path—as considered in Fig. 10 in Sect. 6, where model validation is described. Moreover, the phenomenon of spontaneous phase transitions is strictly related to the variation of temperature field. Hence, the required condition of isothermal phase transitions in Eq. (7) may be verified either by direct temperature measurements or, indirectly, analyzing the shape of the stress–strain curve. The above-stated relation between the stress–strain path and the temperature field was observed using an infrared camera. It also, eventually, allowed to identify the maximum speed for the extension test performed for an SMA wire made of Nitinol, which assures the required constraints regarding the scale of the phenomenon of spontaneous phase changes. This speed was found to be approximately $0.05\,\hbox {mm}/\hbox {s}$. The length of the used SMA wire equals 133 mm. It means that the allowed strain rate obtained for nearly isothermal phase transitions is about $0.00038\,\hbox {s}^{-1}$. This condition also assures sufficient thermal energy flow, i.e., its exchange with the surrounding area. This prevents from other possible source of significant variation of the temperature field that should be additionally taken into account in Eq. (7) for more realistic modeling of the stress–strain relationship. Even the experimentally identified allowed value of the absolute extensions rate is relatively small, i.e., of the order of tens of micrometers per second, it still allows for reliable transient simulations to investigate the superelasticity effect in SMA wires mounted in the supporting layers of GFB, as long as a long-period steady-state operation of GFB under a constant load is taken into account.

All the material properties declared in Eq. (7) are considered as the resultant quantities defined using the fraction $\xi$. Hence, the properties of the two contributing phases are used in the linear combinations to find the following parameters

$$\begin{aligned}&\rho =\rho \left( \xi \right) =\rho ^{A}+\xi \left( {\rho ^{M}-\rho ^{A}} \right) =\rho ^{A}+\xi \Delta \rho \end{aligned}$$

(8)

$$\begin{aligned}&{} \mathbf{C}_{\mathbf{ijkl}} =\mathbf{C}_{\mathbf{ijkl}} \left( \xi \right) =\mathbf{C}_{\mathbf{ijkl}}^\mathbf{A} +\xi \left( {\mathbf{C}_{\mathbf{ijkl}}^\mathbf{M} -\mathbf{C}_{\mathbf{ijkl}}^\mathbf{A} } \right) \nonumber \\&\qquad =\mathbf{C}_{\mathbf{ijkl}}^\mathbf{A} +\xi \Delta \mathbf{C}_{\mathbf{ijkl}} \end{aligned}$$

(9)

$$\begin{aligned}&s_0 =s_0 \left( \xi \right) =s_0^A +\xi \left( {s_0^M -s_0^A } \right) =s_0^A +\xi \Delta s_0 \nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned}&u_0 =u_0 \left( \xi \right) =u_0^A +\xi \left( {u_0^M -u_0^A } \right) =u_0^A +\xi \Delta u_0\nonumber \\ \end{aligned}$$

(11)

The austenite and martensite phases are denoted using the indexes $\hbox {A}$ and $\hbox {M}$, respectively. For a 1-D model of an SMA rod undergoing uniaxial tension, Eq. (7) takes the form

$$\begin{aligned} G\left( {\sigma ,T,\xi ,\varepsilon ^{t}} \right)= & {} -\frac{1}{2\rho }C\sigma ^{2}-\frac{1}{\rho }\sigma \varepsilon ^{t}\nonumber \\&-\,s_0 T_0 +u_0 +\frac{1}{\rho }f\left( \xi \right) \end{aligned}$$

(12)

where the compliance tensor $\mathbf{C}_{\mathbf{ijkl}}$ becomes a scalar $C_{1111} =C$ defined using the inversions of the Young’s moduli for both phases $C^{A}=\left( {E^{A}} \right) ^{-1}$ and $C^{M}=\left( {E^{M}} \right) ^{-1}$, with their contributions calculated according to the martensite percentage volume fraction

$$\begin{aligned} C=C\left( \xi \right) =C^{A}+\xi \left( {C^{M}-C^{A}} \right) =C^{A}+\xi \Delta C \end{aligned}$$

(13)

The resultant strain equals

$$\begin{aligned} \varepsilon =C\sigma +\varepsilon ^{t} \end{aligned}$$

(14)

where $\varepsilon ^{t}$ is the transformation strain found based on the formula

$$\begin{aligned} {\dot{\varepsilon }^t} = \varLambda {\dot{\xi }} \end{aligned}$$

(15)

The general form of the transformation tensor ${\varvec{\Lambda }}$ is depended upon both the phase transition direction, identified by the sign of the strain rate $\dot{\xi }$, and the stresses. However, for a 1-D model the tensor ${\varvec{\Lambda }}$ may be eventually assumed a scalar $\varLambda$ being independent from any of the above-mentioned quantities

$$\begin{aligned} \varLambda =\sqrt{\frac{3}{2}}H\quad \hbox {for }\dot{\xi }>0\hbox { and }\dot{\xi }<0 \end{aligned}$$

(16)

The parameter $\varLambda$ is formulated based on the SMA material property—the maximum uniaxial transformation strain H. The conditions $\dot{\xi }>0$ and $\dot{\xi }<0$ mean an increase and decrease in the amount of martensite phase in the model, respectively. These conditions adequately concern the cases when the stress $\sigma$ grows and decreases. It should be noted that, even though the two independent cases are initially considered to conditionally define the value of $\varLambda$, namely $\dot{\xi }>0$ and $\dot{\xi }<0$, as found in the applications of both the elaborated FE and peridynamic codes, these cases effectively make a reference to the two overlapping conditions $\dot{\xi }\ge 0$ and $\dot{\xi }\le 0$. In fact, from a practical point of view, the value of the strain rate $\dot{\xi }$ never equals to zero during simulations.

Next, the entropy of the model is assured to either remain constant or increase after introduction of the second law of thermodynamics. The respective Clausius–Planck inequality is defined

$$\begin{aligned} \sigma {\dot{\varepsilon }^t} - \rho \frac{{\partial G}}{{\partial \xi }}\dot{\xi } \ge 0 \end{aligned}$$

(17)

After introduction of Eq. (15), Eq. (17) becomes

$$\begin{aligned} \left( {\sigma \varLambda -\rho \frac{\partial G}{\partial \xi }} \right) \dot{\xi } \ge 0 \end{aligned}$$

(18)

Based on Eq. (12) and neglecting change of the mass density $\rho$ during phase transitions, there may be found the partial derivative $\frac{\partial G}{\partial \xi }$ required to be declared in Eq. (18)

$$\begin{aligned} \frac{\partial G}{\partial \xi }= & {} -\frac{1}{2\rho }\frac{\partial C\left( \xi \right) }{\partial \xi }\sigma ^{2}-\frac{1}{\rho }\sigma \frac{\partial \varepsilon ^{t}\left( \xi \right) }{\partial \xi }-\frac{\partial s_0 \left( \xi \right) }{\partial \xi }T_0\nonumber \\&+\,\frac{\partial u_0 \left( \xi \right) }{\partial \xi }+\frac{1}{\rho }\frac{\partial f\left( \xi \right) }{\partial \xi } \end{aligned}$$

(19)

After introduction of Eqs. (10–11), (13) and (15) in Eq. (19), one may obtain

$$\begin{aligned} -\rho \frac{\partial G}{\partial \xi }=\frac{1}{2}\Delta C\sigma ^{2}+\sigma \varLambda +\rho \Delta s_0 T_0 -\rho \Delta u_0 -\frac{\partial f\left( \xi \right) }{\partial \xi } \end{aligned}$$

(20)

Then, substitution of the expression $-\rho \frac{\partial G}{\partial \xi }$ in Eq. (18) by Eq. (20) leads to

$$\begin{aligned} \left( {2\sigma \varLambda +\frac{1}{2}\Delta C\sigma ^{2}+\rho \Delta s_0 T_0 -\rho \Delta u_0 -\frac{\partial f\left( \xi \right) }{\partial \xi }} \right) \dot{\xi } \ge 0 \end{aligned}$$

(21)

which constitutes the conditional expression

$$\begin{aligned} \varPi \dot{\xi } \ge 0 \end{aligned}$$

(22)

in terms of the thermodynamic force $\varPi$.

The remaining contributor to the thermodynamic force $\varPi$—the transformation hardening function $f\left( \xi \right)$—is found as follows [54]:

$$\begin{aligned} f\left( \xi \right) = \left\{ \begin{array}{l@{\quad }l} \frac{1}{2}\rho {b^M}{\xi ^2} + \left( {{\mu _1} + {\mu _2}} \right) \xi ,&{} \dot{\xi } > 0\\ \frac{1}{2}\rho {b^A}{\xi ^2} + \left( {{\mu _1} - {\mu _2}} \right) \xi ,&{} \dot{\xi } < 0 \end{array} \right. \end{aligned}$$

(23)

which leads to the expression defying the partial derivative $\frac{\partial f\left( \xi \right) }{\partial \xi }$

$$\begin{aligned} \frac{{\partial f\left( \xi \right) }}{{\partial \xi }} = \left\{ {\begin{array}{l@{\quad }l} \rho {b^M}\xi + {\mu _1} + {\mu _2}, &{} \dot{\xi } > 0\\ \rho {b^A}\xi + {\mu _1} - {\mu _2}, &{} \dot{\xi } < 0 \end{array}} \right. \end{aligned}$$

(24)

The material properties $b^{A}$, $b^{M}$, $\mu _1$ and $\mu _2$ can be calculated using the Kuhn–Tucker conditions

$$\begin{aligned} b^{A}= & {} -\Delta s_0 \left( {A_{f} -A_{s} } \right) \end{aligned}$$

(25)

$$\begin{aligned} b^{M}= & {} -\Delta s_0 \left( {M_{s} -M_{f} } \right) \end{aligned}$$

(26)

$$\begin{aligned} \mu _1= & {} \frac{1}{2}\rho \Delta s_0 \left( {M_{s} +A_{f} } \right) -\rho \Delta u_0 \end{aligned}$$

(27)

$$\begin{aligned} \mu _2= & {} \frac{1}{4}\rho \Delta s_0 \left( {A_{s} -A_{f} -M_{f} +M_{s} } \right) \end{aligned}$$

(28)

based on the characteristic phase transition temperatures $A_{s}$, $A_{f}$, $M_{s}$ and $M_{f}$, as previously explained in Sect. 3.

After introduction of Eqs. (24–28) in Eq. (21), the thermodynamic force $\varPi$ can be found as

$$\begin{aligned} \varPi =\frac{1}{2}\Delta C\sigma ^{2}+\rho \Delta s_0 T_0 +\varPi _1 \end{aligned}$$

(29)

where

$$\begin{aligned} {\varPi _1} = \left\{ {\begin{array}{l@{\quad }l} \sqrt{6} H\sigma + \rho \Delta {s_0}\left( {{M_{s}} - {M_{f}}} \right) \xi - \frac{1}{4}\rho \Delta {s_0}\left( {3{M_{s}} + {A_{f}} + {A_{s}} - {M_{f}}} \right) , &{} \dot{\xi } > 0\\ \sqrt{6} H\sigma + \rho \Delta {s_0}\left( {{A_{f}} - {A_{s}}} \right) \xi - \frac{1}{4}\rho \Delta {s_0}\left( {{M_{s}} + 3{A_{f}} - {A_{s}} + {M_{f}}} \right) , &{} \dot{\xi } < 0 \end{array}} \right. \end{aligned}$$

(30)

Finally, the transformation function $\varPhi$ is calculated according to the conditionally defined formula

$$\begin{aligned} \varPhi = \left\{ {\begin{array}{l@{\quad }l} \varPi - Y, &{} \dot{\xi }> 0 \left( {{\hbox {austenite}} \rightarrow {\hbox {martensite}}} \right) \\ - \varPi - Y, &{} \dot{\xi }< 0 \left( {{\hbox {martensite}} \rightarrow {\hbox {austenite}}} \right) \end{array}} \right. \nonumber \\ \end{aligned}$$

(31)

which depends on both the thermodynamic force $\varPi$ and the parameter Y, used to define the critical value of the quantity for internal dissipation of energy while phase transition occurs

$$\begin{aligned} Y=\frac{1}{4}\rho \Delta s_0 \left( {M_{s} +M_{f} -A_{f} -A_{s} } \right) \end{aligned}$$

(32)

Taking into account the value of the transformation function $\varPhi$ as well as condition (22), the following two cases are distinguished to specify the required change of $\xi$:

• if the stress $\sigma$ increases and if $\varPhi ( \dot{\xi }>0)>0$, then phase transition from austenite to martensite is identified and further growth of the fraction $\xi$ is necessary; note, $\xi$ cannot take the values greater than 1

• if the stress $\sigma$ decreases and if $\varPhi ( \dot{\xi }<0)>0$, then phase transition from martensite to austenite is identified and further reduction in the fraction $\xi$ is necessary; note, $\xi$ cannot take the values less than 0

Based on verification, performed for the above-stated conditions, which refer to the transformation function $\varPhi$ and the martensitic volume fraction $\xi \in \left[ {0,1} \right]$, static, quasi-static and dynamic simulations may be carried out considering gradual increase or decrease in the stress and the hysteretic character of the modeled superelasticity effect. During simulations, the condition $\varPhi \le 0$ must be satisfied at any time, irrespectively from the sign of $\dot{\xi }$, to assure that the Clausius–Planck inequality (17) is fulfilled.

The above-introduced approach represents the phenomenological modeling technique, specifically making use of the free energy concept. As shown, it allows for representation of both thermally and mechanically induced phase transformations. Dedicated model parameters, e.g., $\xi$ and $\dot{\xi }$, assure effective control over the percentage contribution of martensite and austenite phases as well as the rate of the martensitic transformation. The idea of the use of additional internal variables in the model of SMA is not a new one [55]; however, it has been continuously widely applied for decades to allow for convenient modeling kinetics of phase transformations [53, 56]. The authors of the present paper take an advantage of both more physical interpretation of the model behavior offered by the free-energy-based approach and the relatively newly reported capabilities of a nonlocal modeling via peridynamics.

It should be, however, noted that the above-mentioned comprehensive understanding of the state of the simulated material—in terms of transformation kinetics, energy flow and the entropy of the model—requires relatively complicated mathematical description and therefore leads to implementation inconveniences. Alternatively, another group of phenomenological models can be used, which introduce approximate description for macroscopic material behavior.

In the work [57], the authors consider thermomechanical properties of the modeled SMA to simulate the shape memory effect and superelasticity. The applied phenomenological approach makes use of a polynomial approximation to build an SMA model, successfully followed by its application to a biomechanical system (a rod-type prosthesis of a human middle ear), as reported in [58]. In the work [57], nonlinear properties of the modeled SMA material are addressed by the analytical description based on a fifth-order polynomial. Moreover, the authors of the referenced work confirmed the reliability and usability of the developed first-order approximate SMA model dedicated to operate at the arbitrarily selected frequency range, close to the resonance conditions. The developed model was verified using FE simulations. Another interesting phenomenological approach is presented in [59]. The authors of the cited work propose a straightforward polynomial- based definition of the constitutive model for SMA. The properties of a single and 2-degree-of-freedom (DOF) oscillators are investigated with the introduced SMA components, including bifurcation diagrams. The presented modeling approach allows to conveniently simulate the effects of shape memory and superelasticity.

In the following, the theory of peridynamic model for SMA is provided based on the previously presented fundamentals in the introductory sections.

5 Peridynamic model for SMA

Making the reference to both the former authors’ modeling approaches used for SMA [51, 60, 61] and the theory of the superelasticity effect provided in Sect. 4, a peridynamic model is introduced in the following.

Considering Eq. (1), the governing equation for a 1-D case of a continuum solid body (a rod) takes the form [40]

$$\begin{aligned} \rho \ddot{u}\left( {x,t} \right)= & {} \int _H f\left( {u\left( {\hat{x},t} \right) - u\left( {x,t} \right) ,\hat{x}- x} \right) \mathrm{d}{V_{\hat{x}}} \nonumber \\&+ \,b\left( {x,t} \right) \end{aligned}$$

(33)

which may be transformed into a discrete form for the ith DOF

$$\begin{aligned} \rho \ddot{u}_i^t= & {} \sum \nolimits _{\begin{array}{l} {j = - N}\\ {j \ne 0} \end{array}}^N f\left( u_{i + j}^t - u_i^t,\left( {i + j} \right) L \right. \nonumber \\&\left. -\, iL \right) {V_j} + {b_i} \end{aligned}$$

(34)

with the pairwise interaction force f

$$\begin{aligned} f\left( {u_{i+j}^t -u_i^t ,jL} \right) =\left\{ {{\begin{array}{l@{\quad }l} cs_i ,&{} \hbox {if}\,\left| j \right| L\le \delta \\ 0, &{} \hbox {otherwise} \\ \end{array} }} \right. \end{aligned}$$

(35)

strain $s_i$

$$\begin{aligned} s_i =\frac{u_{i+j}^t -u_i^t }{\left| j \right| L} \end{aligned}$$

(36)

and the volume $V_j$

$$\begin{aligned} V_j =\beta _{i,j} AL \end{aligned}$$

(37)

$u_i^t$, $u_{i+j}^t$ are the displacements at the time step indexed by t, respectively, for the actual central ith particle and the particle, which is located within the horizon H at the jth relative position with respect to the ith particle. The index j takes any discrete value pointing the particle’s location within the horizon of the radius $\delta =NL$, where L equals the distance between particles. Note, that in the following, the parameter L also becomes $\Delta x$, i.e., $\Delta x=L$, which is more readable in the context of both stability and convergence studies. A denotes the area of the cross section of the modeled rod. The factor $\beta _{i,j}$ is introduced to correctly determine the value of the volume for the neighboring particle $V_j$ at the boundaries of the horizon, and it is determined conditionally

$$\begin{aligned} \beta _{i,j} =\left\{ {{\begin{array}{l@{\quad }l} 1, &{} j\ne N\wedge j\ne -N \\ \frac{1}{2},&{} j=N\vee j=-N \\ \end{array} }} \right. \end{aligned}$$

(38)

Next, Eq. (34) evolves into the following form for the ith particle, i.e., for the ith DOF

$$\begin{aligned} \rho \ddot{u}_i^t = \sum \nolimits _{\begin{array}{l} {j = - N}\\ {j \ne 0} \end{array}}^N c\frac{{u_{i + j}^t - u_i^t}}{{\left| j \right| }}{\beta _{i,j}}A + {b_i} \end{aligned}$$

(39)

It should be noted that Eq. (39) takes a general form allowed to be used within the body of a modeled rod excluding its two ends. In detail, if the horizon radius $\delta$ exceeds the distance between the current ith particle and the location of one of the rod’s ends, Eq. (39) should undergo further modification to limit the number of permitted values for the j index.

The micromodulus function c takes the following fundamental, widely applied value for a 1-D case, which stays constant within the horizon of a peridynamic model [41]

$$\begin{aligned} c=\frac{2E^{A}}{\delta ^{2}A} \end{aligned}$$

(40)

hence

$$\begin{aligned} \rho \ddot{u}_i^t = \sum \nolimits _{\begin{array}{l} {j = - N}\\ {j \ne 0} \end{array}}^N \frac{{2{E^A}}}{{{{\left( {NL} \right) }^2}}}\frac{{u_{i + j}^t - u_i^t}}{{\left| j \right| }}{\beta _{i,j}} + {b_i} \end{aligned}$$

(41)

When multiplying both sides of Eq. (41) by the volume of the ith particle $V_i$

$$\begin{aligned} V_i = {\upgamma }_i AL \end{aligned}$$

(42)

we may find

$$\begin{aligned} {m_i}\ddot{u}_i^t = 2\sum \nolimits _{\begin{array}{l} {j = - N}\\ {j \ne 0} \end{array}}^N {\beta _{i,j}}{\gamma _i}\frac{{{E^A}A}}{L}\frac{{u_{i + j}^t - u_i^t}}{{\left| j \right| {N^2}}} + {F_i} \end{aligned}$$

(43)

or

$$\begin{aligned} {m_i}\ddot{u}_i^t = 2\sum \nolimits _{\begin{array}{l} {j = - N}\\ {j \ne 0} \end{array}}^N {\beta _{i,j}}{\gamma _i}{k^A}\frac{{u_{i + j}^t - u_i^t}}{{\left| j \right| {N^2}}} + {F_i} \end{aligned}$$

(44)

where $k^{A}$ is the classically formulated stiffness coefficient (similarly to a 1-D FE formulation) for an initial austenite phase

$$\begin{aligned} k^{A}=\frac{E^{A}A}{L} \end{aligned}$$

(45)

$m_i$ and $F_i$ are the mass and external force considered for the ith particle. Similarly to the parameter $\beta _{i,j}$, the auxiliary factor $\gamma _i$ assures, in turn, the correct volume for the current central particle $V_i$ at the ends of the rod, i.e., where $i=1\vee i=i_{MAX}$. Hence,

$$\begin{aligned} \gamma _i =\left\{ {{\begin{array}{l@{\quad }l} 1, &{}i\ne 1\wedge i\ne i_{MAX} \\ \frac{1}{2},&{} i=1\vee i=i_{MAX}\\ \end{array} }} \right. \end{aligned}$$

(46)

For the sake of simplicity, the case of a uniform rod made of SMA is considered in the work. Taking into account Eq. (14), which defines the total strain in SMA, as well as Eqs. (13), (15) and (16), one may obtain

$$\begin{aligned} \varepsilon =\left( {\frac{1}{E^{A}}+\xi \left( {\frac{1}{E^{M}}-\frac{1}{E^{A}}} \right) } \right) \sigma +\sqrt{\frac{3}{2}}H\xi \end{aligned}$$

(47)

and

$$\begin{aligned} \varepsilon =\left( {\left( {\frac{1}{E^{M}}-\frac{1}{E^{A}}} \right) \sigma +\sqrt{\frac{3}{2}}H} \right) \xi +\frac{\sigma }{E^{A}} \end{aligned}$$

(48)

After introduction of the two expressions, based on the ith particle’s force and displacement $F_i$ and $u_i$, i.e., $\sigma =F_i /A$ and $\varepsilon =u_i /L$ into Eq. (48), the following relationship may be found

$$\begin{aligned} \frac{u_i }{L}=\left( {\left( {\frac{1}{E^{M}}-\frac{1}{E^{A}}} \right) \frac{F_i }{A}+\sqrt{\frac{3}{2}}H} \right) \xi _i +\frac{F_i }{E^{A}A} \end{aligned}$$

(49)

which evolves to the form

$$\begin{aligned} k^{A}u_i =\left( {\left( {\frac{E^{A}}{E^{M}}-1} \right) F_i +\sqrt{\frac{3}{2}}HE^{A}A} \right) \xi _i +F_i \end{aligned}$$

(50)

and, then,

$$\begin{aligned} k^{A}u_i =\left( {\alpha _E F_i +F_M^*} \right) \xi _i +F_i \end{aligned}$$

(51)

$\alpha _{{E}}$ and $F_M^*$ are the auxiliary constant parameters expressing the relationship between the Young’s moduli for the two SMA phases and the resultant phase transformation force

$$\begin{aligned} \alpha _E= & {} \frac{E^{A}}{E^{M}}-1 \end{aligned}$$

(52)

$$\begin{aligned} F_M^*= & {} \sqrt{3/2}HE^{A}A \end{aligned}$$

(53)

Next, Eq. (51) may be rewritten in the form

$$\begin{aligned} k^{A}u_i =F_M^*\xi _i +\left( {\alpha _E \xi _i +1} \right) F_i \end{aligned}$$

(54)

and

$$\begin{aligned} k_i^*u_i =F_i^*+F_i \end{aligned}$$

(55)

where the two equivalent resultant parameters are proposed to be used in a peridynamic model, namely stiffness coefficient $k_i^*$ and the modified phase transformation force $F_i^*$

$$\begin{aligned} k_i^*= & {} \frac{k^{A}}{\alpha _E \xi _i +1} \end{aligned}$$

(56)

$$\begin{aligned} F_i^*= & {} \frac{F_M^*}{\alpha _E \xi _i +1}\xi _i \end{aligned}$$

(57)

to follow the standard compacted expression for the static problem description of the know general form $ku=F$.

Finally, making the reference between Eqs. (55) and (44), an alternative 1-D peridynamic model for SMA is proposed to take the form

$$\begin{aligned} {m_i}\ddot{u}_i^t= & {} 2\sum \nolimits _{\begin{array}{l} {j = - N}\\ {j \ne 0} \end{array}}^N \left( {{\beta _{i,j}}{\gamma _i}\frac{{{k^A}}}{{{\alpha _E}{\xi _i} + 1}}\frac{{u_{i + j}^t - u_i^t}}{{\left| j \right| {N^2}}}} \right) \nonumber \\&+\, \frac{{F_M^*}}{{{\alpha _E}{\xi _i} + 1}}{\xi _i} + {F_i} \end{aligned}$$

(58)

where $m_i$, $k^{A}$, $\alpha _E$, $F_M^*$ are the constant parameters and $\xi _i$ is the control parameter considered for the ith particle to declare the current contributions of the austenite and martensite phases in the mentioned particle.

Application of the governing equation (58) allows for solution of static, quasi-static and dynamic problems. In all cases, it is required to aggregate the system of linear equations making use of the parameters $k_i^*$ and $F_i^*$ in the global stiffness matrix and the force vector, respectively. A general flowchart for applications of the proposed peridynamic model is shown in Fig. 6.

Fig. 6

Flowchart for applications of the elaborated peridynamic model of SMA

The first step of calculations is performed to parameterize the model using geometric and material properties. Moreover, the initial and boundary conditions are defined to introduce the data regarding both fixed displacement areas and external loads. Finally, simulation data referring to total simulation time, time step (temporal discretization), distances between particles (spatial discretization), range of the horizon and the maximum error for the particle displacement are provided. During the second step, initial calculations are conducted to determine auxiliary constants in a model: masses, volumes, stiffness coefficients, resultant phase transformation force as well as critical elongations for the established bonds between particles. If required, initial cracks are introduced into the model by breaking selected bonds.

Iterative part of the procedure deals with the calculation of the particles’ displacements and velocities via solving the matrix equation based on the updated values of external loads. For an SMA model, the conditions regarding the transformation function $\varPhi _i \le 0$ and martensitic volume fraction $\xi _i \in \left[ {0,1} \right]$ are checked during each iteration. If required, the displacements are repeatedly updated to assure that the above-mentioned parameters are kept within the specified limits, which guarantees proper hysteretic behavior of modeled SMA sample. Moreover, a search for the bonds with exceeded critical elongations is carried out in case of growing cracks. The final step (postprocessing) shows the obtained results making use of both numerical and graphical presentations.

To assess the property of the elaborated numerical peridynamic model for SMA (58), the stability condition is determined for explicit formulation, applying von Neumann stability analysis. An exemplary representative case of $N=2$ is taken into account. The central scheme for finite difference (FD) method is used for time integration

$$\begin{aligned} \ddot{u}_i^t = \frac{{u_i^{t - 1} - 2u_i^t + u_i^{t + 1}}}{\Delta t^2} \end{aligned}$$

(59)

For the case when $i\ne 1\wedge i\ne i_{MAX}$ and excluding the external force $F_i$, Eq. (58) becomes

$$\begin{aligned}&m_i \frac{u_i^{t-1} -2u_i^t +u_i^{t+1} }{\Delta t^{2}}\nonumber \\&\quad =2\sum \nolimits _{{\begin{array}{l} {j=-N} \\ {j\ne 0} \\ \end{array} }}^N \left( {\beta _{i,j} \frac{k^{A}}{\alpha _E \xi _i +1}\frac{u_{i+j}^t -u_i^t }{\left| j \right| N^{2}}} \right) \nonumber \\&\qquad +\,\frac{F_M^*}{\alpha _E \xi _i +1}\xi _i \end{aligned}$$

(60)

$$\begin{aligned}&m_i \frac{u_i^{t-1} -2u_i^t +u_i^{t+1} }{\Delta t^{2}} \nonumber \\&\quad =2\left( \frac{k_i^*}{16}\left( {u_{i-2}^t -u_i^t } \right) +\frac{k_i^*}{4}\left( {u_{i-1}^t -u_i^t } \right) \right. \nonumber \\&\qquad \left. +\,\frac{k_i^*}{4}\left( {u_{i+1}^t -u_i^t } \right) +\frac{k_i^*}{16}\left( {u_{i+2}^t -u_i^t } \right) \right) +F_i^*\nonumber \\\end{aligned}$$

(61)

$$\begin{aligned}&u_i^{t-1} -2u_i^t +u_i^{t+1} \nonumber \\&\quad =\frac{\Delta t^{2}k_i^*}{m_i }\left( \frac{1}{8}u_{i-2}^t +\frac{1}{2}u_{i-1}^t -\frac{5}{4}u_i^t \right. \nonumber \\&\qquad \left. +\,\frac{1}{2}u_{i+1}^t +\frac{1}{8}u_{i+2}^t \right) +\frac{\Delta t^{2}}{m_i }F_i^*\end{aligned}$$

(62)

Hence, the equation for the numerical error takes the form

$$\begin{aligned}&\varepsilon _i^{t-1} -2\varepsilon _i^t +\varepsilon _i^{t+1} =r_1 \left( \frac{1}{8}\varepsilon _{i-2}^t +\frac{1}{2}\varepsilon _{i-1}^t \right. \nonumber \\&\quad \left. -\,\frac{5}{4}\varepsilon _i^t +\frac{1}{2}\varepsilon _{i+1}^t +\frac{1}{8}\varepsilon _{i+2}^t \right) +r_2 \end{aligned}$$

(63)

where the axillary parameters $r_1$ and $r_2$ equal

$$\begin{aligned} r_1= & {} \frac{\Delta t^{2}}{m_i }k_i^*\end{aligned}$$

(64)

$$\begin{aligned} r_2= & {} \frac{\Delta t^{2}}{m_i }F_i^*\end{aligned}$$

(65)

The considered error includes both the temporal and spatial terms

$$\begin{aligned} \varepsilon _{i+j}^{t+q} =\hbox {exp}\left( {a\left( {t+q} \right) \Delta t} \right) \hbox {exp}\left( {\hbox {j}\kappa _\varepsilon \left( {i+j} \right) \Delta x} \right) \end{aligned}$$

(66)

where ${\mathrm{j}}=\sqrt{-1}$ is the imaginary unit, a and $\kappa _\varepsilon$ are constants. Consequently, Eq. (63) becomes

$$\begin{aligned}&\hbox {exp}\left( {-a\Delta t} \right) +\hbox {exp}\left( {a\Delta t} \right) \nonumber \\&\quad =2+r_1 \left( {\frac{1}{4}\hbox {cos}\left( {2r} \right) +\hbox {cos}\left( r \right) -\frac{5}{4}} \right) \nonumber \\&\qquad +\,r_2 \hbox {exp}\left( {-at\Delta t} \right) \hbox {exp}\left( {-\mathrm{j}ir} \right) \end{aligned}$$

(67)

where $r=\kappa _\varepsilon \Delta x$. For the most demanding case of $\xi _i =0$, when the velocity for the longitudinal wave reaches the maximum value $c^{A}=\sqrt{E^{A}/\rho }$, for austenitic phase, since $E^{A}>E^{M}$, the condition for numerical stability becomes

$$\begin{aligned} \left| {1+\frac{\Delta t^{2}}{2\Delta x^{2}}\left( {c^{A}} \right) ^{2}\left( {\frac{1}{4}\hbox {cos}\left( {2r} \right) +\hbox {cos}\left( r \right) -\frac{5}{4}} \right) } \right| \le 1 \end{aligned}$$

(68)

which finally allows to determine the constraint for the time step

$$\begin{aligned} \Delta t\le \sqrt{2}\frac{\Delta x}{c^{A}} \end{aligned}$$

(69)

Condition (69) should be normally taken for proper selection of $\Delta t$ for a numerical model in case of explicit integration. It is especially required when high-frequency excitations are applied and the wavelength of the generated elastic wave is comparable with the length of the model. It should be noted that this is, however, not the case for the numerical model studied in Sect. 7. Due to the low-frequency excitation (time period equals 30 s to assure isothermal phase transition), small dimensions of the model (its length equals 4 mm) and limited number of DOFs, i.e., 5, a significantly higher value of the time step $\Delta t=10\,\hbox {ms}$ was arbitrarily selected with respect to the one specified by Eq. (69), i.e., $0.38\,\upmu \hbox {s}$. It should be clearly stated that the choice made for $\Delta t$ was valid for the considered specific nearly quasi-static simulations carried out for SMA.

Similarly, the convergence of Eq. (61) to the analytical case was confirmed. For an exemplary case of $\xi _i =0$, Eq. (61) becomes

$$\begin{aligned}&m_i \frac{u_i^{t-1} -2u_i^t +u_i^{t+1} }{\Delta t^{2}} \nonumber \\&\quad =k^{A}\left( \frac{1}{8}\left( {u_{i-2}^t -u_i^t } \right) +\frac{1}{2}\left( {u_{i-1}^t -u_i^t } \right) \right. \nonumber \\&\qquad \left. +\,\frac{1}{2}\left( {u_{i+1}^t -u_i^t } \right) +\frac{1}{8}\left( {u_{i+2}^t -u_i^t } \right) \right) \end{aligned}$$

(70)

and then

$$\begin{aligned}&m_i \frac{u_i^{t-1} -2u_i^t +u_i^{t+1} }{\Delta t^{2}}\nonumber \\&\quad =k^{A}\left( {\frac{1}{8}u_{i-2}^t +\frac{1}{2}u_{i-1}^t -\frac{5}{4}u_i^t +\frac{1}{2}u_{i+1}^t +\frac{1}{8}u_{i+2}^t } \right) \nonumber \\ \end{aligned}$$

(71)

After introduction of a standard wave solution

$$\begin{aligned} u_{i+j}^{t+q}= & {} \hbox {exp}\left( {\hbox {j}\left( {\omega \left( {t+q} \right) \Delta t-\kappa \left( {i+j} \right) \Delta x} \right) } \right) \nonumber \\= & {} \hbox {exp}\left( {\hbox {j}\left( {\omega t\Delta t-\kappa {i}\Delta x} \right) } \right) \hbox {exp}\left( {\hbox {j}\left( {\omega q \Delta t-\kappa {j} \Delta x} \right) } \right) \nonumber \\ \end{aligned}$$

(72)

Eq. (71) becomes

Fig. 7

Fatigue testing machine Instron 8872 with mounted SMA wire used in the validation experiments for the FE and peridynamic models

$$\begin{aligned}&\frac{m_i }{\Delta t^{2}}\left( {\hbox {exp}\left( {\mathrm{j}\left( {-\omega \Delta t} \right) } \right) -2+\hbox {exp}\left( {\mathrm{j}\left( {\omega \Delta t} \right) } \right) } \right) \nonumber \\&\quad =k^{A}\left( {{\begin{array}{l} {\frac{1}{8}\hbox {exp}\left( {\mathrm{j}\left( {2\kappa \Delta x} \right) } \right) +\frac{1}{2}\hbox {exp}\left( {\mathrm{j}\left( {\kappa \Delta x} \right) } \right) -\frac{5}{4}+} \\ {+\frac{1}{2}\hbox {exp}\left( {\mathrm{j}\left( {-\kappa \Delta x} \right) } \right) +\frac{1}{8}\hbox {exp}\left( {\mathrm{j}\left( {-2\kappa \Delta x} \right) } \right) } \\ \end{array} }} \right) \nonumber \\ \end{aligned}$$

(73)

and then

$$\begin{aligned}&\frac{m_i }{\Delta t^{2}}\left( {2\hbox {cos}\left( {\omega \Delta t} \right) -2} \right) \nonumber \\&\quad =k^{A}\left( {\frac{1}{4}\hbox {cos}\left( {2\kappa \Delta x} \right) +\hbox {cos}\left( {\kappa \Delta x} \right) -\frac{5}{4}} \right) \end{aligned}$$

(74)

After introduction of the two fundamental terms of the Taylor series for the trigonometric components, Eq. (74) takes the form

$$\begin{aligned}&\frac{m_i }{\Delta t^{2}}\left( {2\left( {1-\frac{\left( {\omega \Delta t} \right) ^{2}}{2}} \right) -2} \right) \nonumber \\&\quad =k^{A}\left( {\frac{1}{4}\left( {1-\frac{\left( {2\kappa \Delta x} \right) ^{2}}{2}} \right) +1-\frac{\left( {\kappa \Delta x} \right) ^{2}}{2}-\frac{5}{4}} \right) \nonumber \\ \end{aligned}$$

(75)

$$\begin{aligned}&\frac{m_i }{\Delta t^{2}}\left( {\omega \Delta t} \right) ^{2}=\frac{E^{A}A}{\Delta x}\left( {\frac{\left( {2\kappa \Delta x} \right) ^{2}}{8}+\frac{\left( {\kappa \Delta x} \right) ^{2}}{2}} \right) \end{aligned}$$

(76)

$$\begin{aligned}&m_i \omega ^{2}=\frac{E^{A}A}{\Delta x}\left( {\kappa \Delta x} \right) ^{2} \end{aligned}$$

(77)

$$\begin{aligned}&\omega ^{2}=\kappa ^{2}\frac{E^{A}}{\rho } \end{aligned}$$

(78)

$$\begin{aligned}&\omega ^{2}=\left( {c^{A}} \right) ^{2}\kappa ^{2} \end{aligned}$$

(79)

which, finally, stands for an analytical form of the dispersion relation for an isotropic, homogeneous material.

In the following Sect. 6, the results of experimental validation and numerical verification confirm the applicability of the above-presented theory making use of the stress–strain relationship obtained for the elaborated peridynamic code for SMA.

6 Experimental validation and verification using commercial FE code

As mentioned earlier, both experimental validation and numerical verification were carried out to confirm the demanded functionalities of the elaborated peridynamic model of SMA. In the performed validation experiments, an SMA wire made of Nitinol was used. The length and the diameter of the wire are 133 mm and 1 mm, respectively. Figure 7 shows the test stand used in experiments, equipped with a fatigue testing machine Instron 8872 with the maximum load of 10 kN. During tensile tests, the stress–strain paths for the SMA sample were registered.

The experimental tests were conducted at room temperature $22\,^{\circ }\hbox {C}$. Since, for the used SMA material, the characteristic temperature $A_{f}$ equals $10\,^{\circ }\hbox {C}$ (based on the manufacturer data), the condition regarding the presence of austenite phase before application of mechanical load was satisfied, which is required for testing the superelasticity effect.

The undertaken tests consisted in the following consecutive phases: (step 1) an initial 5-s long pause, (step 2) gradual stretching of the SMA wire until the absolute extension of 11 mm is achieved with the stretching rate 0.05 mm/s, (step 3) 30-s long pause, (step 4) compression by 11 mm with the stretching release rate 0.05 mm/s.

For verification reason, the respective three-dimensional (3-D) FE model of the SMA wire was created to generate the stress–strain path using a commercial software MSC.Software/Marc, which is shown in Fig. 8. It consists of 101080 FEs.

Fig. 8

FE model of an SMA wire used for verification of the peridynamic model. The cross-sectional view is shown on the right

The FE modeling approach is employed since it is a common and convenient verification tool. The same experimental data were applied to validate both the FE code and the elaborated peridynamic model of SMA to assure the correct assessment of the convergence between these two approaches during numerical verification.

The theory of superelasticity effect, which is implemented in the used commercial FE code, was proposed by Auricchio and is presented in detail in [62, 63]. Even though different mathematical formalisms are used by Lagoudas and Auricchio in their theoretical works for SMA—including constitutive equation and the definition for the characteristic points in the stress–strain plots—the theory applied in the FE code is in line with the analytical formulations used in the peridynamic model provided in Sect. 5. As shown below, the results convergence was achieved for the superelasticity effect, satisfying the condition of isothermal phase transition. In both modeling approaches, various elastic moduli are separately considered for martensite and austenite phases, and the martensite percentage volume fraction $\xi$ is introduced as the control property to assure hysteretic character of the stress–strain relationships for SMA. Although different parameters are used to declare the characteristic points in the stress–strain curve, their conversion relationships may be effectively found via either verification or validation process.

Finally, the stress–strain curve for the tested peridynamic model of an SMA sample was generated using the theory described in Sect. 5. The details of the peridynamic model used for validation and verification are described in the following. A generic 1-D peridynamic model of a 4-mm-long piece of an SMA wire was created to investigate the phenomenon of superelasticity. More specifically, the model constitutes the structure of a rod, exhibiting axial loads only. One of the model ends is clamped, whereas the external axial force P is attached at the opposite edge. The external excitation may be static, quasi-static or dynamic, as demanded. The model is shown in Fig. 9.

Fig. 9

Tested 1-D peridynamic model of an SMA wire used for numerical simulations of the superelasticity phenomenon

The tested model is built of 5 particles. Their cross-sectional area A equals $1\,{\hbox {mm}}^{2}$. The distance between particles and the horizon radius is, respectively, $L=1\,{\hbox {mm}}$ and $\delta =2\,{\hbox {mm}}$. An equivalent global stiffness matrix $\mathbf{K}$ is aggregated for the model—making the reference to the components of the derived governing equation (58) to visualize the nonlocal elastic interactions in the peridynamic model. The matrix $\mathbf{K}$ takes the form

$$\begin{aligned} \mathbf{K}=\left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\frac{5}{16}k_1^*}&{} {-\frac{1}{4}k_1^*}&{} {-\frac{1}{16}k_1^*}&{} 0&{} 0 \\ {-\frac{1}{4}k_2^*}&{} {\frac{7}{8}k_2^*}&{} {-\frac{1}{2}k_2^*}&{} {-\frac{1}{8}k_2^*}&{} 0 \\ {-\frac{1}{8}k_3^*}&{} {-\frac{1}{2}k_3^*}&{} {\frac{5}{4}k_3^*}&{} {-\frac{1}{2}k_3^*}&{} {-\frac{1}{8}k_3^*} \\ 0&{} {-\frac{1}{8}k_4^*}&{} {-\frac{1}{2}k_4^*}&{} {\frac{7}{8}k_4^*}&{} {-\frac{1}{4}k_4^*}\\ 0&{} 0&{} {-\frac{1}{16}k_5^*}&{} {-\frac{1}{4}k_5^*}&{} {\frac{5}{16}k_5^*} \\ \end{array} }} \right) \end{aligned}$$

(80)

where the resultant stiffness coefficients $k_i^*=k_i^*\left( {\xi _i } \right)$ may be found according to formula (56). Similarly, the force vector $\mathbf{F}$ for the modeled system is as follows

$$\begin{aligned} \mathbf{F}=\left[ {{\begin{array}{c} {-P-F_2^*} \\ {P+F_2^*-P-F_3^*} \\ {P+F_3^*-P-F_4^*} \\ {P+F_4^*-P-F_5^*} \\ {P+F_5^*} \\ \end{array} }} \right] \end{aligned}$$

(81)

Hence,

$$\begin{aligned} \mathbf{F}=\left[ {{\begin{array}{c} {-P-F_2^*} \\ {F_2^*-F_3^*} \\ {F_3^*-F_4^*} \\ {F_4^*-F_5^*} \\ {P+F_5^*} \\ \end{array} }} \right] \end{aligned}$$

(82)

where the resultant modified phase transformation forces $F_i^*=F_i^*\left( {\xi _i } \right)$ are found according to formula (57).

The global mass matrix $\mathbf{M}$ takes a standard diagonal form populated with the mass of the consecutive particles $m_i$

$$\begin{aligned} \mathbf{M}=\hbox {diag}\left( {m_1 ,\ldots ,m_5 } \right) \end{aligned}$$

(83)

where

$$\begin{aligned} m_i =\rho \gamma _i AL \end{aligned}$$

(84)

The coefficients $\gamma _i$ are found using Eq. (46). After fixation of the first particle, the final form for the equivalent matrix governing equation for the peridynamic model becomes

$$\begin{aligned} {\mathbf{M}}'\ddot{\mathbf{u}} +\mathbf{K}'{} \mathbf{u}=\mathbf{F}' \end{aligned}$$

(85)

with:

$$\begin{aligned} \mathbf{M}^{\prime }= & {} \hbox {diag}\left( {m_2 ,m_3, m_4 ,m_5 } \right) \end{aligned}$$

(86)

$$\begin{aligned} \mathbf{K}^{\prime }= & {} \left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\frac{7}{8}k_2^*}&{} {-\frac{1}{2}k_2^*}&{} {-\frac{1}{8}k_2^*}&{} 0 \\ {-\frac{1}{2}k_3^*}&{} {\frac{5}{4}k_3^*}&{} {-\frac{1}{2}k_3^*}&{} {-\frac{1}{8}k_3^*}\\ {-\frac{1}{8}k_4^*}&{} {-\frac{1}{2}k_4^*}&{} {\frac{7}{8}k_4^*}&{} {-\frac{1}{4}k_4^*} \\ 0&{} {-\frac{1}{16}k_5^*}&{} {-\frac{1}{4}k_5^*}&{} {\frac{5}{16}k_5^*} \\ \end{array} }} \right) \end{aligned}$$

(87)

$$\begin{aligned} \mathbf{F}^{\prime }= & {} \left[ {{\begin{array}{c} {F_2^*-F_3^*} \\ {F_3^*-F_4^*} \\ {F_4^*-F_5^*} \\ {P+F_5^*} \\ \end{array} }} \right] \end{aligned}$$

(88)

$$\begin{aligned} \ddot{\mathbf{u}}= & {} \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\ddot{u}}_2&{\ddot{u}}_3&{\ddot{u}}_4&{\ddot{u}}_5 \end{array}} \right] ^{\mathrm{T}} \end{aligned}$$

(89)

$$\begin{aligned} \mathbf{u}= & {} \left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {u_2 }&{} {u_3 }&{} {u_4 }&{} {u_5 } \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$

(90)

Figure 10 presents the comparison between the results obtained using both experiments and numerical simulations for the elaborated peridynamic model after its validation and verification. The stress–strain curve for the peridynamic model, which is shown in Fig. 10, is obtained using Eq. (85), excluding the acceleration component $\mathbf{M}'\ddot{\mathbf{u}}$ to consider a quasi-static case.

Fig. 10

Comparison between the experimental and simulation results (quasi-static numerical analysis) after validation and verification procedure carried out for the tested peridynamic model. Two validation experiments were conducted taking into account one and two cycles for the hysteresis loop in the stress–strain relationship. The curves identified during experiments exhibit irregularities resulting from spontaneous phase changes—the issue is discussed in Sect. 4

The experimental validation procedure has confirmed the applicability of both the FE and peridynamic modeling for SMA components. The results for the numerical simulations were generated using the models parameterized based on the experimental data. The identified Young’s moduli for the austenite and martensite phases are $E^{A}=66\,\hbox {GPa}$ and $E^{M}=48\,\hbox {GPa}$. In case of the FE model, the four characteristic stresses in the Auricchio model were found: $\sigma _{f}^{AS} =600\,\hbox {MPa}$, $\sigma _{f}^{SA} =630\,\hbox {MPa}$, $\sigma _{s}^{AS} =420\,\hbox {MPa}$ and $\sigma _{s}^{SA} =350\,\hbox {MPa}$, as well as the uniaxial transformation strain $\varepsilon _L =0.075$. Moreover, a standard value of 0.3 was assumed for the Poisson ratios $\nu ^{A}$ and $\nu ^{M}$. Alternatively, for the peridynamic model—making the reference to the Lagoudas model—the following properties were identified: the characteristic phase transition temperatures: $A_{s} =2\,{^{\circ }}\hbox {C}$, $M_{s} =-29 \,{^{\circ }}\hbox {C}$, $M_{f} =-39\, {^{\circ }}\hbox {C}$, and the factors $\rho \Delta s_0 =-1.27\,\hbox {MPa}/\hbox {K}$ and $H=5.24\%$. The temperature $A_{f}$ and the mass density $\rho$ are assumed to be known and equal $10\,{^{\circ }}\hbox {C}$ and $6450\,\hbox {kg}/\hbox {m}^{3}$, respectively. As visible in Fig. 10, the used material properties assure correct shape of the hysteretic stress–strain relationship for both numerical approaches. In addition, the relationship between the axial force and total elongation found in the peridynamic model of an SMA wire is presented in Fig. 11.

Fig. 11

Relationship between the axial force and total elongation in the peridynamic model of an SMA wire used to calculate the amount of dissipated energy per a single cycle of the simulated tension test

Fig. 12

Scheme of the structure and a photograph of a typical radial GFB. The magnified part of GFB shows the proposed localizations for mounting the SMA wires on both top and bump foils. With a standard operation of GFB, the SMA wires are stretched and compressed. Hence, they exhibit the phenomenon of superelasticity that allows to control the properties of the GFB structure

The identified amount of energy dissipated in the modeled SMA wire—originating from the hysteretic character of the superelasticity phenomenon—equals $0.103\,\hbox {J}$ per single cycle of the simulated tension test. The quantity was calculated as the area covered by the hysteresis loop shown in Fig. 11.

7 Numerical case study, application to GFB

The practical applicability of the proposed peridynamic modeling is confirmed with numerical simulations carried out for the model of a mechanical damper made of a piece of an SMA wire. The studied case is of great importance in the field of structural dynamics. More specifically, the structures equipped with SMA may offer the functionality of effective structural stiffness control when installed in mechanical systems. Moreover, SMA dampers provide means for energy dissipation; hence, they may help to reduce mechanical vibrations. Based on the above-mentioned properties of SMA components, a particular authors’ attention is paid on the capability of efficient control of the characteristics of a nonlinear supporting structure mounted in GFB [64]. Figure 12 presents the scheme and the photograph of a typical construction of GFB. The construction is compact. Basically, there are no moving parts in GFB apart from the shaft; what makes this type of journal bearings relatively reliable and robust [65, 66]. The nonlinear supporting structure of a GFB consists of the two types of metallic foils: top foil, which directly covers the journal, and bump foil, which constitutes an elastic-damping element. The bump foil is mounted to continuously align the journal, air film and inner surface of GFB. As shown in Fig. 12, there are several options regarding installation of SMA wires on the bearing foils to modify their properties and, therefore, to help maintaining stable operation of GFB.

Below, the elaborated nonlocal peridynamic modeling tool is adapted to make a suggestion regarding SMA material, which may be applied to suppress low-frequency and low-amplitude vibrations of the shaft mounted in GFB, via reduction in its transverse displacement drift and low-frequency fluctuations. The analyzed construction of GFB is considered to be modeled properly as long as its long-period steady-state operation is taken into account, under a constant load. This condition results from the limit of the present version of the elaborated peridynamic model, as already mentioned in Sect. 4. When satisfied, it allows to maintain isothermal character of the simulated phase transitions, which is the case, if the externally induced strain rate does not exceed the experimentally specified approximate value $0.00038\,\hbox {s}^{-1}$. Further development of the peridynamic model extending its functionality is the subject of future work.

To simulate the phenomenon of energy dissipation, similarly to the case presented in Sect. 6, a peridynamic model of an SMA wire is built using 5 particles. The following values of the selected geometric properties apply: cross-sectional area $A=0.1\,{\hbox {mm}}^{2}$, the distance between particles $L=1\,{\hbox {mm}}$ and the horizon radius $\delta =2\,{\hbox {mm}}$. Table 1 summarizes the material properties of the modeled SMA, which are proposed to parameterize the peridynamic model. Figure 13 shows both the stress–strain and force–elongation curves obtained for the considered material.

Table 1 Material properties proposed for the examined SMA damper

Fig. 13

Stress–strain and force–elongation relationships for the tested SMA material, which is used as a damper to perform mechanical energy dissipation

To observe energy dissipation in the modeled structure during isothermal phase transition, the arbitrary course of the external low-frequency force P is chosen, as shown in Fig. 14. Explicit time integration procedure is used to solve dynamic problems. The central scheme for FD method (59) for temporal derivatives is applied.

Hence, the particle displacements for the time step indexed by $\left( {t+1} \right)$ are found based on Eq. (85), using the formula

$$\begin{aligned} {{\mathbf{u}}^{t + 1}} = \Delta {t^2}{\left( {{\mathbf{M'}}} \right) ^{ - 1}}\left( {{\mathbf{F}}{'^t} - {{{\mathbf{K'}}}^t}{{\mathbf{u}}^t}} \right) + 2{{\mathbf{u}}^t} - {{\mathbf{u}}^{t - 1}} \end{aligned}$$

(91)

Since the components $\mathbf{F}^{\prime t}$ and ${{\mathbf{K'}}^t}$ depend upon the fractions $\xi _i$, each temporal step is performed as an iterative procedure to assure that the conditions referring to the transformation function $\varPhi _i \le 0$ and martensitic volume fraction $\xi _i \in \left[ {0,1} \right]$ are satisfied.

The results of peridynamic calculations are visualized in Figs. 14, 15 and 16. The generated curves consecutively present: the temporal plots for model elongation, stress and strain, as well as the hysteresis in the stress–strain and force–elongation coordinates. Figure 15 presents the plot of the strain rate to make the reference to its maximum allowed value, which is $0.00038\,\hbox {s}^{-1}$, as determined in Sect. 4.

Fig. 14

Temporal plots of the external force applied during simulated tension and the identified model elongation

Fig. 15

Temporal plots of stress, strain and strain rate for the peridynamic model of SMA. The plot of the strain rate is bounded by the allowed limits for isothermal phase transition, which is $\pm 0.038\% \,\hbox {s}^{-1}$

Fig. 16

Hysteretic response of the SMA model for the applied sinusoidal force

The elaborated peridynamic model allowed to investigate the superelasticity phenomenon in case of low-frequency and low-amplitude external force excitation in an SMA wire. Thanks to the performed change of the mechanical properties for the modeled SMA component—dealing with the resultant stiffness at most—control of the properties of the GFB structure is considered to be feasible.

Although a tiny amount of the dissipated energy $0.16\,\upmu \hbox {J}$ was identified in the modeled SMA wire for a single cycle of the hysteresis loop, the mentioned energy dissipation is expected to dramatically increase, in case when many pieces of SMA wires are spread circumferentially in the foils (as their structural parts) to control the behavior of GFB. The described application of SMA wires mounted in the structure of GFB is considered as a complementary passive solution with respect to the active methods applied to control the operational properties [67]. The choice made on both the SMA diameter and its initial tension may lead to the specific ranges of the reaction forces in GFB, at which the desired deformation of the order of micrometers and allowed energy dissipation may be achieved in the supporting structure.

The functionality of the investigated peridynamic model allows for simulation sub-loops within the hysteresis curve defying the material stress–strain relationship. It should be noted that the received results are in line with the recently reported outcomes, e.g., in [68]. In the referenced work, various shapes of internal sub-loops are found for incomplete processes of phase transformations. The idealized conditional piece-wise description is used to model the hysteresis effect which is observed under various external excitation, making use of numerical simulations.

The proposed peridynamic model of SMA is elaborated to address geometric discontinuities regarding the structural parts of the modeled GFB, which is in general an issue for other numerical approaches. Moreover, a nonlocal problem formulation used in peridynamics allows to properly model physical dispersion of the propagating waves, especially in case of limited number of DOFs in the spatial domain being discretized [14]. Finally, even though the planned elaboration of the peridynamic approach will allow to go beyond the limit of isothermal phase transitions, the preliminary results of the simulations carried out for GFB’s component are valuable due to the rigorous requirement regarding the temperature gradient in GFB that must be kept within specific limits of the order of several ${^{\circ }}\hbox {C}$ only [69].

8 Summary and final conclusions

The paper is devoted to the theory and applications for the proposed peridynamic model of SMA. The preliminary study deals with 1-D modeling and isothermal phase transitions, which is of the authors’ concern in the practical case study on the properties of nonlinear supporting structure in GFB. The mechanism of energy dissipation was studied via dynamic simulations. The model of an SMA wire exhibited the phenomenon of superelasticity, as demanded.

SMA undergoes unique phase transitions in the presence of mechanical and thermal loads. Hence, many practical applications of the phenomena observed in SMA are known, including the critical ones as in case of stents used in medicine. In contrast, there exist still significant deficiencies regarding understanding the physics of SMA as well as the theoretical descriptions of the observed effects. This inconveniences motivated the authors to propose a peridynamic model for SMA. The obtained results should be considered as a step toward more realistic modeling for SMA.

As reported in the paper, the two approaches were successfully used to develop the experimentally validated models of SMA. Namely, the Lagoudas and Auricchio theoretical contributions were employed to both build the peridynamic model and perform verification procedure. The elaborated peridynamic model of SMA was validated using the experimental data. The convergence regarding the hysteretic character of the stress–strain curves was achieved after parameterization of the model using the experimentally identified material properties. The considered conditions regarding the Clausius–Planck inequality led to the demanded nonlinear material behavior. As shown in the work, the superelasticity effect was properly modeled making use of the SMA model. The volumetric contributions of the martensite and austenite phases correctly follow the externally induced stress in the material.

The authors made an attempt of peridynamics application to SMA due to very specific properties of this modeling tool. The inherent nonlocality allows for more arbitrariness with respect to the properties of the modeled body, especially in terms of physical dispersion. Moreover, an integral-based problem formulation means that model discontinuities (material, geometric nonlinearities) may be relatively easily handled. The authors are aware of the existing deficiencies of the proposed modeling approach; therefore, future development of the peridynamic SMA model is scheduled to introduce all thermal-based components in the governing equation.