Transient dynamic analysis of cracked structures with multiple contact pairs using generalized HSNC

Abstract

The development of efficient computational methods for cracked structures is critical in the fields of civil, mechanical, and aerospace engineering since the influence of cracks on structural dynamics can play an important role in design, prognosis, and health monitoring. The nonlinearity caused by the intermittent contact on the crack surfaces typically excludes the use of fast linear methods, without which the computation of the dynamics of complex cracked structures becomes very challenging. In this paper, an efficient computational scheme for predicting both the transient and steady-state responses of cracked structures with multiple contact pairs is introduced. The new algorithm is referred to as the generalized hybrid symbolic–numeric computational (HSNC) method. The generalized HSNC method extends the original HSNC method, which was recently developed for bilinear systems, to general piecewise-linear nonlinear systems. This work also combines the HSNC with the $\hbox {X}-\hbox {X}_{r}$ method, a reduced-order modeling technique for cracked structures, to efficiently predict the dynamics of complex structures with cracks. The generalized HSNC approach is based on the idea that the nonlinear response of a cracked structure with multiple contact pairs can be obtained by combining linear responses of the system in each of its linear states. These linear responses can be symbolically expressed as functions of the initial conditions at starting time points in each time range where the system behaves linearly. The transition time where the system switches from one linear state to another is found using a nonlinear optimization solver with the initial values provided by an incremental search process. The method is able to individually track status of each contact pair; therefore, it can be used to predict the dynamics of the system when the crack surfaces are not completely open or closed. Moreover, both the transient and steady-state responses of complex cracked structures under various forcing conditions can be captured by the new method. The generalized HSNC method provides a flexible computational framework that is several orders of magnitude faster than traditional numerical integration methods. The dynamics of a spring–mass system and cantilever beam models that contain one crack and multiple cracks are investigated using the proposed method.

Appendices

Appendix A: Changing coordinates along crack surfaces

This appendix details how the local coordinates along the crack surfaces are defined and the transformation that is applied to the system matrices.

Fig. 19

Normal vector of the pth contact pair with $N_e^p=4$

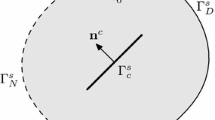
The normal vector of the pth contact pair schematically shown in Fig. 13 is defined as the mean norm of the vectors normal to the adjacent element surfaces [32]:

$$\begin{aligned} \mathbf{n}^{p} = \frac{\sum _{m=1}^{N_{e}^{p}}\mathbf{c}_{m}^{p}}{||\sum _{m=1}^{N_{e}^{p}}{} \mathbf{c}_{m}^{p}||}, \text {where }{} \mathbf{c}_{m}^{p} = \frac{\mathbf{a}_{1}^{m}\times \mathbf{a}_{2}^{m}}{||\mathbf{a}_{1}^{m}\times \mathbf{a}_{2}^{m}||}. \end{aligned}$$

(19)

Note that $\mathbf{a}_{1}^{m}$ and $\mathbf{a}_{2}^{m}$ are the vectors from the contacting node to its adjacent nodes on the mth element, and $N_{e}^{p}$ is the number of elements on the crack surfaces that share the contacting node. For example, $N_{e}^{p} = 4$ represents the case where the contacting node forms a vertex of four elements as shown in Fig. 13. The contact status of the pth contact pair is tracked along the $\mathbf{n}^{p}$ direction for $p=1 \cdots N_{p}$, where $N_{p}$ is the number of contact pairs in the structure.

Next, a coordinate transformation is applied such that the coordinates of the contacting nodes are aligned along the normal direction. The new local coordinates are defined using three mutually perpendicular unit vector $\mathbf{n}^{p}$, $\mathbf{t}_{1}^{p}$, and $\mathbf{t}_{2}^{p}$, where ($\mathbf{t}_{1}^{p}$, $\mathbf{t}_{2}^{p}$) is an arbitrary set of perpendicular unit vectors tangent to the contacting surface and perpendicular to $\mathbf{n}^{p}$. The coordinate transformation can be expressed as

$$\begin{aligned} \mathbf{x}_{c1}^{p}= & {} \mathbf{P}_{c}^{p}\hat{\mathbf{x}}_{c1}^{p},\nonumber \\ \mathbf{x}_{c2}^{p}= & {} \mathbf{P}_{c}^{p}\hat{\mathbf{x}}_{c2}^{p}, \end{aligned}$$

(20)

where $\mathbf{P}_{c}^{p} = \begin{bmatrix}{} \mathbf{n}^{p}&\mathbf{t}_{1}^{p}&\mathbf{t}_{2}^{p}\end{bmatrix}$. The transformation matrix can be assembled into the global form

$$\begin{aligned} \mathbf{x}= \begin{bmatrix} \mathbf{x}_{c1} \\ \mathbf{x}_{c2} \\ \mathbf{x}_{l} \end{bmatrix} = \begin{bmatrix} \mathbf{P}_{c}&\mathbf{0}&\mathbf{0}\\ \mathbf{0}&\mathbf{P}_{c}&\mathbf{0}\\ \mathbf{0}&\mathbf{0}&\mathbf{I} \end{bmatrix} \begin{bmatrix} \hat{\mathbf{x}}_{c1} \\ \hat{\mathbf{x}}_{c2} \\ \mathbf{x}_{l} \end{bmatrix} =\mathbf{P}{\hat{\mathbf{x}}}, \end{aligned}$$

(21)

where $\mathbf{P}_{c}$ is a block diagonal matrix with submatrices $\mathbf{P}_{c}^{p}$ on the diagonal. Applying this transformation to Eq. (4) yields

$$\begin{aligned}&\hat{\mathbf{M}}{\ddot{\hat{\mathbf{x}}}}(t)+\hat{\mathbf{C}}{\dot{\hat{\mathbf{x}}}}(t)+\hat{\mathbf{K}}{\hat{\mathbf{x}}}(t) = \hat{\mathbf{A}}_{0}^{*} \nonumber \\&\quad + \sum _{k=1}^{N_k}\big [{\hat{\mathbf{A}}}_{k}\cos (\alpha _{k}{t} + \tau _{k}) + {\hat{\mathbf{B}}}_{k}\sin (\alpha _{k}{t} + \tau _{k})\big ],\nonumber \\ \end{aligned}$$

(22)

where

$$\begin{aligned} \hat{\mathbf{M}}= & {} \mathbf{P}^{T}{} \mathbf{M}{} \mathbf{P} = \begin{bmatrix} \hat{\mathbf{M}}_{c1,c1}&\hat{\mathbf{M}}_{c1,c2}&\hat{\mathbf{M}}_{c1,l}\\ \hat{\mathbf{M}}_{c1,c2}^{T}&\hat{\mathbf{M}}_{c2,c2}&\hat{\mathbf{M}}_{c2,l}\\ \hat{\mathbf{M}}_{c1,l}^{T}&\hat{\mathbf{M}}_{c2,l}^{T}&\mathbf{M}_{l,l} \end{bmatrix},\nonumber \\ \hat{\mathbf{C}}= & {} \mathbf{P}^{T}{} \mathbf{C}{} \mathbf{P} = \begin{bmatrix} \hat{\mathbf{C}}_{c1,c1}&\hat{\mathbf{C}}_{c1,c2}&\hat{\mathbf{C}}_{c1,l}\\ \hat{\mathbf{C}}_{c1,c2}^{T}&\hat{\mathbf{C}}_{c2,c2}&\hat{\mathbf{C}}_{c2,l}\\ \hat{\mathbf{C}}_{c1,l}^{T}&\hat{\mathbf{C}}_{c2,l}^{T}&\mathbf{C}_{l,l} \end{bmatrix},\nonumber \\ \hat{\mathbf{K}}= & {} \mathbf{P}^{T}{} \mathbf{K}{} \mathbf{P} = \begin{bmatrix} \hat{\mathbf{K}}_{c1,c1}&\hat{\mathbf{K}}_{c1,c2}&\hat{\mathbf{K}}_{c1,l}\\ \hat{\mathbf{K}}_{c1,c2}^{T}&\hat{\mathbf{K}}_{c2,c2}&\hat{\mathbf{K}}_{c2,l}\\ \hat{\mathbf{K}}_{c1,l}^{T}&\hat{\mathbf{K}}_{c2,l}^{T}&\mathbf{K}_{l,l} \end{bmatrix},\nonumber \\ \hat{\mathbf{A}}_{0}^{*}= & {} \mathbf{P}^{T}{} \mathbf{A}_{0}^{*}, \nonumber \\ \hat{\mathbf{A}}_{k}= & {} \mathbf{P}^{T}{} \mathbf{A}_{k}, \nonumber \\ \hat{\mathbf{B}}_{k}= & {} \mathbf{P}^{T}{} \mathbf{B}_{k}. \end{aligned}$$

(23)

The submatrices of $\hat{\mathbf{M}}$ in Eq. (23) can be expressed as

$$\begin{aligned} \hat{\mathbf{M}}_{c1,c1}= & {} \mathbf{P}_{c}^{T}{} \mathbf{M}_{c1,c1} \mathbf{P}_{c}, \nonumber \\ \hat{\mathbf{M}}_{c1,c2}= & {} \mathbf{P}_{c}^{T}{} \mathbf{M}_{c1,c2} \mathbf{P}_{c}, \nonumber \\ \hat{\mathbf{M}}_{c1,l}= & {} \mathbf{P}_{c}^{T}{} \mathbf{M}_{c1,l}, \nonumber \\ \hat{\mathbf{M}}_{c2,c2}= & {} \mathbf{P}_{c}^{T}{} \mathbf{M}_{c2,c2} \mathbf{P}_{c}, \nonumber \\ \hat{\mathbf{M}}_{c2,l}= & {} \mathbf{P}_{c}^{T}{} \mathbf{M}_{c2,l}. \end{aligned}$$

(24)

Note that $\hat{\mathbf{C}}$ and $\hat{\mathbf{K}}$ have the same expressions in their submatrices.

Appendix B: $\hbox {X}-\hbox {X}_{r}$ reduction method

This appendix discusses the creation of a ROM of a cracked structure using the $\hbox {X}-\hbox {X}_r$ method and CB-CMS [28]. First, the relative coordinate transformation is performed

$$\begin{aligned} \hat{\mathbf{x}}= & {} \begin{bmatrix} \hat{\mathbf{x}}_{c1} \\ \hat{\mathbf{x}}_{c2} \\ \mathbf{x}_{l} \end{bmatrix} ={{\varvec{\alpha }}} \begin{bmatrix} \hat{\mathbf{x}}_{r} \\ \hat{\mathbf{x}}_{c2} \\ \mathbf{x}_{l} \end{bmatrix} ={{\varvec{\alpha }}} \begin{bmatrix} \hat{\mathbf{x}}_{r} \\ \mathbf{x}_{h} \end{bmatrix} ={{\varvec{\alpha }}}{\overline{\mathbf{x}}},\nonumber \\&\text {where } {{\varvec{\alpha }}} = \begin{bmatrix} \mathbf{I}&\mathbf{I}&\mathbf{0}\\ \mathbf{0}&\mathbf{I}&\mathbf{0}\\ \mathbf{0}&\mathbf{0}&\mathbf{I} \end{bmatrix}. \end{aligned}$$

(25)

Note that $\hat{\mathbf{x}}_{r} = \hat{\mathbf{x}}_{c1} - \hat{\mathbf{x}}_{c2}$ represents the relative displacement between the contact pairs and $\mathbf{x}_{h}$ = $[\hat{\mathbf{x}}^{T}_{c2},\mathbf{x}^{T}_{l}]^{T}$ represents the coordinates of the healthy structure (i.e., the structure where the crack does not exist). A new set of equations of motion can be obtained by applying the transformation to Eq. (22)

$$\begin{aligned}&\overline{\mathbf{M}}{\ddot{\overline{\mathbf{x}}}}(t) + \overline{\mathbf{C}}{\dot{\overline{\mathbf{x}}}}(t)+\overline{\mathbf{K}}{\overline{\mathbf{x}}}(t) = \overline{\mathbf{A}}_{0}^{*}\nonumber \\&\quad + \sum _{k=1}^{N_k}\big [{\overline{\mathbf{A}}}_{k}\cos (\alpha _{k}{t} + \tau _{k}) + {\overline{\mathbf{B}}}_{k}\sin (\alpha _{k}{t} + \tau _{k})\big ], \end{aligned}$$

(26)

where

$$\begin{aligned} \overline{\mathbf{M}}= & {} {{\varvec{\alpha }}}^{T}\hat{\mathbf{M}}{{\varvec{\alpha }}} = \begin{bmatrix} \overline{\mathbf{M}}_{{\mathbf{x}_{r}}}&\overline{\mathbf{M}}_{{{\mathbf{x}_{r}},{\mathbf{x}_{h}}}}\\ \overline{\mathbf{M}}_{{{\mathbf{x}_{r}},{\mathbf{x}_{h}}}}^{T}&\overline{\mathbf{M}}_{{\mathbf{x}_{h}}} \end{bmatrix},\nonumber \\ \overline{\mathbf{C}}= & {} {{\varvec{\alpha }}}^{T}\hat{\mathbf{C}}{{\varvec{\alpha }}} = \begin{bmatrix} \overline{\mathbf{C}}_{{\mathbf{x}_{r}}}&\overline{\mathbf{C}}_{{{\mathbf{x}_{r}},{\mathbf{x}_{h}}}}\\ \overline{\mathbf{C}}_{{{\mathbf{x}_{r}},{\mathbf{x}_{h}}}}^{T}&\overline{\mathbf{C}}_{{\mathbf{x}_{h}}} \end{bmatrix},\nonumber \\ \overline{\mathbf{K}}= & {} {{\varvec{\alpha }}}^{T}\hat{\mathbf{K}}{{\varvec{\alpha }}} = \begin{bmatrix} \overline{\mathbf{K}}_{{\mathbf{x}_{r}}}&\overline{\mathbf{K}}_{{{\mathbf{x}_{r}},{\mathbf{x}_{h}}}}\\ \overline{\mathbf{K}}_{{{\mathbf{x}_{r}},{\mathbf{x}_{h}}}}^{T}&\overline{\mathbf{K}}_{{\mathbf{x}_{h}}} \end{bmatrix},\nonumber \\ \overline{\mathbf{A}}_{0}^{*}= & {} {{\varvec{\alpha }}}^{T}\hat{\mathbf{A}}_{0}^{*}, \nonumber \\ \overline{\mathbf{A}}_{k}= & {} {{\varvec{\alpha }}}^{T}\hat{\mathbf{A}}_{k}, \nonumber \\ \overline{\mathbf{B}}_{k}= & {} {{\varvec{\alpha }}}^{T}\hat{\mathbf{B}}_{k}. \end{aligned}$$

(27)

Specific expressions for the submatrices of $\overline{\mathbf{M}}$ in Eq. (27) can be expressed as

$$\begin{aligned}&\overline{\mathbf{M}}_{{\mathbf{x}_{r}}} = \hat{\mathbf{M}}_{c1,c1},\nonumber \\&\overline{\mathbf{M}}_{{{\mathbf{x}_{r}}{\mathbf{x}_{h}}}} = \begin{bmatrix} \hat{\mathbf{M}}_{c1,c1}+\hat{\mathbf{M}}_{c1,c2}~~~&\hat{\mathbf{M}}_{c1,l} \end{bmatrix},\nonumber \\&\overline{\mathbf{M}}_{{\mathbf{x}_{h}}} = \begin{bmatrix} \hat{\mathbf{M}}_{c1,c1}+\hat{\mathbf{M}}_{c1,c2}^{T}+\hat{\mathbf{M}}_{c1,c2}+\hat{\mathbf{M}}_{c2,c2}~&\hat{\mathbf{M}}_{c1,l}+\hat{\mathbf{M}}_{c2,l}\\ \hat{\mathbf{M}}_{c1,l}^{T}+\hat{\mathbf{M}}_{c2,l}^{T}~~~&\mathbf{M}_{l,l} \end{bmatrix}.\nonumber \\ \end{aligned}$$

(28)

Note that $\overline{\mathbf{C}}$ and $\overline{\mathbf{K}}$ have the same expressions in their submatrices.

Next, the CB-CMS method is used to reduce the model size by reducing all the DOFs in $\mathbf{x}_{h}$ using a truncated set of normal modes. The Craig–Bampton transformation matrix ${{\varvec{\beta }}}$ can be expressed as

$$\begin{aligned} {{\varvec{\beta }}} = \begin{bmatrix} \mathbf{I}&\mathbf{0}\\ {{\varvec{\Psi }}}_{c}&{{\varvec{\Phi }}}_{n}\\ \end{bmatrix}, \end{aligned}$$

(29)

where ${{\varvec{\Psi }}_{c}}$ includes the constraint modes and ${{\varvec{\Phi }}}_{n}$ includes the fixed interface normal modes of the healthy structure. The constraint modes are a set of static displacements of the DOFs in $\mathbf{x}_{h}$ that can be calculated by enforcing successive unit displacements of each relative DOF in $\mathbf{x}_{r}$ while keeping all other relative DOFs fixed. The normal modes can be obtained by solving for the eigenvectors of ($\overline{\mathbf{K}}_{\mathbf{x}_{h}}$, $\overline{\mathbf{M}}_{\mathbf{x}_{h}}$). The model size is reduced by truncating the normal modes over the frequency range of interest. The coordinates are reduced using the Craig–Bampton transformation

$$\begin{aligned} \overline{\mathbf{x}}= \begin{bmatrix} \hat{\mathbf{x}}_{r} \\ \mathbf{x}_{h} \end{bmatrix} ={{\varvec{\beta }}} \begin{bmatrix} \hat{\mathbf{x}}_{r} \\ {{\varvec{\eta }}} \end{bmatrix} ={{\varvec{\beta }}}{} \mathbf{u}, \end{aligned}$$

(30)

where all the contacting DOFs $\hat{\mathbf{x}}_{r}$ are kept active in the reduced coordinate system $\mathbf{u}$. The equations of motion can also be reduced to

$$\begin{aligned}&\mathbf{M}_{\mathrm{ROM}}{\ddot{\mathbf{u}}}(t) + \mathbf{C}_{\mathrm{ROM}}{\dot{\mathbf{u}}}(t) + \mathbf{K}_{\mathrm{ROM}}{\mathbf{u}}(t) = \mathbf{A}_{\mathrm{ROM},0}^{*} \nonumber \\&\quad + \sum _{k=1}^{N_k}\big [{\mathbf{A}}_{\mathrm{ROM},k}\cos (\alpha _{k}{t} + \tau _{k})\nonumber \\&\quad +\, {\mathbf{B}}_{\mathrm{ROM},k}\sin (\alpha _{k}{t} + \tau _{k})\big ], \end{aligned}$$

(31)

where

$$\begin{aligned} \mathbf{M}_{\mathrm{ROM}}= & {} {{\varvec{\beta }}}^{T}\overline{\mathbf{M}}{{\varvec{\beta }}} = \begin{bmatrix} {\mathbf{M}}_{\mathbf{x}_{r}}&{\mathbf{M}}_{\mathbf{x}_{r},{{\varvec{\eta }}}}\\ {\mathbf{M}}_{\mathbf{x}_{r},{{\varvec{\eta }}}}^{T}&{\mathbf{M}}_{{\varvec{\eta }}} \end{bmatrix}, \nonumber \\ \mathbf{C}_{\mathrm{ROM}}= & {} {{\varvec{\beta }}}^{T}\overline{\mathbf{C}}{{\varvec{\beta }}} = \begin{bmatrix} {\mathbf{C}}_{\mathbf{x}_{r}}&{\mathbf{C}}_{\mathbf{x}_{r},{{\varvec{\eta }}}}\\ {\mathbf{C}}_{\mathbf{x}_{r},{{\varvec{\eta }}}}^{T}&{\mathbf{C}}_{{\varvec{\eta }}} \end{bmatrix}, \nonumber \\ \mathbf{K}_{\mathrm{ROM}}= & {} {{\varvec{\beta }}}^{T}\overline{\mathbf{K}}{{\varvec{\beta }}} = \begin{bmatrix} {\mathbf{K}}_{\mathbf{x}_{r}}&{\mathbf{K}}_{\mathbf{x}_{r},{{\varvec{\eta }}}}\\ {\mathbf{K}}_{\mathbf{x}_{r},{{\varvec{\eta }}}}^{T}&{\mathbf{K}}_{{\varvec{\eta }}} \end{bmatrix}, \nonumber \\ \mathbf{A}_{\mathrm{ROM},0}^{*}= & {} {{\varvec{\beta }}}^{T}\overline{\mathbf{A}}_{0}^{*}, \nonumber \\ \mathbf{A}_{\mathrm{ROM},k}= & {} {{\varvec{\beta }}}^{T}\overline{\mathbf{A}}_{k}, \nonumber \\ \mathbf{B}_{\mathrm{ROM},k}= & {} {{\varvec{\beta }}}^{T}\overline{\mathbf{B}}_{k}. \end{aligned}$$

(32)

The explicit expressions for the submatrices of $\mathbf{M}_{\mathrm{ROM}}$ in Eq. (32) can be expressed as

$$\begin{aligned}&{\mathbf{M}}_{\mathbf{x}_{r}} = \overline{\mathbf{M}}_{{\mathbf{x}_{r}}} + {{\varvec{\Psi }}}_{c}^{T}\overline{\mathbf{M}}_{{{\mathbf{x}_{r}},{\mathbf{x}_{h}}}}^{T}+ \overline{\mathbf{M}}_{{{\mathbf{x}_{r}},{\mathbf{x}_{h}}}}{{\varvec{\Psi }}}_{c}+{{\varvec{\Psi }}}_{c}^{T}\overline{\mathbf{M}}_{{\mathbf{x}_{h}}}{{\varvec{\Psi }}}_{c},\nonumber \\&{\mathbf{M}}_{{\mathbf{x}_{r}},{{\varvec{\eta }}}}=\overline{\mathbf{M}}_{{{\mathbf{x}_{r}},{\mathbf{x}_{h}}}}{{\varvec{\Phi }}}_{n}+{{\varvec{\Psi }}}_{c}^{T}\overline{\mathbf{M}}_{{\mathbf{x}_{h}}}{{\varvec{\Phi }}}_{n},\nonumber \\&{\mathbf{M}}_{{\varvec{\eta }}} = {{\varvec{\Phi }}}_{n}^{T}\overline{\mathbf{M}}_{{\mathbf{x}_{h}}}{{\varvec{\Phi }}}_{n}. \end{aligned}$$

(33)

Note that $\mathbf{C}_{\mathrm{ROM}}$ and $\mathbf{K}_{\mathrm{ROM}}$ have the same expressions in their submatrices. Moreover, ${\mathbf{M}}_{{\varvec{\eta }}} = {{\varvec{\Phi }}}_{n}^{T}\overline{\mathbf{M}}_{{\mathbf{x}_{h}}}{{\varvec{\Phi }}}_{n} = \mathbf{I}$ and ${\mathbf{K}}_{{\varvec{\eta }}} = {{\varvec{\Phi }}}_{n}^{T}\overline{\mathbf{K}}_{{\mathbf{x}_{h}}}{{\varvec{\Phi }}}_{n} = {{\varvec{\Lambda }}}$, where ${{\varvec{\Lambda }}}$ is the eigenvalue matrix of the healthy structure.

Appendix C: Expressions for modal responses

This appendix gives the solutions for the ordinary differential equation given in Eq. (15) subject to known initial conditions, for both underdamped and overdamped modes.

For underdamped modes, the modal response can be written as

$$\begin{aligned} {q}_{j}^{i}(t)= & {} {D}_{j}^{i} e^{-\zeta _{j}^{i} \omega _{j}^{i}t}\sin (\omega _{d,j}^{i}{t}+{\psi }_{j}^{i})\nonumber \\&+ \sum _{k=1}^{N_k}\big [{X}_{k,j}^{i}{\cos ({\alpha }_{k}{t} + {\tau }_{k}^{i} - {\theta }_{k,j}^{i})}\nonumber \\&+ {Y}_{k,j}^{i}{\sin ({\alpha }_{k}{t} + {\tau }_{k}^{i} - {\theta }_{k,j}^{i})}\big ], \end{aligned}$$

(34)

where $\omega _{d,j}^{i}$ is the damped frequency corresponding to the natural frequency $\omega _{j}^{i}$; $\theta _{k,j}^{i}=\tan ^{-1}\Big [\frac{2\zeta _{j}^{i} \omega _{j}^{i} {\alpha }_{k}}{({\omega }_{j}^{i})^2-{\alpha }_{k}^2}\Big ]$; ${X}_{k,j}^{i}= \frac{G_{k,j}^{i}}{\root \of {[({\omega }_{k,j}^{i})^2 - {\alpha }_{k}^2]^2+(2\zeta _{j}^{i} \omega _{j}^{i} {\alpha }_{k})^2}}$ and ${Y}_{k,j}^{i}= \frac{H_{k,j}^{i}}{\root \of {[({\omega }_{k,j}^{i})^2 - {\alpha }_{k}^2]^2+(2\zeta _{j}^{i} \omega _{j}^{i} {\alpha }_{k})^2}}$ are the steady-state amplitudes; ${D}_{j}^{i}$ is the transient response amplitude; and ${\psi }_{j}^{i}$ is the phase angle of the transient response. Note that ${D}_{j}^{i}$ and ${\psi }_{j}^{i}$ depend on the initial modal positions ${q}_{0,j}^{i}$ and velocity $\dot{q}_{0,j}^{i}$ that can be calculated using

$$\begin{aligned} {q}_{0,j}^{i}= & {} ({{\varvec{\Phi }}}_{j}^{i})^{T}{} \mathbf{M}_{\mathrm{ROM}}({\tilde{\mathbf{u}}}_{0}^{i} - {\varvec{\delta }}^{i}),\nonumber \\ \dot{q}_{0,j}^{i}= & {} ({{\varvec{\Phi }}}_{j}^{i})^{T}\mathbf{M}_{\mathrm{ROM}}{\dot{\tilde{\mathbf{u}}}}{_{0}^{i}}. \end{aligned}$$

(35)

The explicit expressions for ${D}_{j}^{i}$ and ${\psi }_{j}^{i}$ can be obtained by enforcing the initial conditions in Eq. (34) and its derivative, namely,

$$\begin{aligned} {q}_{j}^{i}(0)= & {} {q}_{0,j}^{i}, \nonumber \\ \dot{q}_{j}^{i}(0)= & {} \dot{q}_{0,j}^{i}. \end{aligned}$$

(36)

These transient parameters can be expressed as

$$\begin{aligned} {\psi }_{j}^{i}= & {} \tan ^{-1}\bigg \{{{\omega }_{d,j}^{i}\Big [{q_{0,j}^{i} - \sum _{k=1}^{N}(X_{k,j}^{i}{{\mathbb {C}}}_{k,j}^{i} + Y_{k,j}^{i}{{\mathbb {S}}}_{k,j}^{i})}\Big ]}\Big / \nonumber \\&\Big [{{\dot{q}}_{0,j}^{i} + {q}_{0,j}^{i}{\zeta }_{j}^{i}{\omega }_{j}^{i} - {\sum _{k=1}^{N}}\Big (({\zeta }_{j}^{i}{\omega }_{j}^{i}{X_{k,j}^{i}} + {\alpha }_{k}{Y_{k,j}^{i}}){{\mathbb {C}}}_{k,j}^{i}}\nonumber \\&+ {({\zeta }_{j}^{i}{\omega }_{j}^{i}{Y_{k,j}^{i}} - {\alpha }_{k}{X_{k,j}^{i}}){{\mathbb {S}}}_{k,j}^{i}\Big )}\Big ]\bigg \}\nonumber \\ {D}_{j}^{i}= & {} \frac{{q}_{0,j}^{i} - \sum _{k=1}^{N}(X_{k,j}^{i}{{\mathbb {C}}}_{k,j}^{i} + Y_{k,j}^{i}{{\mathbb {S}}}_{k,j}^{i})}{\sin {\psi }_{j}^{i}}, \end{aligned}$$

(37)

where

$$\begin{aligned} {{\mathbb {C}}}_{k,j}^{i}= & {} \cos ({\tau }_{k}^{i} - {\theta }_{k,j}^{i}),\nonumber \\ {{\mathbb {S}}}_{k,j}^{i}= & {} \sin ({\tau }_{k}^{i} - {\theta }_{k,j}^{i}). \end{aligned}$$

(38)

For overdamped modes, the modal response can be expressed as

$$\begin{aligned} {q}_{j}^{i}(t)= & {} {E}_{1,j}^{i} e^{s_{1,j}^{i}t} + {E}_{2,j}^{i} e^{s_{2,j}^{i}t} \nonumber \\&+ \sum _{k=1}^{N_k}\big [{X}_{k,j}^{i}{\cos ({\alpha }_{k}{t} + {\tau }_{k}^{i} - {\theta }_{k,j}^{i})}\nonumber \\&+\, {Y}_{k,j}^{i}{\sin ({\alpha }_{k}{t} + {\tau }_{k}^{i} - {\theta }_{k,j}^{i})}\big ], \end{aligned}$$

(39)

where ${s_{1,j}^{i}}$ and ${s_{2,j}^{i}}$ are the roots of the characteristic polynomial of the system that can be expressed as ${s_{1,j}^{i}} = {\omega }_{j}^{i}\big [-\zeta _{j}^{i} +\root \of {({\zeta _{j}^{i}})^2-1}\big ]$ and ${s_{2,j}^{i}} = {\omega }_{j}^{i}\big [-\zeta _{j}^{i} -\root \of {({\zeta _{j}^{i}})^2-1}\big ]$, respectively. ${E}_{1,j}^{i}$ and ${E}_{2,j}^{i}$ are the transient response amplitudes that can also be obtained by enforcing the initial conditions in Eq. (39) and its derivative. These parameters can be expressed as

$$\begin{aligned} {E}_{1,j}^{i}= & {} \frac{-s_{2,j}^{i}{q_{0,j}^{i}} + \dot{q}_{0,j}^{i}}{s_{1,j}^{i} - s_{2,j}^{i}}\nonumber \\&+ \frac{1}{s_{1,j}^{i} - s_{2,j}^{i}} \Bigg \{ {\sum _{k=1}^{N_k}} \big [{\alpha }_{k}({{X}_{k,j}^{i}} {{{\mathbb {S}}}_{k,j}^{i}} - {{Y}_{k,j}^{i}} {{{\mathbb {C}}}_{k,j}^{i}})\big ]\nonumber \\&+\,s_{2,j}^{i} {\sum _{k=1}^{N_k}} ({{X}_{k,j}^{i}} {{{\mathbb {C}}}_{k,j}^{i}} + {{Y}_{k,j}^{i}} {{{\mathbb {S}}}_{k,j}^{i}}) \Bigg \}, \nonumber \\ {E}_{2,j}^{i}= & {} \frac{s_{1,j}^{i}{q_{0,j}^{i}} - \dot{q}_{0,j}^{i}}{s_{1,j}^{i} - s_{2,j}^{i}}\nonumber \\&- \frac{1}{s_{1,j}^{i} - s_{2,j}^{i}} \Bigg \{ {\sum _{k=1}^{N_k}} \big [{\alpha }_{k}({{X}_{k,j}^{i}} {{{\mathbb {S}}}_{k,j}^{i}} - {{Y}_{k,j}^{i}} {{{\mathbb {C}}}_{k,j}^{i}})\big ]\nonumber \\&+\,s_{1,j}^{i} {\sum _{k=1}^{N_k}} ({{X}_{k,j}^{i}} {{{\mathbb {C}}}_{k,j}^{i}} + {{Y}_{k,j}^{i}} {{{\mathbb {S}}}_{k,j}^{i}}) \Bigg \}. \end{aligned}$$

(40)