1 Introduction

Since the pioneering work by Geniet and Léon [1] on the energy transmission in a nonlinear medium by a periodic driven boundary whose period falls inside a forbidden band gap of the medium, the study of supratransmission in nonlinear systems has attracted considerable theoretical and experimental interest. At the birth, the nonlinear supratransmission provides an understanding of the mechanism of the generation of gap solitons in photonic band-gap materials [2,3,4]. Nowadays as a universal phenomenon, it finds direct application: in nonlinear arrays as a weak signal detector [5, 6]; in a birefringent quadratic medium to degenerate three-wave resonant interaction [7, 8]; in mechanical systems of coupled oscillators and discrete Josephson-junction arrays to the propagation of binary signals [9,10,11]; in finite granular chains to study the bifurcations [12]; in Sine-Gordon chains [13,14,15]; in systems having multi-stable elements to the energy transport [16]; in electrical lattice for the propagation of signals [17,18,19,20,21,22,23]; in Fermi–Pasta–Ulam chains with near and different ranges of interactions [24,25,26]; in Riesz space-fractional Josephson transmission lines and sine-Gordon systems [27,28,29]; in saturable medias [30, 31].

The knowledge of the threshold amplitude is important in supratransmission process. In addition to the analytical thresholds obtained using a continuous approximation, several techniques have been proposed, including saddle node bifurcation [31, 32] and homoclinic orbit approach [33]. The latter approach is useful for the systems where the discreteness appears as an effect of weak or strong interaction between separated elements and allow to understand certain disagreement between numerical and analytical thresholds found using a continuous approximation for the higher frequency.

Beside the natural gap transmission which consists of choosing the driving amplitude above the supratransmission threshold, Togueu Motcheyo et al. [23] had proposed a way to generate nonlinear supratransmission phenomenon using collision between two plane waves. This way works very well for the mechanism of amplification of phonons by phonons in anharmonic oscillator ladder [34], in the chain of coupled cantilever arrays [35] and to the generation of the magnetic soliton [36]. Another way is the soliton creation from resonantly excited localized waves [37].

Up to now, the legacy of the supratransmission phenomenon is the generation of the train of bright solitons by the lattice submitted to a time-periodic driving plane wave. However, dark soliton which has also drawn considerable interest in recent years is not yet generated by supratransmission way in our knowledge. This work is mainly concerned by the construction of a train of dark solitons by nonlinear gap transmission way. Additionally, to the best of our knowledge, there is no report yet on the nonlinear band-gap transmission in the lattice with cubic–quintic nonlinearity. Another aspect of this work investigated the condition for the occurrence of nonlinear supratransmission in the latter mentioned lattice.

The outline of the work is the following: In Sect. 2, we introduce the model and derive the phonon band. In Sect. 3, we derive the homoclinic gap threshold of the discrete nonlinear Schrödinger equation. In Sect. 4, we perform the full integration of the equation and found different solutions. Section 5 concludes the work.

2 Model description

Before explaining the phenomena, building the model and investigating the physical meaning of the equation are necessary for comprehensive understanding. The model considered in this work is a system with weak interaction between separated elements described by the following discrete nonlinear Schrödinger (DNLS) equation with cubic–quintic on-site nonlinearity [38,39,40,41,42]

$$\begin{aligned}&i\frac{\mathrm{d} b_{n}}{\mathrm{d}z}+C(b_{n+1}+b_{n-1})+ \gamma \mid b_{n}\mid ^{2}b_{n}\nonumber \\&\quad +\,\nu \mid b_{n}\mid ^{4}b_{n}=0. \end{aligned}$$
(1)

Here C is the positive coupling constant, and \(\gamma \) and \(\nu \) are the constants of cubic and quintic on-site nonlinearities, respectively. In the case of the optical waveguide arrays, \(b_{n}\) is the electromagnetic wave amplitude in the nth guiding core and z the propagation variable. The cubic–quintic nonlinearity can be obtained via the expansion of the saturable nonlinearity in the waveguide (see [39]). This leads to focusing cubic term (\(\gamma >0\)) and the defocusing quintic nonlinearity (\(\nu <0\)). Both nonlinearities are competitive [40]. The criteria for experimental determination of self-focusing cubic and defocusing constants in the continuum media have been addressed in [43].

In the BECs loaded into a deep optical lattice, \(b_{n}\) is the wave function and the dynamical variable is time. However, the cubic and quintic nonlinearities occur due to the two- and three-body interactions, respectively. Of course, the DNLS equation is obtained after applying the tight-binding approximation and using Wannier functions on the Gross–Pitaevskii (GP) equation (see Refs. [44, 45] for the cubic DNLS equation). \(\gamma \) can be positive (negative) in case of attractive (repulsive) interparticle interactions [46]. For rubidium atoms, the three-body interactions is attractive (\(\nu >0\)) [47, 48]. In the nonlinear Eq. (1), we will focus our study on two cases: cooperative cubic and quintic nonlinearities; competitive nonlinearities.

The important feature of the supratransmission phenomenon is highlighted after recognizing the forbidden bands in the dispersion relation. For infinitesimal amplitude waves, the dispersion relation can be obtained analytically by neglecting the nonlinear terms in the equation of motion and solving for a harmonic discrete solution in the form \(b_{n}=\exp i(kn -\varDelta z)\), where \(\varDelta \) and k are the angular frequency and the wave number. By replacing this solution in the linearized Eq. (1), we obtain the phonon spectrum given by the following linear dispersion law

$$\begin{aligned} \varDelta =-2C\cos (k). \end{aligned}$$
(2)

From this linear dispersion, it appears the linear phonon band \(-2C\le \varDelta \le 2C\) and two forbidden bands outward of the allowed linear wave band given by \(\varDelta <-2C\) and \(\varDelta >2C\). After recognizing the forbidden linear band, we have to find the nonlinear supratransmission threshold of Eq. (1). As the lattice is discrete, we will follow the way proposed by Togueu Motcheyo et al. [33] for the strongly discrete systems.

3 Homoclinic nonlinear band-gap threshold

As the homoclinic nonlinear band-gap threshold is based on the two-dimensional (2D) map approach [33] (which is different to small Hamiltonian perturbation of a Hamiltonian system [49]), to find it, let us follow Refs. [50,51,52,53,54,55,56,57,58] to construct homoclinic manifolds. The starting point is the analysis of the following stationary modes of Eq. (1)

$$\begin{aligned} -\varDelta x_{n}+C(x_{n+1}+x_{n-1})+ \gamma x_{n}^{3}+\nu x_{n}^{5}=0, \end{aligned}$$
(3)

obtained by inserting the ansatz of the stationary solutions in the usual form \(b_{n}=x_{n}\exp (i\varDelta z)\) into Eq. (1). \(\varDelta \) is a driven frequency, and \(x_{n}\) a real stationary function. If we now define \(y_{n}=x_{n-1}\), the mapping (3) takes the 2D form given by:

$$\begin{aligned} x_{n+1}=\frac{1}{C}\left[ \varDelta x_{n}-\gamma x_{n}^{3}-\nu x_{n}^{5}\right] - y_{n},\quad y_{n+1}=x_{n}.\nonumber \\ \end{aligned}$$
(4)

The most straightforward orbit that can be described by the 2D map approach is a fixed point. As the fixed points of the map (4) are in the function of the cooperativity and competition of the cubic–quintic nonlinearity, let us consider the following cases:

3.1 Model with self-focusing cubic and quintic nonlinearities (\(\gamma >0\), \(\nu >0\))

The fixed points of the map (4) corresponding to the cooperative cubic–quintic nonlinearity are located at:

$$\begin{aligned} x_{0}=0;\quad x_{1\pm }=\displaystyle \pm \sqrt{\frac{-\gamma +\sqrt{\gamma ^{2}+4\nu (\varDelta -2C)}}{2\nu }}; \end{aligned}$$
(5)

where the last two exist only if \(\varDelta >2C\). As we are interested in the upper forbidden gap (\(\varDelta >2C\)), all the above fixed point exist. The model has three fixed points as in the case of cubic DNLS, saturable DNLS and Salerno equation [50,51,52,53,54,55,56,57,58] and implies the existence of the same type of orbits. The way to construct the orbits of the map (4) has been addressed several times during the previous years (see [40, 50,51,52,53,54,55,56,57,58,59]). Let us consider \(B_\mathrm{thr}\) the supratransmission threshold emanating from the homoclinic connection. We depict in Fig. 1 the influence of self-focusing quintic (\(\nu >0\)) on \(B_\mathrm{thr}\) for constant self-focusing cubic nonlinearity (\(\gamma =2\)), \(\varDelta =2.04\) and \(C=1\). One can observe that \(B_\mathrm{thr}\) decreases as \(\nu \) increases. This implies that the amplitude slightly above the threshold in the case of cubic DNLS equation (\(\nu =0\)) which achieves a good supratransmission can be a large amplitude in the case of CQ-DNLS and probably induces trapping of moving gap soliton by the lattice. The numerical integration of Eq. (1) in the section below can give the exact behaviors of the wave.

Fig. 1
figure 1

Dependence of the homoclinic driving threshold according to the self-focusing quintic nonlinearity for \(\gamma =2\), \(\varDelta =2.04\) and \(C = 1\)

Full size image

3.2 Model with self-focusing cubic and defocusing quintic nonlinearities (\(\gamma >0\), \(\nu <0\))

The fixed points of the map (4) in case of the self-focusing cubic and defocusing quintic nonlinearities are located at:

$$\begin{aligned} x_{0}=0;\quad x_{2\pm \pm }=\displaystyle \pm \sqrt{\frac{\gamma \pm \sqrt{\gamma ^{2}-4\nu (2C-\varDelta )}}{-2\nu }}; \end{aligned}$$
(6)

where the last four exist only if \(\varDelta <2C-\displaystyle \frac{\gamma ^{2}}{4\nu }\). Within the forbidden gap, \(\varDelta >2C\); then to obtain five fixed points with the frequency in the gap, the following condition shall be verified: \(2C<\varDelta <2C-\displaystyle \frac{\gamma ^{2}}{4\nu }\). Contrary to the cooperative CQ-DNLS, there exist the extra set of fixed points in the competitive CQ-DNLS model. Those extra set of fixed points can support heteroclinic orbits which do not exist in the cooperative model above and the cubic DNLS model study in [33]. The stability of the fixed points has been performed in [40].

Fig. 2
figure 2

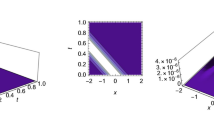
Homoclinic connection of the 2D map (4) for \(\gamma =2\)\(\nu =-2\), \(\varDelta =2.04\) and \(C = 1\). The inset shows the zoom of the homoclinic orbit started at the fixed point \(x=0\)

Full size image

In Fig. 2, we depict homoclinic and heteroclinic orbits emanating from the saddle points. One can see in the inset the turning point of the homoclinic orbit equal to 0.2. As predicted in [33], this value is the threshold of generation of the train of bright solitons in the upper forbidden gap by the plane wave. From the heteroclinic orbit of the 2D map, one can derive dark soliton (see [57]). Also, the tails of the dark soliton cannot be large than the value of the fixed point that supports heteroclinic orbit. Can the value of the latest mentioned fixed points be the threshold of the generation of dark soliton by the supratransmission way? If so, what is the behavior of the lattice with driving amplitude between the value of the first turning point of the homoclinic orbit and the fixed point that supports heteroclinic orbit? The numerical integration of driven Eq. (1) shall give more information.

4 Numerical experiment

This section is devoted to the numerical integration of DNLS equation (1) submitted to the boundary driving \(b_{0}=B\exp (i\varDelta z)\). \(\varDelta \) and B are the driving frequency and amplitude of the boundary, respectively. The initial shocks shall be avoided by increasing smoothly the driving amplitude from 0 to the constant value B (see [5]). To understand how the quintic coefficient of Eq. (1) affects the full integration, we will consider two cases as for the study of the homoclinic thresholds above.

Fig. 3
figure 3

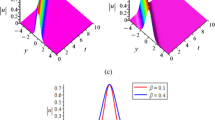
Space–time evolution of a typical numerical simulation of the boundary-driven DNLS equation (1) for \(C = 1\) , \(\varDelta =2.04\), \(B=0.22\), \(\gamma =2\) and different values of \(\nu \). For relatively large quintic coefficient, the gap wave is trapped by a site

Full size image

4.1 Model with self-focusing cubic and quintic nonlinearities (\(\gamma >0\), \(\nu >0\))

In Fig. 3, the intensity of the wave of the driven Eq. (1) as a function of the quintic coefficient is plotted with the driving amplitude and frequency given by \(B=0.22\) and \(\varDelta =2.04\), respectively. The cubic coefficient is constant and equal to 2. In the case of the cubic DNLS (\(\nu =0\)), as the frequency is the band gap and the amplitude is slightly above the threshold, an energy flows in the lattice naturally (see Refs. [5, 33]). When the self-focusing quintic nonlinear term increases, an energy also flows in the lattice, but the transmission of discrete nonlinear band-gap wave is suppressed. For example, if \(\nu =0.44\), one can see the merging of discrete band-gap waves generated and then a localization in space. This corresponds to the large amplitude of the cubic DNLS equation [5], but the difference here is that the trapping of the waves is not only done in the first sites. As in the case of the mobility of discrete soliton [38], one can say that discrete band-gap waves overcome the potential barriers for the first sites, loses the energy through radiation before trapped or rebounded. It is important to underline the fact that the train of waves generated here is different from multi-soliton [60].

For the relatively large quintic term (\(\nu =1; 1.5\)), the discrete band-gap wave starts to move, but further the lattice traps it. This corresponds to the large amplitude for the cubic DNLS equation (see [5]). The curiosity here is the localization of a fraction of the wave, while others travel. Does that mean that CQ-DNLS equation is also a fractional lattice (as in Ref. [61])? The fractional lattice here is not in terms of fractional derivative as Riesz-fractional [27] which takes into account the memory effect of the lattice but the decomposition of the wave in many independent parts. The future explorations can give a good answer to this question.

4.2 Model with self-focusing cubic and defocusing quintic nonlinearities (\(\gamma >0\), \(\nu <0\))

Here, as in the homoclinic threshold above, we consider the following parameters for the full integration: \(C = 1\); \(\varDelta =2.04\); \(\gamma =2\); \(\nu =-2\). The driving amplitude B is a free parameter, but its value will be chosen in function of the supratransmission threshold. From Fig. 2 (inset), we can deduce the homoclinic nonlinear gap threshold \(B_\mathrm{th}=0.2\). In Fig. 4, we depict the full integration of driven Eq. (1) for the amplitude below the threshold \(B = 0.19\) (left panel) and above the threshold \(B = 0.21\) (right panel). A rapid decrease in the amplitude of the evanescent wave occurs for B below the threshold, while for B above the threshold the energy flows and the train of pulses is generated (see Fig. 5). That means that the homoclinic threshold matches very well with the numerical one for the CQ-DNLS model with competition between cubic and quintic nonlinearities.

However, when the driving amplitude increases (see Fig. 6), the train of pulse disappears, but it appears that the train envelope soliton has the form of a density dip with a phase jump across its density minimum (dark soliton) carried by a traveling kink. To the best of our knowledge, this is the first time that this type of the nonlinear transmission of the band gap has been achieved. However, contrary to the optical fibers and the nonlinear plasmonic nanoparticles where dark soliton is created, respectively, by small driving pulse [62] and by modulation instability [63], the lattice is submitted to a periodic driving plane wave with appropriate amplitude.

Fig. 4
figure 4

Space–time evolution of a typical numerical simulation of the boundary-driven DNLS equation (1) for \(C = 1\), \(\varDelta =2.04\), \(\gamma =2\) and \(\nu =-2\). The left panel corresponds to the driving amplitude \(B = 0.19\) below the threshold and the right one to \(B = 0.21\) slightly above

Full size image
Fig. 5
figure 5

Train of pulses generated by the boundary-driven DNLS equation (1) for \(C = 1\) , \(\varDelta =2.04\), \(\gamma =2\) , \(\nu =-2\) and the amplitude \(B = 0.21\) slightly above the threshold

Full size image
Fig. 6
figure 6

(Left panels) Space–time evolution of a typical numerical simulation of the boundary-driven DNLS equation (1) for \(C = 1\), \(\varDelta =2.04\), \(\gamma =2\) and \(\nu =-2\). (Right panels) Behavior of site 50 in a function of time

Full size image

Figure 6 is depicted with the driving amplitude \({B}\in {]}0.2; x_{2++}=0.989{[}\). Knowing that \(x_{2++}\) is a positive value of the fixed points that support heteroclinic orbit in Fig. 2, what happens if \(B\ge x_{2++}\)?

Fig. 7
figure 7

Space–time evolution of a typical numerical simulation of the boundary-driven DNLS equation (1) for \(C = 1\) , \(\varDelta =2.04\), \(\gamma =2\) and \(\nu =-2\). (Left) \(B=x_{2++}=0.989\); (Right) \(B=5\)

Full size image

In Fig. 7 (left), we depict the full integration of the lattice with \(B= x_{2++}\). It appears that only one dark soliton survives and is carried by a traveling kink. When the driving amplitude increases [Fig. 7(Right)], the depth of the dark soliton decreases, but the traveling kink remains. Then, large amplitude induces the generation of the traveling kink in self-focusing cubic and defocusing quintic DNLS equation. The traveling kink has been also observed (not by supratransmission way) in soft media using stored elastic energy [64], in the cation layer in a silicate mica crystal [65] and discrete electrical lattice with nonlinear dispersion [66].

Notice that there is no generation of train of waves by the supratransmission way in the purely defocusing cubic DNLS equation. That is due to the rapid decay of static soliton that exists and is stable for any driving amplitude.

5 Conclusion

In summary, we have investigated the nonlinear band-gap transmission in discrete one-dimensional lattices with cooperative and competitive cubic–quintic nonlinearity. In the case of the self-focusing cubic and focusing quintic nonlinearities, the discrete gap waves generated merge and localize. This corresponds to the relatively large amplitude in the case of cubic DNLS equation. The positive quintic nonlinear term contributes to the localization of the band gap wave as in the problem of mobility. Considering the case of the competition between both nonlinearities, we show that the homoclinic nonlinear band-gap threshold is valid and observes the following scenarios using the supratransmission way: generation of the train of pulses for the driving amplitude slightly above the threshold; generation of the train of dark solitons carried by a traveling kink for the driving amplitude below the great value of the fixed point that supports heteroclinic orbit; generation of the traveling kink for the large amplitude. We think that the obtained results may be used in fabrication of new devices for the generation of discrete gap solitons. Also, it will be important to see the effect of next-nearest-neighbor couplings [67] on nonlinear band-gap transmission.