Skip to main content
SpringerLink
Log in

Exact solutions, conservation laws, bifurcation of nonlinear and supernonlinear traveling waves for Sharma–Tasso–Olver equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

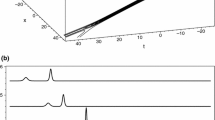
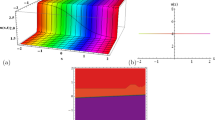
In the present work, we observe the dynamical behavior of nonlinear and supernonlinear traveling waves for Sharma–Tasso–Olver (STO) equation. Exact solutions are derived using \({1}/{G^{^{\prime }}}\) expansion and modified Kudryashov methods. The wave transformation is used to transform STO equation into an ordinary differential equation. Combining Runge–Kutta fourth-order and Fourier spectral technique, we use a mixed scheme for the numerical study of STO equation. Since spectral methods expand the solution in trigonometric series resulting into higher-order technique and Runge–Kutta produces improved accuracy, we extract these qualities for a mixed scheme. Results so produced are presented graphically which provide a useful information about the dynamical behavior. Bifurcation behavior of nonlinear and supernonlinear traveling waves of STO equation is studied with the help of bifurcation theory of planar dynamical systems. It is observed that STO equation supports nonlinear solitary wave, periodic wave, shock wave, stable oscillatory wave and most important supernonlinear periodic wave.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Ak, T., Triki, H., Dhawan, S., Bhowmik, S.K., Moshokoa, S.P., Ullah, M.Z., Biswas, A.: Computational analysis of shallow water waves with Korteweg–de Vries equation. Sci. Iran. (2017). https://doi.org/10.24200/SCI.2017.4518

    Article  Google Scholar 

  2. Ak, T., Dhawan, S.: A practical and powerful approach to potential KdV and Benjamin equations. Beni-Suef Univ. J. Basic Appl. Sci. 6(4), 383–390 (2017)

    Article  Google Scholar 

  3. Ak, T., Dhawan, S., Karakoc, S.B.G., Bhowmik, S.K., Raslan, K.R.: Numerical study of Rosenau–KdV equation using finite element method based on collocation approach. Math. Modell. Anal. 22(3), 373–388 (2017)

    Article  MathSciNet  Google Scholar 

  4. Yan, Z.-Y., Zhang, H.-Q.: Symbolic computation and new families of exact soliton-like solutions to the integrable Broer–Kaup (BK) equations in \((2+1)\)-dimensional spaces. J. Phys. A Math. Gen. 34, 1785–1792 (2001)

    Article  MathSciNet  Google Scholar 

  5. Daghan, D., Donmez, O.: Exact solutions of the Gardner equation and their applications to the different physical plasmas. Braz. J. Phys. 46(3), 321–333 (2016)

    Article  Google Scholar 

  6. Dubinov, A.E., Kolotkov, DYu., Sazonkin, M.A.: Supernonlinear waves in plasma. Plasma Phys. Rep. 38(10), 833–844 (2012)

    Article  Google Scholar 

  7. Nguetcho, A.S.T., Jibin, L., Bilbault, J.M.: Bifurcations of phase portraits of a singular nonlinear equation of the second class. Commun. Nonlinear Sci. Numer. Simul. 19(8), 2590–2601 (2014)

    Article  MathSciNet  Google Scholar 

  8. Jiang, B., Lu, Y., Zhang, J., Bi, Q.: Bifurcations and some new traveling wave solutions for the CH-\(\gamma \) equation. Appl. Math. Comput. 228, 220–233 (2014)

    MathSciNet  MATH  Google Scholar 

  9. Saha, A.: Bifurcation of travelling wave solutions for the generalized KP–MEW equations. Commun. Nonlinear Sci. Numer. Simul. 17(9), 3539–3551 (2012)

    Article  MathSciNet  Google Scholar 

  10. Dhawan, S., Kapoor, S., Kumar, S., Rawat, S.: Contemporary review of distinguish simulation process for the solution of nonlinear Burgers equation. J. Comput. Sci. 3(5), 405–419 (2012)

    Article  Google Scholar 

  11. Zhang, S., Zhang, H.-Q.: Fractional sub-equation method and its applications to nonlinear PDEs. Phys. Lett. A 375(7), 1069–1073 (2011)

    Article  MathSciNet  Google Scholar 

  12. Lu, B.: The first integral method for some time fractional differential equations. J. Math. Anal. Appl. 395(2), 684–693 (2012)

    Article  MathSciNet  Google Scholar 

  13. Wazwaz, A.-M.: A sine–cosine method for handling nonlinear wave equations. Math. Comput. Modell. 40(5–6), 499–508 (2004)

    Article  MathSciNet  Google Scholar 

  14. Abdel-Salam, E.A.B.: Quasi-periodic, periodic waves, and soliton solutions for the combined KdV–mKdV equation. Z. Naturforschung 64a, 639–645 (2009)

    Google Scholar 

  15. He, J.-H., Elagan, S.K., Li, Z.B.: Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 376(4), 257–259 (2012)

    Article  MathSciNet  Google Scholar 

  16. Chen, A.: Multi-kink solutions and soliton fission and fusion of Sharma–Tasso–Olver equation. Phys. Lett. A 374(23), 2340–2345 (2010)

    Article  MathSciNet  Google Scholar 

  17. Ablowitz, M.A., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  Google Scholar 

  18. Wang, S., Tang, X.-Y., Lou, S.-Y.: Soliton fission and fusion: Burgers equation and Sharma–Tasso–Olver equation. Chaos Solitons Fractals 21(1), 231–239 (2004)

    Article  MathSciNet  Google Scholar 

  19. Wazwaz, A.-M., El-Tantawy, S.A.: New \((3+1)\)-dimensional equations of Burgers type and Sharma–Tasso–Olver type: multiple-soliton solutions. Nonlinear Dyn. 87, 2457–2461 (2017)

    Article  MathSciNet  Google Scholar 

  20. Wazwaz, A.-M.: New \((3+1)\)-dimensional nonlinear evolution equations with Burgers and Sharma–Tasso–Olver equations constituting the main parts. Proc. Rom. Acad. Ser. A 16, 32–40 (2015)

    MathSciNet  Google Scholar 

  21. Guckenheimer, J., Holmes, P.J.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York (1983)

    Book  Google Scholar 

  22. Saha, A.: Bifurcation, periodic and chaotic motions of the modified equal width-Burgers (MEW-Burgers) equation with external periodic perturbation. Nonlinear Dyn. 87(4), 2193–2201 (2017)

    Article  MathSciNet  Google Scholar 

  23. Chow, S.-N., Hale, J.K.: Methods of Bifurcation Theory. Springer, New York (1981)

    MATH  Google Scholar 

  24. Daghan, D., Donmez, O.: Exact solutions of Gardner equation and their application to the different physical plasma. Braz. J. Phys. 46(3), 321–333 (2016)

    Article  Google Scholar 

  25. Hosseini, K., Ansari, R.: New exact solutions of nonlinear conformable time-fractional Boussinesq equations using the modified Kudryashov method. Waves Random Complex Media 27(4), 628–636 (2017)

    Article  MathSciNet  Google Scholar 

  26. Anco, S.C., Bluman, G.: Direct construction method for conservation laws of partial differential equations. Part I: examples of conservation law classifications. Eur. J. Appl. Math. 13(5), 545–566 (2002)

    MATH  Google Scholar 

  27. Bhowmik, S.K.: Stability and convergence analysis of a one step approximation of a linear partial integro-differential equation. Numer. Methods Partial Differ. Equ. 27(5), 1179–1200 (2011)

    Article  MathSciNet  Google Scholar 

  28. Bhowmik, S.K.: Stable numerical schemes for a partly convolutional partial integro-differential equation. Appl. Math. Comput. 217(8), 4217–4226 (2010)

    MathSciNet  MATH  Google Scholar 

  29. Bhowmik, S.K., Stolk, C.C.: Preconditioners based on windowed fourier frames applied to elliptic partial differential equations. J. Pseudo Differ. Oper. Appl. 2(3), 317–342 (2011)

    Article  MathSciNet  Google Scholar 

  30. Mallat, S.: A Wavelet Tour of Signal Processing, 3rd edn. Academic Press, Cambridge (2008)

    MATH  Google Scholar 

  31. Trefethen, L.N.: Spectral Methods in MATLAB. Society for Industrial and Applied Mathematics, Philadelphia (2000)

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Sciences and Humanities, National University of Computer and Emerging Sciences, Fast, Lahore Campus, Lahore, Pakistan

    Muhammad Nasir Ali & Syed Muhammad Husnine

  2. Department of Mathematics, Sikkim Manipal Institute of Technology, Sikkim Manipal University, Majitar, Rangpo, East-Sikkim, 737136, India

    Asit Saha

  3. Department of Mathematics, University of Dhaka, Dhaka, 1000, Bangladesh

    Samir Kumar Bhowmik

  4. Department of Mathematics, Central University of Haryana, Haryana, 123029, India

    Sharanjeet Dhawan

  5. Armutlu Vocational School, Yalova University, 77500, Armutlu, Yalova, Turkey

    Turgut Ak

Authors
  1. Muhammad Nasir Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Syed Muhammad Husnine
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Asit Saha
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Samir Kumar Bhowmik
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Sharanjeet Dhawan
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Turgut Ak
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Turgut Ak.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest concerning the publication of this manuscript.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ali, M.N., Husnine, S.M., Saha, A. et al. Exact solutions, conservation laws, bifurcation of nonlinear and supernonlinear traveling waves for Sharma–Tasso–Olver equation. Nonlinear Dyn 94, 1791–1801 (2018). https://doi.org/10.1007/s11071-018-4457-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4457-x

Keywords

Mathematics Subject Classification

Search

Navigation