Asymptotic analysis of passive mitigation of dynamic instability using a nonlinear energy sink network

Abstract

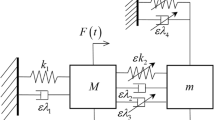
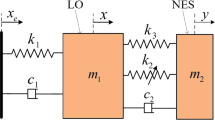
The present work studies a one-DOF nonlinear unstable primary system, which undergoes harmful limit cycle oscillations, coupled to a network of several parallel nonlinear energy sinks (NESs). As usual, in the framework of NES properties exploration and particularly in the context of dynamic instabilities mitigation, four steady-state response regimes are observed. They are classified into two categories depending on whether the NESs mitigate or not the instability and therefore separating harmless situations from harmful situations. An asymptotic analysis shows that the critical manifold of the system can be reduced to a one-dimensional parametric curve evolving in a N-dimensional space. The shape of the critical manifold and the associated stability properties provide an analytical tool to predict the nature of the possible response regimes mentioned above. In particular, the mitigation limit of the NESs, defined as the value of the chosen bifurcation parameter which separates harmful situations from harmless situations, is predicted. Using more restrictive assumptions, i.e., neglecting the nonlinearity of the primary system and assuming N identical NESs, a literal expression of the mitigation limit is obtained. Using a Van de Pol oscillator as a primary system, theoretical results are compared, for validation purposes, to the numerical integration of the system. The comparison shows a good agreement as long as we remain within the limits of use of the asymptotic approach.

Appendices

A Projection of the super-slow dynamics on the critical manifold

Equation (32) is developed into the following form

$$\begin{aligned} \dot{s}&=\epsilon \mathscr {F}\left( s,r_1,\ldots ,r_N,\vartheta _1\,\ldots ,\vartheta _N\right) \end{aligned}$$

(62a)

$$\begin{aligned} \dot{r}_n&=\mathscr {G}_n\left( s,r_1,\ldots ,r_N,\vartheta _1\,\ldots ,\vartheta _N,\epsilon \right) , \text {for}\; n=1,\ldots ,N \end{aligned}$$

(62b)

$$\begin{aligned} \dot{\vartheta }_{n}&=\mathscr {H}_n\left( s,r_1,\ldots ,r_N,\vartheta _1\,\ldots ,\vartheta _N,\epsilon \right) , \text {for}\; n=1,\ldots ,N, \end{aligned}$$

(62c)

where functions $\mathscr {F}$, $\mathscr {G}_n$ and $\mathscr {H}_n$ are deduced from functions f and $g_n$ in systems of Eqs. (10) and (11) as

$$\begin{aligned} \mathscr {F}&=\text {Re}\left\{ f e^{-j\delta }\right\} \end{aligned}$$

(63a)

$$\begin{aligned} \mathscr {G}_n&=\text {Re}\left\{ g_n e^{-j\theta _n}\right\} \end{aligned}$$

(63b)

$$\begin{aligned} \mathscr {H}_n&=\frac{s \, \text {Im}\left\{ g_n e^{-j\theta _n}\right\} -r_n \, \text {Im}\left\{ f e^{-j\delta }\right\} }{r_n \, s}. \end{aligned}$$

(63c)

From system of Eqs. (62), we obtain the real form of the slow and super-slow subsystems (13) and (14) as

$$\begin{aligned} \dot{s}&=0 \end{aligned}$$

(64a)

$$\begin{aligned} \dot{r}_n&=\mathscr {G}_n\left( s,r_1,\ldots ,r_N,\vartheta _1\,\ldots ,\vartheta _N,0\right) , \text {for}\; n=1,\ldots ,N \end{aligned}$$

(64b)

$$\begin{aligned} \dot{\vartheta }_{n}&=\mathscr {H}_n\left( s,r_1,\ldots ,r_N,\vartheta _1\,\ldots ,\vartheta _N,0\right) , \text {for}\; n=1,\ldots ,N, \end{aligned}$$

(64c)

and

$$\begin{aligned} s'&=\mathscr {F}\left( s,r_1,\ldots ,r_N,\vartheta _1\,\ldots ,\vartheta _N\right) \end{aligned}$$

(65a)

$$\begin{aligned} 0&=\mathscr {G}_n\left( s,r_1,\ldots ,r_N,\vartheta _1\,\ldots ,\vartheta _N,0\right) , \text {for}\; n=1,\ldots ,N \end{aligned}$$

(65b)

$$\begin{aligned} 0&=\mathscr {H}_n\left( s,r_1,\ldots ,r_N,\vartheta _1\,\ldots ,\vartheta _N,0\right) , \text {for}\; n=1,\ldots ,N, \end{aligned}$$

(65c)

respectively.

We assume that fixed points of (62) exist only at the super-slow timescale and they are therefore fixed points of (65). Of course, the CM can be also obtained solving Eqs. (65b) and (65c). Then, substituting system of Eq. (19) with $n=1$ (any $n\in [1,\,N]$ can be chosen) into (65a) , we obtain

$$\begin{aligned}&\left( \sqrt{H_1\left( r_1 \right) }\right) '=\frac{1}{2 \sqrt{H_1\left( r_1 \right) }}\frac{\mathrm{d} H_1\left( r_1 \right) }{\mathrm{d}r_1}r_1'\nonumber \\&\quad =\mathscr {F}\left( \sqrt{H_1\left( r_1 \right) },r_1,\ldots ,r_N,\right. \nonumber \\&\qquad \left. -\,\arg \left( F_1(r_1)\right) ,\ldots ,-\arg \left( F_N(r_N)\right) \right) , \end{aligned}$$

(66)

which can be reduced to

$$\begin{aligned} \frac{\mathrm{d }H_1\left( r_1 \right) }{\mathrm{d }r_1}r_1'= f_{r_1}\left( r_1,\ldots ,r_N\right) , \end{aligned}$$

(67)

where $f_{r_1}=2 \sqrt{H_1\left( r_1 \right) } \mathscr {F}$. In reality, $f_{r_1}\left( r_1,\ldots ,r_N\right)$ is a single-valued function because all variables $r_n$ (with $n\in [1,\,N]$) are linked to each other through Eq. (22) (any $n\in [1,\,N]$ can be chosen as master component, we choose $r_1$).

B Proof of Result 4.1

Because N identical NESs are assumed, the function $H_n(x)$ is now denoted H(x). Considering also a linear primary system ($\tilde{f}_{\mathrm{NL}} = 0$), system of Eq. (37) becomes

$$\begin{aligned} \rho H(r_1)-\sum _{k= 1}^{N} r_k^2 \mu&=0 \end{aligned}$$

(68a)

$$\begin{aligned} H(r_n) - H(r_1)&= 0, \quad \text {for}\; n = 2,\ldots ,N. \end{aligned}$$

(68b)

Equation (68b) is a third-order polynomial equation with respect to $r_n^2$ having the three following roots as a function of $r_1$

$$\begin{aligned} r_n^2&= f_1(r_1^2)=r_1^2\ \end{aligned}$$

(69a)

$$\begin{aligned} r_n^2&= f_2(r_1^2)\nonumber \\&=-\frac{r_1^2}{2}+\frac{8 a+\sqrt{3 \alpha r_1^2 \left( 16 a-9 \alpha r_1^2\right) -64 \mu ^2}}{6 \alpha } \end{aligned}$$

(69b)

$$\begin{aligned} r_n^2&= f_3(r_1^2)\nonumber \\&=-\frac{r_1^2}{2}+\frac{8 a-\sqrt{3 \alpha r_1^2 \left( 16 a-9 \alpha r_1^2\right) -64 \mu ^2}}{6 \alpha }. \end{aligned}$$

(69c)

The functions $f_2(r_1^2)>f_3(r_1^2)$. If $\mu >a/\sqrt{3}$, $r_n^2 = f_1(r_1^2)=r_1^2$ is the only real solution.

Using system of Eqs. (69), (68a) is written as follows

$$\begin{aligned} H(r_1)=\frac{\mu }{\rho }\left( r_1^2+\sum _{k=2}^{N}g_n(r_1^2) \right) , \end{aligned}$$

(70)

where $g_n(r_1^2)$ can be, for each term of the sum, $f_1(r_1^2)$, $f_2(r_1^2)$ or $f_3(r_1^2)$.

If $\forall n \in [2,N], g_n(r_1^2)=f_1(r_1^2)=r_1^2$, Eq. (70) becomes

$$\begin{aligned} H(r_1)=\frac{\mu }{\rho } N r_1^2. \end{aligned}$$

(71)

Ignoring the trivial solution, Eq. (71) is reduced to a second-order polynomial equation with respect to $r_1^2$ with the following solutions

$$\begin{aligned} r_{1,1}^{*2} =\frac{4 \left( a \rho -\sqrt{\mu \rho \left( a^2 N-\mu \rho \right) }\right) }{3 \alpha \rho }, \end{aligned}$$

(72)

and

$$\begin{aligned} r_{1,2}^{*2} =\frac{4 \left( a \rho +\sqrt{\mu \rho \left( a^2 N-\mu \rho \right) }\right) }{3 \alpha \rho }, \end{aligned}$$

(73)

which are real if $\rho <\frac{a^2 N}{\mu }$. In this case, $r_{1,1}^{*2}<r_{1,2}^{*2}$.

Considering first the case $\mu >a/\sqrt{3}$, $r_n^2 = f_1(r_1^2)$ is the only real solution, $r_{1,1}^{*2}$ and $r_{1,2}^{*2}$ are therefore the only solutions given Eq. (48) with $w=r_{1,2}^*$.

We consider now the case for which $\mu <a/\sqrt{3}$. Solving $f_1(r_1^2)=f_2(r_1^2)$ (to find the intersection between the functions $f_1$ and $f_2$) and $\mathrm{d}f_2(x)/\mathrm{d}x=0$ (to find the maximum of $f_2$) gives the same value of $r_1^2$ as

$$\begin{aligned} r_{1}^{\star 2}=\frac{4 \left( 2 a+\sqrt{a^2-3 \mu ^2}\right) }{9 \alpha }, \end{aligned}$$

(74)

which corresponds also to one of the solutions of $H'\left( r_1\right) =0$ (see Eq. (25b)), i.e., $r_{1}^{\star }=r^m$ (where $r^m$ is $r_n^m$ in the case of identical NESs).

The difference between $r_{1,2}^{*2}$ and $r_{1}^{\star 2}$ is

$$\begin{aligned} r_{1,2}^{*2}-r_{1}^{\star 2}=\frac{4 \left( a \rho +3 \sqrt{\mu \rho \left( a^2 N-\mu \rho \right) }-\rho \sqrt{a^2-3 \mu ^2}\right) }{9 \alpha \rho }, \nonumber \\ \end{aligned}$$

(75)

which is a real positive number until $\rho =\frac{a^2 N}{\mu }$. Therefore, for $r_1^2>r_{1}^{\star 2}$, $f_1(r_1^2)>f_2(r_1^2)$ and the right-hand side of Eq. (70) is bounded as follows

$$\begin{aligned}&R_l= \frac{\mu }{\rho }\left( r_1^2+ (N-1) f_2(r_1^2)\right) \nonumber \\&\quad<R_c =\frac{\mu }{\rho }\left( r_1^2+\sum _{k=2}^{N}g_n(r_1^2)\right) < R_r=\frac{\mu }{\rho }N r_1^2. \end{aligned}$$

(76)

Let $\mathscr {R}_l$, $\mathscr {R}_c$ and $\mathscr {R}_r$ be the sets of fixed points $\mathbf r^*$, the solutions of $H(r_1)=R_l$, $H(r_1)=R_c$ and $H(r_1)=R_r$, respectively. Consequently, because for $r_1^2>r_{1}^{\star 2}$, $H(r_1)$ in an increasing function and because of Eq. (76), the following inequalities hold

$$\begin{aligned} \forall n \in [1,\,N], \quad \max _{\mathbf{r^*} \in \mathscr {R}_l} r^*_{n}< \max _{\mathbf{r^*} \in \mathscr {R}_c} r^*_{n}< \max _{\mathbf{r^*} \in \mathscr {R}_r} r^*_{n}, \end{aligned}$$

(77)

with

$$\begin{aligned} \max _{\mathbf{r^*} \in \mathscr {R}_r} r^*_{n}=r_{1,2}^{*}, \end{aligned}$$

(78)

giving also Eq. (48) with $w=r_{1,2}^*$.

To finish the proof, one must show that $\mathbf{r^*}= \left[ r_1=w,\ldots ,r_N=w \right]$ is an unstable fixed point on a stable part of S. To this end, the derivative with respect to $r_1$ of the function

$$\begin{aligned} f(r_1)=2 \frac{\rho H(r_1)-\mu N r_1^2}{\frac{dH_1(r_1)}{\mathrm{d}r_1}}, \end{aligned}$$

(79)

defined by Eq. (39), is computed as

$$\begin{aligned} \frac{\mathrm{d}f}{\mathrm{d} r_1} ({r_1})= & {} 2\left( \frac{\rho \frac{\mathrm{d}H_1(r_1)}{\mathrm{d}r_1}-\mu N \, r_1}{\frac{dH_1(r_1)}{\mathrm{d}r_1}}\right. \nonumber \\&\left. -\frac{d^2H_1(r_1)}{\mathrm{d}r_1^2}\frac{\rho H(r_1)-\mu N \, r_1^2}{\left( \frac{\mathrm{d}H_1(r_1)}{\mathrm{d}r_1}\right) ^2}\right) . \end{aligned}$$

(80)

By definition, the term $\rho H(r_1)-\mu N \, r_1^2=0$ if $r_1=r_{1,2}^{*2}$ (see Eq. (71)). Moreover, because $r_{1,2}^{*2}>r_{1}^{\star 2}=r^m$

$$\begin{aligned} \left. \frac{\mathrm{d}H_1(r_1)}{\mathrm{d}r_1}\right| _{r_1=\sqrt{r_{1,2}^{*2}}}>0. \end{aligned}$$

(81)

Therefore, the sign of Eq. (80) is given by the sign of $\rho H'(r_1)-2 \mu N \, r_1$. One can be shown that $\rho \frac{dH_1(r_1)}{\mathrm{d}r_1}-2 \mu N \, r_1$ is a real-valued function if $r_1>\kappa$ with

$$\begin{aligned} \kappa =\frac{2}{3} \sqrt{\frac{2 a+\sqrt{\frac{a^2 (3 \mu N+\rho )}{\rho }-3 \mu ^2}}{\alpha }}, \end{aligned}$$

(82)

and that $r_{1,2}^{*}>\kappa$ until $\rho =\frac{a^2 N}{\mu }$. Consequently, using Result 3.2 ($\frac{\mathrm{d}f}{\mathrm{d} r_1} ({r_1})>0$), $r_{1,2}^{*}$ is an unstable fixed point and Result 4.1 is demonstrated.