Abstract
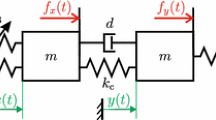
Coupled strongly nonlinear oscillators, whose characteristic is close to linear for low amplitudes but becomes infinitely growing as the amplitude approaches certain limit, are considered in this paper. Such a model may serve for understanding the dynamics of elastic structures within the restricted space bounded by stiff constraints. In particular, this study focuses on the evolution of vibration modes as the energy is gradually pumped into or dissipates out of the system. For instance, based on the two degrees of freedom system, it is shown that the in-phase and out-of-phase motions may follow qualitatively different scenarios as the system’ energy increases. So the in-phase mode appears to absorb the energy with equipartition between the masses. In contrast, the out-of-phase mode provides equal energy distribution only until certain critical energy level. Then, as a result of bifurcation of the 1:1 resonance path, one of the masses becomes a dominant energy receiver in such a way that it takes the energy not only from the main source but also from another mass.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Jaffe, C., Brumer, P.: Local and normal modes: a classical perspective. J. Chem. Phys. 73(11), 5646–5658 (1980)
Manevich, L.I., Pilipchuk, V.N.: Localization of oscillations in linear and nonlinear chains. Adv. Mech. 13(3/4), 107–134 (1990)
Ormondroyd, J., Den Hartog, J.: The theory of the dynamic vibration absorber. Trans. Am. Soc. Mech. Eng. 50, A9–A22 (1928)
Den Hartog, J.: Mechanical Vibration. McGraw-Hill, New York (1947)
Roberson, R.: Synthesis of a nonlinear dynamic vibration absorber. J. Franklin Inst. 254, 205–220 (1952)
Lee, Y., Kerschen, G., Vakakis, A., Panagopoulos, P., Bergman, L., McFarland, D.: Complicated dynamics of a linear oscillator with a light, essentially nonlinear attachment. Physica D 204, 41–69 (2005)
Pierre, C., Castanier, M.P., Chen, W.J.: Wave localization in multi-coupled periodic structures: application to truss beams. ASME Mech. Rev. 49, 65–86 (1996)
Vakakis, A.F., Manevitch, L.I., Mikhlin, Y.V., Pilipchuk, V.N., Zevin, A.A.: Normal Modes and Localization in Nonlinear Systems. Wiley, New York (1996)
Gendelman, O., Vakakis, A.F.: Transitions from localization to nonlocalization in strongly nonlinear damped oscillators. Chaos Solitons Fractals 11(10), 1535–1542 (2000)
Pouget, J., Remoissenet, M., Tamga, J.M.: Energy self-localization and gap local pulses in a two-dimensional nonlinear lattice. Phys. Rev. B 47, 14866–14874 (1993)
Nesterov, S.V.: Examples of nonlinear Klein–Gordon equations, solvable in terms of elementary functions. Proc. Moscow Inst. Power Eng. 357, 68–70 (1978)
Dimentberg, M.F., Bratus, A.S.: Bounded parametric control of random vibrations. R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 456(2002), 2351–2363 (2000)
Dimentberg, M., Iourtchenko, D., Bratus, A.: Transition from planar to whirling oscillations in a certain nonlinear system. Nonlinear Dyn. 23, 165–174 (2000)
Zhuravlev, V.F., Klimov, D.M.: Prikladnye metody v teorii kolebanii. Nauka, Moscow (1988) (in Russian)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pilipchuk, V.N. Transient mode localization in coupled strongly nonlinear exactly solvable oscillators. Nonlinear Dyn 51, 245–258 (2008). https://doi.org/10.1007/s11071-007-9207-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-007-9207-4