Skip to main content
SpringerLink
Log in

Periodic and rational solutions of variable-coefficient modified Korteweg–de Vries equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

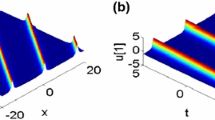
With the aid of multivariate transformation technique, we obtain periodic and rational solutions for variable-coefficient modified Korteweg–de Vries (vc-mKdV) equation. The rational solutions can be obtained as limiting cases of periodic solutions in analogy with the rational solutions of nonlinear Schrödinger equation (NLSE). Further, the effect of variation of parameters on solutions is studied for physically relevant periodic form. Unlike the effect of variation of parameters on solutions of NLSE, where both amplitude and width can be controlled, only path or trajectory of solutions of vc-mKdV equation can be modulated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Helfrich, K.R., Melville, W.K., Miles, J.W.: On interfacial solitary waves over slowly varying topography. J. Fluid Mech. 149, 305–317 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  2. Khater, A.H., El-Kakaawy, O.H., Callebaut, D.K.: Bäcklund transformations and exact solutions for Alfvén solitons in a relativistic electron–positron plasma. Phys. Scr. 58, 545–548 (1998)

    Article  Google Scholar 

  3. Lonngren, K.E.: Ion acoustic soliton experiments in a plasma. Opt. Quantum Electron. 30, 615–630 (1998)

    Article  Google Scholar 

  4. Watanabe, S.: Ion acoustic soliton in plasma with negative ion. J. Phys. Soc. Jpn. 53, 950–956 (1984)

    Article  Google Scholar 

  5. Ono, H.: Soliton fission in anharmonic lattices with reflectionless inhomogeneity. J. Phys. Soc. Jpn. 61, 4336–4343 (1992)

    Article  Google Scholar 

  6. Ziegler, V., Dinkel, J., Setzer, C., Lonngren, K.E.: On the propagation of nonlinear solitary waves in a distributed Schottky barrier diode transmission line. Chaos Solitons Fractals 12, 1719–1728 (2001)

    Article  MATH  Google Scholar 

  7. Nagatani, T.: TDGL and MKdV equations for jamming transition in the lattice models of traffic. Phys. A 264, 581–592 (1999)

    Article  Google Scholar 

  8. Komatsu, T.S., Sasa, S.I.: Kink soliton characterizing traffic congestion. Phys. Rev. E 52, 5574–5582 (1995)

    Article  Google Scholar 

  9. Liu, F., Cheng, R., Zheng, P., Ge, H.: TDGL and MKdV equations for car-following model considering traffic jerk. Nonlinear Dyn. 83, 793–800 (2016)

    Article  Google Scholar 

  10. Wadati, M.: The modified Korteweg–de Vries equation. J. Phys. Soc. Jpn. 34, 1289–1296 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chan, W.L., Li, K.S.: Nonpropagating solitons of the nonisospectral and variable coefficient modified Korteweg–de Vries equation. J. Phys. A 27, 883–902 (1994)

    Article  MathSciNet  Google Scholar 

  12. Yeung, T.C.A., Fung, P.C.W.: Hamiltonian formulation of the inverse scattering method of the modified KdV equation under the non-vanishing boundary condition u (x, t) to b as x to+ or-infinity. J. Phys. A 21, 3575–3592 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  13. Yao, R.X., Qu, C.Z., Li, Z.: Painlevé property and conservation laws of multi-component mKdV equations. Chaos Solitons Fractals 22, 723–738 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  14. Miura, R.M.: Korteweg–de Vries equation and generalizations. I. A remarkable explicit nonlinear transformation. J. Math. Phys. 9, 1202–1204 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  15. Miura, R.M.: The Korteweg–deVries equation: a survey of results. SIAM Rev. 18, 412–459 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  16. Bi, J.B.: Novel solutions of mkdv equation with the modified Bäcklund transformation. J. Shanghai Univ. 3, 286–288 (2004)

    Article  MATH  Google Scholar 

  17. Zha, Q.L., Li, Z.B.: Darboux transformation and multi-solitons for complex mKdV Equation. Chin. Phys. Lett. 25, 8–11 (2008)

    Article  Google Scholar 

  18. Li, D.S., Yu, Z.S., Zhang, H.Q.: New soliton-like solutions to variable coefficients mKdV equation. Commun. Theor. Phys. 42, 649–654 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  19. Serkin, V.N., Hasegawa, A.: Exactly integrable nonlinear Schrödinger equation models with varying dispersion, nonlinearity and gain: application for soliton dispersion. IEEE J. Sel. Top. Quantum Electron. 8, 418–431 (2002)

    Article  Google Scholar 

  20. Serkin, V.N., Hasegawa, A., Belyaeva, T.L.: Comment on exact self-similar solutions of the generalized nonlinear Schrödinger equation with distributed coefficients. Phys. Rev. Lett. 92, 199401 (2004)

    Article  Google Scholar 

  21. Serkin, V.N., Hasegawa, A., Belyaeva, T.L.: Nonautonomous solitons in external potentials. Phys. Rev. Lett. 98, 074102 (2007)

    Article  Google Scholar 

  22. Serkin, V.N., Hasegawa, A., Belyaeva, T.L.: Solitary waves in nonautonomous nonlinear dispersive systems: nonautonomous solitons. J. Mod. Opt. 57, 1087–1099 (2010)

    Article  MATH  Google Scholar 

  23. Serkin, V.N., Hasegawa, A., Belyaeva, T.L.: Nonautonomous matter wave solitons near the Feshbach resonance. Phys. Rev. A 81, 023610 (2010)

    Article  Google Scholar 

  24. Kruglov, V.I., Peacock, A.C., Harvey, J.D.: Exact self-similar solutions of the generalized nonlinear Schrödinger equation with distributed coefficients. Phys. Rev. Lett. 90, 113902 (2003)

    Article  Google Scholar 

  25. Kruglov, V.I., Peacock, A.C., Harvey, J.D.: Exact solutions of the generalized nonlinear Schrödinger equation with distributed coefficients. Phys. Rev. E 71, 056619 (2005)

    Article  MathSciNet  Google Scholar 

  26. Ponomarenko, S.A., Agrawa, G.P.: Do solitonlike self-similar waves exist in nonlinear optical media? Phys. Rev. Lett. 97, 013901 (2006)

    Article  Google Scholar 

  27. Ponomarenko, S.A., Agrawa, G.P.: Optical similaritons in nonlinear waveguides. Opt. Lett. 32, 1659–1661 (2007)

    Article  Google Scholar 

  28. Ilday, F.Ö., Buckley, J., Wise, F.W.: Self-similar evolution of parabolic pulses in a laser cavity. Phys. Rev. Lett. 92, 213902 (2004)

    Article  Google Scholar 

  29. Ilday, F.Ö., Kaertner, F.X., Wise, F.W.: Possibility of self-similar pulse evolution in a Ti: sapphire laser. Opt. Express 12, 2731 (2004)

    Article  Google Scholar 

  30. Oktem, B., Ülgüdür, C., Ilday, F.Ö.: Soliton-similariton fiber laser. Nat. Photon. 4, 307 (2010)

    Article  Google Scholar 

  31. Jirauschek, C., Ilday, F.Ö.: Semianalytic theory of self-similar optical propagation and mode-locking using a shape adaptive model pulse. Phys. Rev. A 83, 063809 (2011)

    Article  Google Scholar 

  32. Yu, X., Liu, Z.Y.: Solitonic propagation and interaction for a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Phys. Rev. E 83, 056601 (2011)

    Article  Google Scholar 

  33. Yu, X., Gao, Y.T., Sun, Z.Y., Liu, Y.: Wronskian solutions and integrability for a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Nonlinear Dyn. 67, 1023–1030 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  34. Sun, Z.Y., Gao, Y.T., Liu, Y., Yu, X.: Soliton management for a variable-coefficient modified Korteweg–de Vries equation. Phys. Rev. E 84, 026606 (2011)

    Article  Google Scholar 

  35. Pradhan, K., Panigrahi, P.K.: Parametrically controlling solitary wave dynamics in the modified Korteweg–de Vries equation. J. Phys. A 39, L343–L348 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  36. Tian, B., Gao, Y.T.: Variable-coefficient balancing-act method and variable-coefficient KdV equation from fluid dynamics and plasma physics. Eur. Phys. J. B 22, 351–360 (2001)

    Article  Google Scholar 

  37. Zhang, Y., Li, J., Lv, Y.N.: The exact solution and integrable properties to the variable-coefficient modified Korteweg–de Vries equation. Ann. Phys. (NY) 323, 3059–3064 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  38. Wazwaz, A.M., Xu, G.Q.: An extended modified KdV equation and its Painlevé integrability. Nonlinear Dyn. (2016). doi:10.1007/s11071-016-2971-2

  39. Biswas, A.: Solitary waves for power-law regularized long-wave equation and R(m, n) equation. Nonlinear Dyn. 59, 423–426 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  40. Wazwaz, A.M., El-Tantawy, S.A.: A new integrable (3 + 1)-dimensional KdV-like model with its multiple-soliton solutions. Nonlinear Dyn. 83, 1529–1534 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  41. He, B., Meng, Q.: Three kinds of periodic wave solutions and their limit forms for a modified KdV-type equation. Nonlinear Dyn. 86, 811–822 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  42. Biswas, A.: Solitary wave solution for KdV equation with power-law nonlinearity and time-dependent coefficients. Nonlinear Dyn. 58, 345 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  43. Gao, Y.T., Tian, B.: Cosmic dust-ion-acoustic waves, spherical modified Kadomtsev–Petviashvili model, and symbolic computation. Phys. Plasmas 13, 112901 (2006)

    Article  Google Scholar 

  44. Tian, B., Gao, Y.T.: Symbolic computation on cylindrical-modified dust-ion-acoustic nebulons in dusty plasmas. Phys. Lett. A 362, 283–288 (2007)

    Article  MATH  Google Scholar 

  45. Yan, Z.: The modified KdV equation with variable coefficients: exact uni/bi-variable travelling wave-like solutions. Appl. Math. Comput. 203, 106–112 (2008)

    MathSciNet  MATH  Google Scholar 

  46. Zheng, X., Shang, Y., Huang, Y.: Abundant explicit and exact solutions for the variable coefficient mKdV equations. Abstr. Appl. Anal. 2013, 1–7 (2013)

  47. Salas, A.H.: Exact solutions to mKdV equation with variable coefficients. Appl. Math. Comput. 216, 2792–2798 (2010)

    MathSciNet  MATH  Google Scholar 

  48. Ye, C., Zhang, W.: New exact solutions for the generalized mKdV equation with variable coefficients. Appl. Math. Sci. 5, 3715–3721 (2011)

    MathSciNet  MATH  Google Scholar 

  49. Chowdury, A., Ankiewicz, A., Akhmediev, N.: Periodic and rational solutions of modified Korteweg–de Vries equation. Eur. Phys. J. D 70, 104 (2016)

    Article  Google Scholar 

  50. Akhmediev, N., Ankiewicz, A., Taki, M.: Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 373, 675–678 (2009)

    Article  MATH  Google Scholar 

  51. Goyal, A., Gupta, R., Loomba, S., Kumar, C.N.: Riccati parameterized self-similar waves in tapered graded-index waveguides. Phys. Lett. A 376, 3454–3457 (2012)

    Article  Google Scholar 

  52. Dai, C.Q., Wang, Y.Y., Tian, Q., Zhang, J.F.: The management and containment of self-similar rogue waves in the inhomogeneous nonlinear Schrödinger equation. Ann. Phys. 327, 512–521 (2012)

    Article  MATH  Google Scholar 

  53. Landau, R.H., Páez, M.J.: Chapter 28, Computational Physics. Wiley, New York (1997)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Physics, Panjab University, Chandigarh, 160014, India

    Ritu Pal, Harleen Kaur & C. N. Kumar

  2. Indian Institute of Science Education and Research (IISER) Tirupati, Tirupati, Andhra Pradesh, 517507, India

    Thokala Soloman Raju

Authors
  1. Ritu Pal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Harleen Kaur
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thokala Soloman Raju
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. C. N. Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thokala Soloman Raju.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pal, R., Kaur, H., Raju, T.S. et al. Periodic and rational solutions of variable-coefficient modified Korteweg–de Vries equation. Nonlinear Dyn 89, 617–622 (2017). https://doi.org/10.1007/s11071-017-3475-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3475-4

Keywords

Search

Navigation