Abstract
Global attitude stabilization of a rigid spacecraft with unknown actuator delay time is an important problem that has rarely been studied. In this paper, first we investigate a Lyapunov-based controller for attitude regulation of a rigid spacecraft with delayed inputs. Simple conditions for global asymptotical stability are obtained by assuming that the true delay value is unknown, but approximation of its upper bound is available. It is also shown that a proper design of the controller prevents the unwinding phenomenon. Then, we extend the results for the system while taking disturbance effects into account. Based on Lyapunov–Krasovskii methodology, it is proven that the proposed controller can drive the closed-loop trajectories to a small region in the neighborhood of the origin in the presence of external disturbances and model uncertainties. Various numerical simulations are carried out to illustrate the effectiveness of the proposed control system.







Similar content being viewed by others
Abbreviations
- C :
-
Direction cosine matrix
-
 :
: -
Principal axis of rotation
- f, g :
-
Generic functions
- I :
-
\(3\times 3\) Identity matrix
- J :
-
Nominal inertial matrix
- \(J_\mathrm{r}\) :
-
Real inertial matrix
- P :
-
Positive definite controller gain matrix
- \(\mathfrak {R}^n\) :
-
n-Dimensional space of real vectors
- \(\mathfrak {R}_+\) :
-
Set of nonnegative real numbers
- T :
-
Actuator torque vector \([T_1, T_2, T_3]^T\)
- \(T_\mathrm{d}\) :
-
Disturbance torque
- \(T_\mathrm{g}\) :
-
Gravity gradient torque
- t :
-
Time
- V, v :
-
Lyapunov function (functional)
- \(\gamma \) :
-
Positive scalar constant
- \(\kappa \) :
-
\(\mathcal {K}_\infty \) Function
- \(\varrho \) :
-
Negative controller gain scalar
- \(\sigma \) :
-
Modified Rodrigues parameter vector \([\sigma _1, \sigma _2, \sigma _3]^T\)
- \(\tau \) :
-
Time delay
- \(\varPhi \) :
-
Principal rotation angle
- \(\omega \) :
-
Angular velocity vector, \([\omega _1, \omega _2, \omega _3]^T\)
References
Ailon, A., Segev, R., Arogeti, S.: A simple velocity-free controller for attitude regulation of a spacecraft with delayed feedback. IEEE Trans. Autom. Control 49(1), 125–130 (2004). doi:10.1109/TAC.2003.821406
Aleksandrov, A.Y., Zhabko, A.P.: Delay-independent stability of homogeneous systems. Appl. Math. Lett. 34, 43–50 (2014). doi:10.1016/j.aml.2014.03.016
Artstein, Z.: Linear systems with delayed controls: a reduction. IEEE Trans. Autom. Control 27(4), 869–879 (1982). doi:10.1109/TAC.1982.1103023
Bahrami, S., Namvar, M., Aghili, F.: In: IEEE International Conference on Robotics and Automation (ICRA), Attitude control of satellites with delay in attitude measurement, pp. 947–952. IEEE, Karlsruhe (2013). doi:10.1109/ICRA.2013.6630687
Bekiaris-Liberis, N.: Simultaneous compensation of input and state delays for nonlinear systems. Syst. Control Lett. 73, 96–102 (2014). doi:10.1016/j.sysconle.2014.08.014
Bekiaris-Liberis, N., Krstic, M.: Nonlinear Control under Nonconstant Delays. SIAM, Philadelphia, PA (2013)
Bharadwaj, S., Osipchuk, M., Mease, K.D., Park, F.C.: Geometry and inverse optimality in global attitude stabilization. J. Guid. Control Dyn. 21(6), 930–939 (1998). doi:10.2514/2.4327
Bustan, D., Sani, S., Pariz, N.: Adaptive fault-tolerant spacecraft attitude control design with transient response control. IEEE/ASME Trans. Mechatron. 19(4), 1404–1411 (2014). doi:10.1109/TMECH.2013.2288314
Bustan, D., Sani, S., Pariz, N.: Immersion and invariance based fault tolerant adaptive spacecraft attitude control. Int. J. Control Autom. Syst. 12(2), 333–339 (2014). doi:10.1007/s12555-012-0536-9
Chen, W., Jiao, L., Li, J., Li, R.: Adaptive NN backstepping output-feedback control for stochastic nonlinear strict-feedback systems with time-varying delays. IEEE Trans. Syst. Man Cybern. Part B: Cybern. 40(3), 939–950 (2010). doi:10.1109/TSMCB.2009.2033808
Chen, Z., Cong, B., Liu, X.: A robust attitude control strategy with guaranteed transient performance via modified Lyapunov-Based control and integral sliding mode control. Nonlinear Dyn. 78(3), 2205–2218 (2014). doi:10.1007/s11071-014-1598-4
Chunodkar, A.A., Akella, M.R.: Attitude stabilization with unknown bounded delay in feedback control implementation. J. Guid. Control Dyn. 34(2), 533–542 (2011). doi:10.2514/1.50352
Fischer, N.: Lyapunov-based control of saturated and time-delayed nonlinear systems. Ph.D. thesis, Graduate School, University of Florida (2012). Available at: http://ncr.mae.ufl.edu/dissertations/nic.pdf
Forbes, J.R.: Passivity-based attitude control on the special orthogonal group of rigid-body rotations. J. Guid. Control Dyn. 36(6), 1596–1605 (2013). doi:10.2514/1.59270
Fortescue, P., Swinerd, G., Stark, J. (eds.): Spacecraft Systems Engineering, 4th edn. Wiley, United Kingdom (2011)
Haddad, W.M., Chellaboina, V.: Nonlinear Dynamical Systems and Control:A Lyapunov-Based Approach. Princeton University Press, New Jersey (2008)
Hu, Q., Li, B., Zhang, A.: Robust finite-time control allocation in spacecraft attitude stabilization under actuator misalignment. Nonlinear Dyn. 73(1–2), 53–71 (2013). doi:10.1007/s11071-013-0766-2
Hu, Q., Li, B., Zhang, Y.: Nonlinear proportional-derivative control incorporating closed-loop control allocation for spacecraft. J. Guid. Control Dyn. 37(3), 799–812 (2014). doi:10.2514/1.61815
Hu, Q., Xiao, B., Wang, D., Poh, E.K.: Attitude control of spacecraft with actuator uncertainty. J. Guid. Control Dyn. 36(6), 1771–1776 (2013). doi:10.2514/1.58624
Hua, C., Feng, G., Guan, X.: Robust controller design of a class of nonlinear time delay systems via backstepping method. Automatica 44(2), 567–573 (2008). doi:10.1016/j.automatica.2007.06.008
Jankovic, M.: Forwarding, backstepping, and finite spectrum assignment for time delay systems. Automatica 45(1), 2–9 (2009). doi:10.1016/j.automatica.2008.04.021
Jankovic, M.: Recursive predictor design for state and output feedback controllers for linear time delay systems. Automatica 46(3), 510–517 (2010). doi:10.1016/j.automatica.2010.01.021
Karafyllis, I.: Finite-time global stabilization by means of time-varying distributed delay feedback. SIAM J. Control Optim. 45(1), 320–342 (2006). doi:10.1137/040616383
Karafyllis, I.: Stabilization by means of approximate predictors for systems with delayed input. SIAM J. Control Optim. 49(3), 1100–1123 (2011). doi:10.1137/100781973
Krstic, M.: Input delay compensation for forward complete and strict-feedforward nonlinear systems. IEEE Trans. Autom. Control 55(2), 287–303 (2010). doi:10.1109/TAC.2009.2034923
Krstic, M., Bekiaris-Liberis, N.: Nonlinear stabilization in infinite dimension. Annu. Rev. Control 37(2), 220–231 (2013). doi:10.1016/j.arcontrol.2013.09.002
Krstic, M., Tsiotras, P.: Inverse optimal stabilization of a rigid spacecraft. IEEE Tran. Autom. Control 44(5), 1042–1049 (1999). doi:10.1109/9.763225
Lee, T.: Computational geometric mechanics and control of rigid bodies. Ph.D. thesis, University of Michigan (2008)
Liang, Z., Liu, Q.: Design of stabilizing controllers of upper triangular nonlinear time-delay systems. Syst. Control Lett. 75, 1–7 (2015). doi:10.1016/j.sysconle.2014.10.011
Ma, Y., Jiang, B., Tao, G., Cheng, Y.: Actuator failure compensation and attitude control for rigid satellite by adaptive control using quaternion feedback. J. Frankl. Inst. 351(1), 296–314 (2014). doi:10.1016/j.jfranklin.2013.08.028
Malisoff, M., Mazenc, F.: Constructions of Strict Lyapunov Functions. Springer, London (2009). doi:10.1007/978-1-84882-535-2
Mazenc, F., Bliman, P.: Backstepping design for time-delay nonlinear systems. IEEE Trans. Autom. Control 51(1), 149–154 (2006). doi:10.1109/TAC.2005.861701
Mazenc, F., Malisoff, M., Lin, Z.: Further results on input-to-state stability for nonlinear systems with delayed feedbacks. Automatica 44(9), 2415–2421 (2008). doi:10.1016/j.automatica.2008.01.024
Mazenc, F., Niculescu, S.I.: Generating positive and stable solutions through delayed state feedback. Automatica 47(3), 525–533 (2011). doi:10.1016/j.automatica.2011.01.029
Mazenc, F., Niculescu, S.I., Bekaik, M.: Backstepping for nonlinear systems with delay in the input revisited. SIAM J. Control Optim. 49(6), 2263–2278 (2011). doi:10.1137/100819023
Nazari, M., Butcher, E.A., Schaub, H.: Spacecraft attitude stabilization using nonlinear delayed multiactuator control and inverse dynamics. J. Guid. Control Dyn. 36(5), 1440–1452 (2013). doi:10.2514/1.58249
Pepe, P., Jiang, Z.P.: A Lyapunov–Krasovskii methodology for ISS and iISS of time-delay systems. Syst. Control Lett. 55(12), 1006–1014 (2006). doi:10.1016/j.sysconle.2006.06.013
Samiei, E., Nazari, M., Butcher, E., Schaub, H.: Delayed feedback control of rigid body attitude using neural networks and Lyapunov–Krasovskii functionals. In: AAS/AIAA Space flight Mechanics Meeting. Charleston, SC (2012)
Schaub, H., Junkins, J.L.: Analytical Mechanics of Space Systems, 2nd edn. AIAA Education Series, Reston, VA (2009). doi:10.2514/4.867231
Sepulchre, R., Janković, M., Kokotović, P.V.: Constructive Nonlinear Control, chap. Construction of Lyapunov Functions. Springer, New York (1997)
Sidi, M.J.: Spacecraft Dynamics and Control: a Practical Engineering Approach, vol. 7. Cambridge University Press, New York (1997)
Slotine, J.J.E., Li, W.: Applied Nonlinear Control, chap. Krasovskii’s Method. Prentice-Hall, Englewood Cliffs, New Jersey (1991)
Sontag, E.D.: Input-to-state stability: Basic concepts and results. In: Paolo Nistri, G.S. (ed.) Nonlinear and Optimal Control Theory, vol. 1932, pp. 163–220. Springer, Berlin, Heidelberg (2008)
Teel, A.: Connections between Razumikhin-type theorems and the ISS nonlinear small gain theorem. IEEE Trans. Autom. Control 43(7), 960–964 (1998). doi:10.1109/9.701099
Tsiotras, P.: Stabilization and optimality results for the attitude control problem. J. Guid. Control Dyn. 19(4), 772–779 (1996). doi:10.2514/3.21698
Xiao, B., Hu, Q., Singhose, W., Huo, X.: Reaction wheel fault compensation and disturbance rejection for spacecraft attitude tracking. J. Guid. Control Dyn. 36(6), 1565–1575 (2013). doi:10.2514/1.59839
Xiao, B., Hu, Q., Zhang, Y., Huo, X.: Fault-tolerant tracking control of spacecraft with attitude-only measurement under actuator failures. J. Guid. Control Dyn. 37(3), 838–849 (2014). doi:10.2514/1.61369
Zhang, F., Duan, G.R.: Robust adaptive integrated translation and rotation finite-time control of a rigid spacecraft with actuator misalignment and unknown mass property. Int. J. Syst. Sci. 45(5), 1007–1034 (2014). doi:10.1080/00207721.2012.743618
Zhang, R., Li, T., Guo, L.: \({H_\infty }\) control for flexible spacecraft with time-varying input delay. Math. Probl. Eng. 2013, 1–6 (2013). doi:10.1155/2013/839108
Acknowledgments
The authors would like to thank the Associated Editor and the anonymous reviewers for their insightful and constructive comments that greatly contributed to improving the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Some useful inequalities
In what follows, we recall some well-known inequalities.
Jensen’s inequality: For any positive scalar \(\gamma \) and a real-valued function f such that the considered integrations are well defined, we have
Cauchy–Schwarz inequality: Let \( x, y \in \mathfrak {R}\). The Cauchy–Schwarz inequality says that
Young’s inequality: Let \(1 < p,q < \infty \) satisfy the constraint \(1/p+1/q = 1\), and \(x,y \in \mathfrak {R}_+\). Then
An elementary case of Young’s inequality is
From above inequalities, one can immediately follow that
Appendix 2: Extracting upper bound of \(\Vert \varXi \Vert \)
Let rewrite \(\varXi \) as
where
\(\varXi _1\) can expand to
where
Property 2 implies \(\Vert \mathrm {diag}\left[ \frac{J_3-J_2}{J_1},\frac{J_1-J_3}{J_2},\frac{J_2-J_1}{J_3} \right] \Vert \le 1 \). On the other hand, Property 3 deduces \(\Vert \sigma \Vert \le 1\). Hence, considering these inequalities and successive application of the triangular inequality, from (34), we obtain
Also \(\varXi _2\) satisfies
where Eq. (8) in Property 1 is used to drive (36).
Finally, combining (35) and (36) yields (20).
Appendix 3: Proof of Theorem 2
Before proving Theorem 2, we introduce a function which plays a key role in the proof. Our approach lies on the application of an operator of new type that leads to develop a delay compensation control law. This algorithm may be seen as classical reduction technique [3] but as pointed in [34], there is a major difference between classical reduction approach and algorithms based on application of this operator. By this consideration, the function \(\mathcal {O}(\sigma ,\alpha ):\mathfrak {R}^3\times \mathfrak {R}^3 \rightarrow \mathfrak {R}^3\) is defined by [21, 22, 34, 35]
and using Leibniz’s rule, its time derivative is obtained as
By substituting dynamics Eq. (18) and the control law (21) in Eq. (38), and also by adding and subtracting \(\varrho \alpha \) to the referenced equation, we have
By the virtue of Krasovskii theorem (see [42, Theorem 3.7] or [16, Theorem 3.6]) and thanks to the negativity of \(\varrho \) which is guaranteed by conditions (22) and (23), one can find that \(\mathcal {O}\) is a solution of exponentially stable system with Lyapunov function \(\mathcal {O}^T\mathcal {O}\). Thus, the existence of \(\gamma _3\in \mathfrak {R}_+\) such that
is guaranteed. This feature will be used in what follows.
Using Sepulchre–Janković–Kokotović approach [40] with the function \(\mathcal {O}\), the L–K functional is constructed as
where
in which \(\gamma _4 = \left( 22.545 \bar{\tau }^3 \bar{P}^4/\underline{P}\right) ^{-1}\) and \(\gamma _5 \in \mathfrak {R}_+\) is a constant which will be defined further ahead.
The derivatives of \(v_i,\, i=0, 1, \ldots , 5\) are obtained as
To show negativity of v, we shall establish the inequalities obtain from Eqs. (42)–(44) and (47).
Since \(\Vert \sigma (t)\Vert ^2\le 1/\underline{P} \sigma (t)^TP\sigma (t)\) for all \(t>0\), we get
Definition of function \(\mathcal {O}\) allows us to have the following inequality
This inequality together with the inequality (20) and the negativity of \(\varrho \) implies that
where \(\gamma _6\) =\(\gamma _2-\varrho \).
Using Jensen’s inequality (26) in conjunction with Cauchy–Schwarz inequality (27), and Young’s inequalities which are specialized for our needs, namely (28) and (29), we conclude
Consequently, by combining (50) with (44), we deduce that the following inequality holds
The functional v is chosen such that its time derivative along the trajectories is negative definite. Hence, this implies that a value for the \(\Vert \alpha (t)\Vert _\infty \) occurs over the initial condition interval, i.e., \(\Vert \alpha (t)\Vert _\infty =\Vert \alpha (0)\Vert _\infty \). Bearing this point in mind, the condition (22) imposes that \(4.01\bar{\tau }^2\gamma _6^2 -1 \le -0.4\bar{\tau }^2\gamma _6^2\). Combining (51) and the previous inequality, we get
Next, we need to extract an inequality for \(\dot{v}_5\) which is useful for our purpose. This is immediately done by considering the inequality (40), so
Consequently, combining the inequalities (43), (45), (46), (48), (52), and (53) together and with some standard algebraic manipulations, we conclude that, for all \(t\ge 0\)
The above inequality can be rewritten as
where \(\mathcal {N} = \left[ \begin{array}{ll} \frac{1}{2} &{} -\frac{1}{2\sqrt{\underline{P}}} \\ -\frac{1}{2\sqrt{\underline{P}}} &{} \gamma _4 \bar{\tau } \end{array} \right] \).
It is clear that the first term of the right-hand side of the inequality (54) is negative definite, if \(\mathcal {N}\) is positive definite matrix, i.e., we have
which implies that the inequality in condition (24) must be satisfied. Furthermore, it is easy to prove that there exists a positive constat \(\gamma _5\) such that \(\lambda ({\mathcal {N}})> 2\gamma _5\) (for instance \(4\gamma _5 = 0.5 + \bar{\tau }\gamma _4 - \sqrt{0.25\left( 1+ \underline{P}\right) +\tau ^2\gamma _4^2-\tau \gamma _4}\)); so
Thus, by recalling the inequality (54), we conclude that for all \(t\ge 0\), the following inequality holds
Notice that, however, we prove the negativity of \(\dot{v}\) along the trajectories, but still we are not allowed to apply L–K theorem [31, Theorem2.6]. For utilizing this theorem and establishing the uniformly asymptotically stability of the closed-loop system, we also need to show that there exist \(\kappa _i \in \mathcal {K}_\infty ,\, i=1,2\) such that
To this end, since
and
from the definition of v, the following inequality is concluded
which guarantees the existence of \(\kappa _2\in \mathcal {K}_\infty \) such that \(v \le \kappa _2\).
The only thing that remains to be shown is a existence of \(\kappa _1\) which satisfy (57).
The definition of the functional v implies that
Considering above inequality, through lengthy but simple calculations and similar procedure which was done to obtain Eq. (50) with utilizing inequality (30), we obtain
where
and \(\epsilon \in (-1, 1)\).
we observe that the \(\varUpsilon \) is a negative functional which is not suitable for our purpose, but this problem is solved efficiently by proper selecting of \(\epsilon \) and considering \(v_3\) and \(v_4\) functionals (at this point, the reason of introducing two functionals \(v_3\) and \(v_4\) in v is clarified). So, it follows that
Since the right-hand side of (60) is a positive definite radially unbounded function, we are able to state that there exists \(\kappa _1\) such that \(\kappa _1 \le v\). Therefore, according to the L–K theorem, we prove that the origin of the attitude system with control law (21) is UGAS. This completes the proof.
Appendix 4: Proof of Theorem 3
To show that the resulting closed-loop system with the proposed control law is ISS with respect to the disturbance \(T_\mathrm{d}\), we just need to show that the functional (41) is an ISS-LKF for the considered system.
Recalling that what we have done in the proof of Theorem 2, from (56), we conclude that
where \(\gamma _7 = 0.4 \bar{\tau }^2\gamma _4 \gamma _6^2\) and \(\gamma _8 =\left( 1+802\bar{\tau }\gamma _4\right) /\gamma _3\).
By the inequality
it follows that for all \(t\ge 0\), we have \(\dot{v} \le - \varGamma (x,\alpha ) + \gamma ^2_8/2 \Vert J^{-1}T_d\Vert ^2\) where
The positive definiteness of \(\varGamma \) implies that there exists a class \(\mathcal {K}_\infty \) function \(\kappa _3\) such that \(\dot{v} \le -\kappa _3 + \gamma ^2_8/2 \Vert J^{-1} T_d\Vert ^2\). This inequality and the positive definiteness condition (57) imply that v is an ISS-LKF. Finally, from Definition 1, we deduce that the system is ISS with respect to \(T_d\).
Rights and permissions
About this article
Cite this article
Safa, A., Baradarannia, M., Kharrati, H. et al. Global attitude stabilization of rigid spacecraft with unknown input delay. Nonlinear Dyn 82, 1623–1640 (2015). https://doi.org/10.1007/s11071-015-2265-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-015-2265-0


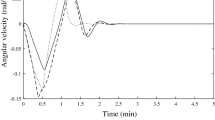

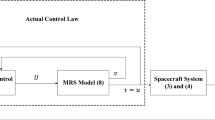
 :
: