1 Introduction

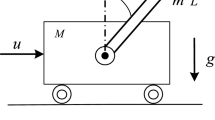
The cart pole system (CPS), also known as the inverted pendulum on a cart, is among the classic mechanical systems that have been studied extensively in control theory during the last four decades. This system was originally used as a benchmark for educational purposes, see [1, 6, 15, 33, 39, 43, 44, 46] .Through the years, this system has attracted attention as an important underactuated mechanical system, because the pendulum angular acceleration cannot be directly controlled [18, 42]. As the CPS dynamics resembles that of many underactuated robot systems, it has been studied as a simplified model such systems (see [7, 27, 30, 38, 40, 43] ). This system is made up of a cart that moves, forward and backward, over a straight line and has a free-moving pendulum hanging from it. The cart is moved by a horizontal force, which is the input of the system. It is well known that several control strategies that were initially conceived for fully actuated systems cannot be applied to drive this system. Actually, the system is not feedback linearizable [23, 42]; also, the system loses controllability when the pendulum passes through the horizontal plane [18, 41]. However, the system can be controlled when located near the unstable equilibrium point, by applying the direct pole placement procedure [25, 42].

In the present authors’ opinion, there are two important problems related to the control of the CPS. The first consists of the upward swing of the pendulum from the hanging position to the upright position. In general, this problem has been tackled by using methods based on energy control and hybrid schemes [2, 3, 8, 9, 22, 26, 31, 44, 45] . The second issue arises when the pendulum is located somewhere in the upper-half plane, and the goal is bringing it to its unstable equilibrium point. Usually, this control challenge has been solved by applying nonlinear control tools. A full review of these tools is beyond the scope of this work; however, we mention, for instance, the well-known energy-based controller or Lyapunov-based techniques, and methods based on the feedforward or the backforward forms, in conjunction with the saturation function or the bounded function approaches [3–5, 13, 14, 22, 30, 45].

In this work, we propose a control strategy to stabilize the damped CPS around to its unstable equilibrium point, assuming that the pendulum starts moving from some position located inside of the upper-half plane and that the damped coefficient is known. Considering the damping force in the non-actuated coordinate makes controlling this system a challenge, because this force can easily destroy the system stability [21, 32, 47]. In addition, managing this force is a very difficult task. Several works have neglected the damping coefficient for this reason.

To develop the proposed control strategy, we transformed the original system into a four-order chain of integrators, with an additional nonlinear perturbation. Then, we proposed the strategy as a combination of a linear PD controller and a modified version of the twisting algorithm [16, 28, 34–36] ,where the first acts over the pendulum position and velocity, while the second brings the whole system state to the origin. The corresponding stability analysis was carried out by using several Lyapunov functions. Convincing numerical simulations were done to assesses the performance of the proposed control strategy. Finally, we mention that this work was inspired by [35, 36]. However, our strategy, when the controller gains are adequately selected, may guarantee global convergence, as long as the position pendulum is initialized into the upper-half plane, though it has the disadvantage of being less robust in the presence of unmodeled perturbations. During the development of this study, we use the following functions:

$$\begin{aligned} \begin{array}{ll} {sgn}[x]=\left\{ \begin{array}{lll} &{}1\qquad \qquad \,\,\,\textit{ if } x> 0, \\ &{}-1\qquad \quad \,\,\,\textit{ if } x<0,\\ &{}\epsilon \, [-1,1]\textit{ if } x=0. \end{array} \right. ;&\quad \displaystyle \frac{{d}}{{d}x}\left| x\right| ={sgn}[x] \end{array}. \end{aligned}$$

The following sections are organized as follows. The nonlinear model of the system is presented in Sect. 2. In Sect. 3, we develop the control strategy. The numerical simulations and the conclusions are in Sects. 4 and 5, respectively.

2 Problem statement

Consider the damped inverted pendulum mounted on a cart. This system can be described by the following set of normalized differential equations [42]:

$$\begin{aligned}&\left( 1+\mu \right) \ddot{x}+\cos \theta \ddot{\theta }-\dot{\theta } ^{2}\sin \theta =f, \nonumber \\&\ddot{x}\cos \theta +\ddot{\theta }-\sin \theta =-d\dot{\theta }, \end{aligned}$$
(1)

where \(x\) is the normalized cart displacement, \(\theta \), is the angle between the pendulum and the vertical, \(f\) is the normalized force applied to the cart, which is also the input to the system, and \(\mu >0\) is a scalar constant dependent on both the cart and pendulum masses. The pendulum viscous friction is considered as a linear function of the angular velocity, \(d\dot{\theta }\), with \(d \ge 0\).

In this work, the physical parameters \(\mu \) and \(d\) are actually given by [42]:

$$\begin{aligned} \begin{array}{cc} \mu =\frac{M}{m};&\quad d=\frac{\gamma }{mL^{1/2}g^{3/2}}, \end{array} \end{aligned}$$

where \(M\) and \(m\) stand for the cart and pendulum masses, respectively, the pendulum length is \(L\), \(g\) is the gravity constant, and \(\gamma \) is the actual dissipation coefficient presented in the non-actuated coordinated \( \theta \). The damping force presented in the actuated coordinate is neglected in order to simplify the methodology presented here. It is important to remark that this force can be easily compensated by using any adaptive control algorithm ([20, 29]).

The control objective consists of bringing the pendulum to its unstable equilibrium point,

$$\begin{aligned} p=(\theta =0,\dot{\theta }=0,x=0,\dot{x}=0), \end{aligned}$$

under the following important considerations:

C1) The system is initialized inside of the following set:

$$\begin{aligned} U=\{(\theta ,\dot{\theta },x,\dot{x}):(-\pi /2,\pi /2)\times R^{3}\} \end{aligned}$$

C2) The state variables are available and the parameters are known.

It should be notice that C1 is not very restrictive, because the pendulum is assumed to be somewhere inside of the upper-half plane; in fact, it can be easily accomplished by using some suitable controller such as those proposed in [26].

Differential equations are understood in the Filippov sense [19] in order to provide for the possibility to use discontinuous signals in controls. Filippov solutions coincide with the usual solutions, when the right-hand sides are Lipschitzian. It is assumed also that all considered inputs allow the existence of solutions and their extension to the whole semi-axis \(t\ge 0\).

3 System transformation

After introducing the following feedback law:

$$\begin{aligned} f=u(\mu +\sin ^{2}\theta )-d\cos \theta \dot{\theta }-\dot{\theta }^{2}\sin \theta +\cos \theta \sin \theta , \nonumber \\ \end{aligned}$$
(2)

the system can be rewritten as:

$$\begin{aligned} \ddot{\theta }&= \sin \theta -\cos \theta u-d\dot{\theta }, \nonumber \\ \ddot{x}&= u, \end{aligned}$$
(3)

Now, in order to represent the system (3) as a four-order chain of integrators plus an additional nonlinear perturbation, we define the following new change of coordinates:

$$\begin{aligned} z_{1}&= x+2\tanh ^{-1}\left( \tan \frac{\theta }{2}\right) ;\quad z_{3}=\tan \theta ; \nonumber \\ z_{2}&= \dot{x}+\dot{\theta }\sec \theta ;\quad z_{4}=\dot{\theta }\sec ^{2}\theta . \end{aligned}$$
(4)

Then, the system (3) can be rewritten as:

$$\begin{aligned} \dot{z}_{1}&= z_{2}; \nonumber \\ \dot{z}_{2}&= z_{3}+\alpha \left( z_{3}\right) z_{4}^{2}-dz_{4}\beta \left( z_{3}\right) ; \nonumber \\ \dot{z}_{3}&= z_{4}; \nonumber \\ \dot{z}_{4}&= \upsilon ; \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{array}{ccc} \alpha (z_{3})=\frac{z_{3}}{\left( 1+z_{3}^{2}\right) ^{\frac{3}{2}}}&;&\quad \beta (z_{3})=\frac{1}{\sqrt{1+z_{3}^{2}}}, \end{array} \end{aligned}$$

and \(\upsilon \) is the new control variable, defined as:

$$\begin{aligned} \upsilon =\sec ^{2}\theta \left( \sin \theta -\cos \theta u-d\dot{\theta } \right) +2\dot{\theta }^{2}\sec ^{2}\theta \tan \theta \nonumber \\ \end{aligned}$$
(6)

It is important to remark that:

$$\begin{aligned} \begin{array}{ccc} \left| \alpha (x)\right| \le \kappa _{0}=\frac{2}{3^{3/2}}&;&\quad \left| \beta (x)\right| \le 1. \end{array} \end{aligned}$$
(7)

Now, to dominate the undesirable term \(d\beta (z_{3})z_{4}\), found in the second equation of (5), we use the following change of coordinates and the following scale of time:

$$\begin{aligned} \begin{array}{ccccc} q_{1}=\epsilon ^{2}z_{1}; &{}\quad q_{2}=\epsilon z_{2};&{}\quad q_{3}=z_{3}; \nonumber \\ &{}\quad q_{4}=z_{4}/\epsilon ;&{}\quad \tau =\epsilon t, \end{array} \nonumber \\ \end{aligned}$$
(8)

where \(\epsilon \) is a strictly positive free parameter. Hence, the system (5) can be written in the new coordinates as:

$$\begin{aligned} \dot{q}_{1}&= q_{2}; \nonumber \\ \dot{q}_{2}&= q_{3}+\epsilon q_{4}\rho (q); \nonumber \\ \dot{q}_{3}&= q_{4} \nonumber \\ \dot{q}_{4}&= \frac{v}{\epsilon ^{2}}=v_{\epsilon }, \end{aligned}$$
(9)

where \(\rho (q)\) is a vanishing perturbation defined by:

$$\begin{aligned} \rho (q)=\epsilon \alpha \left( q_{3}\right) q_{4}-d\beta \left( q_{3}\right) \end{aligned}$$
(10)

Here, the symbol “dot” stands for differentiation with respect to the dimensionless time \(\tau \). We must underscore that the free parameter, \(\epsilon >0\), can be tuned as desired.

Finally, the above system can be expressed in a compact form as:

$$\begin{aligned} \dot{q}=f(q)+Bv_{\epsilon }=F(q,v_{\epsilon }); \end{aligned}$$
(11)

where \(v_{\epsilon }\in R, q\in R^{4}\) and \(f(q): \,R^{4}\rightarrow R^{4}\).

4 Control of the cart pole system

The control law is proposed as:

$$\begin{aligned} v_{\epsilon }(q)=v_{s}(q)+v_{e}(q), \end{aligned}$$

where \(v_{e}(q)\) is a linear controller devoted to bring the states \(q_{3}\) and \(q_{4}\) close enough to the origin, and \(v_{s}(q)\) is a bounded controller designed using the twisting sliding mode algorithm.

The linear control part of the controller, \(v_{\epsilon }\), is selected as:

$$\begin{aligned} v_{e}=-\frac{k_{1}q_{3}+k_{2}q_{4}}{k_{3}}; \end{aligned}$$
(12)

Let us introduce the following auxiliary variables:

$$\begin{aligned} s_{1}&= k_{1}q_{1}+(k_{1}+k_{2})q_{2}+\left( k_{3}+k_{2}\right) q_{3}+k_{3}q_{4}; \nonumber \\ s_{2}&= k_{1}q_{_{2}}+k_{2}q_{3}+k_{3}q_{4}; \end{aligned}$$
(13)

where the set of constants \(k_{i}>0\) should be selected such that they satisfy the following:

$$\begin{aligned} k_{2}&> 1/2+\lambda _{1}\epsilon ^{2}\left( k_{2}+k_{1}\right) \kappa _{0}+\delta _{1}; \nonumber \\ \lambda _{1}^{2}&> \lambda _{2}^{2}+2\lambda _{1}\epsilon d\left( k_{2}+k_{1}\right) \overline{q}_{4}+\delta _{2}; \nonumber \\ \lambda _{2}&> k_{1}\left( \kappa _{0}\epsilon ^{2}\overline{q} _{4}^{2}+\epsilon d\overline{q}_{4}\right) +\delta _{3}; \end{aligned}$$
(14)

where \(\delta _{i}>0, i=\{1,2,3\}\).Footnote 1 The inequities in (14) are referred to in the sequel as assumption A1. Let us propose \(v_{s}\) as a discontinuous injection based on the twisting control algorithm [28, 34–36] .That is,

$$\begin{aligned} v_{s}=-\frac{1}{k_{3}}\left( \lambda _{1}\hbox {sgn}[s_{1}]+\lambda _{2}\hbox {sgn}[s_{2}]\right) =-\frac{\mathfrak {v}_{s}}{k_{3}}; \end{aligned}$$
(15)

where \(\lambda _{1}>\lambda _{2}>0\).

Let us synthesize the main result of this work in the following theorem:

Theorem 1

Consider the system (9) in closed-loop with:

$$\begin{aligned} v=-\frac{1}{k_{3}}\left( k_{1}q_{_{3}}+k_{2}q_{4}+\lambda _{1}\hbox {sig}[s_{1}]+\lambda _{1}\hbox {sig}[s_{2}]\right) , \end{aligned}$$

where

$$\begin{aligned} s_{1}&= k_{1}q_{1}+(k_{1}+k_{2})q_{2}+\left( k_{3}+k_{2}\right) q_{3}+k_{3}q_{4}; \\ s_{2}&= k_{1}q_{_{2}}+k_{2}q_{3}+k_{3}q_{4}. \end{aligned}$$

Under the assumption that the control parameters \(k_{i}>0\); with \( i=\{1,2,3\} \) and \(\lambda _{1}>\lambda _{2}>0\), satisfy the inequalities in (14), then the closed-loop system is asymptotically stable. In particular, the variables \(s_{1}\) converge to zero in finite time.

Proof

Following the application of the linear control, and after some simple algebra, the dynamics of \(s_{1}\) and \(s_{2}\) become:

$$\begin{aligned} \dot{s}_{1}&= s_{2}+(k_{1}+k_{2})\epsilon q_{4}\rho (q)+k_{3}v_{s}; \nonumber \\ \dot{s}_{2}&= k_{1}\epsilon q_{4}\rho (q)+k_{3}v_{s}. \end{aligned}$$
(16)

Then, the system composed by (16) and the last two equations of (9) reads as:

$$\begin{aligned} \dot{s}_{1}&= s_{2}+\epsilon q_{4}\rho (q)(k_{1}+k_{2})+k_{3}v_{s}, \nonumber \\ \dot{s}_{2}&= \epsilon q_{4}\rho (q)k_{1}+k_{3}v_{s} \nonumber \\ \dot{q}_{3}&= q_{4}, \nonumber \\ \dot{q}_{4}&= -\frac{1}{k_{3}}\left( k_{1}q_{_{3}}+k_{2}q_{4}\right) +v_{s}; \end{aligned}$$
(17)

To be able to carry out the convergence analysis, we analyze the boundedness of the states \(q_{3}\) and \(q_{4}\), when the system (17) is feedback by the twisting controller, to assure the boundedness of the vanishing nonlinear perturbation \(\rho (q)\). That is, the system (17), in closed-loop with (15), reads as

$$\begin{aligned} \dot{s}_{1}&= s_{2}+\epsilon q_{4}\rho (q)(k_{1}+k_{2})-\mathfrak {v}_{s}, \nonumber \\ \dot{s}_{2}&= k_{1}\epsilon q_{4}\rho (q)-\mathfrak {v}_{s} \nonumber \\ \dot{q}_{3}&= q_{4}, \nonumber \\ \dot{q}_{4}&= -\frac{1}{k_{3}}\left( k_{1}q_{_{3}}+k_{2}q_{4}\right) -\frac{1}{ k_{3}}\mathfrak {v}_{s} \end{aligned}$$
(18)

where

$$\begin{aligned} \mathfrak {v}_{s}=\lambda _{1}\hbox {sig}[s_{1}]-\lambda _{2}\hbox {sig}[s_{2}]. \end{aligned}$$

Before formally presenting the corresponding proof, we introduce the following auxiliary lemma:

Lemma 1

Consider the following second order system:

$$\begin{aligned} \begin{array}{ccc} \dot{x}=y&;&\quad \dot{y}=-k_{p}x-k_{d}y+\upsilon ; \end{array} \end{aligned}$$

where the set of constants \(k_{i}>0\), for \(i=\{p,d\}\), with \(\left| \upsilon \right| \le \overline{\upsilon }\) . Then, there exits a finite time, \(t_{0}>0\) , such that:

$$\begin{aligned} \begin{array}{ccc} \left| x\right| \le \frac{\overline{\upsilon }+\delta _{0}}{k_{p}};\quad&\left| y\right| \le \frac{\overline{\upsilon }+\delta _{0}}{k_{d}} ;&\quad \forall t\ge t_{0}, \end{array} \end{aligned}$$

where \(\delta _{0}>0\) is sufficiently small. The proof of this lemma is omitted due to its obviousness.

According to this lemma, the last two equations of (17) satisfy the following inequity:

$$\begin{aligned} \begin{array}{ccc} \left| q_{3}\right| \le \frac{\lambda _{1}+\lambda _{2}+\delta _{0} }{k_{1}};\quad&\left| q_{4}\right| \le \overline{q}_{4}=\frac{\lambda _{1}+\lambda _{2}+\delta _{0}}{k_{2}};&\quad \forall t\ge t_{0}, \end{array} \nonumber \\ \end{aligned}$$
(19)

where \(t_{0}\) is a finite period of time and \(\delta _{0}\) is a small positive constant. That is, \(q_{3}\) and \(q_{4}\) are bounded after \(t\ge t_{0}\). This fact assures that the proposed closed-loop system is Lipschitzian, implying that the states \(s_{1}\) and \(s_{2}\) remain bounded during a finite time. Hence, the finite time of scape does not exist—see [24]. On the other hand, from the relations (7) and (10), the inequality,

$$\begin{aligned} \left| \rho (q)\right| \le \kappa _{0}\epsilon \left| q_{4}\right| +d;\quad \forall t\ge t_{0}, \end{aligned}$$
(20)

is fulfilled. Having shown that \(q_{3}\) and \(q_{4}\) are uniformly bounded after some finite time, we are in a position to finally perform the convergence analysis of the whole system, using a continuous and differentiable almost everywhere Lyapunov function. Before to proceeding, we must remember that these kinds of Lyapunov functions have been introduced since the late nineties to prove the stability of discontinuous systems and systems with solutions intended in Filippov’s sense—see for example, [10–12]. Let us introduce our Lyapunov function, as:

$$\begin{aligned} V_{T}(p)=\frac{k_{1}}{2k_{3}}q_{3}^{2}+\frac{1}{2}q_{4}^{2}+\frac{\lambda _{1}}{k_{3}}\left| s_{1}\right| +\frac{1}{2k_{3}}s_{2}^{2}; \end{aligned}$$
(21)

with the vector state \(p=(s_{1},s_{2},q_{3},q_{4})\), whose time derivative around the trajectories of the system (17) is almost everywhere given by:

$$\begin{aligned} \dot{V}_{T}(p)=-\frac{k_{2}}{k_{3}}q_{4}^{2}+\frac{1}{k_{3}}q_{4}\mathfrak {v} _{s}+\overset{W(p)}{\overbrace{\frac{\lambda _{1}}{k_{3}}\hbox {sgn}[s_{1}]\dot{s} _{1}+\frac{1}{k_{3}}s_{2}\dot{s}_{2}}}. \nonumber \\ \end{aligned}$$
(22)

Notice that the derivative of the Lyapunov function (21) exists for all \(s_{1}\) values except the set of measure zero given by \(s_{1}=0\). Notice that \( W(p)\) can be expressed after using (16), as follows:

$$\begin{aligned} W(p)&= \frac{\lambda _{1}}{k_{3}}\left( k_{2}+k_{1}\right) \hbox {sgn}[s_{1}]\rho (q)\epsilon +\frac{k_{1}}{k_{3}}s_{2}\rho (q)\epsilon \\&-\frac{\lambda _{1}^{2}}{k_{3}}-\frac{\lambda _{1}\lambda _{2}\hbox {sgn}[s_{1}]\hbox {sgn}[s_{2}]}{k_{3}}-\frac{\lambda _{2}}{k_{3}}\left| s_{2}\right| . \end{aligned}$$

By using the inequality \(\left| q_{4}\mathfrak {v}_{s}\right| \le (q_{4}^{2}+\mathfrak {v}_{s}^{2})/2\), we have that (22) can be upperbounded, as:

$$\begin{aligned} \dot{V}_{T}(p)\le -\left( \frac{k_{2}}{k_{3}}-\frac{1}{2k_{3}}\right) q_{4}^{2}-\frac{\mathfrak {v}_{s}^{2}}{2k_{3}}+W(p). \end{aligned}$$
(23)

It is easy to see, after some simple algebra that the following inequality

$$\begin{aligned} \frac{\mathfrak {v}_{s}^{2}}{2k_{3}}+W(p)&\le -\frac{\lambda _{1}^{2}}{ 2k_{3}}-\frac{\lambda _{2}}{k_{3}}\left| s_{2}\right| +\frac{1}{ 2k_{3}}\lambda _{2}^{2}+\frac{k_{1}}{k_{3}}\left| s_{2}\right| \epsilon \overline{q}_{4}\overline{\rho } \nonumber \\&+\frac{\lambda _{1}}{k_{3}}\left( k_{2}+k_{1}\right) \left( \kappa _{0}\epsilon ^{2}q_{4}^{2}+\epsilon d\overline{q}_{4}\right) \end{aligned}$$
(24)

holds, for all \(t\ge t_{0}\); where for simplicity, we introduce, \( \overline{\rho }\), such thatFootnote 2

$$\begin{aligned} \left| \rho (q)\right| \le \overline{\rho }=\kappa _{0}\epsilon \overline{q}_{4}+d. \end{aligned}$$
(25)

After substituting (24) into the relation (23), we obtain the following inequality:

$$\begin{aligned} \dot{V}_{T}(p)&\le -\left( \frac{k_{2}}{k_{3}}-\frac{1}{2k_{3}}-\frac{ \lambda _{1}}{k_{3}}\epsilon ^{2}\left( k_{2}+k_{1}\right) \kappa _{0}\right) q_{4}^{2} \\&-\frac{1}{2k_{3}}\lambda _{1}^{2}+\frac{1}{2k_{3}}\lambda _{2}^{2}+\frac{ \lambda _{1}d}{k_{3}}\epsilon \left( k_{2}+k_{1}\right) \overline{q}_{4} \\&-\left| s_{2}\right| \left( \frac{\lambda _{2}}{k_{3}}-\frac{k_{1}}{ k_{3}}\epsilon \overline{q}_{4}\overline{\rho }\right) . \end{aligned}$$

Then, according to the conditions in assumption A1, we have that after a finite time \(t\ge t_{0}\), the following inequity is fulfilled:

$$\begin{aligned} \dot{V}_{T}(p)\le -\frac{\delta _{1}}{k_{3}}q_{4}^{2}-\frac{\delta _{2}}{ 2k_{3}}-\frac{\delta _{3}}{k_{3}}\left| s_{2}\right| . \end{aligned}$$
(26)

From the above, it follows that \(V_{T}(p)<V_{T}(p(0))\) and, from its own definition, \(V_{T}(t)\) is radially bounded and differentially everywhere, except when \(s_{1}=0\). Consequently, the vector state \(p\) is bounded. On the other hand, as \(V_{T}\) is bounded from below, with strictly negative definite time derivative, then \(V\) converges and \(p\) has a limit. Also, \( \overset{.}{p}\) is bounded, according to (18). That is, \(p\) is uniformingly continuous. Now, integrating both sides of the last inequity and using simple algebra, we can claim that the following inequity:

$$\begin{aligned} \frac{\delta _{1}}{k_{3}}\int _{t_{0}}^{t}q_{4}^{2}(s)\hbox {d}s+\frac{\delta _{3}}{ k_{3}}\int _{t_{0}}^{t}\left| s_{2}(s)\right| \hbox {d}s<V_{T}(p(t_{0})), \end{aligned}$$
(27)

holds, for \(t>t_{0}\). It implies that the signals \(s_{2}\) and \(q_{4}\) are, respectively, \(L_{1}\) and \(L_{2}\). According to Barbalat’s lemma, we have that \(s_{2}\rightarrow 0\) and \(q_{4}\rightarrow 0\), as long as \(t\rightarrow \infty \). We proceed to show that \(s_{1}\) converges to zero, in a finite time. So, as the values of \(\left| s_{2}\right| \) and \(\left| q_{4}\right| \) decreasing continuously toward the origin, always exists a finite time \(t_{1}>0\) and a constant \(\mu >0\), such that, \(\lambda _{1}>\left| \Delta (q(t))\right| +\mu \), for all \(t>t_{1}\), where:

$$\begin{aligned} \Delta (q(t))=s_{2}+\epsilon q_{4}\rho (q)(k_{1}+k_{2})-\lambda _{2}\hbox {sgn}[s_{2}], \end{aligned}$$
(28)

because \(\lambda _{1}>>\lambda _{2}\). Hence, the first equation of (18) can be read, as:

$$\begin{aligned} \dot{s}_{1}=-\lambda _{1}\hbox {sgn}[s_{1}]+\Delta (q);\quad t>t_{1}. \end{aligned}$$
(29)

Evidently, the dynamics of \(s_{1}\) concides with the dynamics of a first-order sliding mode.

To see the convergence of \(s_{1}\), we propose \(V_{1}=s_{1}^{2}/2\). According to (28), we have:

$$\begin{aligned} \overset{.}{V}_{1}\le -\mu \left| s_{1}\right| ;\quad t>t_{1}. \end{aligned}$$

From the above inequity, we conclude that \(s_{1}\rightarrow 0\), in a finite time. That is, there is a time \(t_{2}>t_{1}\), such that, \( s_{1}(t)\rightarrow 0\), as long as \(t>t_{2}\). To prove that \(q_{3}\) converges to zero, we introduce the following auxiliary variable \( z=k_{3}q_{4}+k_{2}q_{3}-s_{2}\), whose time derivative can be written, after using simple algebra, as:

$$\begin{aligned} \overset{.}{z}=-\frac{k_{1}}{k_{2}}(z-k_{3}q_{4}+s_{2})-k_{1}\epsilon q_{4}\rho (q). \end{aligned}$$
(30)

According to (20) and the fact that \(s_{1}\rightarrow 0\) and \( q_{4}\rightarrow 0\), the last differential equation turns out to be \(\overset{.}{z}=-k_{1}z/k_{2}\). It imples that \(z\rightarrow 0\) and \( q_{3}\rightarrow 0\). Therefore, the closed-loop system (18) asymptotically converges to the origin, if the control gains are selected according with A1.

Remark 1

The function \(V_{T}\) is continuous but not locally Lipschitz. Therefore, the usual version of the traditional Lyapunov theorem cannot be applied [10, 17]. However, it can be shown that function \(V_{T}(p)\)is absolutely continuous along the trajectories of the closed-loop equation (17), implying that \(V_{T}(p)\) is differentiable almost everywhere, monotone decreasing and converges to zero. These are the conditions needed by the theorem of Zubov [28, 37].

Remark 2

Should the damping parameter \(d\) be very large, assumption A1 becomes a strong condition, because assuring the positiveness of constants \(\delta _{i}\) and \(k_{i},\) \(i=\{1,2,3\}\), in a way that the inequities in (14) hold, needs the parameter \(\epsilon \) to be sufficiently small, which converts the controller into a high-gain controller—see (9). Another way to see it is that when the damping force is very strong, strong control actions must be taken.

It is important to note that the proposed controller has a very simple structure and does not presents singularities, if the system is initialized inside of the upper-half plane.

Tuning the control parameters The correct performance of the control strategy requires control parameters tuning according to the restriction (23). To illustrate this tuning, we fix the pendulum length, mass, and damping as \(L=0.35\) (m), \(m=0.250\) (Kg), and \(\gamma =4\,(\hbox {kgm}^{2}/\hbox {s})\), respectively. Then, according to the expression given in comment C1, the normalized damping coefficient is \(d=0.9\). Now, fixing the control gains as \(k_{1}=0.9, k_{2}=3.5, k_{3}=4, \lambda _{1}=6\), and \(\lambda _{2}=0.8\), and setting the rescale parameter as \(0<\epsilon <0.404\), it is easy to see in a plot that the inequities in (14) hold.

Summarizing Given \(d>0\) and \(\delta _{i}\thickapprox 0.1\), we need to find an admissible parameter vector

$$\begin{aligned} Q=(k_{1},k_{2},k_{3},\lambda _{1},\lambda _{2},\epsilon )\in R_{+}^{6} \end{aligned}$$

fulfilling the restrictions given in (23). This problem can be solved using any numerical optimization program.

5 Numerical simulations

In order to verify the proposed controller performance, we carried out some numerical simulations, where the above proposed control gains were used, with \(\epsilon =0.4\). To make this experiment more interesting, we assume that the knowledge of the damping force has an accuracy of \(85\%\). We ran two experiments with their own different initial conditions. The obtained closed-loop responses for \({p_{1}=(\theta (0)=1.2}\) (rad), \(\dot{\theta } (0)=-0.1\) (rad/s), \(x=0,\dot{x}=0)\) and \(p_{2}=(\theta (0)=-0.7\)[rad], \(\dot{ \theta }(0)=0\), \(x=0.2\) (m/s), \(\dot{x}=0)\) are shown in Fig. 1, where \(p_{i}\) correspond to \((\theta ,\overset{.}{\theta },x,\overset{.}{x})\). As we can see, the control strategy is able to render the system to the origin after 7 (s) elapsed, even when the value of the damping coefficient, \(d\), is partially known.

Fig. 1
figure 1

Closed-loop responses for two initial conditions (\(p_{1}, p_{2}\) ), and a partial knowledge of 85 % of the damping force

Full size image

To provide an idea of how good the proposed control strategy OC is, we compared it with the control technique proposed by Riachy et al. in [35], here referred to as RC. The control parameters of RC were tuning heuristically, but to be fair, we tried to find the values that enable the best transient response. The initial conditions were fixed as \((\theta =0.9,0,0,0)\). The obtained results are shown in Fig. 2, where we can see that the closed-loop response of the propose control strategy is as good as the responses of RC. Furthermore, we can see that our strategy presents a better behavior in the angular variable, if compared with the RF strategy. However, the cart displacements in our strategy are larger that those in RC. Please keep in mind that this is a numeric comparison, a formal comparison is beyond the scope of this work, as is a comparative study between our control strategy and others found in the literature. We must underscore that all the simulations were carried out in the actual coordinates of the pendulum system. Finally, Fig. 3 shows numerically the asymptotic behavior the Lyapunov function \( V_{T}(p)\), and its derivative. To this experiment, we used the same setup as before, but normalized time, and the following two different sets of initial conditions: \((s_{1}=1,s_{2}=0,q_{3}=-5,q_{4}=1)\) and \( (s_{1}=0,s_{2}=0,q_{3}=1,q_{4}=4)\). The numerical similations shown in this figure are the expect results, because \(V_{T}\) converges asymptotically to zero and \(\overset{.}{V}_{T}\) is always strictly negative, with \(\overset{.}{V}_{T}\) tends to \(-4.9\).

Fig. 2
figure 2

Comparison between the closed-loop responses of the OC and the RC strategies, represented with a solid line and a dotted line, respectively

Full size image
Fig. 3
figure 3

Asymptotic behavior of \(V_{T}\) and \(\overset{.}{V}_{T}\), for the initial conditions: \((s_{1}=1,s_{2}=0,q_{3}=-5,q_{4}=1)\) and \( (s_{1}=0,s_{2}=0,q_{3}=1,q_{4}=4)\). The plot on the left side corresponds to the first initial conditions, and the one on the right side to the second initial conditions

Full size image

6 Conclusions

In this work, we introduced a control strategy, based on a PD controller in conjunction with a twisting-like algorithm, to solve the stabilization of the damped cart pole system, assuming that the pendulum is initialized somewhere inside of the upper-half plane. To this end, we first used some nonlinear transformations over the original pendulum system to express it as a four-order chain of integrators, with an additional perturbation that vanishes at the origin. The PD controller was designed to bring the pendulum position and its velocity inside of a compact region simultaneously. At the same time, the twisting-like algorithm renders the whole system state to the origin. For the convergence analysis, we used several Lyapunov functions, thereby assuring that our strategy converges asymptotically once the pendulum position and its velocity are inside of the compact region. The effectiveness and robustness of the strategy was tested running numerical simulations, where uncertainties in the parameters’ values were included. The obtained results allow us to claim that the performance of our controller is satisfactory.