Skip to main content
SpringerLink
Log in

Codimension-two bursting analysis in the delayed neural system with external stimulations

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

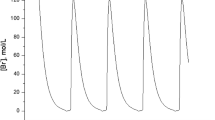
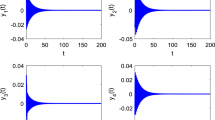
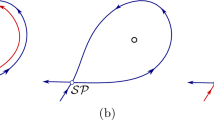
In the neural system, action potentials play a crucial role in many mechanisms of information communication. The quiescent state, spiking and bursting activities are important biological behaviors with the different neurocomputational properties. In this paper, based on the bifurcation mechanisms involved in the generation of action potentials, an interesting mathematical study of bursting behavior is obtained. The transition between the bursting and quiescence state is investigated,which shows that the time delay must be large enough for bursting behavior to occur in a delayed system. Two types of the codimension-two bifurcation, i.e., Bogdanov–Takens (BT) bifurcation and saddle-node homoclinic (SNH) bifurcation are investigated also. The bifurcation curves of the parameters and the phase portraits for the different regions are shown. The local existence of the homoclinic curve is achieved by using the center manifold reduction and normal form method. For occurrence of a periodic stimulation in the neighborhood of the SNH bifurcation, the system can switch over from an equilibrium state to an oscillatory state either through saddle-node on an invariant circle bifurcation (called circle bifurcation for simplicity) or saddle-node (SN) bifurcation, and back from the oscillatory state to the equilibrium state through the circle or homoclinic bifurcation. Complex bursting phenomena are displayed for the different values of delay couplings and stimulation intensities. Some types of bursting behaviors, such as Circle/Circle (Type II or parabolic bursting), Circle/Homoclinic, SN/Circle (triangular bursting), SN/Homoclinic (Type I or square-wave bursting), and Fold/Hopf bursting are obtained in the firing area. The results show that the different burstings are related to the delay coupling and external inputs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York (1983)

    MATH  Google Scholar 

  2. Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory. Springer, New York (1995)

    MATH  Google Scholar 

  3. Hodgkin, A.L., Huxley, A.F.: A quantitative description of membrane and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544 (1952)

    Google Scholar 

  4. Johnston, D., Wu, S.M.: Foundations of Cellular Neurophysiology. MIT Press, Cambridge (1995)

    Google Scholar 

  5. Izhikevich, E.M., Desai, N.S., Walcott, E.C., Hoppensteadt, F.C.: Bursts as a unit of neural information: selective communication via resonance. Trends Neurosci. 26, 161–167 (2003)

    Article  Google Scholar 

  6. Hoppensteadt, F.C., Izhikevich, E.M.: Weakly Connected Neural Networks. Springer, New York (1997)

    Book  Google Scholar 

  7. Izhikevich, E.M.: Neural excitability, spiking and bursting. Int. J. Bifurc. Chaos 10, 1171–1266 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  8. Pakdaman, K., Grotta-Ragazzo, C., Malta, C.P.: Transient regime duration in continuous-time neural networks with delay. Phys. Rev. E 58, 3623–3627 (1998)

    Article  Google Scholar 

  9. Pakdaman, K., Malta, C.P.: A note on convergence under dynamical thresholds with delays. IEEE Trans. Neural Netw. 9, 231–233 (1998)

    Article  Google Scholar 

  10. Pakdaman, K., Grotta-Ragazzo, C., Malta, C.P., Arino, O., Vibert, J.-F.: Effect of delay on the boundary of the basin of attraction in a system of two neurons. Neural Netw. 11, 509–519 (1998)

    Article  Google Scholar 

  11. Pakdaman, K., Malta, C.P., Grotta-Ragazzo, C., Vibert, J.-F.: Effect of delay on the boundary of the basin of attraction in a self-excited single graded-response neuron. Neural Comput. 9, 319–336 (1997)

    Article  MATH  Google Scholar 

  12. Song, Z.G., Xu, J.: Bursting near Bautin bifurcation in a neural network with delay coupling. Int. J. Neural Syst. 19, 359–373 (2009)

    Article  MathSciNet  Google Scholar 

  13. Faria, T., Magalhães, L.T.: Normal form for retarded functional differential equations and applications to Bogdanov–Takens singularity. J. Differ. Equ. 122, 201–224 (1995)

    Article  MATH  Google Scholar 

  14. Giannkopoulos, F., Zapp, A.: Bifurcation in a planar system of differential delay equations modeling neural activity. Physica D 159, 215–232 (2001)

    Article  MathSciNet  Google Scholar 

  15. Jiang, W.H., Yuan, Y.: Bogdanov–Takens singularity in Van der Pol’s oscillator with delayed feedback. Physica D 227, 149–161 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  16. Guo, S.J., Chen, Y.M., Wu, J.H.: Two-parameter bifurcations in a network of two neurons with multiple delays. J. Differ. Equ. 244, 444–486 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  17. Schecter, S.: The saddle-node separatrix-loop bifurcation. SIAM J. Math. Anal. 18, 1142–1156 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  18. Dilao, R., Volford, A.: Excitability in a model with a saddle-node homoclinic bifurcation. arXiv:math-ph/0502049v1 (2005)

  19. Beyn, W.J.: The numerical computation of connecting orbits in dynamical systems. IMA J. Numer. Anal. 9, 379–405 (1990)

    Article  MathSciNet  Google Scholar 

  20. Beyn, W.J., Kleinkauf, J.M.: The numerical computation of homoclinic orbits for maps. SIAM J. Numer. Anal. 34, 1207–1236 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  21. Engelborghs, K.: DDE-BIFTOOL v2.00: a Matlab package for bifurcation analysis of delay differential equations. Tech. Rep. TW-305, Department of Computer Science, K.U. Leuven, Belgium (2000)

  22. Samaey, G., Engelborghs, K., Roose, D.: Numerical computation of connecting orbits in delay differential equations. Numer. Algorithms 30, 335–352 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  23. Izhikevich, E.M.: Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. MIT Press, Cambridge (2007)

    Google Scholar 

  24. Pakdaman, K., Alvarez, F., Diez-Martinez, O., Vibert, J.-F.: Single neuron model with recurrent excitation: response to slow periodic modulation. Biosystems 40, 133–140 (1997)

    Article  Google Scholar 

  25. Glass, L.: Synchronization and rhythmic processes in physiology. Nature 410, 277–284 (2001)

    Article  Google Scholar 

  26. Aihara, K., Matsumoto, G., Ikeyaga, Y.: Periodic and non-periodic responses of a periodically forced Hodgkin-Huxley oscillator. J. Theor. Biol. 109, 249–269 (1984)

    Article  Google Scholar 

  27. Kaplan, D.T., Clay, J.R., Manning, T., Glass, L., Guevara, M.R., Shrier, A.: Subthreshold dynamics in periodically stimulated squid axons. Physiol. Rev. Lett. 76, 4074–4077 (1996)

    Article  Google Scholar 

  28. Chllemi, S., Barbi, M., Garbo, A.D.: Dynamics of neuronal discharge in snail neurons. Biosystems 40, 21–28 (1997)

    Article  Google Scholar 

  29. Glass, L., Shrier, A., Belair, J.: Chaotic cardiac rhythms. In: Holden, A.V. (eds.) Chaos, pp. 237–256. Princeton University Press, Princeton (1986)

    Google Scholar 

  30. Szucs, A., Elson, R.C., Rabinovich, M.I., Abarbanel, H.D.I., Selverston, A.I.: Nonlinear behavior of sinusoidally forced pyloric pacemaker neurons. J. Neurophysiol. 85, 1623–1638 (2001)

    Google Scholar 

  31. Sethia, G.C., Sen, A.: Bursting in a subcritical Hopf oscillator with a nonlinear feedback. http://arxiv.org/abs/nlin.CD/0603053 (2006)

  32. Golubitsky, M., Josic, K., Kaper, T.J.: An unfolding theory approach to bursting in fast-slow systems. In: Broer, H.W., Krauskopf, B., Vegter, G. (eds.) Global Analysis of Dynamical Systems, pp. 277–308. Institute of Physics Publishing, Bristol (2001)

    Google Scholar 

  33. Brusch, L., Lorenz, W., Or-Guil, M., Bar, M., Kummer, U.: Fold-Hopf bursting in a model for calcium signal transduction. http://arxiv.org/pdf/q-bio/0310018 (2003)

  34. Holden, L., Erneux, T.: Slow passage through a Hopf bifurcation: form oscillatory to steady state solutions. SIAM J. Appl. Math. 53, 1045–1058 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  35. de Vries, G.: Multiple bifurcations in a polynomial model of bursting oscillations. J. Nonlinear Sci. 8, 281–316 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  36. Kandel, E.R., Spencer, W.A.: Electrophysiology of hippocampal neurons. II. After-potentials and repetitive firing. J. Neurophysiol. 24, 243–259 (1961)

    Google Scholar 

  37. Smolen, P., Terman, D., Rinzel, J.: Properties of a bursting model with two slow inhibitory variables. SIAM J. Appl. Math. 53, 861–892 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  38. Kohno, T., Aihara, K.: Mathematical-model-based design of silicon burst neurons. Neurocomputing 71, 1619–1628 (2008)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai, 200092, China

    Zigen Song & Jian Xu

Authors
  1. Zigen Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jian Xu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Song, Z., Xu, J. Codimension-two bursting analysis in the delayed neural system with external stimulations. Nonlinear Dyn 67, 309–328 (2012). https://doi.org/10.1007/s11071-011-9979-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-011-9979-4

Keywords

Search

Navigation