Skip to main content
SpringerLink
Log in

Time-fractional KdV equation: formulation and solution using variational methods

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

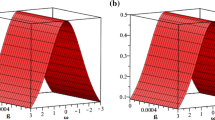
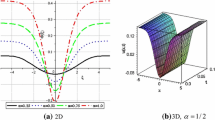
In this work, the semi-inverse method has been used to derive the Lagrangian of the Korteweg–de Vries (KdV) equation. Then the time operator of the Lagrangian of the KdV equation has been transformed into fractional domain in terms of the left-Riemann–Liouville fractional differential operator. The variational of the functional of this Lagrangian leads neatly to Euler–Lagrange equation. Via Agrawal’s method, one can easily derive the time-fractional KdV equation from this Euler–Lagrange equation. Remarkably, the time-fractional term in the resulting KdV equation is obtained in Riesz fractional derivative in a direct manner. As a second step, the derived time-fractional KdV equation is solved using He’s variational-iteration method. The calculations are carried out using initial condition depends on the nonlinear and dispersion coefficients of the KdV equation. We remark that more pronounced effects and deeper insight into the formation and properties of the resulting solitary wave by additionally considering the fractional order derivative beside the nonlinearity and dispersion terms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Riewe, F.: Nonconservative Lagrangian and Hamiltonian mechanics. Phys. Rev. E 53(2), 1890–1899 (1996)

    Article  MathSciNet  Google Scholar 

  2. Riewe, F.: Mechanics with fractional derivatives. Phys. Rev. E 55(3), 3581–3592 (1997)

    Article  MathSciNet  Google Scholar 

  3. Tavazoei, M.S., Haeri, M.: Describing function based methods for predicting chaos in a class of fractional order differential equations. Nonlinear Dyn. 57(3), 363–373 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  4. Bateman, H.: On dissipative systems and related variational principles. Phys. Rev. 38(4), 815–819 (1931)

    Article  MATH  Google Scholar 

  5. Agrawal, O.P.: Formulation of Euler–Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 272(1), 368–379 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  6. Agrawal, O.P.: A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 38(4), 323–337 (2004)

    Article  MATH  Google Scholar 

  7. Agrawal, O.P.: Fractional variational calculus and the transversality conditions. J. Phys. A, Math. Gen. 39, 10375 (2006)

    Article  MATH  Google Scholar 

  8. Agrawal, O.P.: Fractional variational calculus in terms of Riesz fractional derivatives. J. Phys. A, Math. Theor. 40, 6287 (2007)

    Article  MATH  Google Scholar 

  9. Baleanu, D., Avkar, T.: Lagrangians with linear velocities within Riemann–Liouville fractional derivatives. Nuovo Cim. B 119, 73–79 (2004)

    Google Scholar 

  10. Baleanu, D., Muslih, S.I.: Lagrangian formulation of classical fields within Riemann–Liouville fractional derivatives. Phys Scr. 72, 119–123 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  11. Muslih, S.I., Baleanu, D., Rabei, E.: Hamiltonian formulation of classical fields within Riemann–Liouville fractional derivatives. Phys. Scr. 73, 436–438 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  12. Rabei, E.M., Altarazi, I.M.A., Muslih, S.I., Baleanu, D.: Fractional WKB approximation. Nonlinear Dyn. 57(1–2), 171–175 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  13. Baleanu, D.: Fractional variational principles in action. Phys. Scr. T136, 014006 (2009)

    Article  Google Scholar 

  14. Herzallah, M.A.E., Baleanu, D.: Fractional-order Euler–Lagrange equations and formulation of Hamiltonian equations. Nonlinear Dyn. 58(1–2), 385–391 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  15. Baleanu, D., Trujillo, J.I.: A new method of finding the fractional Euler–Lagrange and Hamilton equations within Caputo fractional derivatives. Commun. Nonlinear Sci. Numer. Simul. 15(5), 1111–1115 (2010)

    Article  MathSciNet  Google Scholar 

  16. Tarasov, V.E., Zaslavsky, G.M.: Fractional Ginzburg–Landau equation for fractal media. Phys. A, Stat. Mech. Appl. 354, 249–261 (2005)

    Article  Google Scholar 

  17. Tarasov, V.E., Zaslavsky, G.M.: Nonholonomic constraints with fractional derivatives. J. Phys. A, Math. Gen. 39(31), 9797–9815 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  18. Heymans, N.: Fractional calculus description of non-linear viscoelastic behaviour of polymers. Nonlinear Dyn. 38(1–2), 221–231 (2004)

    Article  MATH  Google Scholar 

  19. Frederico, G.S.F., Torres, D.F.M.: Fractional conservation laws in optimal control theory. Nonlinear Dyn. 53(3), 215–222 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  20. Mendes, R.V.: A fractional calculus interpretation of the fractional volatility model. Nonlinear Dyn. 55(4), 395–399 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  21. Tenreiro Machado, J.A.: Calculation of fractional derivatives of noisy data with genetic algorithms. Nonlinear Dyn. 57(1–2), 253–260 (2009)

    Article  MATH  Google Scholar 

  22. Attari, M., Haeri, M., Tavazoei, M.S.: Analysis of a fractional order Van der Pol-like oscillator via describing function method. Nonlinear Dyn. 61(1–2), 265–274 (2010)

    Article  MATH  Google Scholar 

  23. Agrawal, O.P., Tenreiro Machado, J.A, Sabatier, J. (Guest Editors): Special issue on “Fractional Derivatives and their Applications”. Nonlinear Dyn. 38(4) (2004)

  24. Sabatier, J., Agrawal, O.P., Tenreiro Machado, J.A. (eds.): Advances in Fractional Calculus. Springer, Dordrecht (2007)

    MATH  Google Scholar 

  25. Baleanu, D., Tenreiro Machado, J.A. (Guest Editors): Special issue on “Fractional Differentiation and its Applications (FDA08)”. Phys. Scr. T136 (2009)

  26. Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Philos. Mag. 39(5), 422 (1895)

    Google Scholar 

  27. Fung, M.K.: KdV Equation as an Euler–Poincare’ equation. Chin. J. Phys. 35(6), 789 (1997)

    MathSciNet  Google Scholar 

  28. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  29. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  30. Samko, S.G., Kilbas, A.A., Marichev, O.I.: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, New York (1998)

    Google Scholar 

  31. Luchko, Y., Srivastava, H.M.: The exact solution of certain differential equations of fractional order by using operational calculus. Comput. Math. Appl. 29, 73–85 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  32. Babakhani, A., Gejji, V.D.: Existence of positive solutions of nonlinear fractional differential equations. J. Math. Anal. Appl. 278, 434–442 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  33. Delbosco, D.: Fractional calculus and function spaces. J. Fractal Calc. 6, 45–53 (1996)

    MathSciNet  Google Scholar 

  34. Zhang, S.Q.: Existence of positive solution for some class of nonlinear fractional differential equations. J. Math. Anal. Appl. 278, 136–148 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  35. Saha Ray, S., Bera, R.K.: An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method. Appl. Math. Comput. 167, 561–571 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  36. He, J.-H.: Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Methods Appl. Mech. Eng. 167, 57–68 (1998)

    Article  MATH  Google Scholar 

  37. Momani, S., Odibat, Z., Alawnah, A.: Variational iteration method for solving the space- and time-fractional KdV equation. Numer. Methods Part. Differ. Equ. 24(1), 261–271 (2008)

    Google Scholar 

  38. Molliq, R.Y., Noorani, M.S.M., Hashim, I.: Variational iteration method for fractional heat- and wave-like equations. Nonlinear Anal., Real World Appl. 10, 1854–1869 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  39. Inokuti, M., Sekine, H., Mura, T.: General use of the Lagrange multiplier in non-linear mathematical physics. In: Nemat-Nasser, S. (ed.) Variational Method in the Mechanics of Solids. Pergamon Press, Oxford (1978)

    Google Scholar 

  40. He, J.-H.: A new approach to nonlinear partial differential equations. Commun. Nonlinear Sci. Numer. Simul. 2(4), 230–235 (1997)

    Article  Google Scholar 

  41. He, J.-H.: Variational-iteration—a kind of nonlinear analytical technique: some examples. Int. J. Nonlinear Mech. 34, 699 (1999)

    Article  MATH  Google Scholar 

  42. He, J.-H.: Semi-inverse method of establishing generalized variational principles for fluid mechanics with emphasis on turbo-machinery aerodynamics. Int. J. Turbo Jet-Engines 14(1), 23–28 (1997)

    Article  Google Scholar 

  43. He, J.-H.: Variational principles for some nonlinear partial differential equations with variable coefficients. Chaos Solitons Fractals 19, 847–851 (2004)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Theoretical Physics Research Group, Physics Department, Faculty of Science, Mansoura University, Mansoura, 35516, Egypt

    S. A. El-Wakil, E. M. Abulwafa, M. A. Zahran & A. A. Mahmoud

Authors
  1. S. A. El-Wakil
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. M. Abulwafa
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. A. Zahran
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. A. Mahmoud
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. M. Abulwafa.

Rights and permissions

Reprints and permissions

About this article

Cite this article

El-Wakil, S.A., Abulwafa, E.M., Zahran, M.A. et al. Time-fractional KdV equation: formulation and solution using variational methods. Nonlinear Dyn 65, 55–63 (2011). https://doi.org/10.1007/s11071-010-9873-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-010-9873-5

Keywords

Search

Navigation