Skip to main content

Advertisement

SpringerLink
Log in

Neural Network for a Novel Disturbance Optimal Control Model for Inventory and Production Planning in a Four-Echelon Supply Chain with Reverse Logistic

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

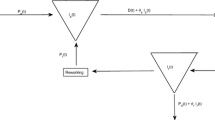
The present paper is devoted to modeling and solving the inventory and production planning in a four-echelon supply chain (SC) with reverse logistics, from supplier to after-sales service center and repair center. To the best of our knowledge, this is the first scientific attempt for modeling and resolving the inventory and production planning in an SC with reverse logistics that the problem is modeled by a disturbance optimal control problem (OCP). Both recycling and reworking are assumed in the reverse logistic. There was a disturbance because we considered the demand time-dependent. From the former points the presented model is so close to the real-world problem in the field of SC. The Pontryagin minimum principle is applied to reformulate the OCP into a system of equations. In continuous, the system of equations is solved by an artificial neural network. In the final step, an example and a case study are presented to depict the performance and validity of the model and the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Garg K, Kannan D, Diabat A, Jha PC (2015) A multi-criteria optimization approach to manage environmental issues in closed loop supply chain network design. J Clean Prod 100:297–314

    Article  Google Scholar 

  2. Giri BC, Sharma S (2015) Optimizing a closed-loop supply chain with manufacturing defects and quality dependent return rate. J Manuf Syst 35:92–111

    Article  Google Scholar 

  3. Soleimani H, Kannan G (2015) A hybrid particle swarm optimization and genetic algorithm for closed-loop supply chain network design in large-scale networks. Appl Math Model 39(14):3990–4012

    Article  MathSciNet  MATH  Google Scholar 

  4. Shohan S, Ali SM, Kabir G, Ahmed SK, Suhi SA, Haque T (2019) Green supply chain management in the chemical industry: structural framework of drivers. Int J Sustain Dev World Ecol 26:752–768

    Article  Google Scholar 

  5. Ahi P, Searcy C (2013) A comparative literature analysis of definitions for green and sustainable supply chain management. J Clean Prod 52:329–341

    Article  Google Scholar 

  6. Cousins PD, Lawson B, Petersen KJ, Fugate B (2019) Investigating green supply chain management practices and performance: The moderating roles of supply chain ecocentricity and traceability. Int J Oper Prod Manag 39:767–786

    Article  Google Scholar 

  7. Zhu W, He Y (2017) Green product design in supply chains under competition. Eur J Oper Res 258:165–180

    Article  MathSciNet  MATH  Google Scholar 

  8. Franchetti M, Elahi B, Ghose S (2017) Green supply chain, logistics, and transportation. In: Machado C, Davim J (eds) Green and Lean Management. Management and Industrial Engineering. Springer, Cambridge

    Google Scholar 

  9. Tseng M-L, Islam MS, Karia N, Fauzi FA, Afrin SA (2019) literature review on green supply chain management: Trends and future challenges. Resour Conserv Recyc 141:145–162

    Article  Google Scholar 

  10. Maditati DR, Munim ZH, Schramm H-J, Kummer SA (2018) A review of green supply chain management: From bibliometric analysis to a conceptual framework and future research directions. Resourc Conserv Recyc 139:150–162

    Article  Google Scholar 

  11. Sethi SP, Thompson GL (2000) Optimal control theory, applications to management science and economics, 2nd edn. Springer, Berlin

    MATH  Google Scholar 

  12. Kistner K-P, Dobos I (2000) Optimal production-inventory strategies for a reverse logistics system. Optim Dyn Econ Anal. Physica-Verlag, HD

  13. Pooya A, Pakdaman M (2021) A new continuous time optimal control model for manpower planning with promotion from inside the system. Int J Oper Res 21(1):349–364

    Article  Google Scholar 

  14. Pooya A, Pakdaman M, Tadj L (2019) Exact and approximate solution for optimal inventory control of two-stock with reworking and forecasting of demand. Oper Res Int J 19(2):333–346

    Article  Google Scholar 

  15. Pooya A, Pakdaman M (2018) A delayed optimal control model for multi-stage production-inventory system with production lead times. J Intell Manuf 94:751–761

    Article  Google Scholar 

  16. Pan X, Li S (2015) Optimal control of a stochastic production-inventory system under deteriorating items and environmental constraints. Int J Prod Res 53:607–628

    Article  Google Scholar 

  17. Benkherouf L, Skouri K, Konstantaras I (2015) Optimal control of production, remanufacturing and refurbishing activities in a finite planning horizon inventory system. J Optim Theory Appl 168:677–698

    Article  MathSciNet  MATH  Google Scholar 

  18. Tadj L, Bounkhel M, Benhadid Y (2006) Optimal control of a production inventory system with deteriorating items. Int J Syst Sci 37:1111–1121

    Article  MathSciNet  MATH  Google Scholar 

  19. Chung S-L, Wee H-M, Yang P-C (2008) Optimal policy for a closed-loop supply chain inventory system with remanufacturing. Math Comput Model Int J 48:867–881

    Article  MathSciNet  MATH  Google Scholar 

  20. Ivanov D, Sokolov B, Kaeschel J (2011) Integrated supply chain planning based on a combined application of operations research and optimal control. CEJOR 19:299–317

    Article  MathSciNet  Google Scholar 

  21. Ivanov D, Dolgui A, Sokolov B (2011) On applicability of optimal control theory to adaptive supply chain planning and scheduling. Proceedings of the 18th World Congress The International Federation of Automatic Control Milano (Italy), pp 423–434

  22. Darla SP, Naiju CD, Annamalai K, Sravan YU (2012) Production and remanufacturing of returned products in supply chain using modified genetic algorithm. Int J Mech Ind Eng 6:175–178

    Google Scholar 

  23. Fahimnia B, Luong L, Marian R (2012) Genetic algorithm optimisation of an integrated aggregate production-distribution plan in supply chains. Int J Prod Res 50(1):81–96

    Article  Google Scholar 

  24. Geunes J, Levi R, Romeijn HE, Shmoys DB (2011) Approximation algorithms for supply chain planning and logistics problems with market choice. Math Program 130:85–106

    Article  MathSciNet  MATH  Google Scholar 

  25. Kenne J-P, Dejax P, Gharbi A (2012) Production planning of a hybrid manufacturing remanufacturing system under uncertainty within a closed-loop supply chain. Int J Prod Econ 135:81–93

    Article  Google Scholar 

  26. Fu D, Aghezzaf E-H, Keyser RD (2014) A model predictive control framework for centralised management of a supply chain dynamical system. Syst Sci Control Eng An Open Access J 2:250–260

    Google Scholar 

  27. Yang K, Wang E (2014) Optimal control of decoupling point with deteriorating items. J Ind Eng Manag 7(5):1368–1384

    Google Scholar 

  28. Li S (2014) Optimal control of the production-inventory system with deteriorating items and tradable emission permits. Int J Syst Sci 45:2390–2401

    Article  MathSciNet  MATH  Google Scholar 

  29. Gaggero M, Tonelli F (2015) Optimal control of distribution chains for perishable goods. IFAC PapersOnLine 48(3):1049–1054

    Article  Google Scholar 

  30. Hedjar R, Garg AK, Tadj L (2015) Model predictive production planning in a three-stock reverse-logistics system with deteriorating items. Int J Syst Sci 2:187–198

    Google Scholar 

  31. Nagarajan V, Shi C (2016) Approximation algorithms for inventory problems with submodular or routing costs. Math Program 160:225–244

    Article  MathSciNet  MATH  Google Scholar 

  32. Ivanov D, Dolgui A, Sokolov B (2016) Robust dynamic schedule coordination control in the supply chain. Comput Ind Eng 94(1):18–31

    Article  Google Scholar 

  33. Kogan K, Herbon A (2016) Inventory control over a short time horizon under unknown demand distribution. IEEE Trans Autom Control 61(10):3058–3063

    Article  MathSciNet  MATH  Google Scholar 

  34. Salviano O, Andres F (2017) On an optimal production-inventory plan for a closed loop supply chain. IFAC PapersOnLine 50(1):4987–4993

    Article  Google Scholar 

  35. Turki S, Didukh S, Sauvey C, Rezg N (2017) Optimization and analysis of a manufacturing-remanufacturing-transport-warehousing system within a closed-loop supply chain. Sustainability 9:561

    Article  Google Scholar 

  36. Dolgui A, Ivanov D, Sethi SP, Sokolov B (2018) Scheduling in production, supply chain and Industry 4.0 systems by optimal control: fundamentals, state-of-the-art and applications. Int J Prod Res 57:411–432

    Article  Google Scholar 

  37. Turki S, Rezg N (2018) Unreliable manufacturing supply chain optimisation based on an infinitesimal perturbation analysis. Int J Syst Sci Oper Logist 5(1):25–44

    Google Scholar 

  38. Xu L, Wang C (2018) Sustainable manufacturing in a closed-loop supply chain considering emission reduction and remanufacturing. Resour Conserv Recyc 131:297–304

    Article  Google Scholar 

  39. Wang Qi, Wu J, Zhao N, Zhu Q (2019) Inventory control and supply chain management: A green growth perspective. Resourc Conserv Recyc 145:78–85

    Article  Google Scholar 

  40. Lagaris IE, Likas A (2012) Hamilton-Jacobi theory over time scales and applications to linear-quadratic problems. IEEE Trans Neural Netw 9(5):987–1000

    Article  Google Scholar 

  41. Vrabie D, Lewis FL (2009) Neural network approach to continuous-time direct adaptive optimal control for partially unknown nonlinear systems. Neural Netw 22:237–246

    Article  MATH  Google Scholar 

  42. Partovi FY, Anandarajan M (2002) Classifying inventory using an artificial neural network approach. Comput Ind Eng 41:389–404

    Article  Google Scholar 

  43. Lee YH, Jung JW, Eum SC, Park SM, Nam HK (2006) Production quantity allocation for order fulfilment in the supply chain: a neural network based approach. Prod Plan Contl 17:378–389

    Article  Google Scholar 

  44. Nik HS, Effati S, Motsa SS, Shirazian M (2014) Spectral homotopy analysis method and its convergence for solving a class of nonlinear optimal control problems. Numer Algor 65(1):171–194

    Article  MathSciNet  MATH  Google Scholar 

  45. Shirazian M, Effati S (2012) Solving a class of nonlinear optimal control problems via He’s variational iteration method. Int J Control Autom Syst 10(2):249–256

    Article  Google Scholar 

  46. Ghasemi S, Effati S (2019) An artificial neural network for solving distributed optimal control of the Poisson’s equation. Neural Process Lett 49:159–175

    Article  Google Scholar 

  47. Zhao J (2020) Neural network-based optimal tracking control of continuous-time uncertain nonlinear system via reinforcement learning. Neural Process Lett 51:2513–2530

    Article  Google Scholar 

  48. Li Z, Li C, Li S, Cao X (2020) A fault-tolerant method for motion planning of industrial redundant manipulator. IEEE Trans Ind Inf 16(12):7469–7478

    Article  Google Scholar 

  49. Li Z, Li S (2021) Saturated PI control for nonlinear system with provable convergence: An optimization perspective. IEEE Trans Circ Syst II Express Briefs 68(2):742–746

    Google Scholar 

  50. Khan AH, Li S, Luo X (2020) Obstacle avoidance and tracking control of redundant robotic manipulator: An RNN-based metaheuristic approach. IEEE Trans Ind Inf 16(7):4670–4680

    Article  Google Scholar 

  51. Khan AH, Cao X, Li S, Katsikis VN, Liao L (2020) BAS-ADAM: an ADAM based approach to improve the performance of beetle antennae search optimizer. IEEE/CAA J Autom Sinica 7(2):461–471

    Article  Google Scholar 

  52. Khan AH, Cao X, Katsikis VN, Stanimirović P, Brajević I, Li S, Kadry S, Nam Y (2020) Optimal portfolio management for engineering problems using nonconvex cardinality constraint: a computing perspective. IEEE Access 8:57437–57450

    Article  Google Scholar 

  53. Khan AT, Li S, Cao X (2021) Control framework for cooperative robots in smart home using bio-inspired neural network. Measurement 167:108253

    Article  Google Scholar 

  54. Khan AT, Li S (2021) Human guided cooperative robotic agents in smart home using beetle antennae search, Science China Information Sciences, Accepted (2021)

  55. Khan AT, Cao X, Li S, Hu B, Katsikis VN (2021) Quantum beetle antennae search: a novel technique for the constrained portfolio optimization problem. Sci China Inf Sci 64:152204

    Article  MathSciNet  Google Scholar 

  56. Mansoori A, Effati S (2019) An efficient neurodynamic model to solve nonlinear programming problems with fuzzy parameters. Neurocomputing 334:125–133

    Article  Google Scholar 

  57. Mansoori A, Effati S (2021) Parametric NCP-based recurrent neural network model: a new strategy to solve fuzzy nonconvex optimization problems. IEEE Trans Syst Man Cybern Syst 51(4):2592–2601

    Article  Google Scholar 

  58. Naidu D (2003) Optimal control systems. CRC Press LLC, Boca Racton

    Google Scholar 

Download references

Acknowledgements

This research is supported by a grant from Ferdowsi University of Mashhad [No: 73209].

Author information

Authors and Affiliations

  1. Department of Management, Ferdowsi University of Mashhad, Mashhad, Iran

    Alireza Pooya & Shila Monazam Ebrahimpour

  2. Department of Applied Mathematics, Ferdowsi University of Mashhad, Mashhad, Iran

    Amin Mansoori & Mohammad Eshaghnezhad

Authors
  1. Alireza Pooya
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amin Mansoori
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohammad Eshaghnezhad
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shila Monazam Ebrahimpour
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alireza Pooya.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pooya, A., Mansoori, A., Eshaghnezhad, M. et al. Neural Network for a Novel Disturbance Optimal Control Model for Inventory and Production Planning in a Four-Echelon Supply Chain with Reverse Logistic. Neural Process Lett 53, 4549–4570 (2021). https://doi.org/10.1007/s11063-021-10612-9

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-021-10612-9

Keywords

Search

Navigation